Revisiting Enhanced AIS Detection Range under Anomalous Propagation Conditions
Abstract
:1. Introduction
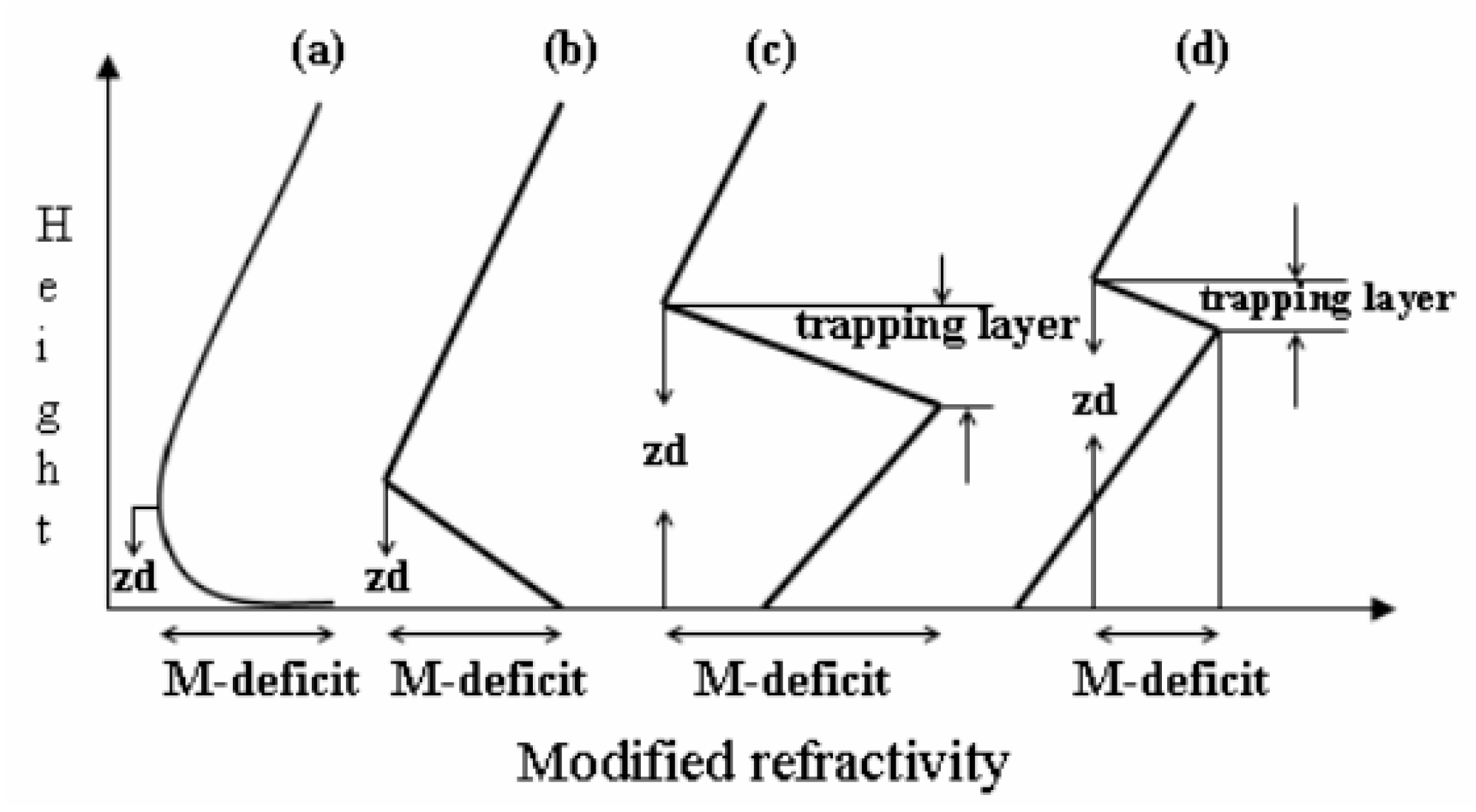
2. Theoretical Background
2.1. Description of the PE Method
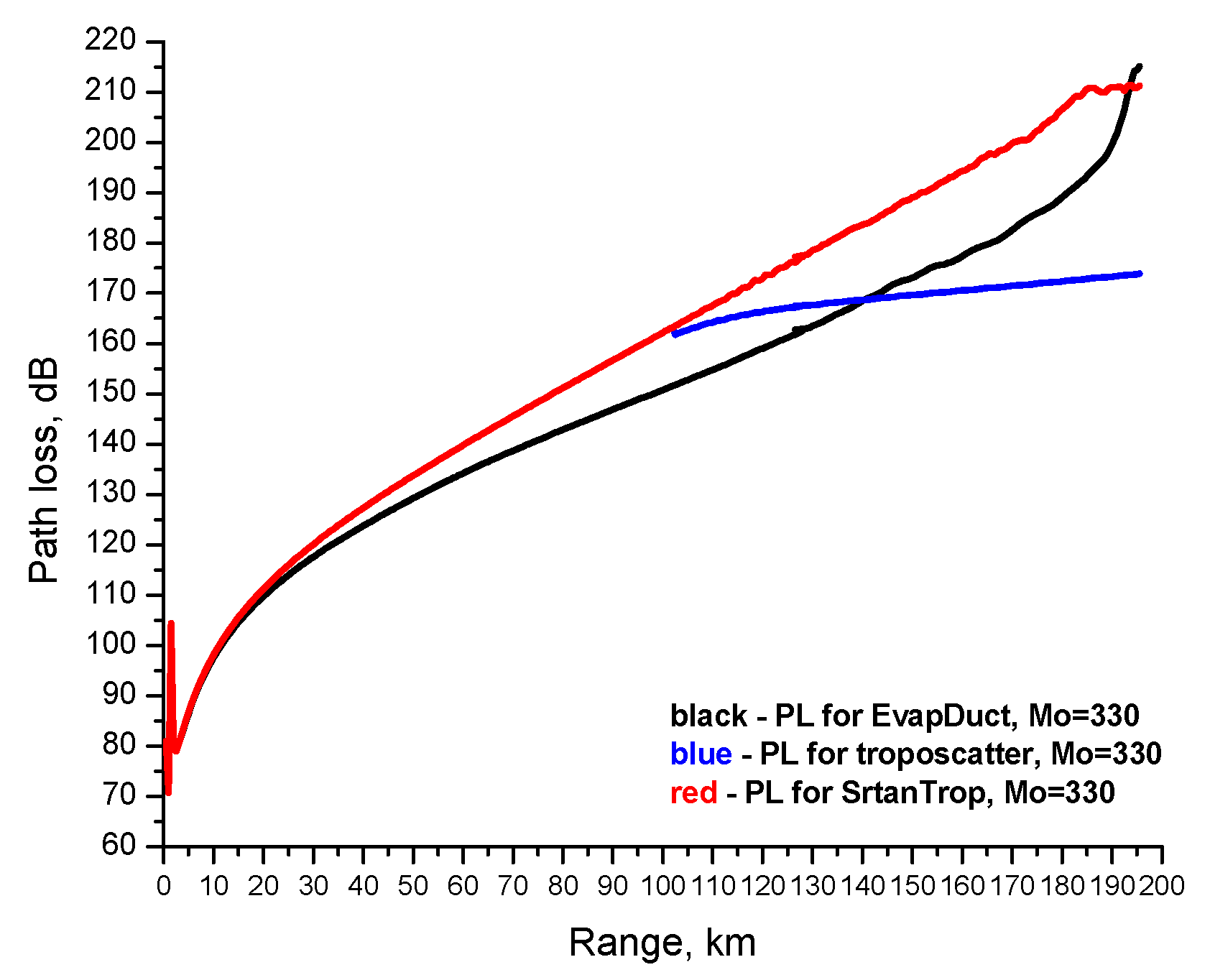
2.2. Troposcatter Model
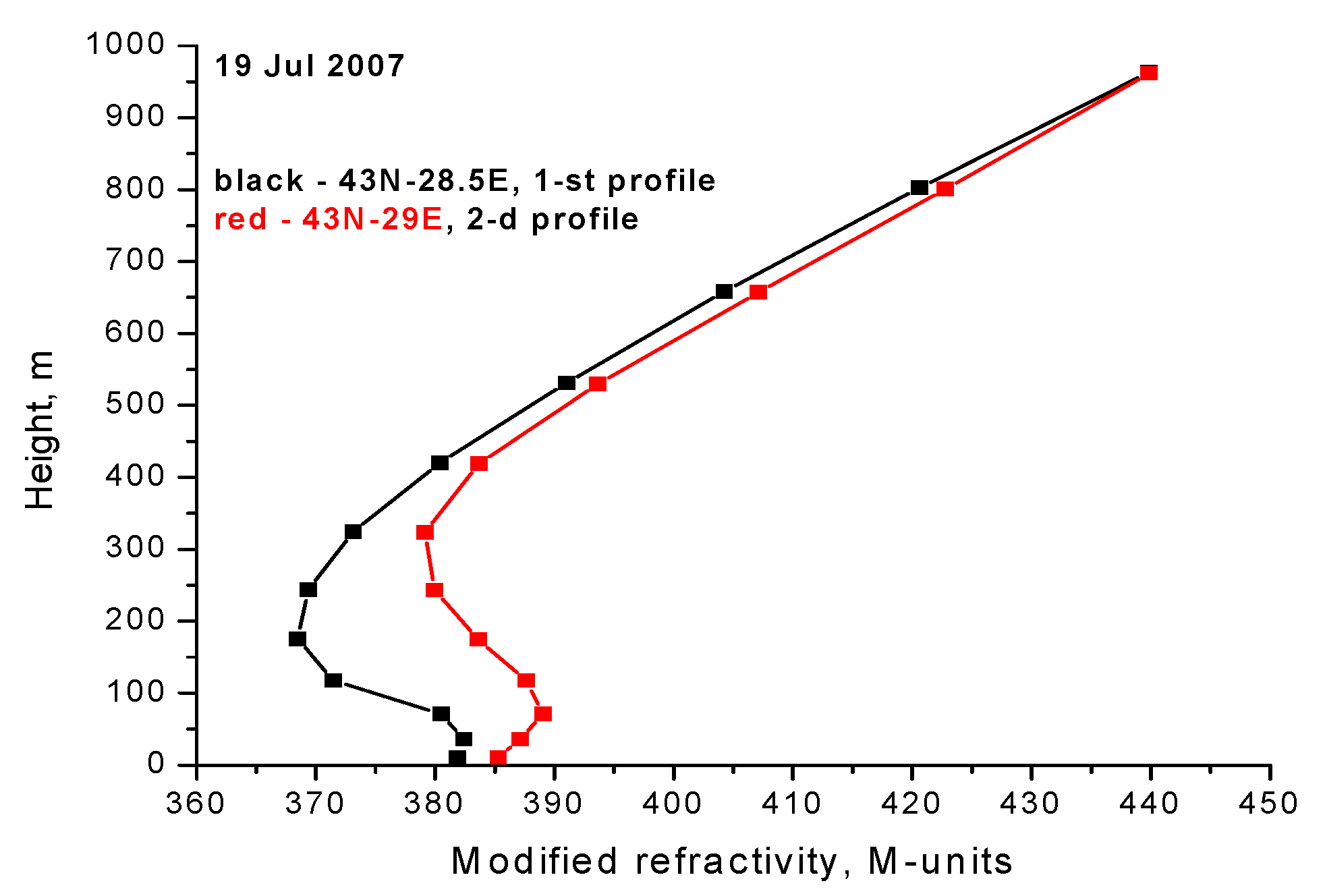
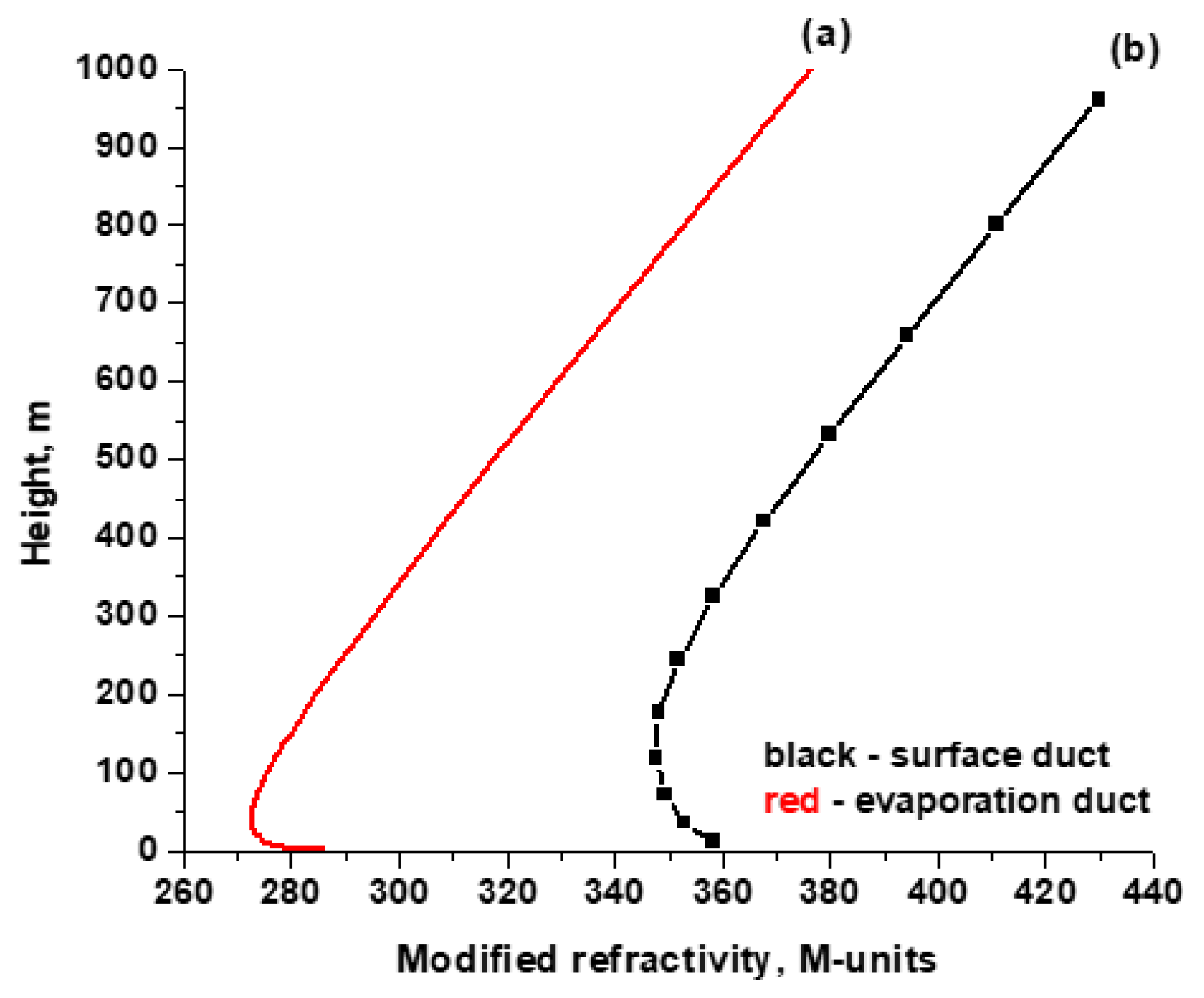
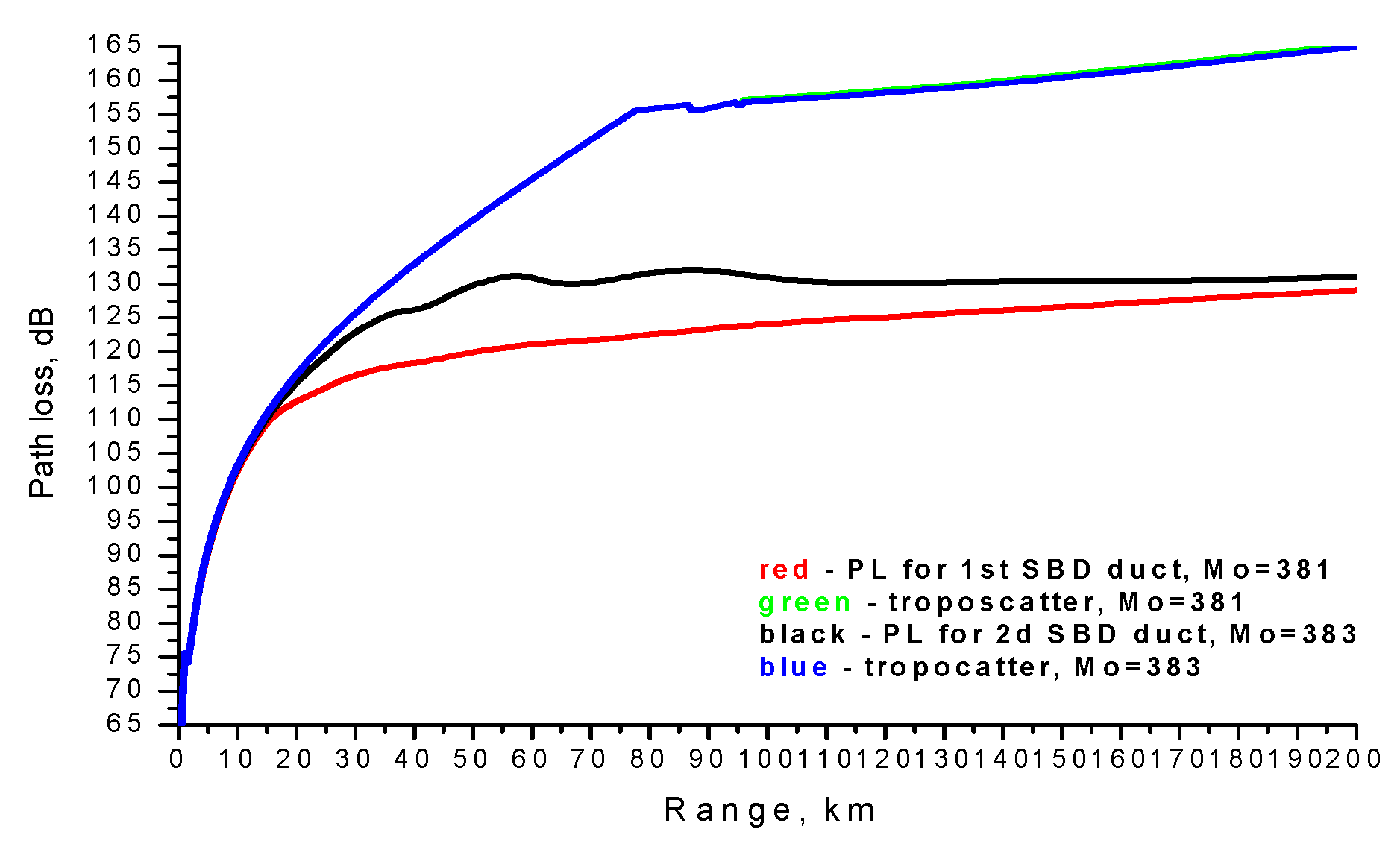
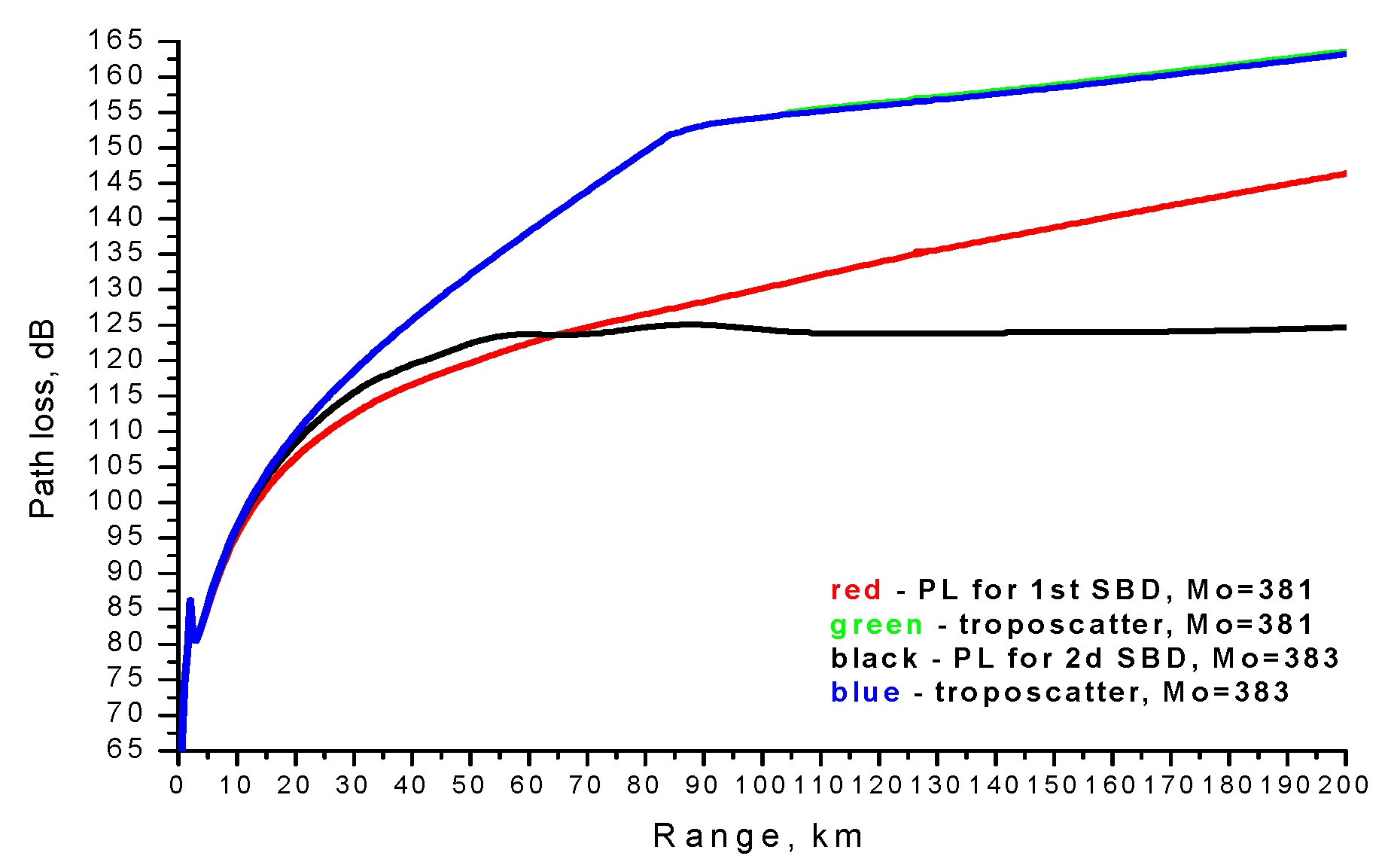
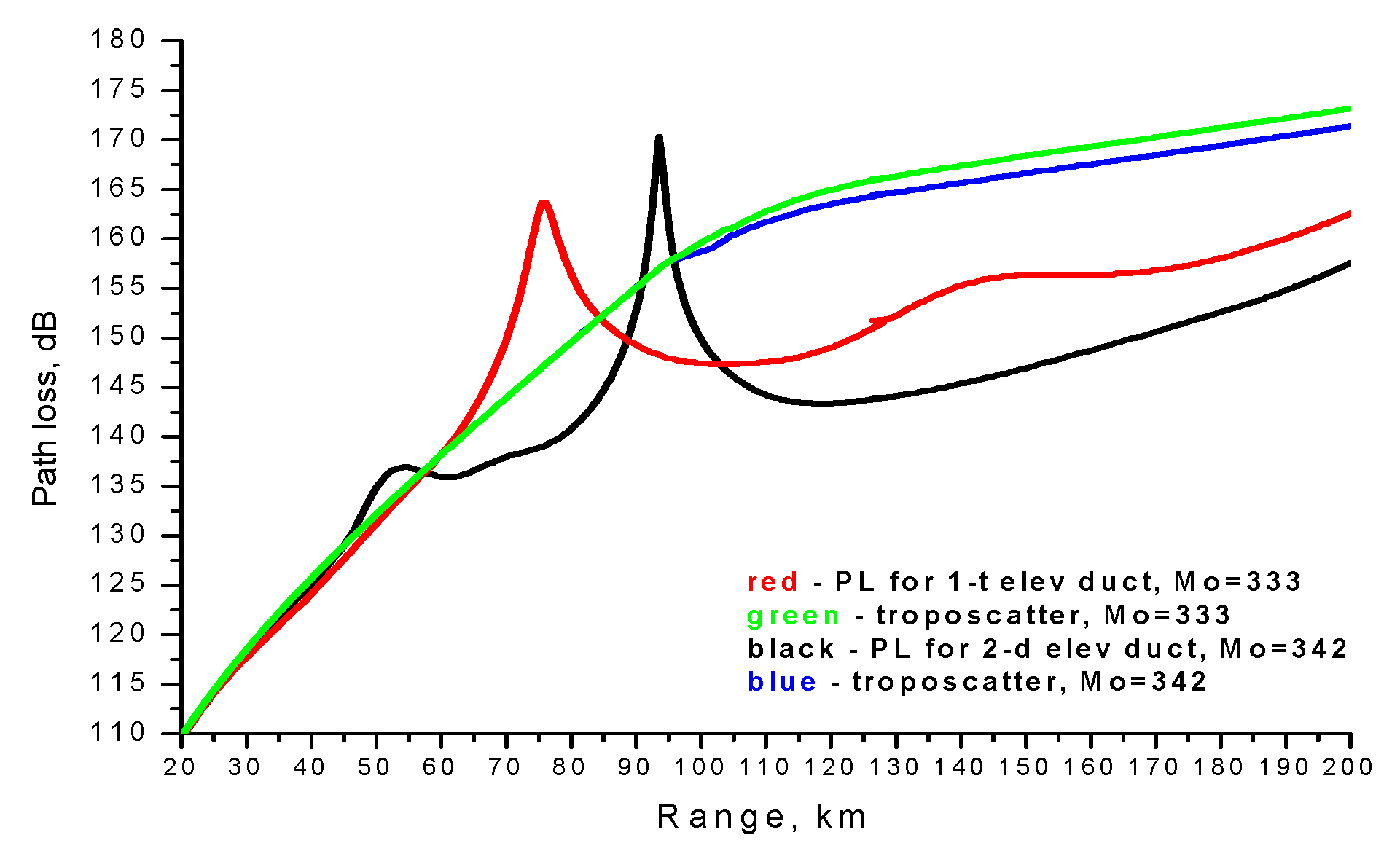
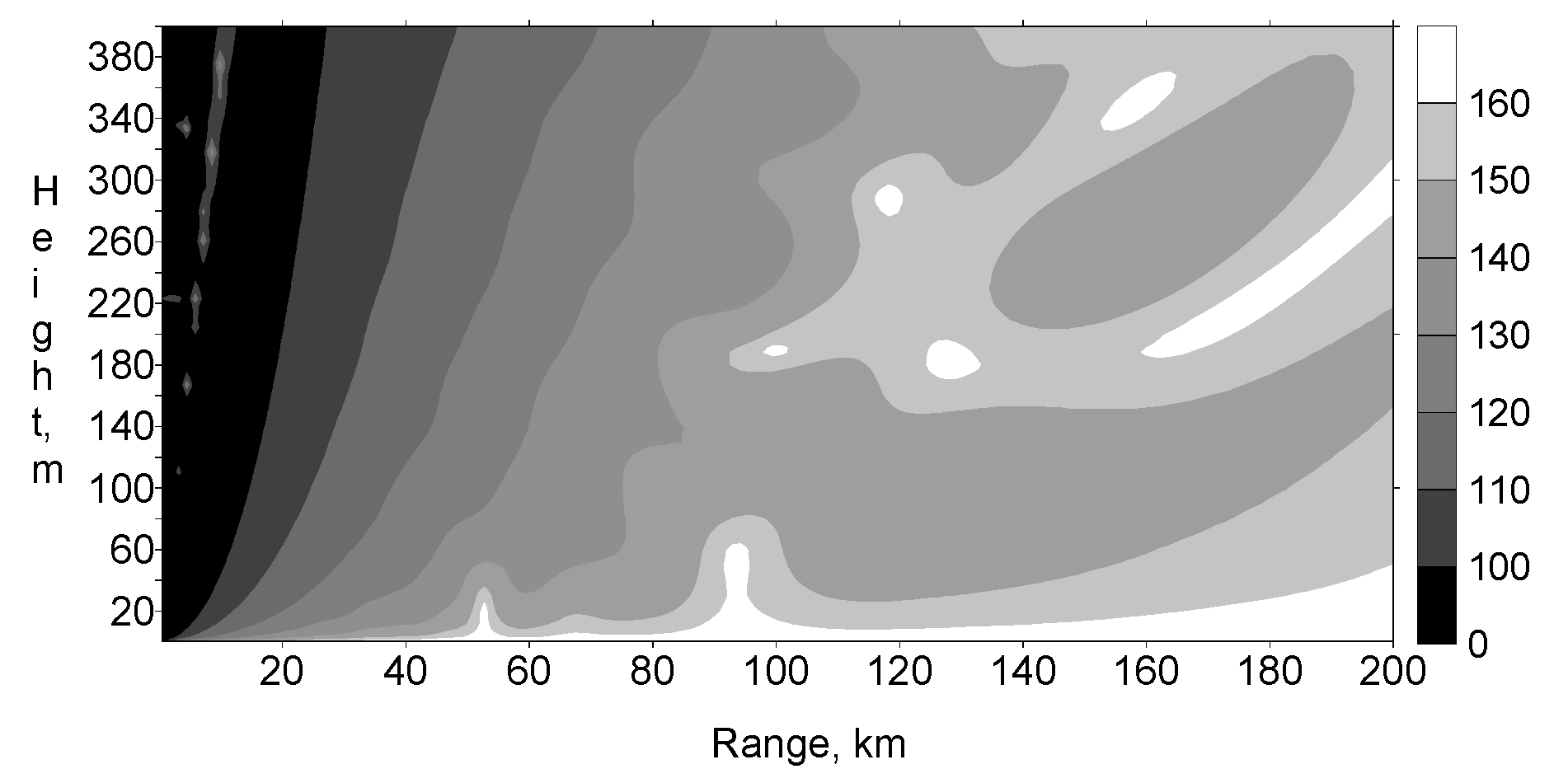
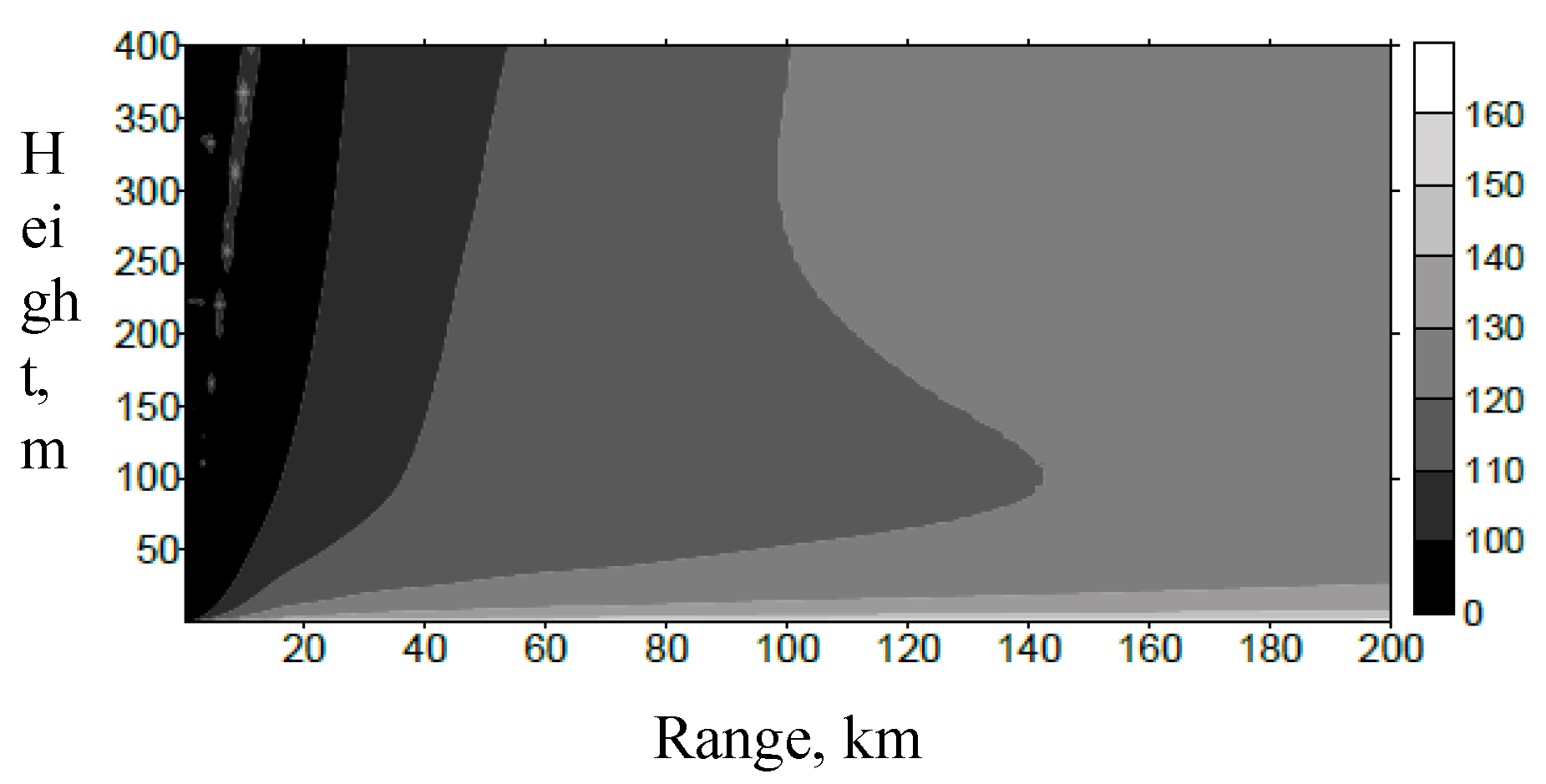
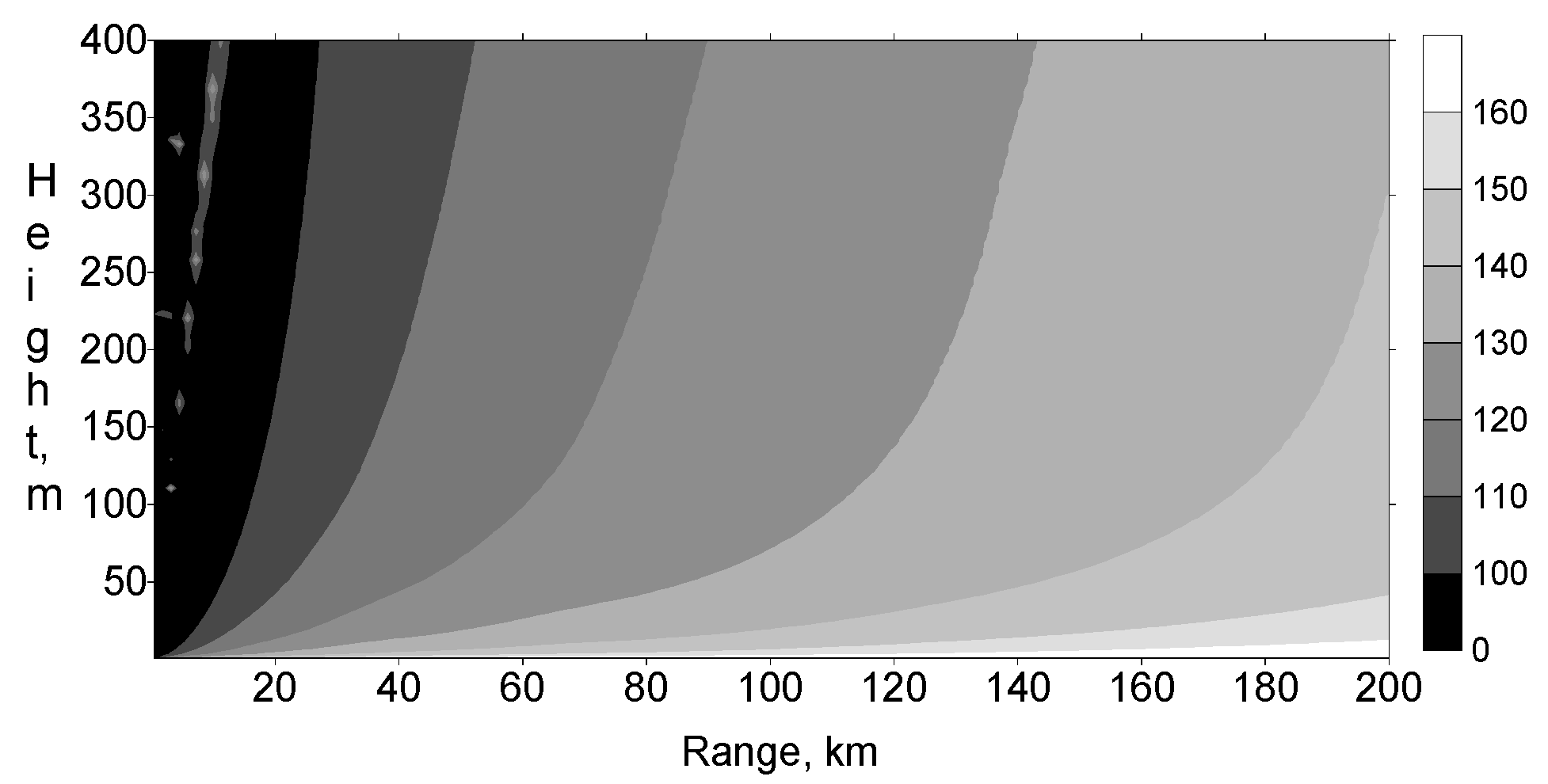
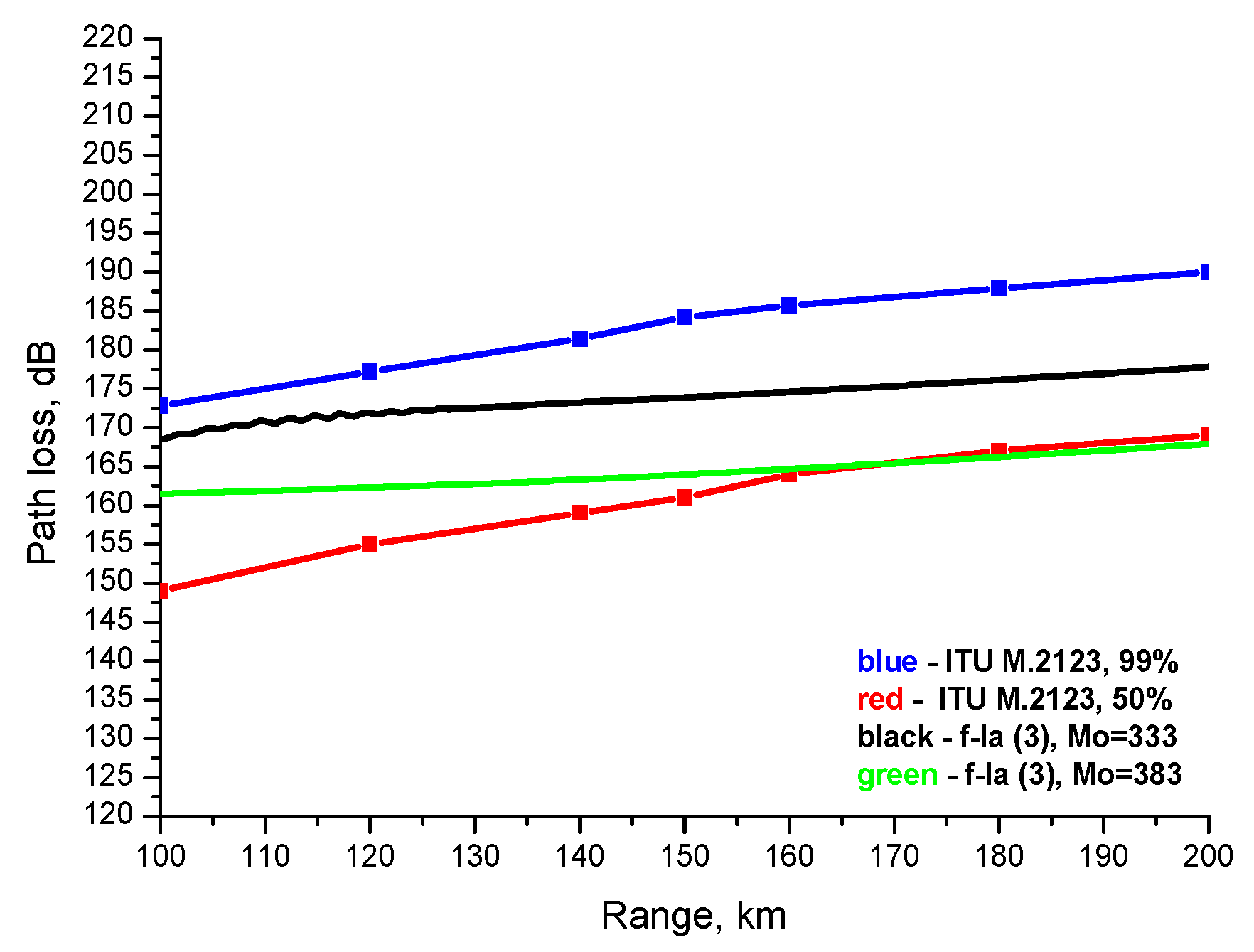
3. Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- International Telecommunication Union. R-REC-M.2092-1: Technical Characteristics for A VHF Data Exchange System in the VHF Maritime Mobile Band; Electronic Publication: Geneva, Switzerland, 2022. [Google Scholar]
- Jiang, S. Networking in ocean: A survey. ACM Comput. Surv. 2022, 54, 13:1–13:33. [Google Scholar] [CrossRef]
- Wright, D.; Janzen, C.; Bochenek, R.; Austin, J.; Page, E. Marine Observing applications using AIS: Automatic Identification System. Front. Mar. Sci. 2019, 6, 537. [Google Scholar] [CrossRef]
- Emmens, T.; Amrit, C.; Abdi, A.; Ghosh, M. The promises and perils of Automatic Identification System data. Expert Sys. Appl. 2021, 178, 114975. [Google Scholar] [CrossRef]
- International Telecommunication Union. ITU-R M.2123: Long Range Detection of Automatic Identification System (AIS) Messages under Various Tropospheric Propagation Conditions; ITU: Geneva, Switzerland, 2007. [Google Scholar]
- Jo, S.-W.; Shim, W.-S. LTE-Maritime: High-speed maritime wireless communication based on LTE technology. IEEE Access 2019, 7, 53172–53181. [Google Scholar] [CrossRef]
- Dinc, E.; Akan, O.B. Beyond-line-of-sight communications with ducting layer. IEEE Commun. Mag. 2014, 52, 37–43. [Google Scholar] [CrossRef]
- Tang, W.; Cha, H.; Wei, M.; Tian, B. Estimation of surface-based duct parameters from automatic identification system using the Levy flight quantum-behaved particle swarm optimization algorithm. JEWA 2019, 33, 827–837. [Google Scholar] [CrossRef]
- Tang, W.; Cha, H.; Wei, M.; Tian, B.; Li, Y. A Study on the Propagation Characteristics of AIS Signals in the Evaporation Duct Environment. ACES J. 2019, 34, 996–1001. [Google Scholar]
- Robinson, L.; Newe, T.; Burke, J.; Toal, D. A simulated and experimental analysis of evaporation duct effects on microwave communications in the Irish Sea. IEEE Trans. AP 2022, 70, 4728–4737. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, S.; Yang, F.; Yang, K. Statistical analysis of hybrid atmospheric ducts over the Northern South China sea and their influence on over-the-horizon electromagnetic wave propagation. J. Mar. Sci. Eng. 2023, 11, 669. [Google Scholar] [CrossRef]
- Bastos, L.; Wietgrefe, H. A Geographical analysis of highly deployable troposcatter systems performance. In Proceedings of the 2013 IEEE Military Communications Conference, San Diego, CA, USA, 18–20 November 2013; pp. 661–667. [Google Scholar] [CrossRef]
- Kerr, D.E. (Ed.) Propagation of Short Radio Waves, 2nd ed.; Peter Peregrinus: London, UK, 1987. [Google Scholar]
- Paulus, R.A. Practical application of an evaporation duct model. Radio Sci. 1985, 20, 887–896. [Google Scholar] [CrossRef]
- Yang, C.; Shi, Y.; Wang, J.; Feng, F. Regional spatiotemporal statistical database of evaporation ducts over the South China Sea for future long-range radio application. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6432–6444. [Google Scholar] [CrossRef]
- Yang, N.; Su, D.; Wang, T. Atmospheric ducts and their electromagnetic propagation characteristics in the Northwestern South China Sea. Remote Sens. 2023, 15, 3317. [Google Scholar] [CrossRef]
- Rautiainen, L.; Tyynelä, J.; Lensu, M.; Siiriä, S.; Vakkari, V.; O’Connor, E.; Hämäläinen, K.; Lonka, H.; Stenbäck, K.; Koistinen, J.; et al. Utö observatory for analysing atmospheric ducting events over Baltic coastal and marine waters. Remote Sens. 2023, 15, 2989. [Google Scholar] [CrossRef]
- von Engeln, A.; Teixeira, J. A ducting climatology derived from ECMWF global analysis fields. J. Geophys. Res. 2004, 109, D18. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J. The investigation of cooperation diversity for communication exploiting evaporation ducts in the South China Sea. IEEE Trans. AP 2022, 70, 8337–8347. [Google Scholar] [CrossRef]
- Zaidi, K.S.; Hina, S.; Jawad, M.; Khan, A.N.; Khan, M.U.S.; Pervaiz, H.B.; Nawaz, R. Beyond the horizon, backhaul connectivity for offshore IoT devices. Energies 2021, 14, 6918. [Google Scholar] [CrossRef]
- Ma, J.; Wang, J.; Yang, C. Long-range microwave links guided by evaporation ducts. IEEE Commun. Mag. 2022, 60, 68–72. [Google Scholar] [CrossRef]
- Sirkova, I. Anomalous tropospheric propagation: Usage possibilities and limitations in radar and wireless communications systems. In Proceedings of the 10th Jubilee International Conference of the Balkan Physical Union, Sofia, Bulgaria, 26–30 August 2018. [Google Scholar] [CrossRef]
- Valčić, S.; Brčić, D. On detection of anomalous VHF propagation over the Adriatic Sea utilizing a software-defined Automatic Identification System receiver. J. Mar. Sci. Eng. 2023, 11, 1170. [Google Scholar] [CrossRef]
- Huang, L.-F.; Liu, C.-G.; Wu, Z.-P.; Zhang, L.-J.; Wang, H.-G.; Zhu, Q.-L.; Han, J.; Sun, M.-C. Comparative analysis of intelligent optimization algorithms for atmospheric duct inversion using Automatic Identification System signals. Remote Sens. 2023, 15, 3577. [Google Scholar] [CrossRef]
- Han, J.; Wu, J.; Zhang, L.; Wang, H.; Zhu, Q.; Zhang, C.; Zhao, H.; Zhang, S. A Classifying-inversion method of offshore atmospheric duct parameters using AIS data based on artificial intelligence. Remote Sens. 2022, 14, 3197. [Google Scholar] [CrossRef]
- Yeh, L. Simple methods for designing troposcatter circuits. IRE Trans. Commun. Syst. 1960, 8, 193–198. [Google Scholar] [CrossRef]
- Rice, P.L.; Longley, A.G.; Norton, K.A.; Barsis, A.P. Transmission Loss Predictions for Tropospheric Communication Circuits; Department of Commerce, National Bureau of Standards: Gaithersburg, MD, USA, 1965. [Google Scholar]
- International Radio Consultative Committee. Recommendations and Reports of the CCIR: Propagation in Non-Ionized Media; CCIR: Geneva, Switzerland, 1986. [Google Scholar]
- International Telecommunication Union. Recommendation ITU-R P.452-16: Prediction Procedure for the Evaluation of Interference Between Stations on the Surface of the Earth at Frequencies above about 0.1 Ghz; Electronic Publication: Geneva, Switzerland, 2015. [Google Scholar]
- International Telecommunication Union. Recommendation ITU-R P.617-2: Propagation Prediction Techniques and Data Required for the Design of Trans-Horizon Radio-Relay Systems; Electronic Publication: Geneva, Switzerland, 2012. [Google Scholar]
- International Telecommunication Union. Recommendation ITU-R P.2001-3: A General Purpose Wide-Range Terrestrial Propagation Model in the Frequency Range 30 Mhz To 50 Ghz; Electronic Publication: Geneva, Switzerland, 2019. [Google Scholar]
- Li, L.; Wu, Z.-S.; Lin, L.-K.; Zhang, R.; Zhao, Z.-W. Study on the prediction of troposcatter transmission loss. IEEE Trans. AP 2016, 64, 1071–1079. [Google Scholar] [CrossRef]
- Yuan, D.; Chen, X. Troposcatter transmission loss prediction based on particle swarm optimization. IET Microw. 2021, 15, 332–341. [Google Scholar] [CrossRef]
- Lee, I.-S.; Noh, J.-H.; Oh, S.-J. A Survey and analysis on a troposcatter propagation model based on ITU-R recommendations. ICT Express 2023, 9, 507–516. [Google Scholar] [CrossRef]
- Levy, M. Parabolic Equation Methods for Electromagnetic Wave Propagation; IEEE: London, UK, 2000. [Google Scholar]
- Kuttler, J.R.; Dockery, G.D. Theoretical description of the parabolic approximation Fourier split-step method of representing electromagnetic propagation in the troposphere. Radio Sci. 1991, 26, 381–393. [Google Scholar] [CrossRef]
- Apaydin, G.; Sevgi, L. Radio Wave Propagation and Parabolic Equation Modeling; Wiley-IEEE Press: Hoboken, NJ, USA, 2017. [Google Scholar]
- Sirkova, I. Brief review on PE method application to propagation channel modeling in sea environment. CEJE 2012, 2, 19–38. [Google Scholar] [CrossRef]
- Zhang, P.; Bai, L.; Wu, Z.; Guo, L. Applying the parabolic equation to tropospheric groundwave propagation: A review of recent achievements and significant milestones. IEEE Antennas Propag. Mag. 2016, 58, 31–44. [Google Scholar] [CrossRef]
- Apaydin, G.; Sevgi, L. The split-step-Fourier and finite-element based parabolic-equation propagation prediction tools: Canonical tests, systematic comparisons, and calibration. IEEE Antennas Propag. Mag. 2010, 52, 66–79. [Google Scholar] [CrossRef]
- Barrios, A.E.; Anderson, K.; Lindem, G. Low altitude propagation effects—A validation study of the Advanced Propagation Model (APM) for mobile radio applications. IEEE Trans. AP 2006, 54, 2869–2877. [Google Scholar] [CrossRef]
- Gunashekar, S.D.; Warrington, E.M.; Siddle, D.R.; Valtr, P. Signal strength variations at 2 GHz for three sea paths in the British Channel islands: Detailed discussion and propagation modeling. Radio Sci. 2007, 42, 1–13. [Google Scholar] [CrossRef]
- Heemskerk, E. RF propagation measurement and model validation during RF/IR synergy trial VAMPIRA. In Proceedings of the SPIE Remote Sensing: Optics in Atmospheric Propagation and Adaptive Systems VIII, Bruges, Belgium, 20–21 September 2005; pp. 598107.1–598107.12. [Google Scholar] [CrossRef]
- Wang, Q.; Alappattu, D.P.; Billingsley, S.; Blomquist, B.; Burkholder, R.J.; Christman, A.J.; Creegan, E.D.; de Paolo, T.; Eleuterio, D.P.; Fernando, H.J.S.; et al. CASPER: Coupled air-sea process and electromagnetic wave ducting research. Bull. Am. Meteor. Soc. 2018, 99, 1449–1471. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, H.; Li, Y.; Sun, Q.; Wu, Y.; Jin, S.; Quek, T.Q.S.; Xu, C. Wireless channel models for maritime communications. IEEE Access 2018, 6, 68070–68088. [Google Scholar] [CrossRef]
- Barrios, A.E. Considerations in the development of the advanced propagation model (APM) for U.S. navy applications. In Proceedings of the International Conference on Radar (IEEE Cat. No.03EX695), Adelaide, SA, Australia, 3–5 September 2003; pp. 77–82. [Google Scholar] [CrossRef]
- Wetzel, L.B. Sea Clutter; Report 9244; Naval Res. Lab.: Washington, DC, USA, 1990. [Google Scholar]
- Sirkova, I. Duct occurrence and characteristics for Bulgarian Black sea shore derived from ECMWF data. J. Atmos. Sol. Terr. Phys. 2015, 135, 107–117. [Google Scholar] [CrossRef]
- Reed, H.R.; Russell, C.M. Ultra High Frequency Propagation; Boston Technical Publishers: Cambridge, MA, USA, 1966. [Google Scholar]
- Hitney, H.V. A practical tropospheric scatter model using the parabolic equation. IEEE Trans. AP 1993, 41, 905–909. [Google Scholar] [CrossRef]
- Turton, J.D.; Bennetts, D.A.; Farmer, S.F.G. An introduction to radio ducting. Meterorolog. Mag. 1988, 117, 245–254. [Google Scholar]
- Rol, M.; Nijboer, R.; Yarovoy, A. Radio wave blind zone in a duct: An analytical approach. In Proceedings of the 24th International Microwave and Radar Conference (MIKON), Gdansk, Poland, 12–14 September 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Couillard, D.; Dahman, G.; GrandMaison, M.-E.; Poitau, G.; Gagnon, F. Robust broadband maritime communications: Theoretical and experimental validation. Radio Sci. 2018, 53, 749–760. [Google Scholar] [CrossRef]
- Sirkova, I. Automatic Identification System Signals propagation in troposphere ducting conditions. In Proceedings of the 10th IEEE International Black Sea Conference on Communications and Networking (BlackSeaCom), Sofia, Bulgaria, 6–9 June 2022; pp. 331–335. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sirkova, I. Revisiting Enhanced AIS Detection Range under Anomalous Propagation Conditions. J. Mar. Sci. Eng. 2023, 11, 1838. https://doi.org/10.3390/jmse11091838
Sirkova I. Revisiting Enhanced AIS Detection Range under Anomalous Propagation Conditions. Journal of Marine Science and Engineering. 2023; 11(9):1838. https://doi.org/10.3390/jmse11091838
Chicago/Turabian StyleSirkova, Irina. 2023. "Revisiting Enhanced AIS Detection Range under Anomalous Propagation Conditions" Journal of Marine Science and Engineering 11, no. 9: 1838. https://doi.org/10.3390/jmse11091838
APA StyleSirkova, I. (2023). Revisiting Enhanced AIS Detection Range under Anomalous Propagation Conditions. Journal of Marine Science and Engineering, 11(9), 1838. https://doi.org/10.3390/jmse11091838






