Analysis of Saturated Impulse for Square Plates under Flat Slamming Impact: Experimental and Numerical Investigation
Abstract
:1. Introduction
2. Experiments
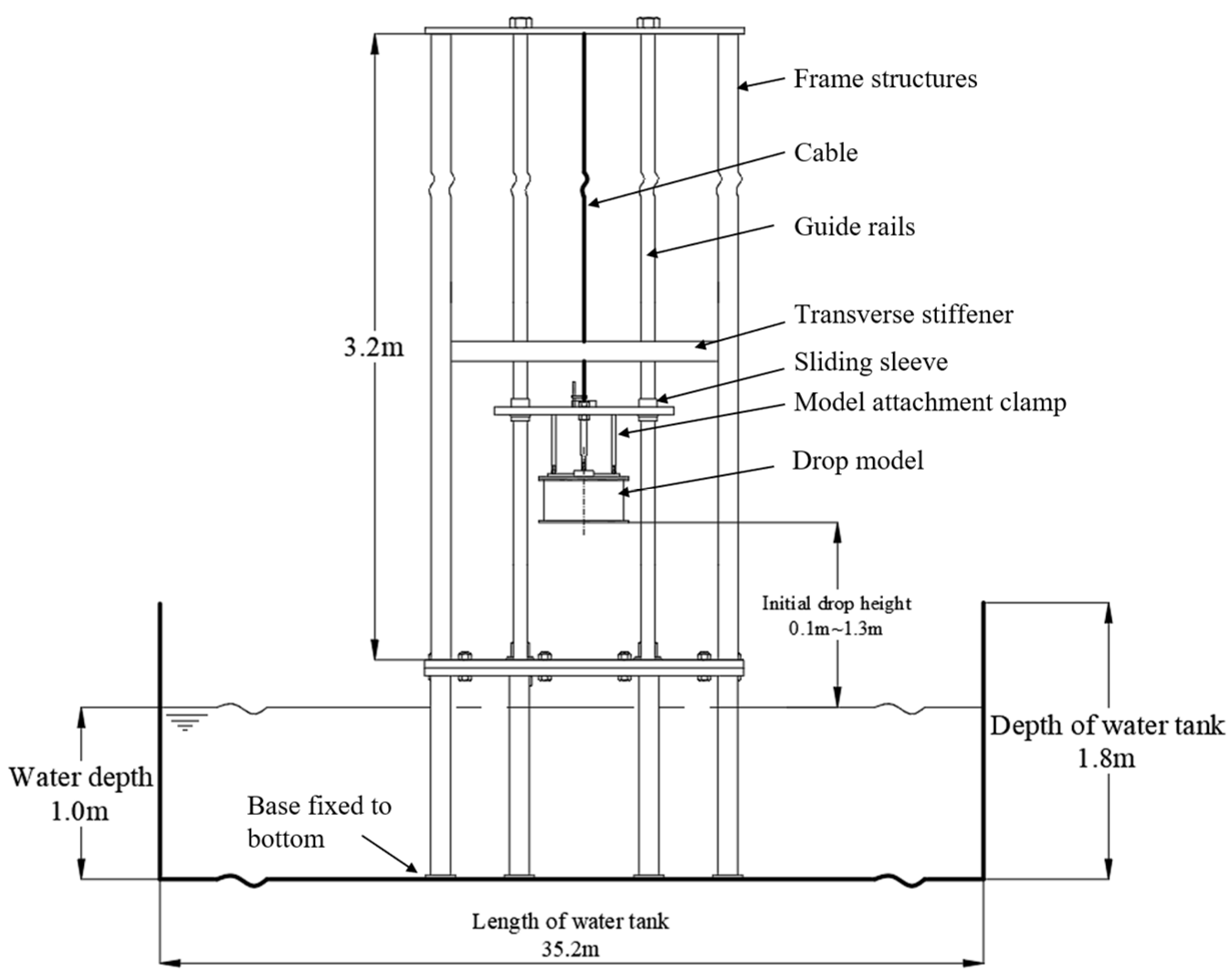
2.1. Experimental Setup
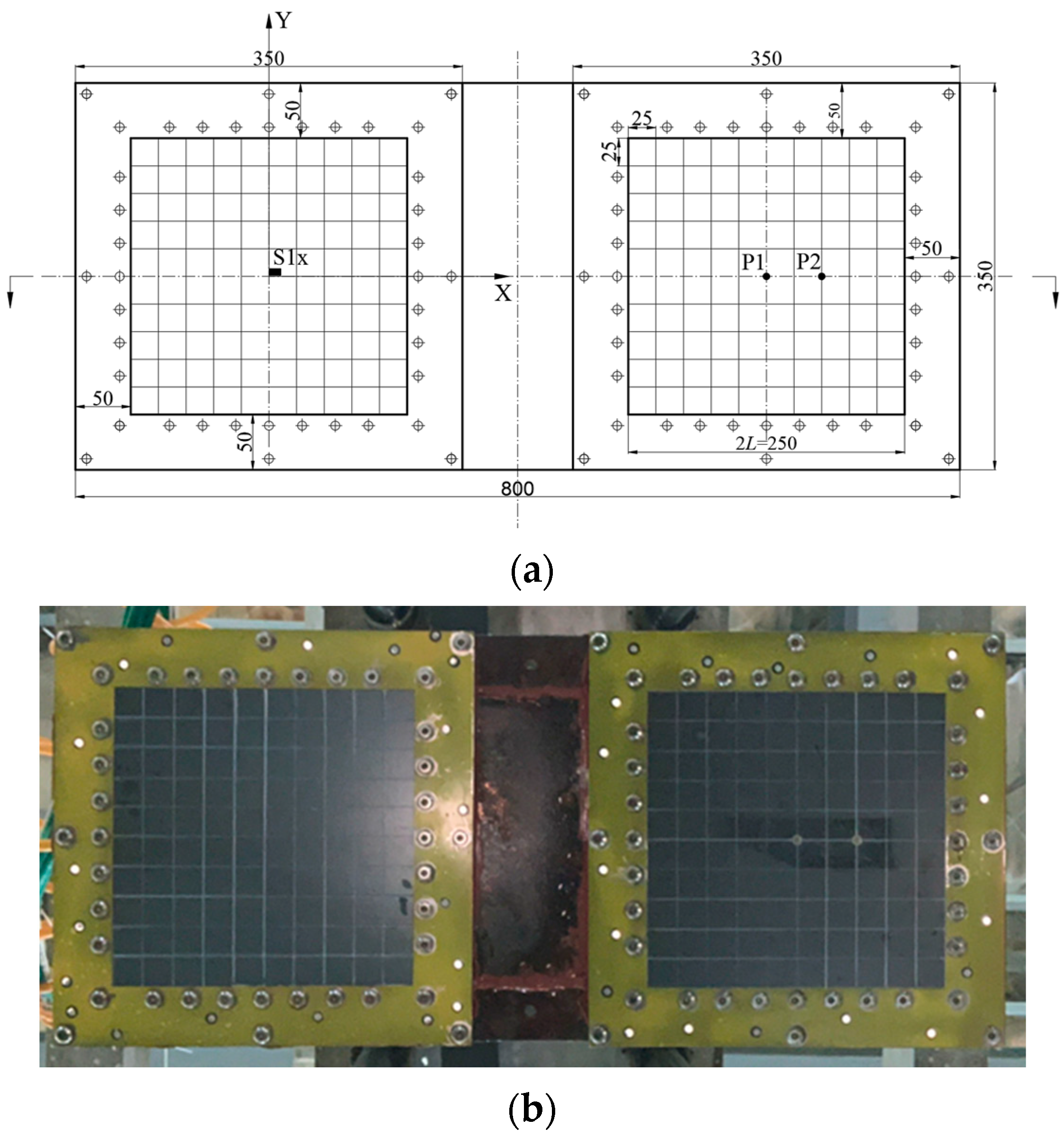
2.2. Specimens and Test Conditions
2.3. Experimental Results
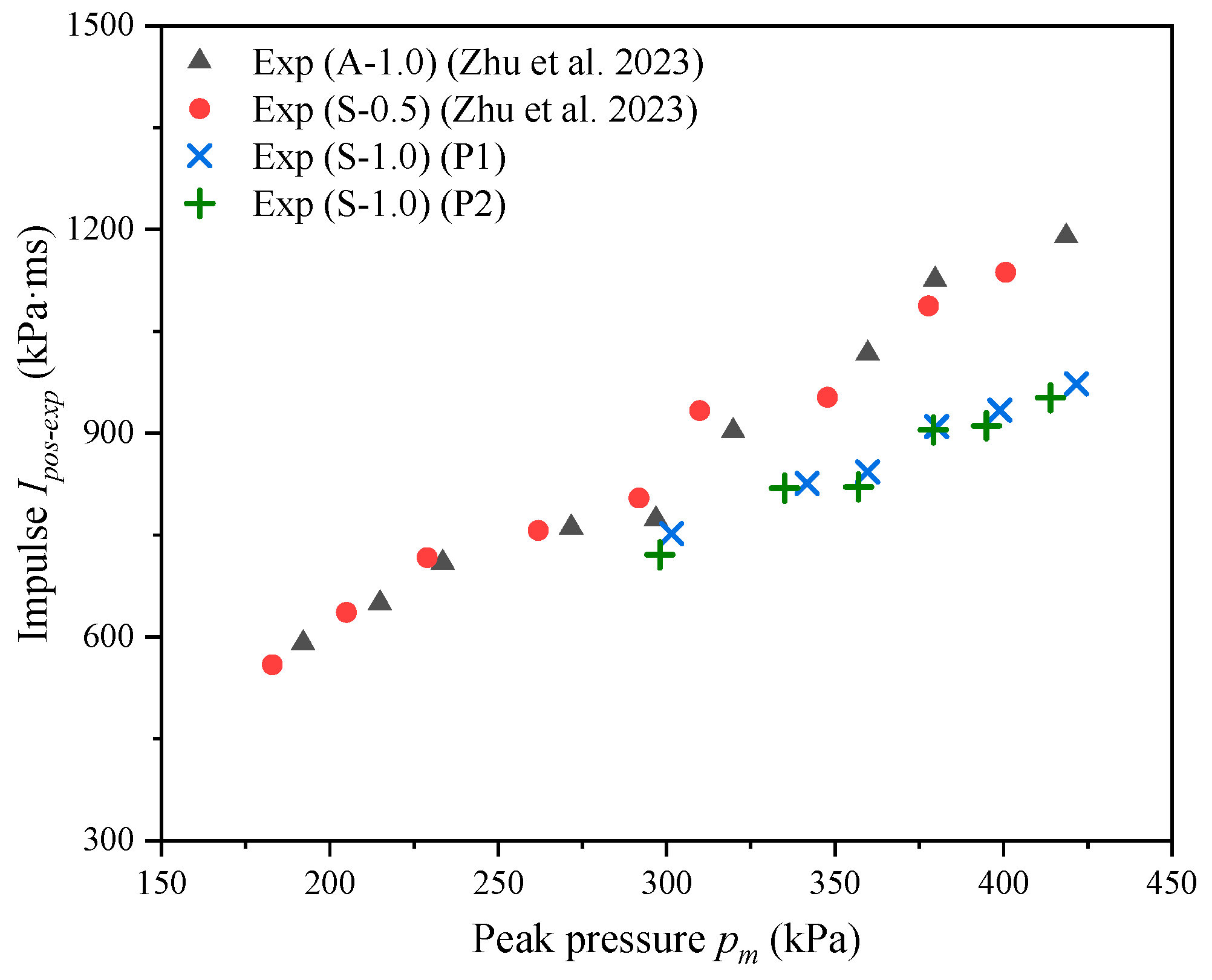
2.3.1. Slamming Pressure and Impulse
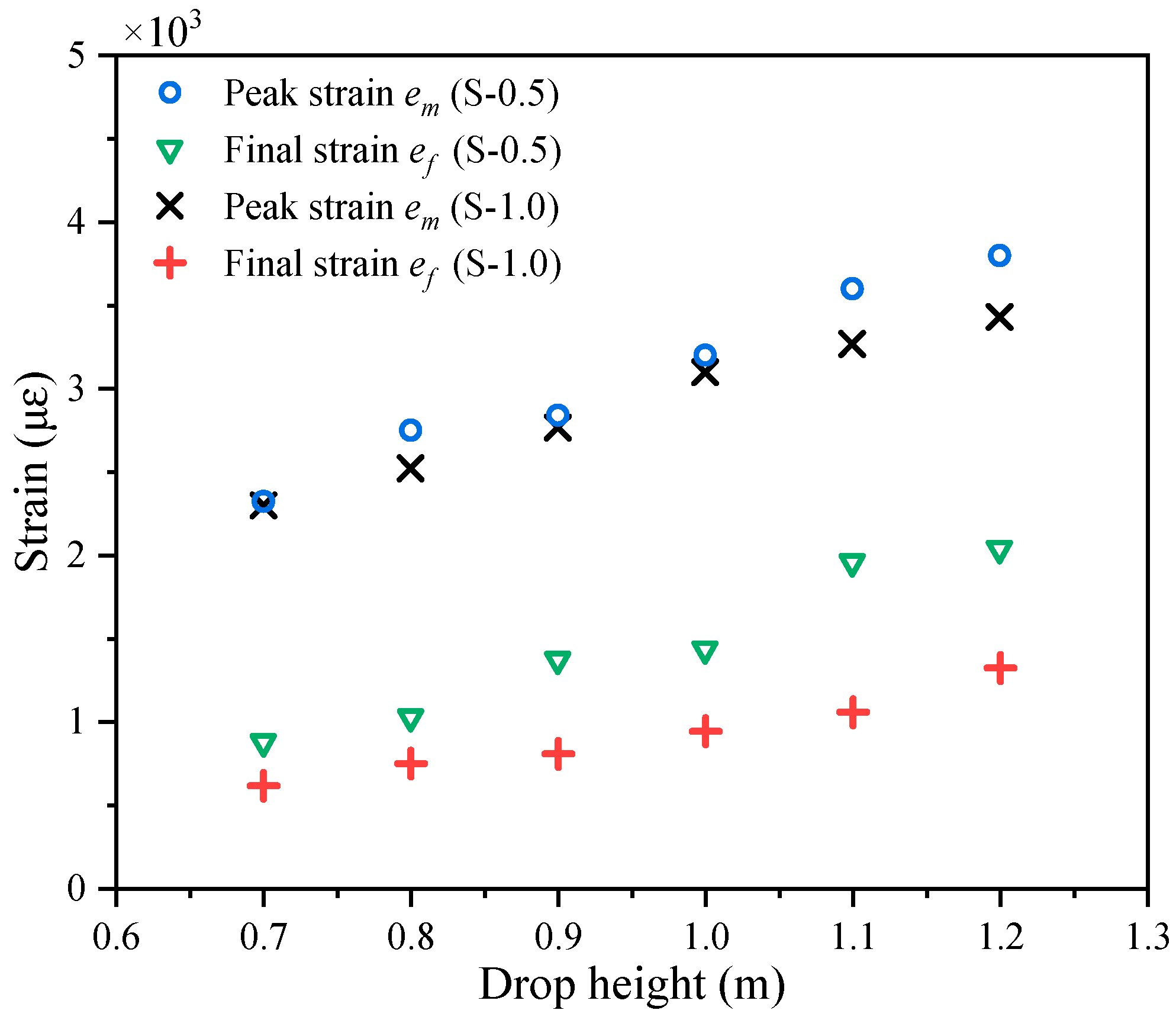
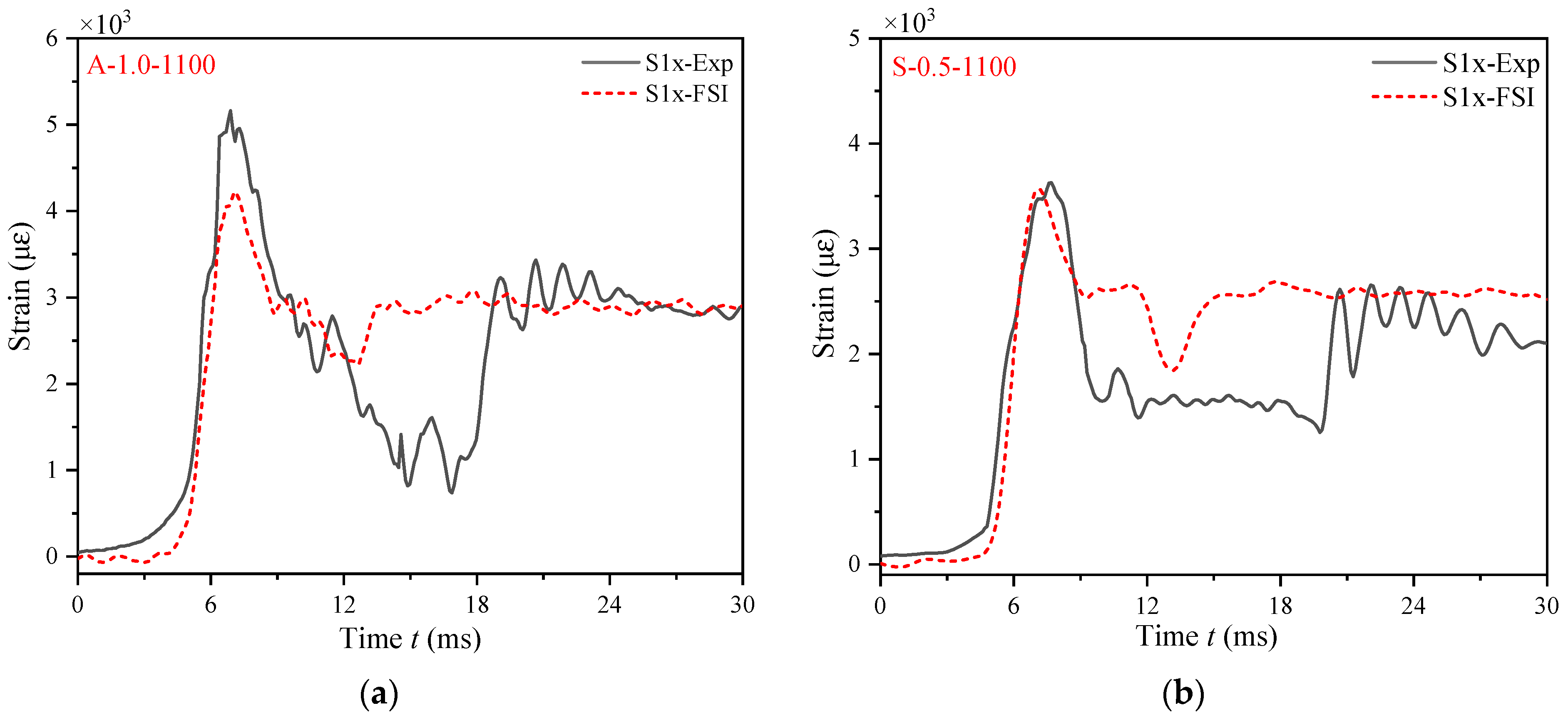
2.3.2. Strain
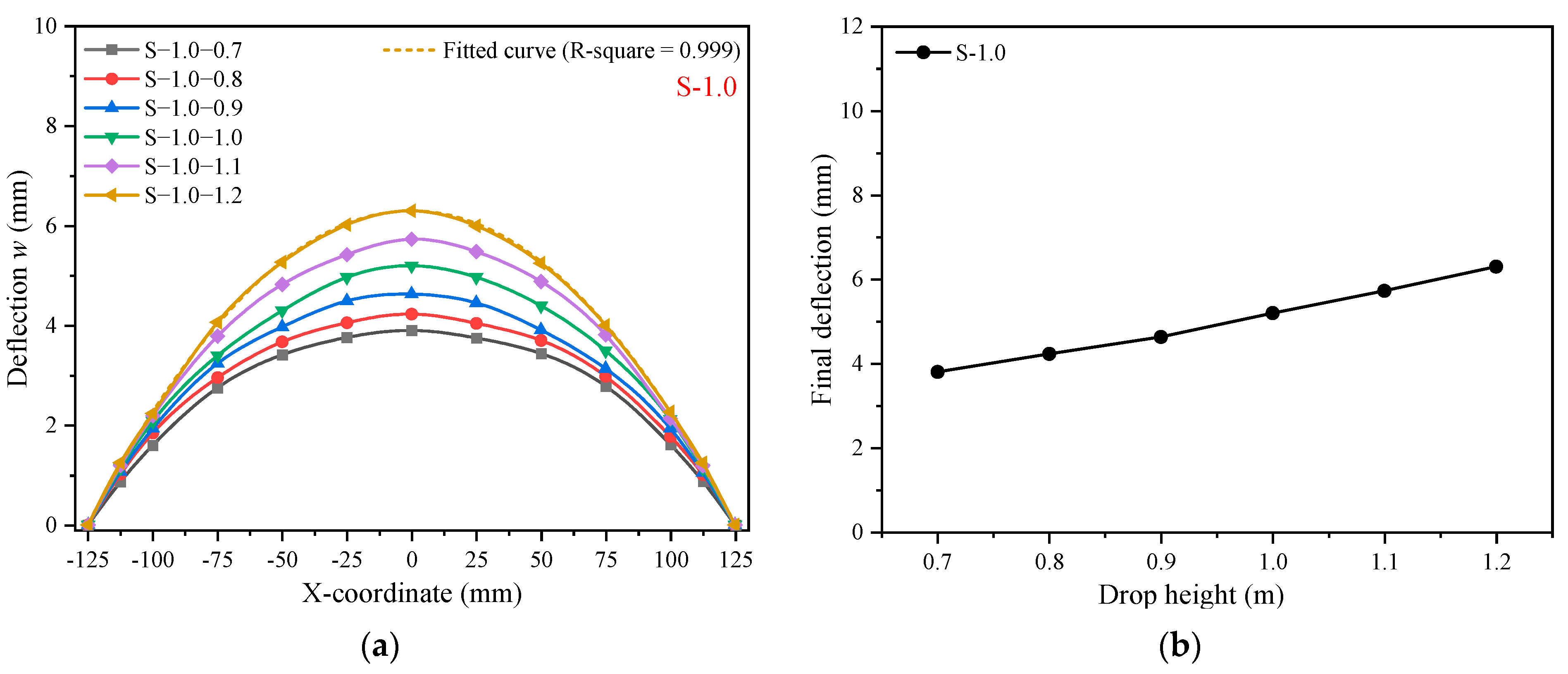
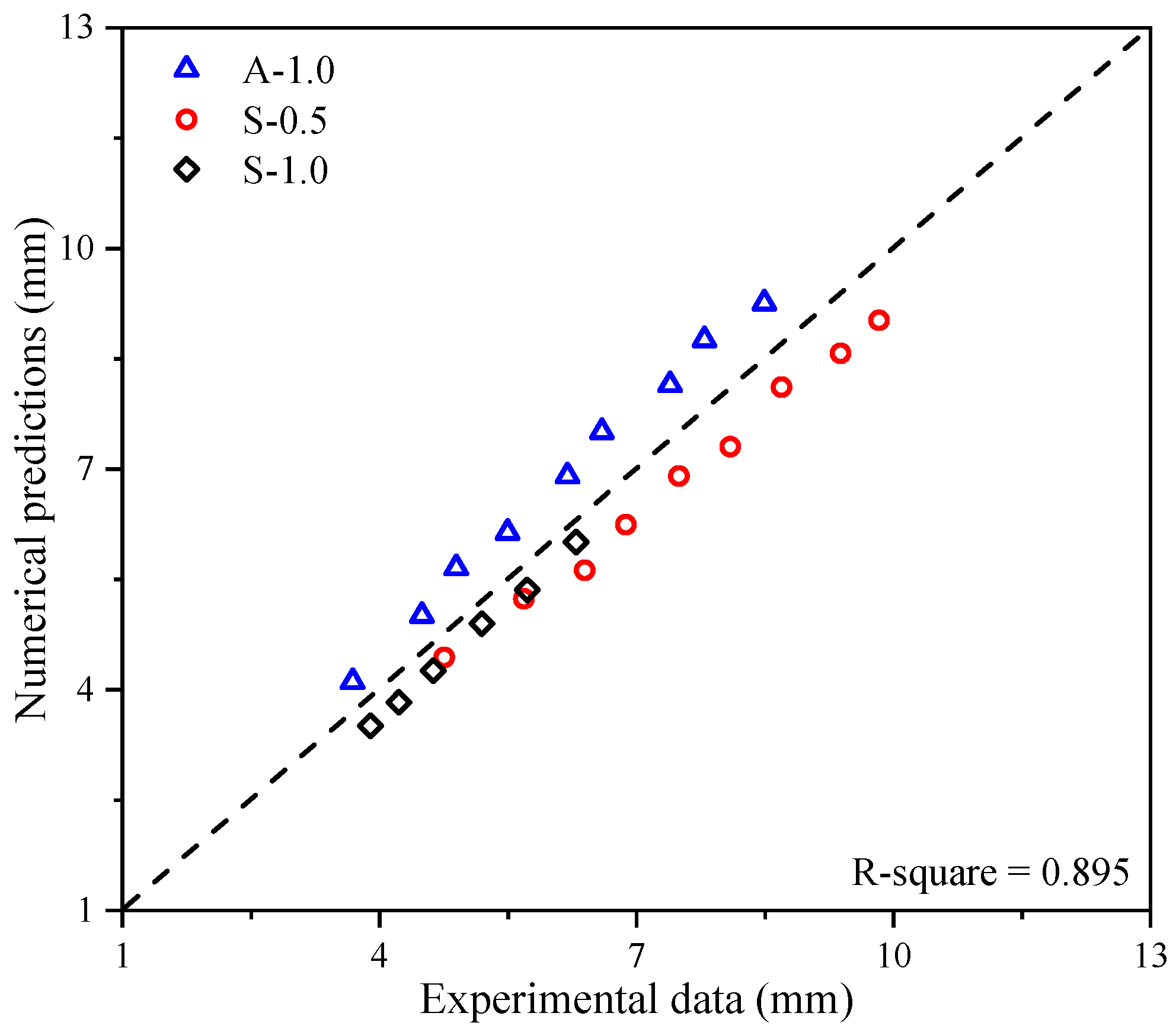
2.3.3. Permanent Deflection and Deformed Profile
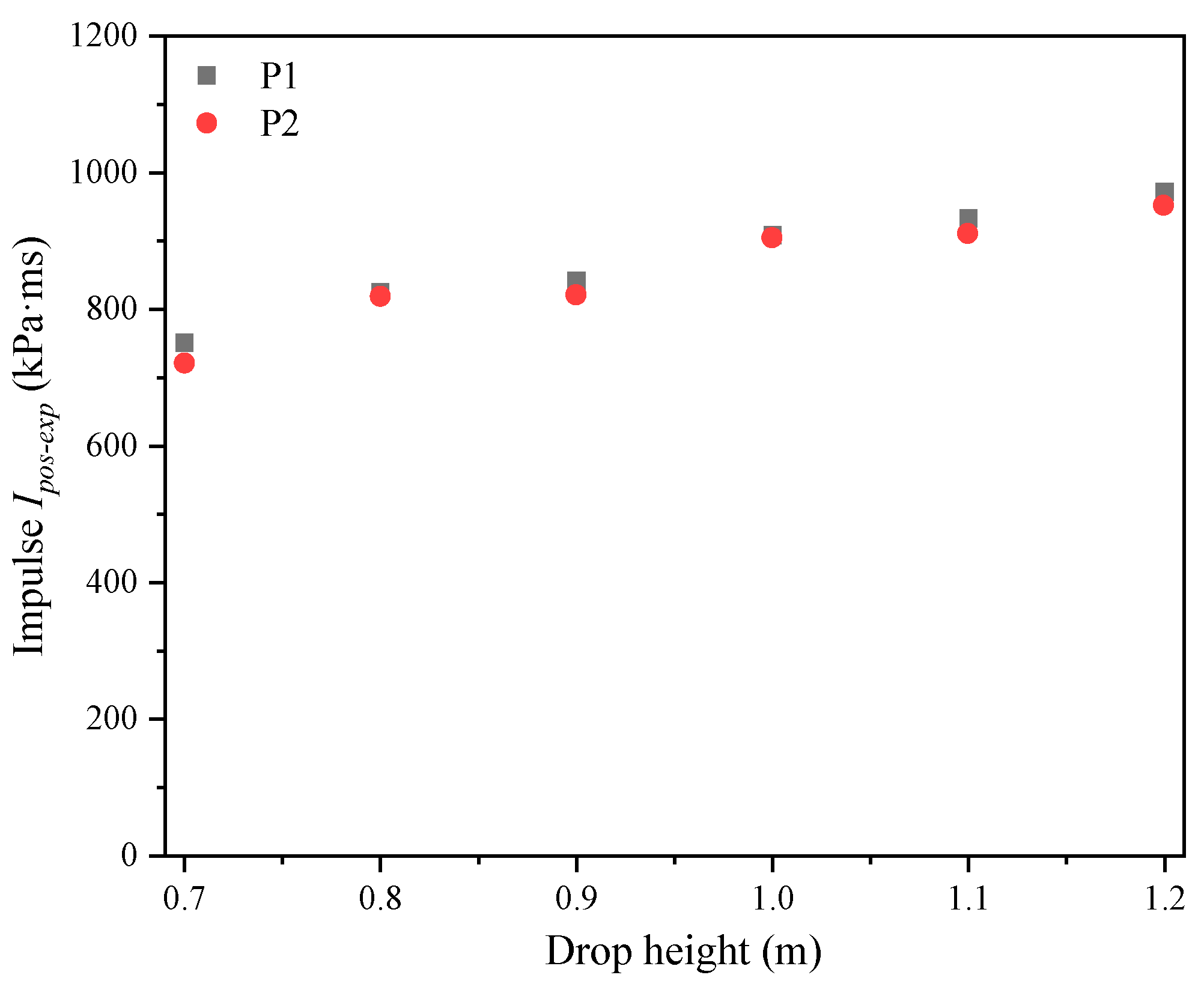
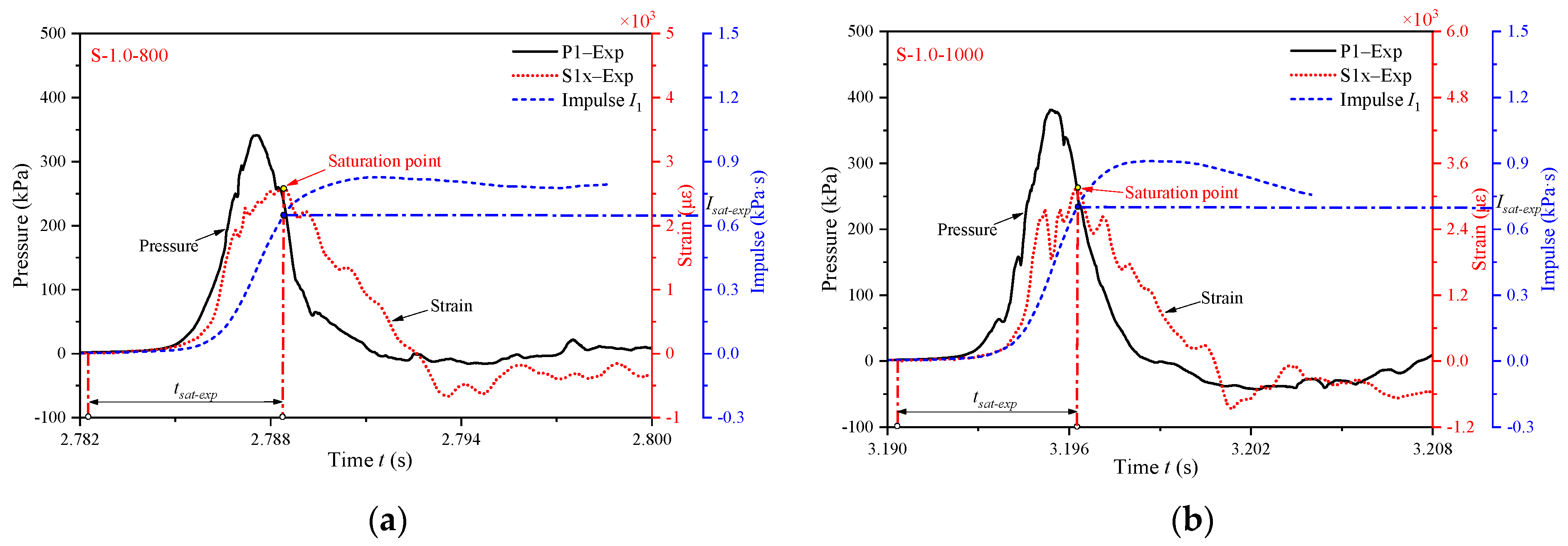
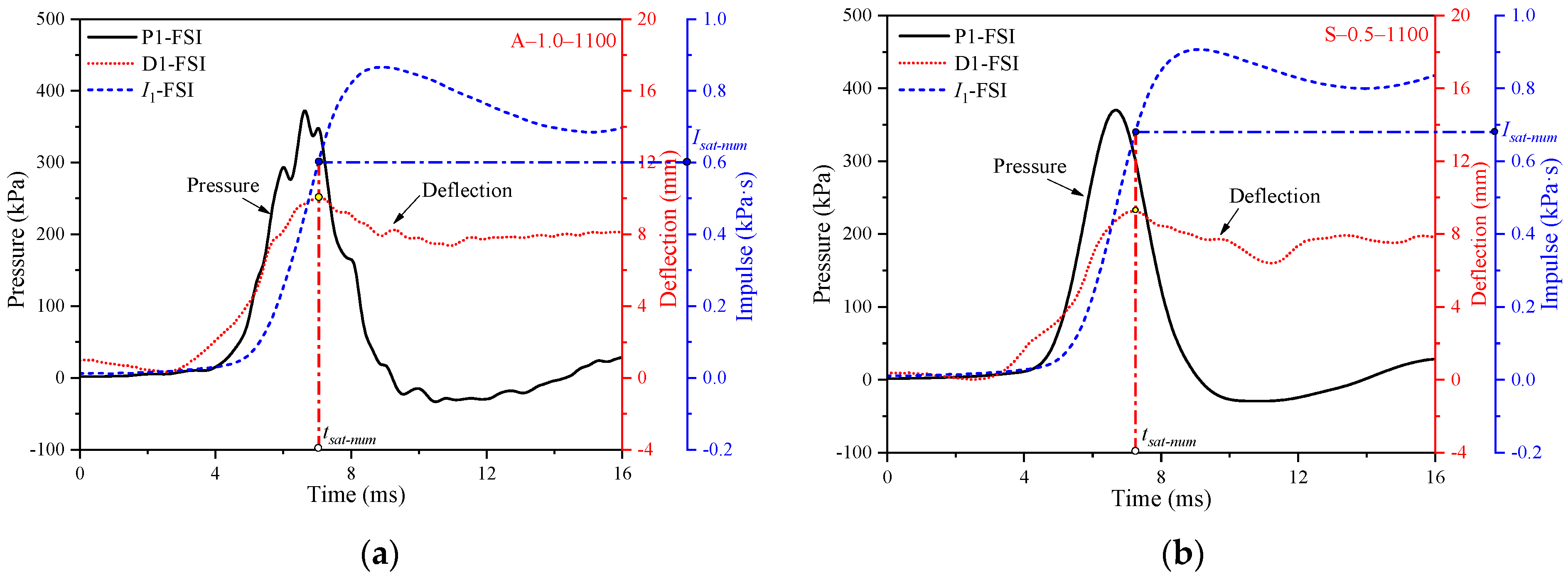
2.3.4. Analysis of Saturated Impulse
3. Numerical Simulations
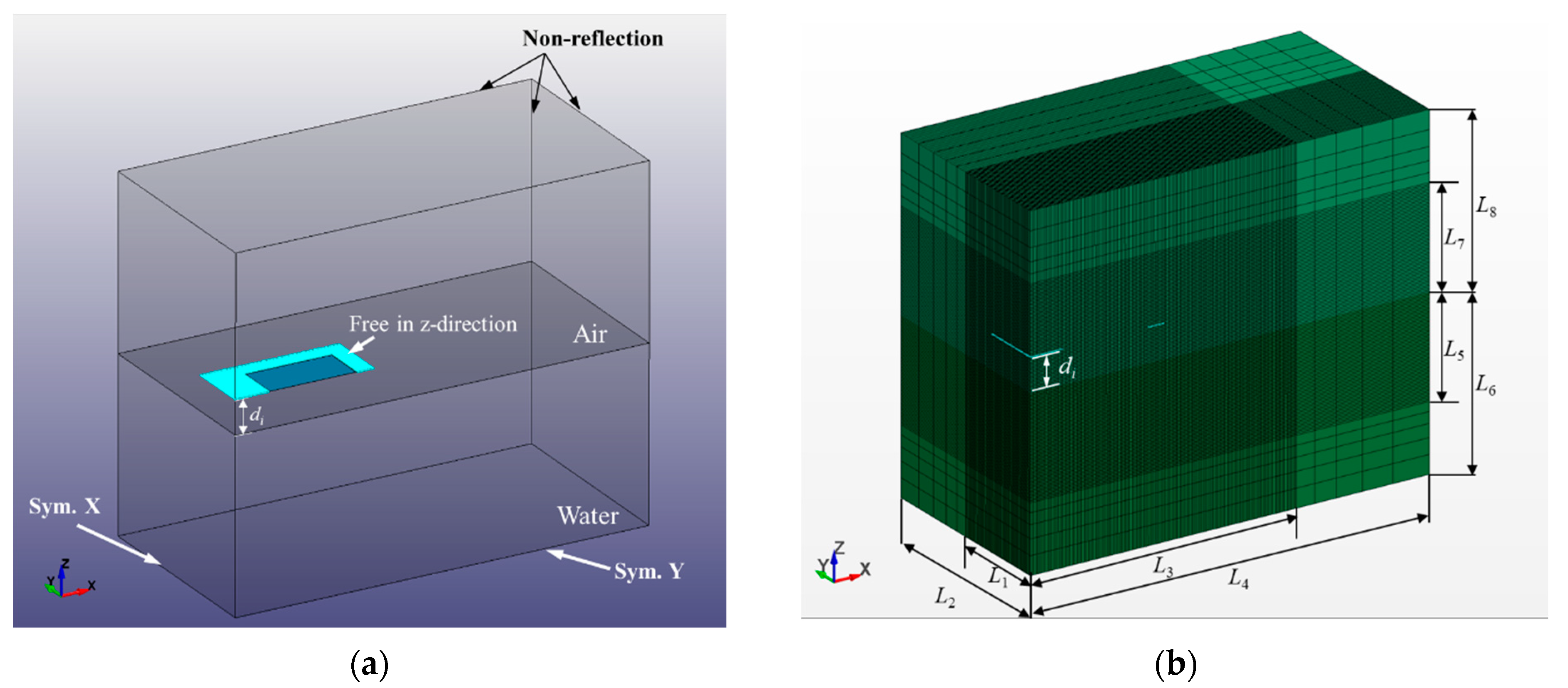
3.1. FSI Model
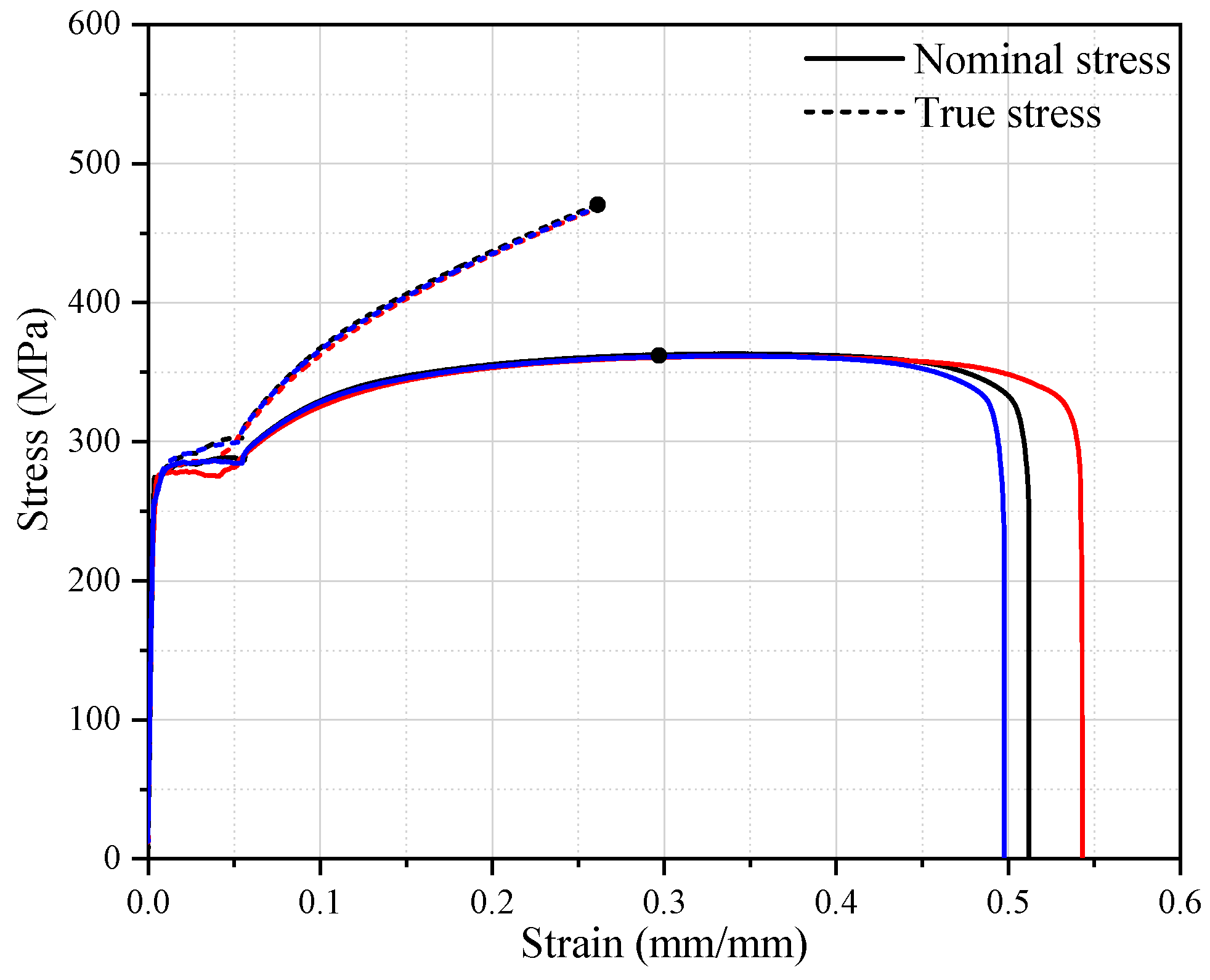
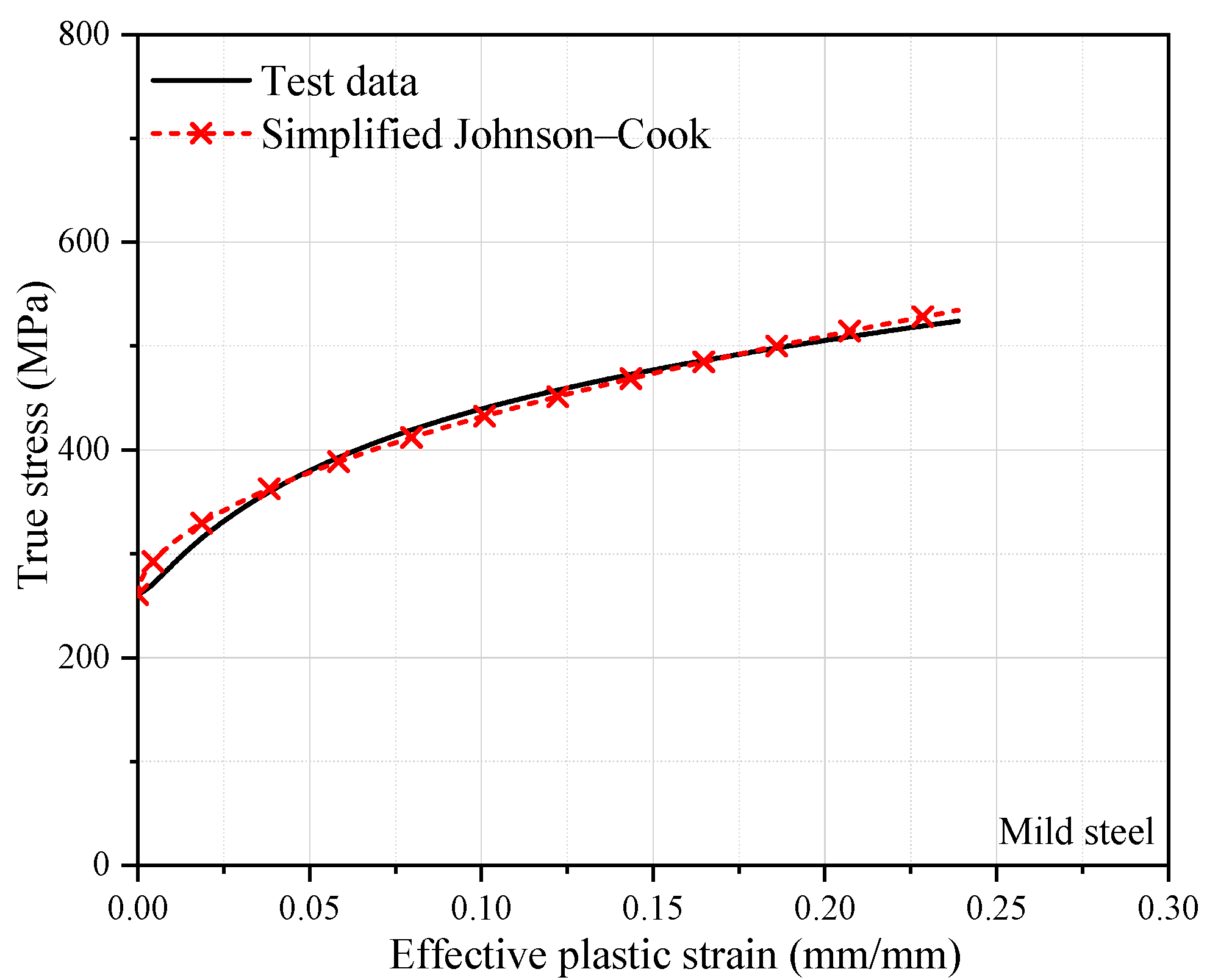
3.2. Materials for Structures and Fluids
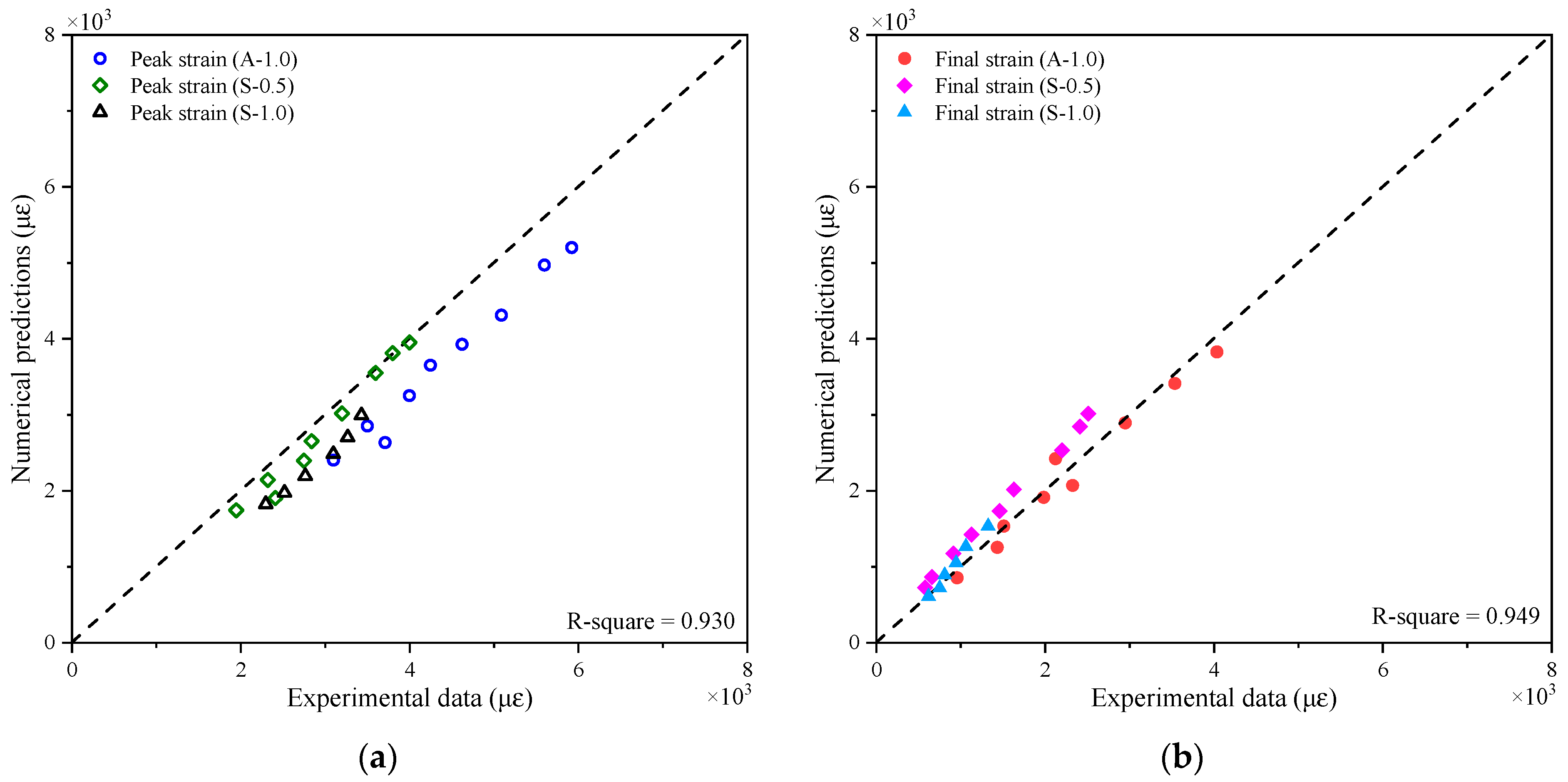
3.3. Validation of Numerical Model
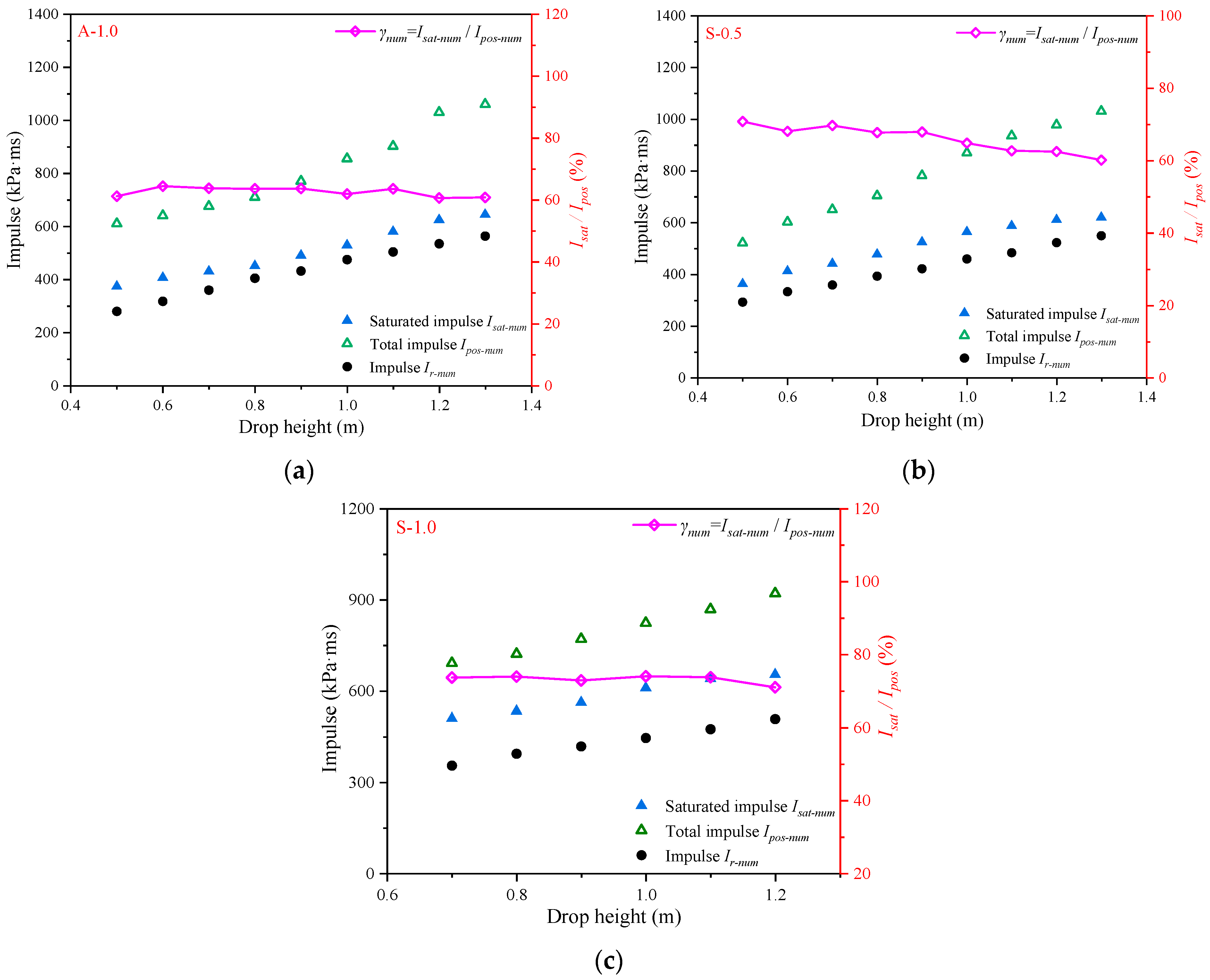
3.4. Numerical Prediction of the Transient Response and Saturated Impulse
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Mesh size (mm) | 12.5 | 5.0 | 4.2 |
| Number of shell elements (structure) | 448 | 2800 | 4032 |
| Number of solid elements (fluid) | 116,058 | 1,394,250 | 2,336,026 |
| Total nodes | 124,395 | 1,438,152 | 2,397,991 |
| CPU time | 1 h 2 min | 13 h 27 min | 25 h 11 min |

References
- Cho, S.; Dessi, D.; Engle, A.; Kukkanen, T. Committee V7: Impulsive Pressure Loading and Response Assessment. In Proceedings of the 17th International Ship and Offshore Structures Congress, ISSC 2009, Seoul, Republic of Korea, 16–21 August 2009; Seoul National University: Seoul, Republic of Korea, 2009; pp. 367–432. [Google Scholar]
- Yamamoto, Y.; Iida, K.; Fukasawa, T.; Murakami, T.; Arai, M.; Ando, A. Structural damage analysis of a fast ship due to bow flare slamming. Int. Shipbuild. Prog. 1985, 32, 124–136. [Google Scholar] [CrossRef]
- Duan, L.L.; Zhu, L.; Chen, M.S.; Pedersen, P.T. Experimental study on the propagation characteristics of the slamming pressures. Ocean Eng. 2020, 217, 107868. [Google Scholar] [CrossRef]
- Sun, Z.; Sui, X.; Deng, Y.; Zou, L.; Korobkin, A.; Xu, L.; Jiang, Y. Characteristics of slamming pressure and force for trimaran hull. J. Mar. Sci. Eng. 2021, 9, 564. [Google Scholar] [CrossRef]
- Meziane, B.; Alaoui, A.E.M.; Nême, A.; Leble, B.; Bellanger, D. Experimental investigation of the influence of the panel stiffness on the behaviour of a wedge under slamming. J. Fluids Struct. 2022, 114, 103702. [Google Scholar] [CrossRef]
- Park, I.C.; Seo, B.C.; Lee, S.H.; Park, J.H.; Seo, H.S. A study on slamming impact load characteristics of energy storage system case for ships. J. Mar. Sci. Eng. 2022, 11, 44. [Google Scholar] [CrossRef]
- Hosseinzadeh, S.; Tabri, K.; Hirdaris, S.; Sahk, T. Slamming loads and responses on a non-prismatic stiffened aluminium wedge: Part I. Experimental study. Ocean Eng. 2023, 279, 114510. [Google Scholar] [CrossRef]
- Chuang, S.L. Investigation of Impact of Rigid and Elastic Bodies with Water; Report for Department of the Navy. Report No. 3248; United States Department of the Navy: Washington, DC, USA, 1970. [Google Scholar]
- Mori, K. Response of the bottom plate of high speed crafts under impulsive water pressure. J. Soc. Nav. Archit. Jpn. 1977, 1977, 297–305. [Google Scholar] [CrossRef]
- Shin, H.; Seo, B.; Cho, S.R. Experimental investigation of slamming impact acted on flat bottom bodies and cumulative damage. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 294–306. [Google Scholar] [CrossRef]
- Abrahamsen, B.C.; Alsos, H.S.; Aune, V.; Fagerholt, E.; Faltinsen, O.M.; Hellan, Ø. Hydroplastic response of a square plate due to impact on calm water. Phys. Fluids 2020, 32, 082103. [Google Scholar] [CrossRef]
- Zhu, L.; Zhu, Z.K.; Yu, T.X.; Jones, N. An experimental study of the saturated impulse for metal plates under slamming. Int. J. Impact Eng. 2023, 178, 104601. [Google Scholar] [CrossRef]
- Truong, D.D.; Jang, B.S.; Quach, H.N.; Dang, X.P.; Duong, H.D.; Cho, S.R. Empirical formulations for prediction of permanent set evolution of steel plates due to repeated impulsive pressure loadings induced by slamming. Ocean Eng. 2023, 268, 113430. [Google Scholar] [CrossRef]
- Pavlović, A.; Minak, G. FEM-SPH Numerical Simulation of Impact Loading on Floating Laminates. J. Mar. Sci. Eng. 2023, 11, 1590. [Google Scholar] [CrossRef]
- Lu, T.; Wang, J.; Liu, K.; Zhao, X. Experimental and Numerical Prediction of Slamming Impact Loads Considering Fluid–Structure Interactions. J. Mar. Sci. Eng. 2024, 12, 733. [Google Scholar] [CrossRef]
- Park, Y.I.; Park, S.H.; Kim, J.H. Numerical Investigation of Plastic Deformation of Flat Plate for Slamming Impact by Coupled Eulerian–Lagrangian Method. Appl. Sci. 2022, 12, 7270. [Google Scholar] [CrossRef]
- Luo, H.; Hu, J.; Soares, C.G. Numerical simulation of hydroelastic responses of flat stiffened panels under slamming loads. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Shanghai, China, 6–11 June 2010; pp. 373–381. [Google Scholar]
- Stenius, I.; Rosén, A.; Kuttenkeuler, J. Hydroelastic interaction in panel-water impacts of high-speed craft. Ocean Eng. 2011, 38, 371–381. [Google Scholar] [CrossRef]
- Wang, S.; Soares, C.G. Numerical study on the water impact of 3D bodies by an explicit finite element method. Ocean Eng. 2014, 78, 73–88. [Google Scholar] [CrossRef]
- Yu, Z.L.; Amdahl, J.; Greco, M.; Xu, H. Hydro-plastic response of beams and stiffened panels subjected to extreme water slamming at small impact angles, Part II: Numerical verification and analysis. Mar. Struct. 2019, 65, 114–133. [Google Scholar] [CrossRef]
- Wang, H.; Cheng, Y.S.; Liu, J.; Zhang, P. Hydroelastic behaviours of laser-welded lightweight corrugated sandwich panels subjected to water impact: Experiments and simulations. Thin-Walled Struct. 2020, 146, 106452. [Google Scholar] [CrossRef]
- Truong, D.D.; Jang, B.S.; Ju, H.B.; Han, S.W. Prediction of slamming pressure considering fluid-structure interaction. Part I: Numerical simulations. Ships Offshore Struct. 2020, 17, 7–8. [Google Scholar]
- Truong, D.D.; Jang, B.S.; Ju, H.B.; Han, S.W. Prediction of slamming pressure considering fluid-structure interaction. Part II: Derivation of empirical formulations. Mar. Struct. 2021, 75, 102700. [Google Scholar] [CrossRef]
- Truong, D.D.; Jang, B.S.; Janson, C.E.; Ringsberg, J.W.; Yamada, Y.; Takamoto, K.; Kawamura, Y.; Ju, H.B. Benchmark study on slamming response of flat-stiffened plates considering fluid-structure interaction. Mar. Struct. 2021, 79, 103040. [Google Scholar] [CrossRef]
- Jones, N. Slamming damage. J. Ship Res. 1973, 17, 80–86. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Yu, T.X.; Fang, J. Large dynamic plastic deflection of a simply supported beam subjected to rectangular pressure pulse. Arch. Appl. Mech. 1994, 64, 223–232. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Yu, T.X.; Fang, J. Saturation impulses for dynamically loaded structures with finite-deflections. Struct. Eng. Mech. 1995, 3, 583–592. [Google Scholar] [CrossRef]
- Zhu, L.; Yu, T.X. Saturated impulse for pulse-loaded elastic-plastic square plates. Int. J. Solids Struct. 1997, 34, 1709–1718. [Google Scholar] [CrossRef]
- Zhu, L.; Bai, X.Y.; Yu, T.X. The saturated impulse of fully clamped square plates subjected to linearly decaying pressure pulse. Int. J. Impact Eng. 2017, 110, 198–207. [Google Scholar] [CrossRef]
- Talioua, A.; Berkane, B.; Martin, M.B.; Perret, G.; Pinon, G. Flat plate pressure impact on a still water surface: The effect of surrounding ambient pressure and plate size. Ocean Eng. 2022, 263, 111926. [Google Scholar] [CrossRef]
- Hu, Q.J.; Zhu, L.; Yu, T.X. Elastic effect on the final deflection of rigid-plastic square plates under pulse loading. Thin-Walled Struct. 2023, 193, 111238. [Google Scholar] [CrossRef]
- ABS. Guide for Slamming Loads and Strength Assessment for Vessels; American Bureau of Shipping: Houston, TX, USA, 2023. [Google Scholar]
- Cheon, J.S.; Jang, B.S.; Yim, K.H.; Lee, H.D.; Koo, B.Y.; Ju, H. A study on slamming pressure on a flat stiffened plate considering fluid–structure interaction. J. Mar. Sci. Technol. 2016, 21, 309–324. [Google Scholar] [CrossRef]
- Guo, Z.T.; Gao, B.; Guo, Z.; Zhang, W. Dynamic constitutive relation based on JC model of Q235 steel. Explosion Shock Waves 2018, 38, 804–810. [Google Scholar]
- Okada, S.; Sumi, Y. Experimental study on the maximum pressure and the duration time of the horizontal water impact of flat plate. J. Soc. Nav. Archit. Jpn. 1995, 178, 381–389. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Li, X.; Zhang, C.; Tan, P.; Chen, P. Impulse saturation in metal plates under confined blasts. Int. J. Impact Eng. 2022, 168, 104308. [Google Scholar] [CrossRef]



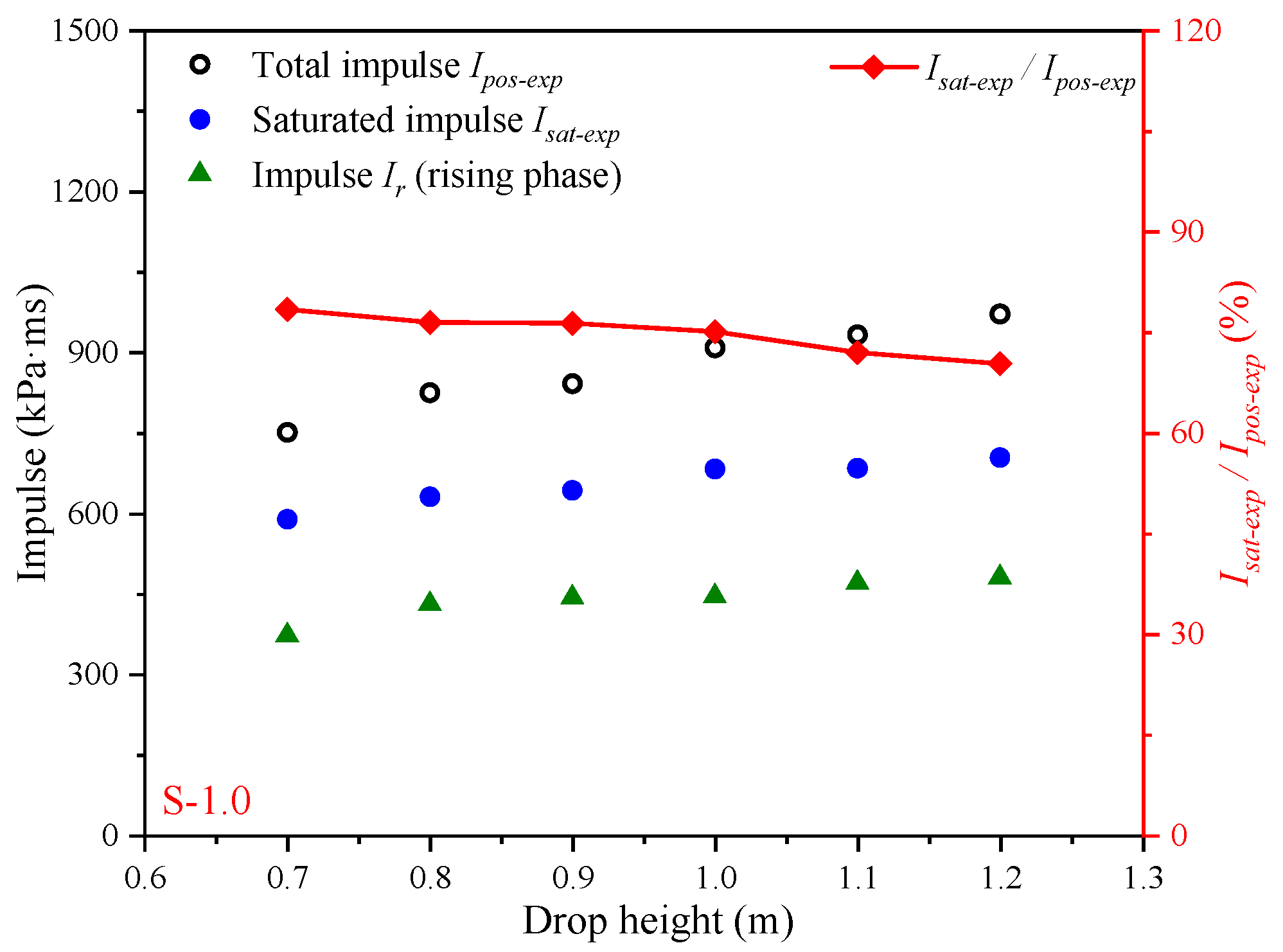
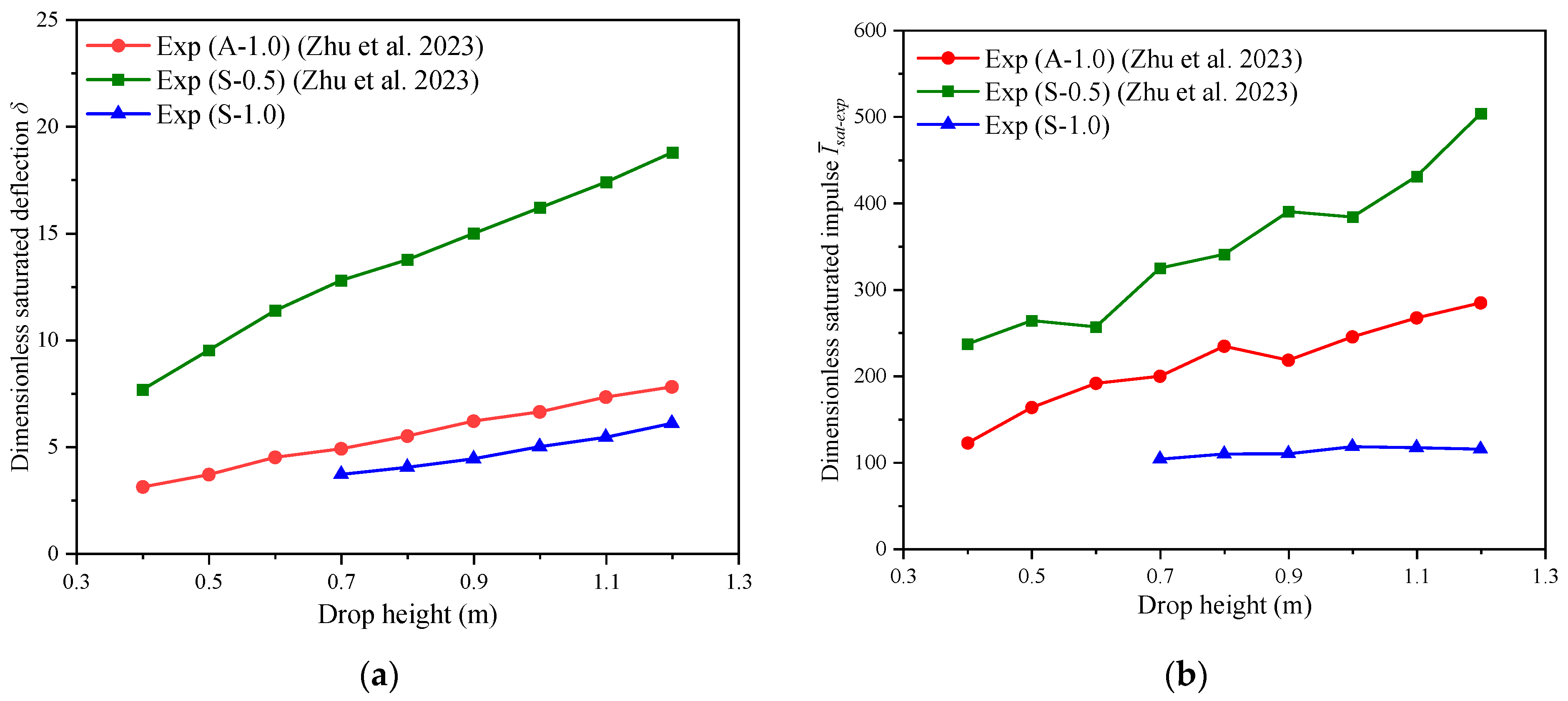




| Test Object | Material | Drop Height (mm) | Series Number * |
|---|---|---|---|
| Drop model | Mild steel | 700 | S-1.0-700 |
| 800 | S-1.0-800 | ||
| 900 | S-1.0-900 | ||
| 1000 | S-1.0-1000 | ||
| 1100 | S-1.0-1100 | ||
| 1200 | S-1.0-1200 |
| Model | Water Domain | Air Domain | Initial Gap | ||||||
|---|---|---|---|---|---|---|---|---|---|
| L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | di | |
| Aluminum/steel plate | 300 | 600 | 800 | 1200 | 300 | 500 | 300 | 500 | 100 |
| Type | Density ρ [kg/m3] | Young’s Modulus [GPa] | A [MPa] | B [MPa] | n [-] | c [-] |
|---|---|---|---|---|---|---|
| Aluminum A1060 | 2700 | 70.0 | 132.74 | 54.13 | 0.32 | - |
| Mild steel (S-0.5) | 7850 | 206.0 | 263.56 | 594.58 | 0.53 | 0.0652 |
| Mild steel (S-1.0) | 7850 | 206.0 | 270.16 | 553.40 | 0.76 | 0.0652 |
| *EOS_Linear_Polynomial | *EOS_Gruneisen | ||||
|---|---|---|---|---|---|
| Parameter | Unit | Value | Parameter | Unit | Value |
| ρ0 | kg/m3 | 1.225 | ρ0 | kg/m3 | 1000 |
| C0 | MPa | 0.0 | C | m/s | 1480 |
| C1 | MPa | 0.0 | S1 | - | 1.921 |
| C2 | MPa | 0.0 | S2 | - | −0.096 |
| C3 | MPa | 0.0 | S3 | - | 0.0 |
| C4 | - | 0.4 | γ0 | - | 0.35 |
| C5 | - | 0.4 | a | - | 0.0 |
| C6 | - | 0.0 | E | MPa | 0.2895 |
| E | MPa | 0.25 | V0 | - | 1.0 |
| V0 | - | 1.0 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Zhu, L.; Guo, K.; Wang, X. Analysis of Saturated Impulse for Square Plates under Flat Slamming Impact: Experimental and Numerical Investigation. J. Mar. Sci. Eng. 2024, 12, 1730. https://doi.org/10.3390/jmse12101730
Zhu Z, Zhu L, Guo K, Wang X. Analysis of Saturated Impulse for Square Plates under Flat Slamming Impact: Experimental and Numerical Investigation. Journal of Marine Science and Engineering. 2024; 12(10):1730. https://doi.org/10.3390/jmse12101730
Chicago/Turabian StyleZhu, Zhikui, Ling Zhu, Kailing Guo, and Xueliang Wang. 2024. "Analysis of Saturated Impulse for Square Plates under Flat Slamming Impact: Experimental and Numerical Investigation" Journal of Marine Science and Engineering 12, no. 10: 1730. https://doi.org/10.3390/jmse12101730
APA StyleZhu, Z., Zhu, L., Guo, K., & Wang, X. (2024). Analysis of Saturated Impulse for Square Plates under Flat Slamming Impact: Experimental and Numerical Investigation. Journal of Marine Science and Engineering, 12(10), 1730. https://doi.org/10.3390/jmse12101730





