Bearing Performance of a Helical Pile for Offshore Photovoltaic under Horizontal Cyclic Loading
Abstract
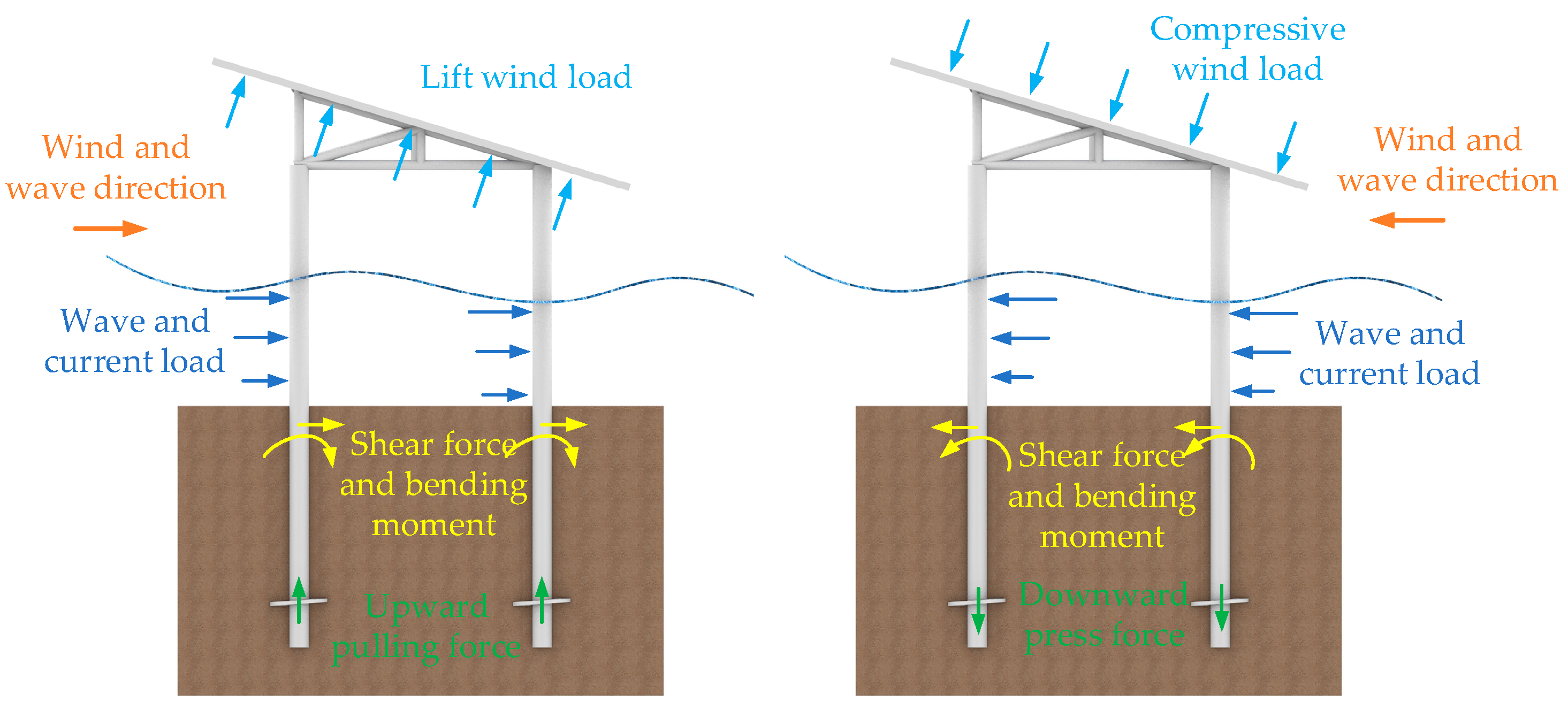
1. Introduction
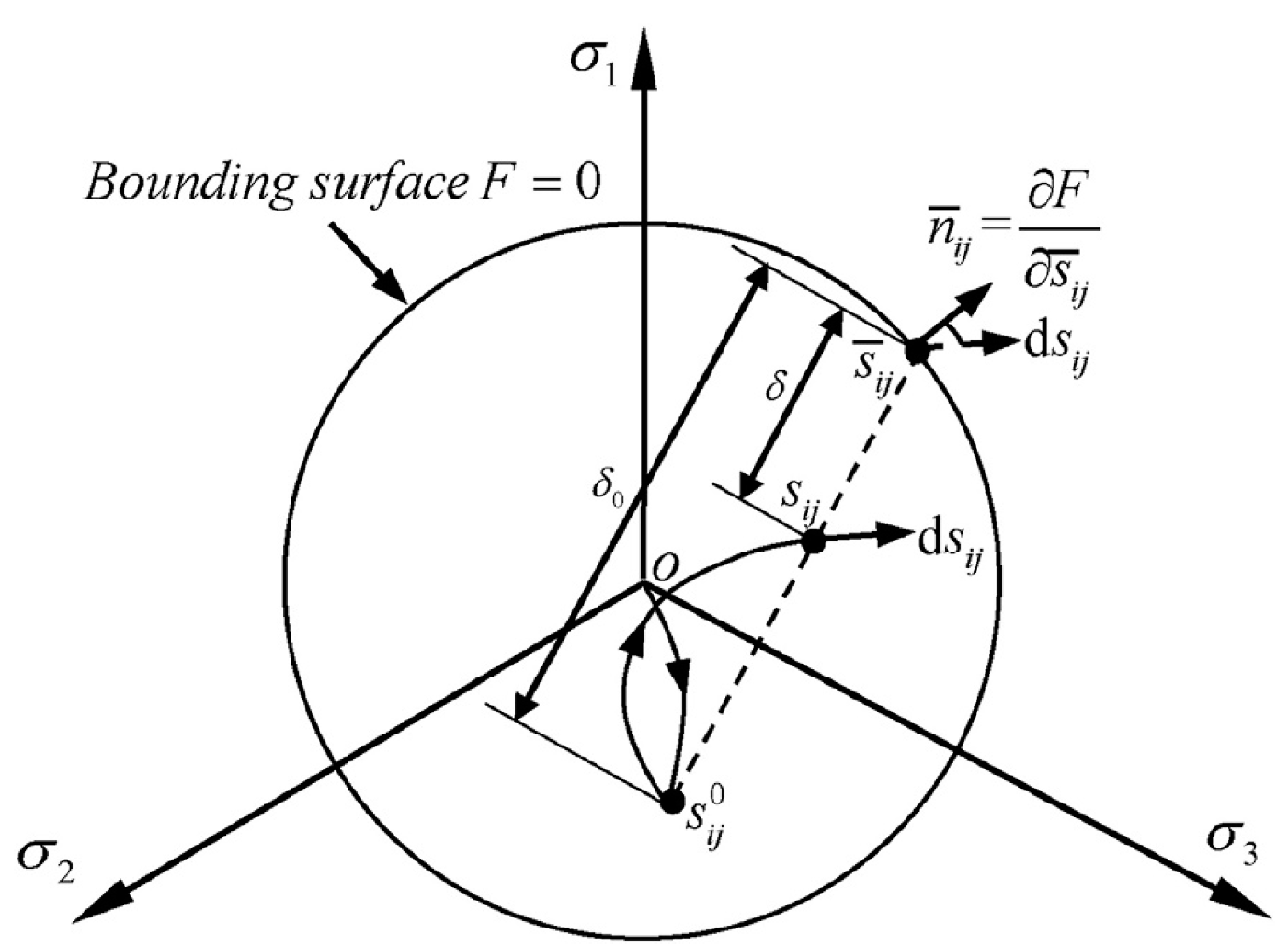
2. Models and Methodology
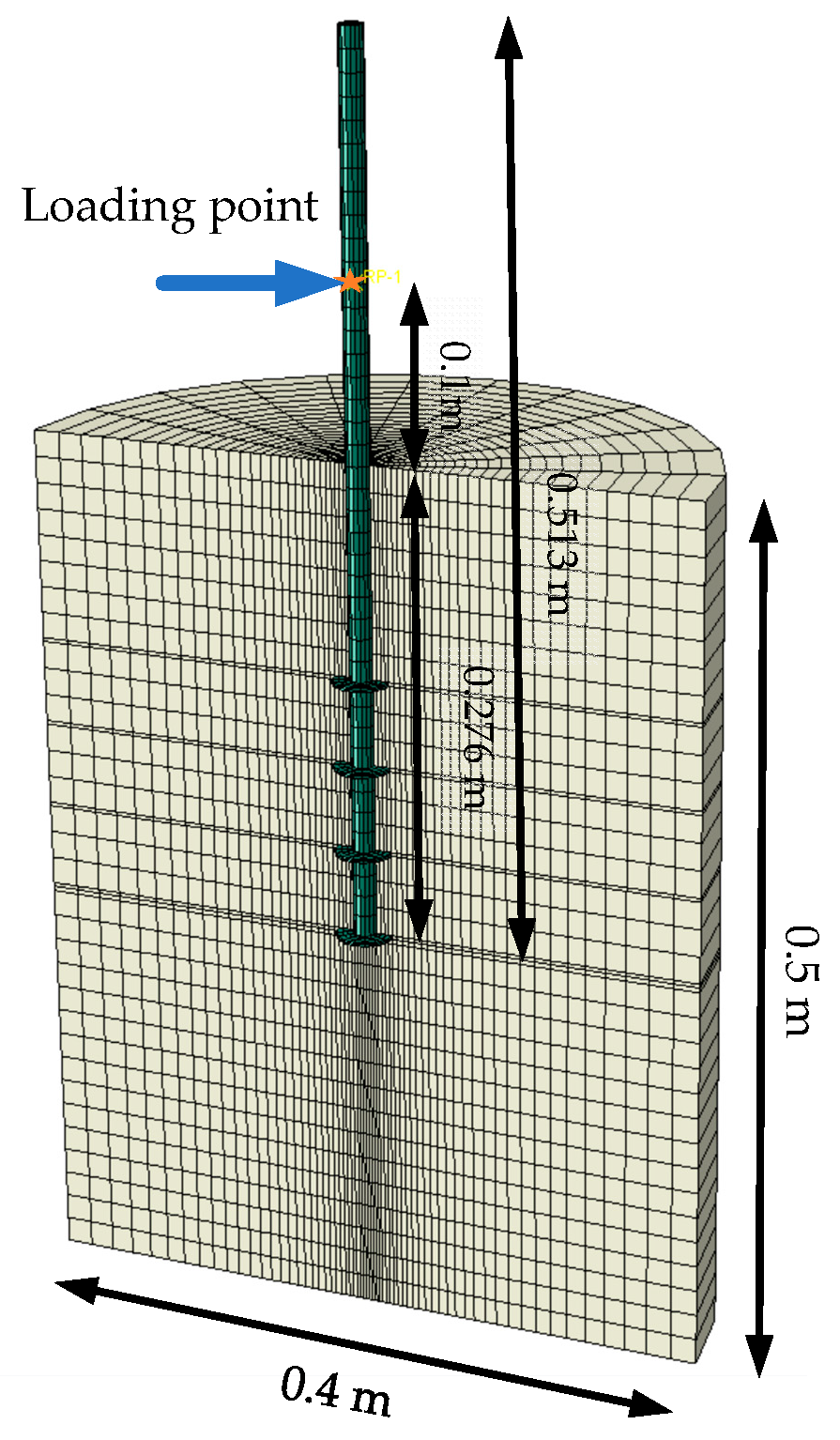
2.1. Numerical Model of the Helical Pile for Offshore PV
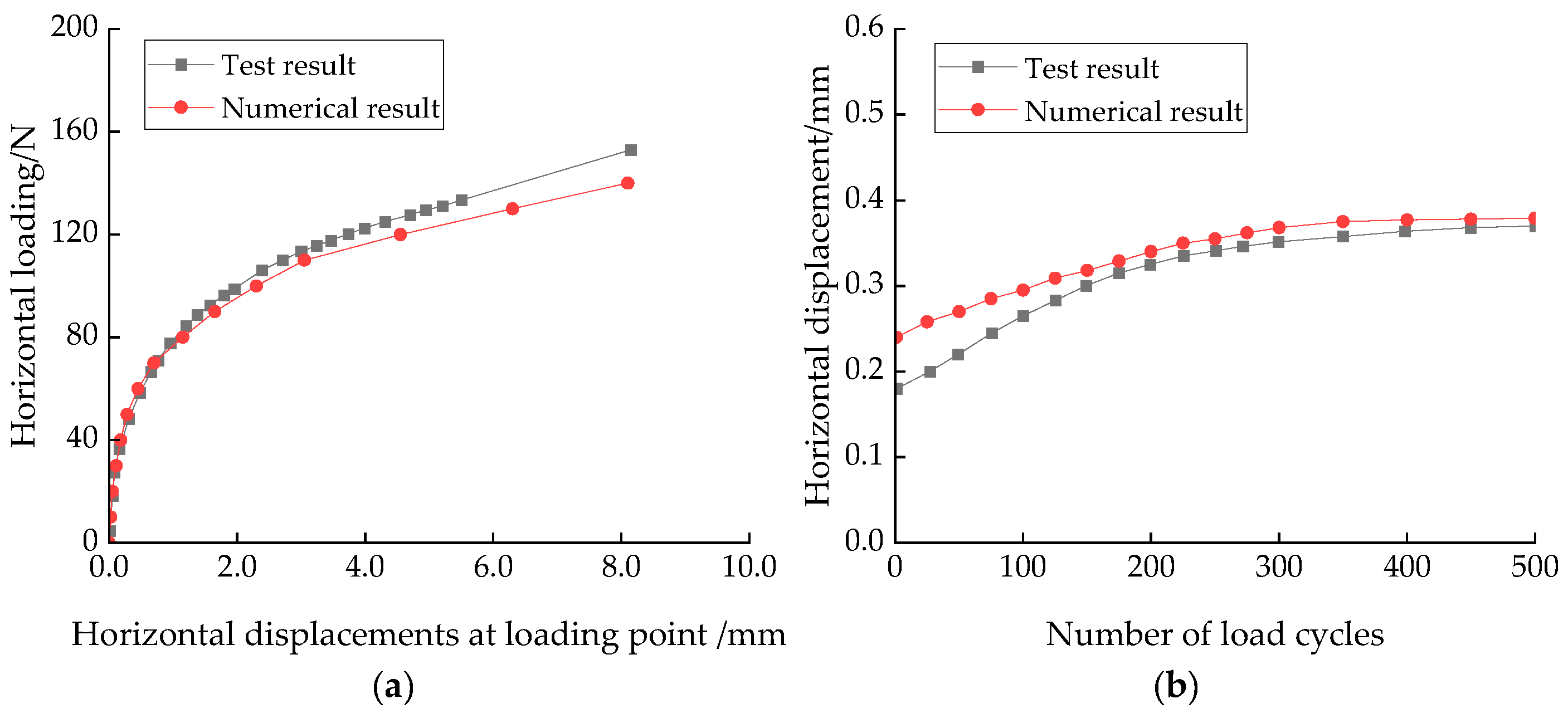
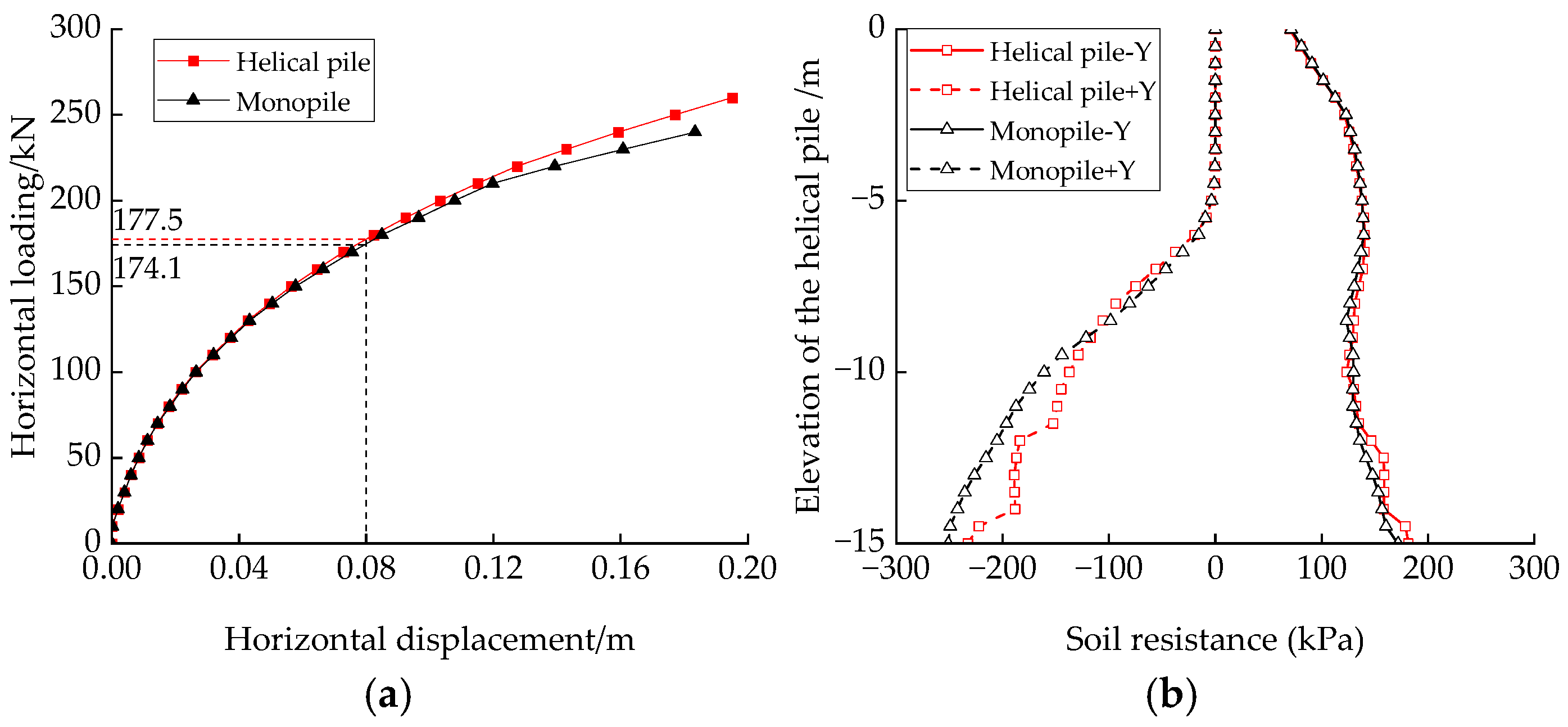
2.2. Validation of the Numerical Analysis Methods
3. Results
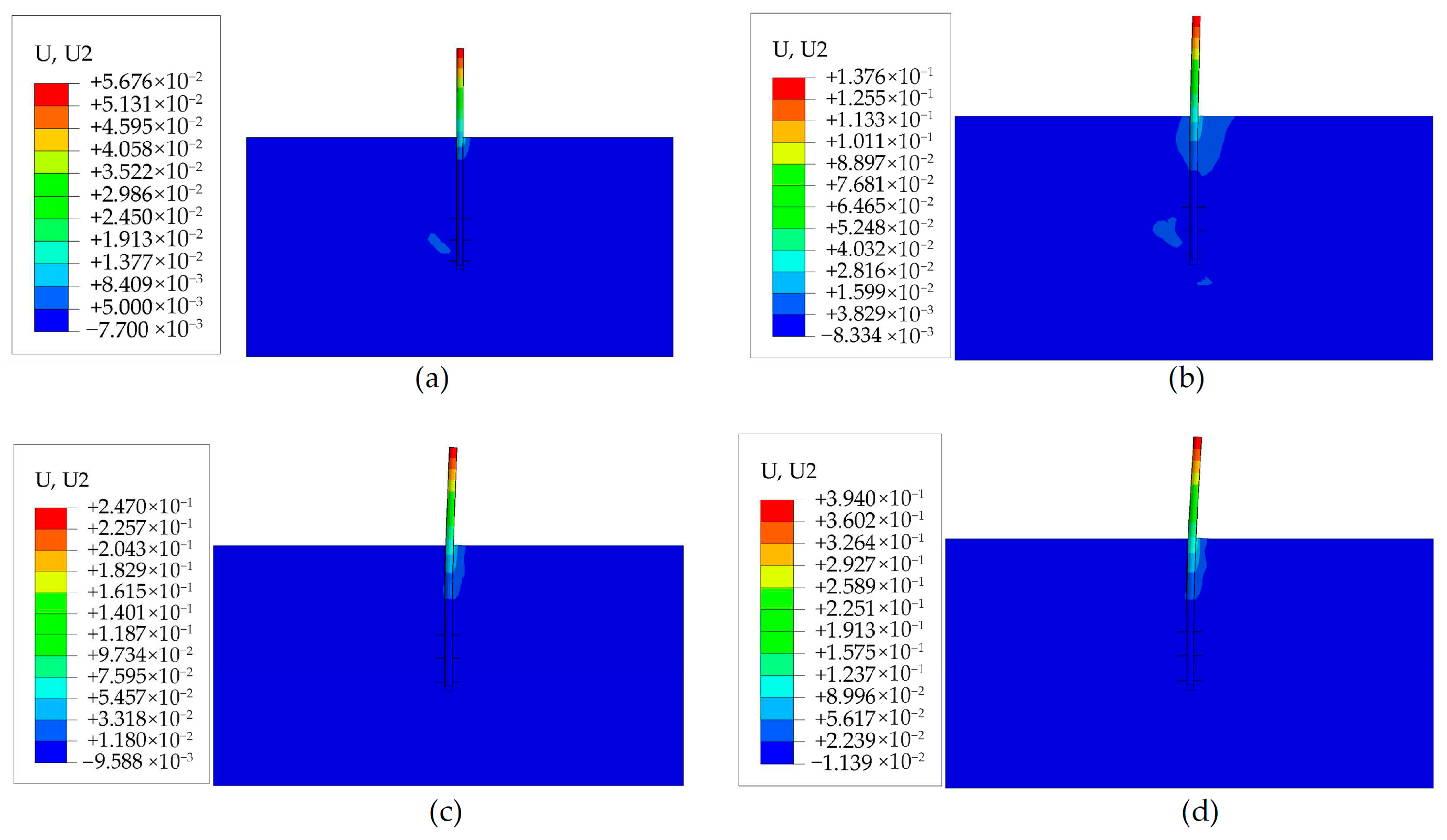
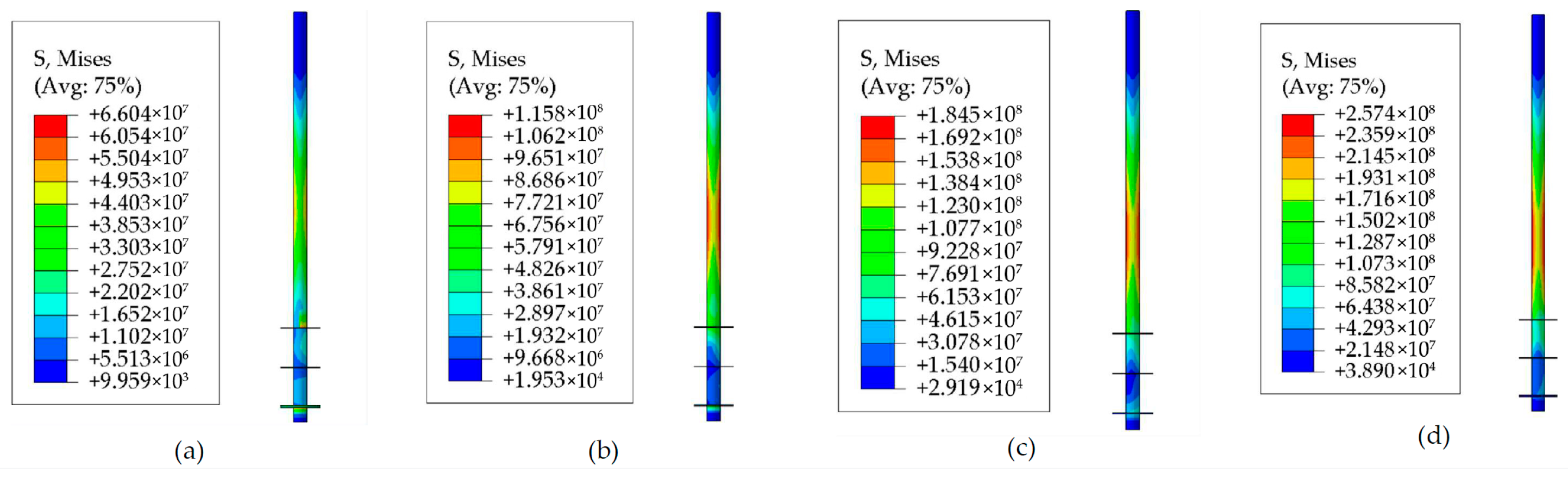
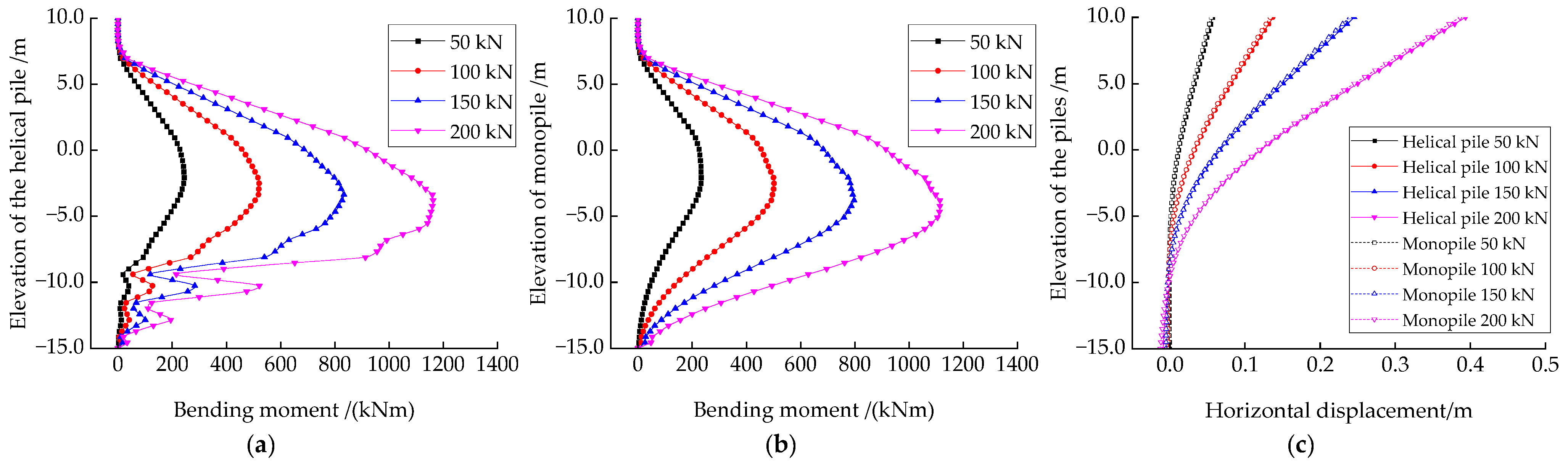
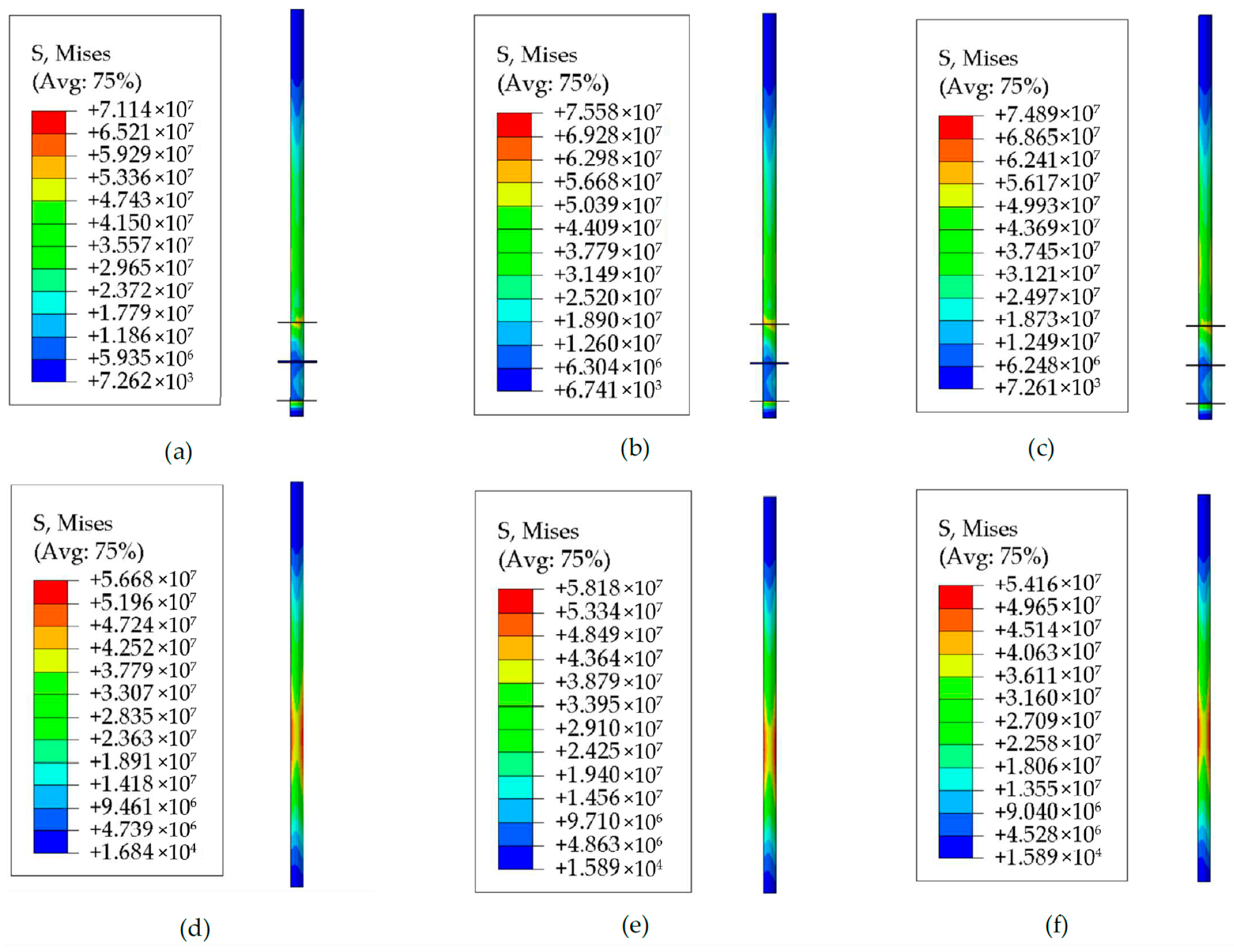
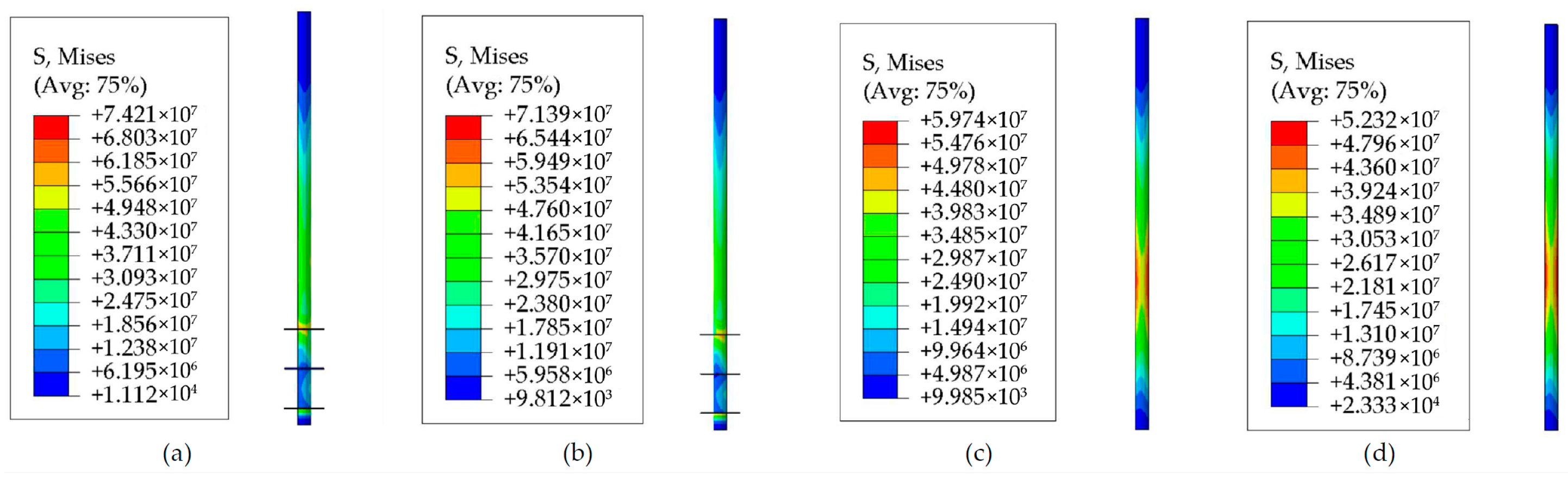
3.1. Bearing Performances of the Helical Pile under Horizontal Monotonic Loadings
3.2. Bearing Performances of the Helical Pile under Horizontal Cyclic Loadings
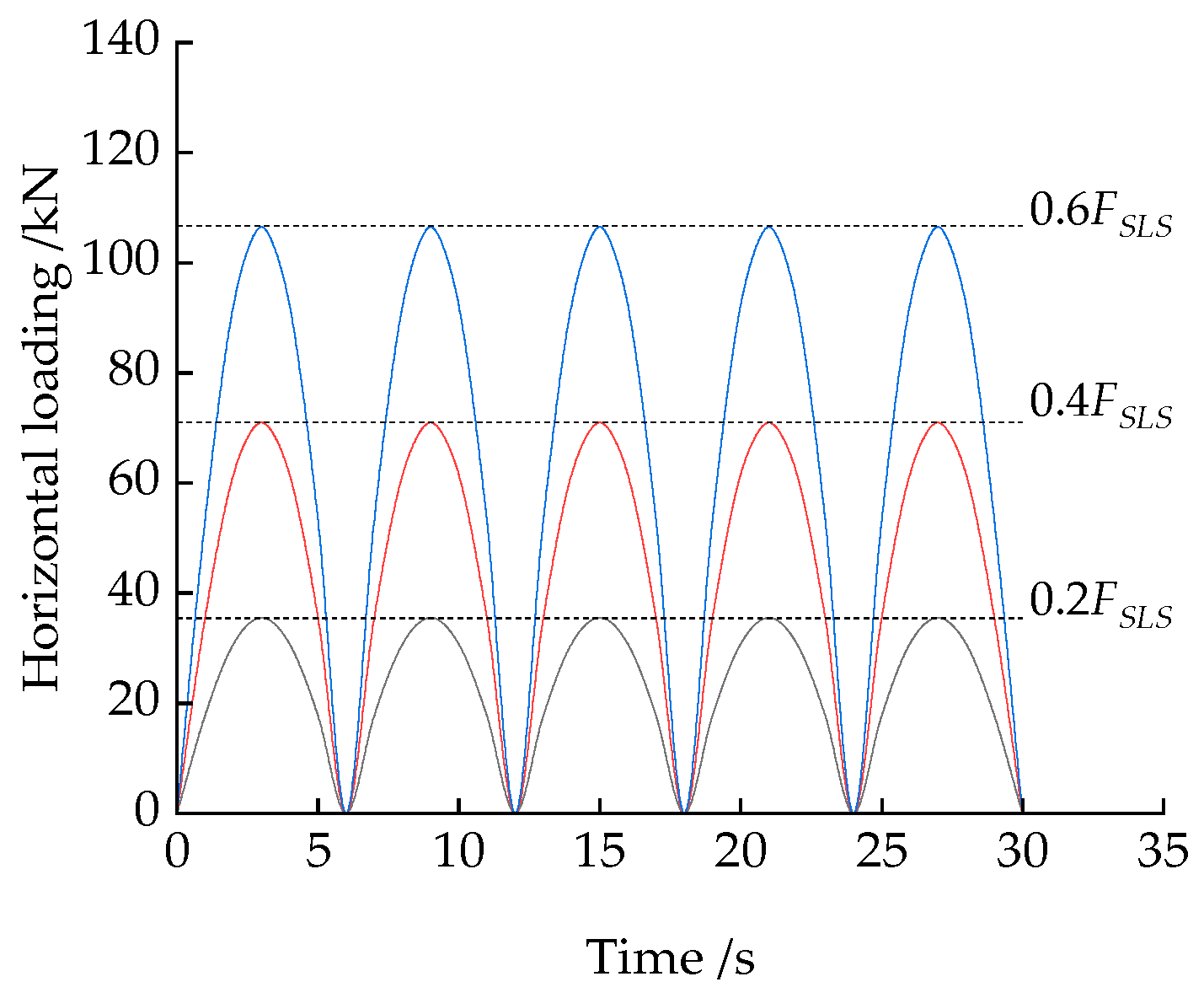
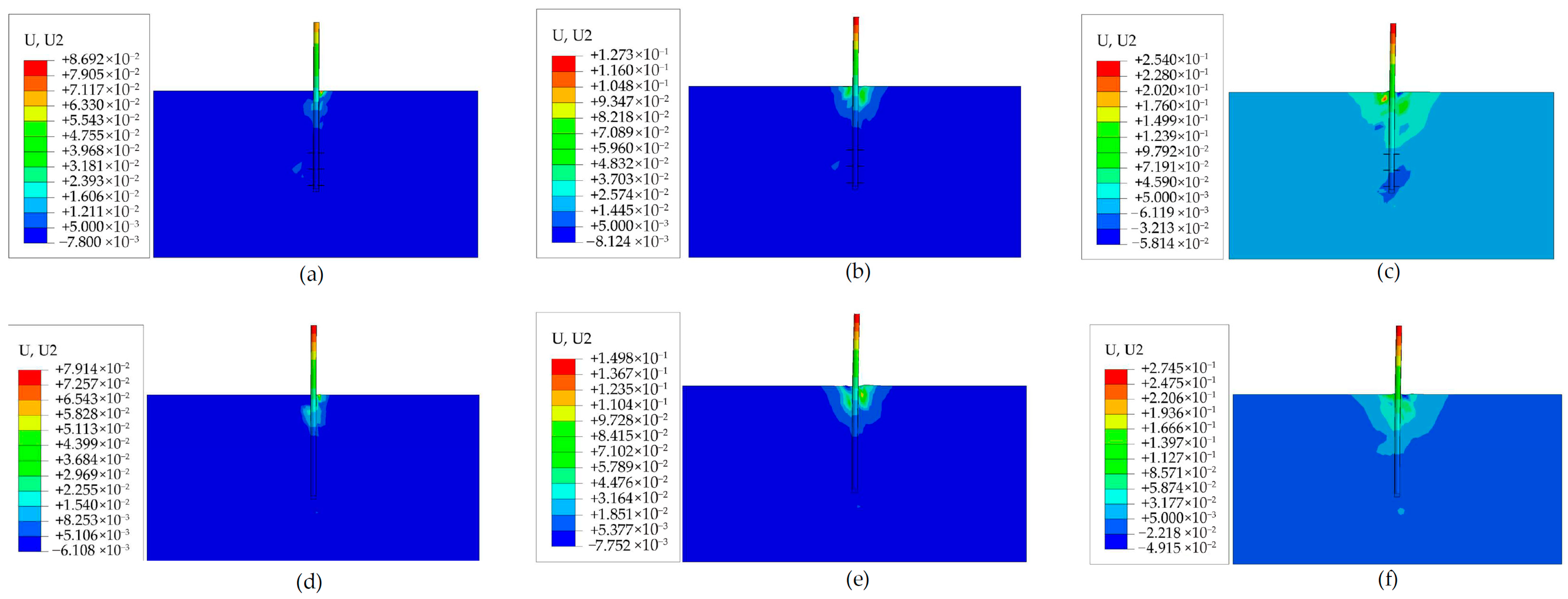
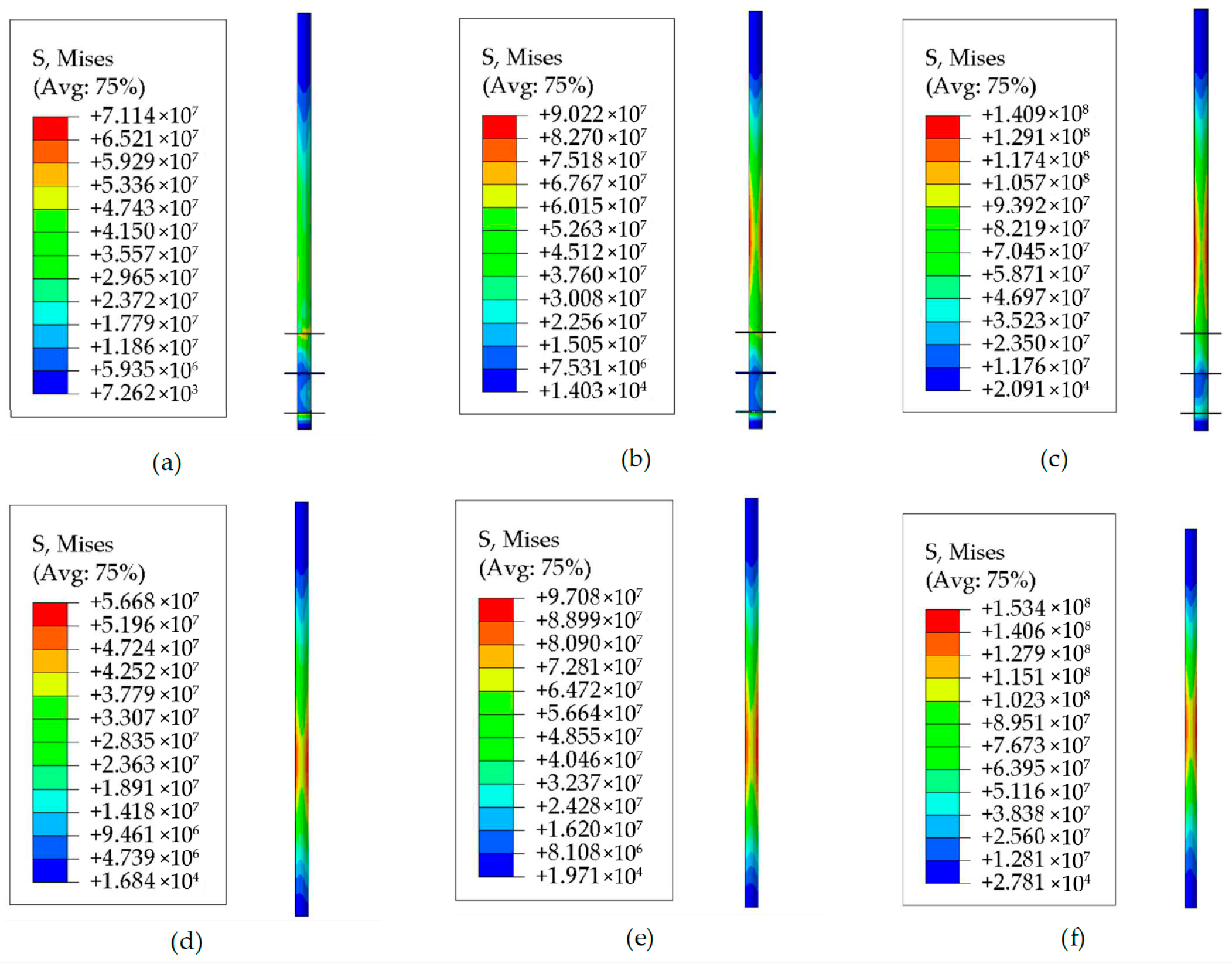
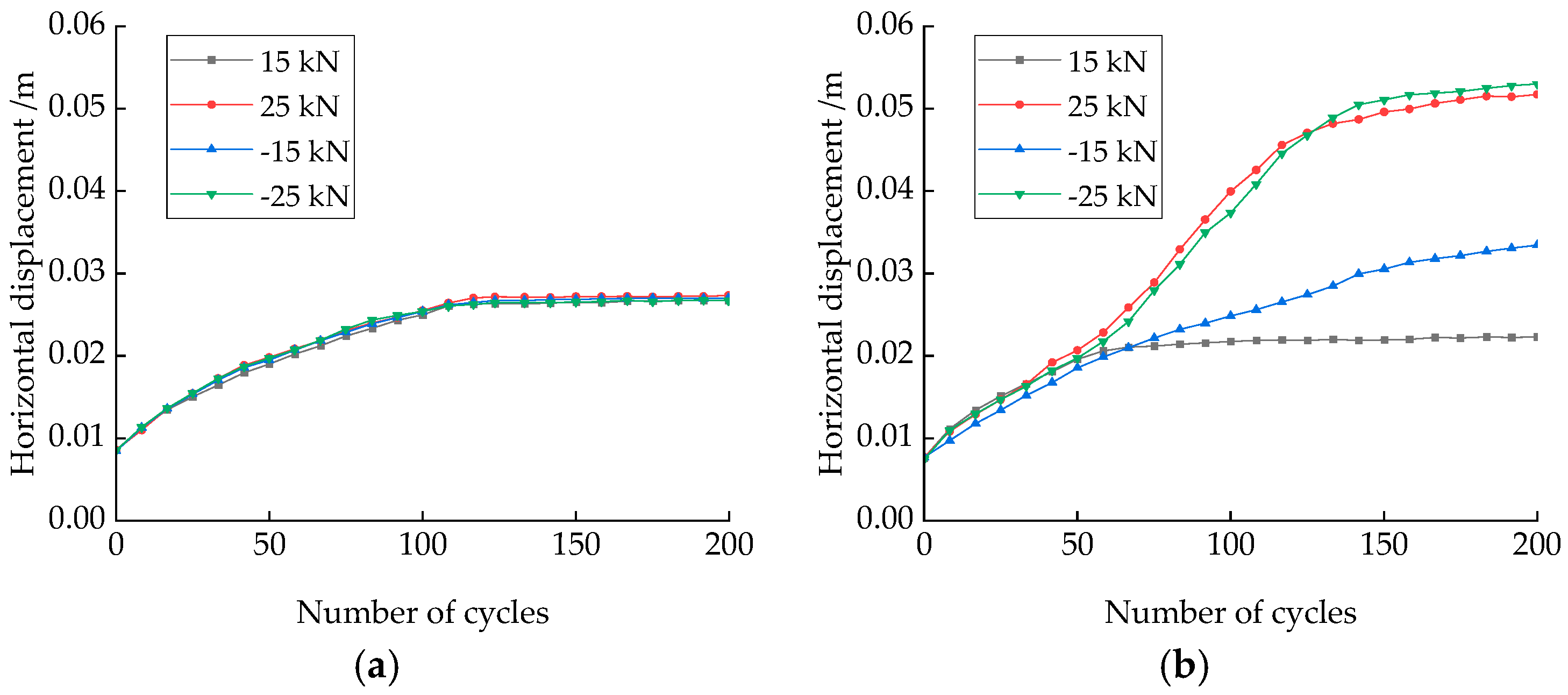
3.2.1. Effects of Cyclic Loadings Amplitude on Horizontal Bearing Performances
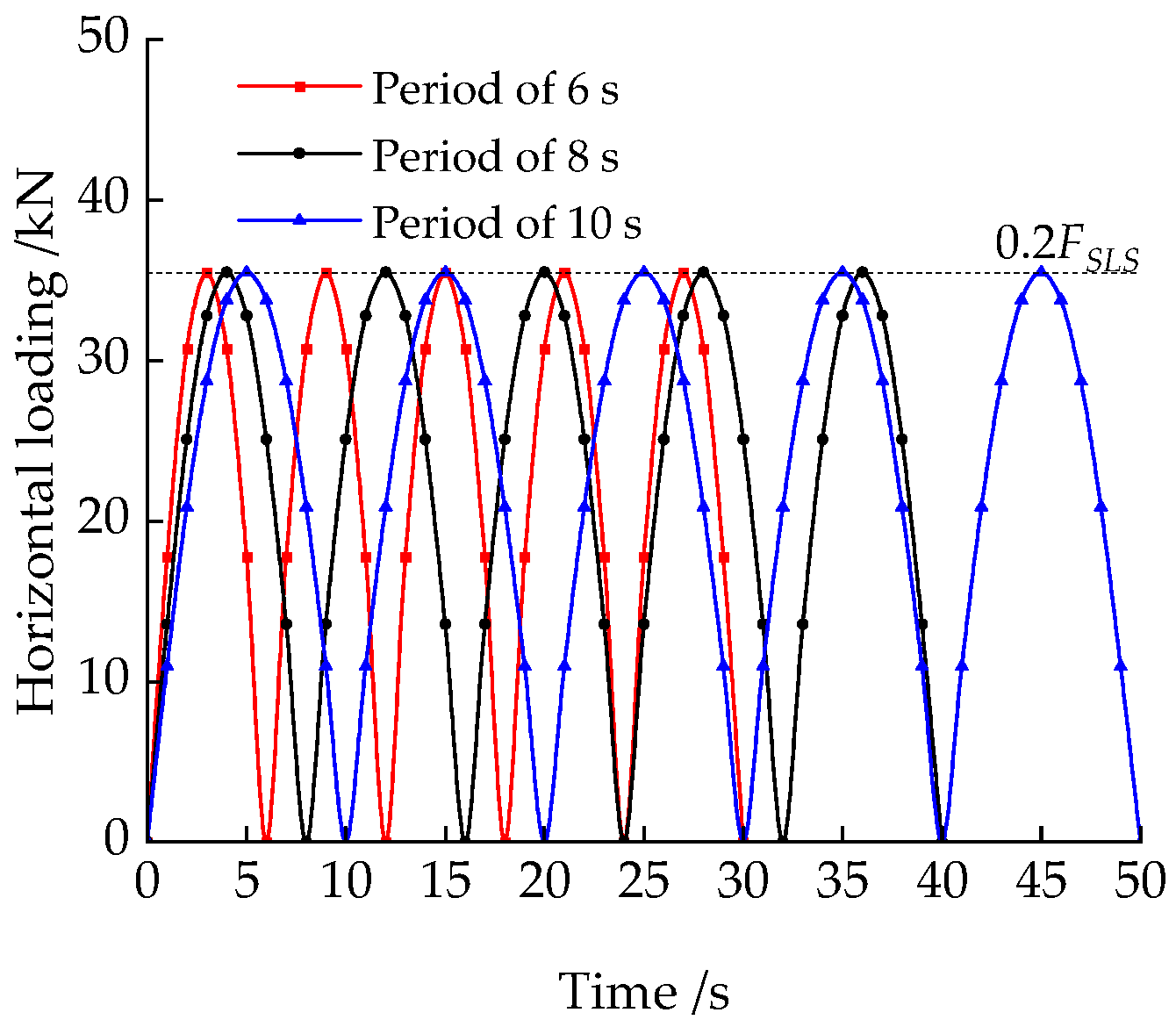
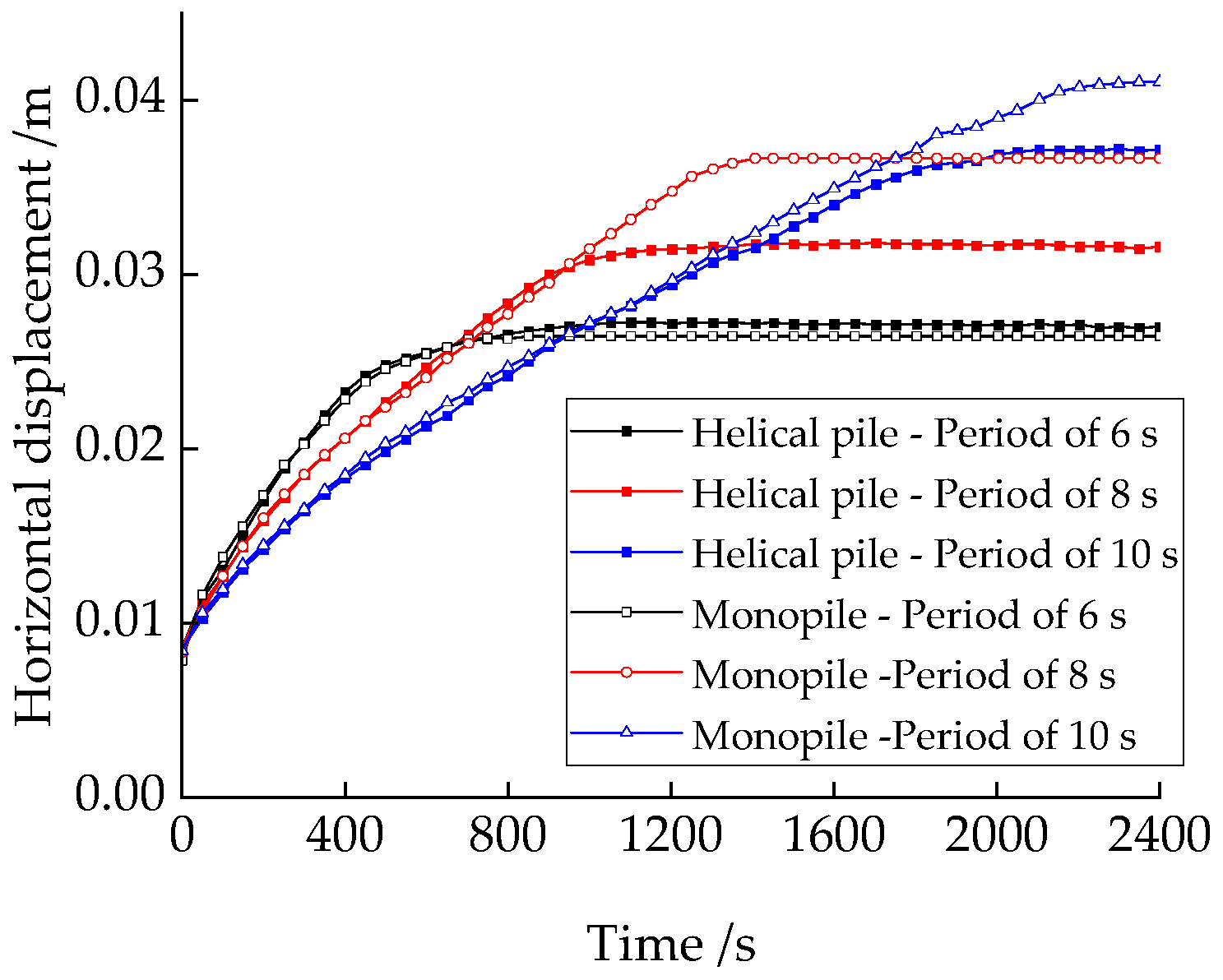
3.2.2. Effects of Cyclic Loadings Period on Horizontal Bearing Performances
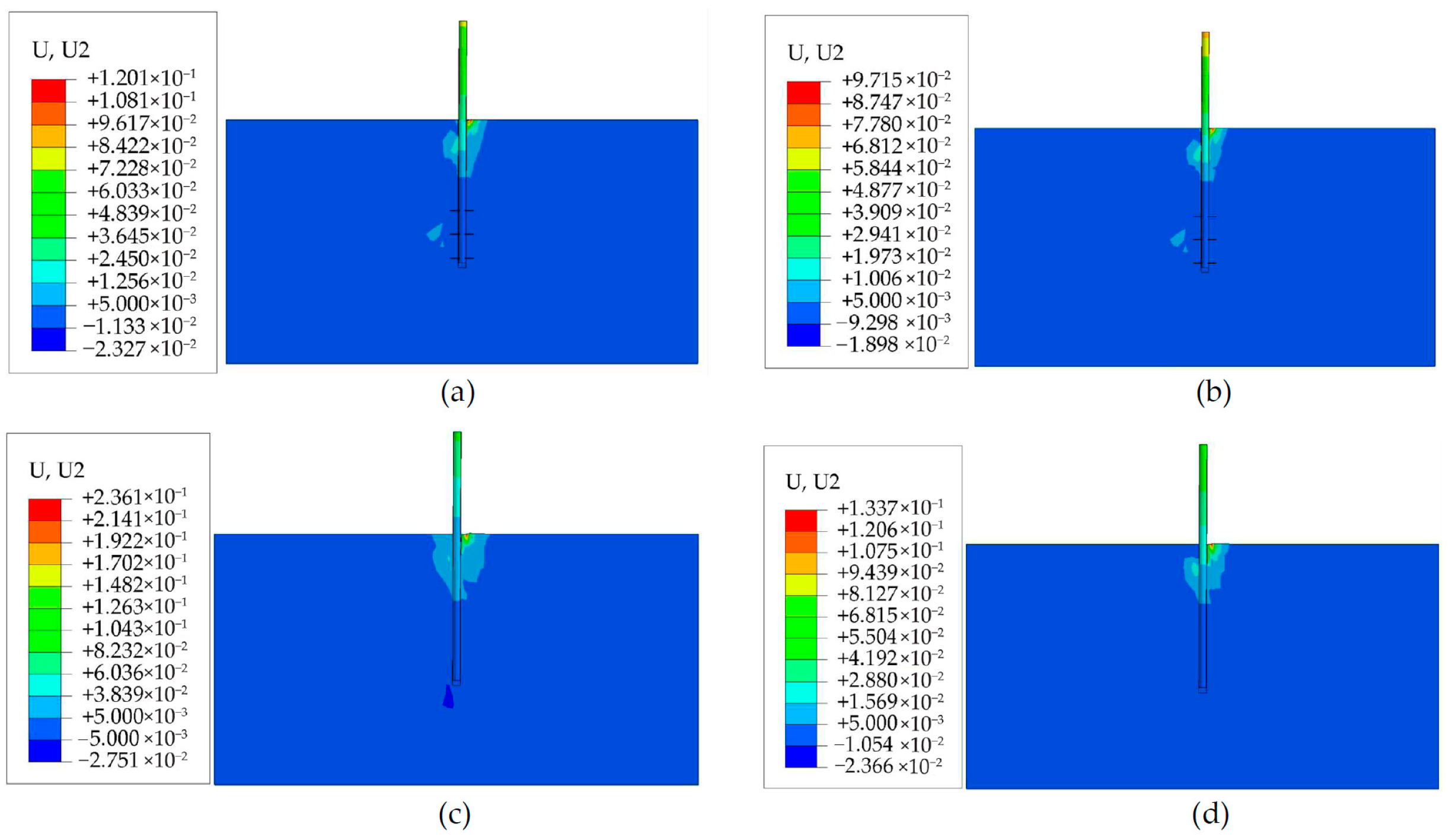
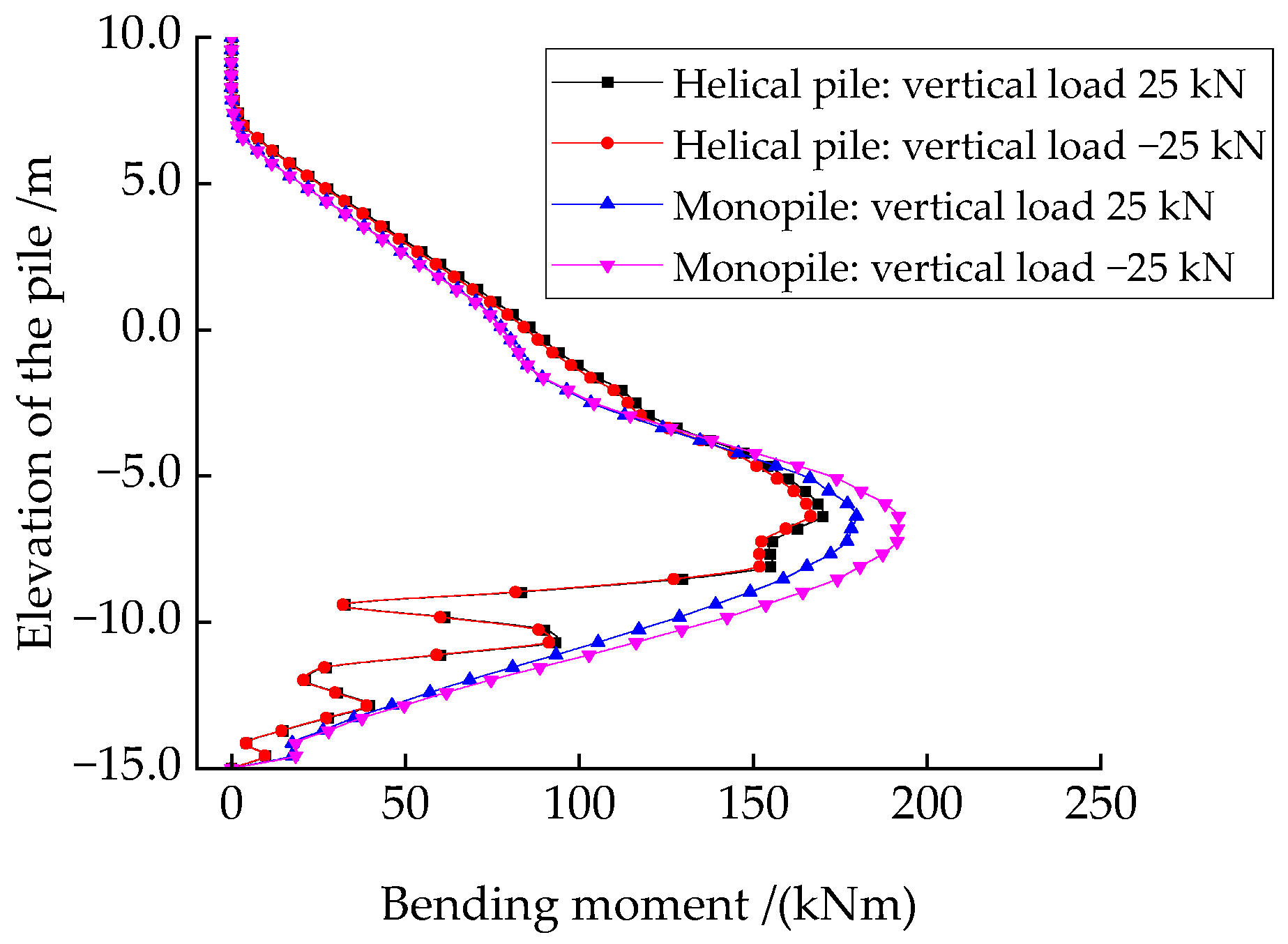
3.2.3. Effects of Vertical Loads on Horizontal Bearing Performances
4. Conclusions
- Under horizontal monotonic loading, the bearing performance of the helical pile and monopile with the same diameter shows little difference in the serviceability limit state.
- Under small horizontal cyclic loadings, the stiffness of the soil around piles stabilizes after a certain number of cycles, and the horizontal displacement no longer increases. Under larger cyclic loads, the stiffness of the soil degrades significantly, leading to more significant accumulated plastic deformation. The horizontal bearing capacity of the helical pile under cyclic loading is approximately 60% of its capacity under monotonic loading, whereas the monopile’s capacity under cyclic loading is less than 60% of its monotonic loading capacity.
- The shorter the cyclic loading period, the greater the initial horizontal displacement accumulation, and the sooner stability is reached. Conversely, the longer the cyclic loading period, the smaller the initial horizontal displacement accumulation, but the accumulated displacement at stabilization is more significant.
- The horizontal cyclic bearing performance of the monopile is greatly affected by vertical loads. However, due to the uplift and compressive resistance provided by the blades, vertical loads have little effect on the horizontal cyclic bearing performance of the helical pile, which exhibits a more stable horizontal cyclic bearing performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Lund, P.D. Review of Recent Offshore Photovoltaics Development. Energies 2022, 15, 7462. [Google Scholar] [CrossRef]
- Ghosh, A. A comprehensive review of water based PV: Flotavoltaics, under water, offshore & canal top. Ocean Eng. 2023, 281, 115044. [Google Scholar]
- Kjeldstad, T.; Lindholm, D.; Marstein, E.; Selj, J. Cooling of floating photovoltaics and the importance of water temperature. Sol. Energy 2021, 218, 544–551. [Google Scholar] [CrossRef]
- Du, J.; Zhang, D.; Zhang, Y.; Xu, K.; Chang, A.; Zhao, S. Design and comparative analysis of alternative mooring systems for offshore floating photovoltaics arrays in ultra-shallow water with significant tidal range. Ocean Eng. 2024, 302, 117649. [Google Scholar] [CrossRef]
- Zheng, Z.; Jin, P.; Huang, Q.; Zhou, B.; Xiang, R.; Zhou, Z.; Huang, L. Motion response and energy harvesting of multi-module floating photovoltaics in seas. Ocean Eng. 2024, 310, 118760. [Google Scholar] [CrossRef]
- Feng, S.-J.; Fu, W.-D.; Chen, H.-X.; Li, H.-X.; Xie, Y.-L.; Lv, S.-F.; Li, J. Field tests of micro screw anchor piles under different loading conditions at three soil sites. Bull. Eng. Geol. Environ. 2021, 80, 127–144. [Google Scholar] [CrossRef]
- Vignesh, V.; Mayakrishnan, M. Design parameters and behavior of helical piles in cohesive soils—A review. Arab. J. Geosci. 2020, 13, 1194. [Google Scholar] [CrossRef]
- Byrne, B.W.; Houlsby, G.T. Helical piles: An innovative foundation design option for offshore wind turbines. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140081. [Google Scholar] [CrossRef]
- Spagnoli, G.; de Hollanda Cavalcanti Tsuha, C. A review on the behavior of helical piles as a potential offshore foundation system. Mar. Georesour. Geotechnol. 2020, 38, 1013–1036. [Google Scholar] [CrossRef]
- Kumar, T.J.; Deendayal, R.; Sahoo, S.K. Behaviour of a laterally loaded rigid helical pile located on a sloping ground surface. Mar. Georesour. Geotechnol. 2024, 1–20. [Google Scholar] [CrossRef]
- Ren, G.; Wang, Y.; Tang, Y.; Zhao, Q.; Qiu, Z.; Luo, W.; Ye, Z. Research on Lateral Bearing Behavior of Spliced Helical Piles with the SPH Method. Appl. Sci. 2022, 12, 8215. [Google Scholar] [CrossRef]
- Lin, Y.F.; Xiao, J.D.; Le, C.H.; Zhang, P.Y.; Chen, Q.S.; Ding, H.Y. Bearing Characteristics of Helical Pile Foundations for Offshore Wind Turbines in Sandy Soil. J. Mar. Sci. Eng. 2022, 10, 889. [Google Scholar] [CrossRef]
- Elkasabgy, M.; El Naggar, H. Axial compressive response of large-capacity helical and driven steel piles in cohesive soil. Can. Geotech. J. 2015, 52, 224–243. [Google Scholar] [CrossRef]
- Ding, H.; Wang, L.; Zhang, P.; Le, C. Study on the Lateral Bearing Capacity of Single-Helix Pile for Offshore Wind Power. In Proceedings of the Volume 9: Offshore Geotechnics; Honoring Symposium for Professor Bernard Molin on Marine and Offshore Hydrodynamics, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Wang, L.; Zhang, P.Y.; Ding, H.Y.; Tian, Y.H.; Qi, X. The uplift capacity of single-plate helical pile in shallow dense sand including the influence of installation. Mar. Struct. 2020, 71, 102697. [Google Scholar] [CrossRef]
- Rao, S.N.; Prasad, Y.V.S.N. Behavior of a helical anchor under vertical repetitive loading. Mar. Geotechnol. 1991, 10, 203–228. [Google Scholar] [CrossRef]
- Wada, M.; Tokimatsu, K.; Maruyama, S.; Sawaishi, M. Effects of cyclic vertical loading on bearing and pullout capacities of piles with continuous helix wing. Soils Found. 2017, 57, 141–153. [Google Scholar] [CrossRef]
- Hao, D.; Che, J.; Chen, R.; Zhang, X.; Yuan, C.; Chen, X. Experimental Investigation on Behavior of Single-Helix Anchor in Sand Subjected to Uplift Cyclic Loading. J. Mar. Sci. Eng. 2022, 10, 1338. [Google Scholar] [CrossRef]
- Yang, X.Y.; Wang, C.Z.; Cao, S.; Wang, F.X.; Wu, W.B.; Luongo, A.; Zhao, Y.L.; Wang, Y.X.; Lin, H.; Guo, P.P. Lateral Dynamic Response of Helical Pile in Viscoelastic Foundation Considering Shear Deformation. Appl. Sci. 2023, 13, 12220. [Google Scholar] [CrossRef]
- Al-Baghdadi, T.A.; Brown, M.J.; Knappett, J.A.; Al-Defae, A.H. Effects of vertical loading on lateral screw pile performance. Proc. Inst. Civ. Eng. Geotech. Eng. 2017, 170, 259–272. [Google Scholar] [CrossRef]
- American Petroleum Institute. Planning, Designing, and Constructing Fixed Offshore Platforms: Working Stress Design; American Petroleum Institute: Washington, DC, USA, 2020. [Google Scholar]
- Merifield, R.S. Ultimate Uplift Capacity of Multiplate Helical Type Anchors in Clay. J. Geotech. Geoenviron. Eng. 2011, 137, 704–716. [Google Scholar] [CrossRef]
- Venkatesan, V.; Mayakrishnan, M. Behavior of Mono Helical Pile Foundation in Clays under Combined Uplift and Lateral Loading Conditions. Appl. Sci. 2022, 12, 6827. [Google Scholar] [CrossRef]
- George, B.E.; Banerjee, S.; Gandhi, S.R. Numerical analysis of helical piles in cohesionless soil. Int. J. Geotech. Eng. 2020, 14, 361–375. [Google Scholar] [CrossRef]
- Cheng, X.; Du, X.; Lu, D.; Ma, C.; Wang, P. A simple single bounding surface model for undrained cyclic behaviours of saturated clays and its numerical implementation. Soil Dyn. Earthq. Eng. 2020, 139, 106389. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, T.; Zhang, J.; Liu, Z.; Cheng, W. Finite element analysis of cyclic lateral responses for large diameter monopiles in clays under different loading patterns. Comput. Geotech. 2021, 134, 104104. [Google Scholar] [CrossRef]
- Das, B.M. Advanced Soil Mechanics, 5th ed.; CRC Press: London, UK, 2019. [Google Scholar]
- Prasad, Y.V.S.N.; Rao, S.N. Pullout behaviour of model pile and helical pile anchors Subjected to lateral cyclic loading. Can. Geotech. J. 1994, 31, 110–119. [Google Scholar] [CrossRef]
- Byrne, B.W.; McAdam, R.A.; Burd, H.J.; Houlsby, G.T.; Martin, C.M.; Gavin, K.; Doherty, P.; Igoe, D.; Zdravkovi, L.; Taborda, D.M.G.; et al. Field testing of large diameter piles under lateral loading for offshore wind applications. In Proceedings of the Geotechnical Engineering for Infrastructure and Development, Edinburgh, UK, 13–17 September 2015; ICE Publishing: London, UK, 2015; Volume 1–7, pp. 1255–1260. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cong, X.; Li, Z.; An, Z.; Liu, J.; Han, Y. Bearing Performance of a Helical Pile for Offshore Photovoltaic under Horizontal Cyclic Loading. J. Mar. Sci. Eng. 2024, 12, 1826. https://doi.org/10.3390/jmse12101826
Cong X, Li Z, An Z, Liu J, Han Y. Bearing Performance of a Helical Pile for Offshore Photovoltaic under Horizontal Cyclic Loading. Journal of Marine Science and Engineering. 2024; 12(10):1826. https://doi.org/10.3390/jmse12101826
Chicago/Turabian StyleCong, Xinfu, Zhe Li, Zhonghai An, Jiangxue Liu, and Yanqing Han. 2024. "Bearing Performance of a Helical Pile for Offshore Photovoltaic under Horizontal Cyclic Loading" Journal of Marine Science and Engineering 12, no. 10: 1826. https://doi.org/10.3390/jmse12101826
APA StyleCong, X., Li, Z., An, Z., Liu, J., & Han, Y. (2024). Bearing Performance of a Helical Pile for Offshore Photovoltaic under Horizontal Cyclic Loading. Journal of Marine Science and Engineering, 12(10), 1826. https://doi.org/10.3390/jmse12101826




