UUV-Assisted Icebreaking Application in Polar Environments Using GA-SPSO
Abstract
:1. Introduction
- Integration of algorithmic advantages. By merging the global search capabilities of SPSO with the local optimization strengths of GA, the proposed GA-SPSO algorithm not only ensures the safety of the navigator but also adeptly addresses the planning challenges in the intricate polar ice environment.
- UUV-assisted icebreaking. This paper introduces a novel icebreaking path-planning method that utilizes the high-accuracy environmental sensing capabilities of UUVs to provide real-time path optimization recommendations for icebreaking vessels. A principal prototype is also designed, enhancing the dynamic adaptability of path planning and navigation safety.
- Real-time path optimization. The GA-SPSO algorithm enables real-time path optimization in the complex and dynamic polar ice environment, significantly reducing the energy consumption and operational time of the icebreaker while concurrently improving its obstacle avoidance capabilities.
2. Relevant Foundations
2.1. Safe Path-Planning Algorithm Basis
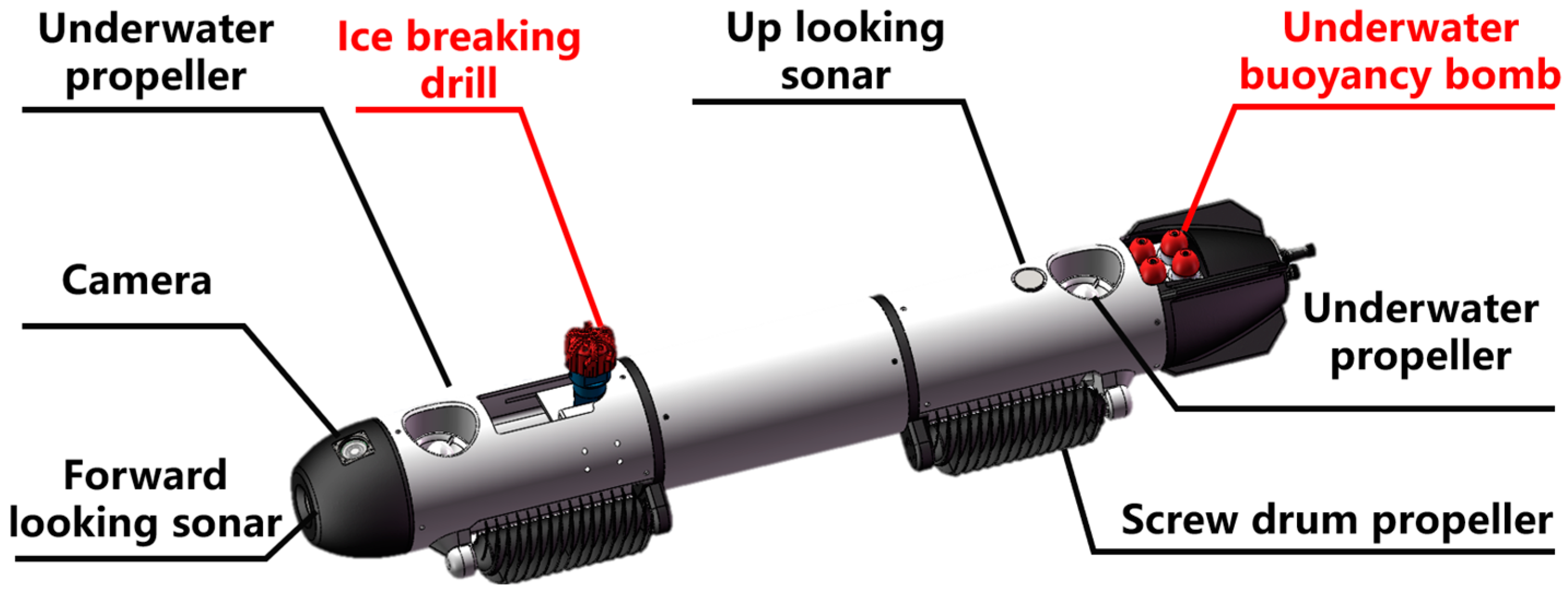
2.2. Design and Application of Unmanned Underwater Vehicles (UUVs)
3. Modeling of the Path Planning Problem
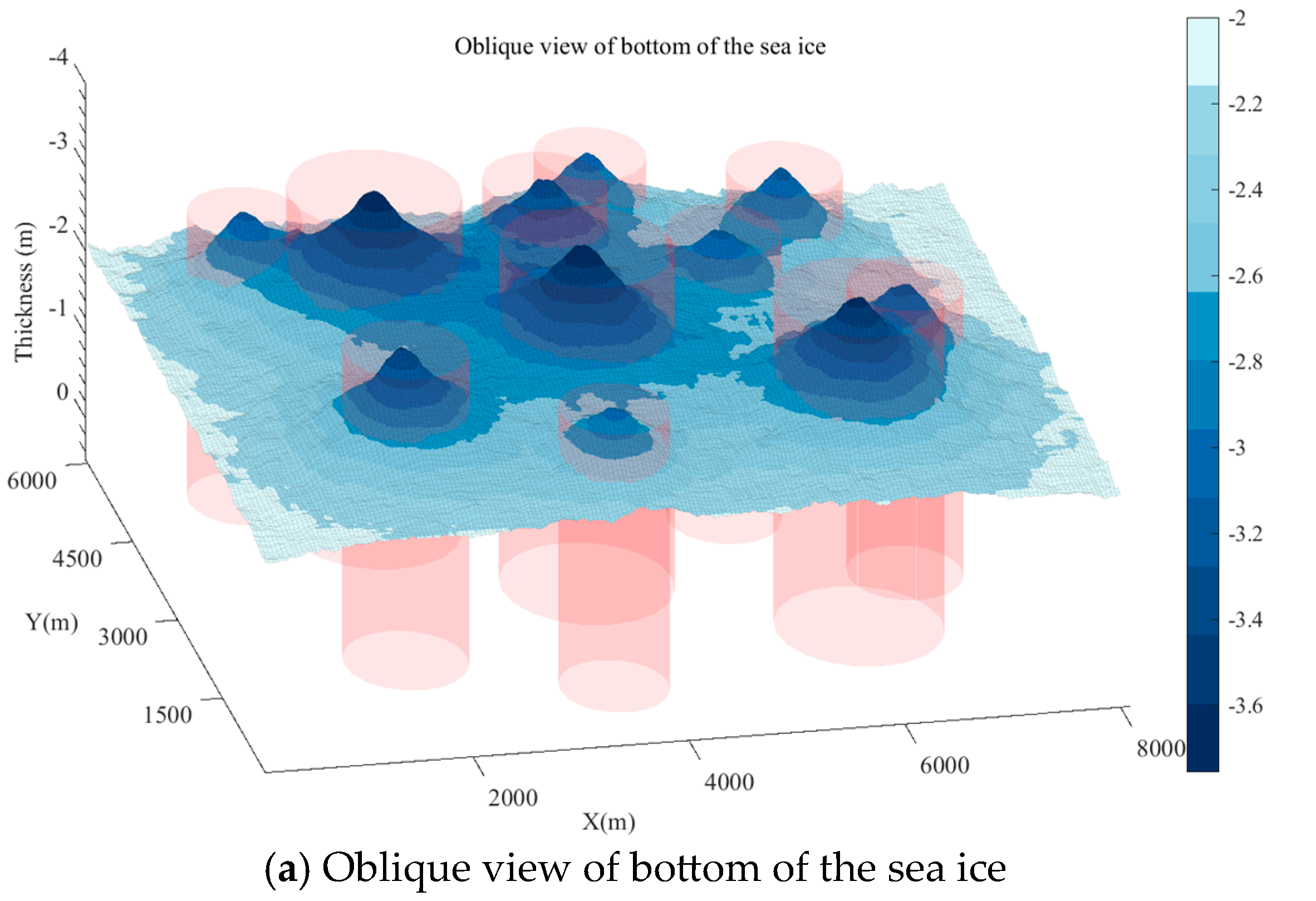
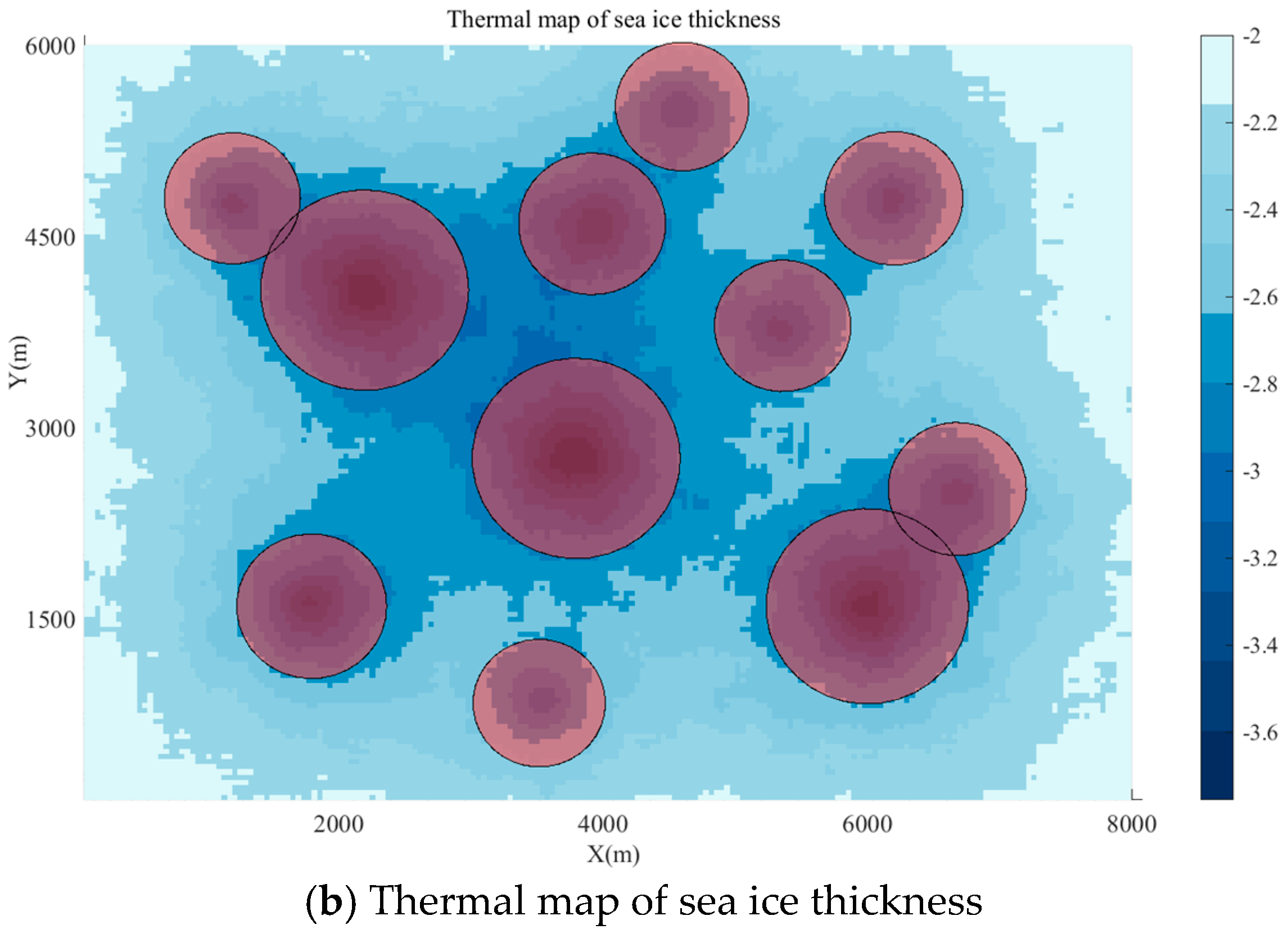
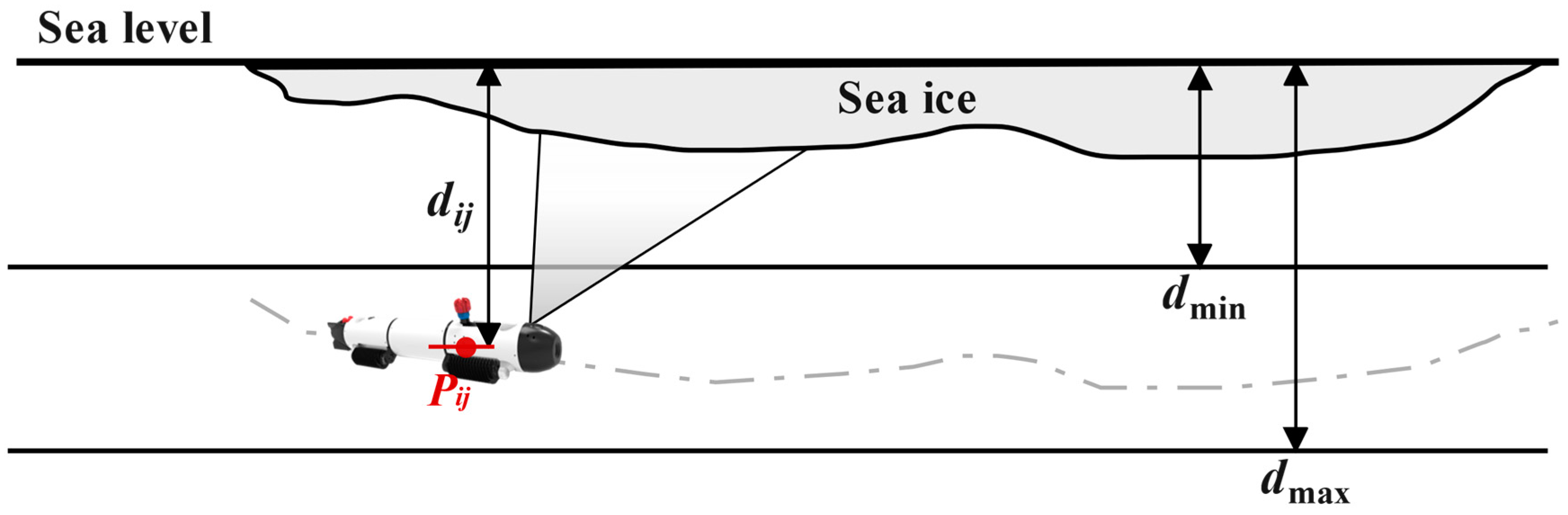
3.1. Establishment of Sea Ice Hazard
- The sea ice is approximately 2 m thick, typical for icebreaking scenarios.
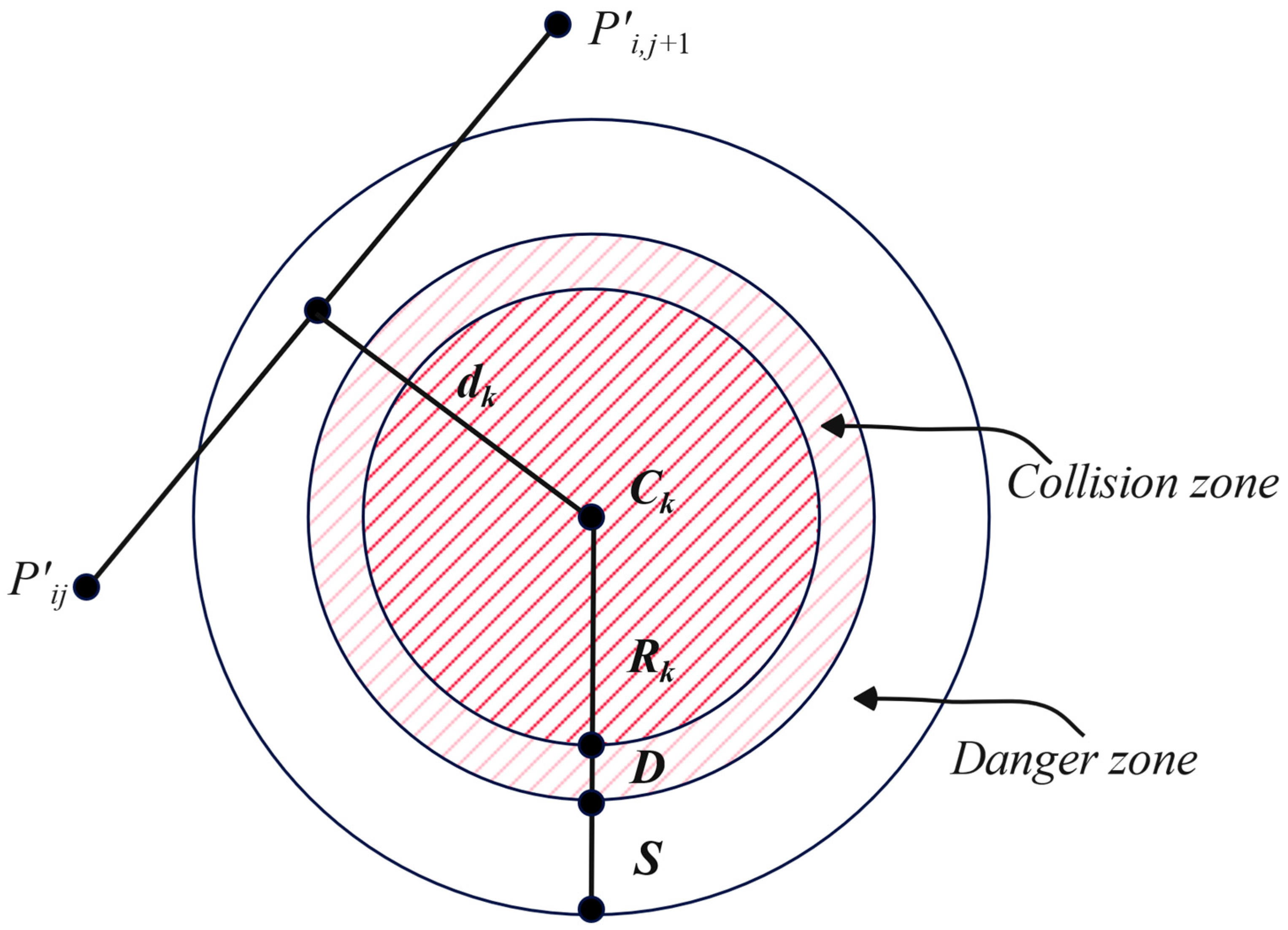
- The threat range of the ice keels is modeled as a cylindrical area during path planning.
- Ice keels are independently and randomly distributed across the sea ice map.
3.2. Construction of Cost Functions
3.2.1. Path Length Cost
3.2.2. Threat Cost
3.2.3. Depth Cost
3.2.4. Smooth Cost
3.2.5. Icebreaking Cost
4. Algorithm Design for GA-SPSO
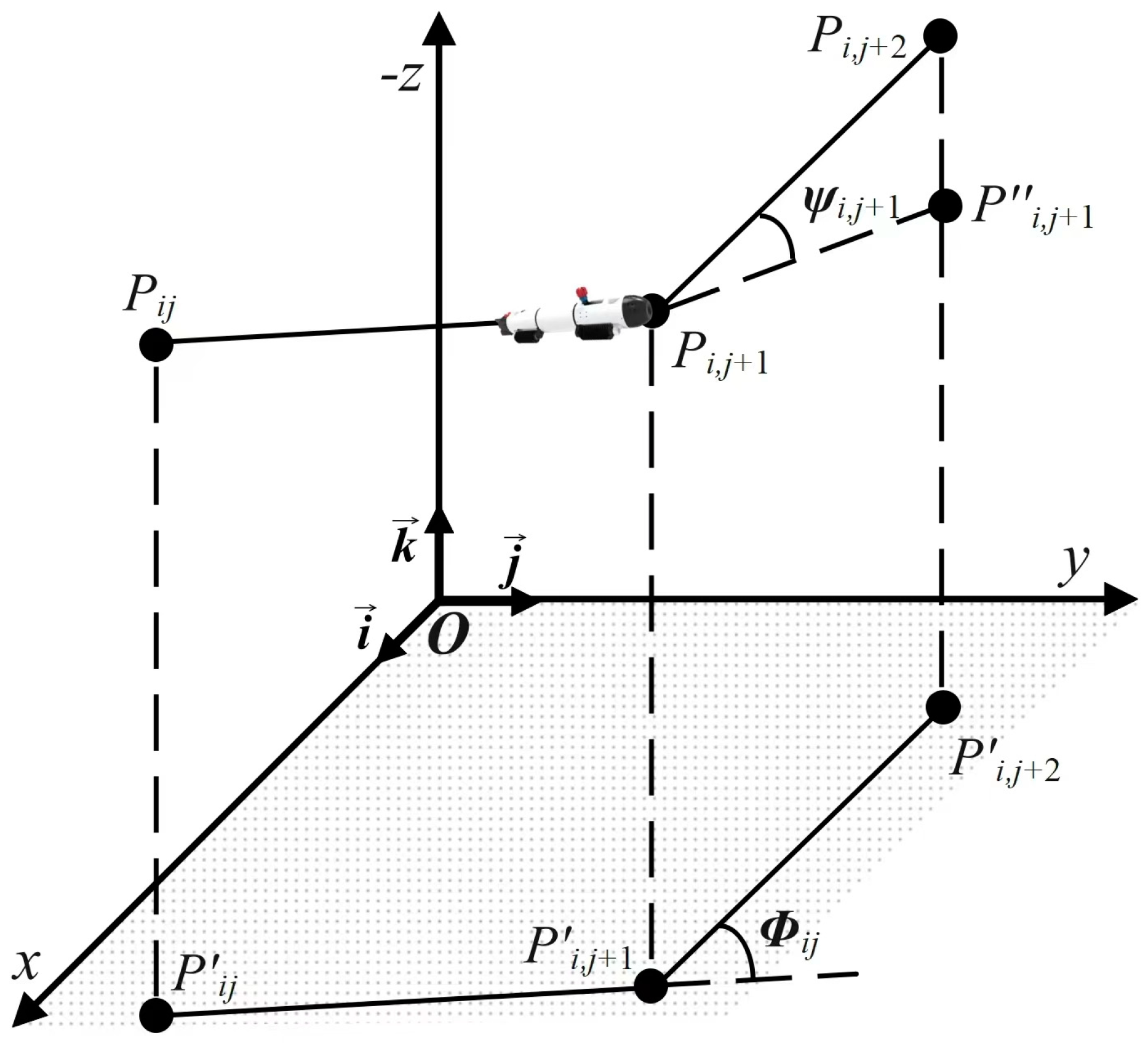
4.1. Principle of SPSO
4.2. Particle Swarm Optimization Strategy
5. Path Planning Implementation and Comparison Analysis
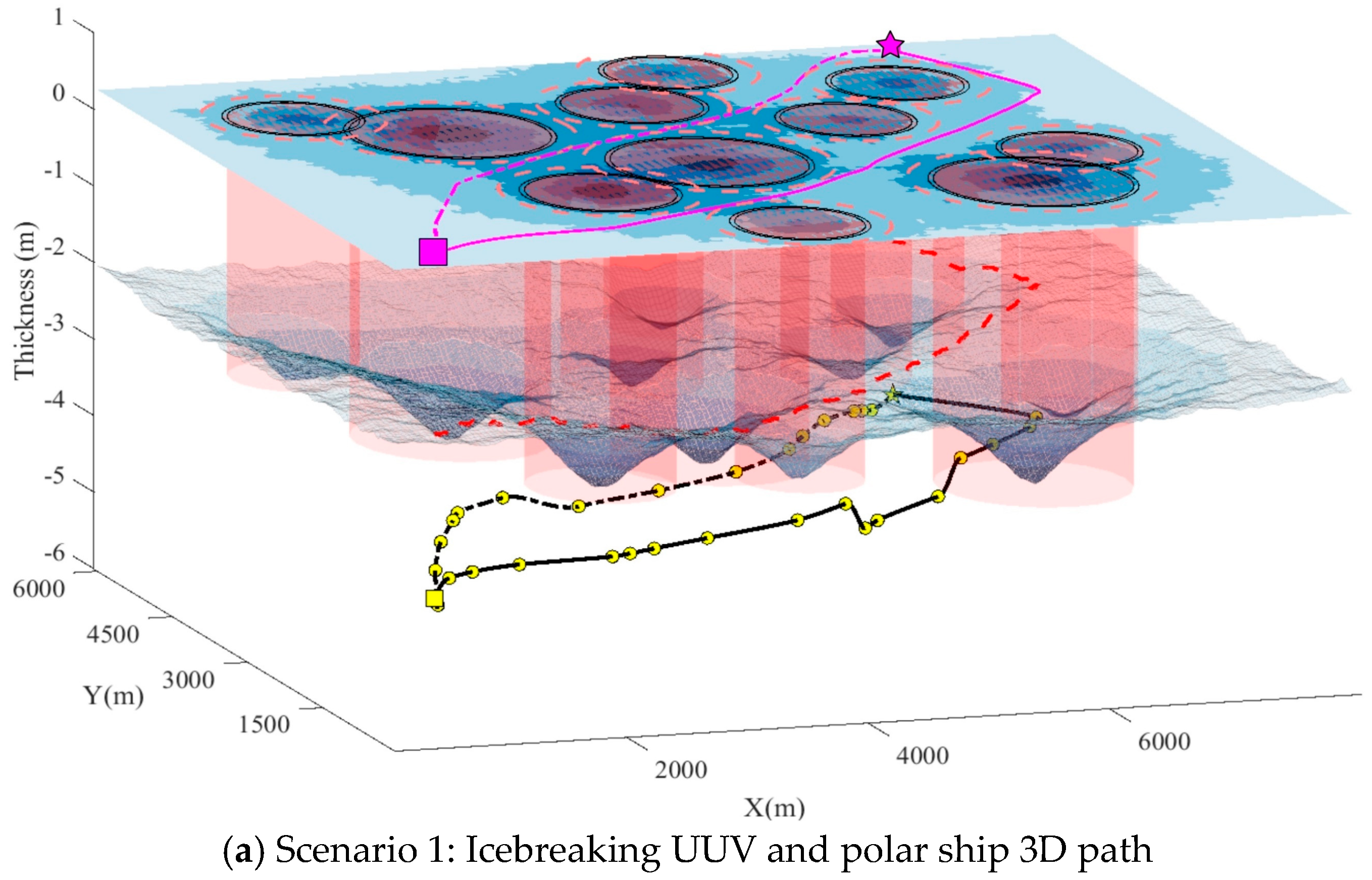
5.1. Path Planning Implementation
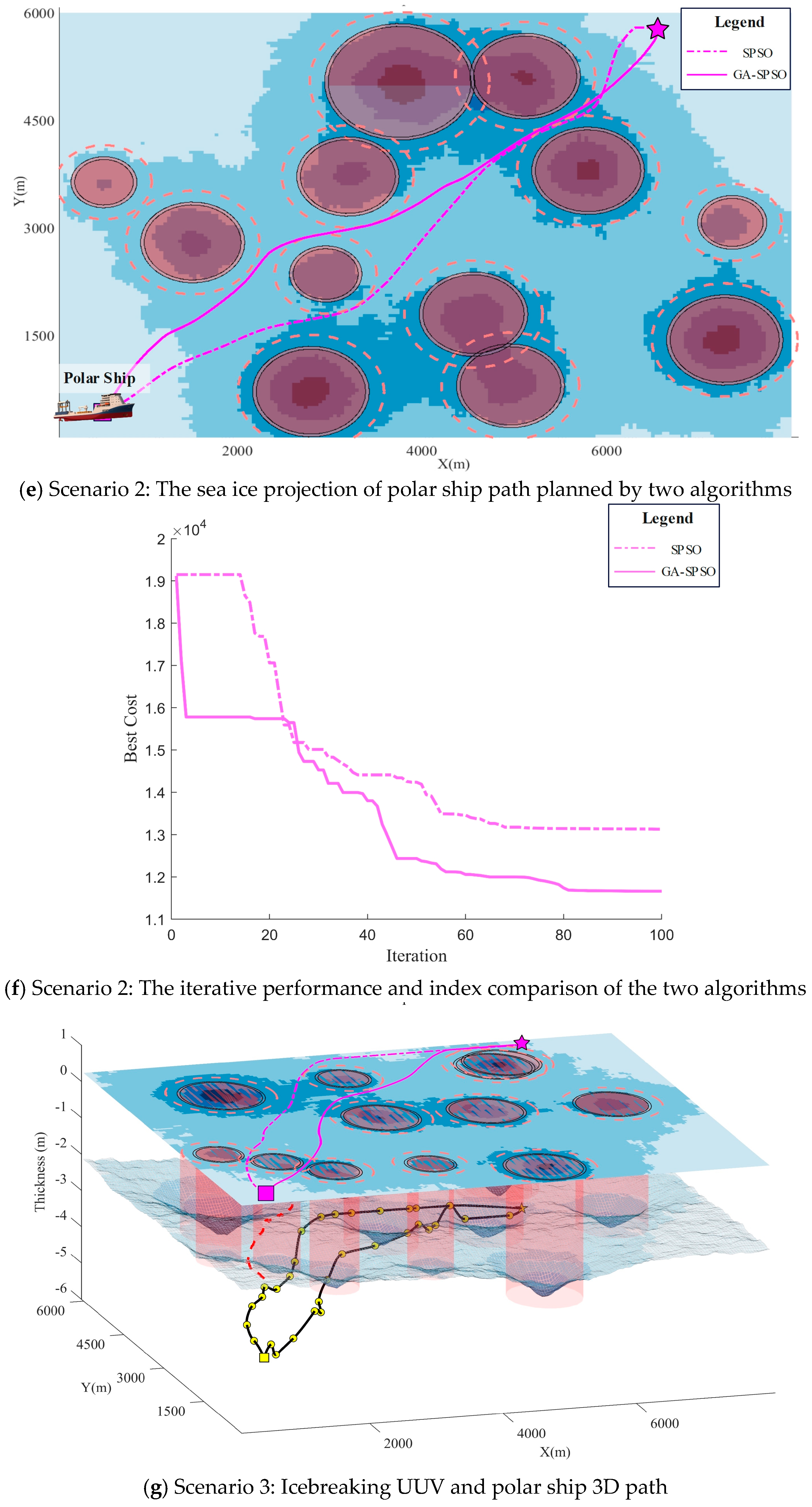
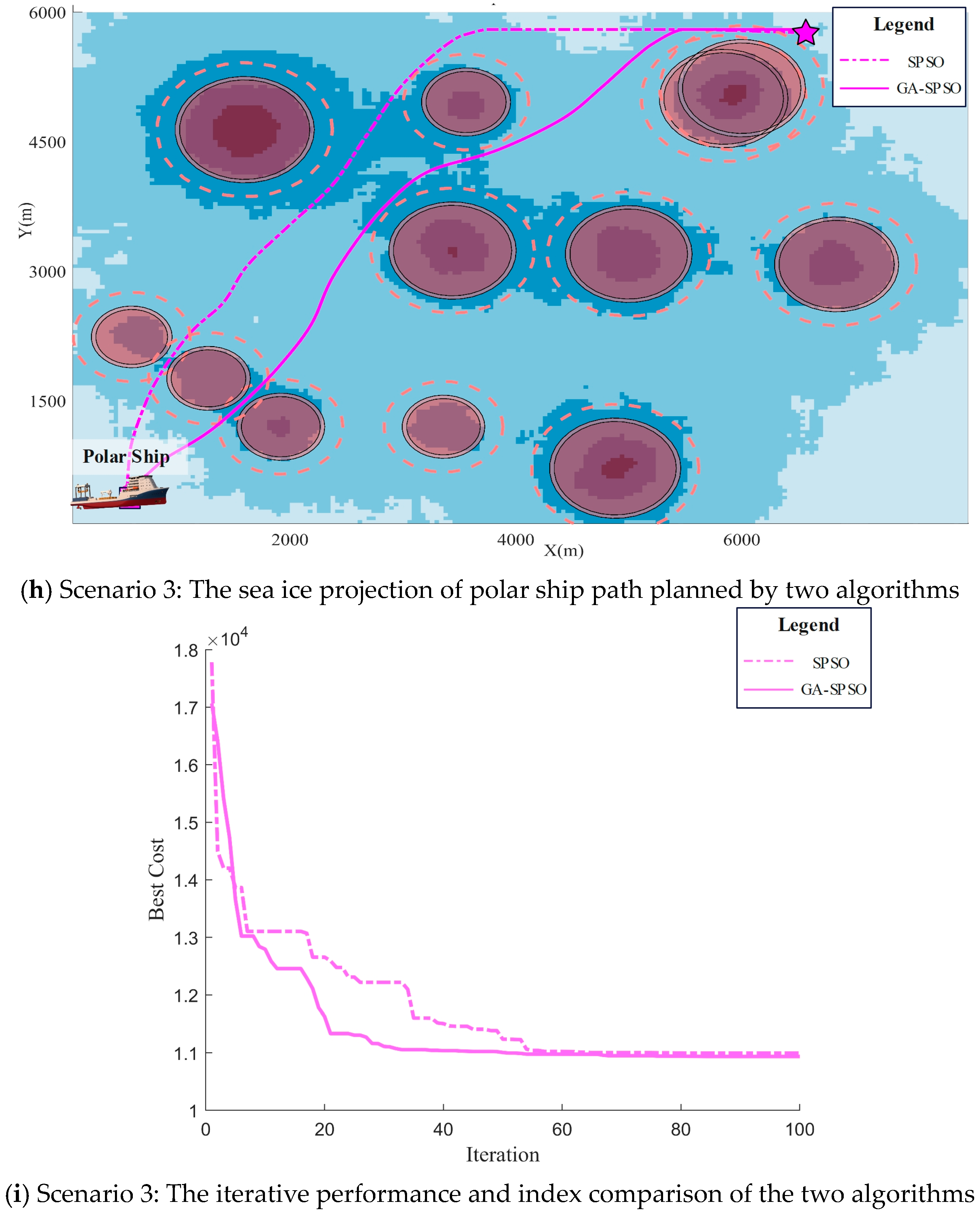
5.2. SPSO vs. GA-SPSO Comparison Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Karimidastenaei, Z.; Avellán, T.; Sadegh, M.; Kløve, B.; Haghighi, A.T. Unconventional Water Resources: Global Opportunities and Challenges. Sci. Total Environ. 2022, 827, 154429. [Google Scholar] [CrossRef] [PubMed]
- Makarova, I.; Makarov, D.; Buyvol, P.; Barinov, A.; Gubacheva, L.; Mukhametdinov, E.; Mavrin, V. Arctic Development in Connection with the Northern Sea Route: A Review of Ecological Risks and Ways to Avoid Them. J. Mar. Sci. Eng. 2022, 10, 1415. [Google Scholar] [CrossRef]
- Zeng, J.; Li, S.; Liu, Y. Application of Unmanned Underwater Vehicles in Polar Research. Adv. Polar Sci. 2021, 32, 173–184. [Google Scholar] [CrossRef]
- Wåhlin, A.; Alley, K.E.; Begeman, C.; Hegrenæs, Ø.; Yuan, X.; Graham, A.G.C.; Hogan, K.; Davis, P.E.D.; Dotto, T.S.; Eayrs, C.; et al. Swirls and scoops: Ice base melt revealed by multibeam imagery of an Antarctic ice shelf. Sci. Adv. 2024, 10, eadn9188. [Google Scholar] [CrossRef] [PubMed]
- Vaquero, T.S.; Daddi, G.; Thakker, R.; Paton, M.; Jasour, A.; Strub, M.P.; Swan, R.M.; Royce, R.; Gildner, M.; Tosi, P.; et al. EELS: Autonomous snake-like robot with task and motion planning capabilities for ice world exploration. Sci. Robot. 2024, 9, eadh8332. [Google Scholar] [CrossRef] [PubMed]
- Ayawli, B.B.K.; Chellali, R.; Appiah, A.Y.; Kyeremeh, F. An Overview of Nature-Inspired, Conventional, and Hybrid Methods of Autonomous Vehicle Path Planning. J. Adv. Transp. 2018, 2018, 8269698. [Google Scholar] [CrossRef]
- Gugan, G.; Haque, A. Path Planning for Autonomous Drones: Challenges and Future Directions. Drones 2023, 7, 169. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, H.; Fan, X.; Lyu, W. Rearch Progress of Path Planning Methods for Autonomous Underwater Vehicle. Math. Probl. Eng. 2021, 2021, 8847863. [Google Scholar] [CrossRef]
- Panda, M.; Das, B.; Subudhi, B.; Pati, B.B. A Comprehensive review of path planning algorithms for autonomous underwater vehicles. Int. J. Autom. Comput. 2020, 17, 321–352. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.; Wu, X.; Hou, X. Research on global path planning for autonomous underwater vehicle considering ocean current. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 790–793. [Google Scholar]
- Yan, Z.; Zhang, J.; Yang, Z.; Tang, J. Two-dimensional optimal path planning for autonomous underwater vehicle using a whale optimization algorithm. Concurr. Comput. Pract. Exp. 2021, 33, e6140. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, M.; Zhang, S.; Zheng, R. AUV path planning based on differential evolution with environment prediction. J. Intell. Robot. Syst. 2022, 104, 23. [Google Scholar] [CrossRef]
- Lim, H.S.; Fan, S.; Chin, C.K.; Chai, S.; Bose, N. Particle swarm optimization algorithms with selective differential evolution for AUV path planning. IAES Int. J. Robot. Autom. (IJRA) 2020, 9, 94–112. [Google Scholar] [CrossRef]
- Zeng, Z.; Sammut, K.; Lian, L.; He, F.; Lammas, A.; Tang, Y. A comparison of optimization techniques for AUV path planning in environments with ocean currents. Robot. Auton. Syst. 2016, 82, 61–72. [Google Scholar] [CrossRef]
- Zhi, L.; Zuo, Y. Collaborative Path Planning of Multiple AUVs Based on Adaptive Multi-Population PSO. J. Mar. Sci. Eng. 2024, 12, 223. [Google Scholar] [CrossRef]
- Fan, S.; Bose, N.; Liang, Z. Polar AUV Challenges and Applications: A Review. Drones 2024, 8, 413. [Google Scholar] [CrossRef]
- Cheng, H.-Y.; Yu, S.-M.; Yu, H.; Zhu, J.-C.; Chu, J.-K. Bioinspired underwater navigation using polarization patterns within snell’s window. China Ocean Eng. 2023, 37, 628–636. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, L.; Zhang, W.; Zhou, J.; Wang, M. Polar Grid Navigation Algorithm for Unmanned Underwater Vehicles. Sensors 2017, 17, 1599. [Google Scholar] [CrossRef] [PubMed]
- Phung, M.D.; Ha, Q.P. Safety-enhanced UAV Path Planning with Spherical Vector-Based Particle Swarm Optimization. Appl. Soft Comput. 2021, 107, 107376. [Google Scholar] [CrossRef]
- Pan, W.; Chen, J.; Lv, B.; Peng, L. Optimization and Application of Improved YOLOv9s-UI for Underwater Object Detection. Appl. Sci. 2024, 14, 7162. [Google Scholar] [CrossRef]




| /* Initialization: */ | |
|---|---|
| 1 | Get a search map and initial path planning information; |
| 2 3 | Set swarm parameters , , , , , and ; Initialize , ; |
| 4 5 6 7 8 9 /* 10 11 12 13 | foreach particle in swarm do | Create a random path ; | Assign to particle’s position ; | Compute fitness as the local_best of the particle; end Set ; Evolutions by SPSO: */ for 1 to do | foreach particle in swarm do | | Compute velocity ; | | Compute new path ; |
| 14 15 16 17 19 20 21 | | | Map to in Cartesian space; | | Update local_best ; | end | Update global_best when ; | Update ; | Save best_position associated with ; end |
| /* Initialization: | |
|---|---|
| 1 | Get a search map and initial path planning information; |
| 2 3 4 | Set swarm parameters , , , , , and ; Set genetic parameters , , , and ; Initialize , ; |
| 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | foreach particle in swarm do | Create a random path ; | Assign to particle’s position ; | Compute fitness as the local_best of the particle; end Set ; Evolutions by GA-SPSO: for 1 to do | Execute selection operation to get the ; | Execute crossover operation on to get ; | Execute mutation operation on ; | Form a new swarm by and ; | foreach particle in swarm do | | Compute velocity ; | | Compute new path ; |
| 19 20 21 22 23 24 25 | | | Map to in Cartesian space; | | Update local_best ; | End | Update global_best when ; | Update and ; | Save best_position associated with ; end |
| Categories | Symbol | Value |
|---|---|---|
| maximum number of iterations | maxiter | 100 |
| particle population size | npop | 200 |
| inertia weight | w | 1 |
| attenuation factor | wdamp | 0.98 |
| learning factors | c1, c2 | 1.5. |
| waypoints | n | 16 |
| selection rate | pSelect | 0.5 |
| crossover rate | pCrossover | 0.7 |
| mutation rate | pMutation | 0.5 |
| final mutation rate | pMutationmin | 0.1 |
| Scenario | Variable | SPSO | GA-SPSO |
|---|---|---|---|
| Scenario 1 | Icebreaking UUV 3D path | 9194.46 m | 9156.09 m |
| Polar ship path | 9186.18 m | 9148.46 m | |
| Iterative performance | 14,166.54 | 12,061.38 | |
| Rate of convergence | slow | fast | |
| Scenario 2 | Icebreaking UUV 3D path | 8849.51 m | 8258.73 m |
| Polar ship path | 8836.61 m | 8249.86 m | |
| Iterative performance | 13,645.98 | 11,069.86 | |
| Rate of convergence | slow | fast | |
| Scenario 3 | Icebreaking UUV 3D path | 9227.74 m | 8548.91 m |
| Polar ship path | 9218.65 m | 8541.77 m | |
| Iterative performance | 11,023.36 | 9963.74 | |
| Rate of convergence | slow | fast |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, W.; Wang, Y.; Song, F.; Peng, L.; Zhang, X. UUV-Assisted Icebreaking Application in Polar Environments Using GA-SPSO. J. Mar. Sci. Eng. 2024, 12, 1845. https://doi.org/10.3390/jmse12101845
Pan W, Wang Y, Song F, Peng L, Zhang X. UUV-Assisted Icebreaking Application in Polar Environments Using GA-SPSO. Journal of Marine Science and Engineering. 2024; 12(10):1845. https://doi.org/10.3390/jmse12101845
Chicago/Turabian StylePan, Wei, Yang Wang, Fei Song, Likun Peng, and Xiaofeng Zhang. 2024. "UUV-Assisted Icebreaking Application in Polar Environments Using GA-SPSO" Journal of Marine Science and Engineering 12, no. 10: 1845. https://doi.org/10.3390/jmse12101845
APA StylePan, W., Wang, Y., Song, F., Peng, L., & Zhang, X. (2024). UUV-Assisted Icebreaking Application in Polar Environments Using GA-SPSO. Journal of Marine Science and Engineering, 12(10), 1845. https://doi.org/10.3390/jmse12101845






