Numerical Simulation and Experimental Validation of the Acoustical Target Strength of Bluefin Tuna Swimbladders Derived from 3D Computed Tomographic Images
Abstract
1. Introduction
2. Materials and Methods
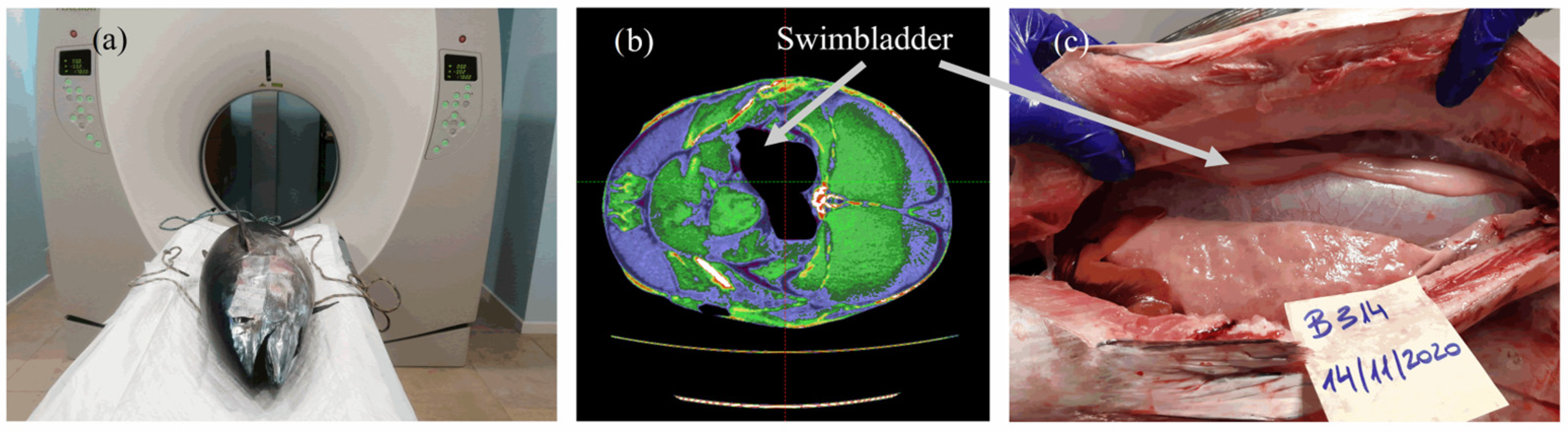
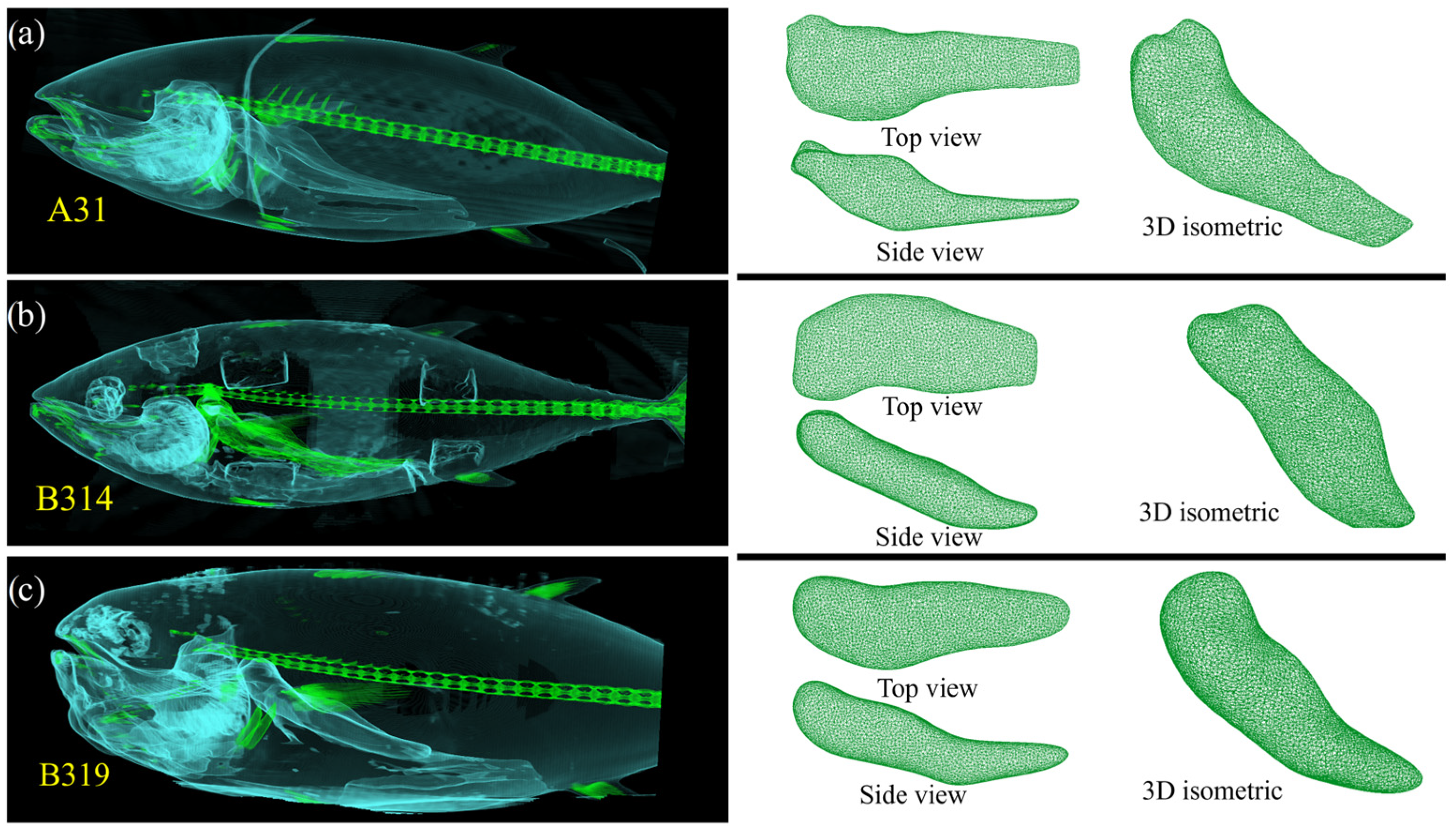
2.1. Tuna Samples and Computed Tomography Imagery
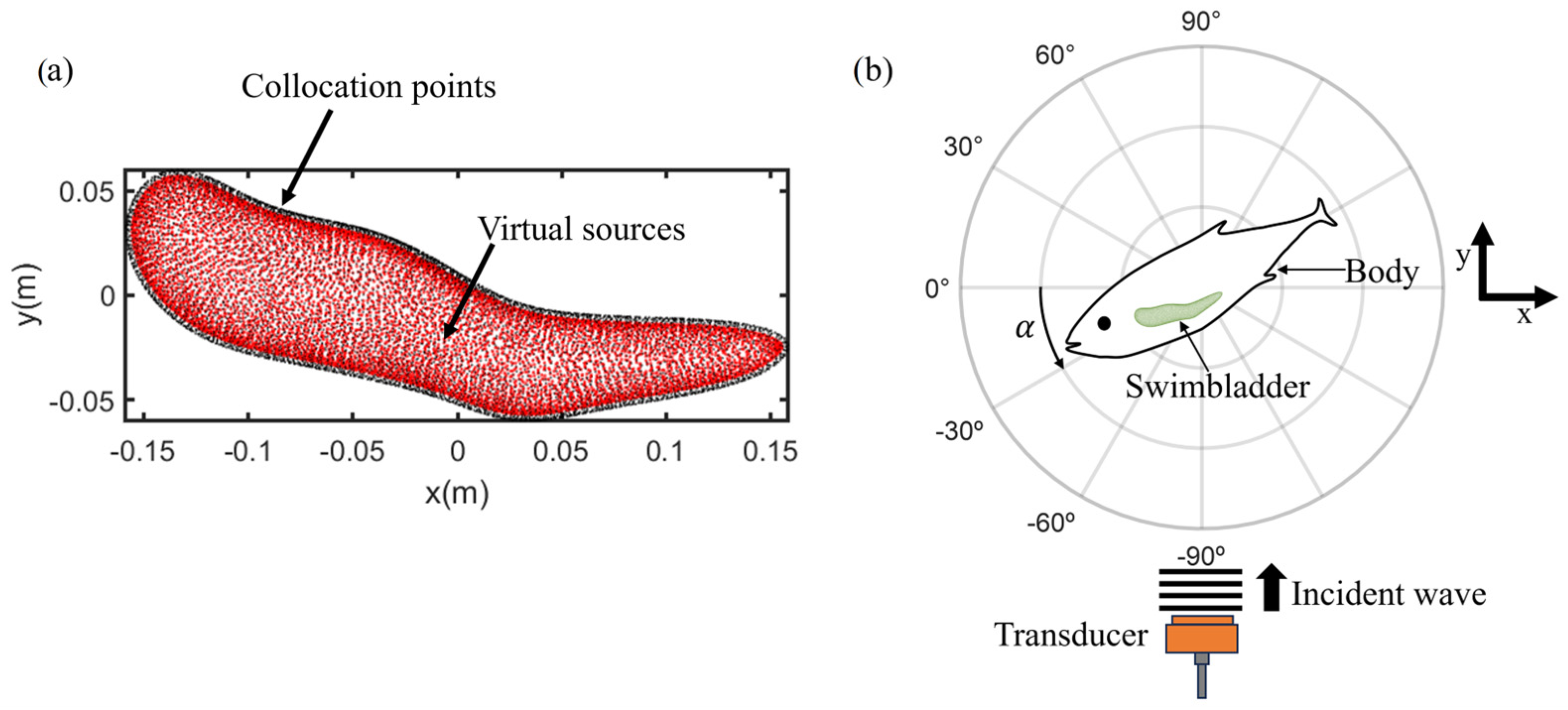
2.2. Numerical Simulation: Method of Fundamental Solutions
2.3. Acoustic Data Acquisition
3. Results
3.1. Computed Axial Tomography (CT)
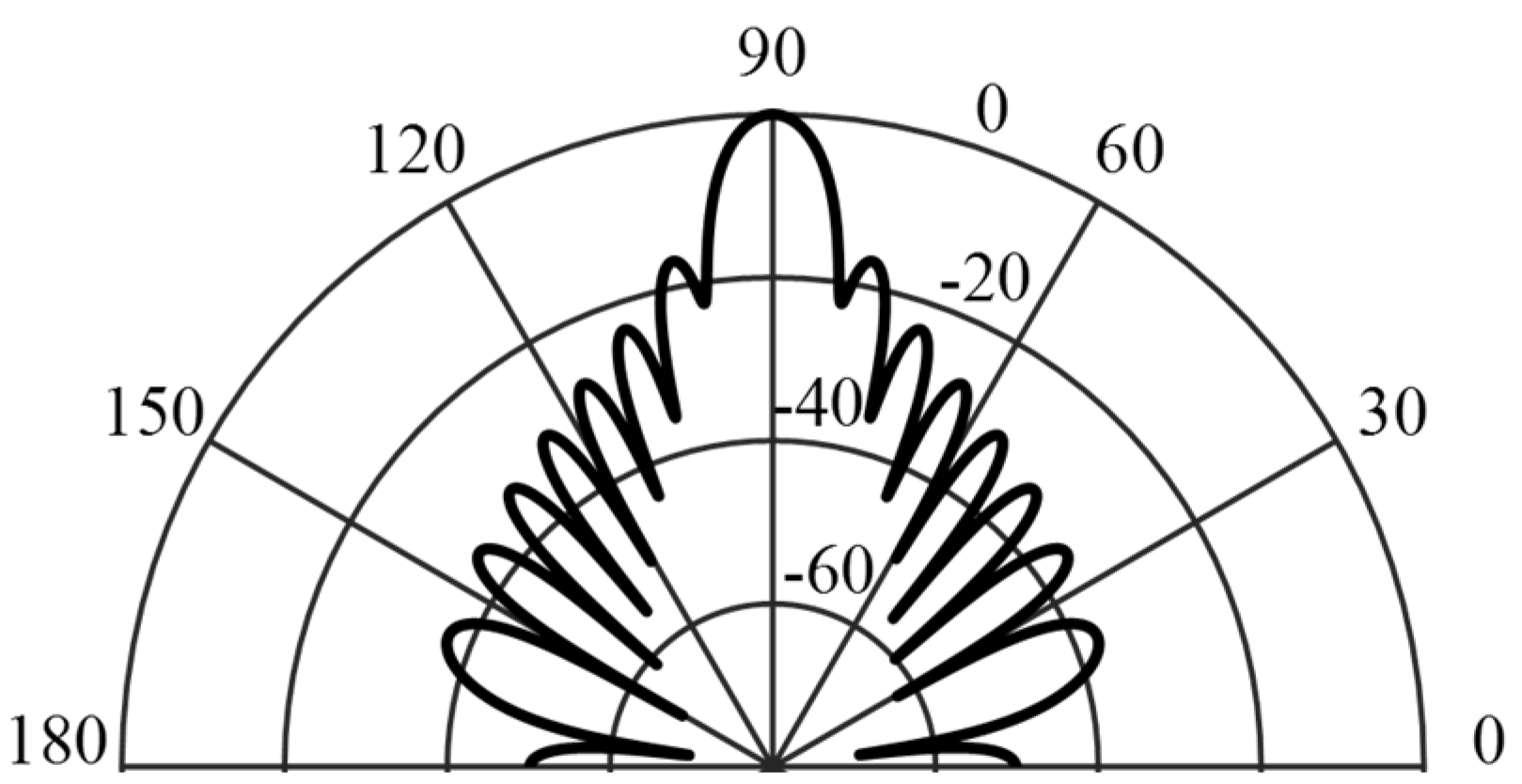
3.2. Backscattering Simulation
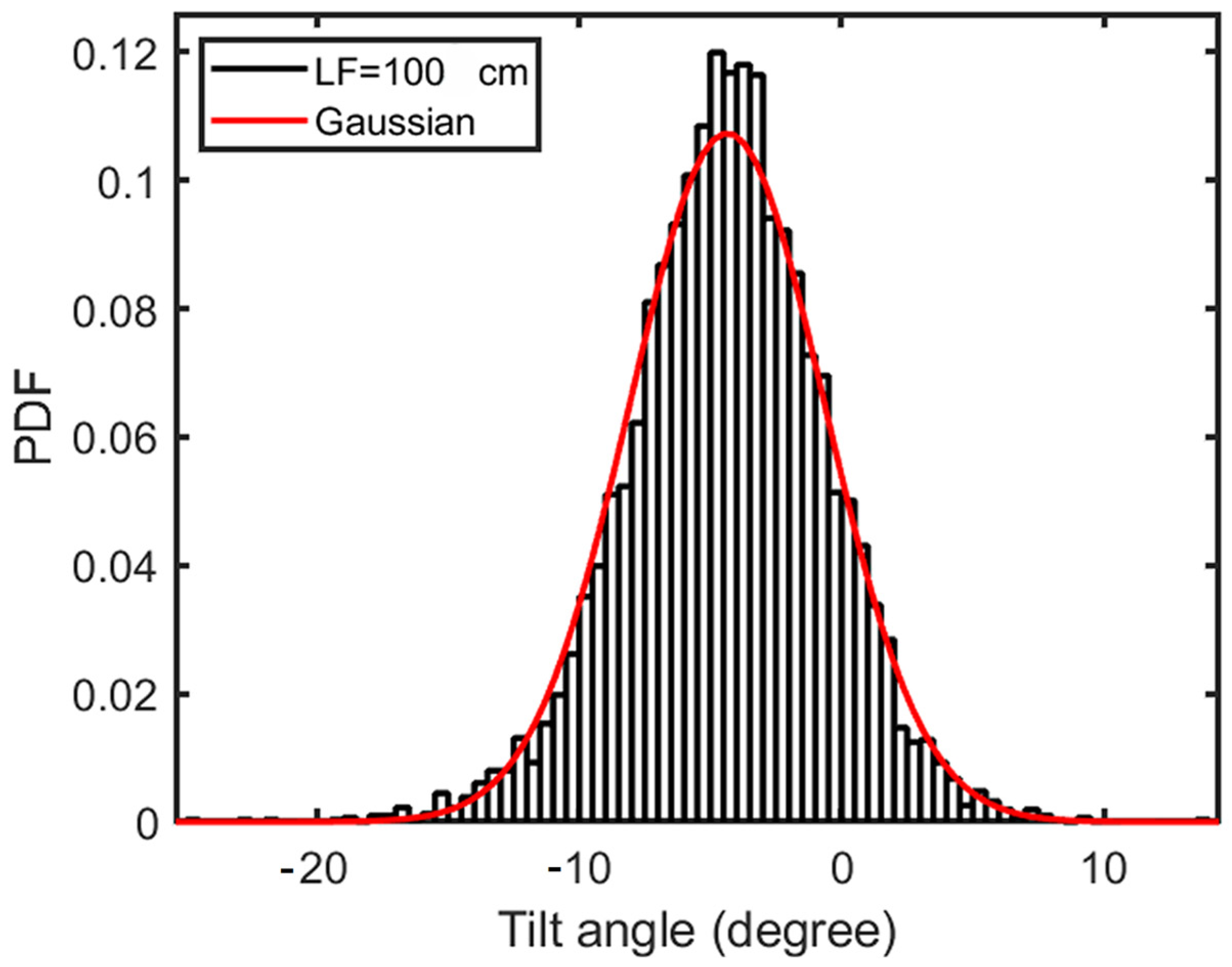
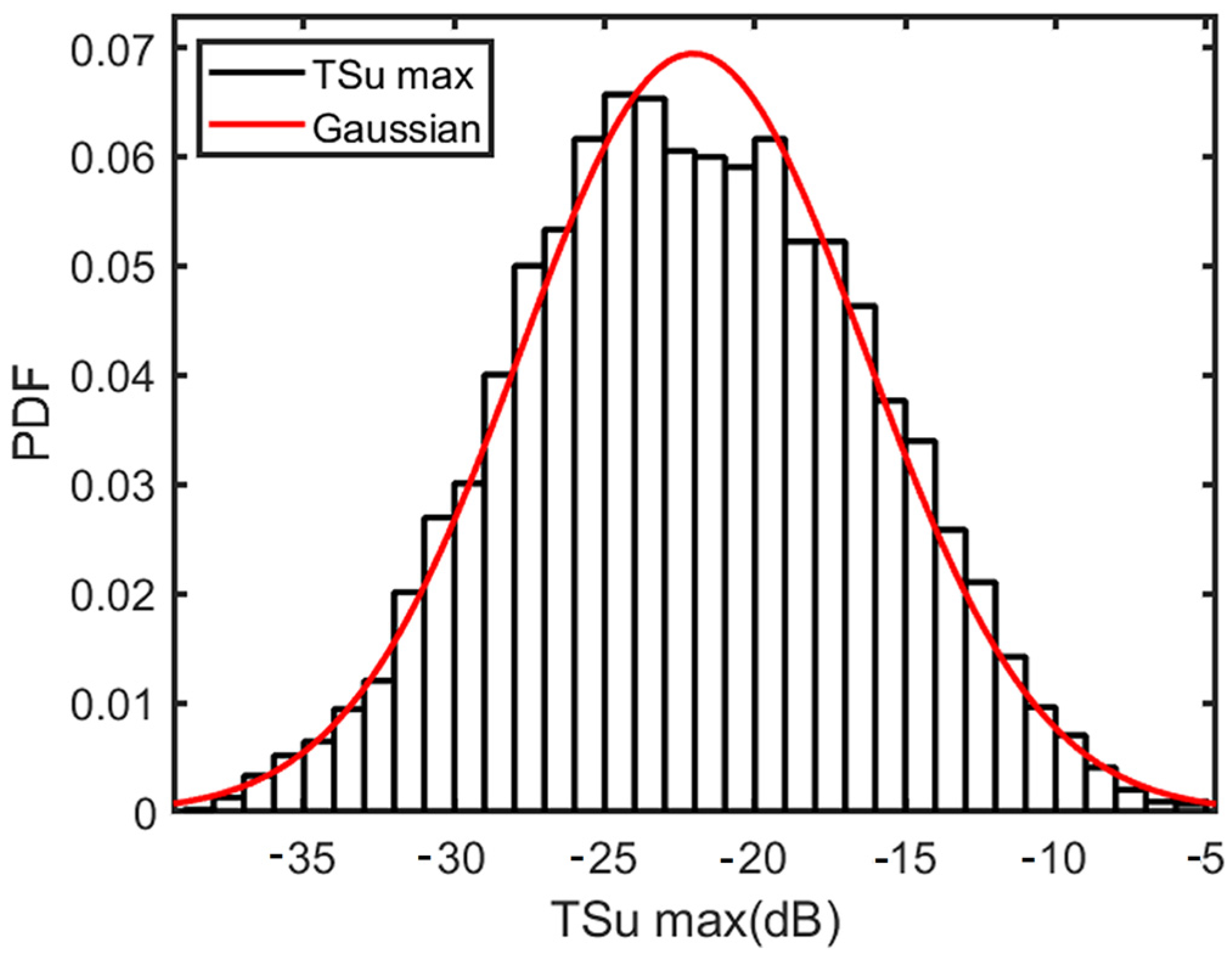
3.3. Comparison of Numerical Simulation and Experimental Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- FAO. Pesca y Acuicultura—Especies Acuáticas—Thunnus Thynnus Linnaeus, 1758. Available online: https://www.fao.org/fishery/es/aqspecies/3296/en (accessed on 18 February 2023).
- Cort, J.L. El Enigma Del Atún Rojo Reproductor Del Atlántico Nororiental; Bedia Artes Gráficas: Santander, Spain, 2007. (In Spanish) [Google Scholar]
- de la Gándara, F.; Ortega, A.; Buentello, A. Tuna Aquaculture in Europe. In Advances in Tuna Aquaculture: From Hatchery to Market; Academic Press: Cambridge, MA, USA, 2016; pp. 115–157. [Google Scholar] [CrossRef]
- Fromentin, J.; Powers, J.E. Atlantic bluefin tuna: Population dynamics, ecology, fisheries and management. Fish Fish. 2005, 6, 281–306. [Google Scholar] [CrossRef]
- Ortega, A.; de la Gándara, F. Closing the life cycle of the Atlantic Bluefin tuna Thunnus thynnus in captivity. In Proceedings of the Aquaculture Europe 17, Dubrovnik, Croatia, 17–20 October 2017; pp. 857–858. [Google Scholar]
- Muñoz-Benavent, P.; Andreu-García, G.; Valiente-González, J.M.; Atienza-Vanacloig, V.; Puig-Pons, V.; Espinosa, V. Automatic Bluefin Tuna sizing using a stereoscopic vision system. ICES J. Mar. Sci. 2018, 75, 390–401. [Google Scholar] [CrossRef]
- Simmonds, J.; MacLennan, D. Fisheries Acoustics: Theory and Practice, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 1. [Google Scholar]
- Kang, D.; Sadayasu, K.; Mukai, T.; Iida, K.; Hwang, D.; Sawada, K.; Miyashita, K. Target strength estimation of black porgy Acanthopagrus schlegeli using acoustic measurements and a scattering model. Fish. Sci. 2004, 70, 819–828. [Google Scholar] [CrossRef]
- Foote, K.G. Summary of methods for determining fish target strength at ultrasonic frequencies. ICES J. Mar. Sci. 1991, 48, 211–217. [Google Scholar] [CrossRef]
- Furusawa, M. Prolate spheroidal models for predicting general trends of fish target strength. J. Acoust. Soc. Jpn. 1988, 9, 13–24. [Google Scholar] [CrossRef]
- Puig-Pons, V.; Muñoz-Benavent, P.; Pérez-Arjona, I.; Ladino, A.; Llorens-Escrich, S.; Andreu-García, G.; Valiente-González, J.M.; Atienza-Vanacloig, V.; Ordóñez-Cebrián, P.; Pastor-Gimeno, J.I.; et al. Estimation of Bluefin Tuna (Thunnus thynnus) mean length in sea cages by acoustical means. Appl. Acoust. 2022, 197, 108960. [Google Scholar] [CrossRef]
- Love, R.H. Dorsal-Aspect Target Strength of an Individual Fish. J. Acoust. Soc. Am. 1971, 49, 816–823. [Google Scholar] [CrossRef]
- Boyra, G.; Uranga, J.; Goñi, N.; Godard, I.; Sobradillo, B. Target strength measurements of Atlantic bluefin tuna (Thunnus thynnus) from a live-bait fishing vessel in the Bay of Biscay. Fish. Res. 2024, 280, 107150. [Google Scholar] [CrossRef]
- Peña, H.; Macaulay, G.J.; Ona, E.; Vatnehol, S.; Holmin, A.J. Estimating individual fish school biomass using digital omnidirectional sonars, applied to mackerel and herring. ICES J. Mar. Sci. 2021, 78, 940–951. [Google Scholar] [CrossRef]
- Jech, J.M.; Horne, J.K.; Chu, D.; Demer, D.A.; Francis, D.T.; Gorska, N.; Jones, B.; Lavery, A.C.; Stanton, T.K.; Macaulay, G.J.; et al. Comparisons among ten models of acoustic backscattering used in aquatic ecosystem research. J. Acoust. Soc. Am. 2015, 138, 3742–3764. [Google Scholar] [CrossRef]
- Foote, K.G. Importance of the swimbladder in acoustic scattering by fish: A comparison of gadoid and mackerel target strengths. J. Acoust. Soc. Am. 1980, 67, 2084–2089. [Google Scholar] [CrossRef]
- Macaulay, G.J.; Peña, H.; Fässler, S.M.M.; Pedersen, G.; Ona, E. Accuracy of the Kirchhoff-Approximation and Kirchhoff-Ray-Mode Fish Swimbladder Acoustic Scattering Models. PLoS ONE 2013, 8, 2–8. [Google Scholar] [CrossRef] [PubMed]
- Peña, H.; Foote, K.G. Modelling the target strength of Trachurus symmetricus murphyi based on high-resolution swimbladder morphometry using an MRI scanner. ICES J. Mar. Sci. 2008, 65, 1751–1761. [Google Scholar] [CrossRef]
- Do, M.A.; Surti, A.M. Estimation of dorsal aspect target strength of deep-water fish using a simple model of swimbladder backscattering. J. Acoust. Soc. Am. 1990, 87, 1588–1596. [Google Scholar] [CrossRef]
- Gorska, N.; Ona, E.; Korneliussen, R. Acoustic backscattering by Atlantic mackerel as being representative of fish that lack a swimbladder. Backscattering by individual fish. ICES J. Mar. Sci. 2005, 62, 984–995. [Google Scholar] [CrossRef]
- Chu, D.; Stanton, T.K.; Jech, J.M.; Reeder, D.B. Modeling of the backscattering by swimbladder-bearing fish. J. Acoust. Soc. Am. 2006, 120, 3105. [Google Scholar] [CrossRef]
- Stanton, K. Simple approximate formulas for backscattering of sound by spherical and elongated objects. J. Acoust. Soc. Am. 1989, 86, 1499–1510. [Google Scholar] [CrossRef]
- Clay, C.S.; Home, J.K. Acoustic models of fish: The Atlantic cod (Gadus morhua). J. Acoust. Soc. Am. 1994, 96, 1661–1668. [Google Scholar] [CrossRef]
- Gauthier, S.; Horne, J.K. Acoustic characteristics of forage fish species in the Gulf of Alaska and Bering Sea based on Kirchhoff-approximation models. Can. J. Fish. Aquat. Sci. 2004, 61, 1839–1850. [Google Scholar] [CrossRef]
- Macaulay, G.J. Anatomically detailed acoustic scattering models of fish. Bioacoustics 2002, 12, 275–277. [Google Scholar] [CrossRef]
- Reeder, D.B.; Jech, J.M.; Stanton, T.K. Broadband acoustic backscatter and high-resolution morphology of fish: Measurement and modeling. J. Acoust. Soc. Am. 2004, 116, 747–761. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Arjona, I.; Godinho, L.M.C.; Espinosa, V. Numerical simulation of target strength measurements from near to far field of fish using the method of fundamental solutions. Acta Acust. United Acust. 2018, 104, 25–38. [Google Scholar] [CrossRef]
- Pérez-Arjona, I.; Godinho, L.; Espinosa, V. Influence of fish backbone model geometrical features on the numerical target strength of swimbladdered fish. ICES J. Mar. Sci. 2020, 77, 2870–2881. [Google Scholar] [CrossRef]
- Zhu, Z.; Tong, J.; Xue, M.; Qiu, C.; Lyu, S.; Liu, B. Investigations on Target Strength Estimation Methods: A Case Study of Chub Mackerel (Scomber japonicus) in the Northwest Pacific Ocean. Fishes 2024, 9, 307. [Google Scholar] [CrossRef]
- Godinho, L.; Tadeu, A.; Mendes, P.A. Wave propagation around thin structures using the MFS. Comput. Mater. Contin. 2007, 5, 117–127. [Google Scholar] [CrossRef]
- Simrad ES120-7C Split Beam Echo Sounder Transducer. Technical Specifications. Available online: https://www.simrad.online/td_120/es120_7c/es120_7c_ds_en_a4.pdf (accessed on 18 October 2024).
- Simrad. Simrad EK80, Wide Band Scientific Echo Sounder. Reference Manual 2008. Volume 1. Available online: https://www.simrad.online/ek80/ins/ek80_ins_en_us.pdf (accessed on 18 October 2024).
- Sarà, G.; Dean, J.M.; d’Amato, D.; Buscaino, G.; Oliveri, A.; Genovese, S.; Ferro, S.; Buffa, G.; Martire, M.L.; Mazzola, S. Effect of boat noise on the behaviour of bluefin Tuna Thunnus thynnus in the Mediterranean Sea. Mar. Ecol. Prog. Ser. 2007, 331, 243–253. [Google Scholar] [CrossRef]
- Voorhees, T.M. Epidemiology of Puffy Snout Syndrome in Tuna. University of Rhode Island. 2015. Available online: http://digitalcommons.uri.edu/theses/820 (accessed on 18 October 2024).
- Partridge, G. Hatchery Production of Yellowfin Tuna. Melbourne, Australia. 2009. Available online: www.issinstitute.org.au (accessed on 18 October 2024).
- Miller, E.A.; Leidholt, S.; Galvin, T.; Norton, A.; Van Houtan, K.S.; Thurber, R.V.; Boustany, A. Electron microscopy reveals viral-like particles and mitochondrial degradation in scombrid puffy snout syndrome. Dis. Aquat. Organ. 2021, 147, 25–31. [Google Scholar] [CrossRef]
- Nakamura, I. A Pugheaded Specimen Found among a School of Bluefin Tuna, Thunnus thynnus. Jpn. J. Ichthyol. 1977, 23, 237–238. [Google Scholar] [CrossRef]


| Calibration Data of the Echosounder | Parameters Selected | ||
|---|---|---|---|
| f (kHz) | 120 | Segmentation threshold (dB) | −50 |
| Transducer | ES120-7C | Area (pixels) | >200 and <2000 |
| Serial number | 1636 | Selection threshold 1 (dB) | −50 |
| Gain (dB) | 26.22 | Selection threshold 2 (dB) | >−40 and <−5 |
| Sa corr (dB) | −0.0462 | Range (m) | >2 and <7.5 |
| BeamWidthAlongship (°) | 6.57 | Minimum pings | 4 |
| BeamWidthAthwartship (°) | 6.6 | Minumum strength | 0.7 |
| AngleOffsetAlongship (°) | −0.02 | ||
| AngleOffsetAthwatship (°) | −0.06 | ||
| TsRmsError (dB) | 0.0366 | ||
| ABFT | A31 | B314 | B319 |
|---|---|---|---|
| Fork Length—FL (cm) | 104 | 96.5 | 98 |
| Total Length—TL (cm) | 116 | 108.5 | 105 |
| Height—H (cm) | 27 | 25 | 33 |
| Circumference—C (cm) | 77 | 70.5 | 81 |
| Width—W (cm) | 21 | 18.5 | 20 |
| Weight—w (Kg) | 21.9 | 18.12 | 21.55 |
| Swimbladder | |||
| Length—SL (cm) | 35.15 | 30.51 | 22.29 |
| Width—SW (cm) | 8.6 | 8.26 | 8.32 |
| Height—SH (cm) | 3.46 | 4.96 | 3 |
| Ratio—SR (%) | 33.8 | 31.6 | 22.7 |
| Angle—(°) | 29.0 | 22 | 21.8 |
| Numerical MFS | Experimental Measurements | ||||
|---|---|---|---|---|---|
| FL (cm) | TS Weighted (dB) | FL (cm) | TS (dB) Median | SD (dB) | Traces |
| 100 | −23.3 | 100 | −22.1 | 5.7 | 5419 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ladino, A.; Pérez-Arjona, I.; Espinosa, V.; Puig-Pons, V.; Gándara, F.d.l.; Ortega, A.; Blanco, E.; Godinho, L. Numerical Simulation and Experimental Validation of the Acoustical Target Strength of Bluefin Tuna Swimbladders Derived from 3D Computed Tomographic Images. J. Mar. Sci. Eng. 2024, 12, 2014. https://doi.org/10.3390/jmse12112014
Ladino A, Pérez-Arjona I, Espinosa V, Puig-Pons V, Gándara Fdl, Ortega A, Blanco E, Godinho L. Numerical Simulation and Experimental Validation of the Acoustical Target Strength of Bluefin Tuna Swimbladders Derived from 3D Computed Tomographic Images. Journal of Marine Science and Engineering. 2024; 12(11):2014. https://doi.org/10.3390/jmse12112014
Chicago/Turabian StyleLadino, Anderson, Isabel Pérez-Arjona, Victor Espinosa, Vicent Puig-Pons, Fernando de la Gándara, Aurelio Ortega, Edurne Blanco, and Luis Godinho. 2024. "Numerical Simulation and Experimental Validation of the Acoustical Target Strength of Bluefin Tuna Swimbladders Derived from 3D Computed Tomographic Images" Journal of Marine Science and Engineering 12, no. 11: 2014. https://doi.org/10.3390/jmse12112014
APA StyleLadino, A., Pérez-Arjona, I., Espinosa, V., Puig-Pons, V., Gándara, F. d. l., Ortega, A., Blanco, E., & Godinho, L. (2024). Numerical Simulation and Experimental Validation of the Acoustical Target Strength of Bluefin Tuna Swimbladders Derived from 3D Computed Tomographic Images. Journal of Marine Science and Engineering, 12(11), 2014. https://doi.org/10.3390/jmse12112014








