Physical Experimental Study on the Wave Reflection and Run-Up of a New Ecological Hollow Cube
Abstract
1. Introduction
2. Materials and Methods
2.1. Block Description
2.2. Physical Model Experiments
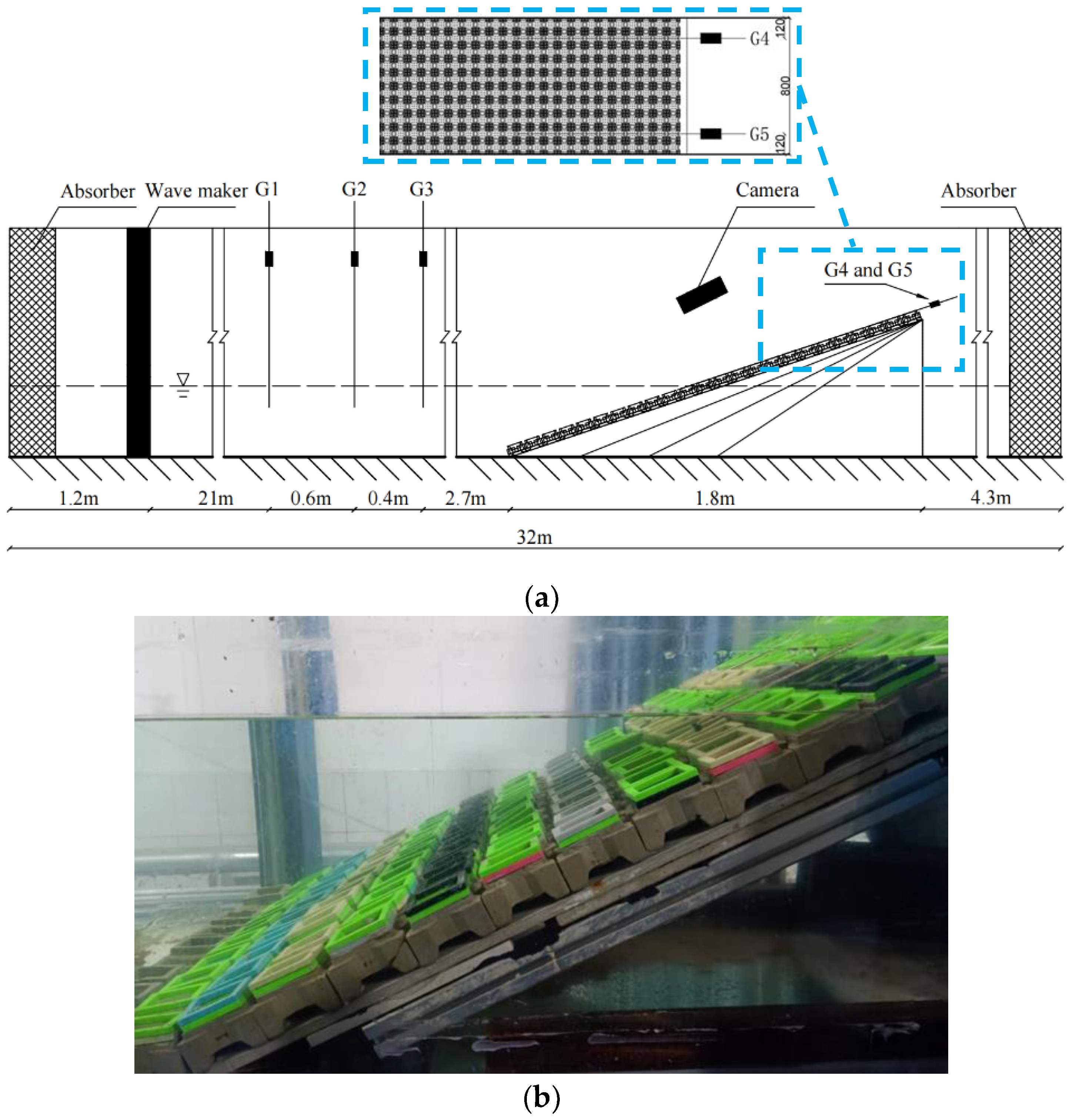
2.2.1. Experimental Equipment and Instruments
2.2.2. Experimental Setup and Procedure
2.2.3. Experimental Layout
3. Results and Discussion
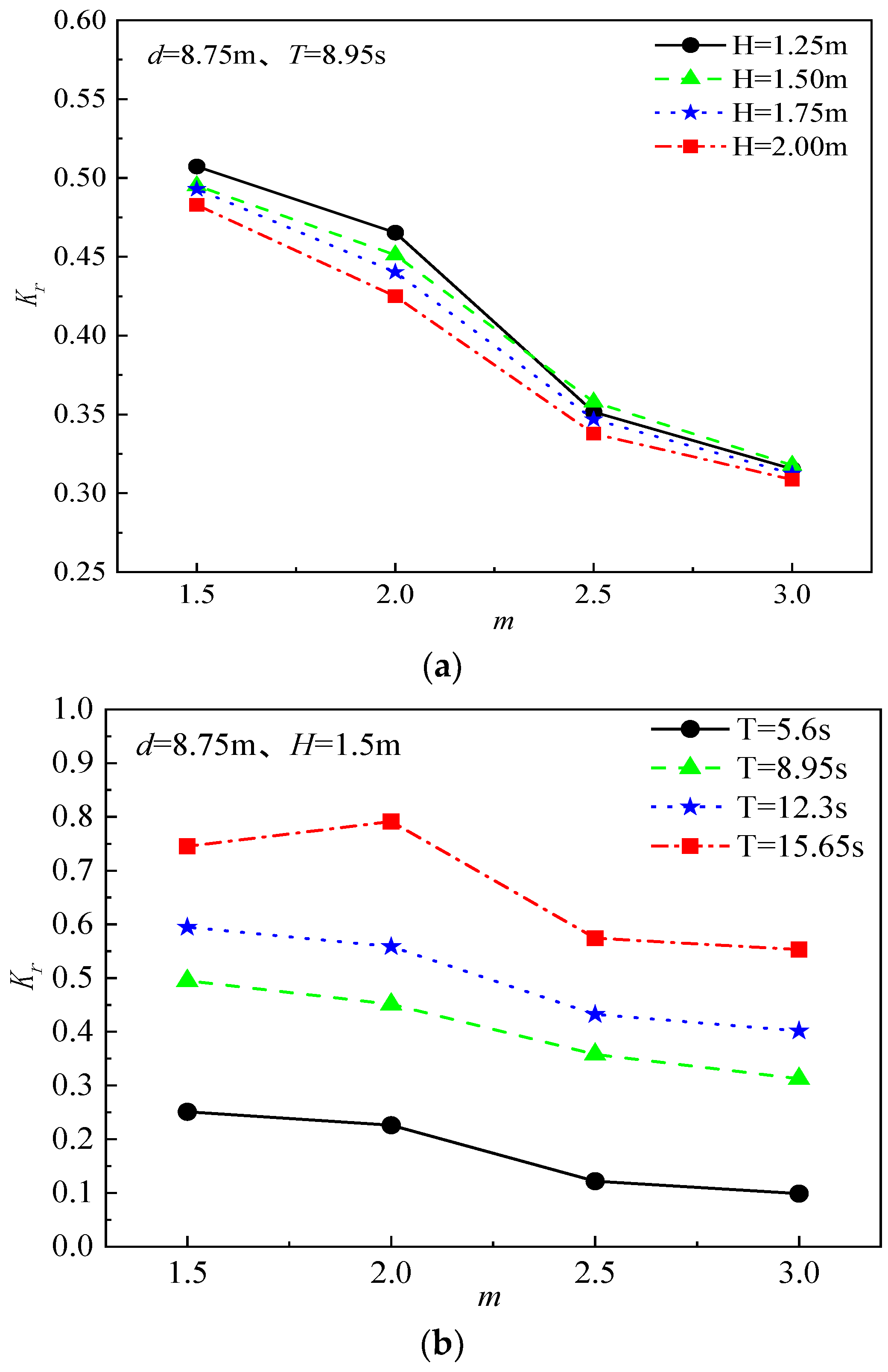
3.1. Analysis of the Reflection Coefficient for the New Block
3.2. Analysis of the Wave Run-Up of the New Block
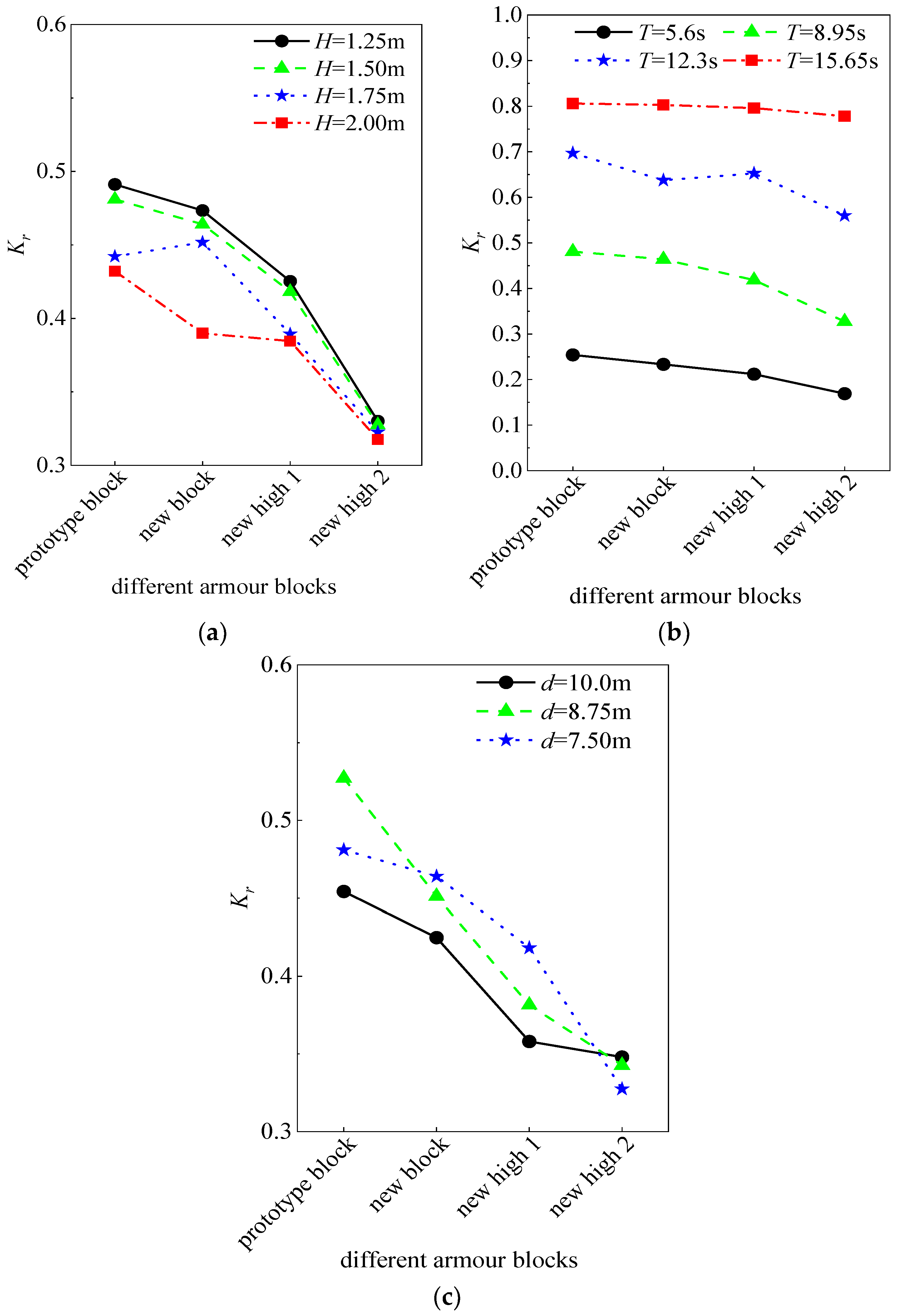
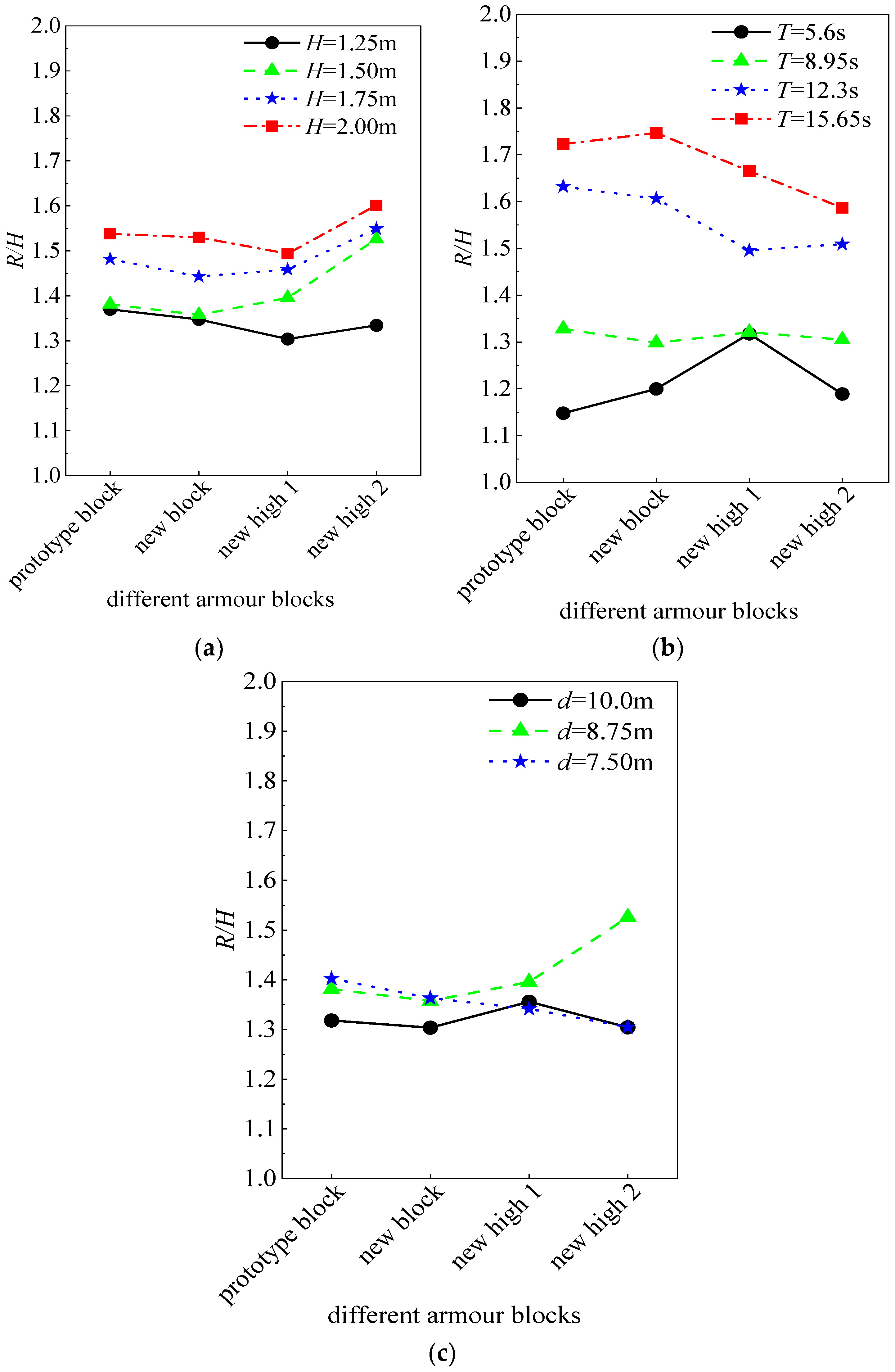
3.3. Comparison of Reflection Coefficient and Wave Run-Up for Different Blocks
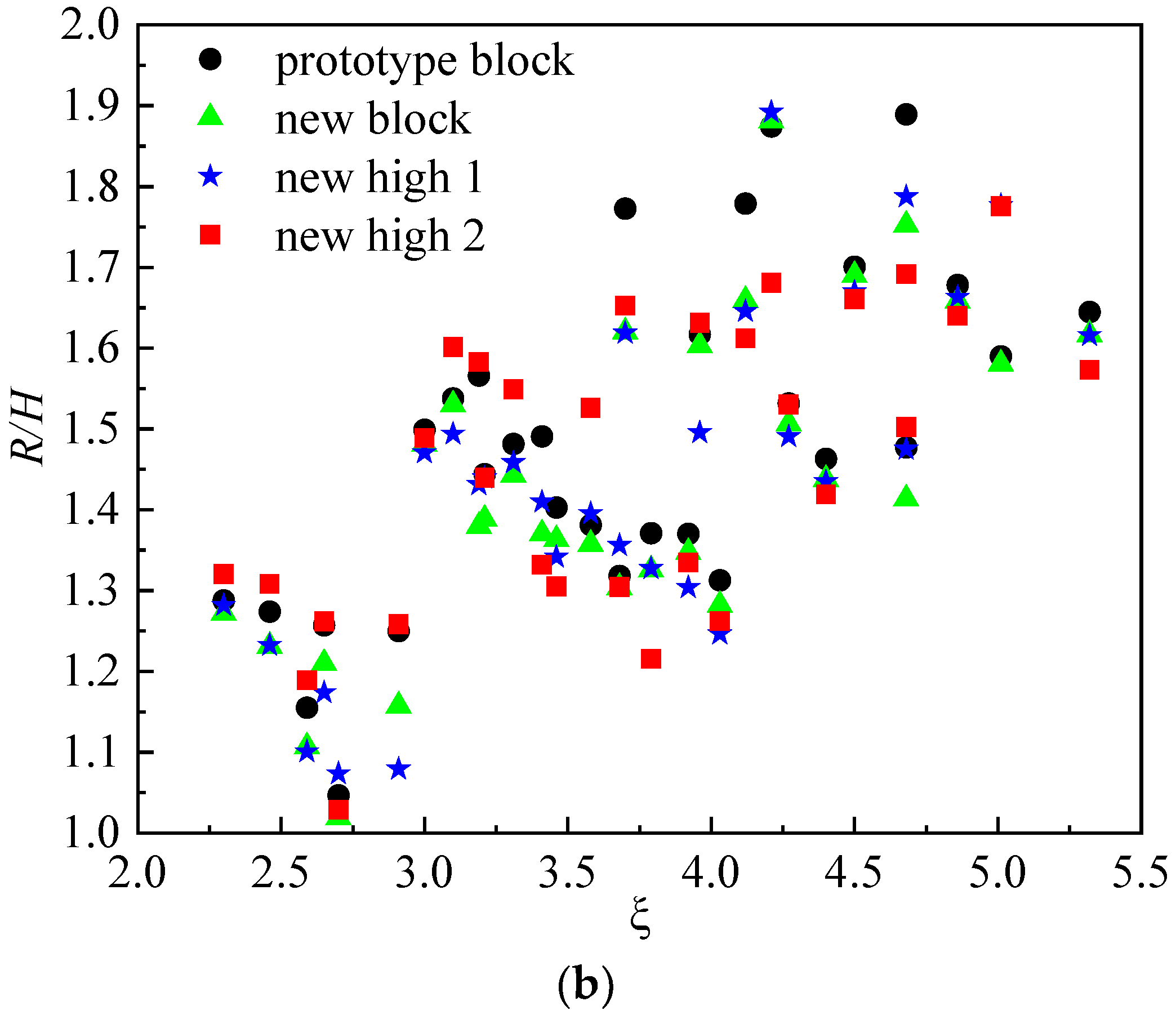
3.4. Influence of the Average Breaking Parameter ξ on the Reflection Coefficient and Wave Run-Up of New Blocks
4. Conclusions
- (1)
- The effects on the reflection coefficients of the new blocks are investigated by varying the incident wave height, period, water depth, and slope gradient. The results show that as the slope gradient increases from 1:1.5 to 1:3, the reflection coefficient of the new block decreases continuously. The reflection coefficient decreases with increasing wave run-up height and decreasing period. In addition, it was found that the relative water depth had little effect on the reflection coefficient.
- (2)
- The effect on the wave run-up height in the new block was investigated by varying the incident wave height, period, water depth, and slope gradient. The results showed that as the slope gradient decreases, the relative run-up height decreases sharply. The wave run-up height increases as the wave height and period increase.
- (3)
- By comparing the reflection coefficient and wave run-up height between the new block and the conventional block, it is concluded that the reflection coefficient of the new block is lower than that of the conventional block and further decreases with the elevation of the frame of the planting groove, but the wave run-up height of the new block does not significantly decrease with the elevation of the frame of the planting groove
- (4)
- Changing the average breaking parameter ξ has an effect on the reflection coefficient and wave run-up in the new block. As ξ increases gradually from 2.3 to 5.32, the reflection coefficient and wave run-up height increase with ξ. When ξ reaches 2.9 and 4.1, the reflection coefficient increases significantly and the wave run-up decreases substantially. Compared to the average reflection coefficients of the conventional quadrilateral hollow blocks, the average reflection coefficients of the new blocks were reduced by 4.25%, the average reflection coefficients of the new height 1 were reduced by 11.66%, and the average reflection coefficients of the new height 2 were reduced by 18.86%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scaravaglione, G.; Latham, J.P.; Xiang, J.; Francone, A.; Tomasicchio, G.R. Historical overview of the structural integrity of Concrete Armour Units. Coast. Offshore Sci. Eng. 2022, 1, 68–98. [Google Scholar]
- Bruce, T.; van der Meer, J.W.; Franco, L.; Pearson, J.M. Overtopping performance of different armour units for rubble mound breakwaters. Coast. Eng. 2009, 56, 166–179. [Google Scholar] [CrossRef]
- Kudale, M.; Prakash, K.; Kudale, A. Performance of concrete armour units of breakwaters in India—A review. Int. J. Civ. Eng. Technol. 2021, 12, 54–66. [Google Scholar] [CrossRef]
- Safari, I.; Mouazé, D.; Ropert, F.; Haquin, S.; Ezersky, A. Hydraulic stability and wave overtopping of Starbloc® armored mound breakwaters. Ocean. Eng. 2018, 151, 268–275. [Google Scholar] [CrossRef]
- Park, Y.H.; Oh, Y.M.; Ahn, S.M.; Han, T.H.; Kim, Y.T.; Suh, K.D.; Won, D. Development of a new concrete armor unit for high waves. J. Coast. Res. 2019, 35, 719–728. [Google Scholar] [CrossRef]
- CN 108385609 B; A Comprehensive Type of Wave Damping Artificial Block and Embankment. Tianjin Research Institute for Water Transport Engineering: Tianjin, China, 2020. (In Chinese)
- Isobe, M. Impact of global warming on coastal structures in shallow water. Ocean. Eng. 2013, 71, 51–57. [Google Scholar] [CrossRef]
- Hosseinzadeh, N.; Ghiasian, M.; Andiroglu, E.; Lamere, J.; Rhode-Barbarigos, L.; Sobczak, J.; Sealey, K.S.; Suraneni, P. Concrete seawalls: A review of load considerations, ecological performance, durability, and recent innovations. Ecol. Eng. 2022, 178, 106573. [Google Scholar] [CrossRef]
- Rella, A.; Perkol-Finkel, S.; Neuman, A.; Sella, I. Challenges in applying ecological enhancement factors into coastal and marine concrete construction. In Coasts, Marine Structures and Breakwaters 2017: Realising the Potential; ICE Publishing: London, UK, 2018; pp. 823–832. [Google Scholar]
- Firth, L.B.; Thompson, R.C.; Bohn, K.; Abbiati, M.; Airoldi, L.; Bouma, T.J.; Bozzeda, F.; Ceccherelli, V.U.; Colangelo, M.A.; Evans, A.; et al. Between a rock and a hard place: Environmental and engineering considerations when designing coastal defence structures. Coast. Eng. 2014, 87, 122–135. [Google Scholar] [CrossRef]
- Gedan, K.B.; Kirwan, M.L.; Wolanski, E.; Barbier, E.B.; Silliman, B.R. The present and future role of coastal wetland vegetation in protecting shorelines: Answering recent challenges to the paradigm. Clim. Change 2011, 106, 7–29. [Google Scholar] [CrossRef]
- Meyer, D.L.; Townsend, E.C.; Thayer, G.W. Stabilization and erosion control value of oyster cultch for intertidal marsh. Restor. Ecol. 1997, 5, 93–99. [Google Scholar] [CrossRef]
- Piazza, B.P.; Banks, P.D.; La Peyre, M.K. The potential for created oyster shell reefs as a sustainable shoreline protection strategy in Louisiana. Restor. Ecol. 2005, 13, 499–506. [Google Scholar] [CrossRef]
- Dafforn, K.A.; Glasby, T.M.; Airoldi, L.; Rivero, N.K.; Mayer-Pinto, M.; Johnston, E.L. Marine urbanization: An ecological framework for designing multifunctional artificial structures. Front. Ecol. Environ. 2015, 13, 82–90. [Google Scholar] [CrossRef] [PubMed]
- Ido, S.; Shimrit, P.F. Blue is the new green–ecological enhancement of concrete based coastal and marine infrastructure. Eco-Log. Eng. 2015, 84, 260–272. [Google Scholar] [CrossRef]
- Rosenberger, D.; Marsooli, R. Benefits of vegetation for mitigating wave impacts on vertical seawalls. Ocean. Eng. 2022, 250, 110974. [Google Scholar] [CrossRef]
- Chapman, M.G.; Underwood, A.J. Evaluation of ecological engineering of “armoured” shorelines to improve their value as habitat. J. Exp. Mar. Biol. Ecol. 2011, 400, 302–313. [Google Scholar] [CrossRef]
- Sutton-Grier, A.E.; Wowk, K.; Bamford, H. Future of our coasts: The potential for natural and hybrid infrastructure to enhance the resilience of our coastal communities, economies and ecosystems. Environ. Sci. Policy 2015, 51, 137–148. [Google Scholar] [CrossRef]
- Mohamed, T.A.; Alias, N.A.; Ghazali, A.H.; Jaafar, M.S. Evaluation of environmental and hydraulic performance of bio-composite re-vetment blocks. Am. J. Environ. Sci. 2006, 2, 129–134. [Google Scholar]
- Scheres, B.; Schüttrumpf, H. Enhancing the ecological value of sea dikes. Water 2019, 11, 1617. [Google Scholar] [CrossRef]
- Le Xuan, T.; Ba, H.T.; Thanh, V.Q.; Wright, D.P.; Tanim, A.H.; Anh, D.T. Evaluation of coastal protection strategies and proposing multiple lines of defense under climate change in the Mekong Delta for sustainable shoreline protection. Ocean. Coast. Manag. 2022, 228, 106301. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; Shou, Y.; Liu, B.; Li, H.; Liu, B.; Chen, S.; Dong, S. Exploring the Ecological Impacts and Implementation Strategies of Reclamation in Taiping Bay of Dalian Port as an Example. J. Taiwan Inst. Chem. Eng. 2023, in press. [Google Scholar] [CrossRef]
- Martínez, J.G.; Bezner, M.; Molenkamp, A.; van den Bos, J.; Hofland, B.; Leblanc, P.; Rella, A.; Rosenberg, Y.; Sella, I.; Martinez, G.; et al. Physical Evaluation of the Hydrodynamic Stability of an Eco-engineered Armouring Unit. Coast. Eng. Proc. 2022, 37, 35. [Google Scholar] [CrossRef]
- Dutykh, D.; Labart, C.; Mitsotakis, D. Long wave run-up on random beaches. Phys. Rev. Lett. 2011, 107, 184504. [Google Scholar] [CrossRef] [PubMed]
- Torsvik, T.; Abdalazeez, A.; Dutykh, D.; Denissenko, P.; Didenkulova, I. Dispersive and nondispersive nonlinear long wave transformations: Numerical and experimental results. In Applied Wave Mathematics II: Selected Topics in Solids, Fluids, and Mathematical Methods and Complexity; Springer: Cham, Switzerland, 2019; pp. 41–60. [Google Scholar]
- Durán, A.; Dutykh, D.; Mitsotakis, D. Peregrie’s system revisited. In Nonlinear Waves and Pattern Dynamics; Abcha, N., Pelinovsky, E., Mutabazi, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–43. [Google Scholar]
- Dutykh, D.; Katsaounis, T.; Mitsotakis, D. Finite volume schemes for dispersive wave propagation and runup. J. Comput. Phys. 2011, 230, 3035–3061. [Google Scholar] [CrossRef]
- Didenkulova, I.I.; Pelinovsky, E.N. Run-up of long waves on a beach: The influence of the incident wave form. Oceanology 2008, 48, 1–6. [Google Scholar] [CrossRef]
- De Bouard, A.; Craig, W.; Díaz-Espinosa, O.; Guyenne, P.; Sulem, C. Long wave expansions for water waves over random topography. Nonlinearity 2008, 21, 2143. [Google Scholar] [CrossRef][Green Version]
- Ma, Y.; Zhu, L.; Peng, Z.; Xue, L.; Zhao, W.; Li, T.; Lin, S.; Bouma, T.J.; Hofland, B.; Dong, C.; et al. Wave attenuation by flattened vegetation (Scirpus mariqueter). Front. Mar. Sci. 2023, 10, 1106070. [Google Scholar] [CrossRef]
- Bouma, T.J.; Vries, M.D.; Low, E.; Kusters, L.; Herman, P.M.J.; Tanczos, I.C.; Temmerman, S.; Hesselink, A.; Meire, P.; Regenmortel, S.V. Flow hydrodynamics on a mudflat and in salt marsh vegetation: Identifying general relationships for habitat characterisations. Hydrobiologia 2005, 540, 259–274. [Google Scholar] [CrossRef]
- Anderson, M.E.; Smith, J.M. Wave attenuation by flexible, idealized salt marsh vegetation. Coast. Eng. 2014, 83, 82–92. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J. A paradigm shift in the quantification of wave energy attenuation due to saltmarshes based on their standing biomass. Sci. Rep. 2022, 12, 13883. [Google Scholar] [CrossRef]
- Goda, Y.; Suzuki, Y. Estimation of incident and reflected waves in random wave experiments. In Coastal Engineering; American Society of Civil Engineers: Reston, VA, USA, 1976; pp. 828–845. [Google Scholar]
- Mansard, E.P.D.; Funke, E.R. The Measurement of Incident and Reflected Spectra Using a Least Squares Method. In Coastal Engineering; American Society of Civil Engineers: Reston, VA, USA, 1980. [Google Scholar]
- Van der Meer, J.W.; Allsop, N.W.H.; Bruce, T.; de Rouck, J.; Kortenhaus, A.; Pullen, T.; Schüttrumpf, H.; Troch, P.; Zanuttigh, B. EurOtop, 2018. Manual on Wave Overtopping of Sea Defences and Related Structures; University of Bologna: Bologna, Italy, 2018. [Google Scholar]
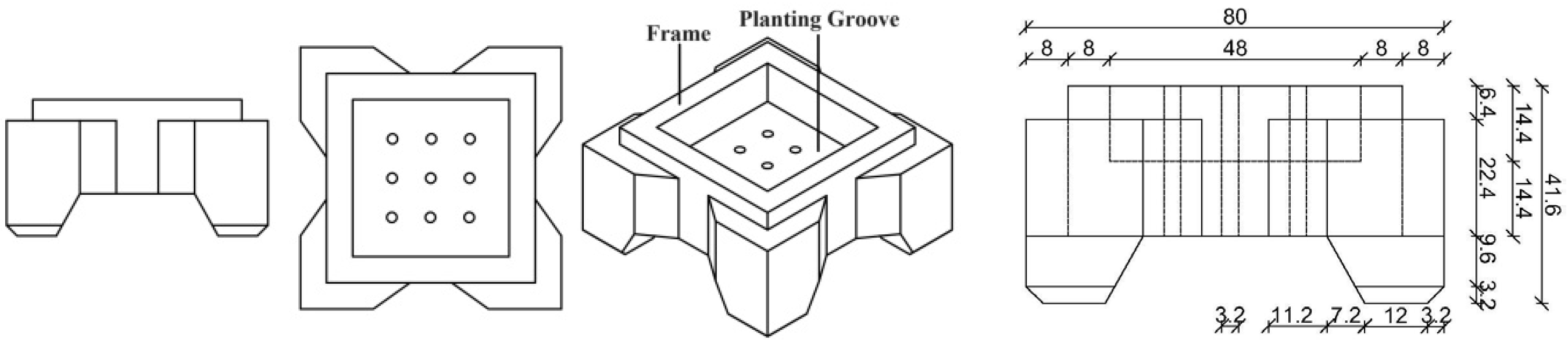







| Block Type | Length/m | Wide/m | Frame Height/m | Height/m |
|---|---|---|---|---|
| Conventional block | 2 | 2 | / | 1.2 |
| New block | 2 | 2 | 0.16 | 1.04 |
| New High 1 | 2 | 2 | 0.32 | 1.2 |
| New High 2 | 2 | 2 | 0.48 | 1.36 |
| Block Type | Slope Gradient m | Water Depth d/m | Period T/s | Wave Height H/m |
|---|---|---|---|---|
| Conventional block | 1:2 | 8.75 | 5.6, 8.95, 12.3, 15.65 | 1.25, 1.5, 1.75, 2.0 |
| 7.5, 10 | 8.95 | 1.25, 1.5, 1.75, 2.0 | ||
| 7.5, 10 | 5.6, 12.3, 15.65 | 1.5 | ||
| New block | 1:1.5, 1:2, 1:2.5, 1:3 | 7.5, 8.75, 10 | 5.6, 8.95, 12.3, 15.65 | 1.25, 1.5, 1.75, 2.0 |
| New High 1 | 1:2 | 8.75 | 5.6, 8.95, 12.3, 15.65 | 1.25, 1.5, 1.75, 2.0 |
| 7.5, 10 | 8.95 | 1.25, 1.5, 1.75, 2.0 | ||
| 7.5, 10 | 5.6, 12.3, 15.65 | 1.5 | ||
| New High 2 | 1:2 | 8.75 | 5.6, 8.95, 12.3, 15.65 | 1.25, 1.5, 1.75, 2.0 |
| 7.5, 10 | 8.95 | 1.25, 1.5, 1.75, 2.0 | ||
| 7.5, 10 | 5.6, 12.3, 15.65 | 1.5 |
| Block Type | Slope Gradient m | Water Depth d/m | Period T/s | Wave Height H/cm |
|---|---|---|---|---|
| Prototype block | 1:2 | 0.35 | 1.12, 1.79, 2.46, 3.13 | 5, 6, 7, 8 |
| 0.3, 0.4 | 1.79 | 5, 6, 7, 8 | ||
| 0.3, 0.4 | 1.12, 2.46, 3.13 | 6 | ||
| New block | 1:1.5, 1:2, 1:2.5, 1:3 | 0.3, 0.35, 0.4 | 1.12, 1.79, 2.46, 3.13 | 5, 6, 7, 8 |
| New High 1 | 1:2 | 0.35 | 1.12, 1.79, 2.46, 3.13 | 5, 6, 7, 8 |
| 0.3, 0.4 | 1.79 | 5, 6, 7, 8 | ||
| 0.3, 0.4 | 1.12, 2.46, 3.13 | 6 | ||
| New High 2 | 1:2 | 0.35 | 1.12, 1.79, 2.46, 3.13 | 5, 6, 7, 8 |
| 0.3, 0.4 | 1.79 | 5, 6, 7, 8 | ||
| 0.3, 0.4 | 1.12, 2.46, 3.13 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Ding, F.; Ye, J.; Jiang, H.; Chen, W.; Gu, W.; Yu, G.; Li, Q. Physical Experimental Study on the Wave Reflection and Run-Up of a New Ecological Hollow Cube. J. Mar. Sci. Eng. 2024, 12, 664. https://doi.org/10.3390/jmse12040664
Zhao H, Ding F, Ye J, Jiang H, Chen W, Gu W, Yu G, Li Q. Physical Experimental Study on the Wave Reflection and Run-Up of a New Ecological Hollow Cube. Journal of Marine Science and Engineering. 2024; 12(4):664. https://doi.org/10.3390/jmse12040664
Chicago/Turabian StyleZhao, Haitao, Feiyue Ding, Junwei Ye, Huabin Jiang, Wei Chen, Weifang Gu, Gengfeng Yu, and Qiang Li. 2024. "Physical Experimental Study on the Wave Reflection and Run-Up of a New Ecological Hollow Cube" Journal of Marine Science and Engineering 12, no. 4: 664. https://doi.org/10.3390/jmse12040664
APA StyleZhao, H., Ding, F., Ye, J., Jiang, H., Chen, W., Gu, W., Yu, G., & Li, Q. (2024). Physical Experimental Study on the Wave Reflection and Run-Up of a New Ecological Hollow Cube. Journal of Marine Science and Engineering, 12(4), 664. https://doi.org/10.3390/jmse12040664






