Dynamic Analysis of a Moored Spar Platform in a Uniform Current: Fluid Load Prediction Using a Surrogate Model

Abstract

A moored spar platform, equipped with various instruments, serves as a crucial tool in hydrological monitoring. However, conducting dynamic analyses of a single spar that endures wind and current requires significant amount of computational time. To address this challenge, this study proposes an efficient surrogate model to represent fluid loads. A database is established to capture the relationship between fluid loads, spar displacements and uniform currents based on a numerical model of the spar. Subsequently, an artificial neural network method is employed to construct the surrogate model. Finally, the surrogate model is integrated with a numerical model of the cable, developed using the lumped mass method, to create a coupled model of the moored spar. The dynamic responses of this coupled model align closely with those obtained from the purely numerical model, demonstrating the efficacy of the surrogate model in capturing fluid loads on the spar. In addition to the surrogate model generation approach, this research provides an efficient method to couple the surrogate model with the numerical model in dynamic analysis of floating systems in uniform currents.

1. Introduction

The development and utilization of marine resources, along with the growth of the marine industry, have garnered significant international attention [1,2]. Notably, the development and utilization of offshore wind energy are currently encountering new opportunities globally [3,4]. Floating offshore wind turbine (FOWT) technology, as a promising new type of wind power technology, provides an effective solution for deep-sea wind energy development. Consequently, it has become a frontier of and hotspot in offshore wind power generation research both domestically and internationally [5,6]. While the potential of offshore wind energy significantly surpasses that of land-based resources, designing FOWTs poses challenges. These challenges primarily stem from the impact forces caused by the motion of the seawater during extreme weather events such as typhoons and rainstorms. FOWTs, thanks to the moored system, experience smaller impact forces compared to fixed offshore wind turbines. However, the fluctuation introduces additional motions to FOWTs. The inertia force caused by this fluctuation is a significant component of external force, necessitating that the design, operation and maintenance of FOWTs consider dynamic responses [7,8]. The multi-body dynamics (MBDs) method is a common simulation method used to analyze the dynamic responses of complex mechanical systems due to its flexible expression of constraints [9]. The mass matrix, external force and constraint equations are the three components of the MBDs method. For FOWTs, the mass matrix is determined by its material and geometrical shape, while constraint equations depend on the kinematic pairs between components. The external forces comprise air-inducted forces acting on the rotor and tower and wave and current-induced forces acting on the platform and the moored system [10,11,12]. Additionally, vortex-induced vibrations (VIVs) are easily generated due to the slender structure, and they affect the fatigue life of spar platforms and mooring cables [13]. The VIVs of FOWTs have been studied by Rodolfo using physical experiments [14,15], and the effects of helical strakes on reducing the s of spar platforms were investigated by Daniel [16]. The dynamic response of wind turbine towers was simulated by combining the van der Pol equation and Hamilton’s principle, taking VIVs into account [17]. Since this article aims to introduce a surrogate model to replace the numerical model, the modeling theory is based on the numerical model of the moored spar platform developed by Zhu [18,19]. The assumptions of this article are listed below:

• The current velocity is uniform across the water depth.
• Wave-induced loads and vortex-induced vibrations are ignored.
• The hydrodynamic loads are expressed by using the Morison formula, and the influence of the structure on the current is ignored.
• The hydrodynamic coefficients in the Morison formula refer to our previous work [18,19], and the differences in the coefficients in different sea states are ignored.
• The three chains used in FOWTS are simplified as three slender ropes herein.

This article aims to study the applicability of a surrogate model, which reduces the computational time of complex parts of external forces in the numerical model. Although some external forces, including wave-induced loads and vortex-induced vibration, are ignored to simplify the verification process, the applicability of the surrogate model can still be verified by comparing a purely numerical model with a numerical–surrogate coupled model. Morison proposed that hydrodynamic force acting on slim cylinder structures comprises a viscous drag force and an additional mass inertia force, which depend on the relative velocities and relative accelerations between structures and fluid, respectively. Because the current-induced force only acts on submerged bodies, determining the submerged part before calculating the force is essential. The submerged part is determined by using the relative positions and attitudes of platforms and seawater. Therefore, the independent variables of current-induced force include positions, attitudes, velocities and accelerations. Considering the Morison formula and the method for calculating the size of the submerged part, the relationship between current-induced force and independent variables becomes complex, which reduces the computational efficiency of a dynamical analysis. To improve the computational efficiency, a surrogate model which calculates the current-induced force efficiently has been established.

The surrogate model method was first proposed in an optimization study, which reduced the computational complexity from design variables to constraints and objective functions [20,21]. In our previous work, an ANN-based surrogate model was established to represent the relationship between viscous drag force and the motions of irregular structures in deep-towed seismic exploration system [22,23]. Due to the advantages of the surrogate model, the surrogate model method is applied to calculate the current-induced force acting on FOWTs herein. To verify the feasibility of the method, a FOWT with moored system is simplified to be a cylinder spar with three moored cables. Variables selection, database establishment and algorithm selection are three important steps in establishing a surrogate model. The fluid loads in uniform current contain the viscous drag force, additional mass inertia force and buoyancy. The viscous drag force is influenced by the submerged part and relative velocities include translational velocities, rotational velocities and current velocity. Therefore, the viscous drag force is affected by heave, roll, pitch, translational velocities, rotational velocities of the spar and the current velocity. The buoyancy depends on the submerged height. The additional mass inertia force can be calculated by using an additional mass inertia matrix and the relative acceleration of the spar. The additional mass inertia matrix of a completely submerged cylinder is a constant matrix in the body coordinate system, while the matrix of a semi-submerged cylinder is a variable of the submerged height. Because the additional mass inertia force is related to acceleration, which should be calculated in the equation for the motion of MBDs, it is calculated directly within body coordinate system. The computational time taken to calculate the viscous drag force constitutes the major part of calculating the fluid loads. Therefore, both the viscous drag force and the apparent weight are calculated by using a surrogate model to reduce the computational time herein. Combined with the above discussion, the output variables of the surrogate model are viscous drag force and apparent weight, and the input variables of the surrogate model are heave, roll, pitch, translational velocities, rotational velocities and current velocity.

The sample distribution in the database is configured to reflect real conditions, resulting in there being two distinct sections in this study: a large fluctuation data section and a steady-state data section. The large amount of fluctuation data correspond to extreme shock conditions, while the steady-state fluctuation data correspond to dynamic equilibrium conditions. To ensure that the database has a reasonable distribution, the input variables of these two sections have uniform distributions, with each section containing 1,000,000 sample data points. A numerical model of a spar, implemented in the MATLAB(R2020a) platform, can be used to calculate the viscous drag force and apparent weight. The input variables set by distribution and the output variables calculated by the MATLAB program are collected to establish the database. There are several algorithms available for establishing a surrogate model, including the Kriging model, Radial basis function (RBF) and artificial neural network (ANN) [24,25,26]. The Kriging model assumes that the mapping relationship is stationary, meaning that the average of the output values corresponding to different input values is the same [27]. This assumption makes it unsuitable for tasks involving viscous drag prediction. RBF is a local approximation method, and it does not provide output values if the input variables are far away from the range of the database [28,29]. On the other hand, ANN is a global approximation method that is widely used for approximating highly nonlinear relationships [30,31,32]. Due to the excellent performance of ANN in nonlinear tasks, it is employed to establish the surrogate model for predicting viscous drag force herein.

The accuracy of the surrogate model is verified in two ways in this study. Firstly, the root mean square error of the test set serves as an index to indicate the accuracy of the surrogate model [33]. Additionally, new external forces, namely wind loads, are introduced to verify the applicability of the surrogate model. Both the numerical–surrogate coupled dynamic model and the purely numerical model are simulated under three conditions: no wind, constant wind and sinusoidal wind, respectively. The simulation results indicated the introduction of the new external loads did not affect the accuracy of the surrogate model in predicting the fluid loads. Therefore, the surrogate model can be used to replace the numerical model, which requires a much longer computational time, and the coupled model holds significant application value in predicting the fluid loads inducted by uniform currents. The remainder of this paper is organized as follows: the numerical modeling of the moored spar platform, including the spar, cable, connection and environment load models, is described in Section 2; the establishment of the surrogate model, including the data acquisition and artificial network neural prediction, is presented in Section 3; and the coupled model and simulation results under three conditions are shown in Section 4. Finally, the conclusions and future prospects are presented in Section 5.

2. Numerical Model

Sample data are the foundation of machine learning, and a sufficient amount of sample data is essential for training the surrogate model. The database is generated by using one numerical model in this research. Subsequently, the accuracy of the surrogate model is also verified by using the numerical model. Therefore, the numerical model of the moored spar is introduced here. The origin of the global frame is located at the still-water level, with the X-axis pointing east, the Z-axis pointing vertically upwards and the Y-axis pointing north according to the right-hand rule, as shown in Figure 1. The numerical model of the system includes the spar model, cable model, constraint model and environmental loads. These will be individually described in the following sections.

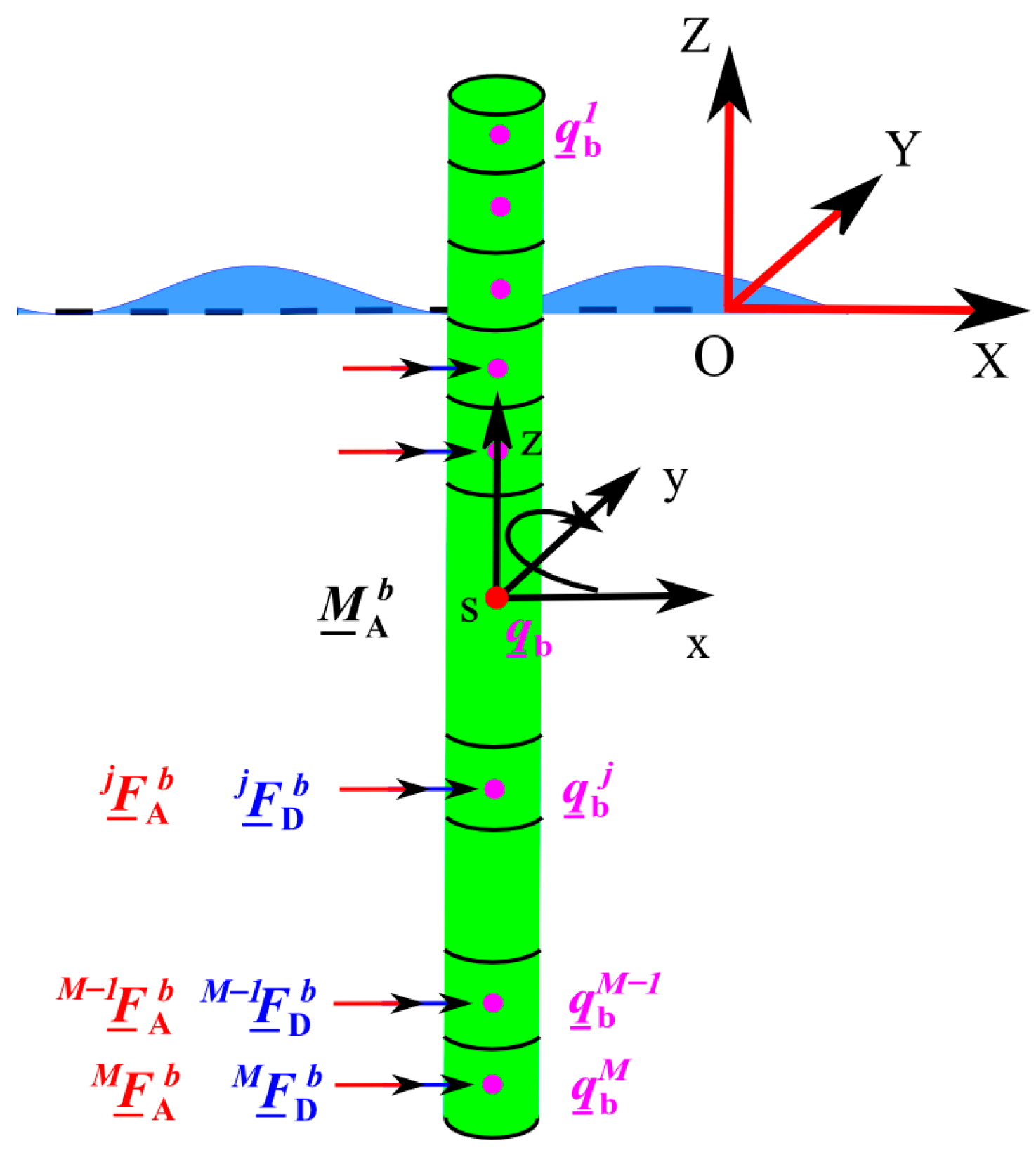
2.1. Spar Model

The origin of the spar frame is located at the geometric center of the spar platform, and the axes coincide with those of the global frame initially. The initial position of the spar is the undisplaced position at the still-water level. The spar modeling is axially divided into 100 elements, as shown in Figure 2. The modelling parameters of the spar are listed in

Table 1. Modelling parameters of spar platform.

Parameter	Value
Diameter Db/m	1.0
Mass Mb/kg	6000
Length Lb/m	12
Center of mass CM/m	−4
$\mathrm{Drag} \mathrm{coefficient} C_D^{\mathrm{b}}$	1.1
Added-mass coefficient $C_A^{\mathrm{b}}$	0.8
Cross-area Ab/m2	0.785

, referring to the DNV report [34].

The external forces acting on the spar platform consist of three parts: buoyancy and gravity ${\underset{\_}{F}}_B^{\mathrm{b}}$, added mass loads ${\underset{\_}{F}}_A^{\mathrm{b}}$ and hydrodynamic drag ${\underset{\_}{F}}_D^{\mathrm{b}}$.${\underset{\_}{F}}_A^{\mathrm{b}}$ and ${\underset{\_}{F}}_D^{\mathrm{b}}$ are concentrated at the center of the spar element, and correlated moments, $M_A^{\mathrm{b}}$, are added to translate these element forces to the origin of the spar frame. Details regarding the spar model can be found in the literature [18,19,35,36].

$$\begin{array}{l}{\underset{\_}{F}}_B^{\mathrm{b}}={\rho }_{\mathrm{f}}g{V}_0{\underset{\_}{\delta }}_{i3}-M^{\mathrm{b}}\underset{\_}{g}+{\underset{\_}{\underset{\_}{C}}}^{\mathrm{b}}{\underset{\_}{q}}^{\mathrm{b}},\\ {\underset{\_}{F}}_A^{\mathrm{b}}=-C_A^{\mathrm{b}}{V}_{\mathrm{s}}{\rho }_{\mathrm{f}}{\ddot{\underset{\_}{q}}}_g^{\mathrm{b}},\\ {\underset{\_}{F}}_D^{\mathrm{b}}=-\frac{1}{2}{C}_D^{\mathrm{b}}{\rho }_f{A}^{\mathrm{b}}‖{\underset{\_}{V}}_g^R‖{\underset{\_}{V}}_g^R,\\ M_A^{\mathrm{b}}={\displaystyle \sum _{j=1}^M{(}^{j,1}{F}_A^{\mathrm{b}}\hspace{0.33em}·\hspace{0.33em}{}^{j,3}{q}^{\mathrm{b}}+{}^{j,\mathrm{l}}{F}_D^{\mathrm{b}}\hspace{0.33em}·\hspace{0.33em}{}^{j,\mathrm{3}}{q}^{\mathrm{b}})}.\end{array}$$

(1)

where the vector ${\underset{\_}{\delta }}_{i3}$ denotes the $\rho g{V}_0$ and is active only in the Z axis, $M^{\mathrm{b}}\underset{\_}{g}$ is the weight of the spar and ${\underset{\_}{\underset{\_}{C}}}^{\mathrm{b}}{\underset{\_}{q}}^{\mathrm{b}}$ represents the buoyancy and restoring moments generated when the spar position is changed. Matrix ${\underset{\_}{\underset{\_}{C}}}^{\mathrm{b}}$ depends on the geometric shape of the spar, as shown in Equation (2). $C_A^{\mathrm{b}}$ is the added mass coefficient normal to the spar axis, $V_s$ represents the submerged volume of the spar, obtained by summing over the submerged spar elements. ${\rho }_{\mathrm{f}}$ and ${\ddot{\underset{\_}{q}}}_g^{\mathrm{b}}$ represent the acceleration of the spar element and the density of seawater, respectively. $C_D^{\mathrm{b}}$ and $A^{\mathrm{b}}$ represent the normal drag coefficient of the spar and the projection area of the spar element in the current direction, respectively. ${\underset{\_}{V}}_g^R$ is the relative velocity of the spar element in the seawater. $F_A^{\mathrm{b}}$ and $F_D^{\mathrm{b}}$ are active only when the spar element is submerged in the fluid. ${}^{j,\mathrm{l}}{F}_A^{\mathrm{b}}$ is the x-component of ${\underset{\_}{F}}_A^{\mathrm{b}}$ at the jth element, and ${}^{j,3}{q}^{\mathrm{b}}$ is the z-component of ${\underset{\_}{q}}^{\mathrm{b}}$, representing the position of the jth spar element in the spar frame.

$${\underset{\_}{\underset{\_}{C}}}^{\mathrm{b}}=\left(\begin{array}{cccccc}0\hfill & 0& 0& 0& 0& \hfill 0\\ 0\hfill & 0& 0& 0& 0& \hfill 0\\ 0\hfill & 0& 7.90\times {10}^3& 0& 0& \hfill 0\\ 0\hfill & 0& 0& -1.62\times {10}^5& 0& \hfill 0\\ 0\hfill & 0& 0& 0& -1.62\times {10}^5& \hfill 0\\ 0\hfill & 0& 0& 0& 0& \hfill 0\end{array}\right).$$

(2)

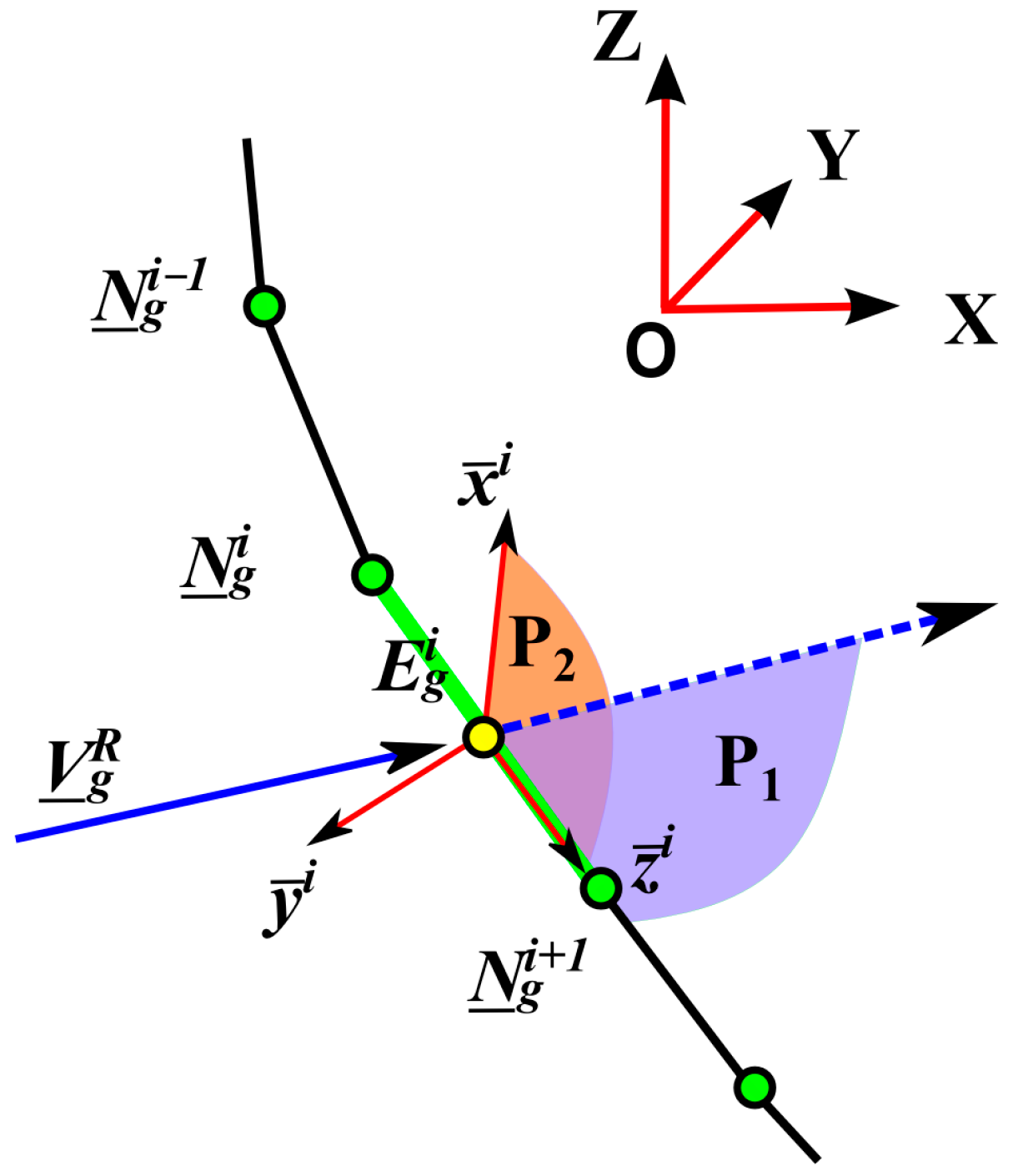
2.2. Cable Model

Each cable is divided into N elements from top to bottom with respect to the lumped mass method, as illustrated in Figure 1. Additionally, the relative velocity element frame is used to express the cable shape and external load [37], through which the rotation transformation matrix and formulas for external load can be effectively expressed. The element orientation vector ${\underset{\_}{E}}_g^i$ is represented by the positions of the terminal nodes ${\underset{\_}{N}}_g^i$ and ${\underset{\_}{N}}_g^{i+1}$, as shown in Equation (3). ${\underset{\_}{\dot{N}}}_g^i$ represents the velocity of the ith node, and the relative velocity ${\underset{\_}{V}}_g^R$ is the average relative velocity acting on the terminal nodes.

$$\begin{array}{l}{\underset{\_}{E}}_g^i={\underset{\_}{N}}_g^{i+1}-{\underset{\_}{N}}_g^i,\\ {\underset{\_}{V}}_g^R={\underset{\_}{V}}_g^f-\frac{{\underset{\_}{\dot{N}}}_g^{i+1}+{\underset{\_}{\dot{N}}}_g^i}{2}.\end{array}$$

(3)

$$\begin{array}{l}{\overline{z}}^i=\frac{{\underset{\_}{E}}_g^i}{‖{\underset{\_}{E}}_g^i‖},\\ {\overline{x}}^i=\frac{{\tilde{z}}^i{\underset{\_}{V}}_g^R}{‖{\tilde{z}}^i{\underset{\_}{V}}_g^R‖},\\ {\overline{y}}^i={\tilde{z}}^i{\overline{x}}^i.\end{array}$$

(4)

The unit axis ${\overline{z}}^i$ of the relative velocity element frame indicates the direction of the ith element, obtained by normalizing the element orientation vector ${\underset{\_}{E}}_g^i$, as shown in Figure 3. The unit axis ${\overline{x}}^i$ is perpendicular to plane $P_1$, which is composed of unit axis ${\overline{z}}^i$ and the relative velocity ${\underset{\_}{V}}_g^R$. According to the right-hand principle, unit axis ${\overline{y}}^i$ is perpendicular to the plane $P_2$ formed by the unit axes ${\overline{z}}^i$ and ${\overline{x}}^i$. The unit axes of the ith element are given specifically by Equation (4).

The forces acting on the cable include the cable tension, ${\underset{\_}{T}}_b^i$, damping force, ${\underset{\_}{D}}_b^i$, hydrodynamic drag forces, $F_z^i$ and $F_y^i$, and apparent weight, ${\underset{\_}{F}}_W^i$. These forces are expressed in detail in references [28,31] and are briefly listed below.

$$\begin{array}{l}{\underset{\_}{T}}_b^i=\frac{\pi d_{\mathrm{c}}^2}{4}E{\epsilon }_b^i\overline{z},\\ {\underset{\_}{D}}_b^i=C_d{\underset{\_}{\underset{\_}{A}}}^{iT}\left({\dot{N}}_g^{i+1}-{\dot{N}}_g^i\right)\overline{z},\\ F_z^i=\frac{\pi }{2}{C}_{\mathrm{f}}{\rho }_{\mathrm{f}}{d}^i{l}^i‖{\underset{\_}{V}}_g^R‖{\overline{z}}^T{\underset{\_}{V}}_g^R,\\ F_y^i=-\frac{1}{2}{C}_n{\rho }_{\mathrm{f}}{d}^i{l}^i‖{\underset{\_}{V}}_g^R‖{\overline{x}}^T\left(\tilde{z}{\underset{\_}{V}}_g^R\right),\\ {\underset{\_}{F}}_W^i=\left(m_{\mathrm{c}}^i-m_{\mathrm{f}}^i\right)\underset{\_}{g},\end{array}$$

(5)

where ${\epsilon }_b^i$ is the axial strain and $l^i$ represents the length of the ith cable element. The cable mass and the mass of displaced fluid $m_{\mathrm{c}}^i$ and $m_{\mathrm{f}}^i$ for the ith element are given as

$$\begin{array}{l}{\epsilon }_b^i=\frac{l^i-l_0^i}{l_0^i},\\ l^i=\sqrt{{\underset{\_}{E}}_g^{iT}{\underset{\_}{E}}_g^i},\\ m_{\mathrm{c}}^i=\frac{\pi d_c^2}{4}{l}_0^i{\rho }_{\mathrm{c}},\\ m_{\mathrm{f}}^i=\frac{\pi d_c^2}{4}{l}_0^i{\rho }_{\mathrm{f}}.\end{array}$$

(6)

The mass matrix of the ith element with respect to the element frame is given by Equation (7). The mass matrix of the nodes with respect to the global frame is represented by the mass matrix of the elements with respect to the element frame, and the added mass effect along the cable axial is ignored. Therefore, the mass matrix $M_I^i$ for the ith node is composed of the element mass matrices $M_b^{i-1}$ and $M_b^i$.

$$\begin{array}{l}{M}_b^i=\left(\begin{array}{ccc}{m}_{\mathrm{c}}^i+C_A{m}_{\mathrm{f}}^i& 0& 0\\ 0& m_{\mathrm{c}}^i+C_A{m}_{\mathrm{f}}^i& 0\\ 0& 0& m_{\mathrm{c}}^i\end{array}\right),\\ M_I^i=\frac{1}{2}{\underset{\_}{\underset{\_}{A}}}^{i-1}{M}_b^{i-1}{\underset{\_}{\underset{\_}{A}}}^{i-1\begin{array}{c} \end{array}\mathrm{T}}+\frac{1}{2}{\underset{\_}{\underset{\_}{A}}}^i{M}_b^i{\underset{\_}{\underset{\_}{A}}}^{i\begin{array}{c} \end{array}\mathrm{T}}.\end{array}$$

(7)

Finally, the forces acting on each cable element are shared equally by the terminal nodes of the element. The governing equation of the ith node is determined by the forces acting on the (i − 1)th and ith elements, as shown in Equation (8). The bottom of the cable is fixed to the seabed through the spring force $T^{\mathrm{spr}}$, and the first node of the cable is connected to the bottom of the floating platform through a ball joint. The modeling parameters of the cable are shown in

Table 2. Modelling parameters of mooring cables.

Parameter	Value
$\mathrm{Diameter} d_c$/m	0.05
$\mathrm{Density} {\rho }_c$/(kg·m–3)	3570
Elastic modulus E/GPa	2.38
$\mathrm{Damping} C_d$/(N·s·m–1)	−10,000
Transversal drag coef. Cn	1.15
Longitudinal drag coef. Cf	0.001
Added-mass coef. $C_A$	1
$\mathrm{Position} \mathrm{of} {\underset{\_}{N}}_g^1$/m $\mathrm{Position} \mathrm{of} {\underset{\_}{N}}_g^2$/m $\mathrm{Position} \mathrm{of} {\underset{\_}{N}}_g^3$/m	(1, 0, −1.4531) (−2.5, 0.433, −1.4531) (−2.5, −0.433, −1.4531)
$\mathrm{Position} \mathrm{of} {\underset{\_}{N}}_g^{N1}$/m $\mathrm{Position} \mathrm{of} {\underset{\_}{N}}_g^{N2}$/m $\mathrm{Position} \mathrm{of} {\underset{\_}{N}}_g^{N3}$/m	(120, 0, −50) (−60, 103.923, −50) (−60, −103.923, −50)
Single cable length S/m	142.5

.

$$M_I^i{\ddot{N}}_g^i={\underset{\_}{\underset{\_}{A}}}^i\left({\underset{\_}{T}}_b^i+{\underset{\_}{D}}_b^i+\frac{1}{2}{\underset{\_}{F}}_D^i\right)-{\underset{\_}{\underset{\_}{A}}}^{i-1}\left({\underset{\_}{T}}_b^{i-1}+{\underset{\_}{D}}_b^{i-1}-\frac{1}{2}{\underset{\_}{F}}_D^{i-1}\right)+\frac{1}{2}\left({\underset{\_}{F}}_W^i+{\underset{\_}{F}}_W^{i-1}\right).$$

(8)

2.3. Connection Model

The moored spar platform is composed of three mooring cables and one spar platform, and the spherical joint is defined here as connecting the spar platform to the cables. Additionally, the bottom of the cable is connected to the seabed by using spring forces.

2.3.1. Spherical Joint

A rigid body has six degrees of freedom in three dimensions, while a point mass has only three translational degrees of freedom. A three-dimensional spherical joint model has been well-developed in references [38,39], but it requires suitable modifications to connect the spar and the cable node, because each cable node has only three translational degrees of freedom. The constraint equation ${\underset{\_}{\Phi }}^{\mathrm{sph}}$ is expressed by Equation (9)

$$\begin{array}{l}{\underset{\_}{\Phi }}^{\mathrm{sph}}={\underset{\_}{q}}^{\mathrm{b}}+{\underset{\_}{\underset{\_}{A}}}^{\mathrm{b}}{\underset{\_}{s^{\prime }}}_k^{\mathrm{b}}-{\underset{\_}{q}}^1\\ {\underset{\_}{\underset{\_}{\Phi }}}_q^{\mathrm{sph}}=\left(\underset{\_}{\underset{\_}{I}}\begin{array}{c} \end{array}-{\underset{\_}{\underset{\_}{A}}}^{\mathrm{b}}{\underset{\_}{\underset{\_}{\widetilde{s^{\prime }}}}}_k^{\mathrm{b}}{{\underset{\_}{\underset{\_}{G}}}^{\prime }}^{\mathrm{b}}\begin{array}{c} \end{array}-\underset{\_}{\underset{\_}{I}}\right)\end{array}$$

(9)

where ${\underset{\_}{q}}^{\mathrm{b}}$ represents the origin of the spar frame with respect to the global frame, and ${\underset{\_}{\underset{\_}{A}}}^{\mathrm{b}}$ represents the rotation transformation matrix of the spar. Vector ${\underset{\_}{s^{\prime }}}_k^{\mathrm{b}}$ represents the position of the hinge node with respect to the spar frame. As it is the first node of the cable connected to the spar platform, ${\underset{\_}{q}}^1$ represents the position of the first node of the cable with respect to the global frame. ${\underset{\_}{\underset{\_}{\Phi }}}_q^{\mathrm{sph}}$ represents the Jacobian matrix of the constraint equation.${{\underset{\_}{\underset{\_}{G}}}^{\prime }}^{\mathrm{b}}$ expresses the relationship between the angular velocities and the Euler angles, as instructed by Shabana [39]. The Z-Y-X Euler angle set is adopted here, where ${{\underset{\_}{\underset{\_}{G}}}^{\prime }}^{\mathrm{b}}$ can be carried out according to the research by Greenwood [40]; and ${\underset{\_}{\underset{\_}{\widetilde{s^{\prime }}}}}_k^{\mathrm{b}}$ represents the skew symmetric of the position vector ${\underset{\_}{s^{\prime }}}_k^{\mathrm{b}}$. γ represents the dot product of the Jacobian matrix with the acceleration [38]. ${\underset{\_}{\dot{\theta }}}^{\mathrm{b}}$ and $\underset{\_}{{\omega }^{\prime }}$ are the angle velocities of the Euler angels and the spar platform in the spar frame.

$$\gamma =\left({\underset{\_}{\underset{\_}{A}}}^{\mathrm{b}}{\underset{\_}{\underset{\_}{\widetilde{{\omega }^{\prime }}}}}^{\mathrm{b}}{\underset{\_}{\underset{\_}{\widetilde{s^{\prime }}}}}_k^{\mathrm{b}}{{\underset{\_}{\underset{\_}{G}}}^{\prime }}^{\mathrm{b}}+{\underset{\_}{\underset{\_}{A}}}^{\mathrm{b}}{\underset{\_}{\underset{\_}{\widetilde{s^{\prime }}}}}_k^{\mathrm{b}}{{\underset{\_}{\underset{\_}{\dot{G}}}}^{\prime }}^{\mathrm{b}}\right){\underset{\_}{\dot{\theta }}}^{\mathrm{b}}.$$

(10)

2.3.2. Spring Force

The spring force is a linear function of the relative position and velocity between the bottom node of the cable $q^{N+1}$ and the seabed anchor point $P^{\mathrm{anchor}}$. The spring forces fix the cable on the seabed, and are carried out using three-by-three coefficient matrices K and C, as shown by

$$T^{\mathrm{spr}}=\mathit{K}\left(q^{N+1}-P^{\mathrm{anchor}}\right)+\mathit{C}\left({\dot{q}}^{N+1}-{\dot{P}}^{\mathrm{anchor}}\right)$$

(11)

where K and C are three-by-three coefficient matrices of the stiffness and damping, respectively. They are both diagonal matrices composed of coefficients $k_s$ and $c_s$, respectively. The values are listed in

Table 3. Modelling parameters of spring forces.

Parameter	Value
Stiffness coef. ks/(MN·m–1)	87.8
Damping coef. cs/(MN·s·m–1)	3.3

.

Finally, the equation of motion of the moored spar platform is expressed by

$$\left(\begin{array}{cc}M& {\begin{array}{c}\left({\mathbf{\Phi }}_q^{\mathrm{sph}}\right)\end{array}}^{\mathrm{T}}\\ {\mathbf{\Phi }}_q^{\mathrm{sph}}& 0\end{array}\right)\left(\begin{array}{c}\ddot{q}\\ \lambda \end{array}\right)=\left(\begin{array}{c}Q\\ \gamma \end{array}\right),$$

(12)

where M is the mass matrix of the system, and Q is the external forces of the system. The matrix ${\begin{array}{c}\left({\mathbf{\Phi }}_q^{\mathrm{sph}}\right)\end{array}}^{\mathrm{T}}$ represents the transposed Jacobian matrix.

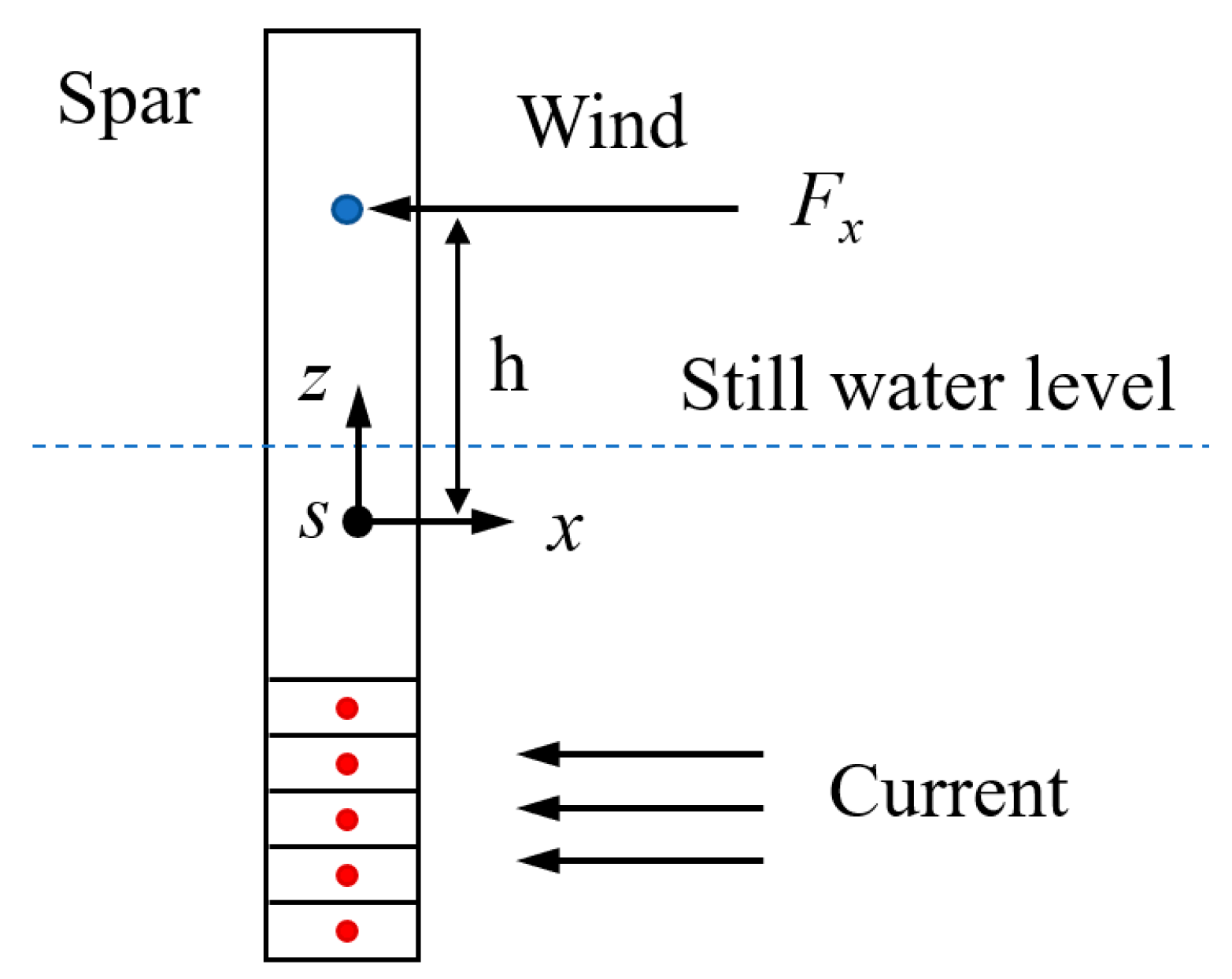
2.4. Environment Loads Model

The environmental loads consist of drag forces generated by the current and wind, which are introduced separately.

2.4.1. Current Model

The current velocity is assumed to be uniform across all water depths. The current velocity is denoted as ${\underset{\_}{V}}_g^{\mathrm{c}}$, which is composed of the X-directional component ${\underset{\_}{V}}_g^x$, and the Y-directional component ${\underset{\_}{V}}_g^y$, as shown in Equation (13).

$${\underset{\_}{V}}_g^c={\left(\begin{array}{ccc}{\underset{\_}{V}}_g^x& {\underset{\_}{V}}_g^y& 0\end{array}\right)}^{\mathrm{T}}$$

(13)

2.4.2. Wind Model

The wind loads are generated to test the applicability of the surrogate model. Because the wind loads are not considered in creating the surrogate model, the influence of the introduction of wind loads on the prediction accuracy of the surrogate model is verified here. Actually, the wind loads can be treated as the interference loads in the coupled model composed by the surrogate model and the numerical model. The wind loads are simplified as one concentrated load acting on a specified location within the spar, as shown in Figure 4. The wind loads are either a constant force or a sinusoidal force as shown in Equation (14).

$$\begin{array}{l}{F}_x=A\sin \left(\omega t\right)\\ M_y=F_x\cdot h\end{array}$$

(14)

where A is the amplitude of the sinusoidal wind loads, and $2\pi /\omega$ represents the period of the sinusoidal load. h is the position of action point in the spar frame. $M_y$ is the correlated moment generated by the X-direction wind loads.

3. Surrogate Model

Training a surrogate model requires a large amount of data. In general, the accuracy of the surrogate model depends primarily on the logical relationship between the selected inputs and outputs, the quantity of sample data and the machine learning algorithm employed.

3.1. Data Acquisition

The surrogate model is used to predict the external loads on the spar platform, which include the apparent weight, restoring moments, hydrodynamic drag forces and correlated moments. Because the mooring loads are not considered in the surrogate model, the surge, sway and yaw motions of the spar are not considered as input variables, while the translational velocities in the X- and Y-directions are considered to calculate the hydrodynamic drag forces. The restoring moments will be generated for the pitch and roll motions because the center of mass is lower than the center of buoyance. The relationships between the restoring moments and rotation angles are studied carefully. Additionally, the direction and magnitude of currents also impact the fluid loads on the spar. Therefore, this study sets the input variables as the heave, roll and pitch motions and the translational and rotational velocities, the current velocity and the output are three translational hydrodynamic drags and three restoring moments, as shown in

Table 4. Input parameters of large fluctuation state.

Parameter	Value Range
X-direction current velocity/(m/s)	[−0.1, 0.4]
Y-direction current velocity/(m/s)	[−0.1, 0.2]
Z-direction displacement/(m)	[−3.9, 1.1]
Roll/(rad)	[−0.35, 0.35]
Pitch/(rad)	[−0.5, 0.5]
X-direction velocity/(m/s)	[−0.6, 0.6]
Y-direction velocity/(m/s)	[−0.5, 0.5]
Z-direction velocity/(m/s)	[−1.5, 1.5]
Roll angular velocity (rad/s)	[−0.4, 0.4]
Pitch angular velocity (rad/s)	[−0.4, 0.4]

. The variable range of each parameter is specified referring to the stability requirements of the spar platform and the environmental conditions.

Considering that the spar platform tends to be in a steady state in a constant current, the occurrence probability of the steady state is high. The density of the steady-state status is increased, as shown in

Table 5. Input parameters of steady state fluctuation.

Parameter	Value Range
X-direction current velocity/(m/s)	[−0.1, 0.4]
Y-direction current velocity/(m/s)	[−0.1, 0.2]
Z-direction displacement/(m)	[−1.9, −0.9]
Roll/(rad)	[−0.05, 0.05]
Pitch/(rad)	[−0.1, 0.1]
X-direction velocity/(m/s)	[−0.05, 0.05]
Y-direction velocity/(m/s)	[−0.03, 0.03]
Z-direction velocity/(m/s)	[−0.05, 0.05]
Roll angular velocity (rad/s)	[−0.05, 0.05]
Pitch angular velocity (rad/s)	[−0.05, 0.05]

. Finally, the database is composed of two parts: large fluctuation data and steady-state fluctuation data. Each part contains 1 million sets of data.

This method enhances the efficiency of data acquisition and, based on the frequency probability of state occurrence in the dynamic process, increases the density of the steady-state data. This is of great significance for subsequent data analysis and model training, contributing to improving the accuracy of model predictions. Based on the numerical model of the spar, a random function is used to generate the sample data. The spar displacements, velocities and current velocity are randomly generated within specified ranges to obtain large and evenly distributed states for the spar platform. Additionally, the density of the steady state is increased according to the frequency probability of state occurrence in the dynamic process. Subsequently, except for the added mass force, the fluid loads on the spar are calculated for each of these states.

3.2. Artificial Neural Network Prediction

Due to the superior performance of regression algorithms in numerical data prediction, the fluid loads of the spar can be predicted by using regression algorithms. Generally, the regression algorithms include normal equations, polynomial regression algorithms, neural network regression algorithms, etc. [33,41,42]. And the artificial neural network (ANN) simulates the working principles of the human brain’s neural network, exhibiting powerful self-learning, self-organization and adaptive capabilities. Compared to other methods, ANN’s advantages are mainly evident in several aspects: 1. nonlinear mapping capabilities for capturing the nonlinear relationships of the fluid loads; 2. the ability to learn from extensive data to adapt to different input patterns, which accommodate variations in the fluid loads of a moored spar under different environmental conditions; 3. the ability to automatically learn the features of fluid dynamics from input data without manual extraction; 4. advantages in handling large-scale data, and 5. strong generalization abilities for predicting fluid loads [43,44,45,46]. The input variables in this study include heave, roll and pitch motions, translational and rotational velocities and current velocity. The output variables consist of three translational hydrodynamic resistances and three restoring moments. The relationship between the input and output variables is not a simple linear one; rather, it involves complex nonlinear connections. With a considerable number of input variables, the surrogate model needs to learn the intricate relationships among them, making the model more complex. Complex surrogate models require a substantial amount of data for training to avoid overfitting. Given the diverse changes in environment conditions and the complex variability of hydrodynamic loads on the spar platform, the surrogate model needs excellent generalization capabilities to predict the fluid loads in various intricate scenarios. Considering these factors, the study ultimately chooses to employ an ANN to construct the surrogate model.

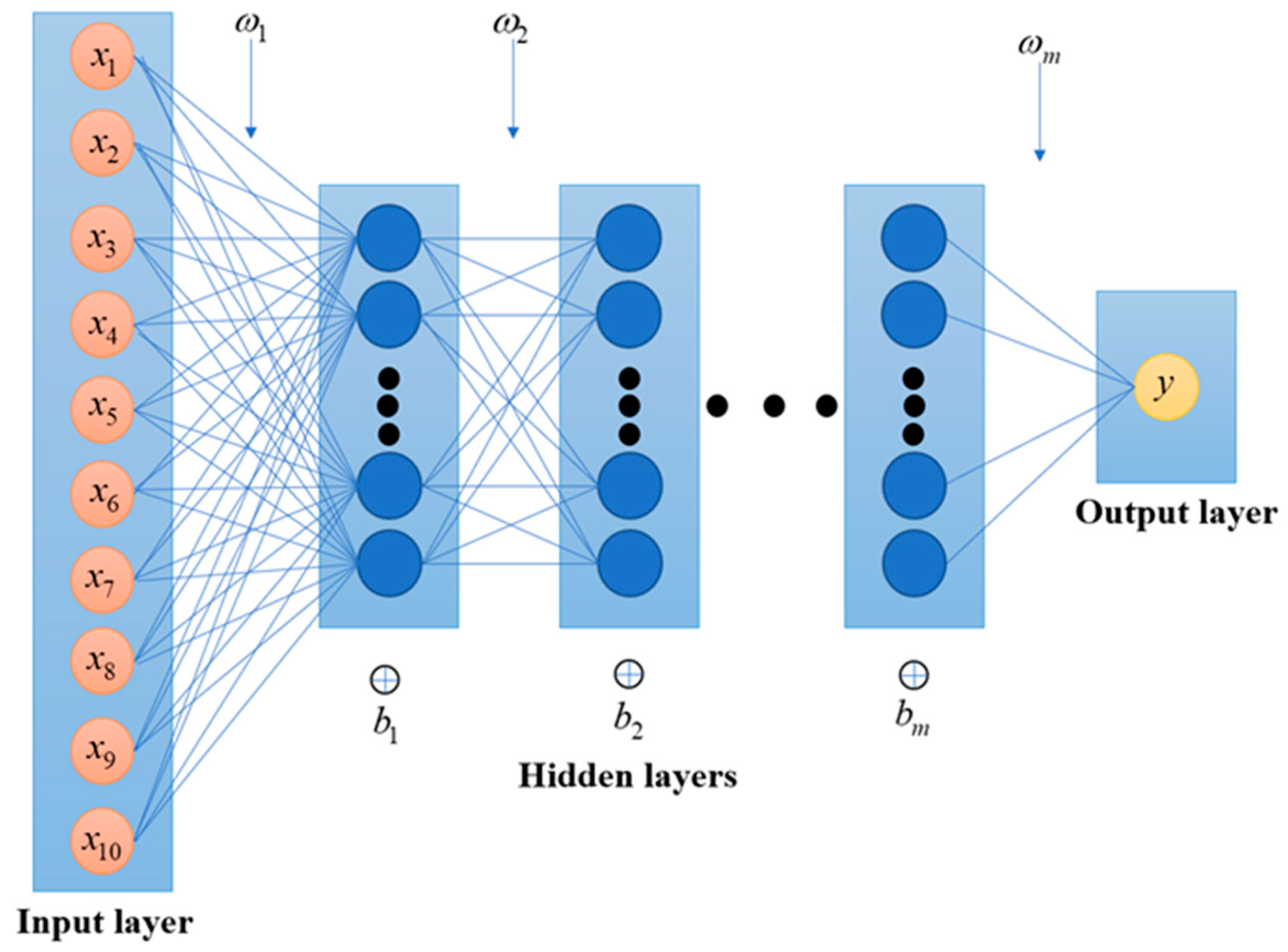
3.2.1. Neural Network Structure

The ANN is a type of multi-layer feedforward network. The key components of the ANN are neurons, forming a complex topology through weighted connections. The backpropagation learning algorithm is employed to construct the network, and the weight parameters are adjusted through gradient descent. To accurately reflect the characteristics of the fluid loads, the construction has ten input variables and five output variables, and each output variable has one independent neural network with all input variables. Each neural network model has ten input nodes and one output node, as illustrated in Figure 5.

3.2.2. Establishment of Neural Networks

The number of hidden layers and nodes in each layer significantly influences how difficult it is to train neural networks and their predictive performance. Generally, as the complexity of the neural network increases, the difficulty in training the network tends to rise, and simultaneously, the predictive performance improves. However, this improvement does not imply that higher complexity is always better, as excessive complexity can lead to overfitting, thereby reducing the model’s generalization ability. Regarding the number of hidden layers, some studies suggest that [47,48,49], with a sufficient number of nodes in the hidden layer, a neural network with a single hidden layer can approximate any nonlinear function. However, there is currently no explicit quantification formula for the number of nodes in the hidden layer. Rough estimates can be made based on empirical formulas [50,51].

$$N=\sqrt{n+m}+a$$

(15)

where N is the number of neurons in the hidden layer, n and m are the numbers of input and output nodes and a is a constant typically ranging between 1 and 10.

Considering the structure and complexity of the neural network, as well as the characteristics of the research problem, preliminary tests were conducted and iteratively adjusted. Based on the test results, the neural network models with six to ten hidden layers have been used to predict the forces and moments on the spar. The number of neurons in the hidden layers is within the range of 32 to 50 to provide a network structure with sufficient expressive power. And a grid search method has been employed to determine the number of neurons in each layer. This approach allows for a comprehensive search over different neuron quantities, facilitating the identification of the optimal network structure. After that, the original dataset is randomly divided into three parts: 60% of the data is allocated as the training set, used for training and fitting the model; 20% serves as the validation set, employed for adjusting the network structure and selecting the optimal number of neurons; and the remaining 20% constitutes the test set, utilized to assess the generalization ability of the final model. After adjustments to and the optimization of the validation set, the neural network model parameters shown in

Table 6. Neural network parameters.

Items	No. of Hidden Layers	No. of Nodes per Layer
Fx	6	32
Fy	10	50
Fz	10	32
Mx	6	50
My	10	32

were obtained for predicting different forces and moments. These parameters were obtained through conducting a grid search and performance evaluation on the validation set, ensuring the provision of the optimal network structure and parameter configuration for predicting each type of force and moment.

The accuracy of the surrogate model was measured using the root mean square error (RMSE): a smaller RMSE indicates higher accuracy of the surrogate model. The specific formula for RMSE is given in Equation (16)

$$RMSE=\sqrt{\frac{1}{N}\times {\displaystyle {\sum }_{i=1}^n{(y_i-f_i)}^2}}$$

(16)

where $f_i$ is the predicted values, and $y_i$ is the actual value.

The RMSE values for $F_x,F_y,F_z,M_x,M_y$ are shown in

Table 7. The RMSE of surrogate model.

Items	Net Structure	Initial Learn Rate	Attenuation Factor	Period	Epoch	RMSE
Fx	Input-32nodes × 6layers-output	0.01	0.99	300	40,000	0.008434
Fy	Input-50nodes × 10layers-output	0.01	0.99	300	40,000	0.009267
Fz	Input-32nodes × 10layers-output	0.01	0.99	300	40,000	0.001079
Mx	Input-50nodes × 6layers-output	0.01	0.9	300	40,000	0.009808
My	Input-32nodes × 10layers-output	0.01	0.99	300	40,000	0.007135

, all of which are at a low level. This clearly indicates that the surrogate model exhibits an extremely high accuracy in predicting the fluid loads on the spar platform.

4. Verification

Although the accuracy of the surrogate model has be verified by the test set from the database, the applicability of the surrogate model with the coupled cable model and the wind loads have not been verified. Therefore, the model of a moored spar platform, coupling the surrogate model and the cable model and wind loads, is introduced before the verification.

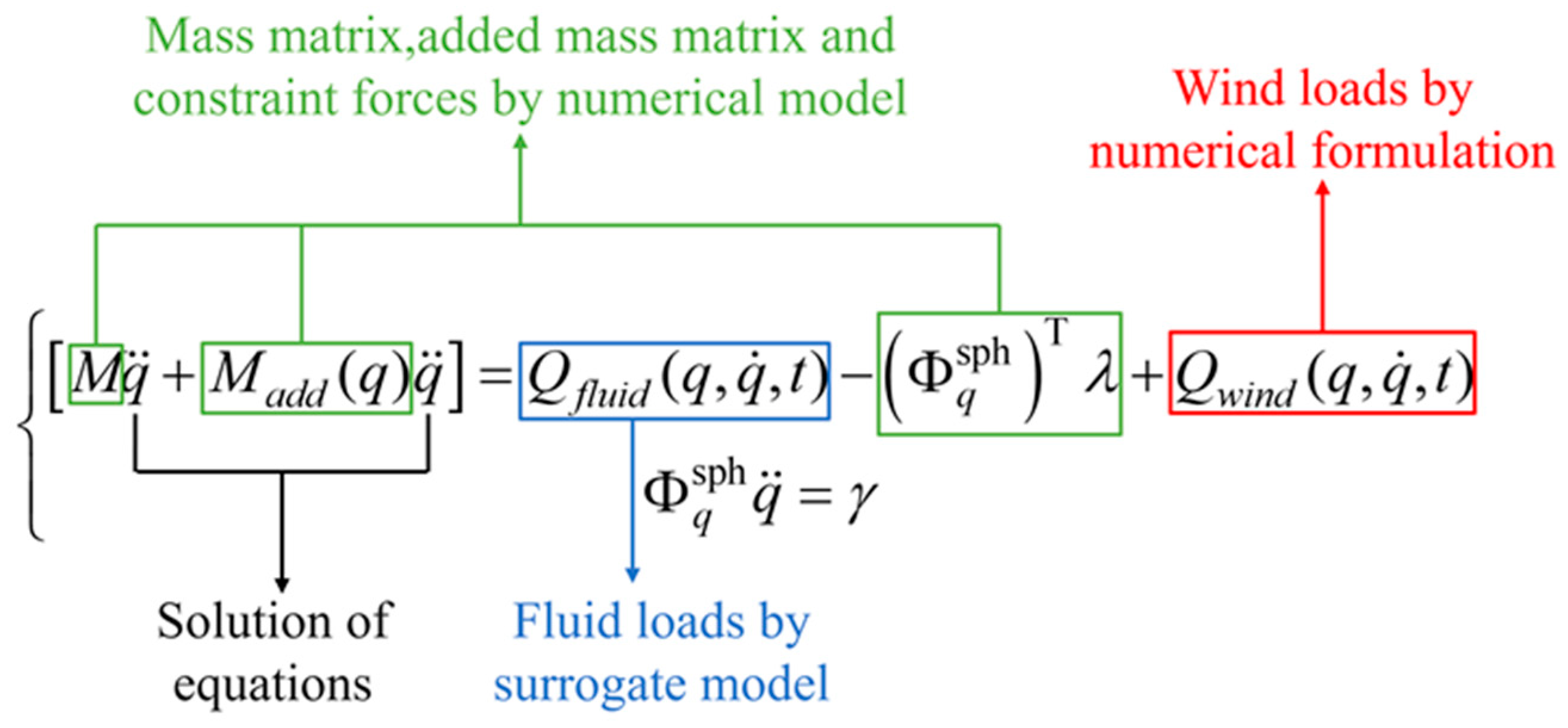
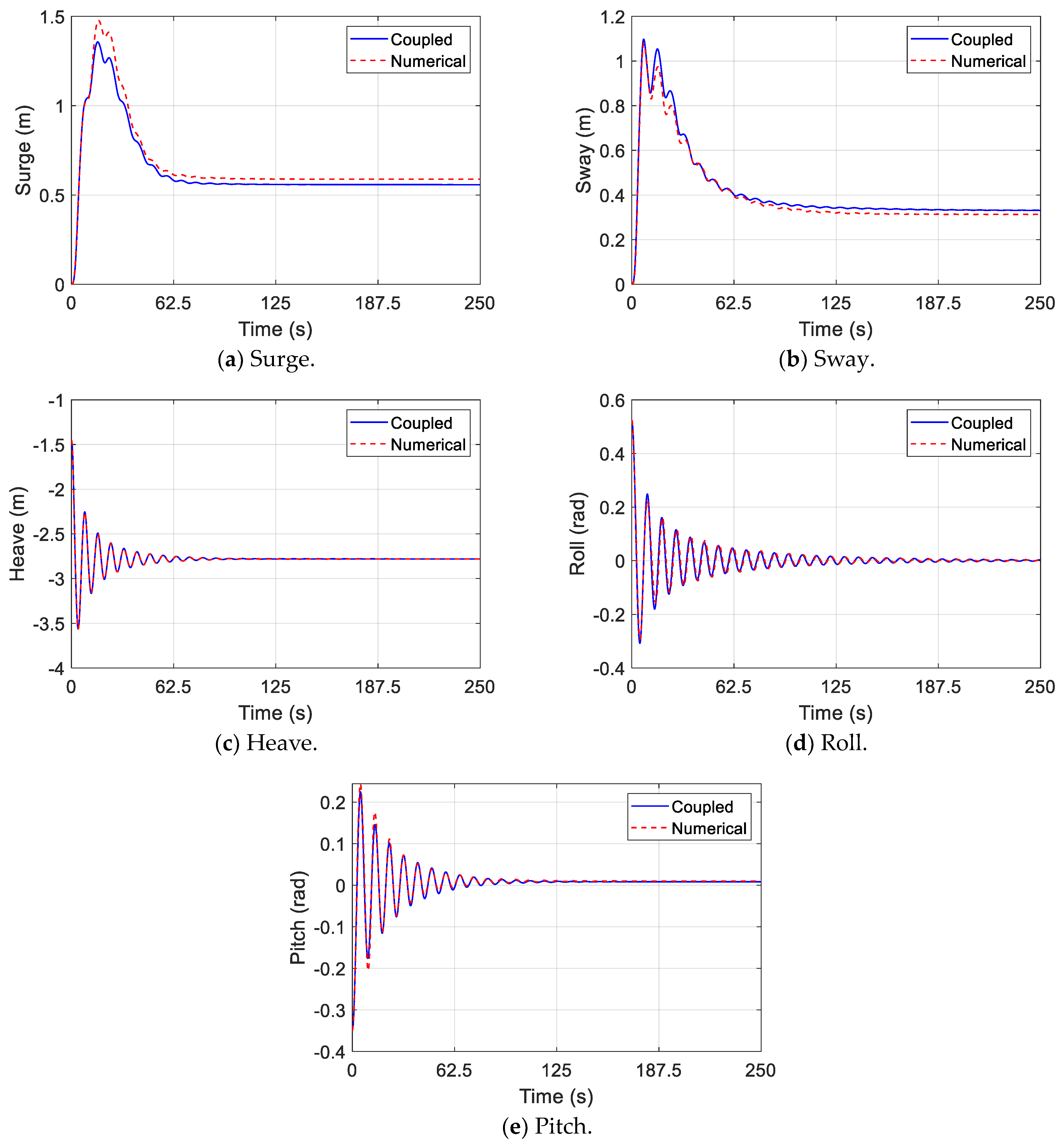
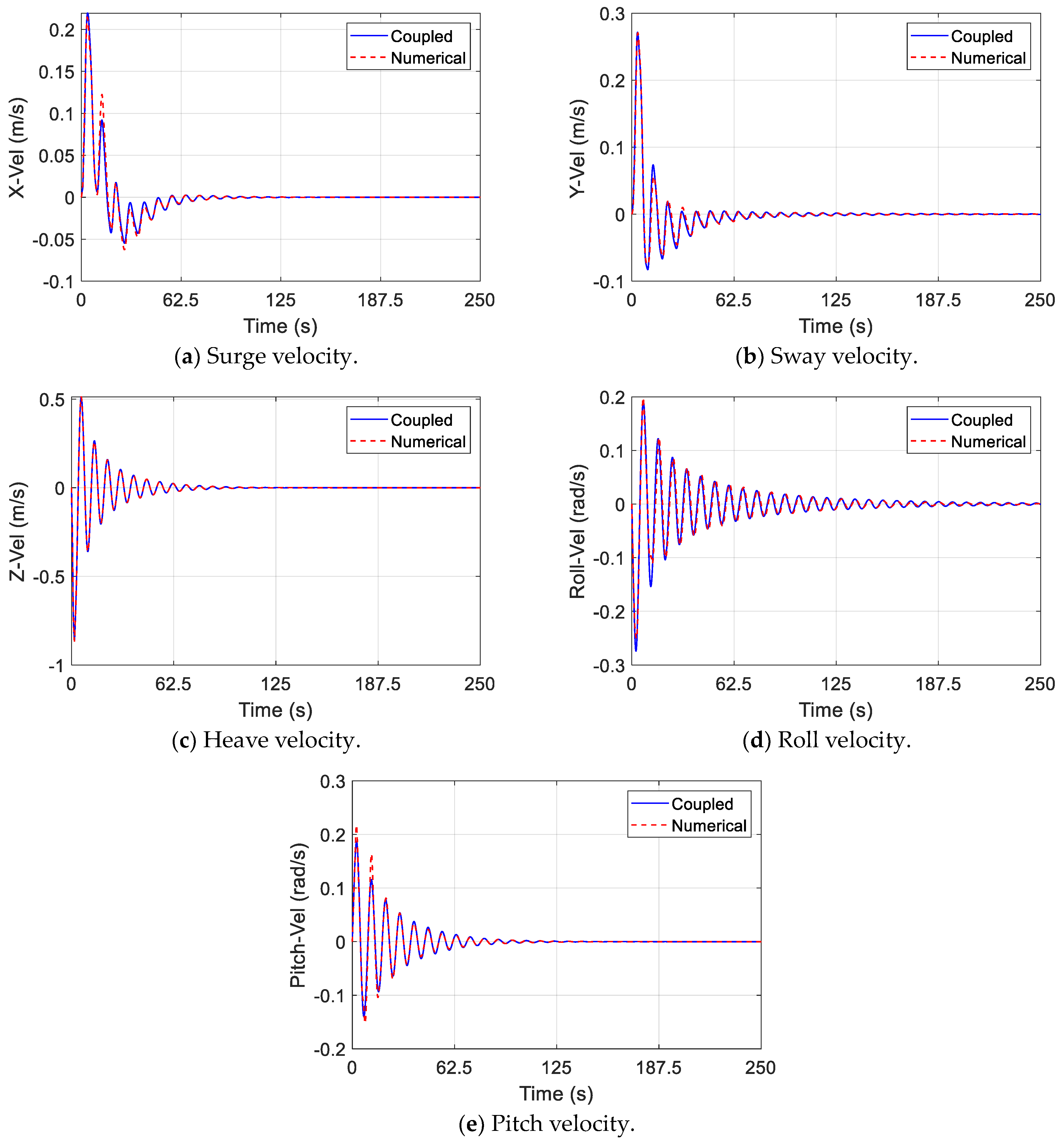
4.1. Coupled Model

According to the cable model and the connection model, three mooring cables are connected to the spar model, which are expressed in the surrogate model. The components of the coupled model are shown in Figure 6. The added mass forces are calculated by using the submerged volume which is a function of the heave, roll and pitch motions of the spar. The constraint loads are calculated by using the connection model and cable model. The wind loads, which can be treated as the interference forces here, are simplified as one sine function, as shown in Equation (14).

The dynamic responses of the moored spar obtained from the coupled model are compared with those obtained from the purely numerical model in three difference conditions: free fall without wind, subjected to constant wind and subjected to sine wind loads. The initial velocity of the spar platform is 0, and the initial displacement of the spar platform, along with the marine environment, are summarized in

Table 8. Initial parameters of the spar platform.

Parameter	Value
X-direction displacement/(m)	0
Y-direction displacement/(m)	0
Z-direction displacement/(m)	0
Roll/(rad)	pi/6
Pitch/(rad)	−pi/9
Yaw/(rad)	0
X-direction current velocity/(m/s)	0.2
Y-direction current velocity/(m/s)	0.1

.

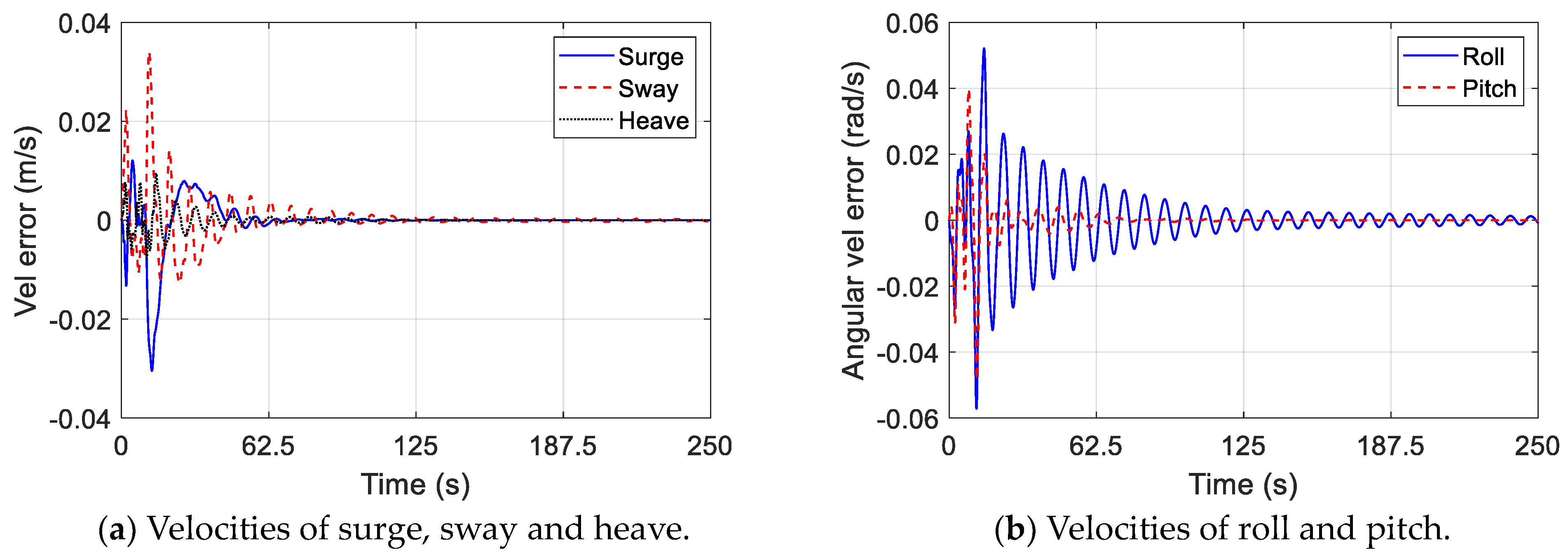
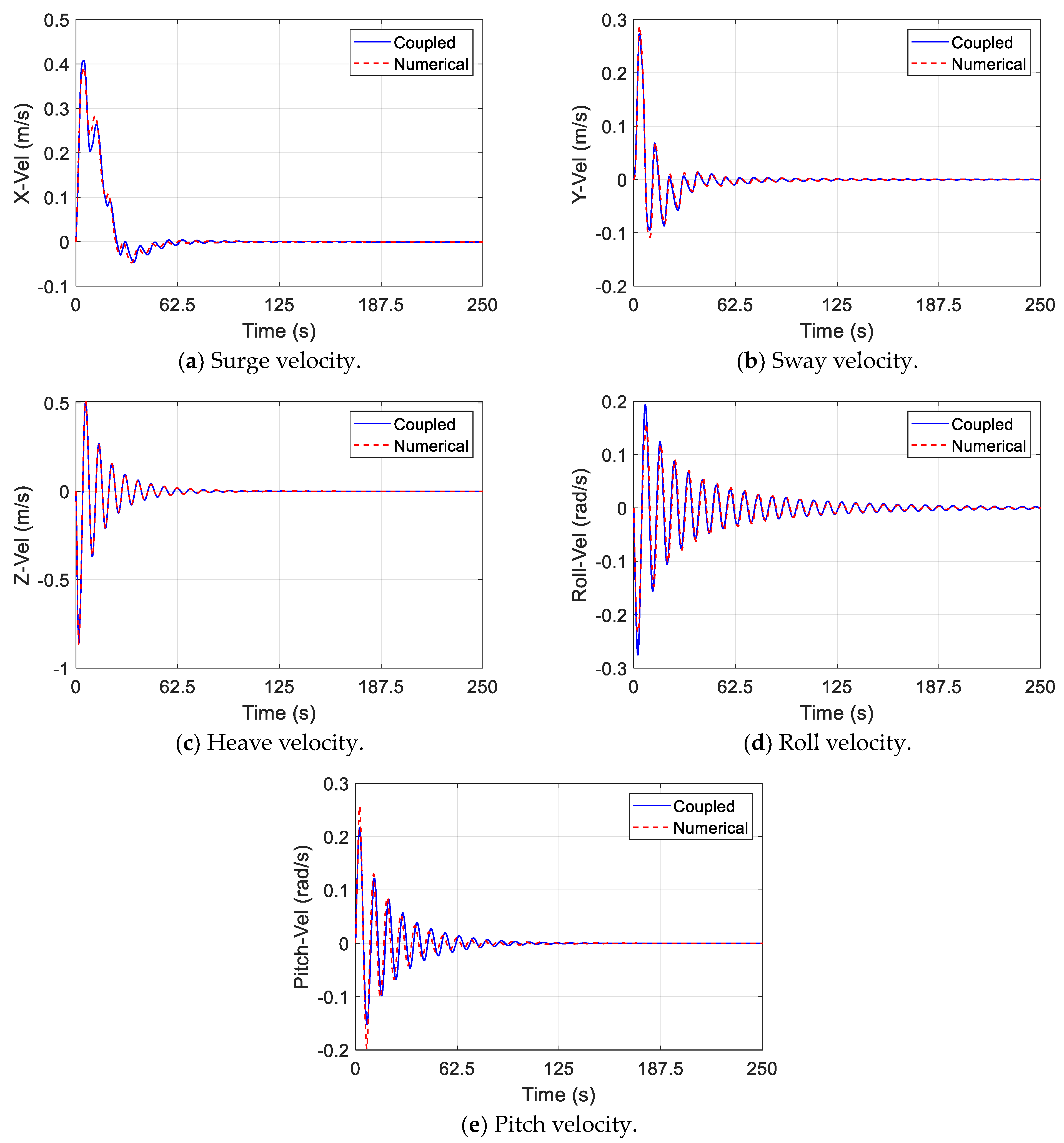
4.2. Without Wind

The first scenario assumes that the spar operates under mild conditions, and no wind acts on it. The simulation results from both the numerical–surrogate coupled model and the numerical model are compared to verify the performance of the surrogate model. In Figure 7, the surge, sway, heave, roll and pitch of the coupled model and numerical model are depicted over a period of 0 to 250 s, as the spar stabilizes after 250 s. Although there are noticeable errors in the surge and sway motions of both models, none exceed 0.05 m. This suggests that the fluid loads predicted by the surrogate model align closely with those calculated by the numerical model.

To investigate the reason for the differences, the velocities of these motions are presented in Figure 8. As shown, the disparities in surge and sway are attributed to the variations in the surge and sway velocities within the first 50 s.

The errors in each direction are correlated with the root mean square error (RMSE) presented in Table 7. As observed in Figure 7 and Figure 8, the smallest errors are found during the heave compared to surge, sway, roll, and pitch. This discrepancy can be attributed to the smallest RMSE being in the vertical force component (Fz) among Fx, Fy, Fz, Mx and My. Additionally, the errors in velocities of the surge, sway, heave, roll and pitch decrease over time. This phenomenon can be explained as follows: When the velocity in the coupled model is smaller than that in the numerical model, the viscous drag force predicted by the surrogate model tends to be smaller than that predicted by the numerical model, resulting in a smaller velocity. However, in the subsequent time step, the velocity differences between the coupled model and the numerical model decrease because the smaller viscous drag force in the coupled model leads to a larger velocity. In essence, the differences in velocity self-correct through feedback regulation, gradually approaching zero with time, as illustrated in Figure 8.

Conversely, the errors in the surge and sway remain constant after 250 s rather than approaching zero. This is because the errors in the surge and sway represent cumulative errors in the surge and sway velocities over time. Unlike heave, where the error is close to zero due to feedback regulation between heave and buoyancy, surge and sway errors persist as they are integral to the velocity errors over time. Figure 9 and Figure 10 illustrate the errors in surge, sway, heave, roll and pitch, and their respective velocities, providing a clear indication of the underlying reasons.

According to Figure 9 and Figure 10, the error in pitch decreases over time. This decreasing trend can be explained as follows: Consider a scenario where the current velocity in the surge direction is 0.2 m/s, and the current velocity in the sway direction is 0.1 m/s. The pitch direction is perpendicular to the surge direction, while the roll direction is perpendicular to the sway direction. When the pitch velocity in the coupled model exceeds that in the numerical model, it indicates that the sway velocity of every point on the submerged part of the spar in the coupled model is greater than that in the numerical model. Consequently, the viscous drag force on the submerged point caused by pitch velocities in the coupled model is larger than that in the numerical model, resulting in a larger viscous drag moment in the coupled model as well. In the subsequent time step, the driven moment in the coupled model becomes smaller than that in the numerical model due to the larger viscous drag moment. Consequently, the pitch acceleration in the coupled model also becomes smaller than that in the numerical model. This leads to the pitch velocity in the coupled model being smaller than that in the numerical model in the subsequent time step. As a result, the angular velocities and viscous drag moment also undergo feedback regulation. Because the current velocity in the surge direction is greater than the current velocity in the sway direction, the feedback regulation in pitch velocity is more pronounced than that in roll velocities.

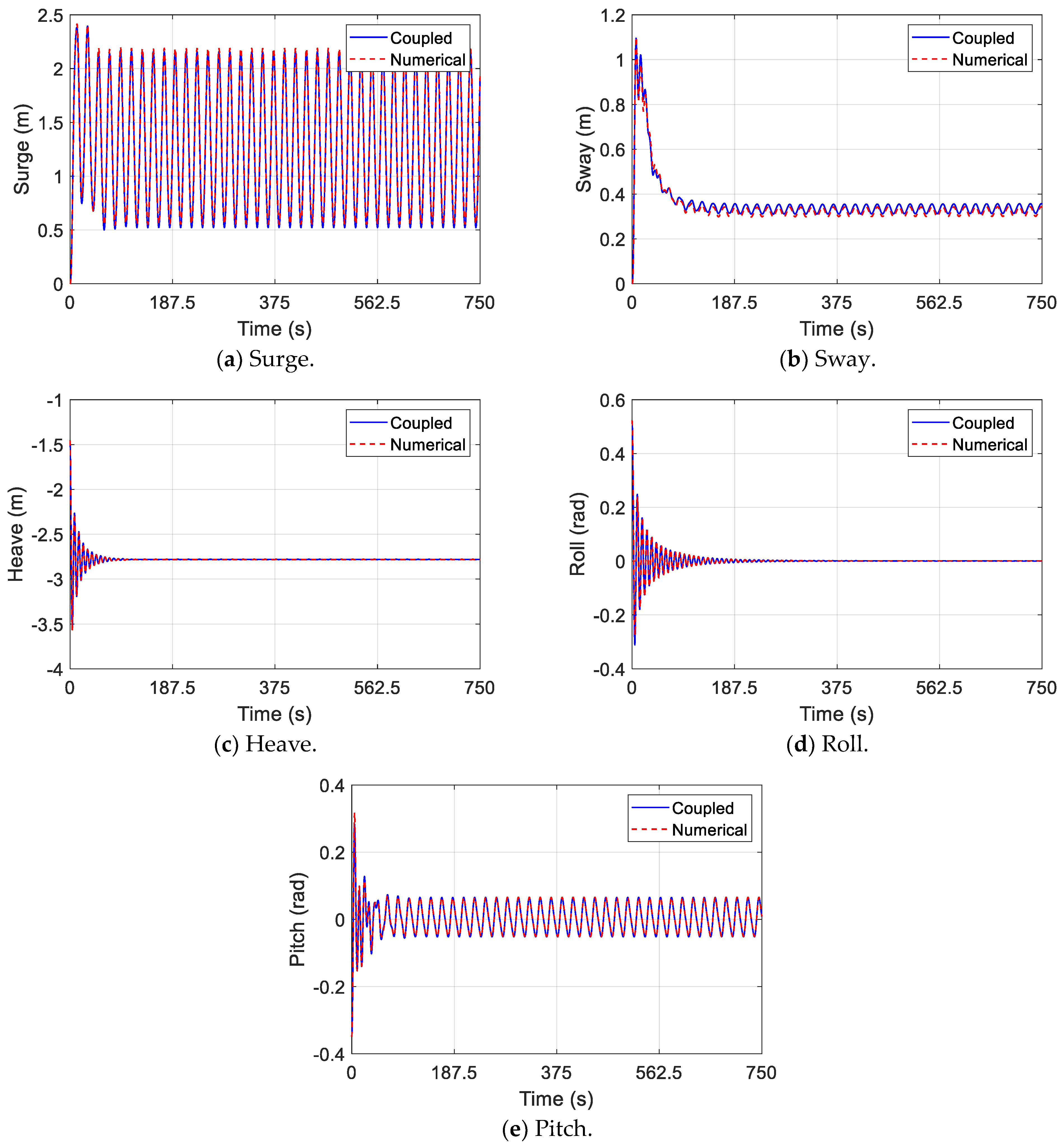
4.3. Constant Wind

This part verified the performance of coupled model under constant wind. Figure 11 and Figure 12 show the simulation results of coupled model and numerical model. According to Figure 11 and Figure 12, the errors between the coupled model and numerical model in constant wind are smaller than those when there is no wind.

Figure 13 and Figure 14 show the errors in the coupled model. Similarly to the errors when there is no wind, the velocity errors in the surge, sway and heave decrease to near zero with time. The heave error also decreases to near zero, and there are steady-state errors in both the surge and sway.

As depicted in Figure 14, the steady-state error in sway is improved compared to the sway error observed in the case of no wind. This improvement can be attributed to the significant external forces generated by wind acting on the sway direction, which outweigh the errors in viscous drag introduced by the surrogate model. Consequently, the motions in the sway direction are primarily influenced by the external forces generated by the wind, with the errors in viscous drag force being caused by the surrogate model having minimal impact on these motions.

4.4. Sinusoidal Wind

This part verifies the performance of surrogate model in the sinusoidal wind. Figure 15 and Figure 16 show the displacements and velocities of the coupled model and numerical model.

Figure 17 and Figure 18 show the errors of displacements and velocities. Similarity with the errors of no wind, the velocity errors in surge, sway and heave decrease to near zero with time. The displacement errors in heave decrease to near zero, and there are steady-state errors in surge and sway.

Figure 17 and Figure 18 illustrate the errors in displacement and velocity. The errors in surge, sway, and heave in sinusoidal wind exhibit consistency with those observed in constant wind conditions. Although the displacement and velocity errors in the roll display noticeable fluctuations during the period of 125–375 s, these fluctuations diminish over time. This can be attributed to the superimposed effect of sinusoidal wind and prediction errors of the surrogate model during the mentioned period. However, this effect diminishes due to the characteristics of viscous drag moment, as discussed in Section 4.3.

Comparing the errors in the coupled model under three different wind styles, it is observed that the errors of heave, surge velocity and sway velocity gradually decrease to zero over time. Steady-state errors are present in surge and sway, with these errors being equal to the integral of the errors of surge and sway velocities.

5. Conclusions

This study establishes a surrogate model that captures the relationship between the position, attitude and velocity of the spar platform, and the viscous drag force. To verify the performance of the surrogate model, the dynamic response of the spar platform under three wind styles, including no wind, constant wind and sinusoidal wind, are analyzed using both a purely numerical model and a numerical–surrogate coupled model. Based on the comparison of simulation results from the purely numerical model and coupled model, the following conclusions are drawn:

(1)

The surrogate model, based on artificial neural networks (ANN), effectively predicts the viscous drag force acting on the spar. Small root mean square error (RMSE) and errors in the coupled model indicate that the surrogate model exhibits excellent performance in predicting the fluid loads on the spar in uniform currents.

(2)

An efficient and reasonable method of database establishment is proposed, integrating two parts of the database including large fluctuation and steady-state fluctuation. The random function is used to acquire the distribution of input variables in the database based on the numerical model.

(3)

The additional mass inertia matrix should be calculated separately so that the acceleration items can be calculated easily.

(4)

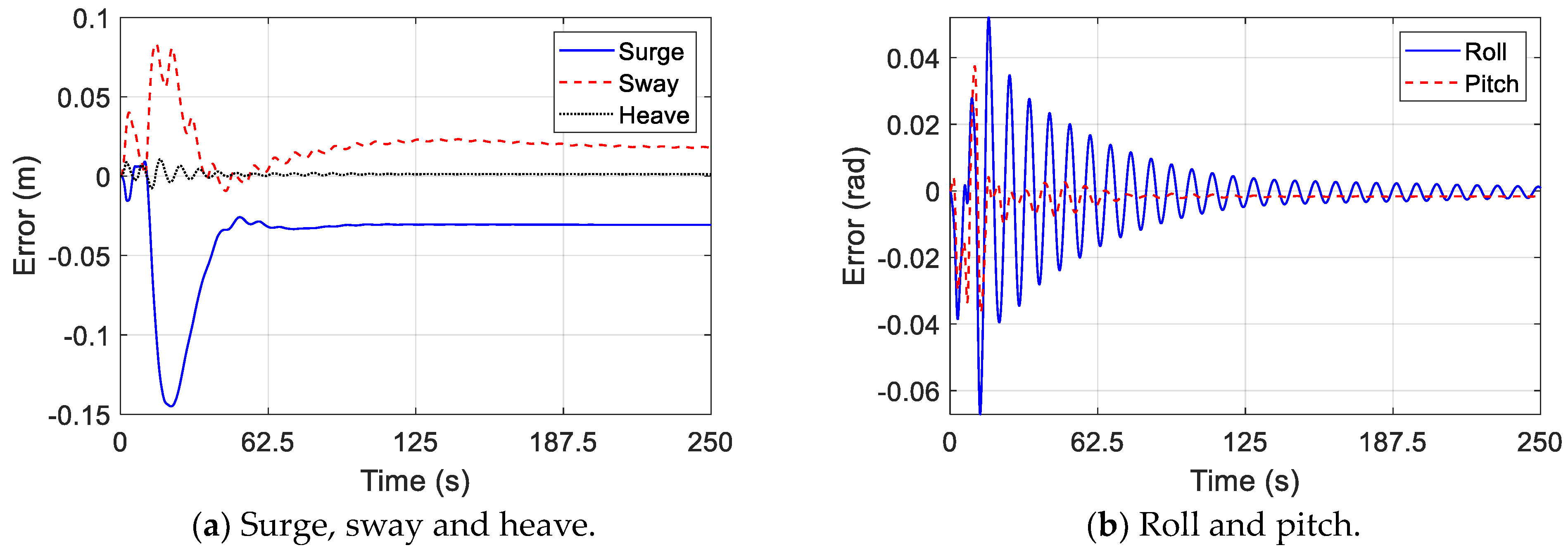
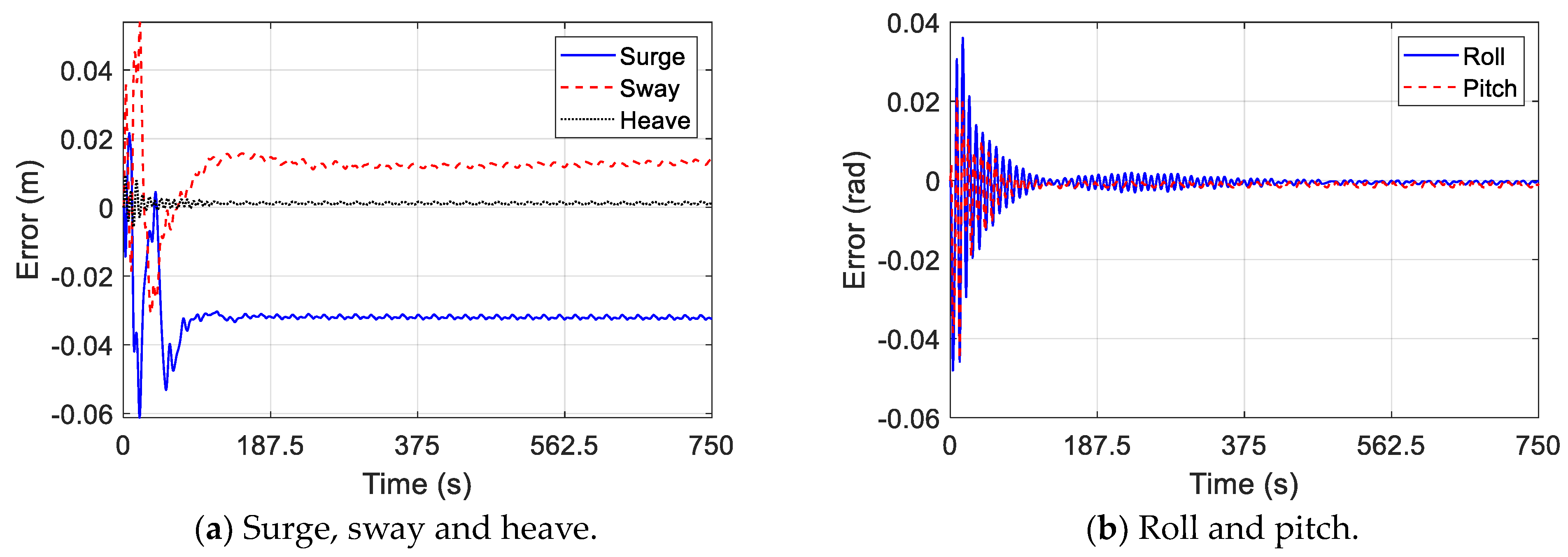
Due to the mooring system, errors in one direction affect the accuracy of the surrogate model in other directions. Therefore, the coupled model is convergent when errors of the surrogate model in all directions are acceptable.

(5)

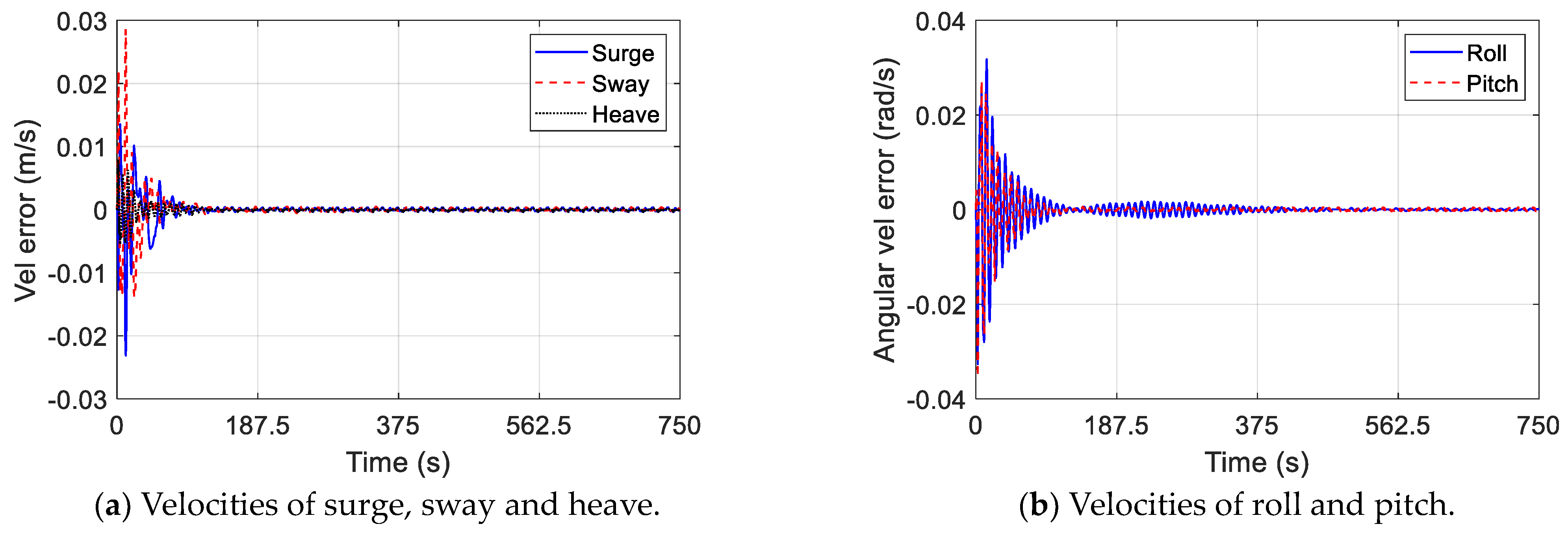
The errors in the numerical–surrogate coupled model have been analyzed to demonstrate the performance of the coupled model in different wind styles. Comparing the errors of the coupled model in three wind styles, it is observed that the errors in the heave, surge velocity and sway velocities decrease to zero with time. Steady-state errors exist in surge and sway, and these errors are equal to the integral of the errors in the surge and sway velocities. Although the errors in roll and pitch imported into the coupled model are generated by the surrogate model, these errors do not diverge. The error analysis indicates that the surrogate model has potential application value in predicting complex external forces of mechanical systems operating in various environments.

In this study, only the fluid loads inducted by uniform currents are considered as the component of hydrodynamic force. While this simplification verifies the feasibility of the surrogate model, future works should focus on establishing an improved surrogate model that could consider the wave-induced loads; additionally, the modeling theory should be extended to consider vortex-induced vibrations.