Obstacle Avoidance Control for Autonomous Surface Vehicles Using Elliptical Obstacle Model Based on Barrier Lyapunov Function and Model Predictive Control
Abstract
1. Introduction
- (1)
- A novel BLF is improved by introducing an elliptical obstacle model. Compared to the literature [10,11], using ellipses instead of circles as equivalent obstacles, especially non-circular obstacles like rectangles, effectively addresses the issue of excessive conservatism caused by excessive area expansion in obstacle equivalence methods. Moreover, compared to the literature [12,13], directly integrating elliptical obstacle avoidance performance metrics into the BLF overcomes the challenges of relying on extensive data for machine learning training, thus simplifying the implementation process.
- (2)
- A design approach for angular velocity based on MPC is established, aiming to achieve precise constraint control over angles. Compared with the literature [10,11], this approach addresses the practical issue of angle limitation by introducing angular error constraints, ensuring that the directional error of the ASV remains within a reasonable threshold. Furthermore, by incorporating a directional error assist function into the ASV’s linear velocity controller, the system ensures that when the ASV’s heading angle deviates significantly from the predetermined value, it can automatically stop and adjust the angle. Compared with the literature [19,20,21,22], it guarantees the linearization of the ASV system, skillfully avoiding the complexity challenges faced by traditional MPC methods in handling nonlinear ASV systems.
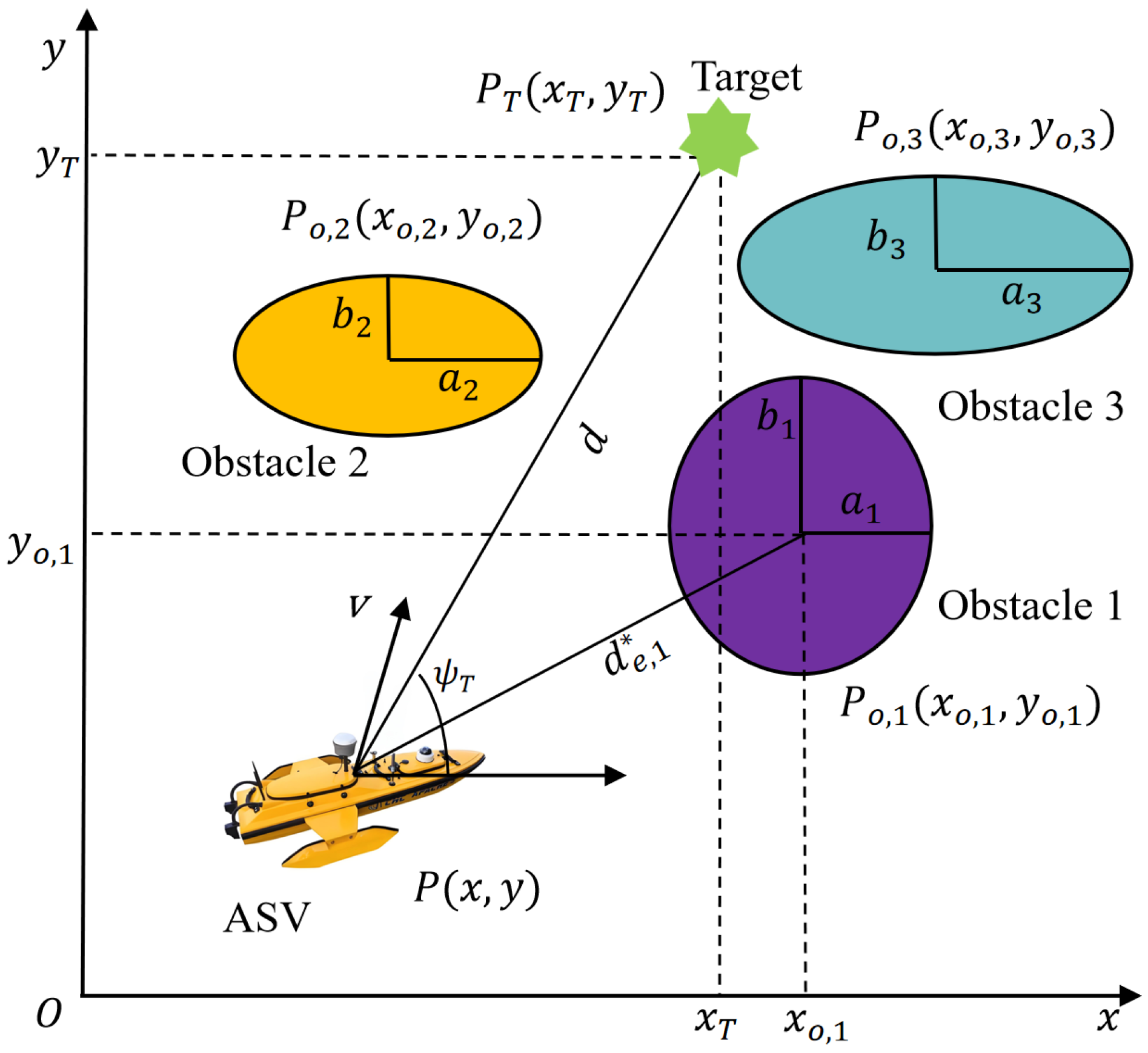
2. System Modeling and Objective
2.1. Kinematic Model
2.2. Objective
- (1)
- When t→∞, the distance d between the ASV and target point converges to zero:
- (2)
- When , the variables satisfy , where is the safety distance function that can predefine the obstacle.
3. Main Results
3.1. The Improved BLF
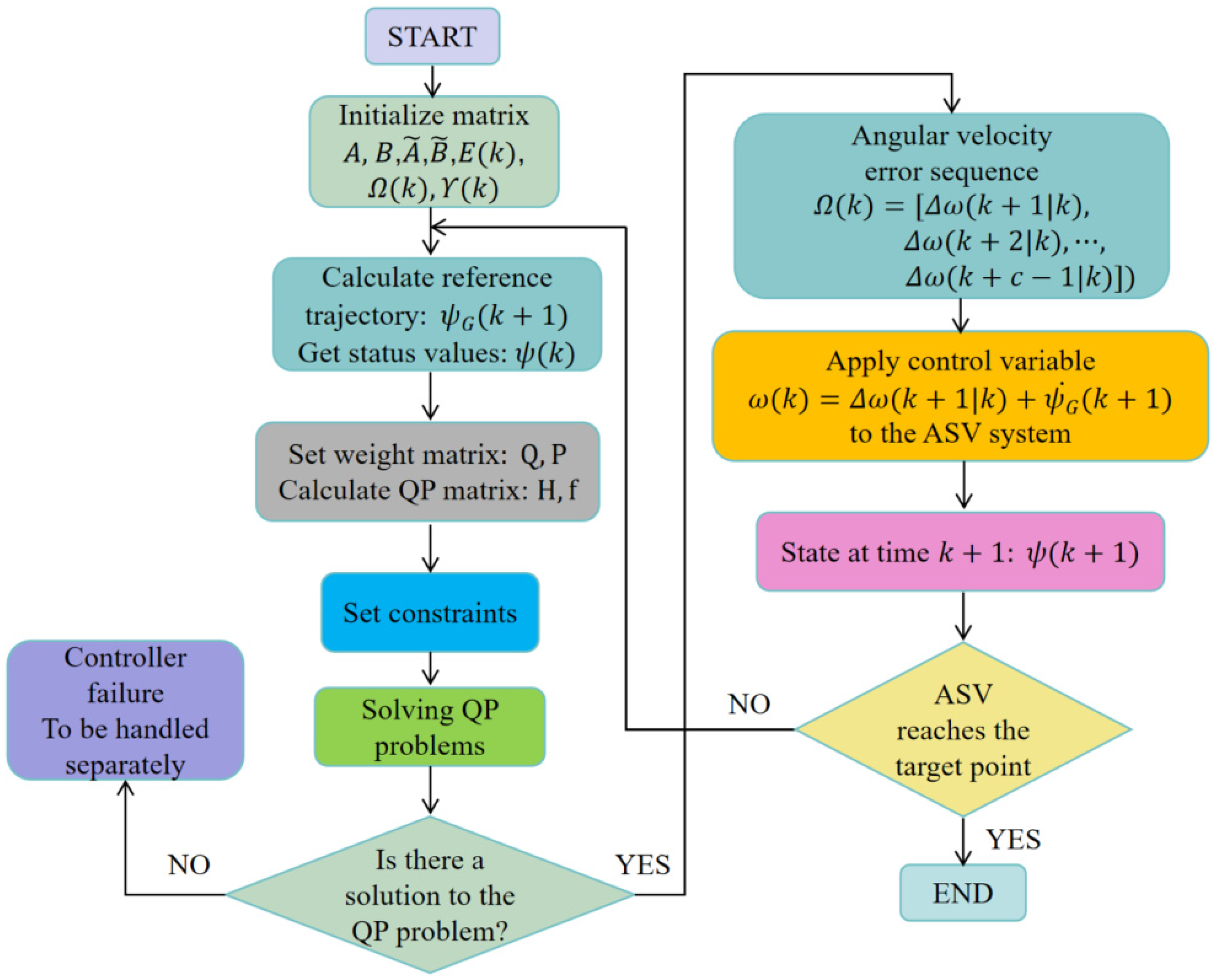
3.2. MPC Controller Design
3.3. Controller Design
- (1)
- , and the variable between the ASV and the obstacles satisfies , where is the equivalent elliptical obstacle safety distance that can predefine the obstacle.
- (2)
- When , the distance between the ASV and target point converges to zero; that is,
4. Simulation Results
4.1. Comprehensive Evaluation of MPC
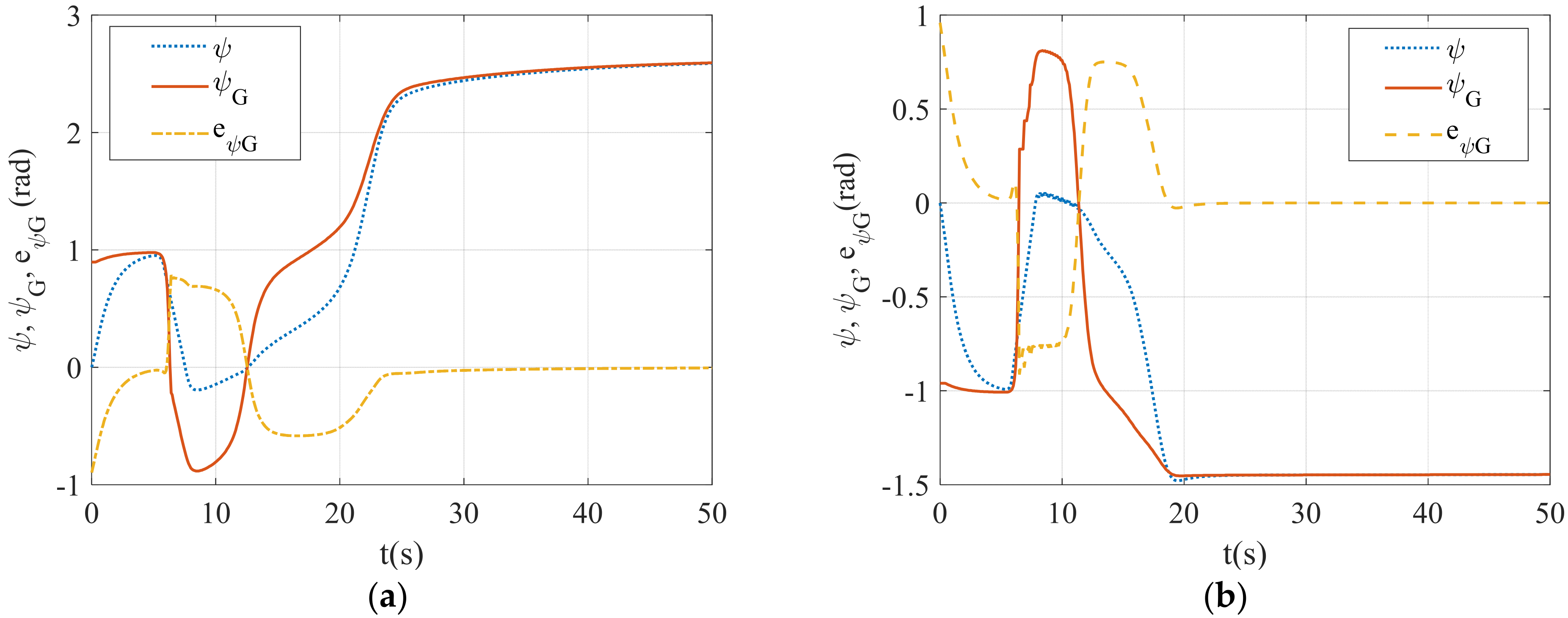
4.1.1. Stability Demonstration
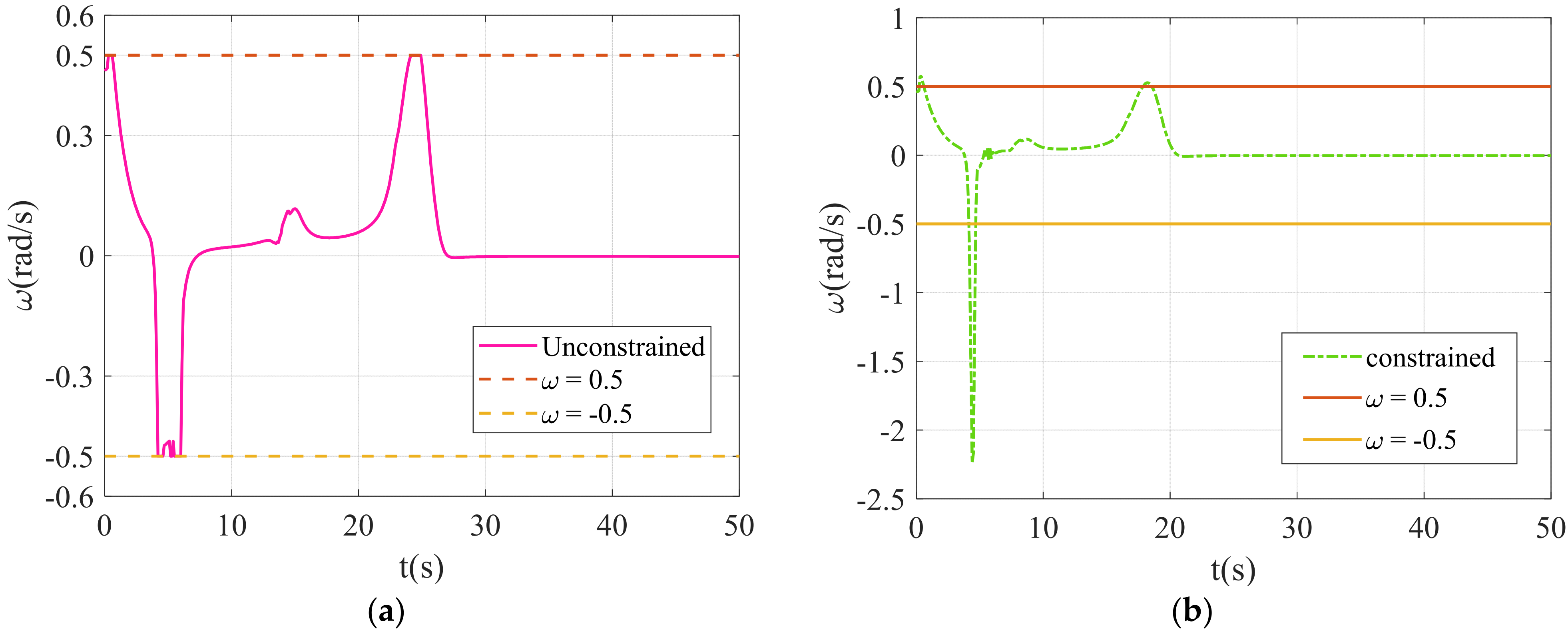
4.1.2. Performance Comparison
4.2. Comprehensive Evaluation of ASV Control
4.2.1. Stability Demonstration
- (1)
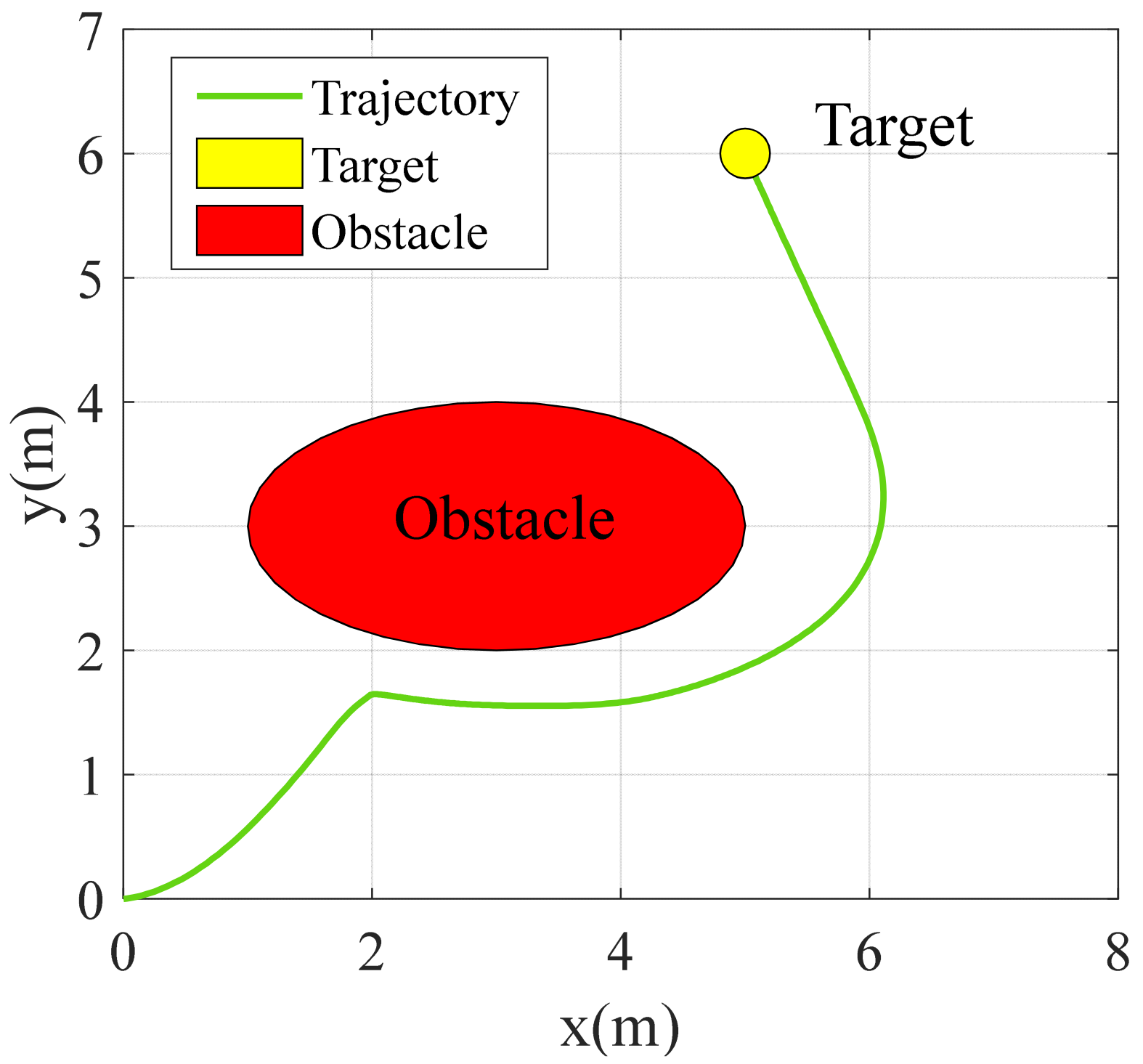
- Obstacle Avoidance of Single Obstacle
- (2)
- Obstacle Avoidance of Multiple Obstacles
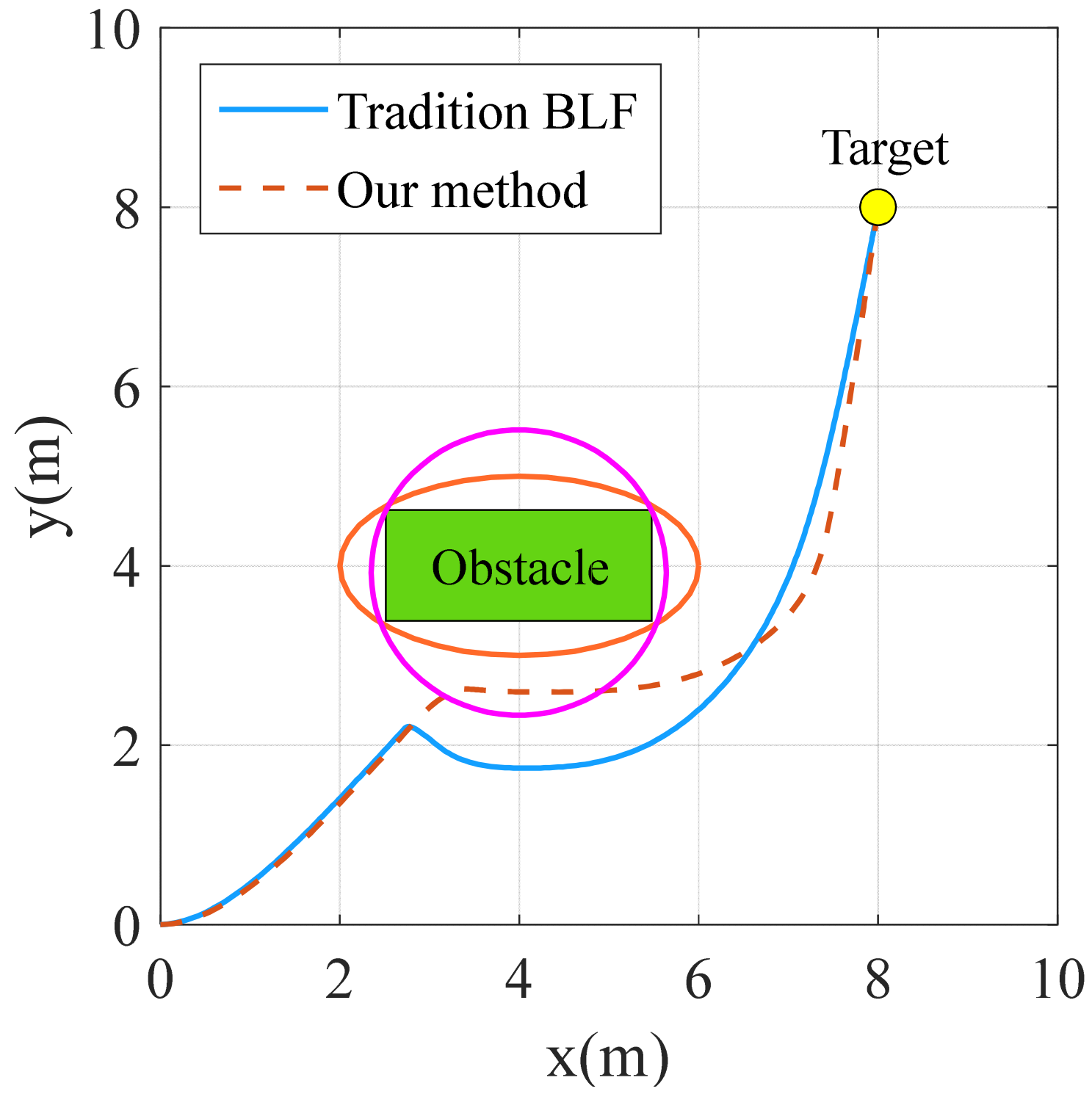
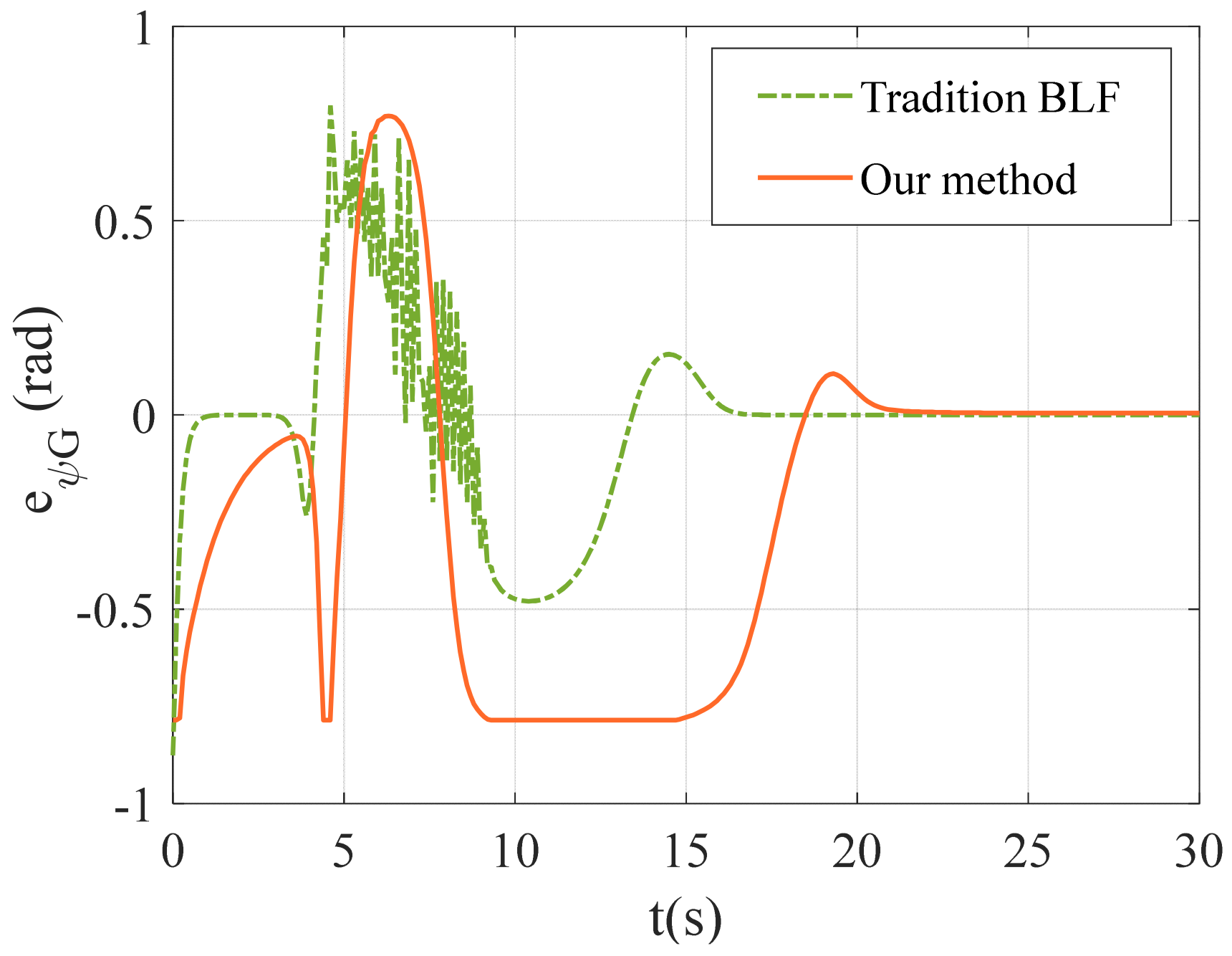
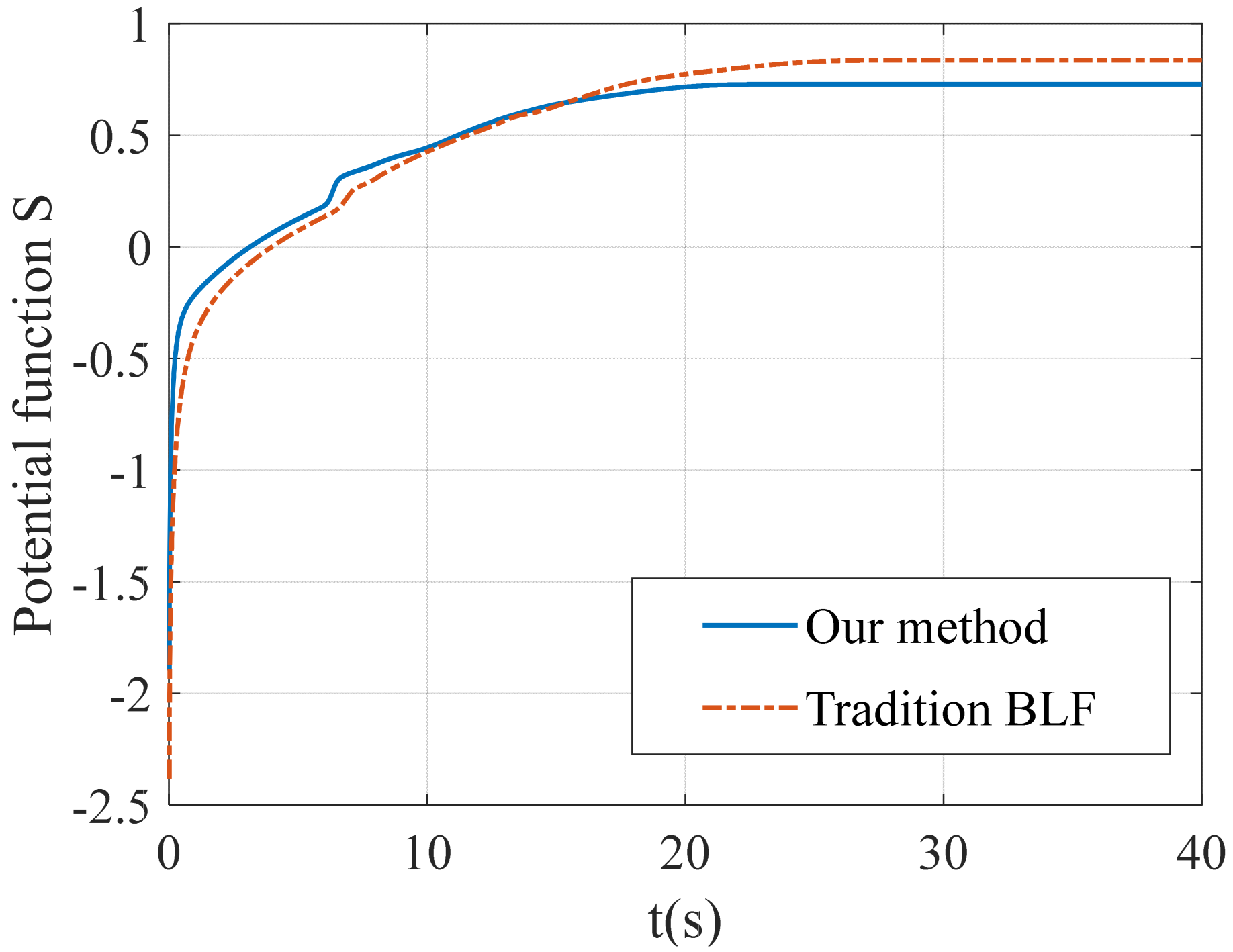
4.2.2. Performance Comparison
5. Conclusions and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma’Arif, A.; Rahmaniar, W.; Vera, M. Artificial potential field algorithm for obstacle avoidance in uav quadrotor for dynamic environment. In Proceedings of the 2021 IEEE International Conference on Communication, Networks and Satellite (COMNETSAT), Online Conference, 17–18 July 2021; pp. 184–189. [Google Scholar]
- Ding, T.; Xu, K.; Ge, M. Fast fixed-time output multi-formation tracking of networked autonomous surface vehicles: A mathematical induction method. IEEE Trans. Veh. Technol. 2023, 72, 5769–5781. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, Z.; Li, Z. Multi-UAV formation control based on a novel back-stepping approach. IEEE Trans. Veh. Technol. 2020, 69, 2437–2448. [Google Scholar] [CrossRef]
- Zhu, G.; Yan, J.; Zhang, P. Event-triggered adaptive neural fault-tolerant control of underactuated MSVs with input saturation. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7045–7057. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Z.; Peng, Z. Cooperative path following ring-networked under-actuated autonomous surface vehicles: Algorithms and experimental results. IEEE Trans. Cybern. 2020, 50, 1519–1529. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Zhang, J.; Cui, Y. Autonomous obstacle avoidance algorithm for unmanned surface vehicles based on an improved velocity obstacle method. ISPRS Int. J. Geo-Inf. 2021, 10, 618. [Google Scholar] [CrossRef]
- Feng, N.; Fan, F.; Xu, G. Deep Reinforcement Learning Based AGV Self-navigation Obstacle Avoidance Method. Instrumentation 2023, 9, 11–16. [Google Scholar]
- Lee, D.; Woo, J. Reactive Collision Avoidance of an Unmanned Surface Vehicle through Gaussian Mixture Model-Based Online Map. J. Mar. Sci. Eng. 2022, 10, 472. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. Auton. Robot. Veh. 1986, 5, 90–98. [Google Scholar]
- Yang, T.; Ma, Y.; Zhang, P. Artificial potential field-based anti-saturation positioning obstacle avoidance control for wheeled robots. Nonlinear Dyn. 2022, 110, 3499–3512. [Google Scholar] [CrossRef]
- Zhang, P.; Ding, Y.; Chen, Y. Obstacle avoidance control of the AGV with Actuator Dead Zones Based on Fixed-time Disturbance Observers and Command Filtering. IEEE Access 2024, 66701–66716. [Google Scholar] [CrossRef]
- Wu, X.; Chen, H.; Chen, C. The autonomous navigation and obstacle avoidance for USVs with ANOA deep rein-forcement learning method. Knowl.-Based Syst. 2020, 196, 105201. [Google Scholar] [CrossRef]
- Mokhtare, Z.; Vu, M.; Mobayen, S.; Rojsiraphisal, T. An adaptive barrier function terminal sliding mode controller for partial seizure disease based on the Pinsky–Rinzel mathematical model. Mathematics 2022, 10, 2940. [Google Scholar] [CrossRef]
- Alattas, K.; Vu, M.; Mofid, O.; El-Sousy, F.F.; Fekih, A.; Mobayen, S. Barrier function-based nonsingular finite-time tracker for quadrotor UAVs subject to uncertainties and input constraints. Mathematics 2022, 10, 1659. [Google Scholar] [CrossRef]
- Singh, R.; Bera, T.; Chatti, N. A real-time obstacle avoidance and path tracking strategy for a mobile robot using machine-learning and vision-based approach. Simulation 2022, 98, 789–805. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, Z.; Qi, S. Autonomous cooperative formation control of underactuated USVs based on improved MPC in complex ocean environment. Ocean. Eng. 2023, 270, 113633. [Google Scholar] [CrossRef]
- Seal, S.; Boulet, B. Centralized MPC for home energy management with EV as mobile energy storage unit. IEEE Trans. Sustain. Energy 2023, 14, 1425–1435. [Google Scholar] [CrossRef]
- Benotsmane, R.; Kovács, G. Optimization of energy consumption of industrial robots using classical PID and MPC controllers. Energies 2023, 16, 3499. [Google Scholar] [CrossRef]
- Kim, E.; Kim, J.; Sunwoo, M.; Sunwoo, M. Model predictive control strategy for smooth path tracking of autonomous vehicles with steering actuator dynamics. Int. J. Automot. Technol. 2014, 15, 1155–1164. [Google Scholar] [CrossRef]
- Kokot, M.; Miklić, D.; Petrović, T. A unified MPC design approach for AGV path following. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 4789–4796. [Google Scholar]
- Xu, J.; Zhang, G. Tracking Control of Wheeled Mobile Robot Based on MMPC. Acad. J. Sci. Technol. 2023, 6, 137–145. [Google Scholar]
- Marrugo, D.; Villa, J. MPC-Based Path Tracking of a Differential-Drive Mobile Robot with Optimization for Improved Control Performance. In Workshop on Engineering Applications; Springer Nature: Cham, Switzerland, 2023; Volume 6, pp. 276–289. [Google Scholar]
- Fabregas, E.; Farias, G.; Aranda-Escolastico, E. Simulation and experimental results of a new control strategy for point stabilization of nonholonomic mobile robots. IEEE Trans. Ind. Electron. 2019, 67, 6679–6687. [Google Scholar] [CrossRef]
- Sui, S.; Zhao, T. Active disturbance rejection control for optoelectronic stabilized platform based on adaptive fuzzy sliding mode control. ISA Trans. 2022, 125, 85–98. [Google Scholar] [CrossRef]
- Kuhne, F.; Lages, W.; da Silva, J., Jr. Model predictive control of a mobile robot using linearization. Nonlinear Dyn. 2004, 4, 525–530. [Google Scholar]
- Najafi, A.; Vu, M.; Mobayen, S.; Asad, J.H.; Fekih, A. Adaptive barrier fast terminal sliding mode actuator fault tolerant control approach for quadrotor UAVs. Mathematics 2022, 10, 3009. [Google Scholar] [CrossRef]






| Params | Value | Params | Value | Params | Value |
|---|---|---|---|---|---|
| 0 | 0 | 0 | |||
| 0 | 0 | 1 | |||
| 5 | 0.5 | 2 | |||
| 1 | 0.25 | Step | 0.01s | ||
| 10 | 10 | 0.2 | |||
| 80 | 10 | 10 |
| Params | |||||
|---|---|---|---|---|---|
| Case1 | Value (m) | (3,3) | (0,0) | (4,5) | 1 |
| Case2 | Value (m) | (4,4) | (7,2) | (0,6) | 1 |
| Params | ||||
| Value (m) | (3,3) | (0,0) | (4,5) | 1 |
| Params | ||||
| Value (m) | (3,3) | (0,0) | (5,6) | 1 |
| Params | |||||
| Value | (8,2) | (3,3) | (6,7) | (10,6) | (0,0) |
| Params | |||||
| Value | 1m | 1m | 1m | 1m | (9,10) |
| Params | |||||
| Value | 2 | 1 | 0.25 | ||
| Params | |||||
| Value | 1 | 2 | 0.36 | ||
| Params | |||||
| Value | 100 | 80 | 80 | 50 | 0.49 |
| Params | |||
| Value (m) | (4,4) | (0,0) | (8,8) |
| Params | |||
| Value (m) | 2 | 1 | 1 |
| Params | ||||||
|---|---|---|---|---|---|---|
| Case 1 | Value (m) | (4,4) | (0,0) | (8,8) | 2 | 1 |
| Case 2 | Value (m) | (4,5) | (0,0) | (14,12) | 1 | 3 |
| Control Strategy | Input Constraints | State Constraints | Potential Energy | Obstacles Conservatism |
|---|---|---|---|---|
| Our method | Yes | Yes | Small | Weak |
| Method [11] | No | No | Big | Strong |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Ding, Y.; Du, S. Obstacle Avoidance Control for Autonomous Surface Vehicles Using Elliptical Obstacle Model Based on Barrier Lyapunov Function and Model Predictive Control. J. Mar. Sci. Eng. 2024, 12, 1035. https://doi.org/10.3390/jmse12061035
Zhang P, Ding Y, Du S. Obstacle Avoidance Control for Autonomous Surface Vehicles Using Elliptical Obstacle Model Based on Barrier Lyapunov Function and Model Predictive Control. Journal of Marine Science and Engineering. 2024; 12(6):1035. https://doi.org/10.3390/jmse12061035
Chicago/Turabian StyleZhang, Pengfei, Yuanpei Ding, and Shuxin Du. 2024. "Obstacle Avoidance Control for Autonomous Surface Vehicles Using Elliptical Obstacle Model Based on Barrier Lyapunov Function and Model Predictive Control" Journal of Marine Science and Engineering 12, no. 6: 1035. https://doi.org/10.3390/jmse12061035
APA StyleZhang, P., Ding, Y., & Du, S. (2024). Obstacle Avoidance Control for Autonomous Surface Vehicles Using Elliptical Obstacle Model Based on Barrier Lyapunov Function and Model Predictive Control. Journal of Marine Science and Engineering, 12(6), 1035. https://doi.org/10.3390/jmse12061035






