Next Article in Journal
Numerical Investigation of Wave Force on Coastal Bridge Decks Close to a Sloping Seabed
Previous Article in Journal
Node Load and Location-Based Clustering Protocol for Underwater Acoustic Sensor Networks
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JMSE
Volume 12
Issue 6
10.3390/jmse12060983
jmse-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Errors of Tropical Cyclone-Induced Ocean Waves in Reanalysis Using Buoy Data

by
Yalan Zhang
1,†,
Wei Zhong
2,†,
Zhihao Feng
1,†,
Ruilin Wang
3,*,
Yuan Sun
2,* and
Zongbao Bai
1
1
College of Meteorology and Oceanography, National University of Defense Technology, Changsha 410073, China
2
College of Advanced Interdisciplinary Studies, National University of Defense Technology, Nanjing 211101, China
3
Institute of Software, Chinese Academy of Sciences, Beijing 100190, China
*
Authors to whom correspondence should be addressed.
†
These authors contribute equally to this work.
J. Mar. Sci. Eng. 2024, 12(6), 983; https://doi.org/10.3390/jmse12060983
Submission received: 26 April 2024 / Revised: 1 June 2024 / Accepted: 10 June 2024 / Published: 12 June 2024
(This article belongs to the Section Ocean and Global Climate)
Browse Figures
Versions Notes

Abstract

:
Due to limited in-situ ocean observations, reanalysis data are often considered as an important source for studying tropical cyclone (TC)-induced ocean waves. Here, we introduced a method to quantitatively evaluate the errors of TC-induced ocean waves in reanalysis datasets. The TC data are from the IBTrACS dataset. We compared TC-induced ocean waves in two reanalysis datasets (i.e., ERA5 and WAVERYS) with those in buoy data when TCs are near the buoy stations. We showed that the errors of TC-induced ocean waves in WAVERYS and ERA5 are similar, because the surface winds in these two datasets are the same. We noticed that the errors in the North Pacific are remarkably smaller than those in the North Atlantic due to more realistic probability density of TC-induced ocean waves in the North Pacific compared with those in the North Atlantic. Moreover, the errors are strongly related to significant wave height (SWH) and the distance from TC center. The larger the SWH and the shorter the distance, the larger the error. Furthermore, the errors in TC-induced ocean waves decreased significantly over the past decades.

1. Introduction

Tropical cyclones (TCs) are classified as one of the most destructive environmental disasters on Earth by the United Nations [1]. They pose a great threat to human society and terrestrial/marine ecosystems [1,2,3]. Though there is significant scientific interest and public concern regarding disasters caused by TC-related wind and rainfall over land [4,5,6,7], relatively fewer studies are focused on the disasters caused by TC-induced ocean waves. Such disastrous effects from TC-induced ocean waves, however, cannot be ignored, not only because TC-induced waves have long been a major concern for vessels and installations at sea [8] but also because more than 90% of the global TC best track data are collected over the ocean [9]. Many previous studies focused on the errors of global ocean waves between reanalysis data and in-situ observation data [10,11,12]. Compared with common ocean wave data, the uncertainty of ocean wave data associated with extreme weather (e.g., TC) is greater, thus affecting the analysis of ocean disasters [13,14,15,16,17]. Shi et al. (2014) noted that TC-induced ocean wave hazards have increased significantly, so much so that such hazards should be a concern [18]. As suggested by Hodges et al. (2017), reanalysis data can act as a bridge between the observations of TCs and the simulations of TCs [19]. Many studies focused on verifying the accuracy of model performance in simulating TC activities such as TC track, intensity, lifetime, size, and precipitation [20,21,22]; however, they did not validate TC-induced ocean wave data in reanalysis data.
The commonly used TC information is mainly recorded in the TC best track datasets from various agencies. These datasets often do not include the information of TC-induced ocean waves, which needs to be extracted from ocean wave data. So far, ocean wave observations mainly depend on buoys and satellites [23]. Wave measurements from satellites are obtained by means of inversions rather than direct measurements, which are subject to systematic errors. In contrast, measurements from buoys are direct measurements with higher accuracy [11]. The datasets from buoys are considered as “true values” and are used to examine the errors in satellite altimeter data and numerical model outputs [24,25,26]. The limited number and uneven distribution of buoys constrain its ability to build gridded global ocean wave data. Different from the in-situ buoy data, satellite altimeter data provide estimates of wave height from empirically calibrated functions of measured backscatter; the satellite data are limited by their narrow tracks, and their global coverage takes 5–10 days [27]. Due to the limitation of the temporal and spatial extent of the observations based on buoys and satellites, numerical models are often used to produce long-term gridded global ocean wave data (e.g., reanalysis data that assimilate the observations from both buoys and satellites) [11,28,29].
As the TC is a moving system and TC-induced wave region also moves with the TC, verification of simulated TC-induced ocean wave data (e.g., data from reanalysis) is not straightforward. Only a few studies focused on the methods of estimating the errors in TC-induced ocean waves. Thus, we developed a new method that can objectively evaluate the performance of a numerical model in simulating TC-induced ocean wave. The aim of this study is to present this new method that can quantitatively evaluate the errors of TC-induced ocean waves in reanalysis datasets, unlike previous studies that focused on the errors of ocean wave. This new method will then be implemented to evaluate TC-induced ocean waves from the European Centre for Medium-Range Weather Forecasts (ECMWF) fifth-generation reanalysis (ERA5) [29] and Copernicus Marine Environment Monitoring Service (CMEMS) global wave reanalysis of Météo-France (WAVERYS) [11], and to reveal possible trends and sources of these errors.

2. Data

The data used in this study include TC best track data, global buoy data, and two global wave reanalysis datasets. The TC best track data are the International Best Track Archive for Climate Stewardship (IBTrACS; https://www.ncei.noaa.gov/data/international-best-track-archive-for-climate-stewardship-ibtracs/v04r00/access/netcdf/IBTrACS.ALL.v04r00.nc, accessed on 1 December 2023) [30]. The global buoy data are obtained from the National Data Buoy Center (NDBC; https://www.ndbc.noaa.gov/data/historical/stdmet/, accessed on 1 December 2023). The global wave reanalysis data are from two sources: the ERA5 product [29] (https://cds.climate.copernicus.eu/cdsapp#!/dataset/, accessed on 1 December 2023) and the WAVERYS product [11] (https://data.marine.copernicus.eu/product/GLOBAL_MULTIYEAR_WAV_001_032, accessed on 1 December 2023).

2.1. TC Best Track Dataset

The IBTrACS dataset is the most complete dataset of global TCs available, which includes TC data from 1841 to the present and uses remote sensing data such as satellite imagery, microwave and infrared imagery, scatterometry, and other data sources to determine the best tracks of TCs [31]. It is a product of collaborative efforts of all the World Meteorological Organization (WMO) Regional Specialized Meteorological Centers, other organizations, and individuals from around the world. The IBTrACS dataset consists of the best estimates of TC central location (latitude and longitude), minimum center pressure (MCP), and maximum sustained wind (MSW) at 6-hourly intervals [30,32]. We selected the TC best track data from 1993 to 2020 for this study.

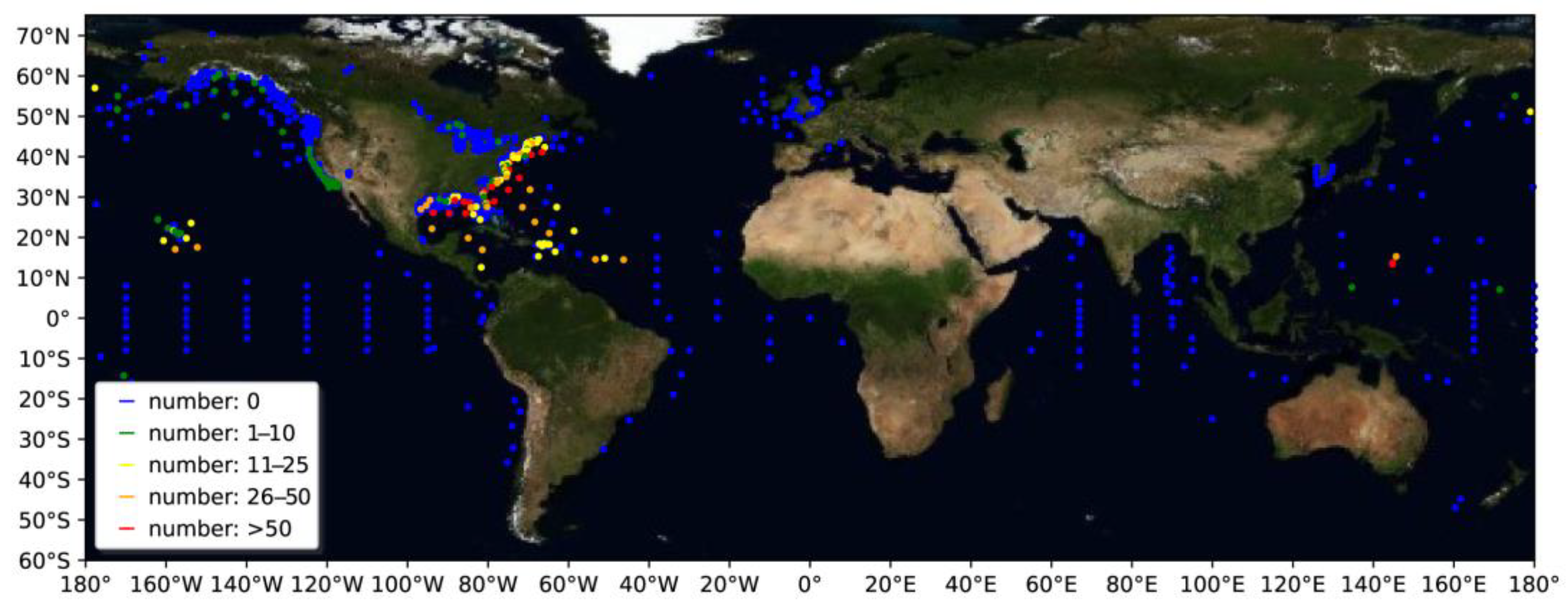
2.2. Global Buoy Data

Although the validity of high-wind-speed buoy data has been questioned [33,34,35], buoy data have been found to be of high quality in general [36,37,38]. They have been widely used for validating model results and calibrating satellite observations. For calibration purposes, we need a high-quality database of buoy wind speed, direction, and significant wave height (SWH) over a long period. The most extensive dataset that includes these fields is the standard meteorological data in the Historical NDBC data, which are quality controlled and contain data from the beginning of each station (1329 stations) up to and including December 2021 [39] (https://www.ndbc.noaa.gov/data/historical/stdmet/, accessed on 1 December 2023). The period of the Historical NDBC data is from 1970 to 2022. The variables in the buoy data include wind direction, wind speed, SWH, dominant wave period, average wave period, sea-level pressure, etc. (https://www.ndbc.noaa.gov/measdes.shtml, accessed on 1 December 2023).

2.3. Global Ocean Wave Reanalysis Data

In this study, we examined the performances of two reanalysis datasets (i.e., ERA5 and WAVERYS) in reproducing TC-induced ocean waves. These two reanalysis datasets are widely used in studying TC activities and ocean waves, which contain long-term global wave information and assimilate data from various satellite sensors, including those onboard NOAA, MetOp, and Sentinel satellites [40].
The ERA5 is a global reanalysis, produced using the Integrated Forecast System cycle CY41R2 release, covering the period from 1979 to 2022. The ERA5 (similar to its predecessor of the ERA-Interim reanalysis) [41] was produced using an improved data assimilation technique (4D-Var scheme). The horizontal resolution of the atmospheric (ocean wave) model used for producing the ERA5 is about 30 km (40 km). The temporal resolution of model outputs is 3 h. Note that the temporal resolutions of the outputs of both ERA5 and the WAVERYS are 3 h, but this does not mean that the wind and wave model exchanged data every three hours. The exchange of air-sea data within the model depends on the time step set by the model itself. This reanalysis dataset includes surface wind, mean wave direction, mean wave period, SWH, etc. Details about the ERA5 reanalysis can be found at the website of the Copernicus Climate Change Service [42] and in Hersbach et al. [29].
The global ocean reanalysis wave system of Météo-France (WAVERYS), with a resolution of 1/5°, provides reanalysis for global ocean surface waves covering the period 1993–2020. It includes 3-h integrated wave parameters describing the sea state at the ocean surface (significant height, period, direction, Stokes drift, etc.). Note that the wave model used in producing the WAVERYS is driven by sea-ice fraction and wind provided by ERA5 [11].

3. Evaluation Method

We propose a new method to evaluate the errors of the reanalysis data with respect to the buoy data. Specifically, we collect the SWH information from numerous NDBC buoys when TCs are close to the buoy stations, compare the SWH in buoy data with that in reanalysis data, and evaluate the errors of SWH in reanalysis data. Though many previous studies validated models simulating ocean waves [10,11,12], none was found on model simulated TC-induced ocean waves.

3.1. Observed TC-Induced Ocean Waves

We define TC-induced ocean wave as the ocean wave within a radius of 600 km from the TC center and use the recorded TC-induced ocean waves of the buoy data when the buoy station is within a radius of 600 km from the TC center in the IBTrACS dataset. We combined the global ocean buoy data and the best track data to collect the records of TC-induced ocean waves. Figure 1 shows the spatial distribution of the buoy stations marked by numbers of times (6-h interval; the temporal resolution of the TC tracks in the IBTrACS) when the stations are close to TCs from 1993 to 2020, which is the period covered by the aforementioned datasets (i.e., IBTrACS, NDBC, ERA5, and WAVERYS). The color represents the number of the records with a 6-h interval. When a TC passes near a buoy and the buoy is within a radius of 600 km from the TC center, it is considered as a record of TC-induced ocean wave. There are 3327 observed records of TC-induced ocean waves. Most of them are distributed in the Northern Hemisphere, especially in the ocean waters near the east coast of the United States.

3.2. Errors of TC-Induced Ocean Waves in ERA5 and WAVERYS Reanalysis Datasets

For each record of TC-induced ocean wave at a buoy station, we applied the nearest-neighbor interpolation method to obtain the values of various fields (e.g., SWH, wave period, surface wind, etc.) from the reanalysis datasets. As the reanalysis datasets are gridded, with relatively high resolutions (i.e., no more than 40 km), if the nearest gridded point neighboring the station is over land, the next nearest gridded point over water is selected. As a result, we obtained 3327 reanalysis records of TC-induced ocean wave data from each of the ERA5 and WAVERYS reanalysis datasets.
We use root mean squared error (RMSE) (Equation (1)), average differences (bias) (Equation (2)), scatter index (SI) (Equation (3)), the corrected indicator introduced by Hanna and Heinold (HH) (Equation (4)) [43], and capacity prediction (C) (Equation (5)) of SWH to describe the deviation of the reanalysis data from the buoy data. The SI of SWH gives the dispersion between the model and altimeter data. Mentaschi et al. (2013) highlighted some concerns with RMSE-derived metrics that favor negatively biased model outputs [44]. The authors suggested the use of the unbiased HH metric proposed by Hanna and Heinold (1985) [43]. As for capacity prediction (C), the positive value means overestimate, and vice versa. Through the above-mentioned indices, we can quantitatively and comprehensively evaluate the errors.
The RMSE is given by
RMSE = 1 n − 1 ∑ i = 1 n ( V r e a , i − V b u o , i ) 2
The bias is given by
bias = 1 n ∑ i = 1 n | V r e a , i − V b u o , i |
The SI is given by
S I = ∑ i = 1 n [ ( V r e a , i − V r e a ¯ ) − ( V b u o , i − V b u o ¯ ) ] 2 ∑ i = 1 n V b u o , i 2
The HH is given by
H H = ∑ i = 1 n ( V r e a , i − V b u o , i ) 2 ∑ i = 1 n V r e a , i · V b u o , i
The C is given by
C = 100 × 1 n ∑ 1 n V r e a , i − V b u o , i ( V r e a , i + V b u o , i ) / 2
where V r e a , i and V b u o , i are the records of TC-induced ocean waves (i.e., SWH) of the reanalysis and buoy data, respectively; V r e a ¯ and V b u o ¯ are the average values of V r e a , i and V b u o , i , respectively; n is the total number of 6-h records of TC-induced ocean waves (n = 3327 from 1993 to 2020). The RMSE of surface wind speed is also calculated to investigate possible source for the RMSE of SWH, as SWH is largely affected by surface wind speed [45].

4. Results

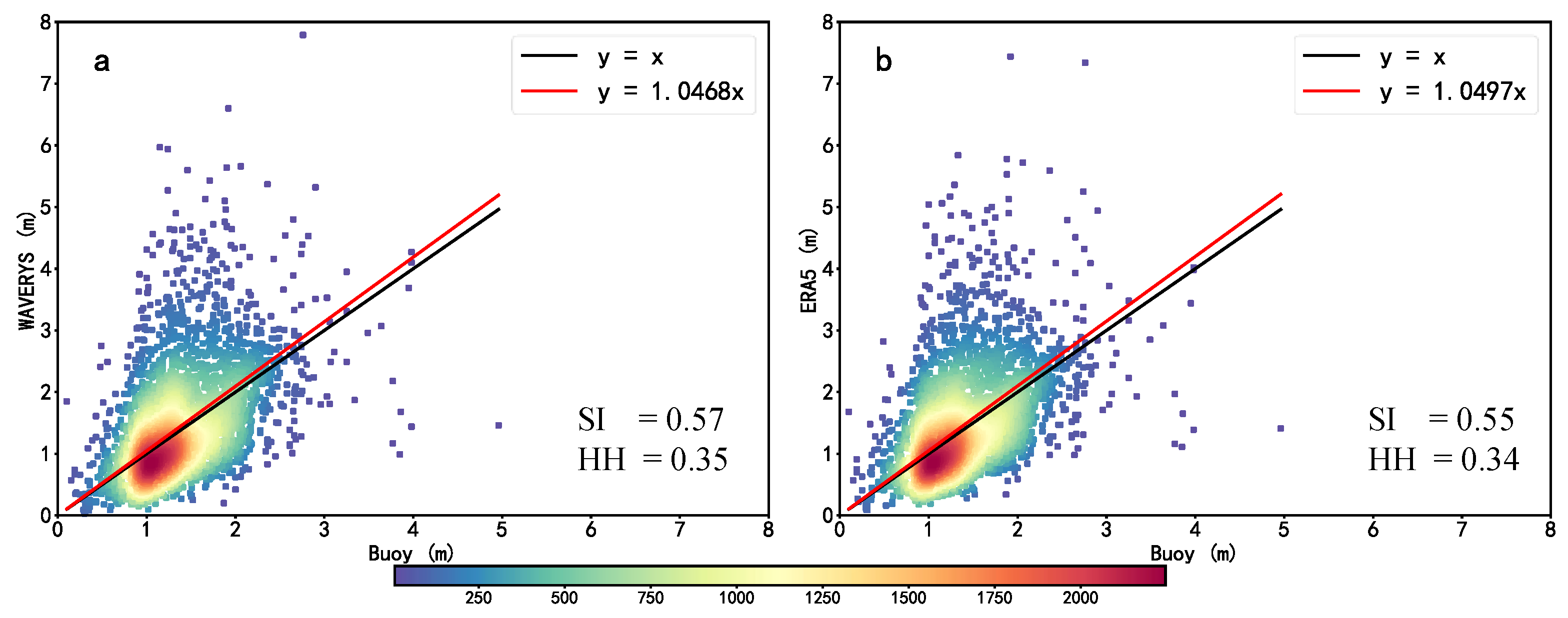
4.1. Errors in the Two Reanalysis Datasets

First, we perform TC-induced ocean wave validation using the global wave buoy data obtained from the Historical NDBC data [39]. Figure 1 shows that the NDBC global buoys are mostly distributed near the coasts, except for the North Pacific (NP) and central tropical Indian Ocean. More importantly, as the North Atlantic (NA) is one of the most active TC basins [46] and a large number of buoys are moored in the North Atlantic, most of the TC records are concentrated in the NA, especially in the areas near the east coast of the United States. Note that some stations in TC-active regions do not have TC records, largely due to the short records at these stations. As for the spatial distribution of the errors in the two reanalysis datasets, most of the stations have RMSEs within 0.5 m, but a few stations at high latitudes, in the U.S. interior lakes, and in remote regions have larger RMSEs above 0.5 m (Figure S1). We mainly focus on the NP and NA in the rest of the paper.
Figure 2 shows scatter plots of SWH from the two reanalysis datasets and the buoy data during the period 1993–2020. The correlations between reanalysis datasets, and observations are all above 0.99. However, the linear regression shows a slope of 1.047 for the WAVERYS (Figure 2a), and of 1.050 for the ERA5 (Figure 2b). Note that the two slopes are similar and both are notably larger than not only the ideal value of 1.0 but also the slopes reported in [11], which focused on global ocean wave rather than on TC-induced ocean waves (e.g., 0.97 in WAVERYS and 0.93 in ERA5). This indicates that, different from the global ocean waves in [11], the SWH of TC-induced ocean waves in the reanalysis datasets is overall larger compared to the buoy data (+0.11 m in both WAVERYS and ERA5). This is consistent with the results in Bethel et al. [47], which showed that the model simulations of large waves (e.g., TC-induced ocean waves) tend to be larger than those observed. Specifically, the differences between the WAVERYS data and buoy data are quite small when the SWH is less than 1 m, and the differences gradually increase with a larger SWH (Figure 2a). The differences between the ERA5 data and buoy data are also quite small with smaller SWH, and increase with large SWH (Figure 2b). Thereby, both the WAVERYS and ERA5 datasets are more accurate in smaller SWH. When comparing the scatter plots of the WAVERYS and ERA5, the distribution of the points in the WAVERYS is quite similar to those in the ERA5 (e.g., most of the points are concentrated around 1 m, and slopes of both reanalysis datasets are similar) (Figure 2a,b), which is due to the fact that the wave model that produced the WAVERYS reanalysis data is also driven by the wind field of the ERA5 [11], and wind plays a decisive role in the development and extinction of ocean waves [48]. Moreover, we see a better SI (Equation (3)) of SWH for the ERA5 of 0.55, in comparison with 0.57 for the WAVERYS. We also see a better HH (Equation (4)) of SWH for the ERA5 of 0.34, in comparison with 0.35 for the WAVERYS. It indicates that the errors of ERA5 are smaller compared with those of WAVERYS.
Figure 3 shows the probability density function for SWH from buoy, ERA5, and WAVERYS in the NP and NA. The global reanalysis data distributions of the ERA5 and WAVERYS are similar to those of the NP and NA (Figure S2). The distributions of the two reanalysis datasets are consistent with that of the buoy data as the probability density is mainly concentrated in the range from 1.0 to 2.0 m of SWH, which is consistent with the probability density of the global ocean wave data (e.g., the ERA5 and WAVERYS) in [11]. However, there are still notable differences in detail. In the NP (NA), there are notable (slight) differences between the ERA5 and WAVERYS. As shown as Figure 3a (Figure 3b), the error is quite small when the SWH is more than 2.75 m (less than 1.25 m), which indicates that reanalysis data perform well with high SWH in the NP (with low SWH in the NA). Besides, in the NP, the probability density of the buoy (WAVERYS, ERA5) data in 0–1 m is 5.04% (16.04%, 7.65%), in 1–2 m is 48.13% (46.83%, 52.42%), in 2–3 m is 43.47% (30.78%, 33.02%), and above 3 m is 3.36% (6.36%, 6.91%) (Figure 3a). In the NA, the probability density of the buoy (WAVERYS, ERA5) data in 0–1 m is 25.92% (34.09%, 34.88%), in 1–2 m is 65.47% (44.66%, 45.49%), in 2–3 m is 4.49% (14.09%, 14.31%), and above 3 m is 0.11% (6.33%, 5.33%) (Figure 3b). Note that the percentage of the wave with high SWH in the ERA5 and WAVERYS reanalysis datasets is higher than that in the buoy data (Figure 3 and Figure S2), which partly explains why the SWH values in the two reanalysis datasets are overall larger compared to those in the buoy data (e.g., the slope in Figure 2).
Figure 4 shows the temporal evolution of the errors of TC-induced ocean waves in the reanalysis datasets from 1993 to 2020. The RMSE (Equation (1)) slope for the WAVERYS is −0.10 m ± 0.09 m decades−1 (Figure 4a), and the slope of RMSE for the ERA5 is −0.08 m ± 0.09 m decades−1 (Figure 4b). The slope of bias (Equation (2)) for the WAVERTS is −0.08 m ± 0.06 m decades−1 (Figure 4c), and the slope of bias for the ERA5 is −0.06 m ± 0.06 m decades−1 (Figure 4d). We can see a significant decreasing trend in the RMSE and bias of the reanalysis data over the study period. The RMSE of the WAVERYS and the bias of both WAVERYS and ERA5 pass the 95% significance test, while the RMSE of the ERA5 only passes the 90% significance test. Specifically, for the RMSEs of both WAVERYS and ERA5, the errors in most years before 2012 were higher than 0.7 m, while the errors in most years after 2013 were lower than 0.7 m (Figure 4a,b). For the biases of both WAVERYS and ERA5, the errors in most years before 2012 were higher than 0.5 m, while the errors in most years after 2013 were lower than 0.5 m (Figure 4c,d). This is not a surprise: it is largely due to the increase in computational power running numerical models [49], the incorporation of high-quality observations (e.g., better quality satellite data), and the improvement of the model and its assimilation scheme [31], which led to a significant decrease of errors in the wave model results.

4.2. Possible Causes of Errors in TC-Induced Ocean Wave Intensity, Distance, and Wind Speed

In previous studies, the global multi-year-averaged errors of ocean waves are around 0.24 m, including those around 0.1–0.3 m in the NA [11]. However, the multi-year-averaged errors of TC-induced ocean waves for the ERA5 and WAVERYS reported here are 0.54 and 0.56 m, respectively, which are much larger. We will investigate the cause next.
It is known that the energy source of TC-induced ocean waves comes from TC wind, and thus it is assumed that the bias of TC-induced ocean waves is largely caused by the bias of TC wind. This is partly demonstrated by our results, as the distributions of TC-induced ocean waves in both WAVERYS and ERA5 using the same wind field are similar, and their errors are also similar. Note that the wind information in buoy data is continuous, namely wind speed is averaged over 10 min, while the wind speed in the reanalysis data is instantaneous. Probably due to time averaging, the wind speed in the buoy data has a more concentrated distribution, which mainly distributes in the range of 5–7 m s−1. The instantaneous wind speed in the reanalysis data has a relatively looser distribution compared to the time-averaged wind speed of buoy data, which mainly distributes in the range of 1–10 m s−1 (Figure S2). Therefore, we should not compare the errors of instantaneous wind speed in the reanalysis data with errors of in-situ buoy wind speed averaged over 10 min.
The errors of TC-induced ocean waves are related to wind speed errors associated with TCs, which often come from the limited skills of models in reproducing TCs [50,51]. It is assumed that the closer to TC eyewall, the larger wind speed, and thus the larger errors of wind speed and ocean wave. Table 1 shows errors of TC-induced ocean waves at different distances from TC centers in the NP and NA. Note that the values of the three parameters (i.e., RMSE, bias, and C) for the WAVERYS and ERA5 datasets are similar. According to their RMSE and bias, the errors of the reanalysis data (i.e., ERA5 and WAVERYS) in the NA are obviously lager than those in the NP with various distances from the TC center. The errors of reanalysis data (i.e., WAVERYS and ERA5 and WAVERYS) are obviously lager with the shorter distance from the TC center. It indicates that the errors of TC-induced ocean waves are strongly correlated with the area and distance from the TC center. The errors in the NP and at the short distance from the TC center are larger. According to C (Equation (5)), the SWH values of TC-induced ocean waves are overestimated within a radius of 600 km from the TC center in the NA. As for the NP basin, the SWH values of TC-induced ocean waves are overestimated within a radius of 400 km and are underestimated at distance between 400 and 600 km from the TC center. In most cases, the global ocean waves of the reanalysis data are not within the influence radii of TCs, and the errors are relatively small [10]. This partly explains the reason why the errors of TC-induced ocean waves are larger than the errors of the global ocean waves. In addition, the errors of the models are large when simulating large waves, including TC-induced ocean waves [47].
Table 2 shows errors of TC-induced ocean waves with respect to different SWH values. Similar to Table 1, there are larger (smaller) errors in the NA (NP) in terms of RMSE and bias. Moreover, the errors of TC-induced ocean waves are strongly correlated with the SWH of the wave: the larger the wave, the larger the error. In addition, almost all the SWH values of TC-induced ocean waves in the NP are underestimated except for the errors with SWH of 0.5–1.0 m in the ERA5. In the NA, the SWH values are overestimated (underestimated) with smaller (larger) SWH. Compared with the global wave [11], the SWH of TC-induced ocean waves, along with its errors, are all relatively large. More detailed information of TC-induced ocean waves errors is listed in Table S1.
Table 3 shows errors of TC-induced ocean waves in shallow water and deep ocean. The differences between the NP and NA are similar to those in Table 1. The errors of the shallow water are larger compared with those of the deep ocean according to their RMSE and bias. The errors of TC-induced ocean waves are underestimated except for the errors in the deep ocean of the NA. It is probably due to the effect of terrain in shallow water simulation, resulting in a large error. In the NP, the SWH of both shallow water and deep ocean are underestimated. In the NA, the SWH are underestimated (overestimated) in the shallow water (deep ocean). In conclusion, the errors of TC-induced waves are mainly associated with ocean basin (i.e., NP and NA), SWH, depth of the seawater, and the distance from the TC center.

5. Conclusions

We use a new method to quantitatively evaluate the errors of TC-induced ocean waves in the two reanalysis datasets (i.e., ERA5 and WAVERYS) with respect to the buoy data. This method can be used to assess not only the accuracy of TC-induced ocean waves in reanalysis data but also the accuracy of TC-induced ocean waves simulated or forecasted in other numerical model products, even the accuracy of TC-induced ocean waves in satellite data. Based on the TC-induced ocean wave records collected for this study, we reveal possible trends and sources of errors in the reanalysis datasets with respect to the buoy data.
Due to the identical surface wind used in the two reanalysis systems, the errors of TC-induced ocean waves in the two reanalysis datasets are quite similar. Moreover, the errors of TC-induced ocean waves are much larger than those of global ocean waves in the two reanalysis datasets, and the errors of TC-induced ocean waves are strongly related to ocean basins (i.e., the NP and NA), SWH, depth of the seawater (shallow sea and deep sea), and the distance from the TC center. The errors in the NP and the deep ocean are smaller than those in the NA and the shallow water, and the larger the SWH and the shorter the distance, the larger the error. The errors in the NP are overestimated (underestimated) with the short (long) distance from the TC center. The errors in the NA are overestimated (underestimated) with small (large) SWH in the deep ocean (shallow water). Furthermore, the errors of TC-induced ocean waves decrease significantly over the study period (1993–2020), possibly because of the improvements in computing, observations, and model physics.
Note that the spatial distribution of the buoys in the NDBC data is heterogeneous and varies with time, with more buoys in the NP and NA and relatively fewer in the other sea areas, which brings uncertainty not only to measuring the accuracy of TC-induced ocean waves but also to evaluating the trend of the errors of TC-induced ocean waves in the reanalysis data. Considering the above-mentioned shortcomings in the NDBC data, we present a quantitative method evaluating errors of TC-induced ocean waves in the reanalysis data or model results using the buoy data, rather than provide a robust conclusion on the errors of TC-induced ocean waves and its trend in the study period in this paper.

6. Discussions

Exploring the errors of waves in reanalysis data has always been a focal point in marine research, with increasing attention paid to wave errors during extreme weathers [52,53,54]. Satellite altimeter measurements of SWH have been extensively validated and used to investigate climatological trends, extreme wave events, cyclone structures and associated wave fields, and the performances of operational hindcasts [33,53,55,56,57,58,59,60,61,62,63]. However, satellite-derived wave measurements are acquired through inversion techniques, inherently containing systematic errors, in contrast to the direct and more accurate measurements obtained from buoys [11]. Satellite altimeter measurements are inaccurate in observing not only extreme ocean waves but also near-shore ocean waves [11,61]. As is well known, the ocean waves near TC are extremely large, and the public concerns are more focused on the TC-induced ocean waves nearshore compared with the those far from shore. As such, it is more appropriate to use buoy data to evaluate the errors of TC-induced ocean waves in reanalysis data. In reality, few studies used buoy data to validate and study ocean waves, especially TC-induced ocean waves. On the other hand, despite the abundance of studies using reanalysis data to investigate ocean waves and TC activities (e.g., TC track and intensity) [18,19,20,21,22,64], studies on TC-induced ocean waves are limited. These are our motivations for investigating the errors of TC-induced ocean wave in reanalysis using buoy data.
The weakness of buoy observations is their scarcity and inadequate spatial coverage [11]. In future, the addition of more buoy stations around the globe and the build-up of its global network will help reduce uncertainty in estimating the accuracy of TC-induced ocean waves in the reanalysis and forecast data. Our next step is to study the impacts of TC wind speed errors and buoys update on TC-induced ocean wave errors in the models.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/jmse12060983/s1, Figure S1: Spatial distribution of NDBC ocean wave buoys in terms of RMSE in TC-induced ocean waves at 6-h interval over the period 1993–2020. (a) RMSE between WAVERYS and buoy data; (b) RMSE between ERA5 and buoy data.; Figure S2: Scatter plots of speed wind from buoy and reanalysis data at 6-h interval over the period 1993–2020. The color bar represents the number of samples at each point; Figure S3: Probability density function for SWH from buoy, ERA5, and WAVERYS data in global oceans; Table S1: Errors of TC-induced ocean waves.

Author Contributions

Conceptualization, W.Z., R.W. and Y.S.; methodology, W.Z. and Z.F.; software, Z.F. and Z.B.; validation, W.Z.; formal analysis, Y.Z. and Y.S.; investigation, Y.S.; resources, W.Z.; data curation, Z.F. and Z.B.; writing—original draft preparation, Y.Z.; writing—review and editing Y.Z., W.Z., R.W., Y.S. and Z.F.; visualization, Y.Z.; supervision, R.W. and Y.S.; project administration, R.W.; funding acquisition, Y.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Natural Science Foundation of China (grants 42075035 and 42075011).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

IBTrACS: https://www.ncei.noaa.gov/products/international-best-track-archive, accessed on 1 December 2023; NDBC: http://www.ndbc.noaa.gov, accessed on 1 December 2023; ERA5: https://cds.climate.copernicus.eu/, accessed on 1 December 2023; WAVERYS: https://marine.copernicus.eu/access-data, accessed on 1 December 2023.

Acknowledgments

Yalan Zhang, Wei Zhong and Zhihao Feng contributed equally to this work. We wish to thank Shuo Lv for his advice on experimental design.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Peduzzi, P.; Chatenoux, B.; Dao, H.; De Bono, A.; Herold, C.; Kossin, J.; Mouton, F.; Nordbeck, O. Global trends in tropical cyclone risk. Nat. Clim. Chang. 2012, 2, 289–294. [Google Scholar] [CrossRef]
  2. Lin, T.-C.; Hamburg, S.P.; Lin, K.-C.; Wang, L.-J.; Chang, C.-T.; Hsia, Y.-J.; Vadeboncoeur, M.A.; McMullen, C.M.M.; Liu, C.-P. Typhoon disturbance and forest dynamics: Lessons from a Northwest Pacific subtropical forest. Ecosystems 2011, 14, 127–143. [Google Scholar] [CrossRef]
  3. Wu, X.; Xu, Z.; Liu, H.; Guo, J.; Zhou, L. What Are the Impacts of Tropical Cyclones on Employment? An Analysis Based on Meta-Regression. Weather. Clim. Soc. 2019, 11, 259–275. [Google Scholar] [CrossRef]
  4. Emanuel, K. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef] [PubMed]
  5. Knutson, T.R.; McBride, J.L.; Chan, J.; Emanuel, K.; Holland, G.; Landsea, C.; Held, I.; Kossin, J.P.; Srivastava, A.K.; Sugi, M. Tropical cyclones and climate change. Nat. Geosci. 2010, 3, 157–163. [Google Scholar] [CrossRef]
  6. Lin, Y.; Zhao, M.; Zhang, M. Tropical cyclone rainfall area controlled by relative sea surface temperature. Nat. Commun. 2015, 6, 6591. [Google Scholar] [CrossRef]
  7. Sun, Y.; Zhong, Z.; Li, T.; Yi, L.; Hu, Y.; Wan, H.; Chen, H.; Liao, Q.; Ma, C.; Li, Q. Impact of ocean warming on tropical cyclone size and its destructiveness. Sci. Rep. 2017, 7, 8154. [Google Scholar] [CrossRef]
  8. Sampson, C.R.; Wittmann, P.A.; Tolman, H.L. Consistent tropical cyclone wind and wave forecasts for the U.S. Navy. Weather Forecast. 2010, 25, 1293–1306. [Google Scholar] [CrossRef]
  9. Sun, Y.; Zhong, Z.; Li, T.; Yi, L.; Shen, Y. The slowdown tends to be greater for stronger tropical cyclones. J. Clim. 2021, 34, 5741–5751. [Google Scholar] [CrossRef]
  10. Sharmar, V.; Markina, M. Validation of global wind wave hindcasts using ERA5, MERRA2, ERA-Interim and CFSRv2 reanalyzes. IOP Conf. Ser. Earth Environ. Sci. 2020, 606, 012056. [Google Scholar] [CrossRef]
  11. Law-Chune, S.; Aouf, L.; Dalphinet, A.; Levier, B.; Drillet, Y.; Drevillon, M. WAVERYS: A CMEMS global wave reanalysis during the altimetry period. Ocean Dyn. 2021, 71, 357–378. [Google Scholar] [CrossRef]
  12. Wang, H.; Zhu, J.; Yang, J. Error Analysis on ESA’s Envisat ASAR Wave Mode Significant Wave Height Retrievals Using Triple Collocation Model. Remote. Sens. 2014, 6, 12217–12233. [Google Scholar] [CrossRef]
  13. Caires, S.; Sterl, A. 100-year return value estimates for ocean wind speed and significant wave height from the ERA-40 data. J. Clim. 2005, 18, 1032–1048. [Google Scholar] [CrossRef]
  14. Morim, J.; Hemer, M.; Wang, X.L.; Cartwright, N.; Trenham, C.; Semedo, A.; Young, I.; Bricheno, L.; Camus, P.; Casas-Prat, M.; et al. Robustness and uncertainties in global multivariate wind-wave climate projections. Nat. Clim. Chang. 2019, 9, 711–718. [Google Scholar] [CrossRef]
  15. Morim, J.; Vitousek, S.; Hemer, M.; Reguero, B.; Erikson, L.; Casas-Prat, M.; Wang, X.L.; Semedo, A.; Mori, N.; Shimura, T.; et al. Global-scale changes to extreme ocean wave events due to anthropogenic warming. Environ. Res. Lett. 2021, 16, 074056. [Google Scholar] [CrossRef]
  16. Frölicher, T.L.; Fischer, E.M.; Gruber, N. Marine heatwaves under global warming. Nature 2018, 560, 360–364. [Google Scholar] [CrossRef]
  17. Vousdoukas, M.I.; Mentaschi, L.; Voukouvalas, E.; Verlaan, M.; Jevrejeva, S.; Jackson, L.P.; Feyen, L. Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard. Nat. Commun. 2018, 9, 2360. [Google Scholar] [CrossRef]
  18. Shi, J.; Feng, X.; Toumi, R.; Zhang, C.; Hodges, K.I.; Tao, A.; Zhang, W.; Zheng, J. Global increase in tropical cyclone ocean surface waves. Nat. Commun. 2024, 15, 174. [Google Scholar] [CrossRef]
  19. Hodges, K.; Cobb, A.; Vidale, P.L. How Well Are Tropical Cyclones Represented in Reanalysis Datasets? J. Clim. 2017, 30, 5243–5264. [Google Scholar] [CrossRef]
  20. Schenkel, B.A.; Hart, R.E. An Examination of Tropical Cyclone Position, Intensity, and Intensity Life Cycle within Atmospheric Reanalysis Datasets. J. Clim. 2012, 25, 3453–3475. [Google Scholar] [CrossRef]
  21. Jones, E.; Wing, A.A.; Parfitt, R. A Global Perspective of Tropical Cyclone Precipitation in Reanalyzes. J. Clim. 2021, 34, 8461–8480. [Google Scholar] [CrossRef]
  22. Bian, G.F.; Nie, G.Z.; Qiu, X. How well is outer tropical cyclone size represented in the ERA5 reanalysis dataset? Atmos. Res. 2021, 249, 105339. [Google Scholar]
  23. Collins, C.O.; Lund, B.; Ramos, R.J.; Drennan, W.M.; Graber, H.C. Wave Measurement Intercomparison and Platform Evaluation during the ITOP (2010) Experiment. J. Atmos. Ocean. Technol. 2014, 31, 2309–2329. [Google Scholar] [CrossRef]
  24. Durrant, T.H.; Greenslade, D.J.M.; Simmonds, I. Validation of Jason-1 and envisat remotely sensed wave heights. J. Atmos. Ocean. Technol. 2009, 26, 123–134. [Google Scholar] [CrossRef]
  25. Abdalla, S. SARAL/AltiKa wind and wave products: Monitoring, validation and assimilation. Mar. Geod. 2015, 38, 365–380. [Google Scholar] [CrossRef]
  26. Yu, H.; Jiangyu, L.; Kejian, W.; Zhifeng, W.; Haiqing, Y.; Shaoqing, Z.; Yijun, H.; Ryan, M.K. A global high-resolution ocean wave model improved by assimilating the satellite altimeter significant wave height. Int. J. Appl. Earth Observ. Geoinf. 2018, 70, 43–50. [Google Scholar] [CrossRef]
  27. Houghton, I.A.; Smit, P.B.; Clark, D.; Dunning, C.; Fisher, A.; Nidzieko, N.J.; Chamberlain, P.; Janssen, T.T. Performance Statistics of a Real-Time Pacific Ocean Weather Sensor Network. J. Atmos. Ocean. Technol. 2021, 38, 1047–1058. [Google Scholar] [CrossRef]
  28. Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
  29. Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
  30. Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The International Best Track Archive for Climate Stewardship (IBTrACS): Unifying tropical cyclone data. Bull. Amer. Meteor. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
  31. Kossin, J.P.; Emanuel, K.A.; Vecchi, G.A. The poleward migration of the location of tropical cyclone maximum intensity. Nature 2014, 509, 349–352. [Google Scholar] [CrossRef]
  32. Knapp, K.R.; Kruk, M.C. Quantifying interagency differences in tropical cyclone best-track wind speed estimates. Mon. Weather. Rev. 2010, 138, 1459–1473. [Google Scholar] [CrossRef]
  33. Alves, J.H.G.M.; Young, I.R. On estimating extreme wave heights using combined Geosat, TOPEX/Poseidon and ERS-1 altimeter data. Appl. Ocean Res. 2003, 25, 167–186. [Google Scholar] [CrossRef]
  34. Large, W.G.; Morzel, J.; Crawford, G.B. Accounting for surface wave distortion of the marine wind profile in low-level ocean storms wind measurements. J. Phys. Oceanogr. 1995, 25, 2959–2971. [Google Scholar] [CrossRef]
  35. Vinoth, J.; Young, I.R. Global estimates of extreme wind speed and wave height. J. Clim. 2011, 24, 1647–1665. [Google Scholar] [CrossRef]
  36. Evans, D.; Conrad, C.; Paul, F. Handbook of Automated Data Quality Control Checks and Procedures; NOAA/NDBC Technical; National Data Buoy Center: Hancock County, MS, USA, 2003; 44p. Available online: https://www.ndbc.noaa.gov/publications/NDBCHandbookofAutomatedDataQualityControl2009.pdf (accessed on 9 June 2024).
  37. Ribal, A.; Young, I.R. 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci. Data 2019, 6, 77. [Google Scholar] [CrossRef] [PubMed]
  38. Zieger, S.; Babanin, A.V.; Erick Rogers, W.; Young, I.R. Observation-based source terms in the third-generation wave model WAVEWATCH. Ocean Model. 2015, 96, 2–25. [Google Scholar] [CrossRef]
  39. Ribal, A.; Young, I.R. Calibration and Cross Validation of Global Ocean Wind Speed Based on Scatterometer Observations. J. Atmos. Ocean. Technol. 2020, 37, 279–297. [Google Scholar] [CrossRef]
  40. Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Matsui, N.; Allan, R.J.; Yin, X.; Gleason, B.E.; Vose, R.S.; Rutledge, G.; Bessemoulin, P.; et al. The Twentieth Century Reanalysis Project. Q. J. R. Meteorol. Soc. 2011, 137, 1–28. [Google Scholar] [CrossRef]
  41. Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Vitart, F. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
  42. Copernicus Climate Change Service. ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. Coper-nicus Climate Change Service Climate Data Store (CDS). 2017. Available online: https://cds.climate.copernicus.eu/#!/search?text=ERA5 (accessed on 10 September 2019).
  43. Hanna, S.; Heinold, D. Development and Application of a Simple Method for Evaluating Air Quality; American Petroleum Institute: Washington, DC, USA, 1985. [Google Scholar]
  44. Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Problems in RMSE-based wave model validations. Ocean Model. 2013, 72, 53–58. [Google Scholar] [CrossRef]
  45. Gulev, S.K.; Grigorieva, V. Variability of the Winter Wind Waves and Swell in the North Atlantic and North Pacific as Revealed by the Voluntary Observing Ship Data. J. Clim. 2006, 19, 5667–5685. [Google Scholar] [CrossRef]
  46. Bromirski, P.D.; Kossin, J.P. Increasing hurricane wave power along the U.S. Atlantic and Gulf coasts. J. Geophys. Res. Ocean. 2008, 113. [Google Scholar] [CrossRef]
  47. Bethel, B.J.; Dong, C.; Wang, J. An empirical wind-wave model for hurricane-forced wind waves in the Caribbean Sea. Earth Space Sci. 2021, 8. [Google Scholar] [CrossRef]
  48. Langodan, S.; Cavaleri, L.; Viswanadhapalli, Y.; Hoteit, I. Wind-wave source functions in opposing seas. J. Geophys. Res. Ocean. 2015, 120, 6751–6768. [Google Scholar] [CrossRef]
  49. Sonnewald, M.; Lguensat, R.; Jones, D.C.; Dueben, P.D.; Brajard, J.; Balaji, V. Bridging observations, theory and numerical simulation of the ocean using machine learning. Environ. Res. Lett. 2021, 16, 073008. [Google Scholar] [CrossRef]
  50. Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
  51. Hendricks, E.A.; Peng, M.S.; Ge, X.; Li, T. Performance of a dynamic initialization scheme in the coupled ocean-atmosphere mesoscale prediction system for tropical cyclones (COAMPS-TC). Weather. Forecast. 2011, 26, 650–663. [Google Scholar] [CrossRef]
  52. Rappin, E.D.; Nolan, D.S.; Majumdar, S.J. A highly configurable vortex initialization method for tropical cyclones. Mon. Weather. Rev. 2013, 141, 3556–3575. [Google Scholar] [CrossRef]
  53. Cardone, V.J.; Jensen, R.E.; Resio, D.T.; Swail, V.R.; Cox, A.T. Evaluation of Contemporary Ocean Wave Models in Rare Extreme Events: The ‘Halloween storm’ of October 1991 and the ‘Storm of the century’ of March 1993. J. Atmos. Ocean. Technol. 1996, 13, 198–230. [Google Scholar] [CrossRef]
  54. Lodise, J.; Merrifield, S.; Collins, C.; Behrens, J.; Terrill, E. Performance of ERA5 wind speed and significant wave height within Extratropical cyclones using collocated satellite radar altimeter measurements. Coast. Eng. J. 2024, 66, 89–114. [Google Scholar] [CrossRef]
  55. Lodise, J.; Merrifield, S.; Collins, C.; Rogowski, P.; Behrens, J.; Terrill, E. Global Climatology of Extratropical Cyclones from a New Tracking Approach and Associated Wave Heights from Satellite Radar Altimeter. J. Geophys. Res. Ocean. 2022, 127. [Google Scholar] [CrossRef]
  56. Abdalla, S.; Janssen, P.A.; Bidlot, J.R. Jason-2 OGDR Wind and Wave Products: Monitoring, Validation and Assimilation. Mar. Geod. 2010, 33, 239–255. [Google Scholar] [CrossRef]
  57. Clarence, C.; Hesser, T. Alt WIZ: A System for Satellite Radar Altimeter Evaluation of Modeled Wave Heights; Technical Report; US Army Engineer Research and Development Center: Duck, NC, USA, 2021. [Google Scholar]
  58. de León, S.P.; Bettencourt, J. Composite Analysis of North Atlantic Extra-Tropical Cyclone Waves from Satellite Altimetry Observations. Adv. Space Res. 2019, 68, 762–772. [Google Scholar] [CrossRef]
  59. Queffeulou, P. Long-Term Validation of Wave Height Measurements from Altimeters. Mar. Geod. 2004, 27, 495–510. [Google Scholar] [CrossRef]
  60. Agustinus, R.; Young, I.R. Global Calibration and Error Estimation of Altimeter, Scatterometer, and Radiometerwind Speed Using Triple Collocation. Remote Sens. 2020, 12, 1997. [Google Scholar]
  61. Yang, J.; Zhang, J.; Jia, Y.; Fan, C.; Cui, W. Validation of Sentinel-3A/3B and Jason-3 Altimeter Wind Speeds and Significant Wave Heights Using Buoy and ASCAT Data. Remote. Sens. 2020, 12, 2079. [Google Scholar] [CrossRef]
  62. Zieger, S.; Vinoth, J.; Young, I.R. Joint Calibration of Multiplatform Altimeter Measurements of Wind Speed and Wave Height over the Past 20 Years. J. Atmos. Ocean. Technol. 2009, 26, 2549–2564. [Google Scholar] [CrossRef]
  63. Izaguirre, C.; Méndez, F.J.; Menéndez, M.; Losada, I.J. Global Extreme Wave Height Variability Based on Satellite Data. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
  64. Geng, Q.; Sugi, M. Variability of the North Atlantic Cyclone Activity in Winter Analyzed from NCEP–NCAR Reanalysis Data. J. Clim. 2001, 14, 3863–3873. [Google Scholar] [CrossRef]
Jmse 12 00983 g001
Figure 1. Spatial distribution of buoy stations marked by numbers of times (6-h interval) when the stations are close to TC centers (i.e., within a radius of 600 km from the TC center) during the period from 1993 to 2020.
Figure 1. Spatial distribution of buoy stations marked by numbers of times (6-h interval) when the stations are close to TC centers (i.e., within a radius of 600 km from the TC center) during the period from 1993 to 2020.
Jmse 12 00983 g001
Jmse 12 00983 g002
Figure 2. (a) Scatter plots of SWH from buoy and WAVERYS data. (b) Scatter plots of SWH from buoy and ERA5 data. The color bar represents the density of points.
Figure 2. (a) Scatter plots of SWH from buoy and WAVERYS data. (b) Scatter plots of SWH from buoy and ERA5 data. The color bar represents the density of points.
Jmse 12 00983 g002
Jmse 12 00983 g003
Figure 3. Probability density function for SWH from buoy, ERA5, and WAVERYS data in the two basins. (a) the NP; (b) the NA.
Figure 3. Probability density function for SWH from buoy, ERA5, and WAVERYS data in the two basins. (a) the NP; (b) the NA.
Jmse 12 00983 g003
Jmse 12 00983 g004
Figure 4. Time evolution of errors of TC-induced ocean waves in the reanalysis data from 1993 to 2020. Dots indicates the annual-mean errors, and linear trend lines (dashed) are shown with their 95% two-sided confidence intervals (shaded) which are also given by the annotated values. (a) RMSE of WAVERYS data; (b) RMSE of ERA5 data; (c) bias of WAVERYS data; and (d) bias of ERA5 data.
Figure 4. Time evolution of errors of TC-induced ocean waves in the reanalysis data from 1993 to 2020. Dots indicates the annual-mean errors, and linear trend lines (dashed) are shown with their 95% two-sided confidence intervals (shaded) which are also given by the annotated values. (a) RMSE of WAVERYS data; (b) RMSE of ERA5 data; (c) bias of WAVERYS data; and (d) bias of ERA5 data.
Jmse 12 00983 g004
Table 1. Errors of TC-induced ocean waves at different distances from TC center in the NP and NA.
Table 1. Errors of TC-induced ocean waves at different distances from TC center in the NP and NA.
ErrorDataOceanDistance
0–200 km200–400 km400–600 km
RMSE (m)WAVERYSNP1.210.850.68
NA2.161.170.85
ERA5NP1.400.900.67
NA2.191.170.82
Bias (m)WAVERYSNP0.890.610.47
NA1.410.800.59
ERA5NP0.920.600.46
NA1.420.790.57
C (%)WAVERYSNP10.260.68−10.55
NA43.1717.710.17
ERA5NP16.076.24−4.57
NA43.9619.211.36
Table 2. Errors of TC-induced ocean waves with respect to different SWH (m).
Table 2. Errors of TC-induced ocean waves with respect to different SWH (m).
ErrorDataOceanSWH (m)
ALL0.5–1.01.0–1.51.5–2.02.0–2.52.5–3.0>3.0
RMSE (m)WAVERYSNP0.660.190.360.60.561.151.22
NA0.820.610.830.960.891.152.68
ERA5NP0.650.250.410.60.531.091.23
NA0.80.620.810.910.851.262.75
Bias (m)WAVERYSNP0.690.410.540.690.660.90.95
NA0.760.660.760.850.810.981.6
ERA5NP0.670.440.560.660.640.880.95
NA0.750.660.750.820.81.041.63
C (%)WAVERYSNP−11.09−0.29−13.7−12.93−8.98−8.11−27.62
NA−0.774.77−0.48−5.57−15.85−49.36−89.25
ERA5NP−4.2813.04−3.05−0.42−7.55−8.4−30.19
NA0.618.590.39−6.07−16.54−56.76−93.35
Table 3. Errors of TC-induced ocean waves in shallow water and deep ocean (m). The depth boundary between them is set to 200 m.
Table 3. Errors of TC-induced ocean waves in shallow water and deep ocean (m). The depth boundary between them is set to 200 m.
ErrorDataBasin and Depth
NP 0–200 (m)NP 200+ (m)NA 0–200 (m)NA 200+ (m)
RMSE (m)WAVERYS0.690.530.880.83
ERA50.680.510.800.83
Bias (m)WAVERYS0.480.350.630.58
ERA50.470.370.580.57
C (%)WAVERYS−10.28−13.30−0.480.45
ERA5−4.60−4.21−3.993.66
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhang, Y.; Zhong, W.; Feng, Z.; Wang, R.; Sun, Y.; Bai, Z. Errors of Tropical Cyclone-Induced Ocean Waves in Reanalysis Using Buoy Data. J. Mar. Sci. Eng. 2024, 12, 983. https://doi.org/10.3390/jmse12060983

AMA Style

Zhang Y, Zhong W, Feng Z, Wang R, Sun Y, Bai Z. Errors of Tropical Cyclone-Induced Ocean Waves in Reanalysis Using Buoy Data. Journal of Marine Science and Engineering. 2024; 12(6):983. https://doi.org/10.3390/jmse12060983

Chicago/Turabian Style

Zhang, Yalan, Wei Zhong, Zhihao Feng, Ruilin Wang, Yuan Sun, and Zongbao Bai. 2024. "Errors of Tropical Cyclone-Induced Ocean Waves in Reanalysis Using Buoy Data" Journal of Marine Science and Engineering 12, no. 6: 983. https://doi.org/10.3390/jmse12060983

APA Style

Zhang, Y., Zhong, W., Feng, Z., Wang, R., Sun, Y., & Bai, Z. (2024). Errors of Tropical Cyclone-Induced Ocean Waves in Reanalysis Using Buoy Data. Journal of Marine Science and Engineering, 12(6), 983. https://doi.org/10.3390/jmse12060983

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop