Assessment of a Hybrid Wind–Wave Energy Converter System in Nearshore Deployment
Abstract
:1. Introduction
- A novel conceptual design for a hybrid nearshore wind–wave energy converter system, integrating a high-efficiency wave energy converter with vertical axis wind turbines.
- A comprehensive analytical model in the time domain for the proposed HWWECS, combining the modeling of the WEC, VAWT, hydraulic system, and electric generator.
- Numerical simulations and analysis of the HWWECS performance, including the effects of phase differences between multiple WEC units on the overall efficiency and system response.
- Demonstration of the potential advantages of the proposed HWWECS in increasing total energy conversion efficiency and smoothing the system response by leveraging the complementary nature of wind and wave energy sources in a nearshore deployment scenario.
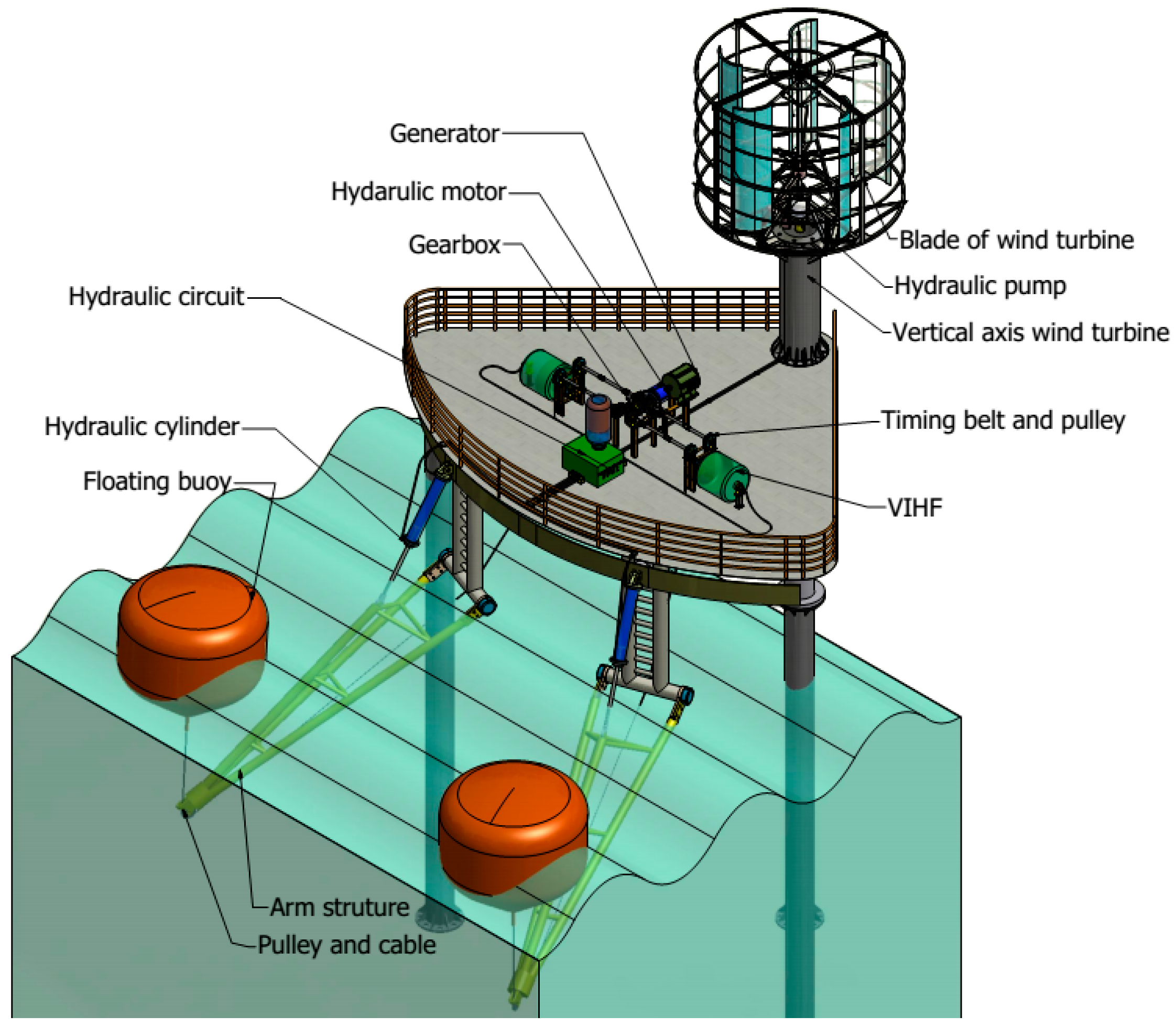
2. Overall Layout of the HWWECS
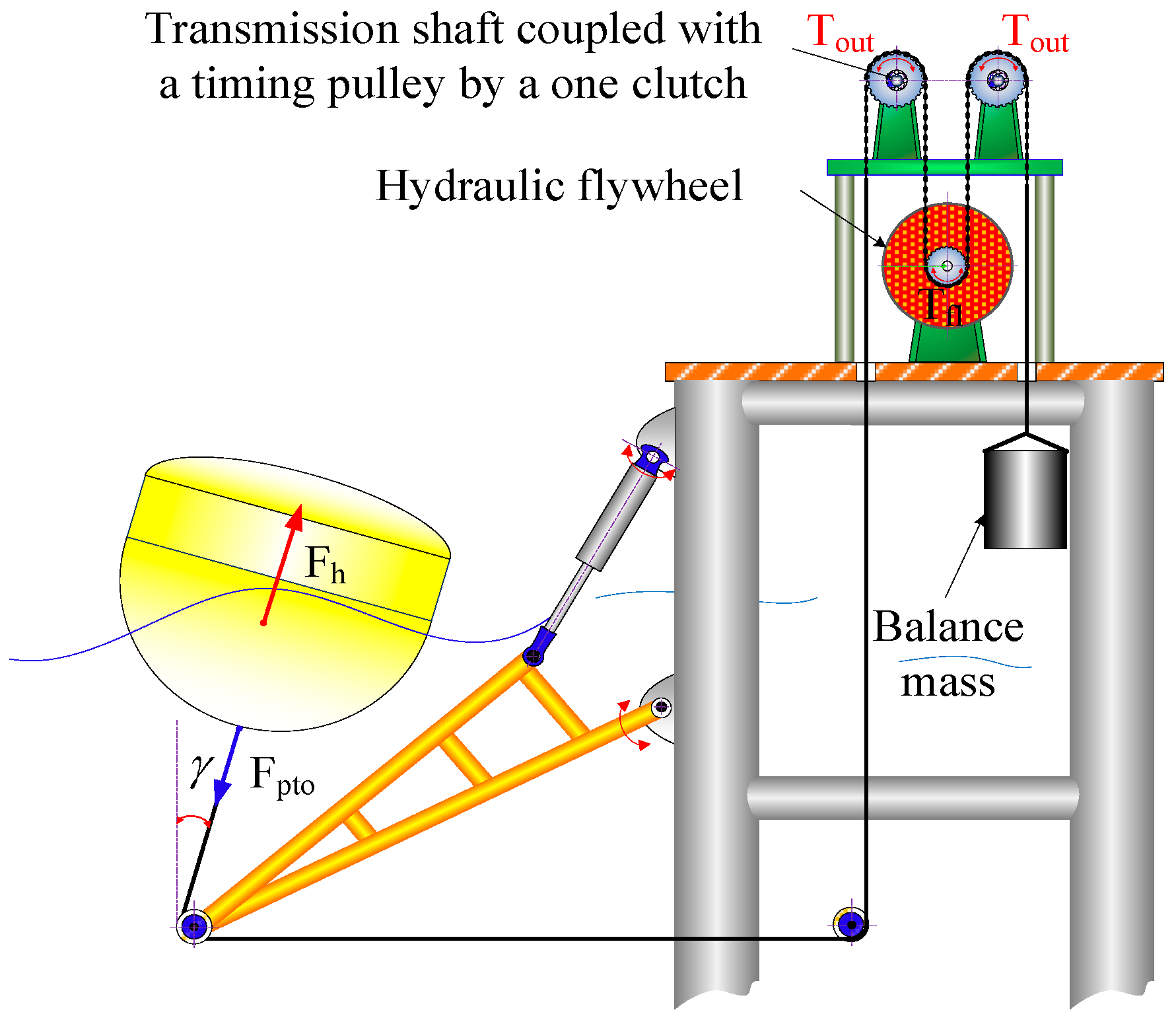
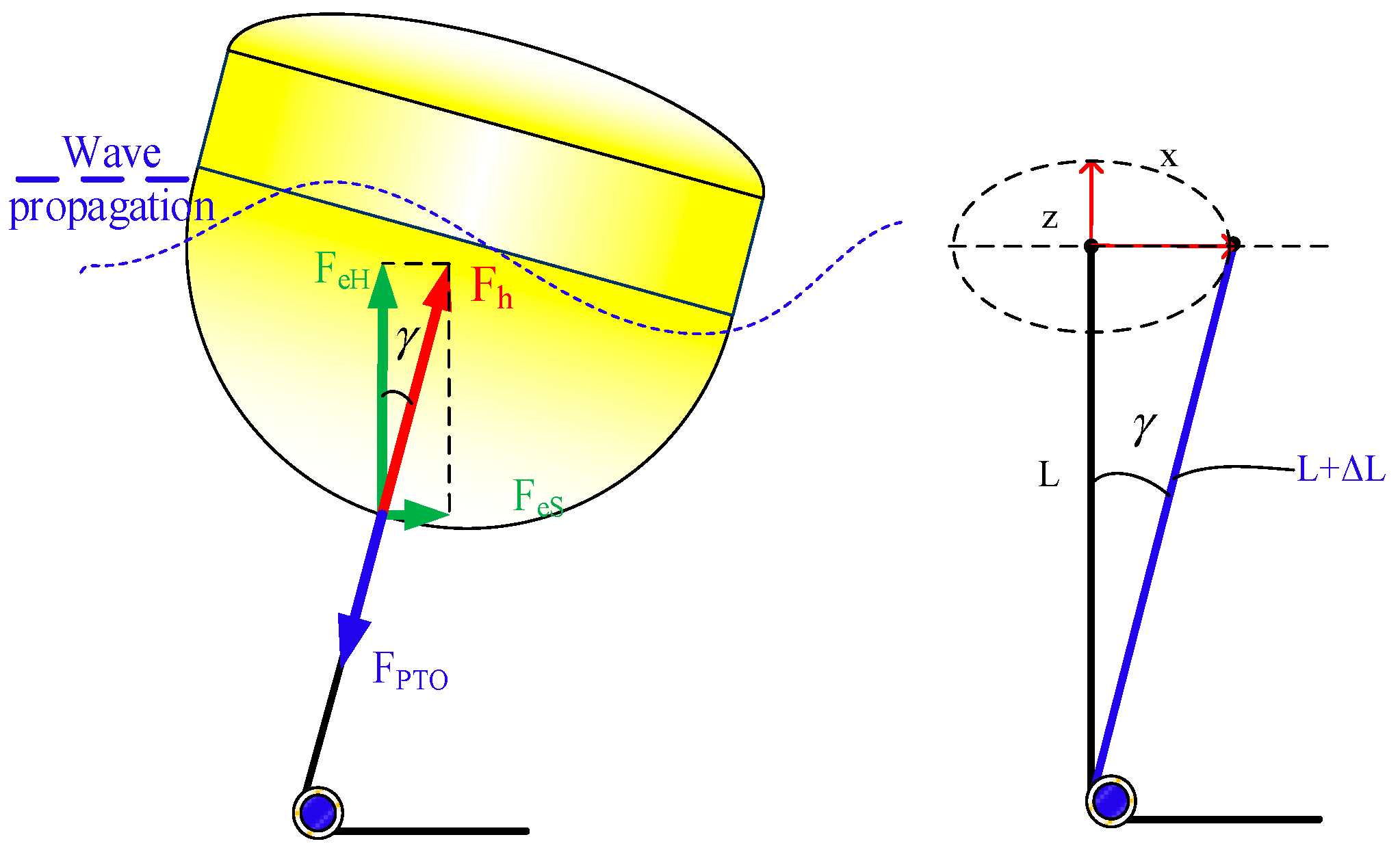
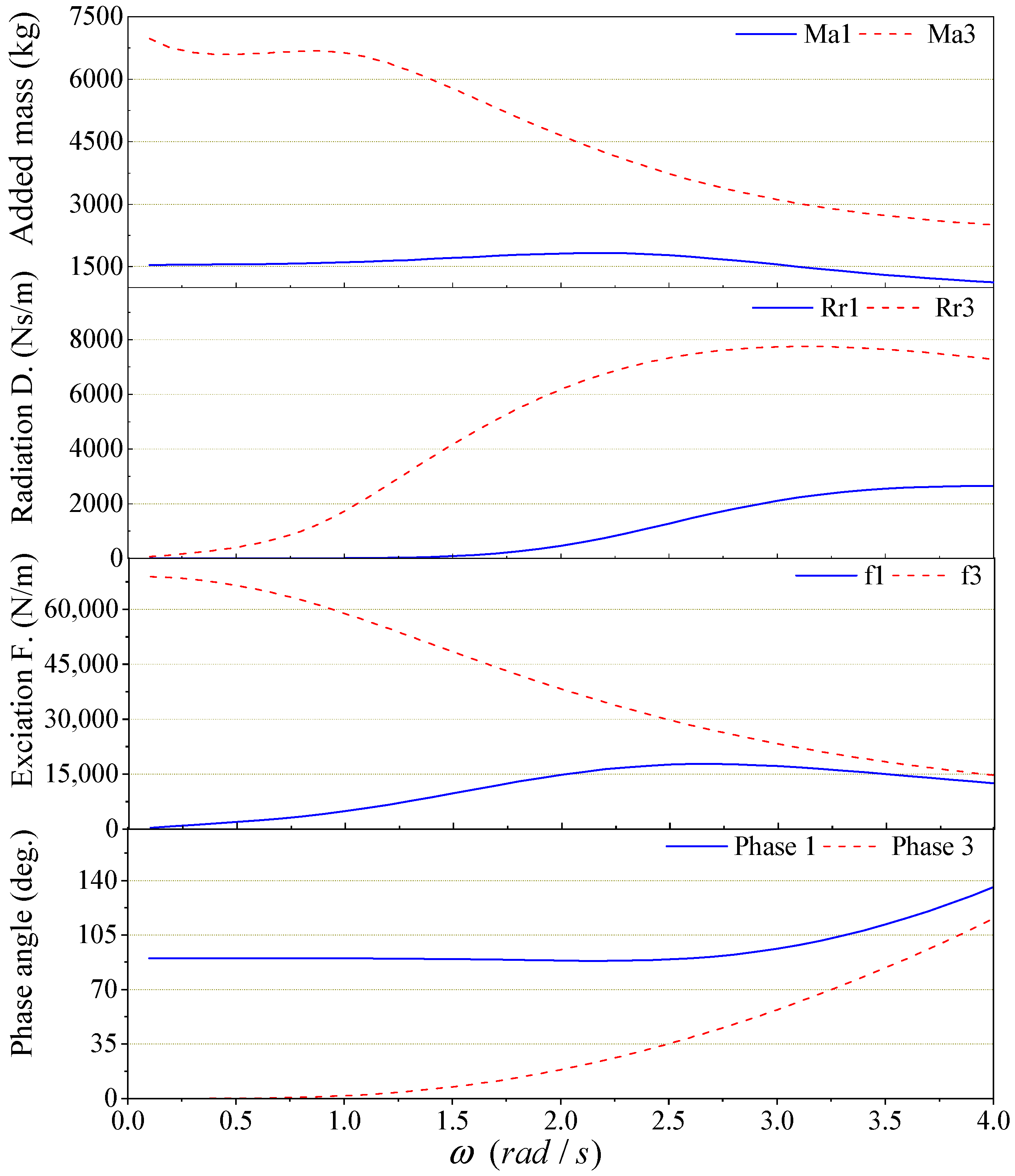
3. WEC System Model
4. Wind Energy Converter System
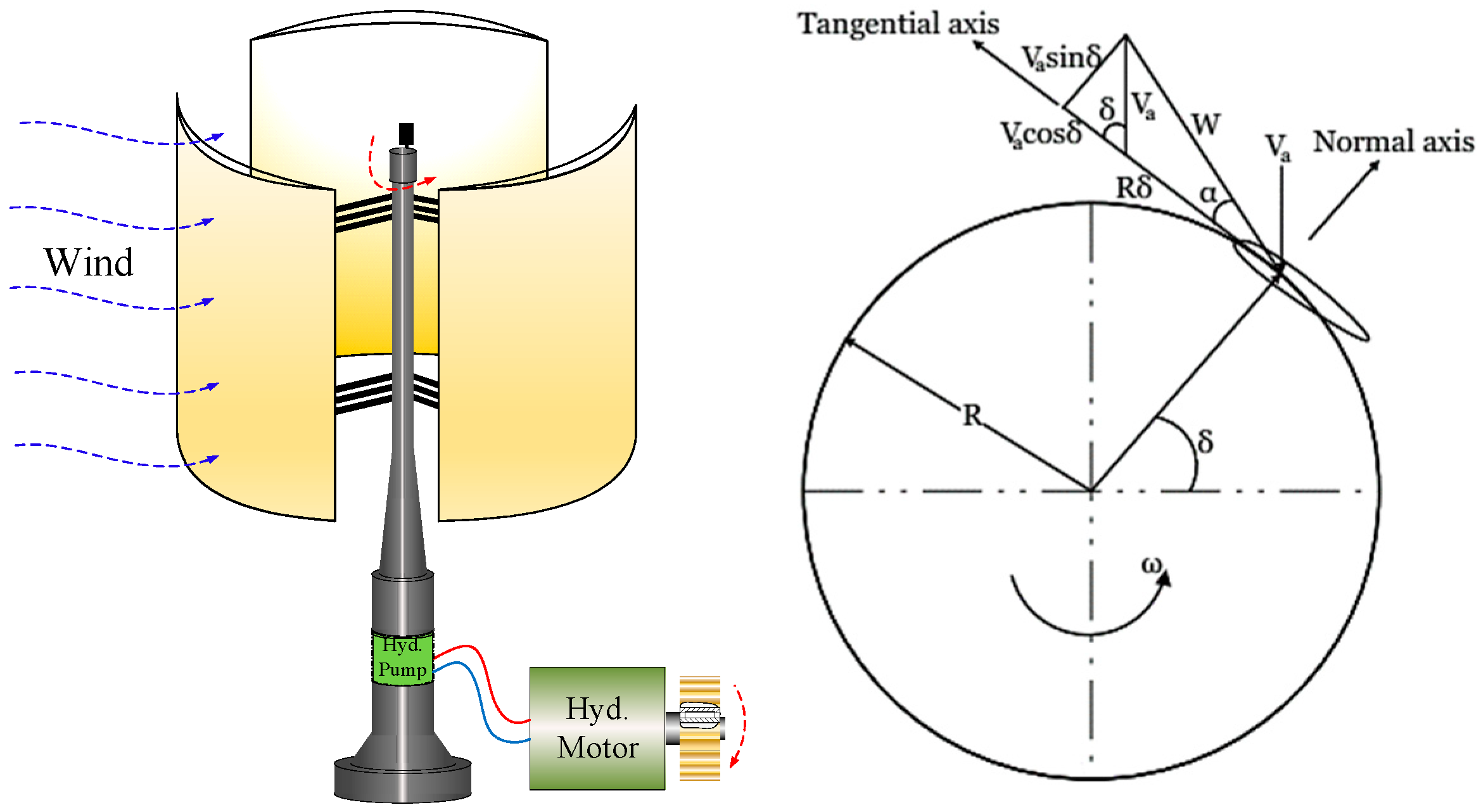
4.1. Modeling of VAWT
4.1.1. The Attack Angle and Relative Flow Velocity
4.1.2. The Tangential and Normal Forces
4.1.3. Calculation of Torque and Power
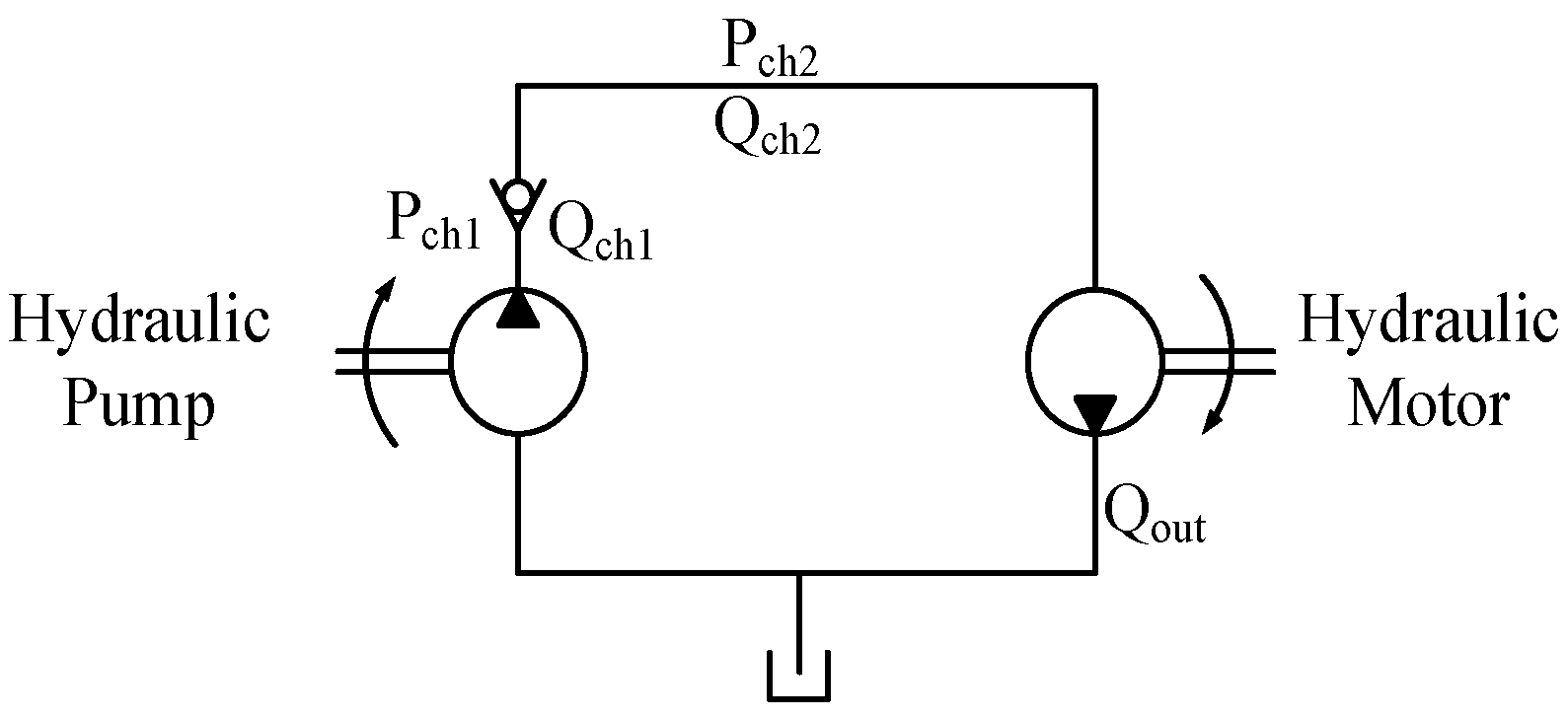
4.2. Hydraulic Circuit
4.2.1. Hydraulic Pump
4.2.2. Hydraulic Motor
4.2.3. Power Calculation
5. Generator Model
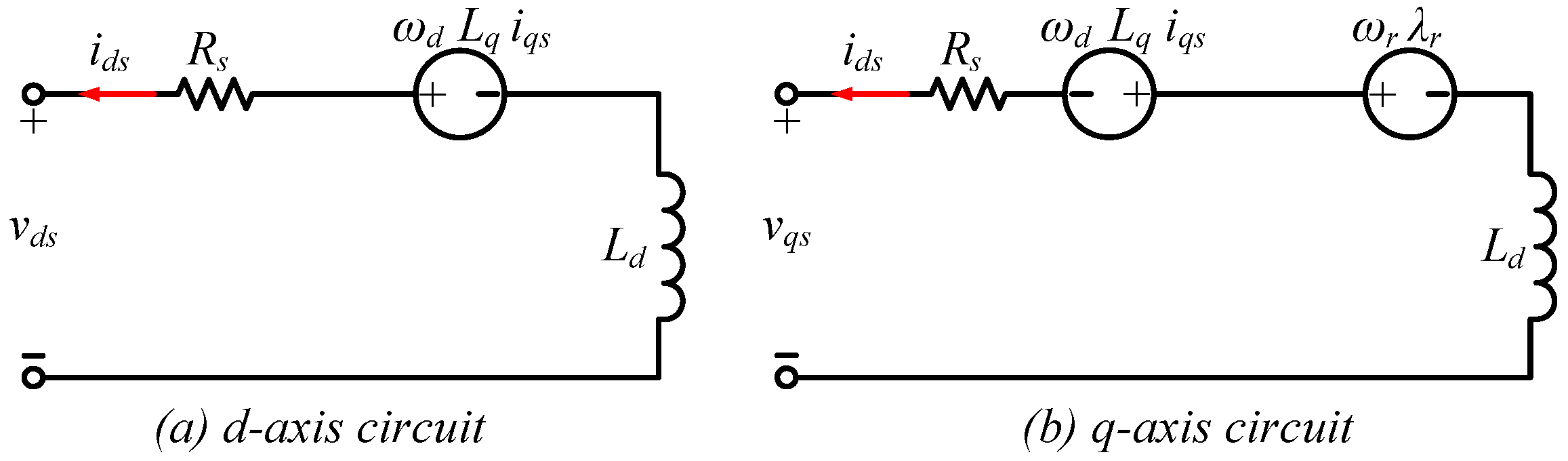
5.1. abc/dq Transformation (Park Transformation)
5.2. Permanent Magnet Generator
5.3. Excitation and Load Model
5.4. Hybrid Mechanism Simulation Model
6. Simulation Results and Discussion
6.1. Parameters
6.2. Results
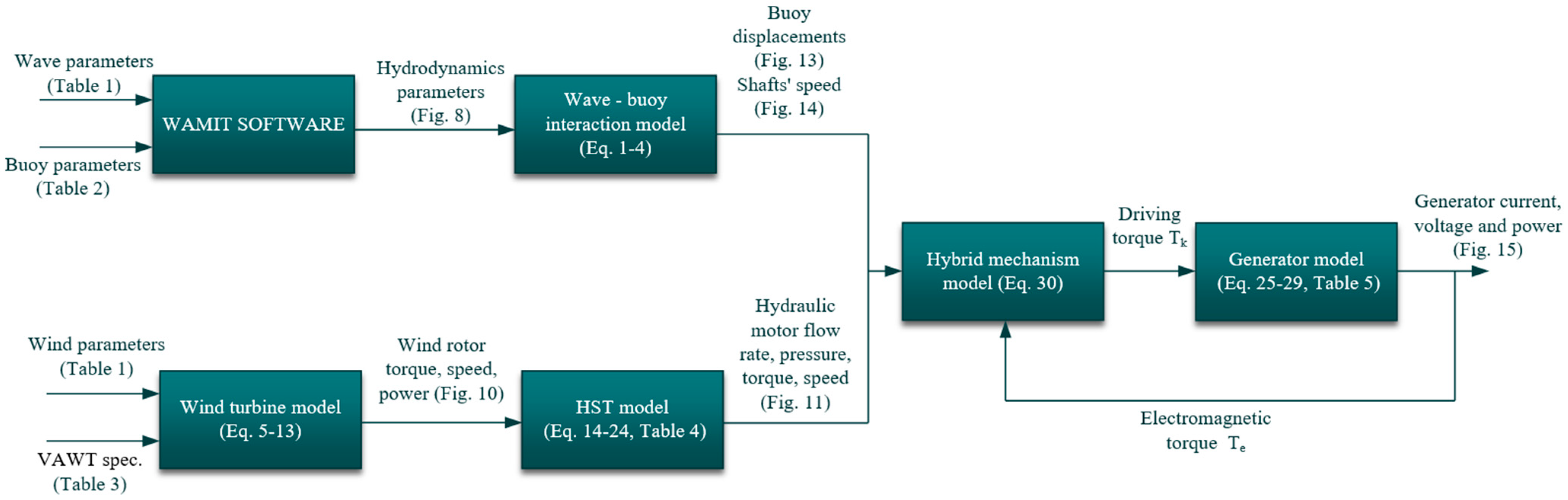
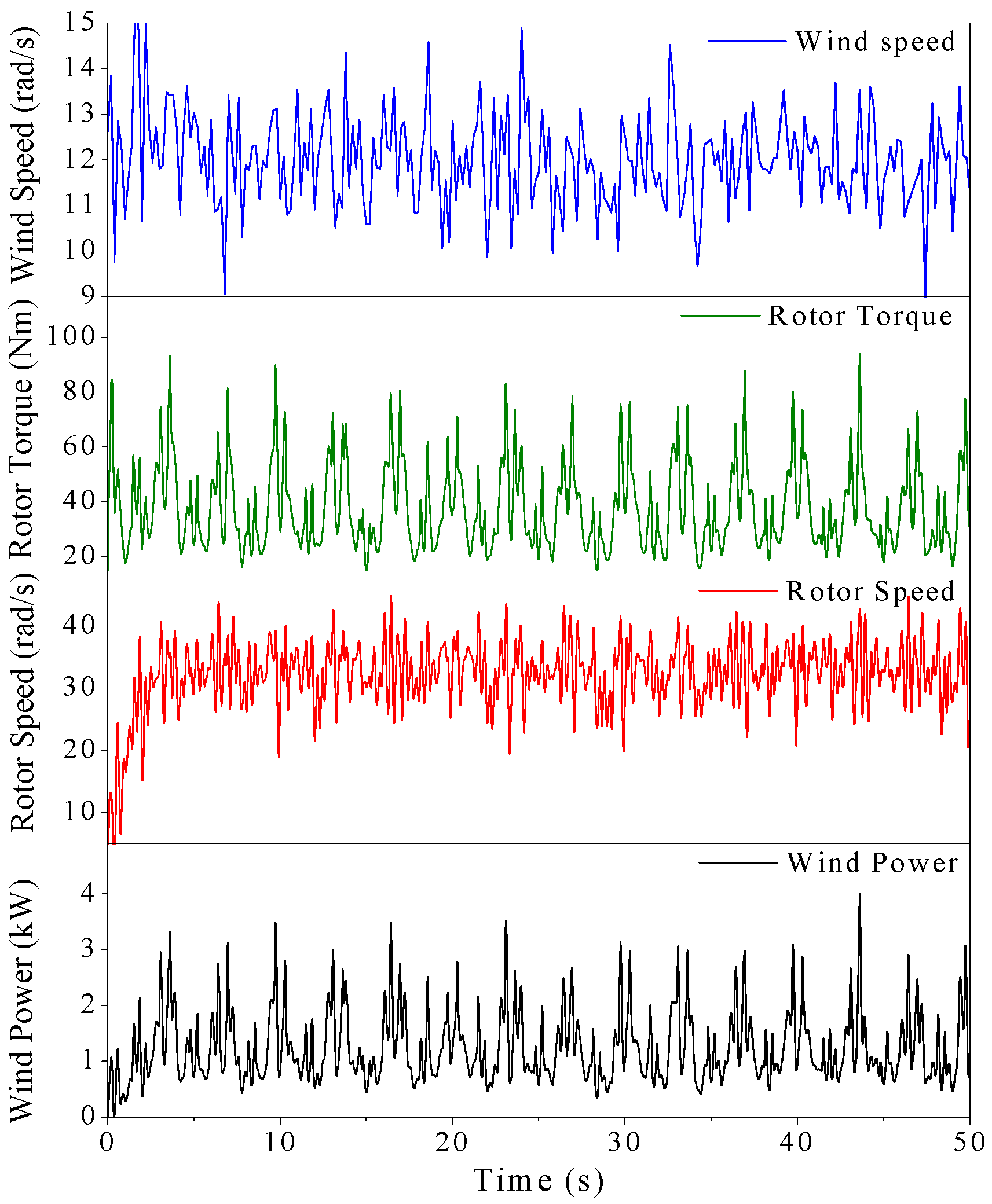

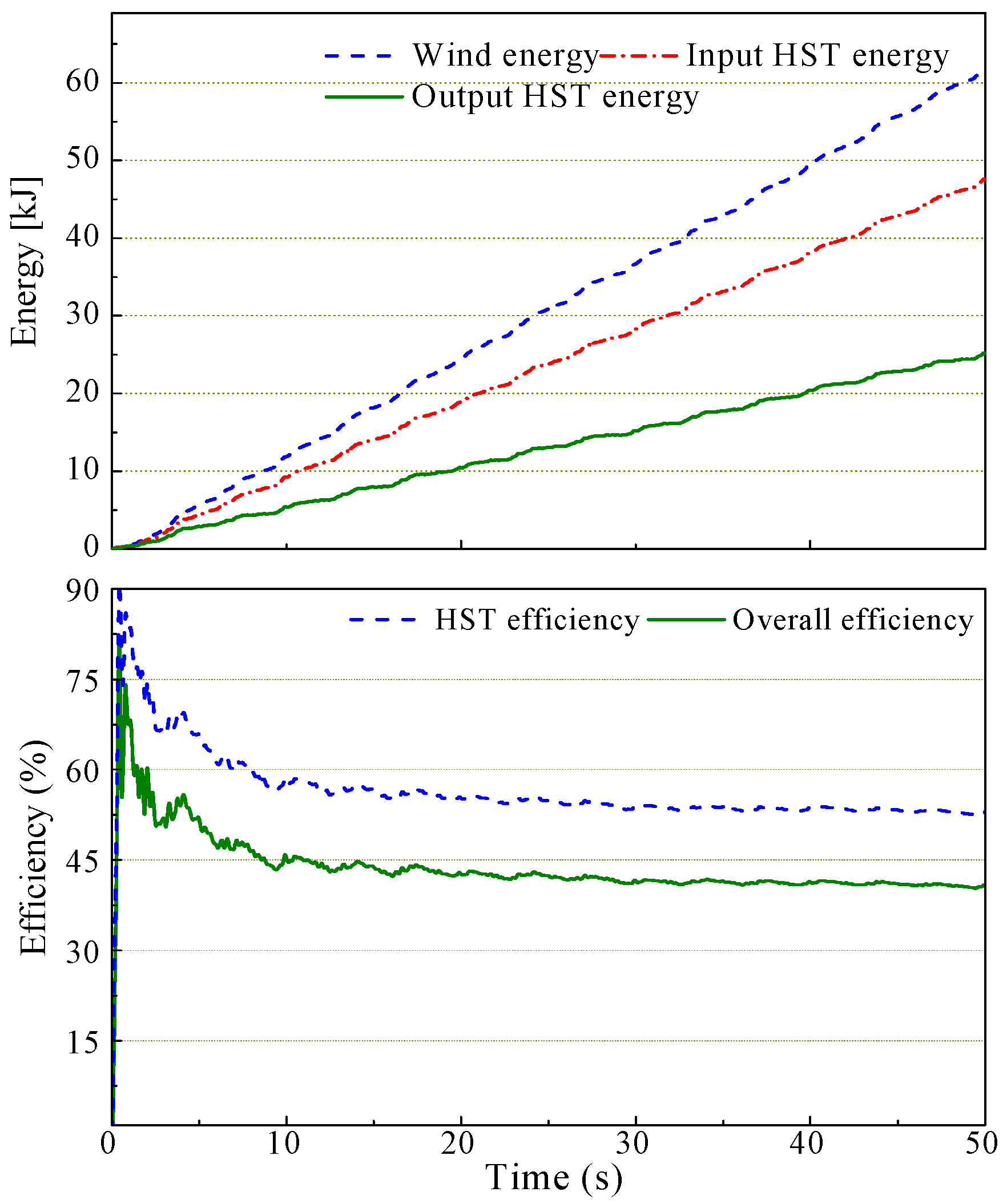

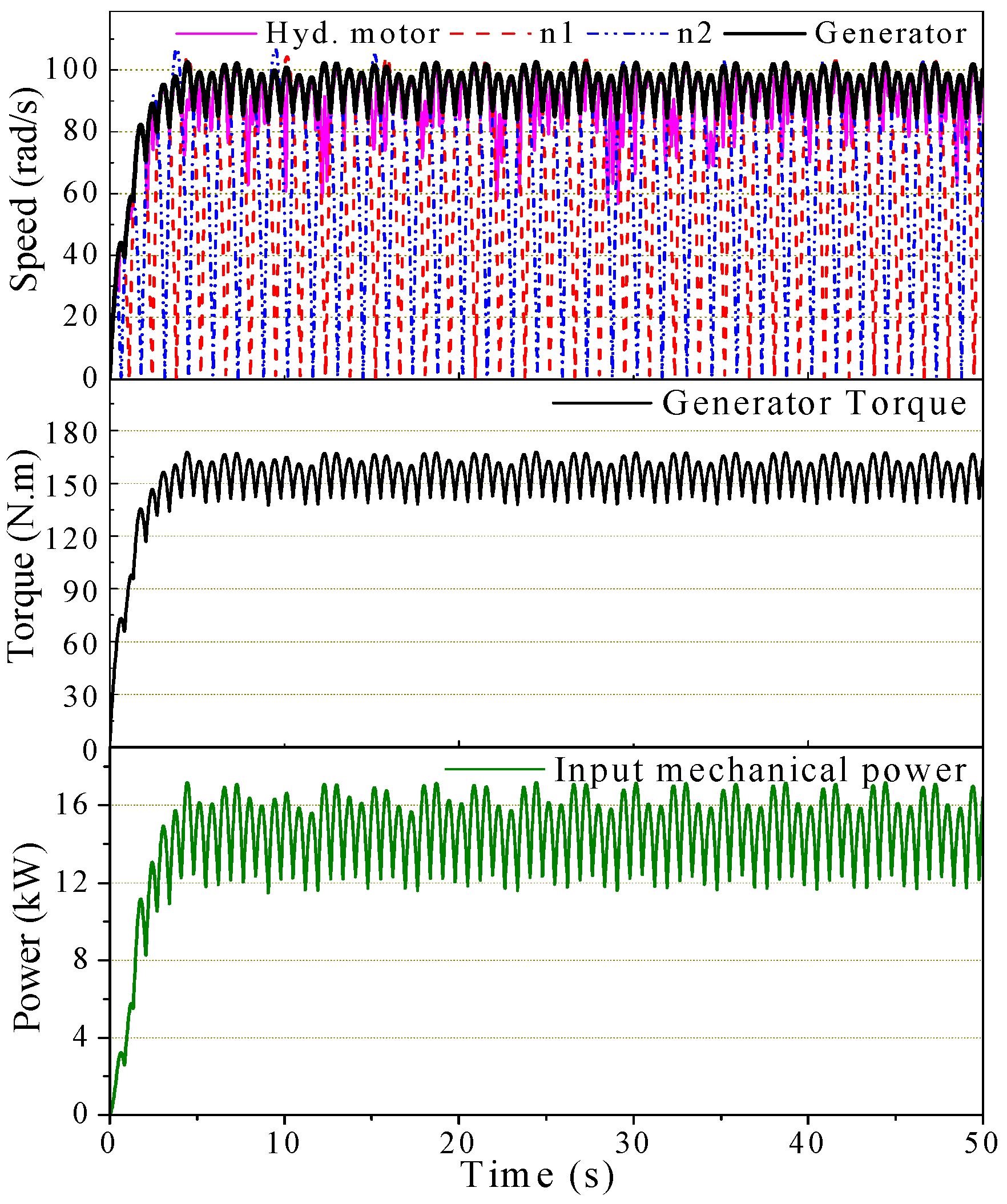

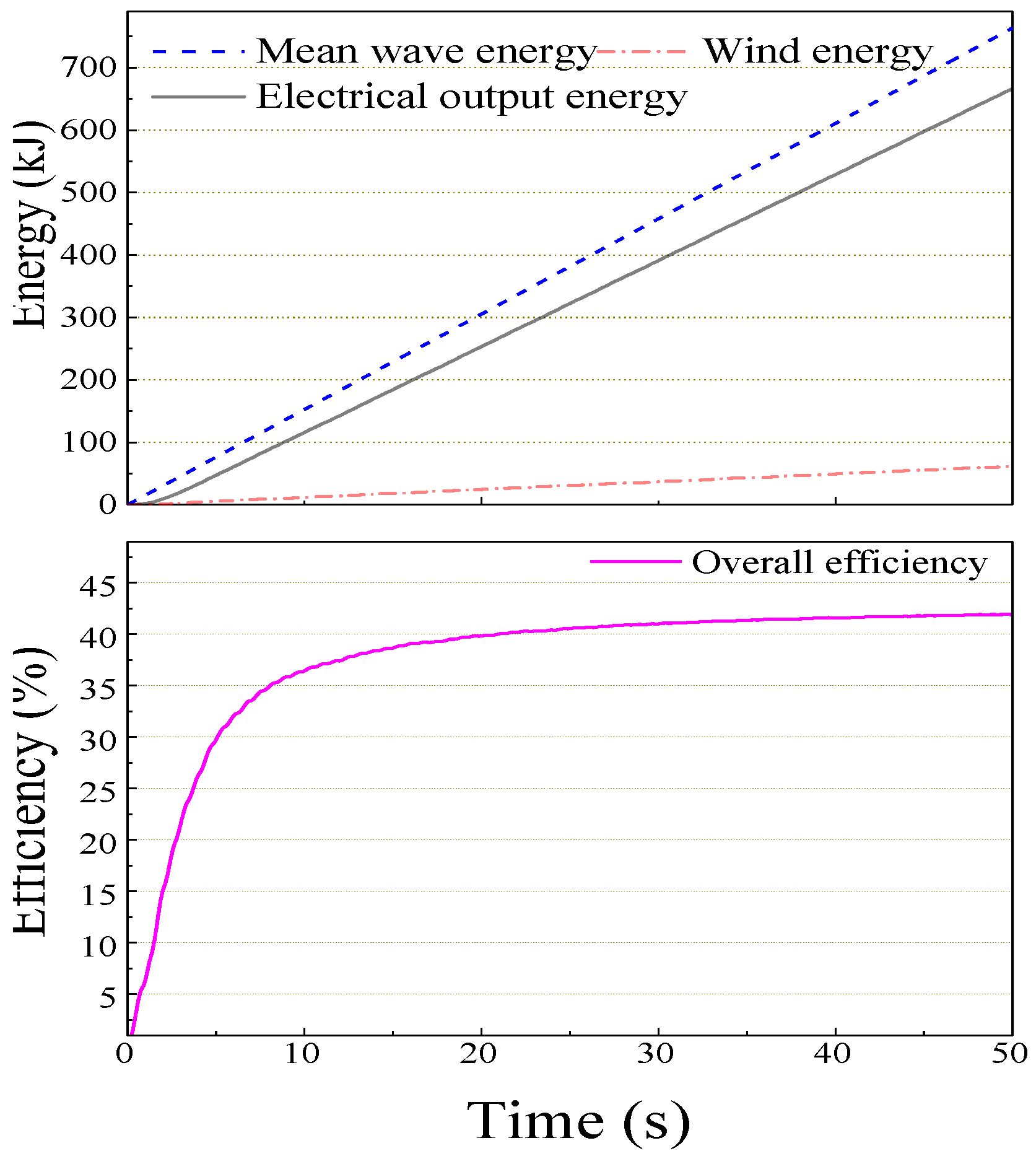
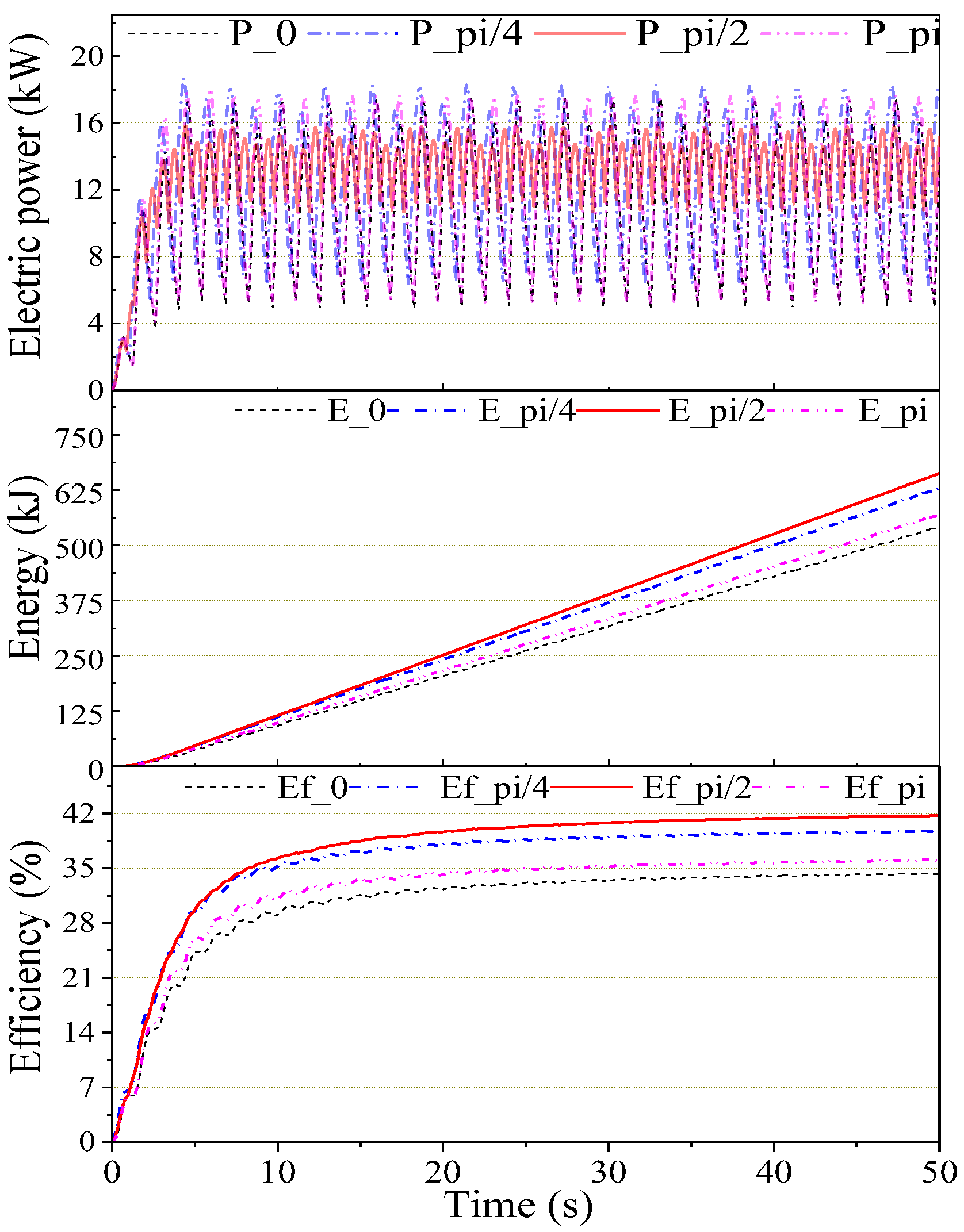
6.3. Challenges and Limitations
6.3.1. Challenges
6.3.2. Limitations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jebaselvi, G.D.A.; Paramasivam, S. Analysis on renewable energy systems. Renew. Sustain. Energy Rev. 2013, 28, 625–634. [Google Scholar] [CrossRef]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- Falcão, A.F.d.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2009, 14, 899–918. [Google Scholar] [CrossRef]
- López, I.; Andreu, J.; Ceballos, S.; de Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Kumar, Y.; Ringenberg, J.; Depuru, S.S.; Devabhaktuni, V.K.; Lee, J.W.; Nikolaidis, E.; Andersen, B.; Afjeh, A. Wind energy: Trends and enabling technologies. Renew. Sustain. Energy Rev. 2015, 53, 209–224. [Google Scholar] [CrossRef]
- Pérez-Collazo, C.; Greaves, D.; Iglesias, G. A review of combined wave and offshore wind energy. Renew. Sustain. Energy Rev. 2014, 42, 141–153. [Google Scholar] [CrossRef]
- McTiernan, K.L.; Sharman, K.T. Review of Hybrid Offshore Wind and Wave Energy Systems. J. Phys. Conf. Ser. 2020, 1452, 12016. [Google Scholar] [CrossRef]
- Dong, X.; Li, Y.; Li, D.; Cao, F.; Jiang, X.; Shi, H. A state-of-the-art review of the hybrid wind-wave energy converter. Prog. Energy 2022, 4, 042004. [Google Scholar] [CrossRef]
- Ayub, M.W.; Hamza, A.; Aggidis, G.A.; Ma, X. A Review of Power Co-Generation Technologies from Hybrid Offshore Wind and Wave Energy. Energies 2023, 16, 550. [Google Scholar] [CrossRef]
- Cao, F.; Yu, M.; Liu, B.; Wei, Z.; Xue, L.; Han, M.; Shi, H. Progress of Combined Wind and Wave Energy Harvesting Devices and Related Coupling Simulation Techniques. J. Mar. Sci. Eng. 2023, 11, 212. [Google Scholar] [CrossRef]
- Wan, L.; Gao, Z.; Moan, T. Experimental and numerical study of hydrodynamic responses of a combined wind and wave energy converter concept in survival modes. Coast. Eng. 2015, 104, 151–169. [Google Scholar] [CrossRef]
- Dang, T.D.; Phan, C.B.; Truong HV, A.; Le, C.D.; Nguyen, M.T.; Ahn, K.K. A study on modeling of a hybrid wind wave energy converter system. In Proceedings of the 2016 16th International Conference on Control, Automation and Systems (ICCAS), Gyeongju, Republic of Korea, 16–19 October 2016; pp. 182–187. [Google Scholar]
- Muliawan, M.J.; Karimirad, M.; Gao, Z.; Moan, T. Extreme responses of a combined spar-type floating wind turbine and floating wave energy converter (STC) system with survival modes. Ocean Eng. 2013, 65, 71–82. [Google Scholar] [CrossRef]
- Wan, L.; Greco, M.; Lugni, C.; Gao, Z.; Moan, T. A combined wind and wave energy-converter concept in survival mode: Numerical and experimental study in regular waves with a focus on water entry and exit. Appl. Ocean Res. 2017, 63, 200–216. [Google Scholar] [CrossRef]
- Homayoun, E.; Ghassemi, H.; Ghafari, H. Power Performance of the Combined Monopile Wind Turbine and Floating Buoy with Heave-type Wave Energy Converter. Pol. Marit. Res. 2019, 26, 107–114. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, C.; Zhu, X. Decoupling control of a dual-stator linear and rotary permanent magnet generator for offshore joint wind and wave energy conversion system. IET Electr. Power Appl. 2020, 14, 561–569. [Google Scholar] [CrossRef]
- Si, Y.; Chen, Z.; Zeng, W.; Sun, J.; Zhang, D.; Ma, X.; Qian, P. The influence of power-take-off control on the dynamic response and power output of combined semi-submersible floating wind turbine and point-absorber wave energy converters. Ocean Eng. 2021, 227, 108835. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, W.; Michailides, C.; Wan, L.; Kim, H.; Li, X. WEC shape effect on the motion response and power performance of a combined wind-wave energy converter. Ocean Eng. 2022, 250, 111038. [Google Scholar] [CrossRef]
- Chen, M.; Xiao, P.; Zhou, H.; Li, C.B.; Zhang, X. Fully Coupled Analysis of an Integrated Floating Wind-Wave Power GenerationPlatform in Operational Sea-states. Front. Energy Res. 2022, 819, 931057. [Google Scholar]
- Folley, M.; Whittaker, T.J.T. Analysis of the nearshore wave energy resource. Renew. Energy 2009, 34, 1709–1715. [Google Scholar] [CrossRef]
- Al-Habaibeh, A.; Su, D.; McCague, J.; Knight, A. An innovative approach for energy generation from waves. Energy Convers. Manag. 2010, 51, 1664–1668. [Google Scholar] [CrossRef]
- Binh, P.C.; Tri, N.M.; Dung, D.T.; Ahn, K.K.; Kim, S.-J.; Koo, W. Analysis, design and experiment investigation of a novel wave energy converter. IET Gener. Trans. Distrib. 2016, 10, 460–469. [Google Scholar] [CrossRef]
- Islam, M.; Ting, D.S.-K.; Fartaj, A. Aerodynamic models for Darrieus-type straight-bladed vertical axis wind turbines. Renew. Sustain. Energy Rev. 2006, 12, 1087–1109. [Google Scholar] [CrossRef]
- Saber, H.E.; Attia, E.M.; El Gamal, H.A. Analysis of Straight Bladed Vertical Axis Wind Turbine. Int. J. Eng. Res. Technol. 2015, 4, 714–723. [Google Scholar]
- Li, Q.; Maeda, T.; Kamada, Y.; Murata, J.; Furukawa, K.; Yamamoto, M. Aerodynamic Models and Wind Tunnel for Straight-bladed Vertical Axis Wind Turbines. IOSR J. Eng. 2014, 4, 35–44. [Google Scholar]
- Ahn, K.K.; Truong, D.Q.; Tien, H.H.; Yoon, J.I. An innovative design of wave energy converter. Renew. Energy 2012, 42, 186–194. [Google Scholar] [CrossRef]
- Falnes, J.; Kurniawan, A. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2020; Volume 8. [Google Scholar]
- Dang, T.D.; Phan, C.B.; Ahn, K.K. Modeling and Experimental Investigation on Performance of a Wave Energy Converter with Mechanical Power Take-Off. Int. J. Precis. Eng. Manuf.-Green Technol. 2019, 6, 751–768. [Google Scholar] [CrossRef]
- Ha, K.; Truong, H.V.A.; Dang, T.D.; Ahn, K.K. Recent control technologies for floating offshore wind energy system: A review. Int. J. Precis. Eng. Manuf.-Green Technol. 2021, 8, 281–301. [Google Scholar] [CrossRef]
- Hung, H.T.; Ahn, K.K. Modeling and simulation of hydrostatic transmission system with energy regeneration using hydraulic accumulator. J. Mech. Sci. Technol. 2010, 24, 1163–1175. [Google Scholar]
- Wu, B.; Lang, Y.; Zargari, N.; Kouro, S. Power Conversion and Control of Wind Energy Systems; Institute of Electrical and Electronics Engineers, Inc.: Piscataway, NJ, USA, 2011. [Google Scholar]
- WAMIT User Manual, Version 7.0; WAMIT, Inc.: Chestnut Hill, MA, USA, 2013; Available online: http://www.wamit.com (accessed on 1 January 2024).
- Paraschivoiu, I. Wind Turbine Design: With Emphasis on Darrieus Concept; Presses Inter Polytechnique: Montreal, QC, Canada, 2002. [Google Scholar]
- Simão Ferreira, C.; Van Kuik, G.; Van Bussel, G.; Scarano, F. Visualization by PIV of dynamic stall on a vertical axis wind turbine. Exp. Fluids 2009, 46, 97–108. [Google Scholar] [CrossRef]
- Castelli, M.R.; Englaro, A.; Benini, E. The Darrieus wind turbine: Proposal for a new performance prediction model based on CFD. Energy 2011, 36, 4919–4934. [Google Scholar] [CrossRef]
- Zanon, A.; Giannattasio, P.; Simão Ferreira, C.J. A vortex panel model for the simulation of the wake flow past a vertical axis wind turbine in dynamic stall. Wind Energy 2013, 16, 661–680. [Google Scholar] [CrossRef]
- Beri, H.; Yao, Y. Double multiple streamtube model and numerical analysis of vertical axis wind turbine. Energy Power Eng. 2011, 3, 262. [Google Scholar] [CrossRef]
- Leishman, J.G.; Beddoes, T.S. A Semi-Empirical model for dynamic stall. J. Am. Helicopter Soc. 1989, 34, 3–17. [Google Scholar]
- Gupta, S.; Leishman, J.G. Dynamic stall modelling of the S809 aerofoil and comparison with experiments. Wind Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2006, 9, 521–547. [Google Scholar] [CrossRef]
- Ferreira, C.S.; Bijl, H.; van Bussel, G.; Van Kuik, G. Simulating dynamic stall in a 2D VAWT: Modeling strategy, verification and validation with particle image velocimetry data. J. Phys. Conf. Ser. 2007, 75, 012023. [Google Scholar] [CrossRef]
- Lain, S.; Osorio, C. Simulation and evaluation of a straight-bladed Darrieus-type cross flow marine turbine. J. Sci. Ind. Res. 2010, 69, 906–912. [Google Scholar]
- Giorgi, G.; Ringwood, J.V. Analytical representation of nonlinear Froude-Krylov forces for 3-DoF point absorbing wave energy devices. Ocean Eng. 2018, 164, 749–759. [Google Scholar] [CrossRef]
- Saeidtehrani, S.; Fazeres-Ferradosa, T.; Rosa-Santos, P.; Taveira-Pinto, F. Review on floating wave-wind energy converter plants: Nonlinear dynamic assessment tools. Sustain. Energy Technol. Assess. 2022, 54, 102753. [Google Scholar] [CrossRef]

| Notation | Name | Value | Unit |
|---|---|---|---|
| Wind speed | 12 | m/s | |
| Water depth | 10 | m | |
| Wave height | 1.5 | m | |
| Wave frequency | 2.2 | rad/s | |
| Phase difference | rad |
| Notation | Name | Value | Unit |
|---|---|---|---|
| Buoy diameter | 3.0 | m | |
| Pinion diameter | 0.1 | m | |
| Gearbox ratio | 4 | ||
| Generator inertia | 1 | kg.m2 | |
| Initial draft | 1.5 | m |
| Name | Value |
|---|---|
| Rotor diameter (m) | 6 |
| Number of blades | 3 |
| Chord length (m) | 0.25 |
| Height of rotor (m) | 4 |
| Induced velocity (m/s) | 7 |
| Components | Notation | Quantity | Value | SI Unit |
|---|---|---|---|---|
| Hydraulic pump | Displacement | 242 | 1 cm3/rev → | |
| Volumetric efficiency | 0.95 | |||
| Mechanical efficiency | 0.98 | |||
| Inertia | 0.046 | |||
| Hydraulic motor | Displacement | 80.4 | 1 cm3/rev → | |
| Volumetric efficiency | 0.95 | |||
| Mechanical efficiency | 0.98 | |||
| Inertia | 0.021 |
| Quantity | Value |
|---|---|
| Number of poles | 20 |
| Stator resistance | 0.62 Ω |
| d-axis and q-axis stator inductance | 0.0122 H |
| Magnetic flux | 0.12 Wb |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Binh, P.C.; Dang, T.D.; Ahn, K.K. Assessment of a Hybrid Wind–Wave Energy Converter System in Nearshore Deployment. J. Mar. Sci. Eng. 2024, 12, 1093. https://doi.org/10.3390/jmse12071093
Binh PC, Dang TD, Ahn KK. Assessment of a Hybrid Wind–Wave Energy Converter System in Nearshore Deployment. Journal of Marine Science and Engineering. 2024; 12(7):1093. https://doi.org/10.3390/jmse12071093
Chicago/Turabian StyleBinh, Phan Cong, Tri Dung Dang, and Kyoung Kwan Ahn. 2024. "Assessment of a Hybrid Wind–Wave Energy Converter System in Nearshore Deployment" Journal of Marine Science and Engineering 12, no. 7: 1093. https://doi.org/10.3390/jmse12071093
APA StyleBinh, P. C., Dang, T. D., & Ahn, K. K. (2024). Assessment of a Hybrid Wind–Wave Energy Converter System in Nearshore Deployment. Journal of Marine Science and Engineering, 12(7), 1093. https://doi.org/10.3390/jmse12071093







