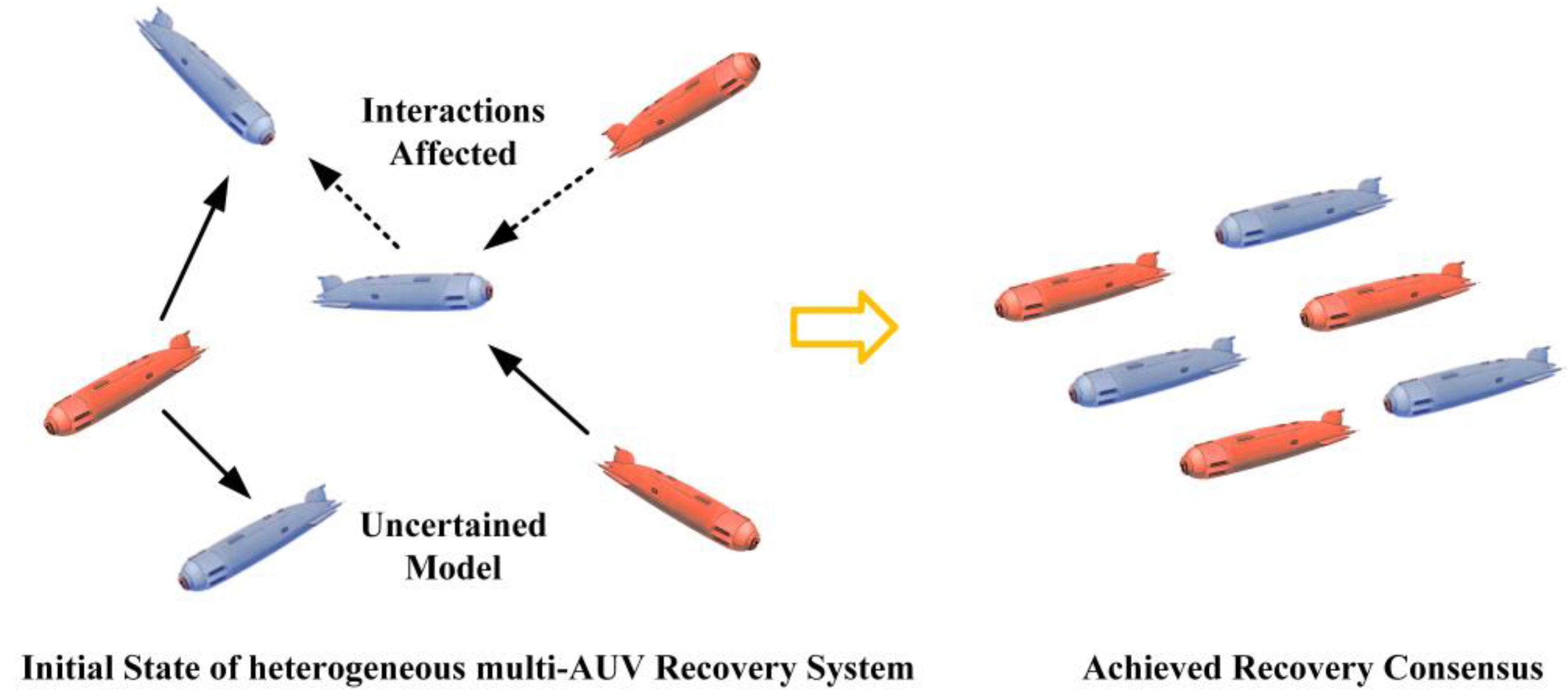
Consensus Control of Heterogeneous Uncertain Multiple Autonomous Underwater Vehicle Recovery Systems in Scenarios of Implicit Reduced Visibility
Abstract
:1. Introduction
- (1)
- Establishment of a heterogeneous visual multi-AUV system: We developed a feedback linearization model for a heterogeneous multi-AUV recovery system that considers both dynamic and visual interaction complexities under conditions of model uncertainty. Unlike the model proposed by Ref. [33], our model accounts for real-world uncertainties, making it more practical and applicable.
- (2)
- Introduction of a reference model approach: We introduced an adaptive consensus controller for heterogeneous multi-AUV systems. This controller is designed to operate using only relative information, effectively managing implicit visual interaction limitations and model uncertainties. Compared to Ref. [34], we extended this approach from linear systems to nonlinear AUV models.
- (3)
- Dual validation: We validated the feasibility of our control approach through both stability proofs and numerical simulations. By incorporating uncertainties and considering different visual scenarios, we significantly enhanced the practical applicability of our method in engineering contexts.
2. Related Works
3. Theoretical Foundations
3.1. Reduced Visibility Interaction Model
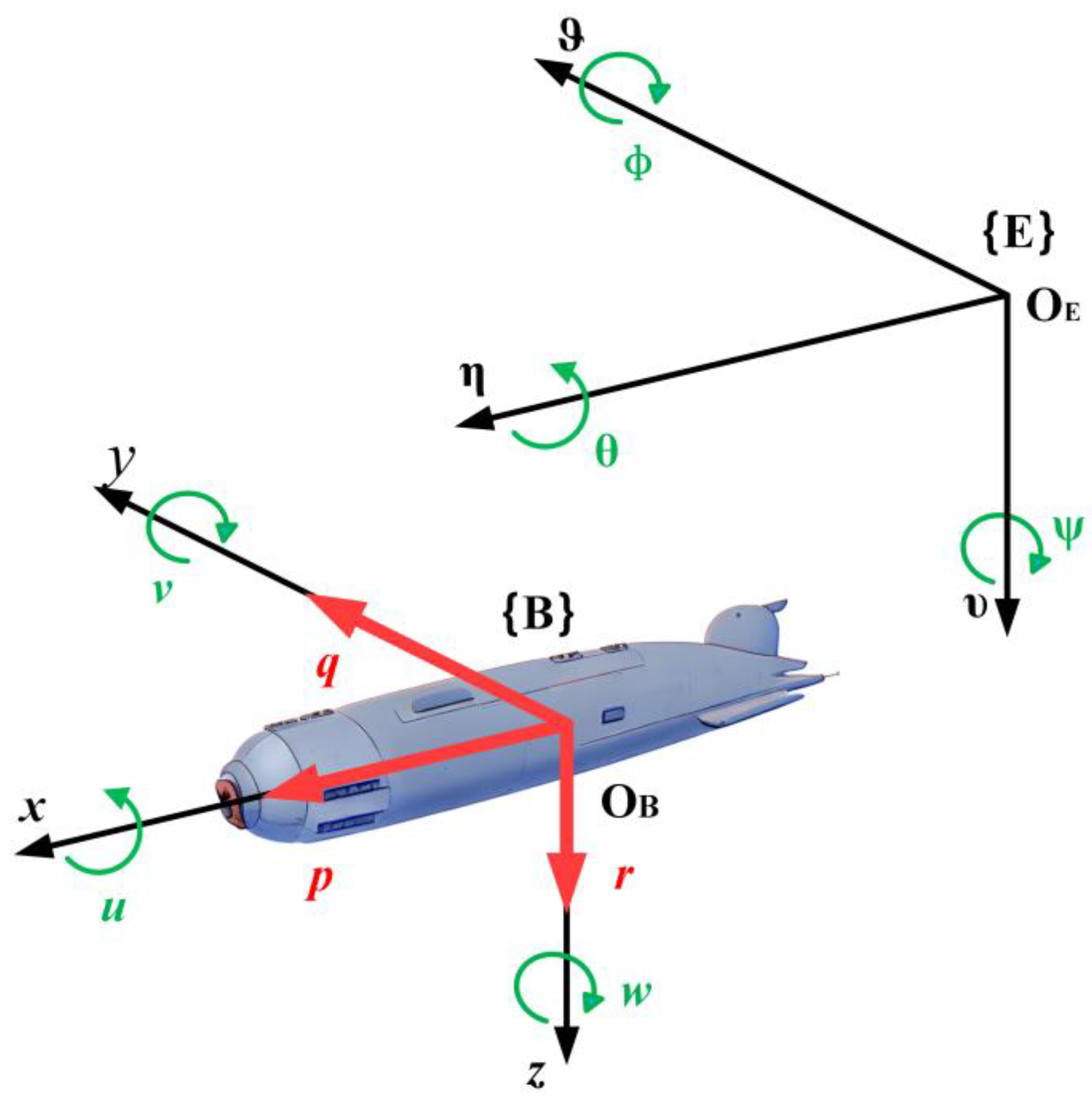
3.2. The AUV Model
3.3. Relevant Lemma
4. Problem Description and Formulation
4.1. Key Definitions and Assumptions
4.2. Modeling of Single AUV with Uncertainties
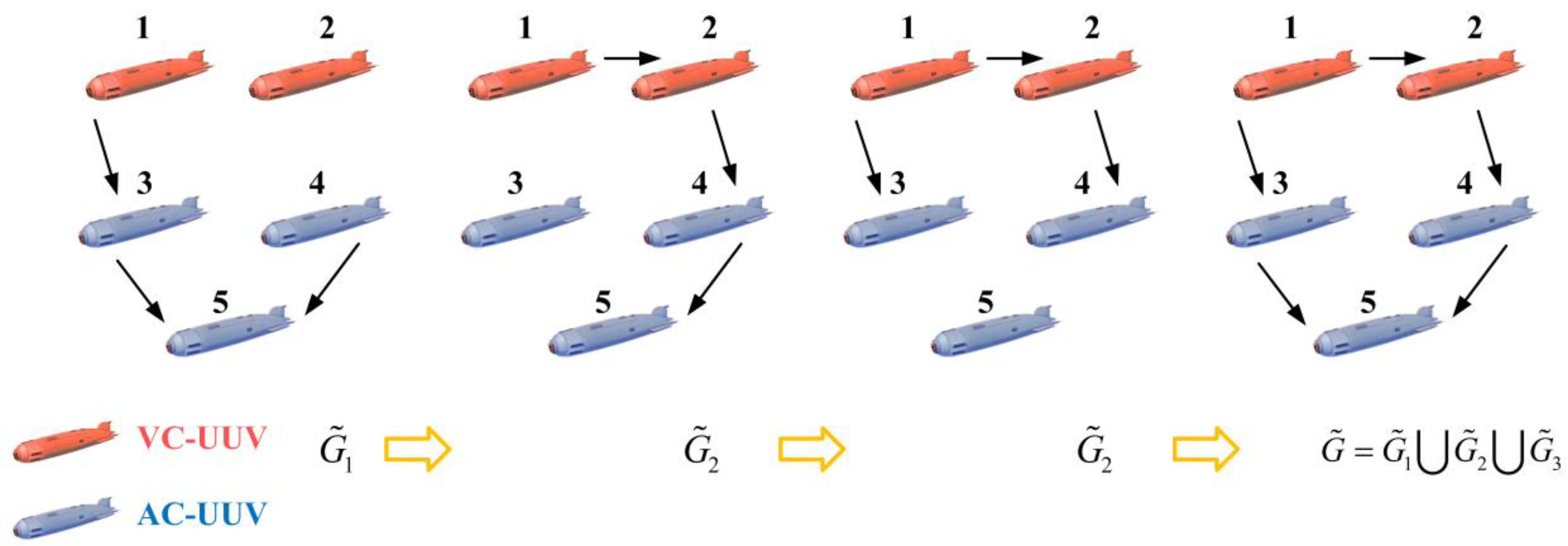
4.3. Modeling of Heterogeneous Multi-AUV Recovery Systems
5. Controller Design and Convergence Analysis
6. Simulation Results
6.1. Validation of Algorithm Efficacy
6.1.1. Simulation Setup and Parameter Selection
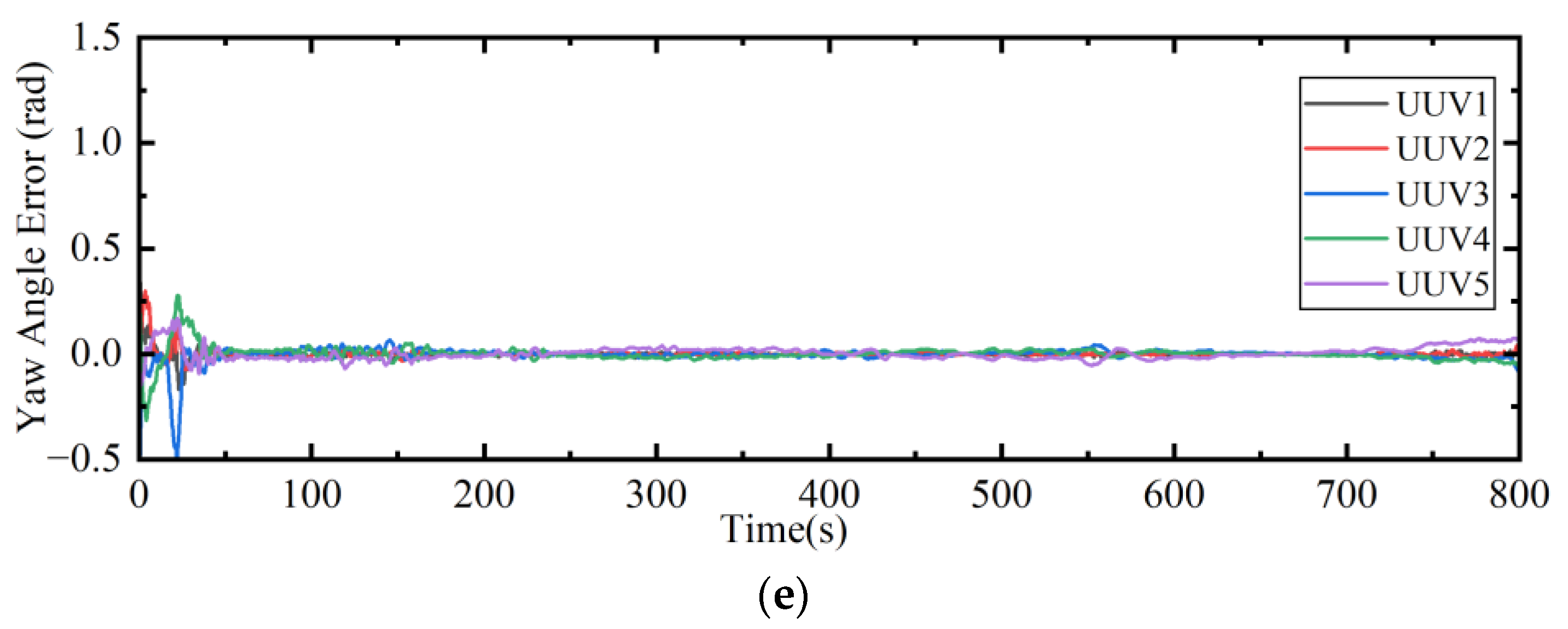
6.1.2. Results and Analysis
6.2. Superiority Comparison and Performance Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Vu, M.T.; Le Thanh, H.N.N.; Huynh, T.-T.; Thang, Q.; Duc, T.; Hoang, Q.-D.; Le, T.-H. Station-Keeping Control of a Hovering over-Actuated Autonomous Underwater Vehicle under Ocean Current Effects and Model Uncertainties in Horizontal Plane. IEEE Access 2021, 9, 6855–6867. [Google Scholar] [CrossRef]
- Li, T.; Bai, W.; Liu, Q.; Long, Y.; Chen, C.P. Distributed Fault-Tolerant Containment Control Protocols for the Discrete-Time Multiagent Systems via Reinforcement Learning Method. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3979–3991. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Zhang, M.; Zhou, J.; Yue, L. Distributed Lyapunov-Based Model Predictive Control for AUV Formation Systems with Multiple Constraints. J. Mar. Sci. Eng. 2024, 12, 363. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, M.; Zhang, S.; Zheng, R.; Dong, S. Multi-AUV Adaptive Path Planning and Cooperative Sampling for Ocean Scalar Field Estimation. IEEE Trans. Instrum. Meas. 2022, 71, 1–14. [Google Scholar] [CrossRef]
- Liao, Y.; Chen, C.; Du, T.; Sun, J.; Xin, Y.; Zhai, Z.; Wang, B.; Li, Y.; Pang, S. Research on Disturbance Rejection Motion Control Method of USV for UUV Recovery. J. Field Robot. 2023, 40, 574–594. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, W.; Fei, M.; Yan, H. An Unmanned Surface Vehicle for the Launch and Recovery of Autonomous Underwater Vehicles: A Novel Design. IEEE Robot. Autom. Mag. 2024, 31, 53–61. [Google Scholar] [CrossRef]
- Xia, G.; Zhang, Y.; Zhang, W.; Zhang, K.; Yang, H. Robust Adaptive Super-Twisting Sliding Mode Formation Controller for Homing of Multi-Underactuated AUV Recovery System with Uncertainties. ISA Trans. 2022, 130, 136–151. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, Z.; Zeng, J.; Wu, W. Distributed Event-Triggered Coordinated Control for Multi-UUV Recovery System with Time Delay. Ocean Eng. 2023, 283, 115138. [Google Scholar] [CrossRef]
- Berlinger, F.; Gauci, M.; Nagpal, R. Implicit Coordination for 3D Underwater Collective Behaviors in a Fish-Inspired Robot Swarm. Sci. Robot. 2021, 6, eabd8668. [Google Scholar] [CrossRef] [PubMed]
- Yao, P.; Sui, X.; Liu, Y.; Zhao, Z. Vision-Based Environment Perception and Autonomous Obstacle Avoidance for Unmanned Underwater Vehicle. Appl. Ocean Res. 2023, 134, 103510. [Google Scholar] [CrossRef]
- Liu, C.; Wen, J.; Huang, J.; Lin, W.; Wu, B.; Xie, N.; Zou, T. Lightweight Underwater Object Detection Algorithm for Embedded Deployment Using Higher-Order Information and Image Enhancement. J. Mar. Sci. Eng. 2024, 12, 506. [Google Scholar] [CrossRef]
- Peng, C.; Jin, S.; Bian, G.; Cui, Y.; Wang, M. Sample Augmentation Method for Side-Scan Sonar Underwater Target Images Based on CBL-sinGAN. J. Mar. Sci. Eng. 2024, 12, 467. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Z.; Gong, P.; Pan, J.; Wu, W. Visual Location Method Based on Asymmetric Guiding Light Array in UUV Recovery Progress. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 2671–2675. [Google Scholar]
- Li, Z.; Zhang, W.; Wu, W.; Du, X.; Han, A. Image-Based Visual Servo Control for UUV Recovery System under Field of View Constraints. In Proceedings of the OCEANS 2023—Limerick, OCEANS Limerick 2023, Limerick, Ireland, 5–8 June 2023. [Google Scholar]
- Yu, B.; Wu, J.; Islam, M.J. Udepth: Fast Monocular Depth Estimation for Visually-Guided Underwater Robots. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; IEEE: New York, NY, USA, 2023; pp. 3116–3123. [Google Scholar]
- Meng, C.; Zhang, W.; Du, X. Finite-Time Extended State Observer Based Collision-Free Leaderless Formation Control of Multiple AUVs via Event-Triggered Control. Ocean Eng. 2023, 268, 113605. [Google Scholar] [CrossRef]
- Wen, L.; Yu, S.; Zhao, Y.; Yan, Y. Adaptive Dynamic Event-Triggered Consensus Control of Multiple Autonomous Underwater Vehicles. Int. J. Control 2023, 96, 746–756. [Google Scholar] [CrossRef]
- Nuño, E.; Loría, A.; Panteley, E. Leaderless Consensus Formation Control of Cooperative Multi-Agent Vehicles without Velocity Measurements. IEEE Control Syst. Lett. 2021, 6, 902–907. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, X.; Luo, G.; Liu, G. A Formation Control Method for AUV Group under Communication Delay. Front. Bioeng. Biotechnol. 2022, 10, 848641. [Google Scholar] [CrossRef] [PubMed]
- Yan, T.; Xu, Z.; Yang, S.X. Consensus Formation Tracking for Multiple AUV Systems Using Distributed Bioinspired Sliding Mode Control. IEEE Trans. Intell. Veh. 2022, 8, 1081–1092. [Google Scholar] [CrossRef]
- Pang, W.; Zhu, D.; Sun, C. Multi-AUV Formation Reconfiguration Obstacle Avoidance Algorithm Based on Affine Transformation and Improved Artificial Potential Field Under Ocean Currents Disturbance. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1469–1487. [Google Scholar] [CrossRef]
- Wang, X.; Fan, X.; Shi, P.; Ni, J.; Zhou, Z. An Overview of Key SLAM Technologies for Underwater Scenes. Remote Sens. 2023, 15, 2496. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, S.; An, D.; Liu, J.; Wang, H.; Feng, Y.; Li, D.; Zhao, R. Visual SLAM for Underwater Vehicles: A Survey. Comput. Sci. Rev. 2022, 46, 100510. [Google Scholar] [CrossRef]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Li, X.; Tan, Y.; Tang, J.; Chen, X. Task-Driven Formation of Nonholonomic Vehicles With Communication Constraints. IEEE Trans. Control Syst. Technol. 2022, 31, 442–450. [Google Scholar] [CrossRef]
- Feng, J.; Yao, Y.; Wang, H.; Jin, H. Multi-AUV Terminal Guidance Method Based on Underwater Visual Positioning. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 13–16 October 2020; IEEE: New York, NY, USA, 2020; pp. 314–319. [Google Scholar]
- Zhang, S.; Li, Z.; Wang, X. Robust H2 Consensus for Multi-Agent Systems With Parametric Uncertainties. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2473–2477. [Google Scholar] [CrossRef]
- Wang, G.; Wang, C.; Ding, Z.; Ji, Y. Distributed Consensus of Nonlinear Multi-Agent Systems With Mismatched Uncertainties and Unknown High-Frequency Gains. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 938–942. [Google Scholar] [CrossRef]
- Long, J.; Wang, W.; Huang, J.; Lü, J.; Liu, K. Adaptive Leaderless Consensus for Uncertain High-Order Nonlinear Multiagent Systems with Event-Triggered Communication. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 7101–7111. [Google Scholar] [CrossRef]
- Mei, J.; Tian, K.; Ma, G. Scaled Position Consensus of High-Order Uncertain Multiagent Systems Over Switching Directed Graphs. IEEE Trans. Cybern. 2023, 54, 3093–3104. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, Z.; Wu, W.; Yang, Y. A Bilevel Task Allocation Method for Heterogeneous Multi-UUV Recovery System. Ocean Eng. 2023, 274, 114057. [Google Scholar] [CrossRef]
- Tian, K.; Mei, J. Consensus of Uncertain Heterogeneous Multi-Agent Systems Under a Directed Graph. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; IEEE: New York, NY, USA, 2020; pp. 6822–6826. [Google Scholar]
- Li, Z.; Zhang, W.; Zhang, Y.; Wu, W. Coordinated Control Strategies for Heterogeneous Multi-UUV Recovery System in Low-Visibility Underwater Implicit Interaction Scenarios. Ocean Eng. 2024, 297, 117076. [Google Scholar] [CrossRef]
- Tian, C.; Tian, K.; Mei, J.; Ma, G. Bipartite Leaderless Position Consensus of Heterogeneous Uncertain Multi-Agent Systems under Switching Directed Graphs. Syst. Control Lett. 2023, 181, 105628. [Google Scholar] [CrossRef]
- Amirkhani, A.; Barshooi, A.H. Consensus in Multi-Agent Systems: A Review. Artif. Intell. Rev. 2022, 55, 3897–3935. [Google Scholar] [CrossRef]
- Schenato, L.; Gamba, G. A Distributed Consensus Protocol for Clock Synchronization in Wireless Sensor Network. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; IEEE: New York, NY, USA, 2007; pp. 2289–2294. [Google Scholar]
- Ismail, Z.H.; Sariff, N.; Hurtado, E. A Survey and Analysis of Cooperative Multi-Agent Robot Systems: Challenges and Directions. Appl. Mob. Robot. 2018, 5, 8–14. [Google Scholar]
- Wang, D.; Wang, Z.; Wang, Z.; Wang, W. Design of Hybrid Event-Triggered Containment Controllers for Homogeneous and Heterogeneous Multiagent Systems. IEEE Trans. Cybern. 2020, 51, 4885–4896. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.; Jouandeau, N.; Cherif, A.A. A Survey and Analysis of Multi-Robot Coordination. Int. J. Adv. Robot. Syst. 2013, 10, 399. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for Multi-Agent Dynamic Systems: Algorithms and Theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, C.; Su, H.; Zhang, K. Echo State Network-Based Decentralized Control of Continuous-Time Nonlinear Large-Scale Interconnected Systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6293–6303. [Google Scholar] [CrossRef]
- Xin, B.; Zhang, J.; Chen, J.; Wang, Q.; Qu, Y. Overview of Research on Transformation of Multi-AUV Formations. Complex Syst. Model. Simul. 2021, 1, 1–14. [Google Scholar] [CrossRef]
- Schmickl, T.; Thenius, R.; Moslinger, C.; Timmis, J.; Tyrrell, A.; Read, M.; Hilder, J.; Halloy, J.; Campo, A.; Stefanini, C.; et al. CoCoRo—The Self-Aware Underwater Swarm. In Proceedings of the 2011 Fifth IEEE Conference on Self-Adaptive and Self-Organizing Systems Workshops, Ann Arbor, MI, USA, 3–7 October 2011; pp. 120–126. [Google Scholar]
- Dorigo, M.; Floreano, D.; Gambardella, L.M.; Mondada, F.; Nolfi, S.; Baaboura, T.; Birattari, M.; Bonani, M.; Brambilla, M.; Brutschy, A. Swarmanoid: A Novel Concept for the Study of Heterogeneous Robotic Swarms. IEEE Robot. Autom. Mag. 2013, 20, 60–71. [Google Scholar] [CrossRef]
- Li, S.; Batra, R.; Brown, D.; Chang, H.-D.; Ranganathan, N.; Hoberman, C.; Rus, D.; Lipson, H. Particle Robotics Based on Statistical Mechanics of Loosely Coupled Components. Nature 2019, 567, 361–365. [Google Scholar] [CrossRef] [PubMed]
- Slavkov, I.; Carrillo-Zapata, D.; Carranza, N.; Diego, X.; Jansson, F.; Kaandorp, J.; Hauert, S.; Sharpe, J. Morphogenesis in Robot Swarms. Sci. Robot. 2018, 3, eaau9178. [Google Scholar] [CrossRef] [PubMed]
- Meng, C.; Mo, T.; Zhang, X. Distributed Fixed-Time Dynamic Event-Triggered Leaderless Formation Control for Multiple AUVs Based on FRBFDO. Ocean Eng. 2024, 307, 118241. [Google Scholar] [CrossRef]
- Hadi, B.; Khosravi, A.; Sarhadi, P. A Review of the Path Planning and Formation Control for Multiple Autonomous Underwater Vehicles. J. Intell. Robot. Syst. 2021, 101, 67. [Google Scholar] [CrossRef]
- Mazare, M. Distributed Adaptive Fault Tolerant Formation Control for Multiple Underwater Vehicles: Free-Will Arbitrary Time Approach. Ocean Eng. 2023, 286, 115601. [Google Scholar] [CrossRef]
- Wang, J.; Dong, H.; Chen, F.; Vu, M.T.; Shakibjoo, A.D.; Mohammadzadeh, A. Formation Control of Non-Holonomic Mobile Robots: Predictive Data-Driven Fuzzy Compensator. Mathematics 2023, 11, 1804. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, D.; Pang, W.; Zhang, Y. A Survey of Underwater Search for Multi-Target Using Multi-AUV: Task Allocation, Path Planning, and Formation Control. Ocean Eng. 2023, 278, 114393. [Google Scholar] [CrossRef]
- Van, M.; Sun, Y.; Mcllvanna, S.; Nguyen, M.-N.; Zocco, F.; Liu, Z. Control of Multiple AUV Systems with Input Saturations Using Distributed Fixed-Time Consensus Fuzzy Control. IEEE Trans. Fuzzy Syst. 2024, 32, 3142–3153. [Google Scholar] [CrossRef]
- Zheping, Y.; Yibo, L.; Jiajia, Z.; Haomiao, Y. Coordinate Control of Multi-UUVs Formation under Double Independent Topologies with Time-Vary Delays. In Proceedings of the 2017 29th Chinese Control And Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; IEEE: New York, NY, USA, 2017; pp. 7202–7207. [Google Scholar]
- Jadbabaie, A.; Lin, J.; Morse, A.S. Coordination of Groups of Mobile Autonomous Agents Using Nearest Neighbor Rules. IEEE Trans. Autom. Control 2003, 48, 988–1001. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons: Hoboken, NJ, USA, 2011; ISBN 1-119-99149-8. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Ren, W.; Beard, R.W. Distributed Consensus in Multi-Vehicle Cooperative Control; Springer: Berlin/Heidelberg, Germany, 2008; Volume 27. [Google Scholar]
- Wolfowitz, J. Products of Indecomposable, Aperiodic, Stochastic Matrices. Proc. Am. Math. Soc. 1963, 14, 733–737. [Google Scholar] [CrossRef]
- Park, J.-Y.; Jun, B.; Lee, P.; Oh, J. Experiments on Vision Guided Docking of an Autonomous Underwater Vehicle Using One Camera. Ocean Eng. 2009, 36, 48–61. [Google Scholar] [CrossRef]
- Bao, J.; Li, D.; Qiao, X.; Rauschenbach, T. Integrated Navigation for Autonomous Underwater Vehicles in Aquaculture: A Review. Inf. Process. Agric. 2020, 7, 139–151. [Google Scholar] [CrossRef]
- Tian, Y.-P.; Zhang, Y. High-Order Consensus of Heterogeneous Multi-Agent Systems with Unknown Communication Delays. Automatica 2012, 48, 1205–1212. [Google Scholar] [CrossRef]
- Jost, J.; Jost, J. Riemannian Geometry and Geometric Analysis; Springer: Berlin/Heidelberg, Germany, 2008; Volume 42005. [Google Scholar]
- Yan, Z.; Wu, Y.; Liu, Y.; Ren, H.; Du, X. Leader-Following Multiple Unmanned Underwater Vehicles Consensus Control under the Fixed and Switching Topologies with Unmeasurable Disturbances. Complexity 2020, 2020, 5891459. [Google Scholar] [CrossRef]
- Mei, J. Model Reference Adaptive Consensus for Uncertain Multi-Agent Systems under Directed Graphs. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; IEEE: New York, NY, USA, 2018; pp. 6198–6203. [Google Scholar]
- Li, Y.; Jiang, Y.; Cao, J.; Wang, B.; Li, Y. AUV Docking Experiments Based on Vision Positioning Using Two Cameras. Ocean Eng. 2015, 110, 163–173. [Google Scholar] [CrossRef]
- Almeida, J.; Silvestre, C.; Pascoal, A. Cooperative Control of Multiple Surface Vessels in the Presence of Ocean Currents and Parametric Model Uncertainty. Int. J. Robust Nonlinear 2010, 20, 1549–1565. [Google Scholar] [CrossRef]



| Project | Types of Agents | Control Architectures | Interaction Mechanisms |
|---|---|---|---|
| Blueswarm [9] | homogeneous | reactive | implicit |
| Coco [43] | heterogeneous | hybrid | explicit |
| Swarmanoid [44] | heterogeneous | hybrid | explicit |
| particle robotics projects [45] | homogeneous | reactive | implicit |
| Kilobot project [46] | homogeneous | deliberative | explicit |
| Category | VC-AUV | AC-AUV |
|---|---|---|
| Uncertain AUV dynamic model | ||
| Uncertain feedback linearization model | ||
| Reference model | ||
| Feedback linearization controller | ||
| Final controller |
| AUV Number | x | y | z | p | AUV Model |
|---|---|---|---|---|---|
| 1 | 22.7 m | 29.2 m | −4.1 m | 0.5 m/s | VC-AUV |
| 2 | 50.7 m | 3.9 m | −1.1 m | 0.5 m/s | VC-AUV |
| 3 | 2.7 m | 26.9 m | −2.1 m | 0.5 m/s | AC-AUV |
| 4 | 43.4 m | 20.5 m | −4.1 m | 0.5 m/s | AC-AUV |
| 5 | 22.1 m | 14.7 m | −5.1 m | 0.5 m/s | AC-AUV |
| Metric | Result |
|---|---|
| Convergence Time | 350 s |
| Accuracy | 0.5 m |
| Position error (VC-AUVs) | less smooth trajectory |
| Position error (AC-AUVs) | smoother trajectory |
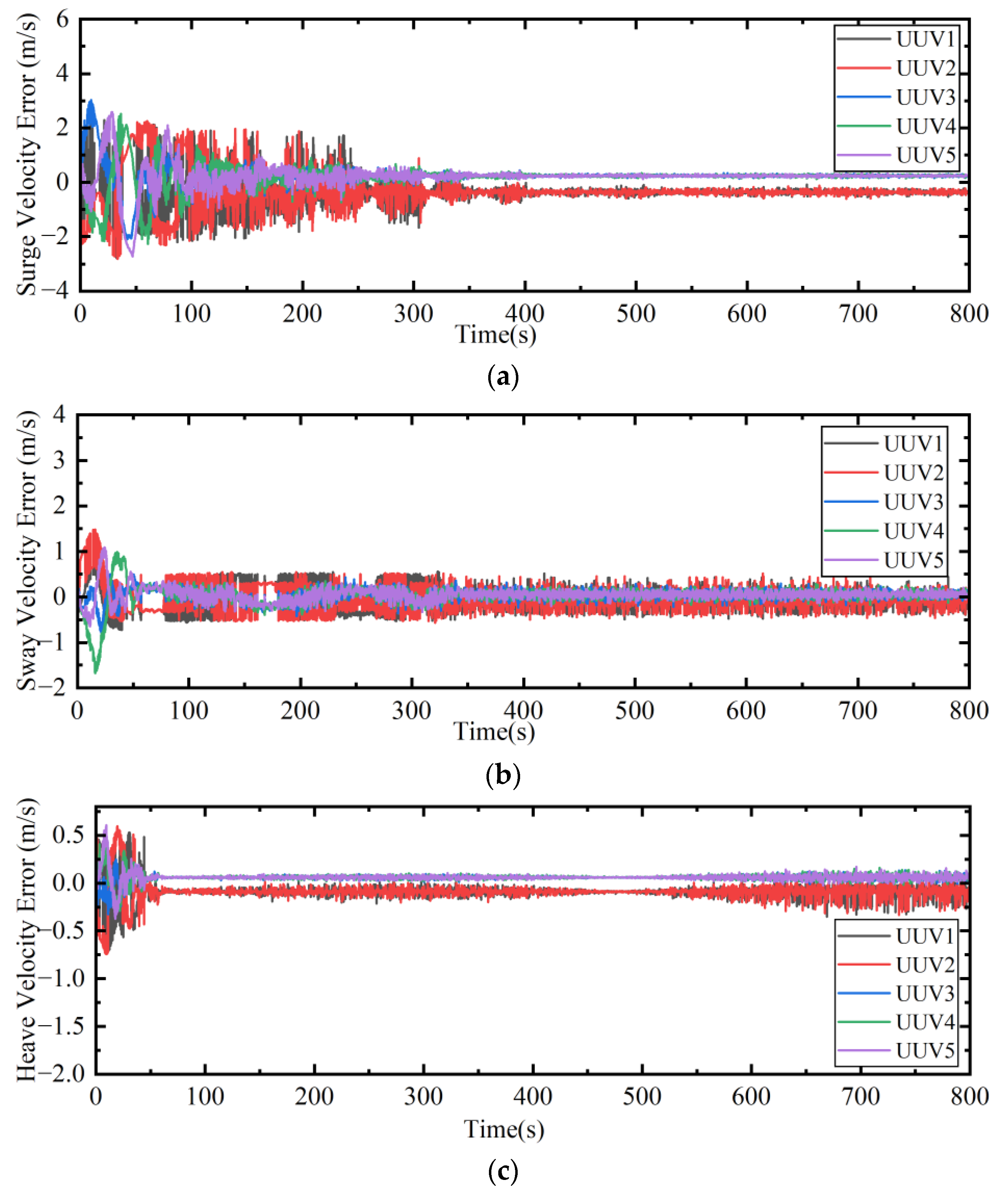
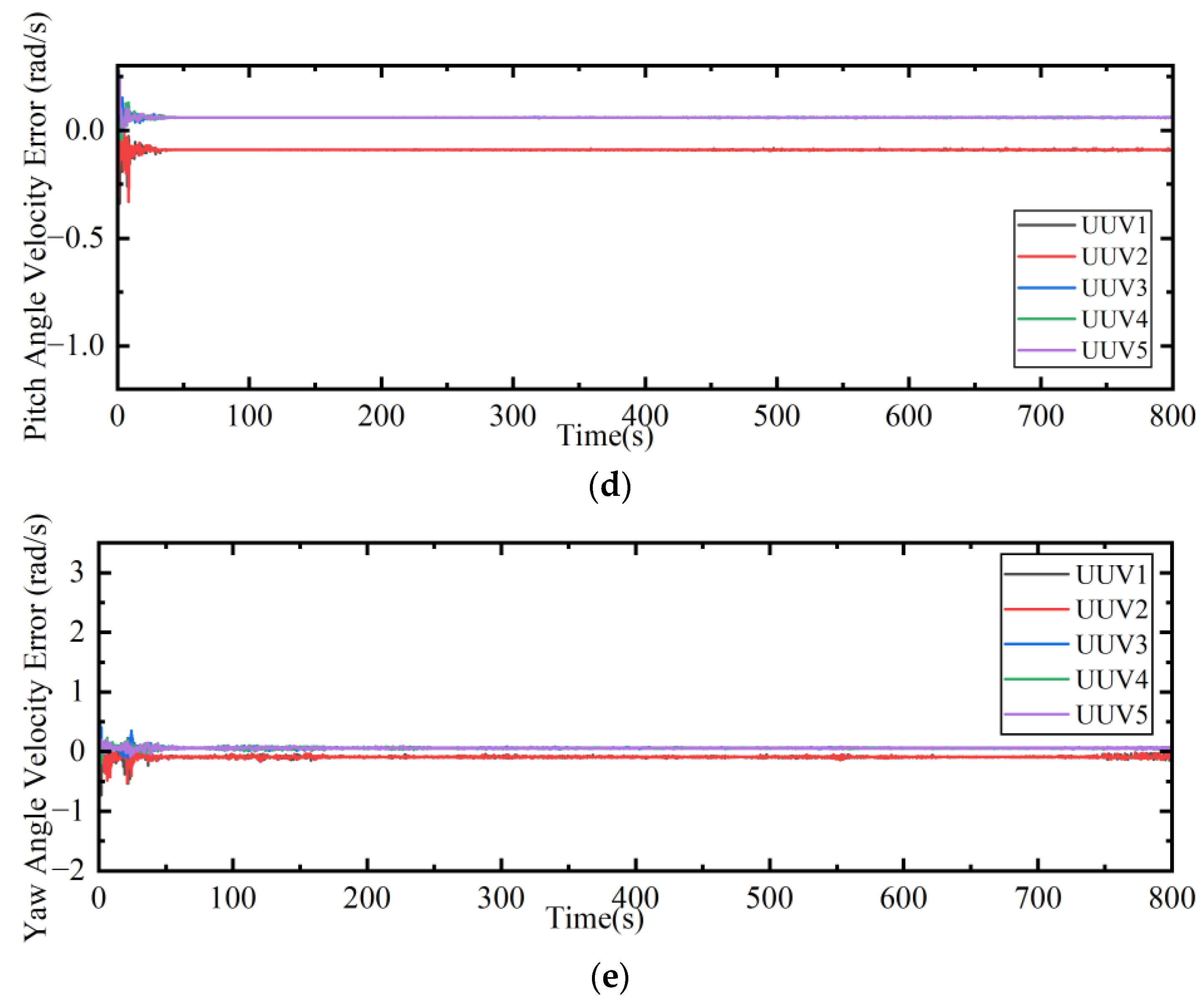
| Velocity error (VC-AUVs) | small steady-state errors |
| Velocity error (AC-AUVs) | converges to zero |
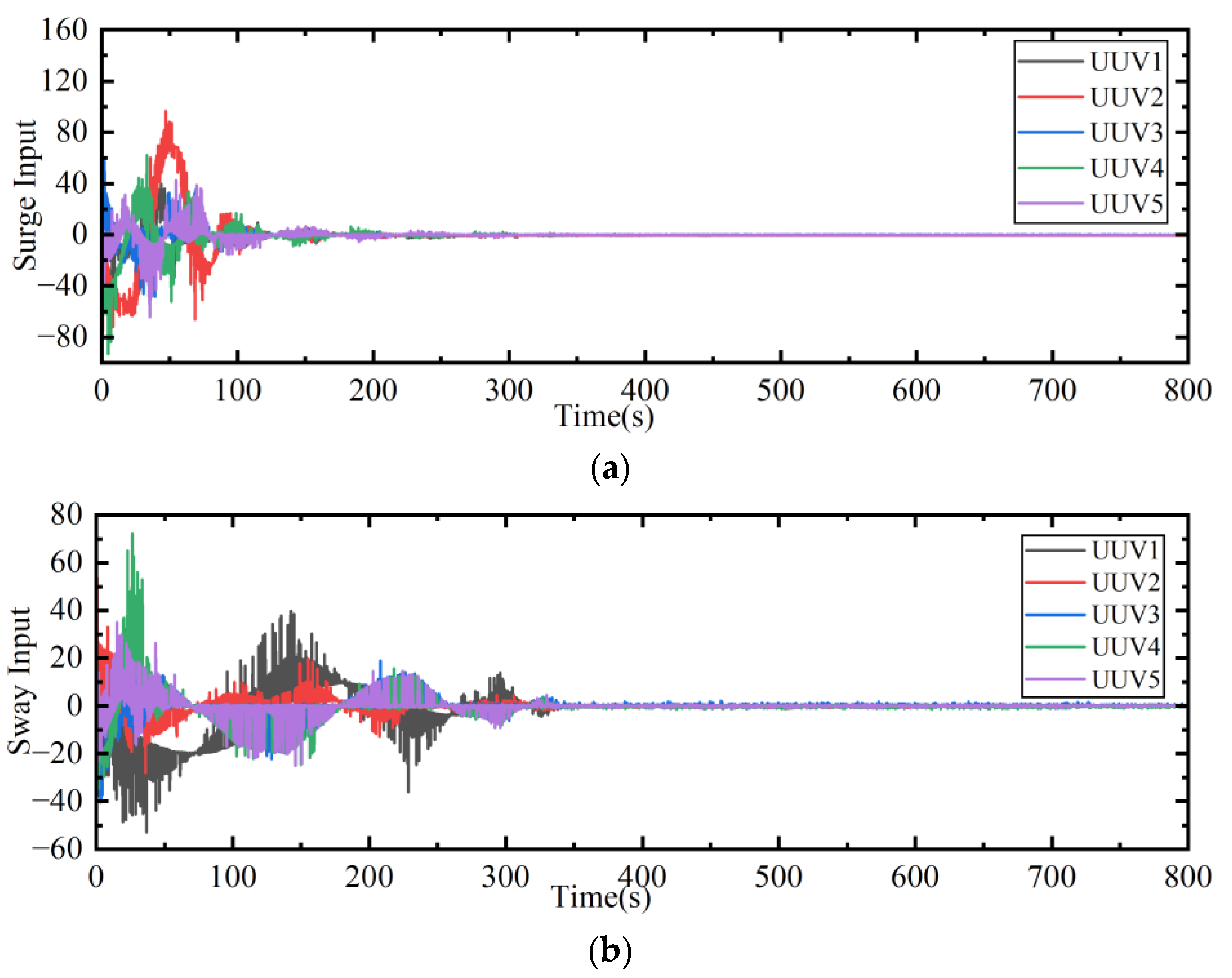
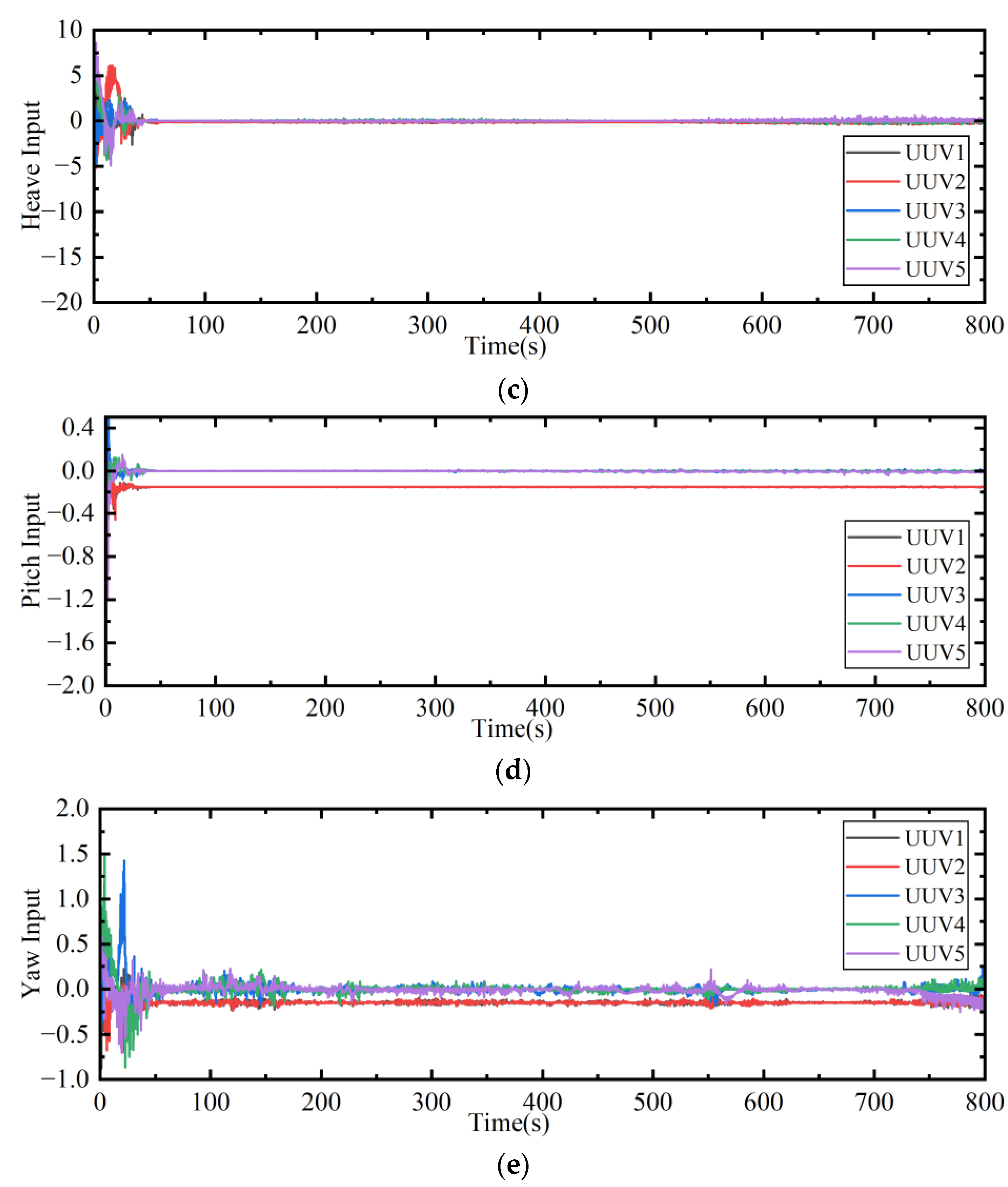
| Control inputs (Surge, Sway, Yaw) | initial peaks, then stabilize |
| Control inputs (Pitch, Heave) | smaller variations, greater stability |
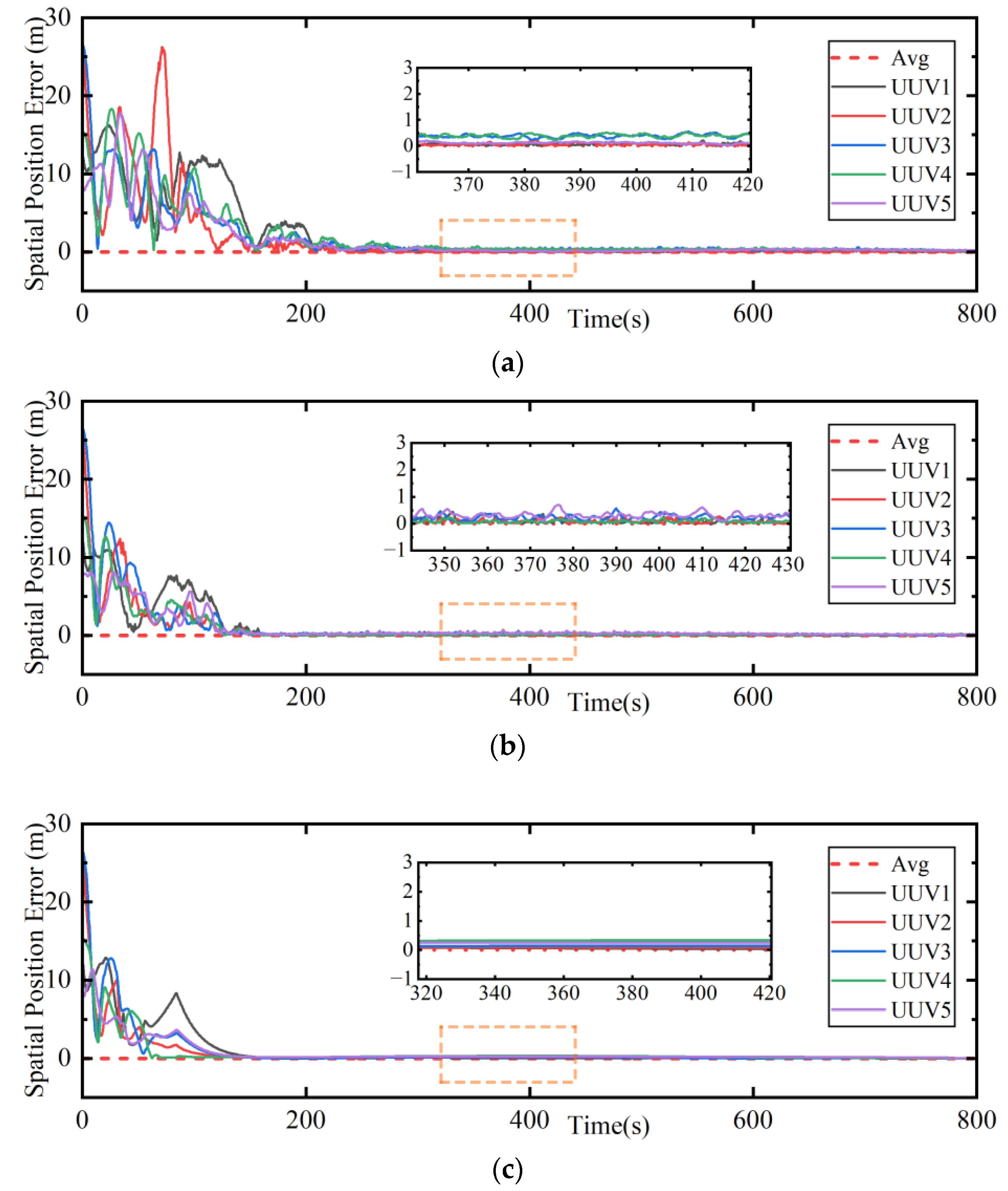
| Scenario | Interaction Network | Convergence Time | Accuracy |
|---|---|---|---|
| Ideal visual interaction | fixed directed spanning tree topology | 180 s | 0.1 m |
| Good visual interaction | switching directed spanning tree topology | 180 s | 0.4 m |
| Regular visual interaction | joint connectivity graph with s | 280 s | 0.4 m |
| Reduced visual interaction | joint connectivity graph with s | 350 s | 0.5 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhang, W.; Wu, W.; Shi, Y. Consensus Control of Heterogeneous Uncertain Multiple Autonomous Underwater Vehicle Recovery Systems in Scenarios of Implicit Reduced Visibility. J. Mar. Sci. Eng. 2024, 12, 1332. https://doi.org/10.3390/jmse12081332
Li Z, Zhang W, Wu W, Shi Y. Consensus Control of Heterogeneous Uncertain Multiple Autonomous Underwater Vehicle Recovery Systems in Scenarios of Implicit Reduced Visibility. Journal of Marine Science and Engineering. 2024; 12(8):1332. https://doi.org/10.3390/jmse12081332
Chicago/Turabian StyleLi, Zixuan, Wei Zhang, Wenhua Wu, and Yefan Shi. 2024. "Consensus Control of Heterogeneous Uncertain Multiple Autonomous Underwater Vehicle Recovery Systems in Scenarios of Implicit Reduced Visibility" Journal of Marine Science and Engineering 12, no. 8: 1332. https://doi.org/10.3390/jmse12081332
APA StyleLi, Z., Zhang, W., Wu, W., & Shi, Y. (2024). Consensus Control of Heterogeneous Uncertain Multiple Autonomous Underwater Vehicle Recovery Systems in Scenarios of Implicit Reduced Visibility. Journal of Marine Science and Engineering, 12(8), 1332. https://doi.org/10.3390/jmse12081332







