Study on Strain Field Reconstruction Method of Long-Span Hull Box Girder Based on iFEM
Abstract
1. Introduction
2. Inverse Finite Element Formulation for Shells
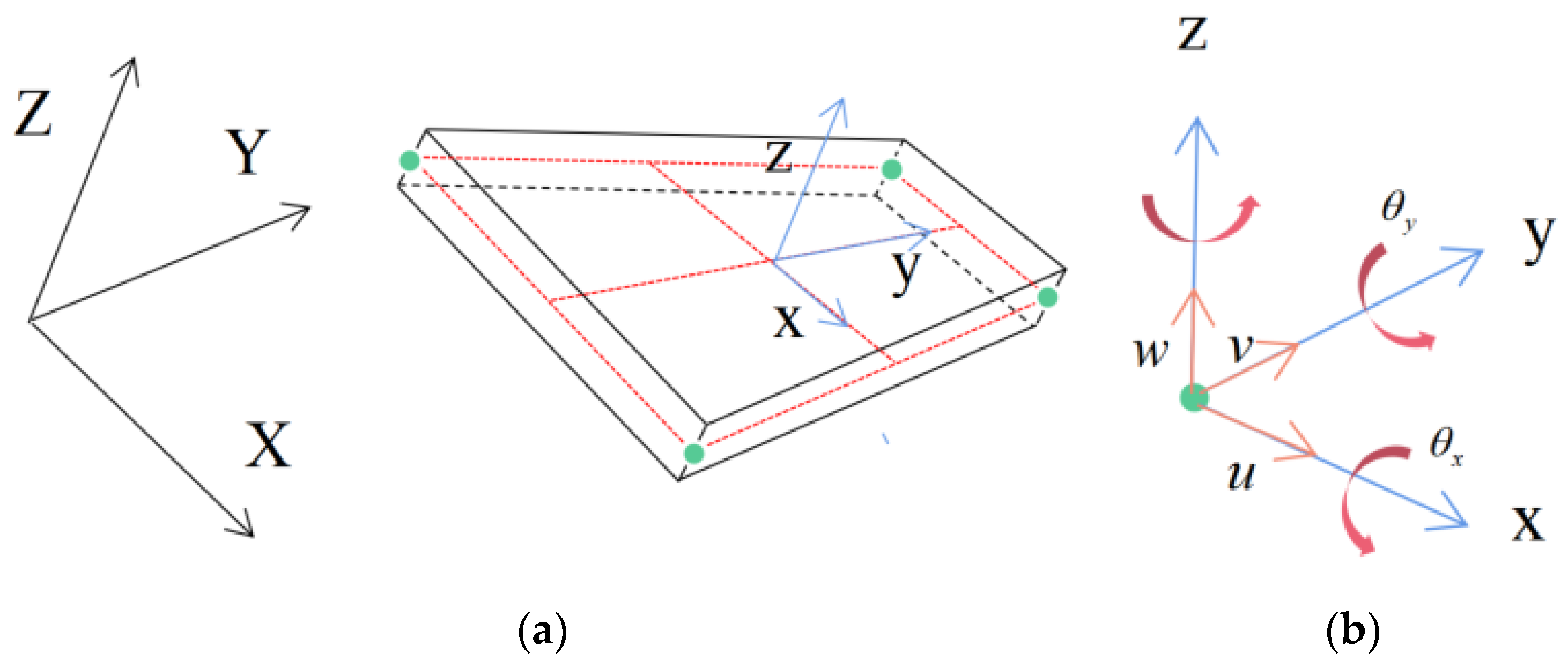
2.1. Constructing Inverse Shell Element
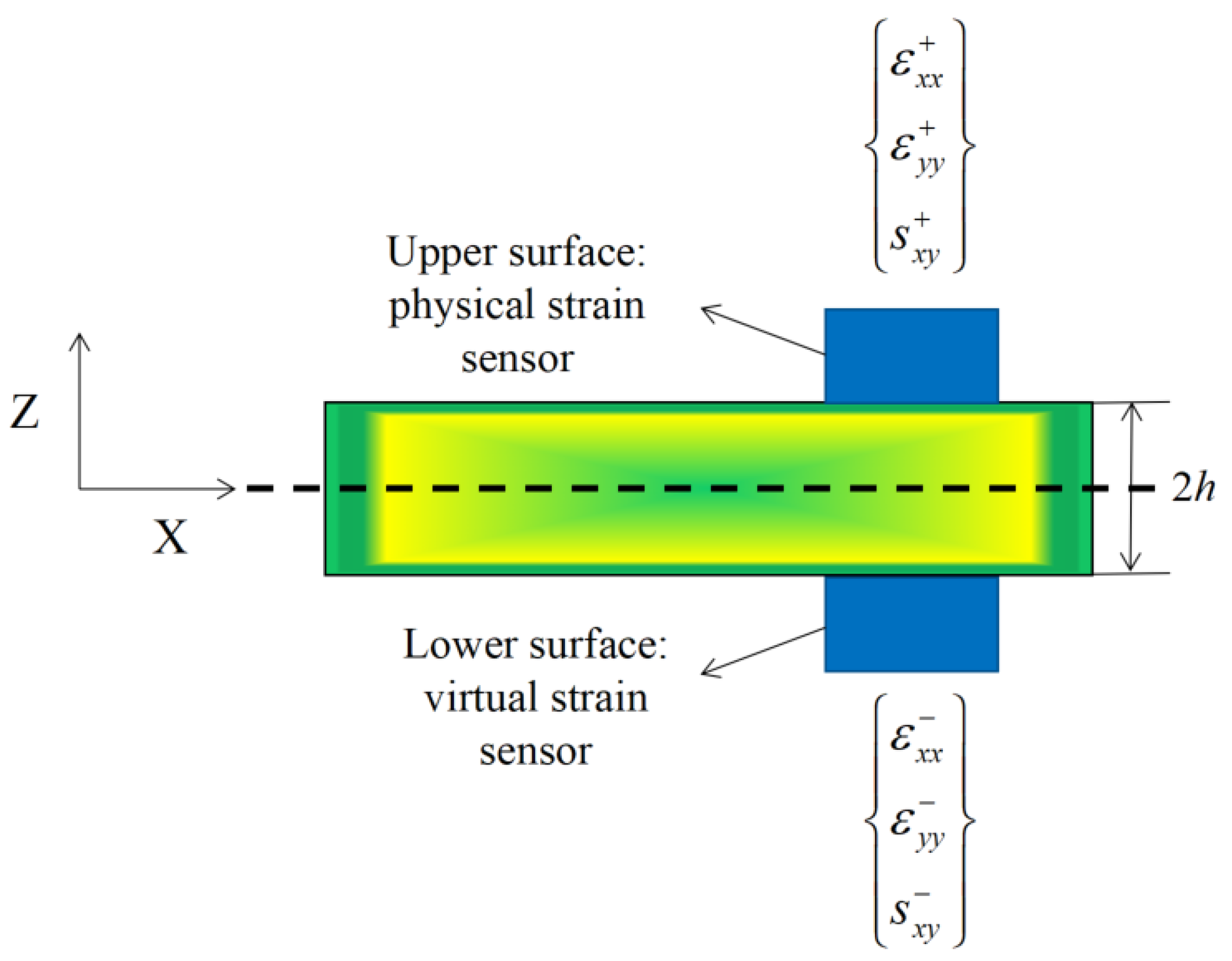
2.2. Data Input
2.3. Least Squares Error Function
3. Model Parameters
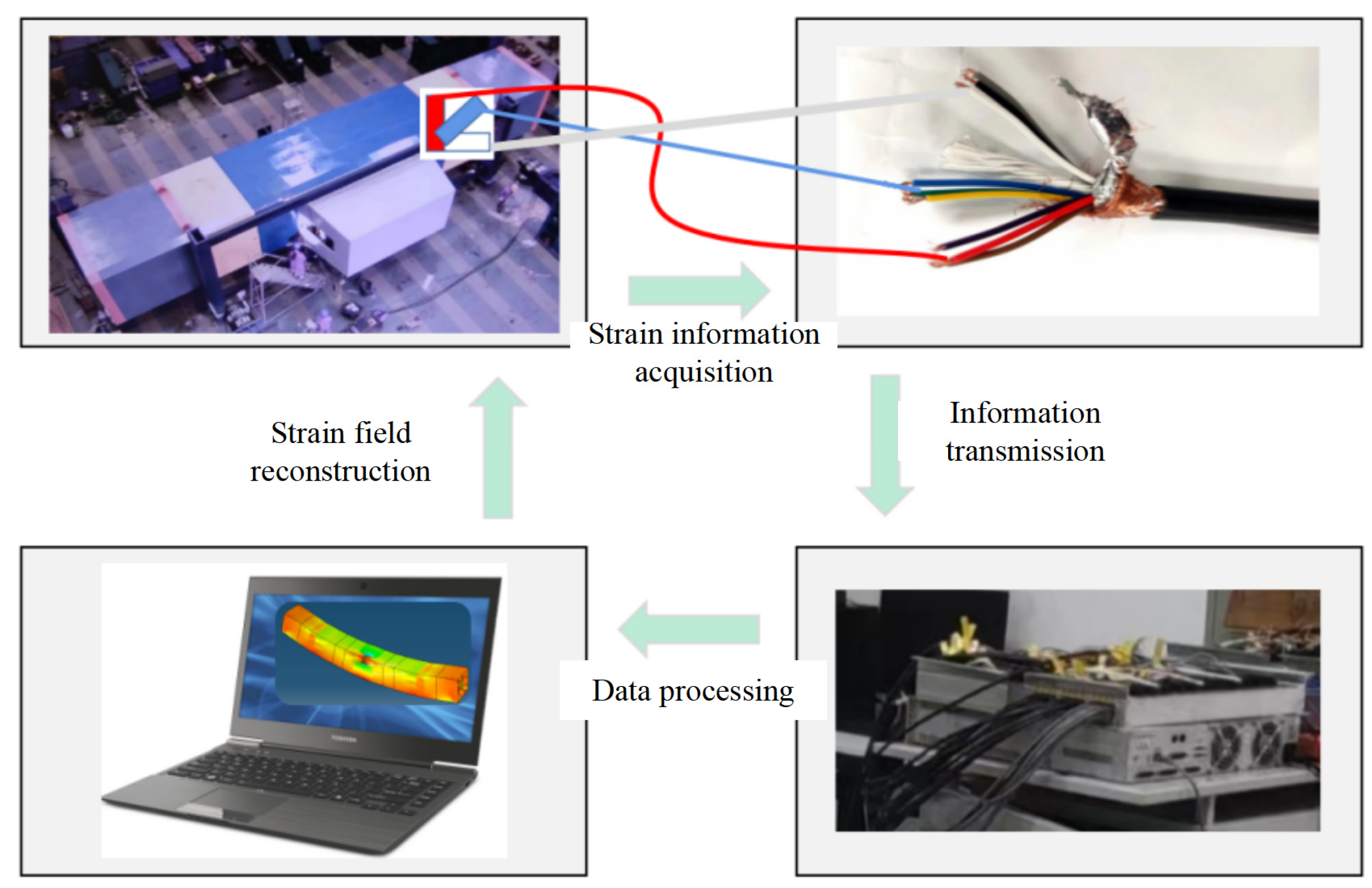
4. Design of Test Scheme for Hull Box Girder
5. Discussion
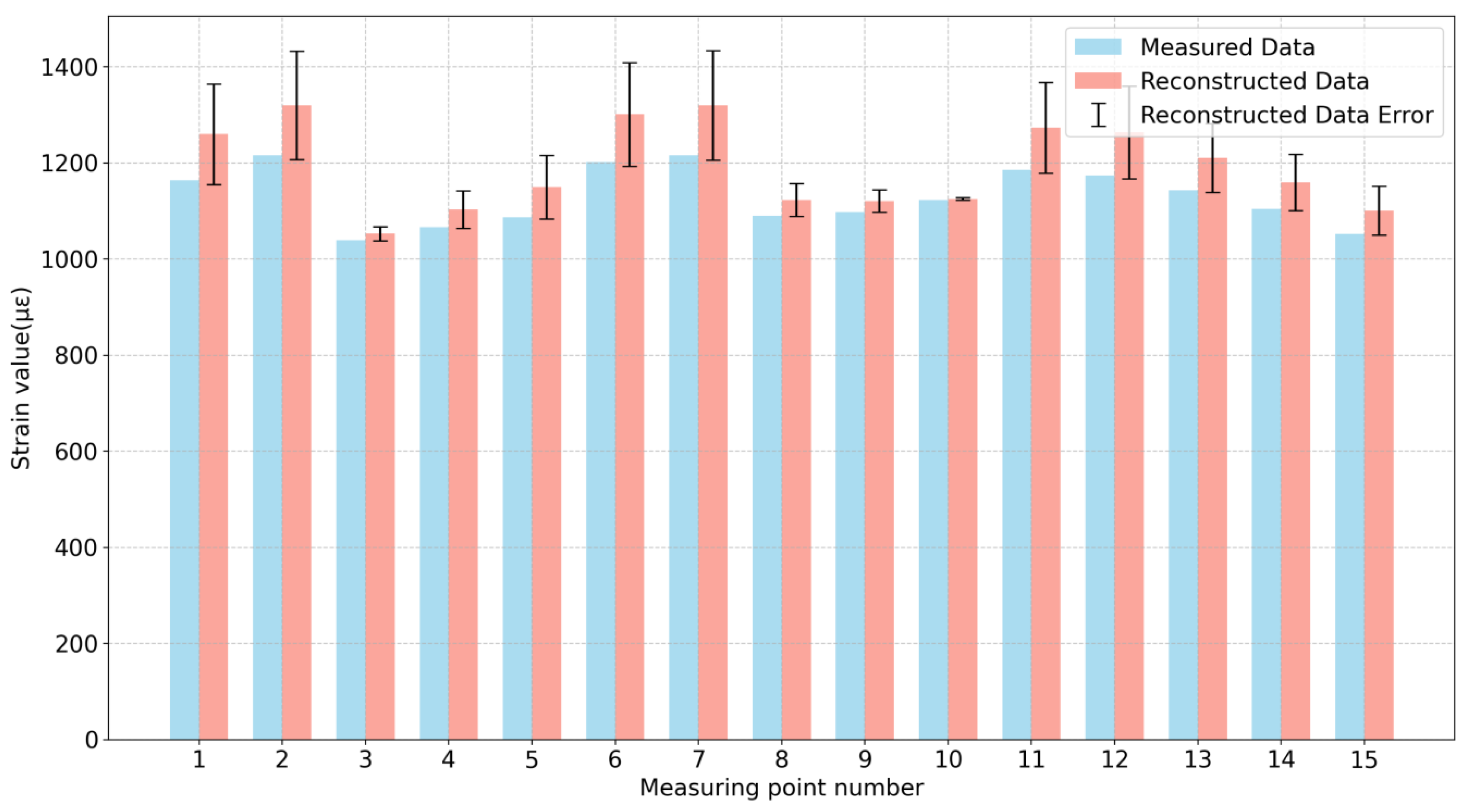
5.1. Analysis of Test Data
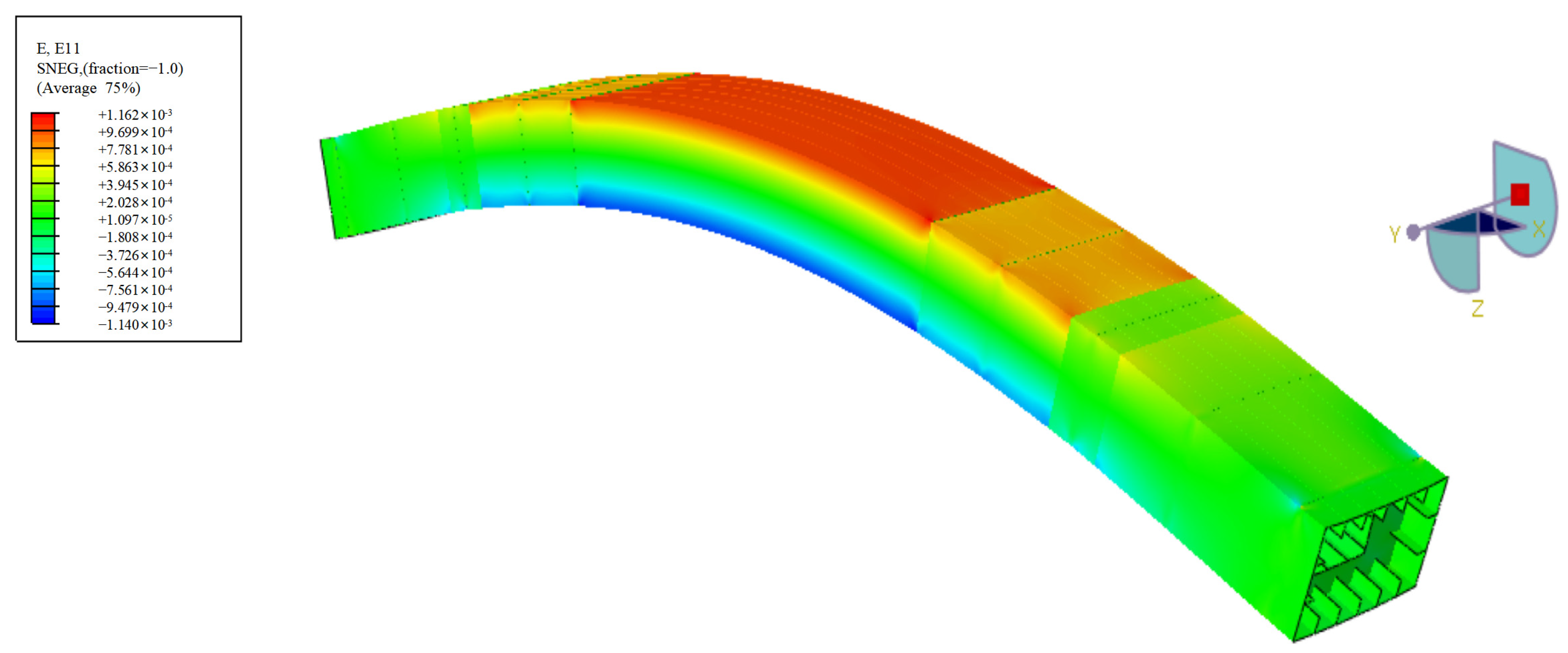
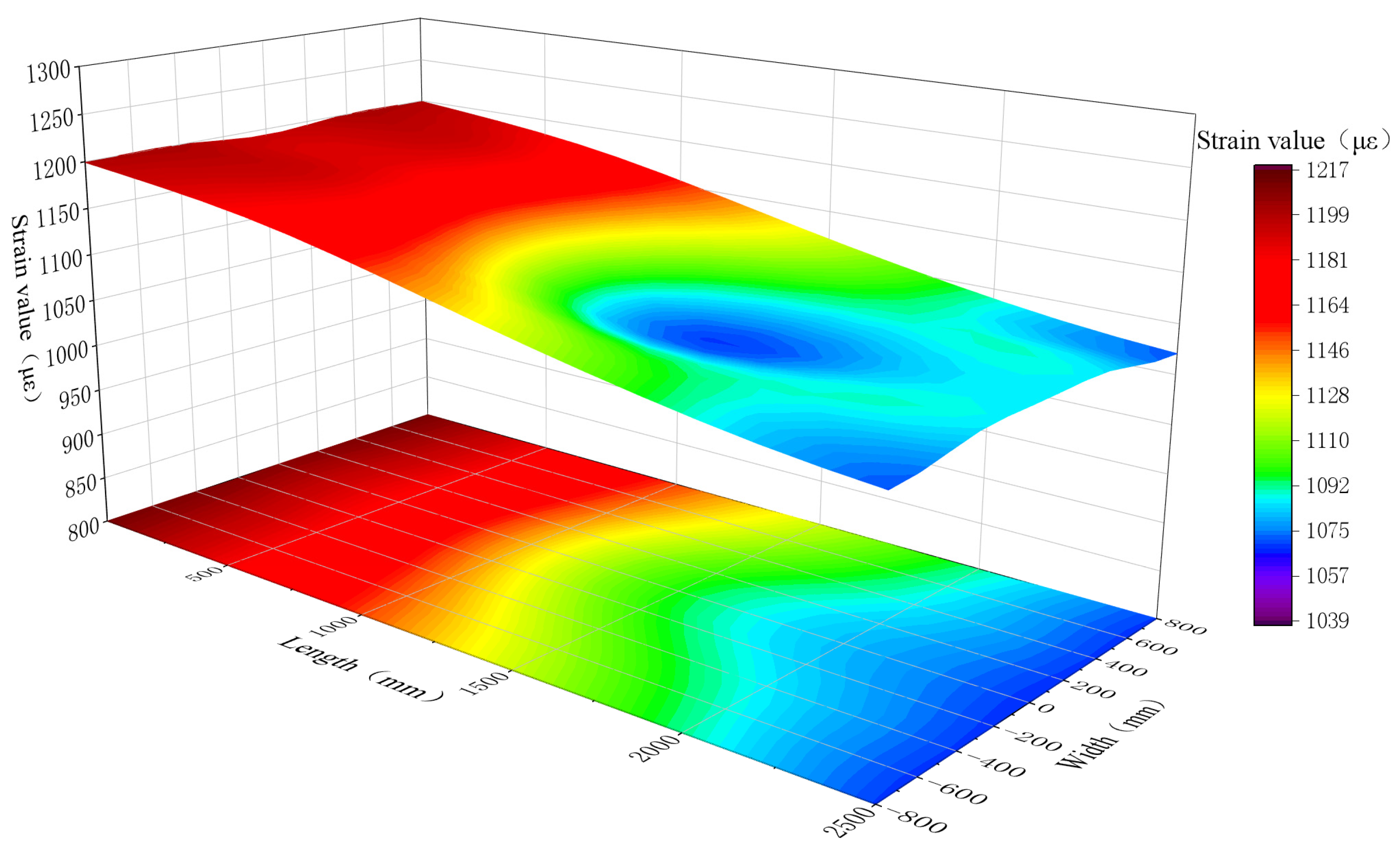
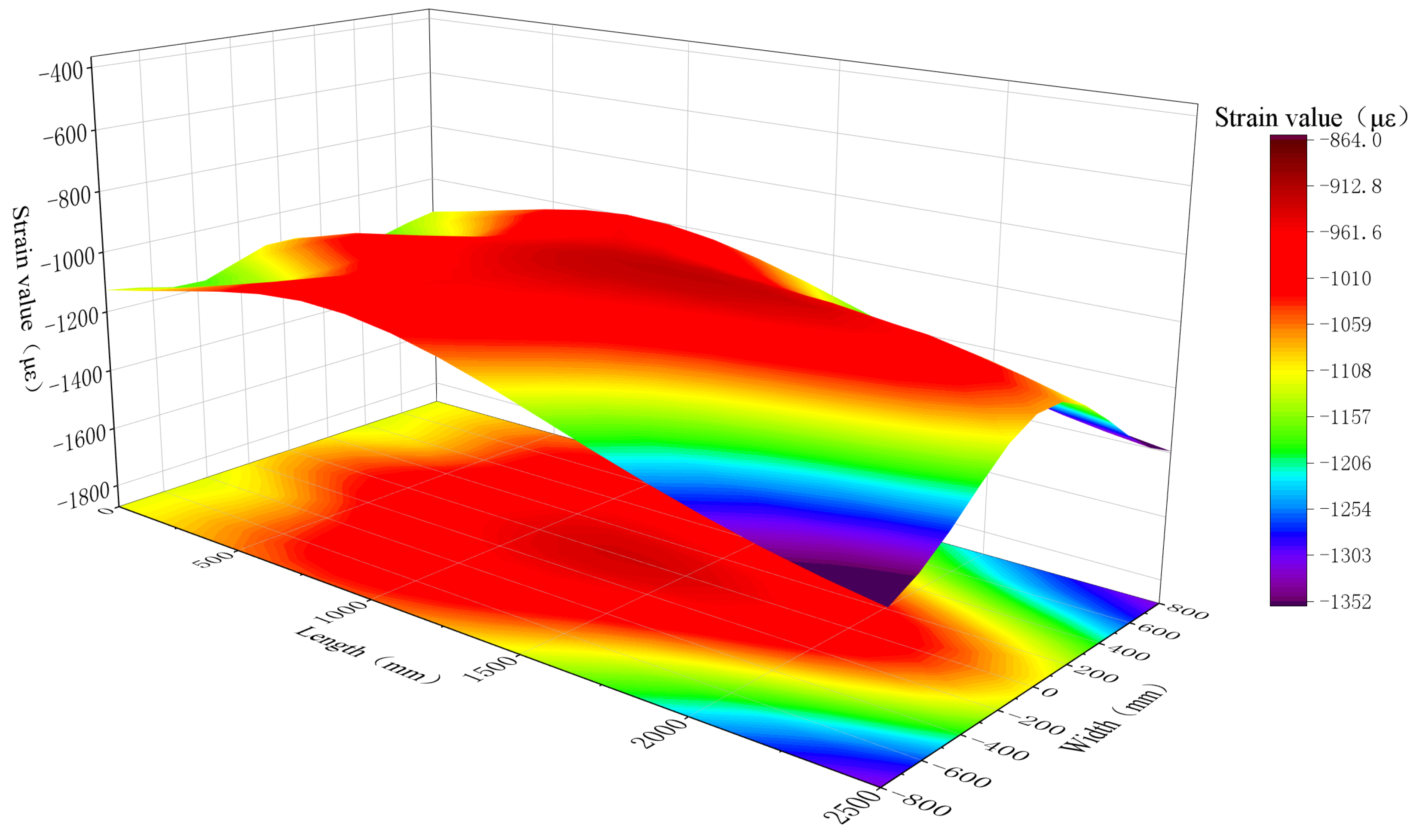
5.2. Strain Field Reconstruction
6. Conclusions
- For the first time, significant quantities of measured data and virtual sensor strain data were used to reconstruct the strain field of the top plate, broadside, and bottom plate of the box girder test section under a certain working environment.
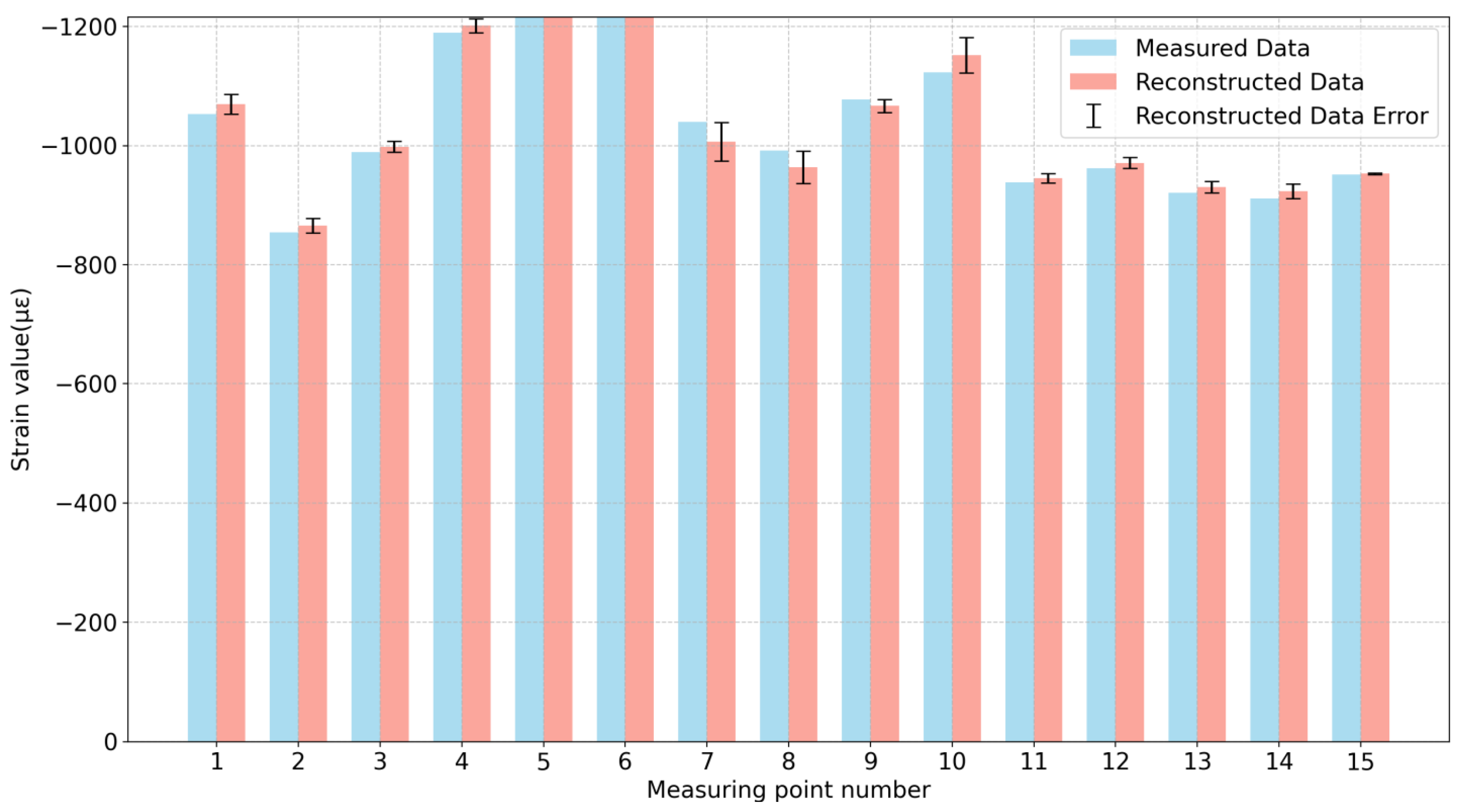
- By confirming the reconstruction results, it was found that the average error between the reconstructed value and the measured value (again, excluding the measurement points near the neutral axis) was 3.42% and the reconstruction error of the verification points ranged from −0.40% to 2.51%.
- In this study, a large number of experimental data were used to reconstruct the strain field of a long-span hull box girder and present it visually, allowing us to quickly evaluate the stress state of the hull structure in complex sea conditions, prevent potential structural damage, and ensure the safety of ship structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, X.; Zhu, Q.; Zhang, T.; Yang, H.; Chen, G. Research progress of ship structure monitoring technology. J. Ship Mech. 2022, 26, 1246–1253. [Google Scholar]
- Zheng, Q.; Wang, X.; Zhao, X.; Yang, H.; Xu, C.; Jiang, Z. Research on strain sensor technology applied to structural safety monitoring of ships and offshore engineering. Equip. Environ. Eng. 2023, 20, 83–89. [Google Scholar]
- Bernasconi, O.; Ewins, D.J. Application of strain modal testing to real structures. In Proceedings of the 7th International Modal Analysis Conference, Las Vegas, NV, USA, 30 January–2 February 1989; Society for Experimental Mechanics: Bethel, CT, USA, 1989; Volume 2, pp. 1453–1464. [Google Scholar]
- Chopra, I. Review of state of art of smart structures and integrated systems. AIAA J. 2002, 40, 2145–2187. [Google Scholar] [CrossRef]
- Sun, J. Inverstigation on Morphing Wing Structures Based on Shape Memory Polymer Composite (SMPC) Skins and Active Honeycomb Structures. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2015. [Google Scholar]
- Ko, W.L.; Richards, W.L.; Tran, V.T. Displacement Theories for In-Flight Deformed Shape Predictions of Aerospace Structures. NASA/TP-2007-214612, 1 October 2007. [Google Scholar]
- Derkevorkian, A.; Masri, S.F.; Alvarenga, J.; Boussalis, H.; Bakalyar, J.; Richards, W.L. Strain-based deformation shape-estimation algorithm for control and monitoring applications. AIAA J. 2013, 51, 2231–2240. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, J.; Wang, X.; Chen, G.; Zhu, Q.; Jiang, Z.; Wang, Z. Solving approach for global stress field of the 3D structures based on artificial intelligence. J. Ship Mech. 2023, 27, 238–249. [Google Scholar]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a Panamax containership using inverse finite element method. Ocean. Eng. 2016, 119, 16–29. [Google Scholar] [CrossRef]
- Kefal, A. An efficient curved inverse-shell element for shape sensing and structural health monitoring of cylindrical marine structures. Ocean. Eng. 2019, 188, 106262. [Google Scholar] [CrossRef]
- Huang, H. Research on Deformation Reconstruction of Plateand Girder Structure Based on Inverse Finite Element Method. Master’s Thesis, University of Science and Technology, Huazhong, China, 2021. [Google Scholar] [CrossRef]
- Mao, Z. Comparison of Shape Reconstruction Strategies in a Complex Flexible Structure. Master’s Thesis, University of California, San Diego, CA, USA, 2008. [Google Scholar]
- Tessler, A.; Spangler, J. A Variational Principle for Reconstruction of Elastic Deformations in Shear Deformable Plates and Shells; National Aeronautics and Space Administration, Langley Research Center: Hampton, VA, USA, 2003. [Google Scholar]
- Hu, M.; Wu, S.; Dong, E. Deformation reconstruction of a three-dimensional panel structure opon IFEM. Eng. Mech. 2024, 41, 235–245. [Google Scholar]
- Ke, Z.; Yuan, S.; Ren, Y.; Xu, Y. Shape reconstruction of self-adaptive morphing wings’ fishbone based on iFEM. Acta Aeronaut. 2020, 41, 250–260. [Google Scholar]
- Kefal, A.; Oterkus, E. Structural health monitoring of marine structures by using inverse finite element method. In Analysis and Design of Marine Structures V, 1st ed.; CRC Press: Boca Raton, FL, USA, 2015; pp. 341–349. [Google Scholar]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a chemical tanker based on inverse finite element method. Ocean. Eng. 2016, 112, 33–46. [Google Scholar] [CrossRef]
- Kefal, A.; Mayang, J.B.; Oterkus, E.; Yildiz, M. Three dimensional shape and stress monitoring of bulk carriers based on iFEM methodology. Ocean. Eng. 2018, 147, 256–267. [Google Scholar] [CrossRef]
- Putranto, T.; Kõrgesaar, M.; Tabri, K. Application of equivalent single layer approach for ultimate strength analyses of ship hull girder. J. Mar. Sci. Eng. 2022, 10, 1530. [Google Scholar] [CrossRef]
- Putranto, T. Equivalent single layer approach for ultimate strength analysis of box girder under bending load. Ocean. Eng. 2024, 292, 116535. [Google Scholar] [CrossRef]
- Yan, H.; Bai, C.; Jia, T.; Liu, C. Application of inverse finite element in deformation and reconstruction of ship reinforced plate structure. Shipbuild. China 2023, 64, 168–179. [Google Scholar]
- Zhu, Q.; Wu, G.; Zeng, J.; Jiang, Z.; Yue, Y.; Xiang, C.; Zhan, J.; Zhao, B. Enhanced Strain Field Reconstruction in Ship Stiffened Panels Using Optical Fiber Sensors and the Strain Function-Inverse Finite Element Method. Appl. Sci. 2023, 14, 370. [Google Scholar] [CrossRef]
- Wei, P.; Li, C.; Jiang, Z.; Wang, D. Real-Time Digital Twin of Ship Structure Deformation Field Based on the Inverse Finite Element Method. J. Mar. Sci. Eng. 2024, 12, 257. [Google Scholar] [CrossRef]
- Vazquez, S.L.; Tessler, A.; Quach, C.C.; Cooper, E.G.; Parks, J.; Spangler, J.L. Structural Health Monitoring Using High-Density Fiber Optic Strain Sensor and Inverse Finite Element Methods. NASA/TM-2005-213761, 1 May 2005. [Google Scholar]
- Tessler, A.; Spangler, J.L. Inverse FEM for full-field reconstruction of elastic deformations in shear deformable plates and shells. In Proceedings of the 2nd European Workshop on Structural Health Monitoring, Munich, Germany, 7–9 July 2004. [Google Scholar]
- Kefal, A.; Oterkus, E.; Tessler, A.; Spangler, J.L. A quadrilateral inverse-shell element with drilling degrees of freedom for shape sensing and structural health monitoring. Eng. Sci. Technol. Int. J. 2016, 19, 1299–1313. [Google Scholar] [CrossRef]
- Cao, Z.; Fei, Q.; Jiang, D.; Zhang, D.; Jin, H.; Zhu, R. Dynamic sensitivity-based finite element model updating for nonlinear structures using time-domain responses. Int. J. Mech. Sci. 2020, 184, 105788. [Google Scholar] [CrossRef]



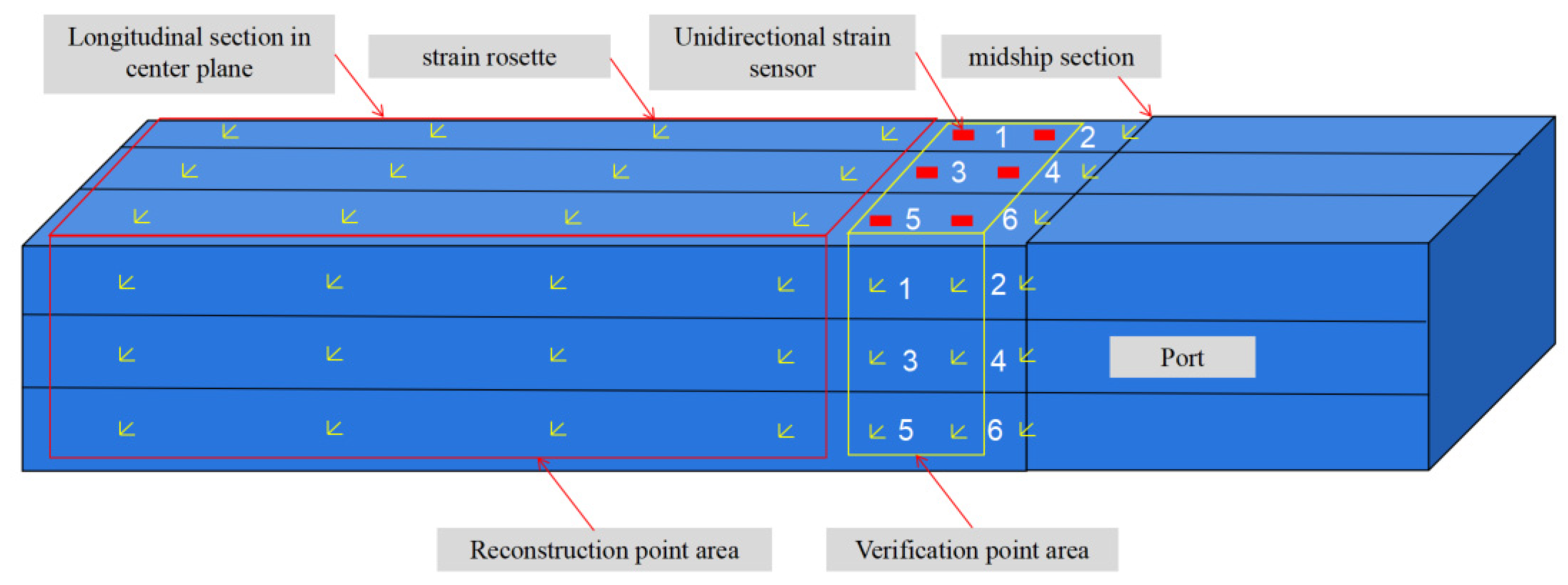

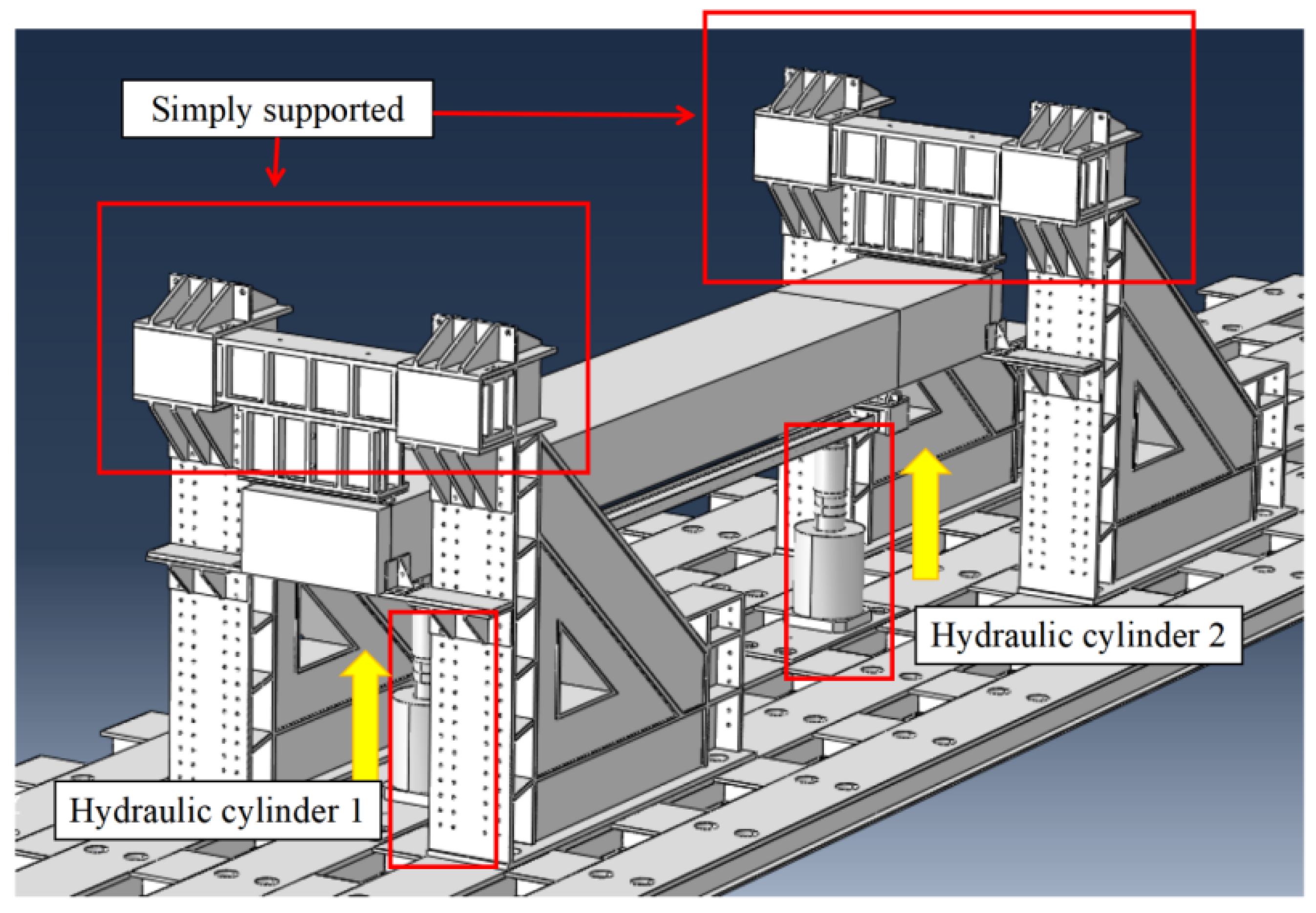


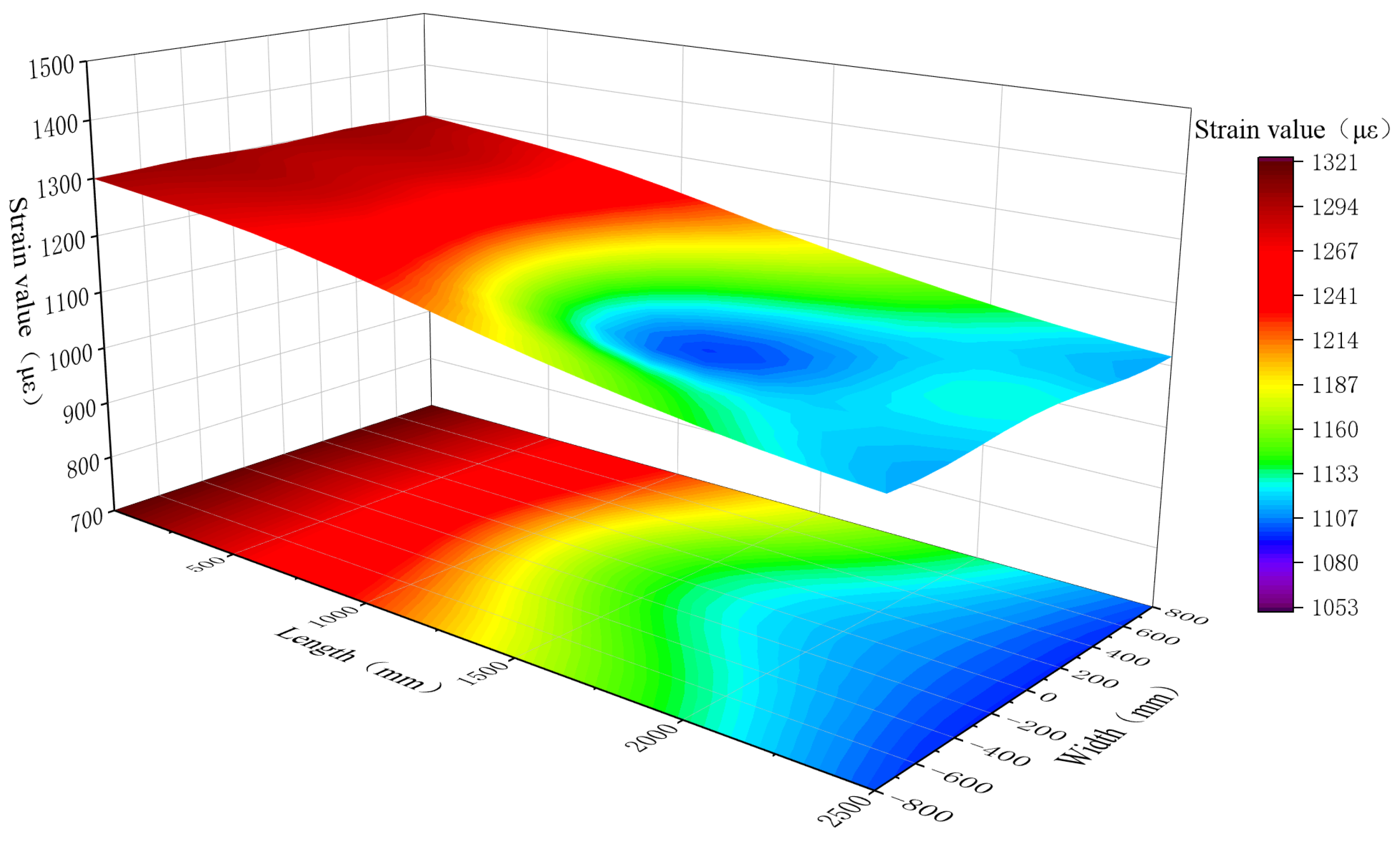

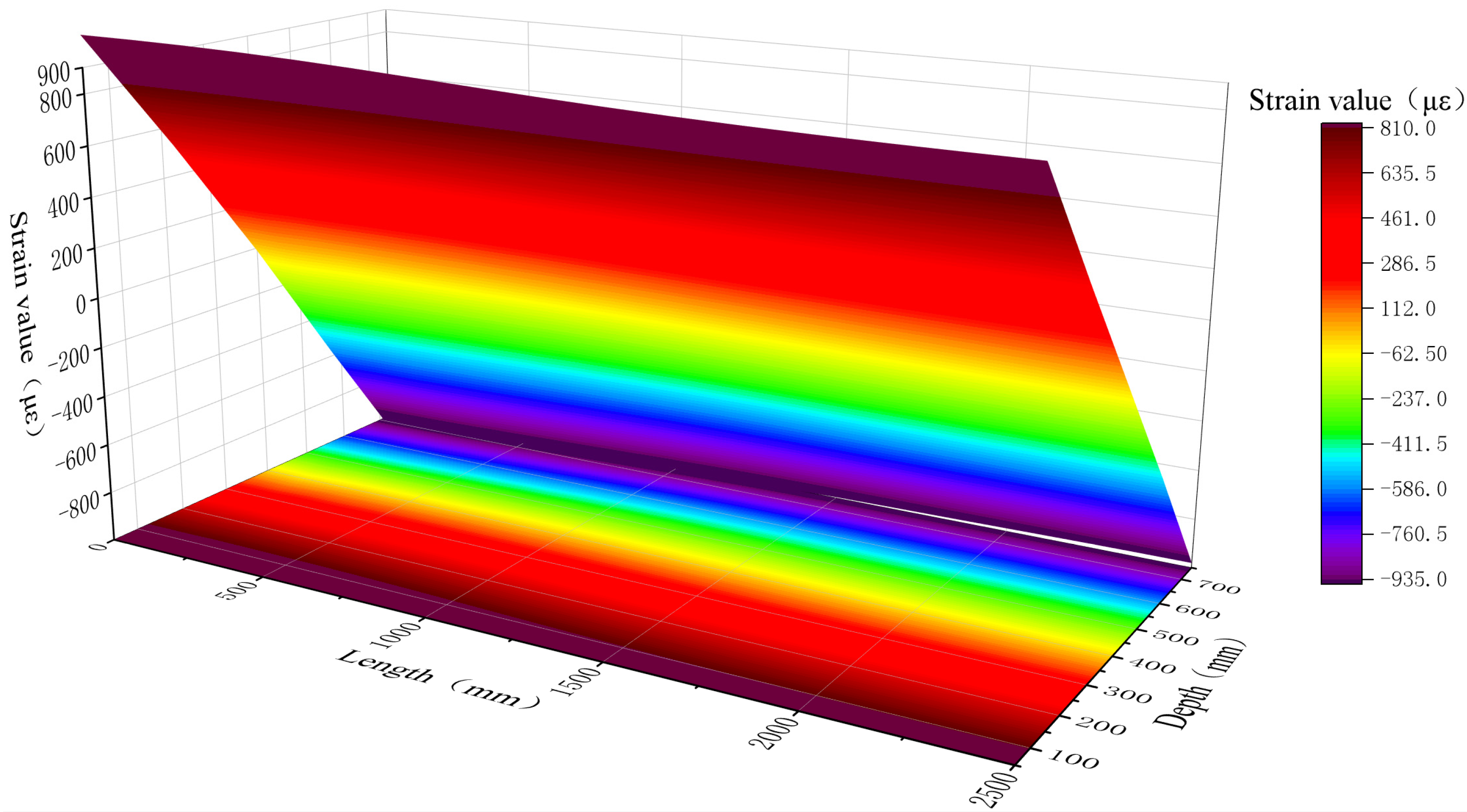
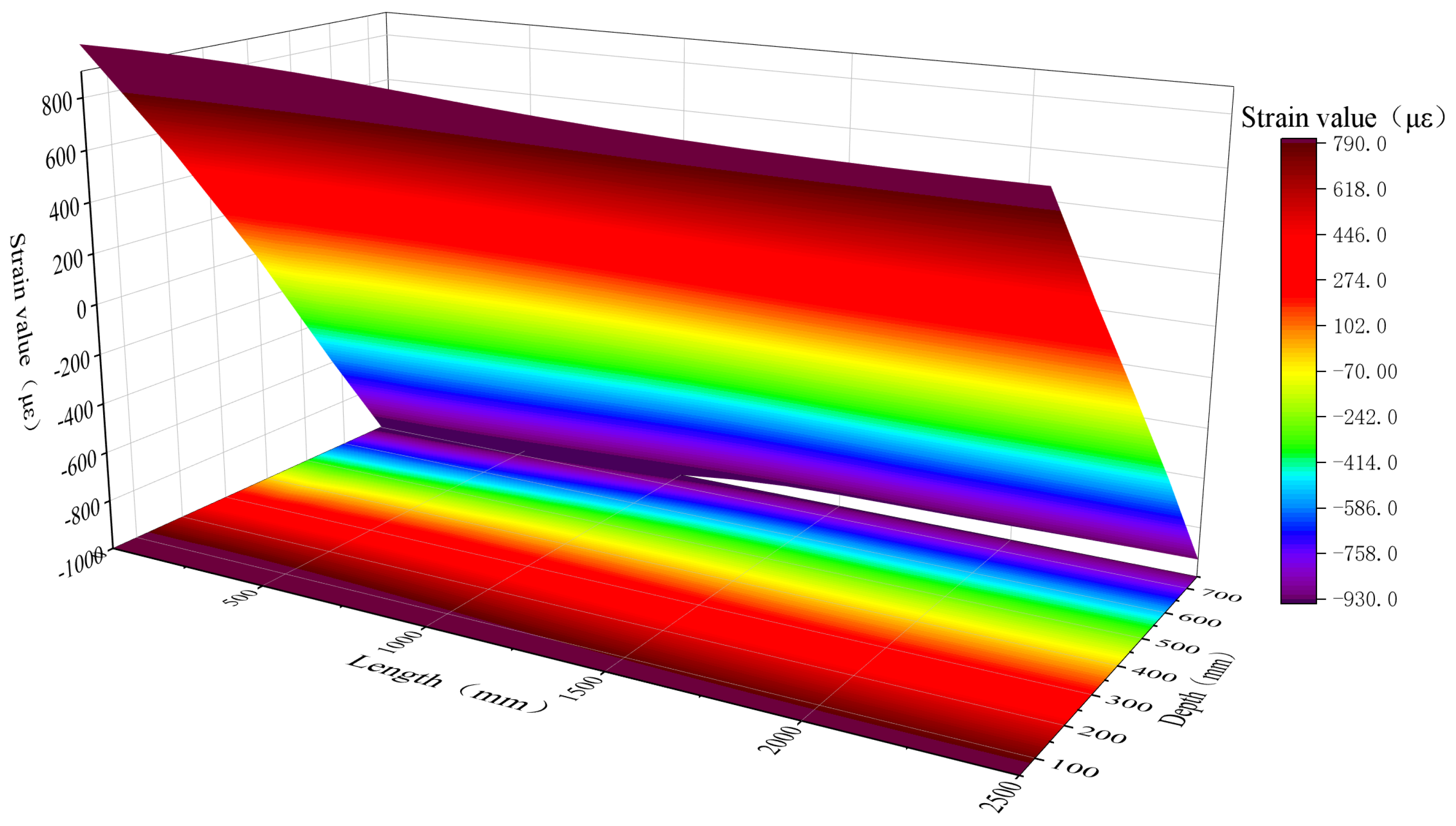

| Box Girder Dimensions (mm) | Division and Size of Box Girder Cabin (mm) | Quantity (pcs) | Thickness of Plate and Shell in Test Section (mm) | Elastic Modulus (GPa) | Poisson’s Ratio | |||
|---|---|---|---|---|---|---|---|---|
| Length | 12,500 | Loading section | 1500 | 2 | Top plate | 5.55 | 205 | 0.3 |
| Width | 1500 | Changeover portion | 1500 | 2 | Port | 5.75 | 205 | 0.3 |
| Height | 800 | Test section | 4500 | 2 | Bottom plate | 5.75 | 205 | 0.3 |
| Tooling occupation section | 500 | 4 | Starboard | 5.75 | 205 | 0.3 | ||
| Loading Type | Load Size (kN) | Number of Replication |
|---|---|---|
| Four-point bending | 0, 200, 400, 600, …1400, 1600, 1700… | 1 |
| Reconstruction Point Area | Reconstruction Point Number | Relative Error | ||
|---|---|---|---|---|
| Top plate | 1 | 1163.68 | 1260.06 | −7.65% |
| 2 | 1216.60 | 1320.45 | −7.86% | |
| 3 | 1039.00 | 1053.30 | −1.36% | |
| 4 | 1066.00 | 1103.55 | −3.40% | |
| 5 | 1087.42 | 1150.11 | −5.45% | |
| 6 | 1201.73 | 1301.33 | −7.65% | |
| 7 | 1215.69 | 1320.24 | −7.92% | |
| 8 | 1090.00 | 1123.39 | −2.97% | |
| 9 | 1098.00 | 1120.86 | −2.04% | |
| 10 | 1122.81 | 1125.56 | −0.24% | |
| 11 | 1185.75 | 1273.76 | −6.91% | |
| 12 | 1174.00 | 1263.91 | −7.11% | |
| 13 | 1143.00 | 1210.53 | −5.58% | |
| 14 | 1104.00 | 1159.82 | −4.81% | |
| 15 | 1052.05 | 1100.87 | −4.43% | |
| Port | 1 | 800.00 | 787.75 | 1.55% |
| 2 | 807.00 | 776.86 | 3.88% | |
| 3 | 708.00 | 669.66 | 5.73% | |
| 4 | 696.00 | 662.56 | 5.05% | |
| 5 | 707.75 | 654.53 | 8.13% | |
| 6 | 27.00 | 23.15 | 16.62% | |
| 7 | 44.00 | 56.00 | −21.43% | |
| 8 | 24.00 | 38.96 | −38.39% | |
| 9 | −15.00 | −36.49 | −58.89% | |
| 10 | −15.00 | 0.61 | −2563.51% | |
| 11 | −933.00 | −926.05 | 0.75% | |
| 12 | −851.00 | −835.38 | 1.87% | |
| 13 | −620.00 | −590.98 | 4.91% | |
| 14 | −814.00 | −771.59 | 5.50% | |
| 15 | −712.29 | −678.83 | 4.93% | |
| Bottom plate | 1 | −1053.00 | −1069.71 | 1.56% |
| 2 | −854.00 | −865.98 | 1.38% | |
| 3 | −989.00 | −998.25 | 0.93% | |
| 4 | −1190.00 | −1201.75 | 0.98% | |
| 5 | −1348.98 | −1350.95 | 0.15% | |
| 6 | −1341.00 | −1340.94 | 0.00% | |
| 7 | −1040.00 | −1006.64 | −3.31% | |
| 8 | −992.00 | −963.82 | −2.92% | |
| 9 | −1078.00 | −1066.70 | −1.06% | |
| 10 | −1123.14 | −1152.12 | 2.52% | |
| 11 | −938.00 | −945.51 | 0.79% | |
| 12 | −962.00 | −971.23 | 0.95% | |
| 13 | −921.00 | −930.39 | 1.01% | |
| 14 | −911.00 | −923.32 | 1.33% | |
| 15 | −951.42 | −952.97 | 0.16% |
| Verification Point Area | Verification Point Number | Relative Error | ||
|---|---|---|---|---|
| Top plate | 1 | 1104 | 1108.94 | −0.45% |
| 2 | 940 | 939.15 | 0.09% | |
| 3 | 1107 | 1111.58 | −0.41% | |
| 4 | 1039 | 1036.08 | 0.28% | |
| 5 | 1128 | 1134.08 | −0.54% | |
| 6 | 1086 | 1090.37 | −0.40% | |
| Port | 1 | 712 | 703.05 | 1.27% |
| 2 | 746 | 732.67 | 1.82% | |
| 3 | −13 | −10.76 | 20.81% | |
| 4 | −6 | 1.11 | −640.95% | |
| 5 | −530 | −517.04 | 2.51% | |
| 6 | −774 | −771.58 | 0.31% | |
| Bottom plate | 1 | −1315 | −1328.41 | 1.01% |
| 2 | −1166 | −1172.55 | 0.56% | |
| 3 | −1131 | −1138.52 | 0.66% | |
| 4 | −1114 | −1123.13 | 0.81% | |
| 5 | −861 | −856.05 | −0.58% | |
| 6 | −1116 | −1121.32 | 0.47% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Wang, X.; Zhao, N.; Jiang, Z.; Li, F.; Chen, H.; Wei, P.; Zhang, T. Study on Strain Field Reconstruction Method of Long-Span Hull Box Girder Based on iFEM. J. Mar. Sci. Eng. 2024, 12, 1482. https://doi.org/10.3390/jmse12091482
Chen G, Wang X, Zhao N, Jiang Z, Li F, Chen H, Wei P, Zhang T. Study on Strain Field Reconstruction Method of Long-Span Hull Box Girder Based on iFEM. Journal of Marine Science and Engineering. 2024; 12(9):1482. https://doi.org/10.3390/jmse12091482
Chicago/Turabian StyleChen, Guocai, Xueliang Wang, Nan Zhao, Zhentao Jiang, Fei Li, Haozheng Chen, Pengyu Wei, and Tao Zhang. 2024. "Study on Strain Field Reconstruction Method of Long-Span Hull Box Girder Based on iFEM" Journal of Marine Science and Engineering 12, no. 9: 1482. https://doi.org/10.3390/jmse12091482
APA StyleChen, G., Wang, X., Zhao, N., Jiang, Z., Li, F., Chen, H., Wei, P., & Zhang, T. (2024). Study on Strain Field Reconstruction Method of Long-Span Hull Box Girder Based on iFEM. Journal of Marine Science and Engineering, 12(9), 1482. https://doi.org/10.3390/jmse12091482







