System Structural Error Analysis in Binocular Vision Measurement Systems
Abstract
:1. Introduction
- The error analysis model for binocular stereo vision measurement systems is refined in this study by considering the relationships among object distance, baseline length, and the angle between the baseline and the optical axis. This provides a comprehensive model for analyzing the impact of system structural parameters on measurement accuracy.
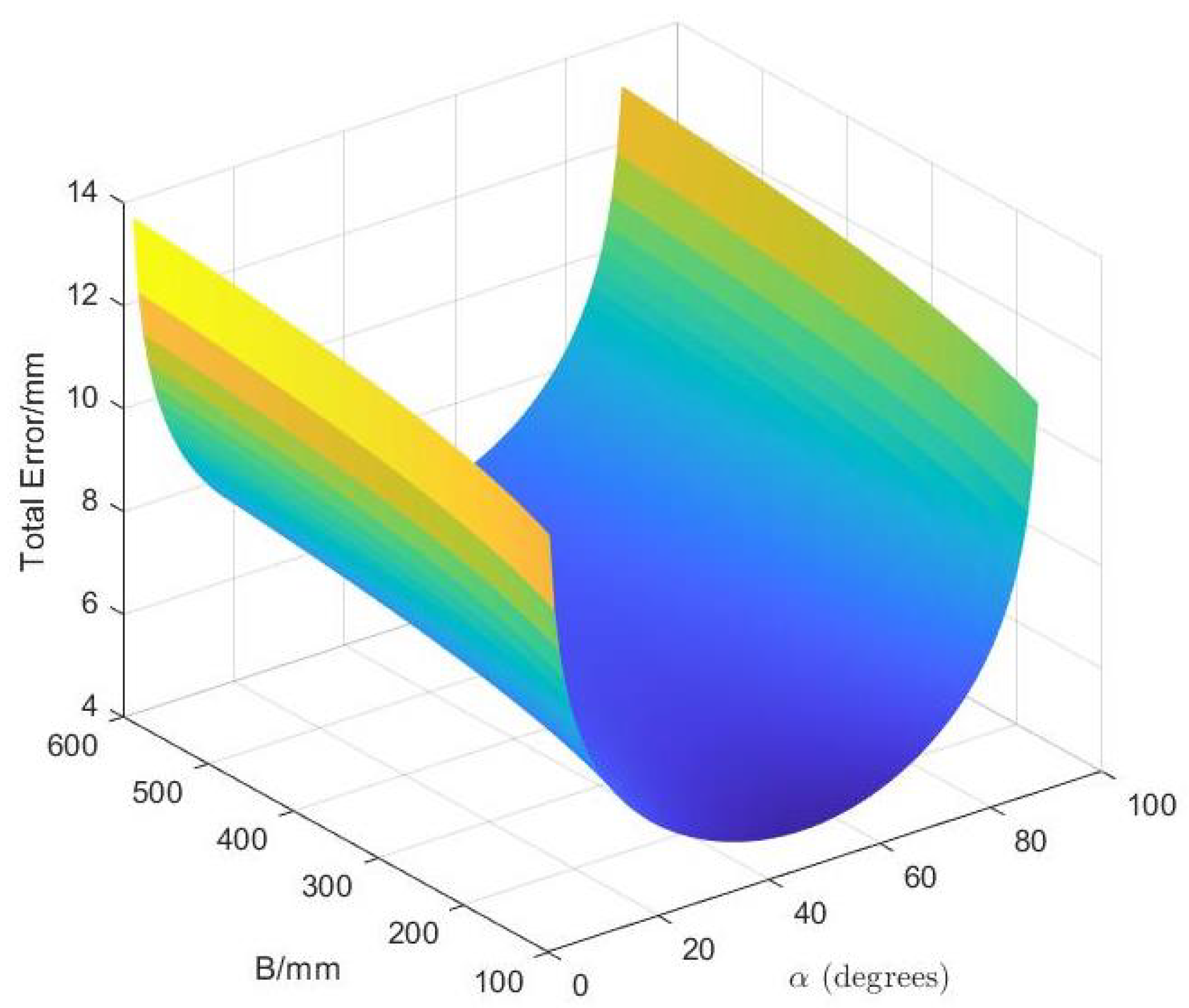
- Experimental verification and nonlinear analysis are conducted to determine the impact of baseline length and object distance variations on binocular measurement errors, suggesting an optimal range for the K value (the ratio of baseline length to object distance).
- The impact of the angle between the optical axis and the baseline on measurement accuracy is analyzed, and the optimal range is determined to be between 30° and 40°.
2. Related Work
2.1. Research on System Intrinsic Parameters
2.2. Research on System Extrinsic Parameters
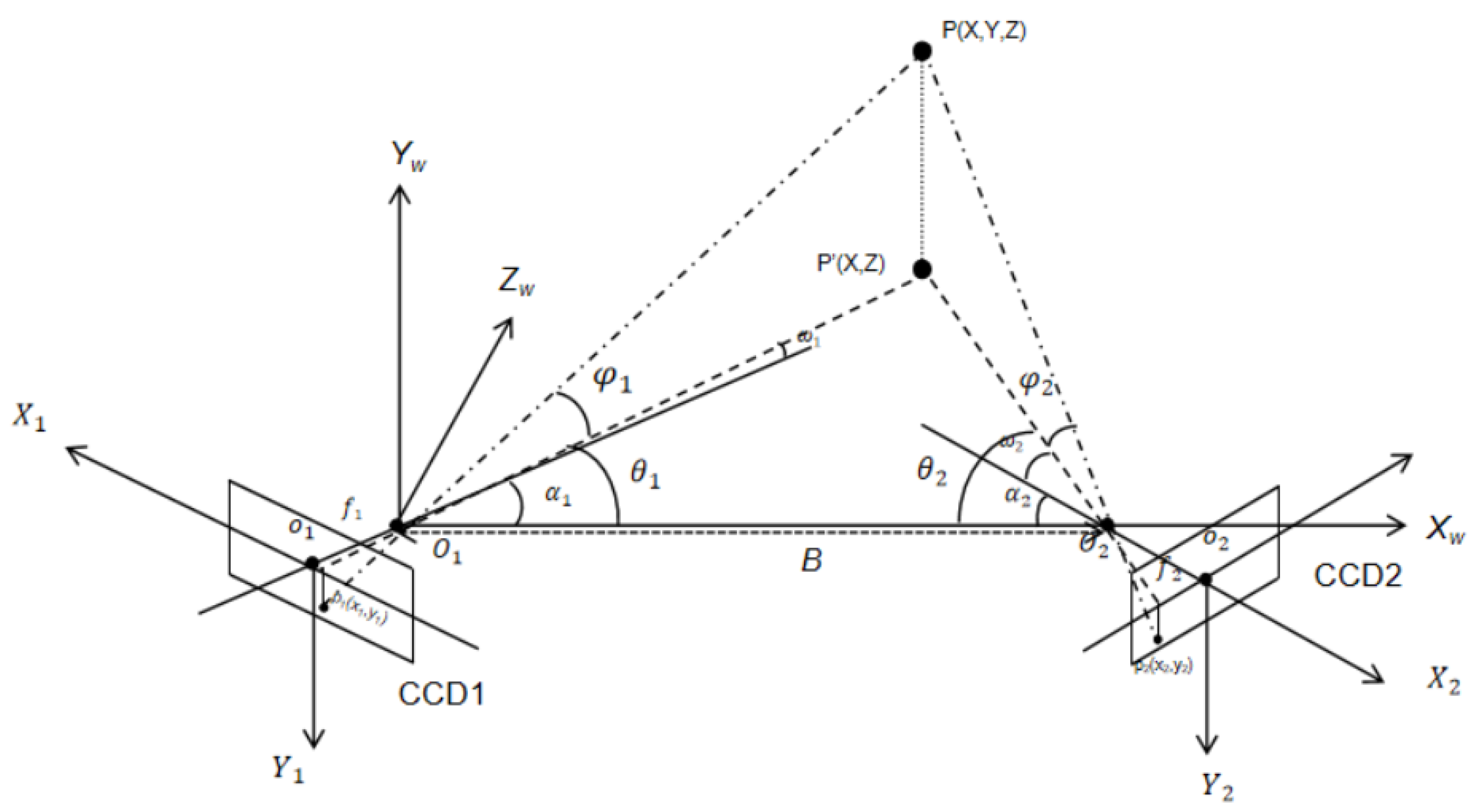
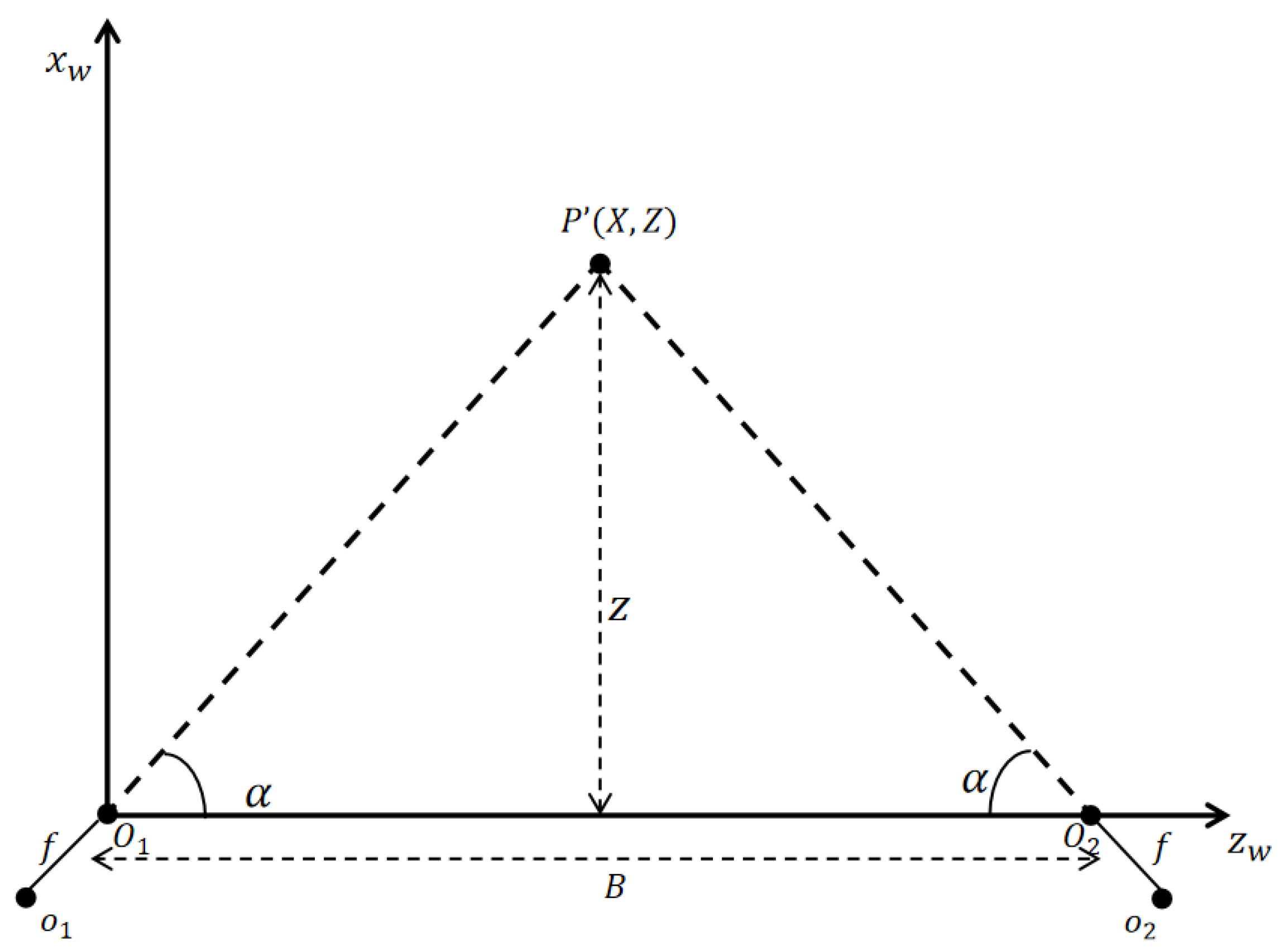
3. Measurement Error Analysis Model for Binocular Vision
4. Experiments and Results
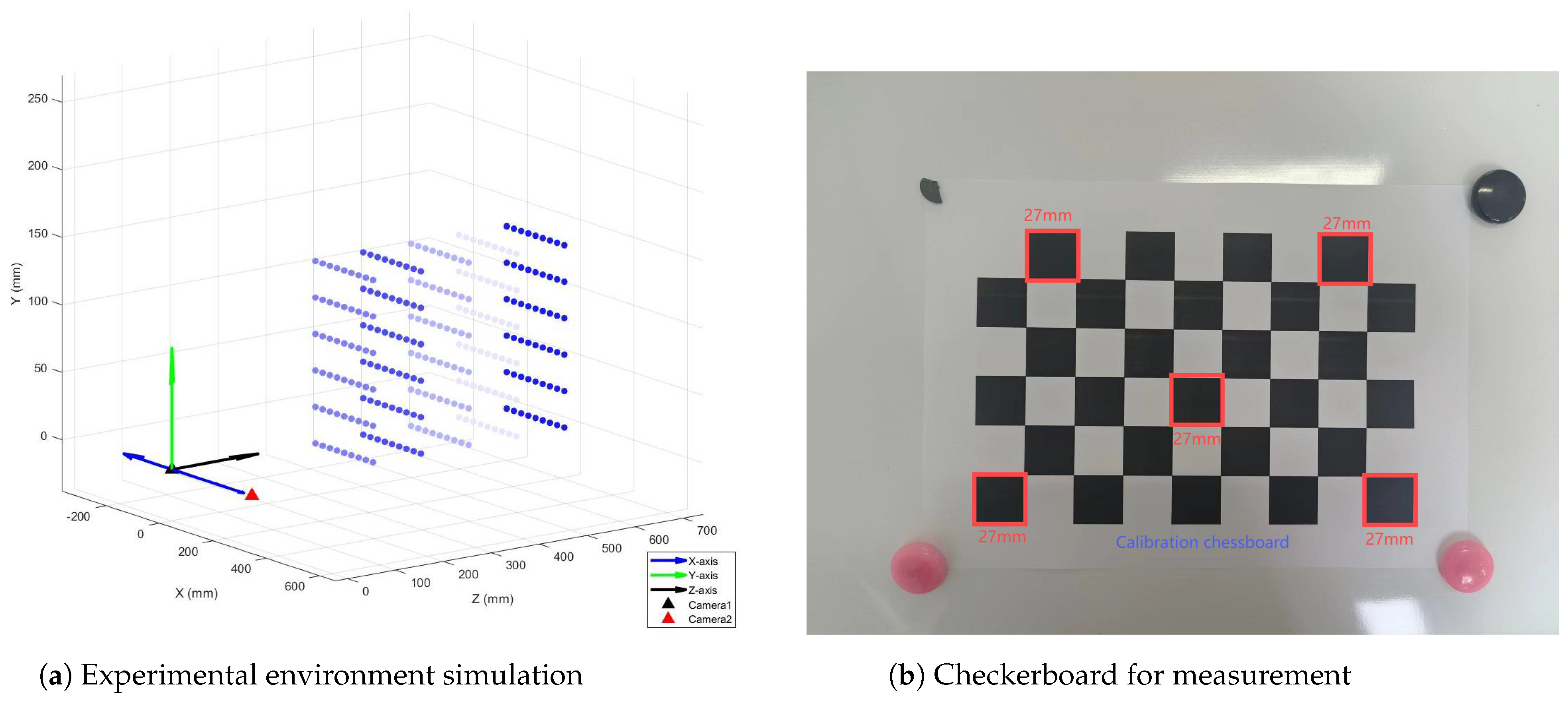
4.1. Experiment System
4.2. Experimental Results
4.2.1. Experiment I
4.2.2. Experiment II
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, P.; Qin, T. Stereo vision-based semantic 3d object and ego-motion tracking for autonomous driving. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 of September 2018; pp. 646–661. [Google Scholar]
- Ma, Y.; Li, Q.; Chu, L.; Zhou, Y.; Xu, C. Real-time detection and spatial localization of insulators for UAV inspection based on binocular stereo vision. Remote Sens. 2021, 13, 230. [Google Scholar] [CrossRef]
- Guan, J.; Yang, X.; Ding, L.; Cheng, X.; Lee, V.C.; Jin, C. Automated pixel-level pavement distress detection based on stereo vision and deep learning. Autom. Constr. 2021, 129, 103788. [Google Scholar] [CrossRef]
- Kahmen, O.; Rofallski, R.; Luhmann, T. Impact of stereo camera calibration to object accuracy in multimedia photogrammetry. Remote Sens. 2020, 12, 2057. [Google Scholar] [CrossRef]
- Hamid, M.S.; Abd Manap, N.; Hamzah, R.A.; Kadmin, A.F. Stereo matching algorithm based on deep learning: A survey. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 1663–1673. [Google Scholar] [CrossRef]
- Sarlin, P.E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 4938–4947. [Google Scholar]
- Adil, E.; Mikou, M.; Mouhsen, A. A novel algorithm for distance measurement using stereo camera. CAAI Trans. Intell. Technol. 2022, 7, 177–186. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, D. Improved Camera Calibration Method and Accuracy Analysis for Binocular Vision. Int. J. Pattern Recognit. Artif. Intell. 2021, 35, 2155010. [Google Scholar] [CrossRef]
- Hua, L.; Lu, Y.; Deng, J.; Shi, Z.; Shen, D. 3D reconstruction of concrete defects using optical laser triangulation and modified spacetime analysis. Autom. Constr. 2022, 142, 104469. [Google Scholar] [CrossRef]
- Pollefeys, M.; Koch, R.; Gool, L.V. Self-calibration and metric reconstruction inspite of varying and unknown intrinsic camera parameters. Int. J. Comput. Vis. 1999, 32, 7–25. [Google Scholar] [CrossRef]
- Chen, B.; Pan, B. Camera calibration using synthetic random speckle pattern and digital image correlation. Opt. Lasers Eng. 2020, 126, 105919. [Google Scholar] [CrossRef]
- Feng, W.; Su, Z.; Han, Y.; Liu, H.; Yu, Q.; Liu, S.; Zhang, D. Inertial measurement unit aided extrinsic parameters calibration for stereo vision systems. Opt. Lasers Eng. 2020, 134, 106252. [Google Scholar] [CrossRef]
- Zimiao, Z.; Hao, Z.; Kai, X.; Yanan, W.; Fumin, Z. A non-iterative calibration method for the extrinsic parameters of binocular stereo vision considering the line constraints. Measurement 2022, 205, 112151. [Google Scholar] [CrossRef]
- Pan, B.; Yu, L.; Wu, D.; Tang, L. Systematic errors in two-dimensional digital image correlation due to lens distortion. Opt. Lasers Eng. 2013, 51, 140–147. [Google Scholar] [CrossRef]
- Claus, D.; Fitzgibbon, A.W. A rational function lens distortion model for general cameras. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 213–219. [Google Scholar]
- Jia, Z.; Yang, J.; Liu, W.; Wang, F.; Liu, Y.; Wang, L.; Fan, C.; Zhao, K. Improved camera calibration method based on perpendicularity compensation for binocular stereo vision measurement system. Opt. Express 2015, 23, 15205–15223. [Google Scholar] [CrossRef] [PubMed]
- Kytö, M.; Nuutinen, M.; Oittinen, P. Method for measuring stereo camera depth accuracy based on stereoscopic vision. In Proceedings of the Three-Dimensional Imaging, Interaction, and Measurement, San Francisco, CA, USA, 24–27 January 2011; Volume 7864, pp. 168–176. [Google Scholar]
- Kopparapu, S.; Corke, P. The effect of noise on camera calibration parameters. Graph. Model. 2001, 63, 277–303. [Google Scholar] [CrossRef]
- Su, Z.; Pan, J.; Zhang, S.; Wu, S.; Yu, Q.; Zhang, D. Characterizing dynamic deformation of marine propeller blades with stroboscopic stereo digital image correlation. Mech. Syst. Signal Process. 2022, 162, 108072. [Google Scholar] [CrossRef]
- Williams, K.; Rooper, C.N.; De Robertis, A.; Levine, M.; Towler, R. A method for computing volumetric fish density using stereo cameras. J. Exp. Mar. Biol. Ecol. 2018, 508, 21–26. [Google Scholar] [CrossRef]
- Pi, S.; He, B.; Zhang, S.; Nian, R.; Shen, Y.; Yan, T. Stereo visual SLAM system in underwater environment. In Proceedings of the OCEANS 2014-TAIPEI, Taipei, Taiwan, 7–10 April 2014; pp. 1–5. [Google Scholar]
- Xu, Y.; Zhao, Y.; Wu, F.; Yang, K. Error analysis of calibration parameters estimation for binocular stereo vision system. In Proceedings of the 2013 IEEE International Conference on Imaging Systems and Techniques (IST), Beijing, China, 22–23 October 2013; pp. 317–320. [Google Scholar]
- Li, X.; Gao, S.; Yang, Y.; Liang, J. The geometrical analysis of localization error characteristic in stereo vision systems. Rev. Sci. Instrum. 2021, 92, 015122. [Google Scholar] [CrossRef]
- Gao, S.; Chen, X.; Wu, X.; Zeng, T.; Xie, X. Analysis of Ranging Error of Parallel Binocular Vision System. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 13–16 October 2020; pp. 621–625. [Google Scholar] [CrossRef]
- Zhang, M.; Cui, J.; Zhang, F.; Yang, N.; Li, Y.; Li, F.; Deng, Z. Research on evaluation method of stereo vision measurement system based on parameter-driven. Optik 2021, 245, 167737. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Q.; Ye, Q.; Yu, D.; Yu, Z.; Liu, Y. A binocular vision-based underwater object size measurement paradigm: Calibration-Detection-Measurement (CDM). Measurement 2023, 216, 112997. [Google Scholar] [CrossRef]
- Llorca, D.F.; Sotelo, M.A.; Parra, I.; Ocaña, M.; Bergasa, L.M. Error analysis in a stereo vision-based pedestrian detection sensor for collision avoidance applications. Sensors 2010, 10, 3741–3758. [Google Scholar] [CrossRef]
- Zhang, T.; Boult, T. Realistic stereo error models and finite optimal stereo baselines. In Proceedings of the 2011 IEEE Workshop on Applications of Computer Vision (WACV), Washington, DC, USA, 5–7 January 2011; pp. 426–433. [Google Scholar]
- Yongkang, L.; Wei, L.; Zhang, Y.; Junqing, L.; Weiqi, L.; Zhang, Y.; Hongwen, X.; Zhang, L. An error analysis and optimization method for combined measurement with binocular vision. Chin. J. Aeronaut. 2021, 34, 282–292. [Google Scholar]
- Gai, S.; Da, F.; Dai, X. A novel dual-camera calibration method for 3D optical measurement. Opt. Lasers Eng. 2018, 104, 126–134. [Google Scholar] [CrossRef]
- Xiang, R.; He, W.; Zhang, X.; Wang, D.; Shan, Y. Size measurement based on a two-camera machine vision system for the bayonets of automobile brake pads. Measurement 2018, 122, 106–116. [Google Scholar] [CrossRef]
- Li, Z.y.; Song, L.m.; Xi, J.t.; Guo, Q.h.; Zhu, X.j.; Chen, M.l. A stereo matching algorithm based on SIFT feature and homography matrix. Optoelectron. Lett. 2015, 11, 390–394. [Google Scholar] [CrossRef]
- Tong, Z.; Gu, L.; Shao, X. Refraction error analysis in stereo vision for system parameters optimization. Measurement 2023, 222, 113650. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, W.; Wang, F.; Lu, Y.; Wang, W.; Yang, F.; Jia, Z. Improved separated-parameter calibration method for binocular vision measurements with a large field of view. Opt. Express 2020, 28, 2956–2974. [Google Scholar] [CrossRef]
- Huang, H.; Liu, J.; Liu, S.; Jin, P.; Wu, T.; Zhang, T. Error analysis of a stereo-vision-based tube measurement system. Measurement 2020, 157, 107659. [Google Scholar] [CrossRef]
- Zhou, Y.; Rupnik, E.; Meynard, C.; Thom, C.; Pierrot-Deseilligny, M. Simulation and analysis of photogrammetric UAV image blocks—Influence of camera calibration error. Remote Sens. 2019, 12, 22. [Google Scholar] [CrossRef]
- Zilly, F.; Kluger, J.; Kauff, P. Production rules for stereo acquisition. Proc. IEEE 2011, 99, 590–606. [Google Scholar] [CrossRef]
- Sha, O.; Zhang, H.; Bai, J.; Zhang, Y.; Yang, J. The analysis of the structural parameter influences on measurement errors in a binocular 3D reconstruction system: A portable 3D system. PeerJ Comput. Sci. 2023, 9, e1610. [Google Scholar] [CrossRef]
- Liu, X.; Chen, W.; Madhusudanan, H.; Du, L.; Sun, Y. Camera orientation optimization in stereo vision systems for low measurement error. IEEE/ASME Trans. Mechatron. 2020, 26, 1178–1182. [Google Scholar] [CrossRef]
- Yang, L.; Wang, B.; Zhang, R.; Zhou, H.; Wang, R. Analysis on location accuracy for the binocular stereo vision system. IEEE Photonics J. 2017, 10, 7800316. [Google Scholar] [CrossRef]



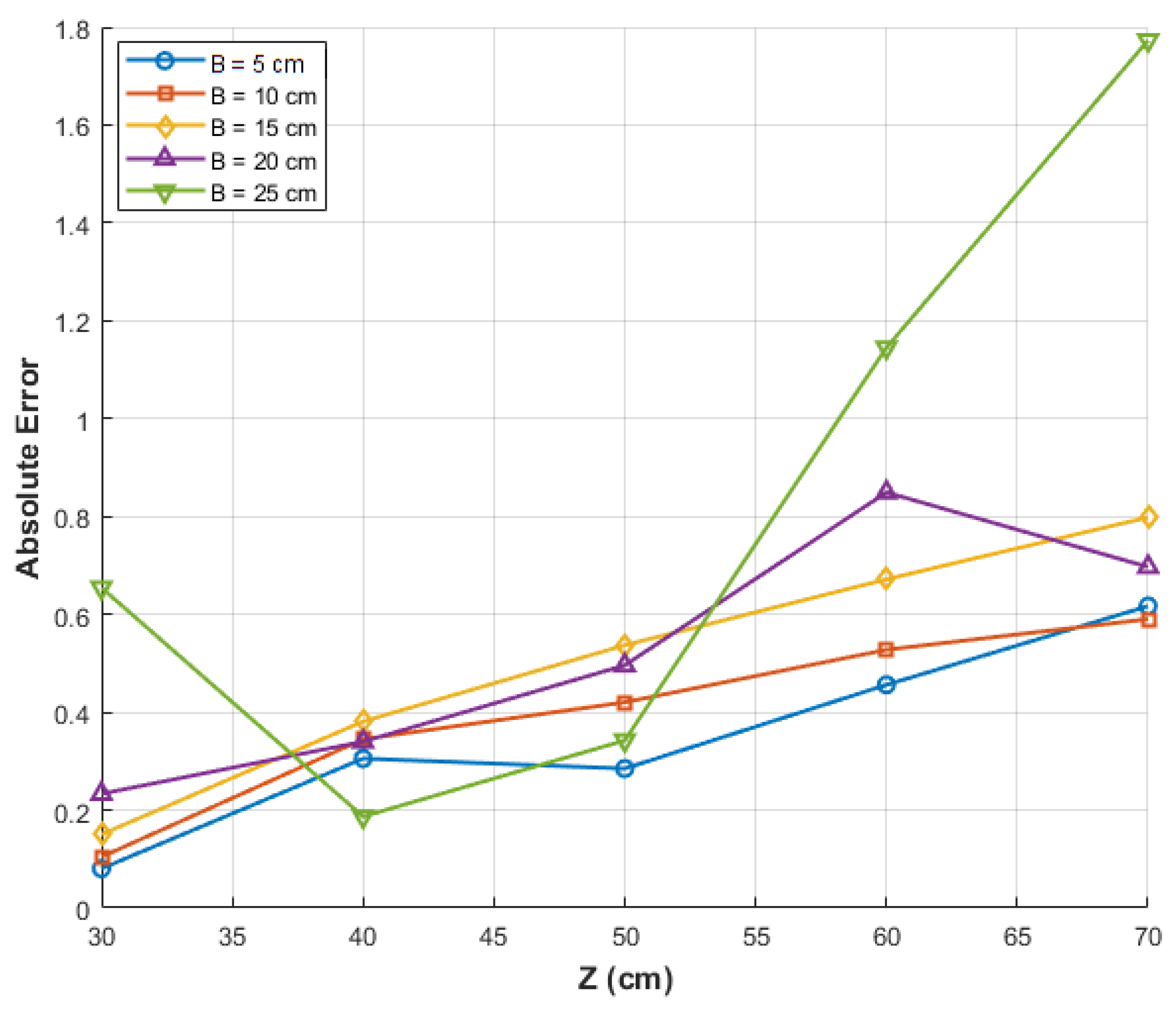

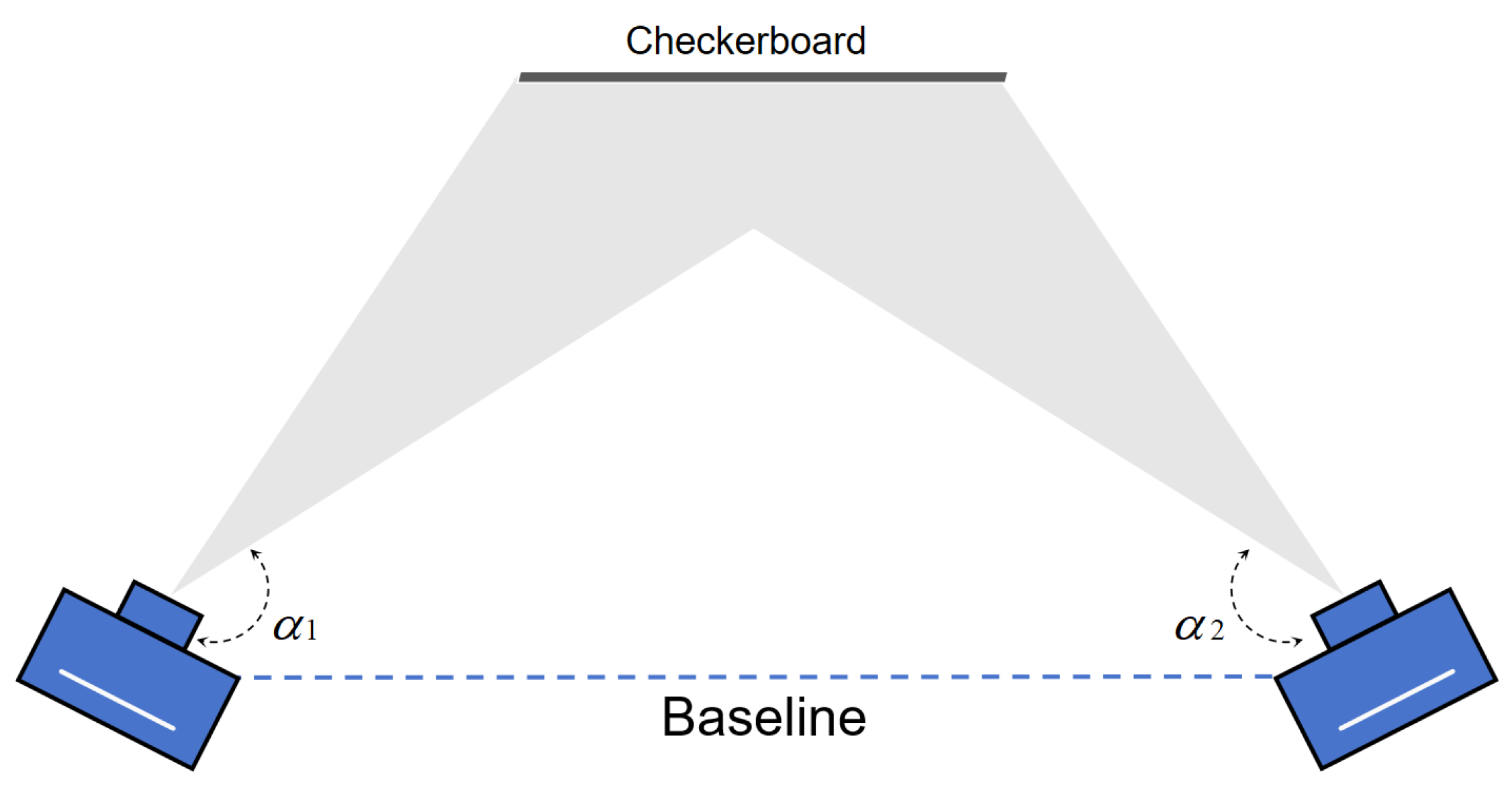

| B/Z | 30 cm | 40 cm | 50 cm | 60 cm | 70 cm |
|---|---|---|---|---|---|
| 5 cm | 26.9195 mm | 27.3054 mm | 26.7151 mm | 26.5440 mm | 26.3830 mm |
| 10 cm | 27.1043 mm | 26.6551 mm | 26.5797 mm | 26.4722 mm | 26.4097 mm |
| 15 cm | 27.1504 mm | 26.6189 mm | 26.4629 mm | 26.3282 mm | 26.2018 mm |
| 20 cm | 26.7665 mm | 26.6601 mm | 27.4959 mm | 27.8492 mm | 26.3031 mm |
| 25 cm | 27.6544 mm | 26.8131 mm | 26.6576 mm | 25.8550 mm | 28.7729 mm |
| Angle | 5° | 15° | 25° | 35° | 45° | 55° |
|---|---|---|---|---|---|---|
| result | 28.0896 mm | 26.3043 mm | 26.7151 mm | 27.1043 mm | 27.3276 mm | 27.433 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Qiu, Y.; Wang, X.; Gu, J.; Xiao, P. System Structural Error Analysis in Binocular Vision Measurement Systems. J. Mar. Sci. Eng. 2024, 12, 1610. https://doi.org/10.3390/jmse12091610
Yang M, Qiu Y, Wang X, Gu J, Xiao P. System Structural Error Analysis in Binocular Vision Measurement Systems. Journal of Marine Science and Engineering. 2024; 12(9):1610. https://doi.org/10.3390/jmse12091610
Chicago/Turabian StyleYang, Miao, Yuquan Qiu, Xinyu Wang, Jinwei Gu, and Perry Xiao. 2024. "System Structural Error Analysis in Binocular Vision Measurement Systems" Journal of Marine Science and Engineering 12, no. 9: 1610. https://doi.org/10.3390/jmse12091610
APA StyleYang, M., Qiu, Y., Wang, X., Gu, J., & Xiao, P. (2024). System Structural Error Analysis in Binocular Vision Measurement Systems. Journal of Marine Science and Engineering, 12(9), 1610. https://doi.org/10.3390/jmse12091610







