Characteristics of Higher Harmonic Forces on Submerged Horizontal Cylinders with Sharp and Round Corners
Abstract
:1. Introduction
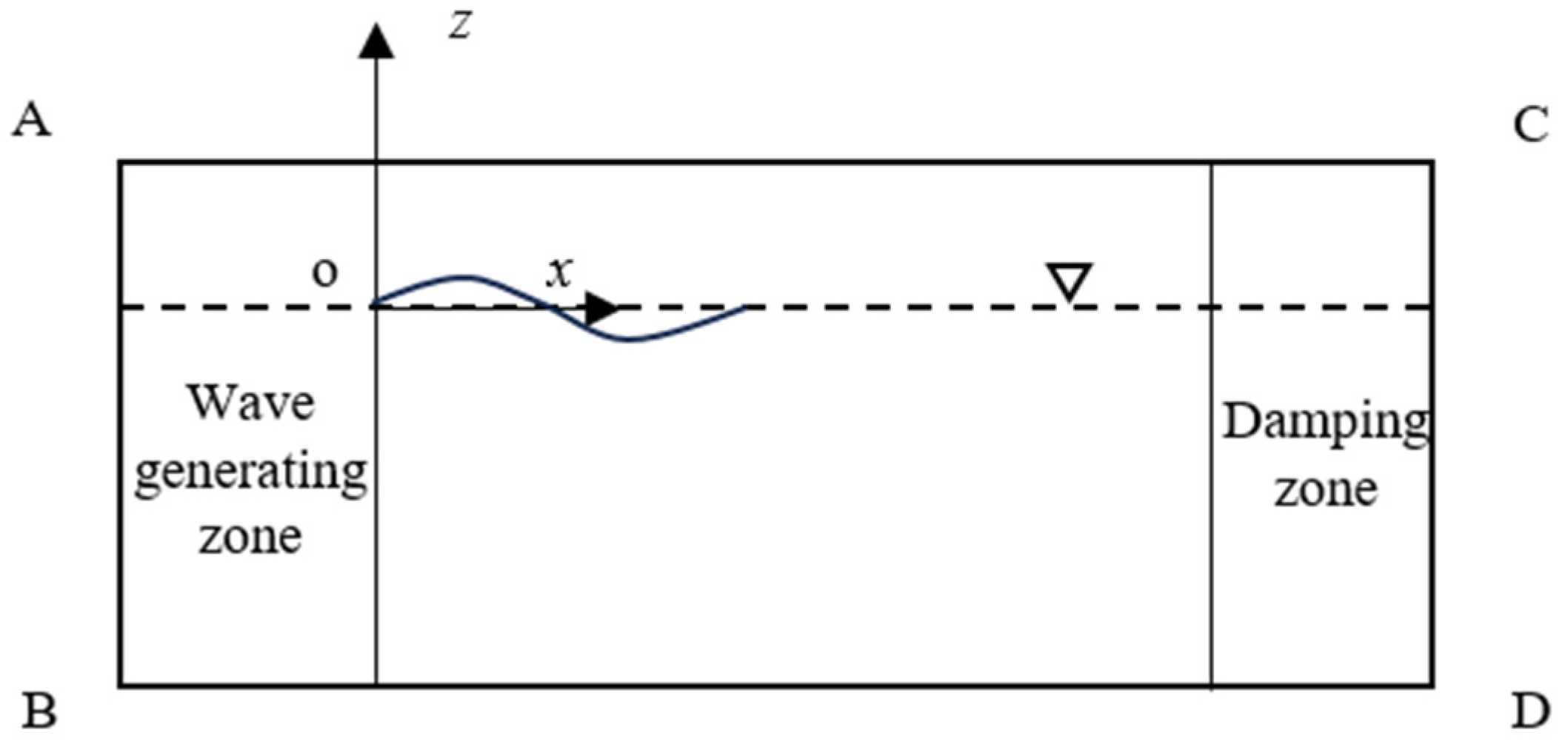
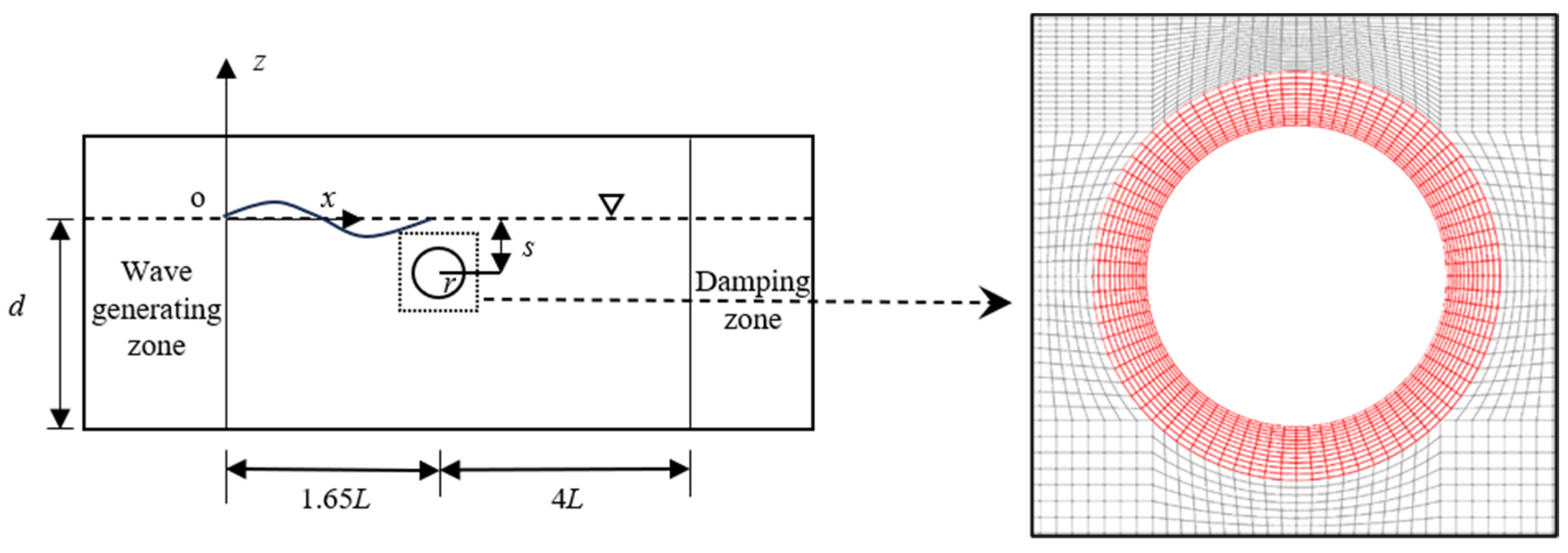
2. Mathematical Model
3. Numerical Verification
3.1. Grid Convergence Verification
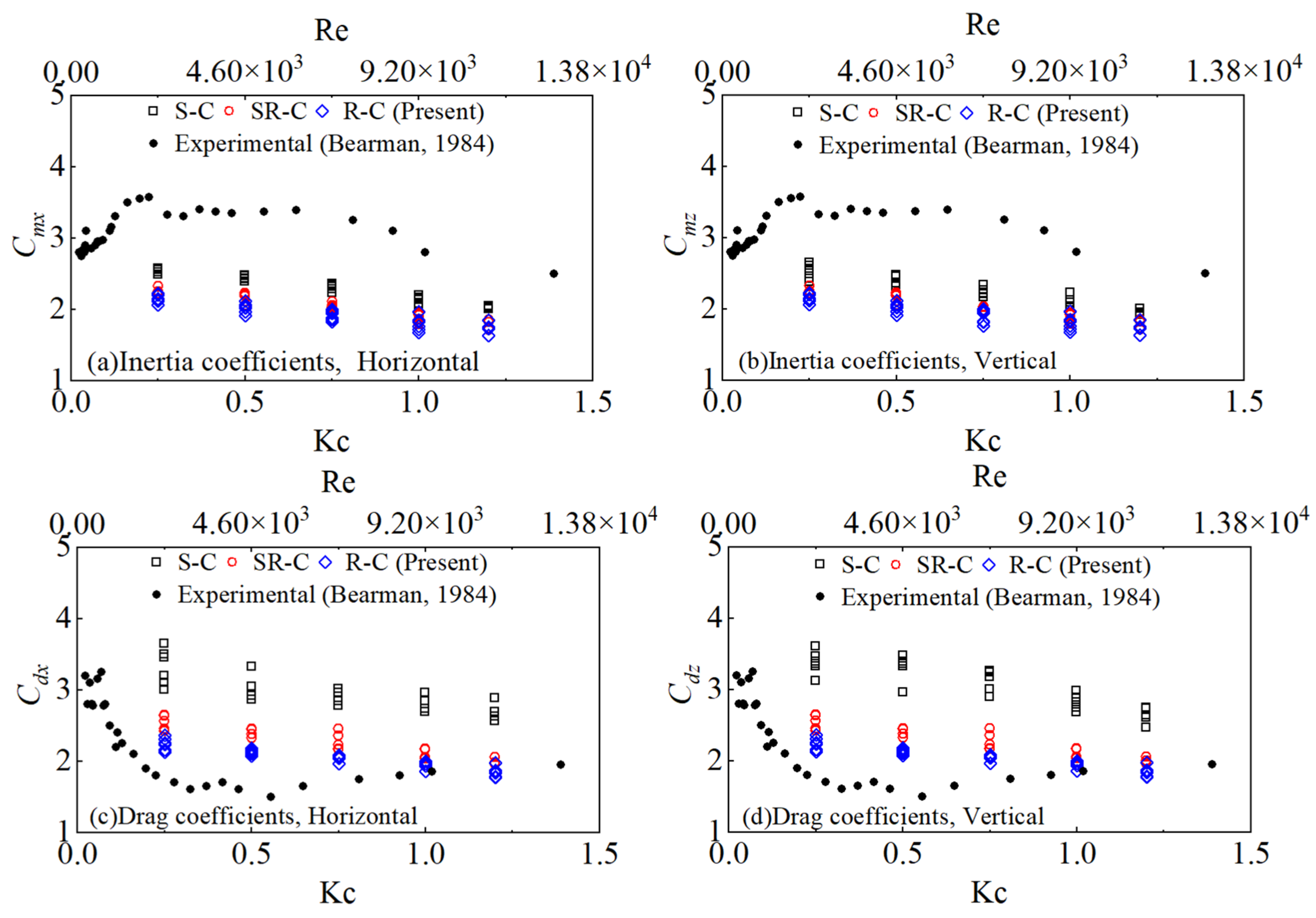
3.2. Verification of Wave Force Calculation
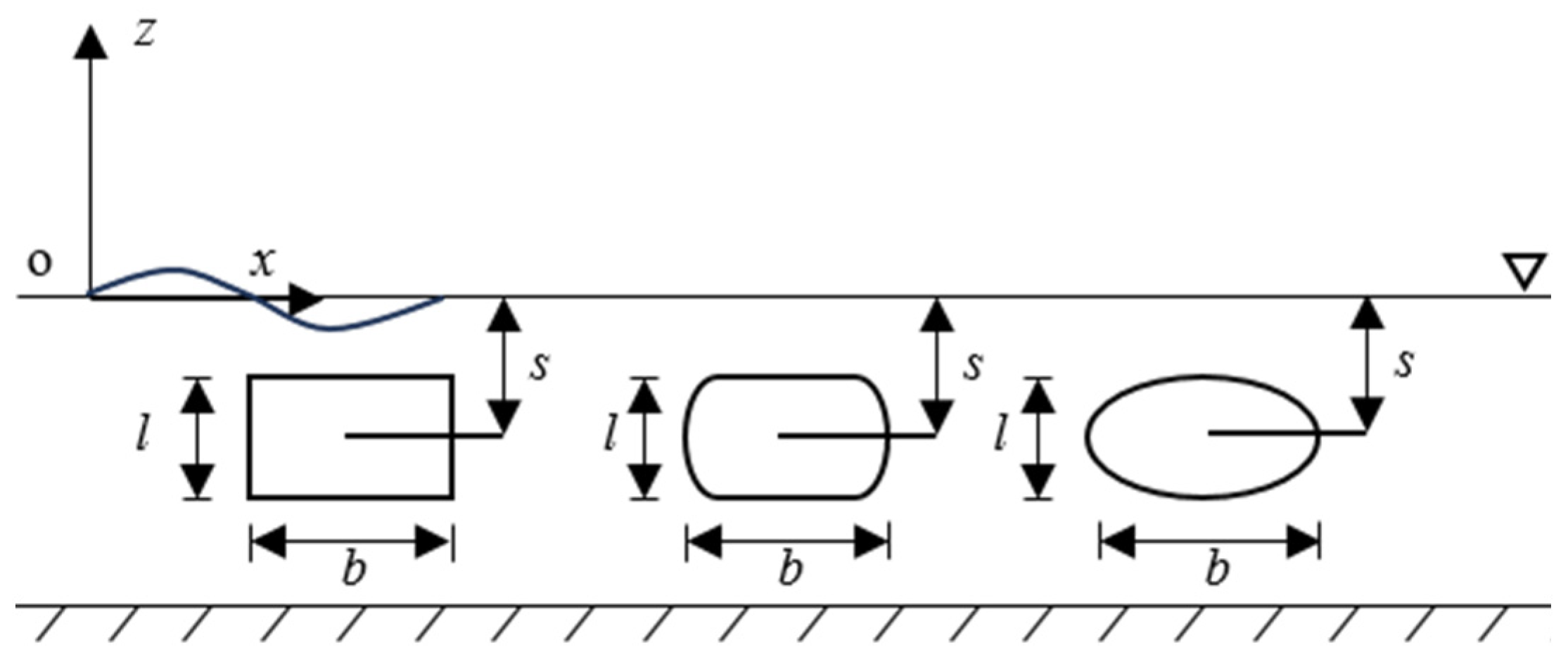
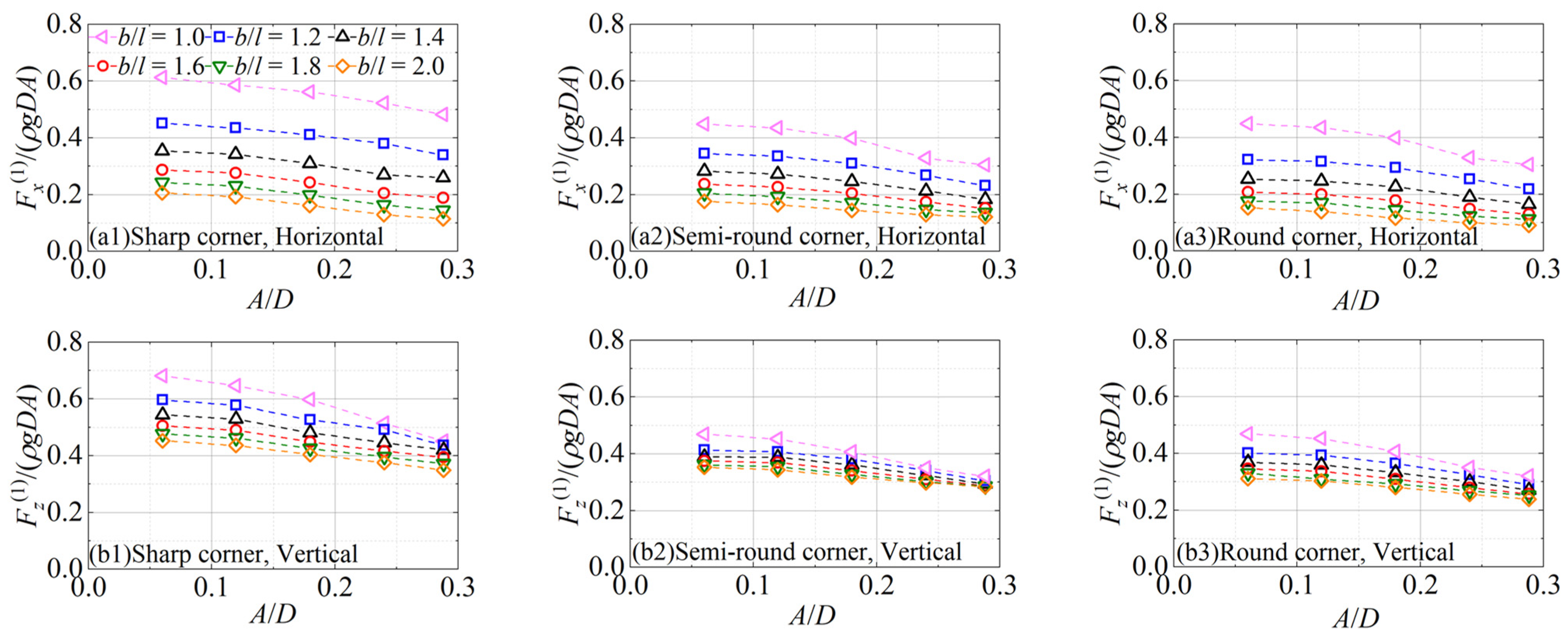
4. Wave Force on Cylinders with Various Section Corners and Aspect Ratios
4.1. Calculation Settings and Parameters
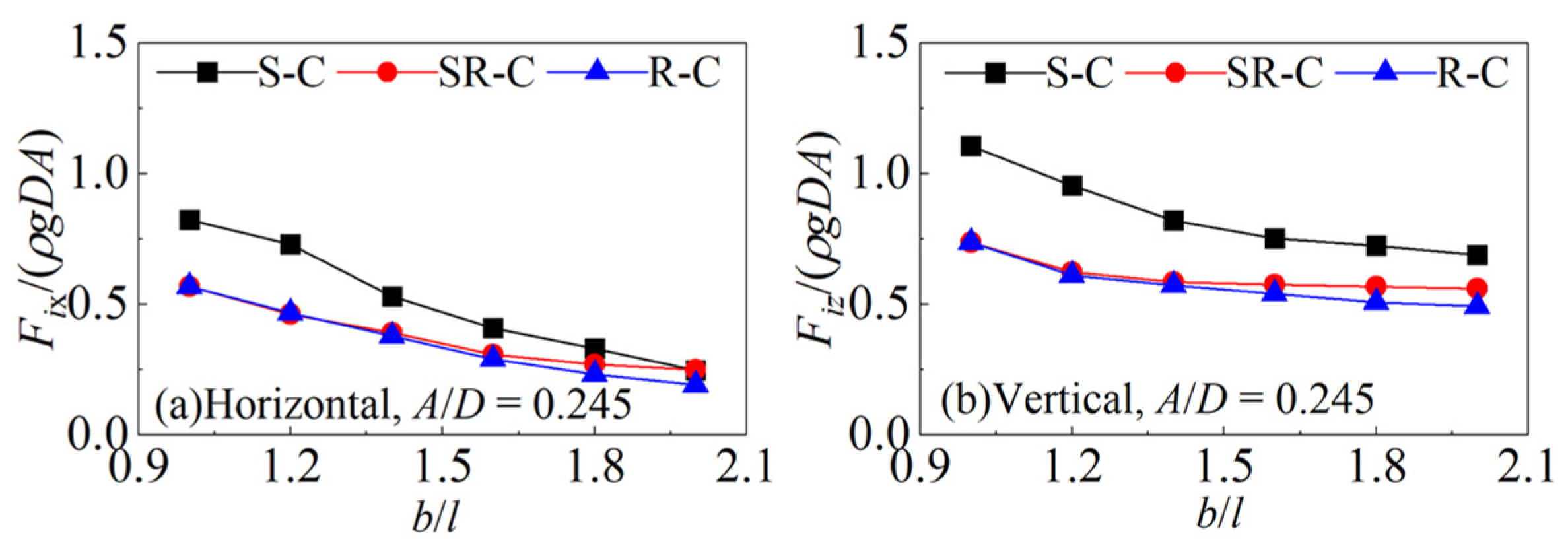
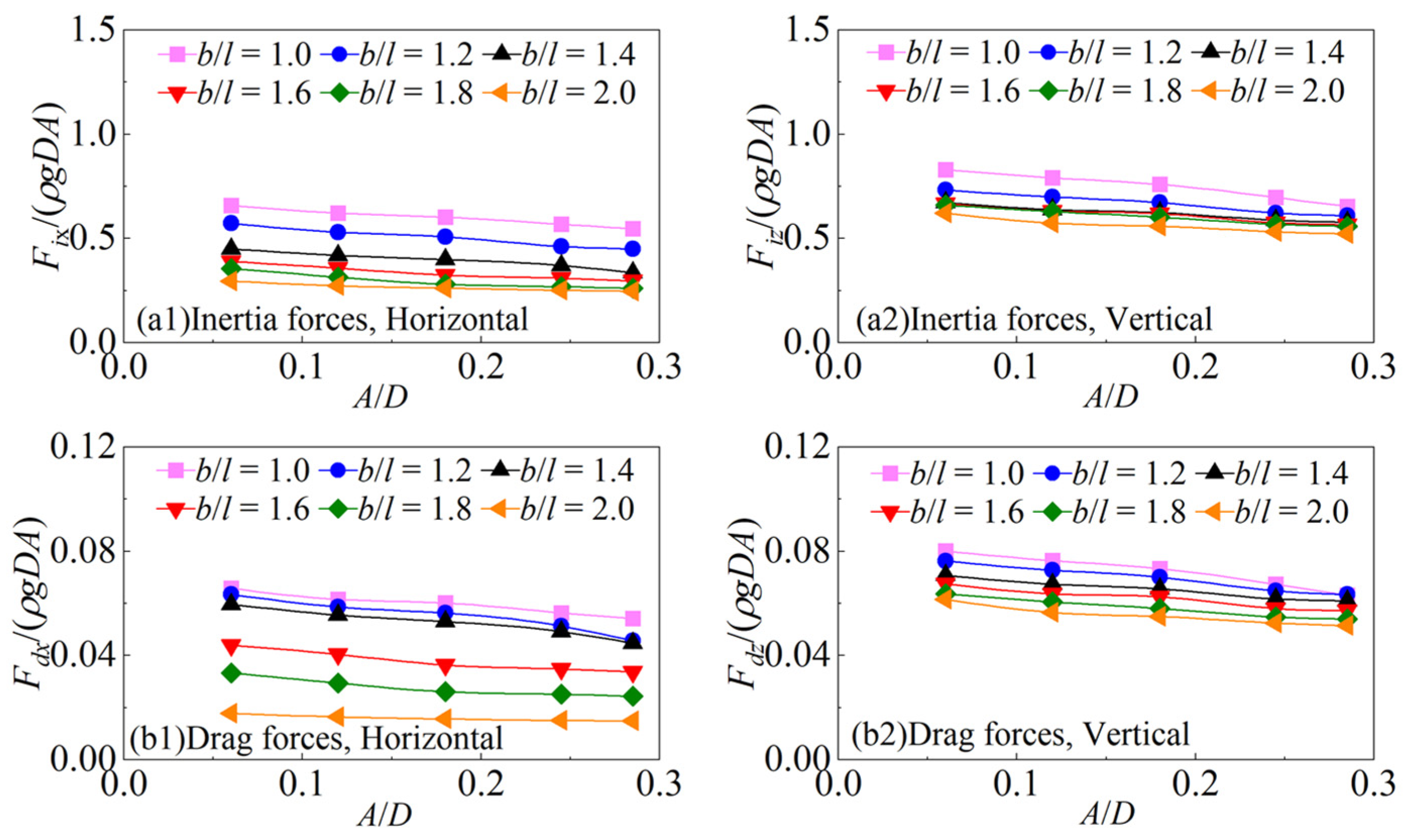
4.2. Wave Force Results
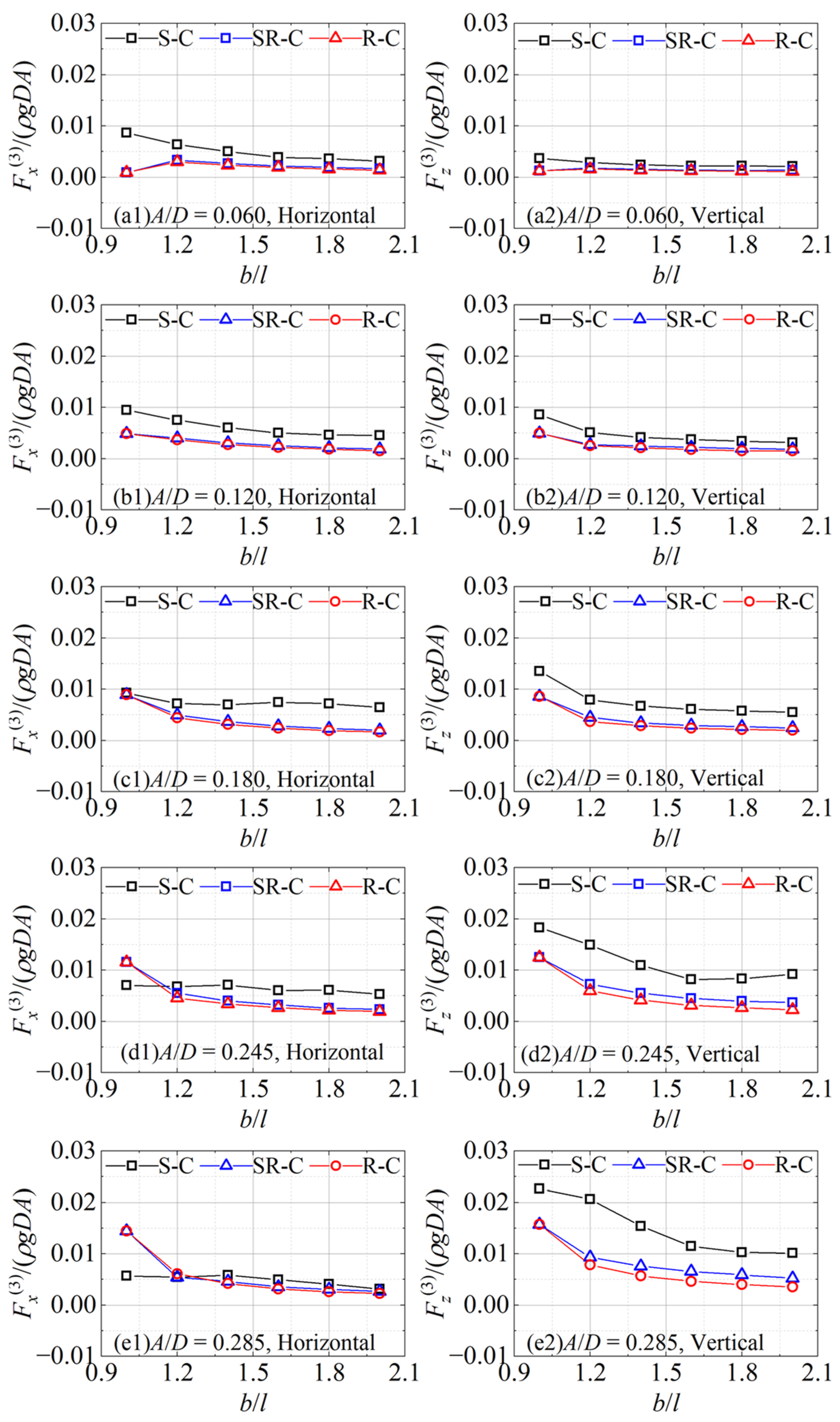
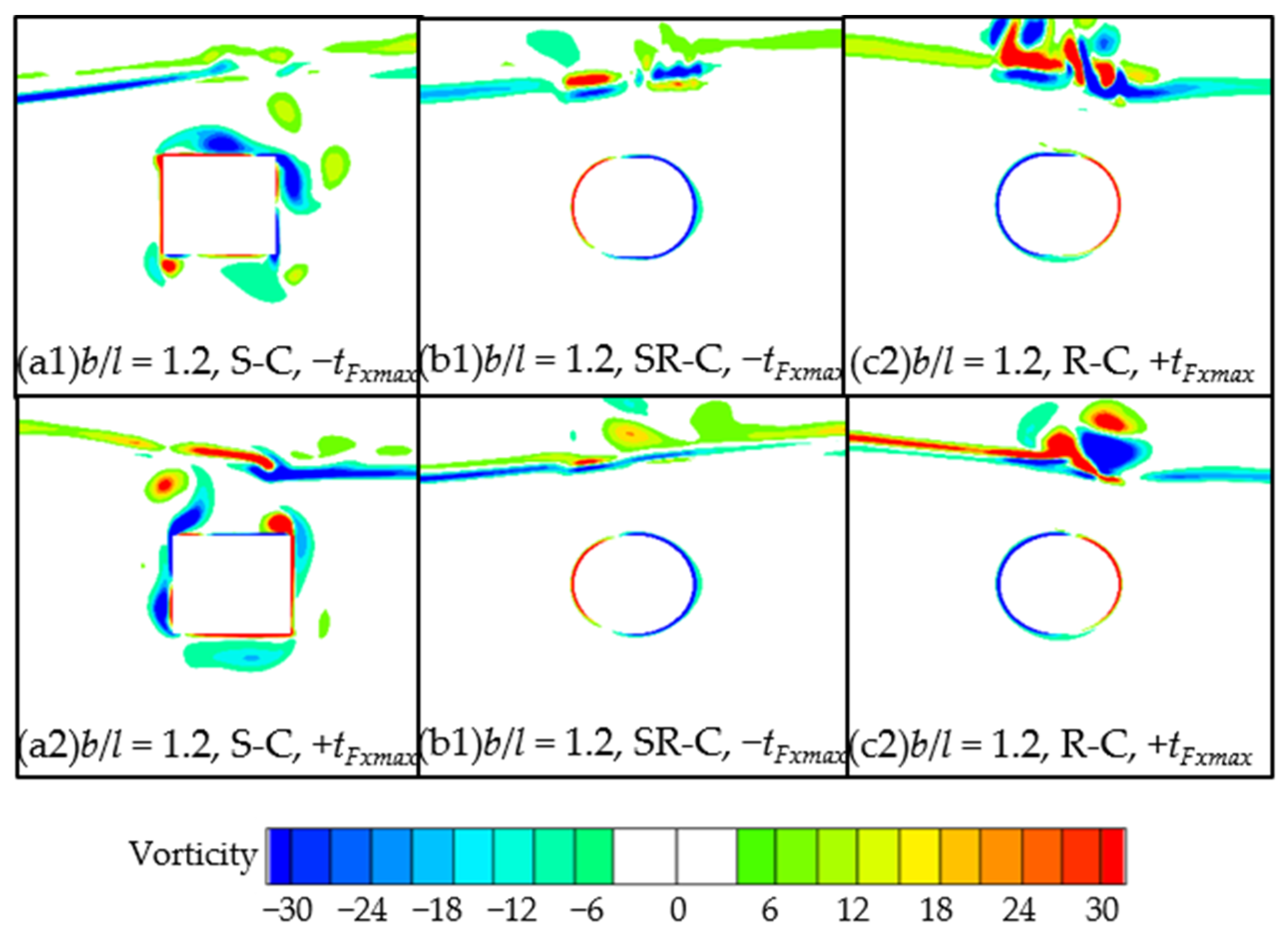
5. Viscous Flow Field and Force Decomposition
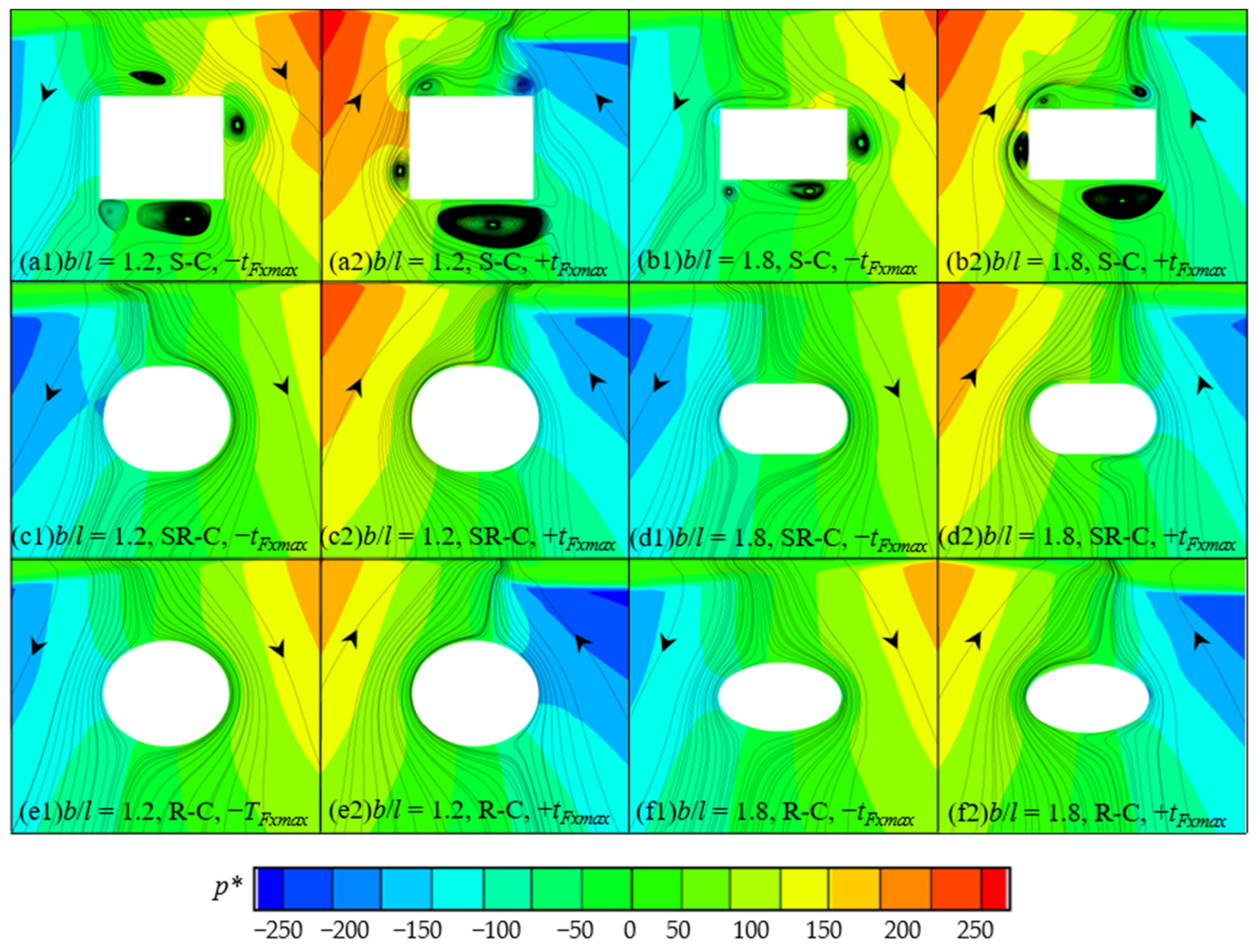
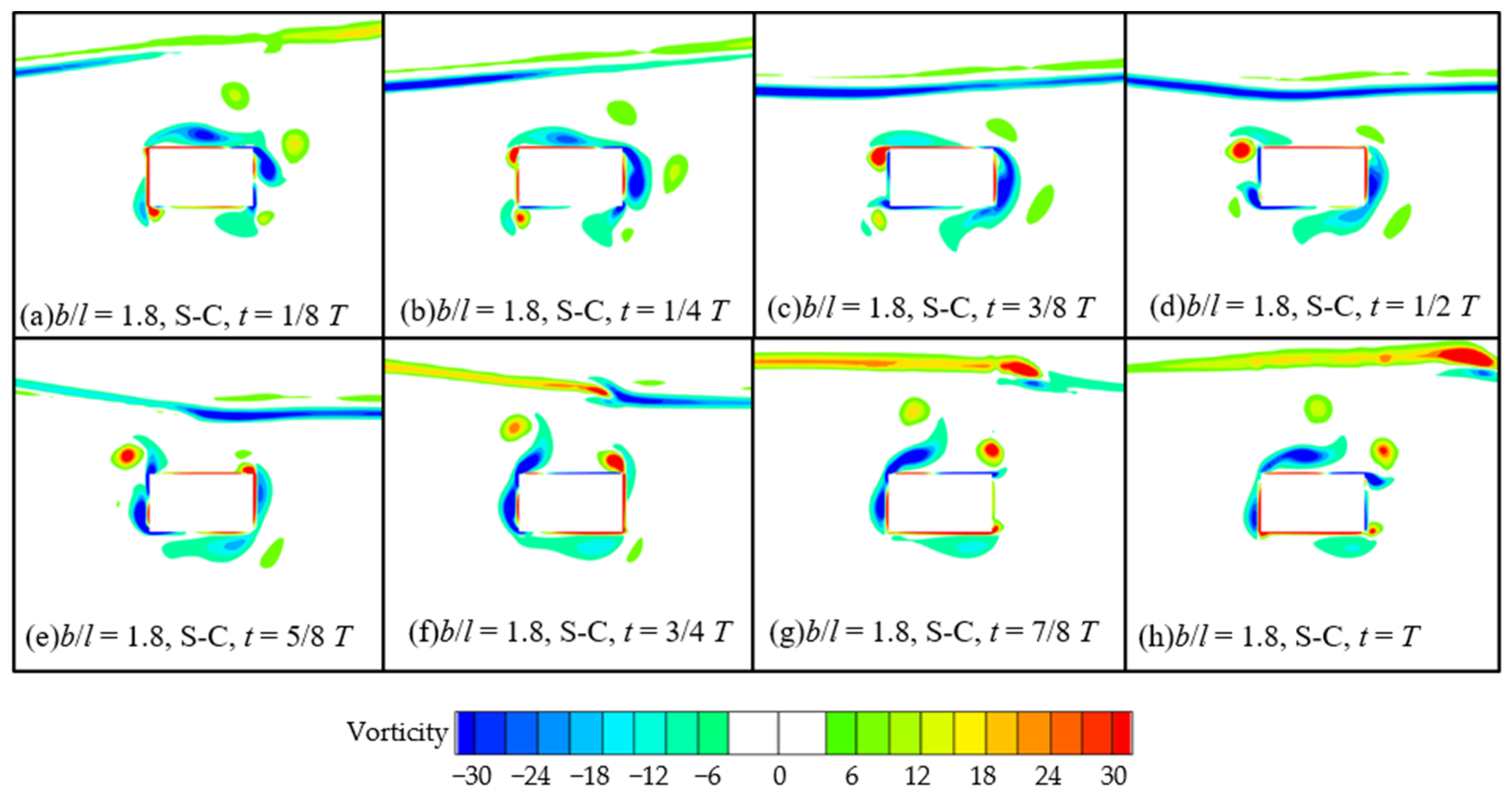
5.1. Flow Field Distribution
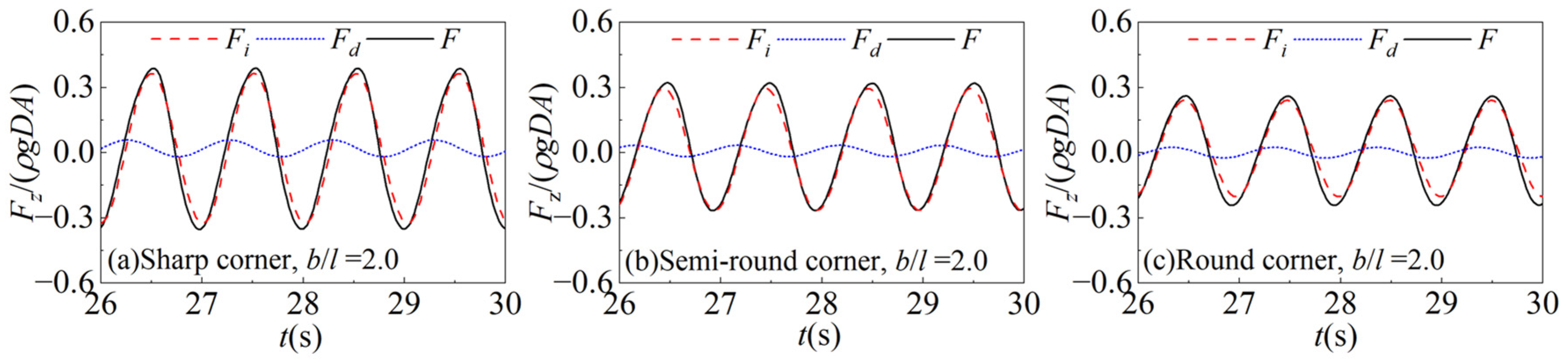
5.2. Decomposition of Wave Force
6. Conclusions
- (1)
- There are similar flow field distributions around the semi-round-corner and round-corner cylinders, while the complex and stronger vortices generated around the sharp-corner cylinder cause a significant difference in the pressure distribution. This leads to larger inertia forces, and larger second and third harmonic forces.
- (2)
- Some vortices are generated from the wave action on the submerged horizontal cylinders rotating periodically clockwise around the cylinder. This contributes to the significant nonlinear effect in the higher harmonic forces, especially on the sharp-corner cylinder, and this effect generally becomes greater with the decrease in the aspect ratio.
- (3)
- The hydrodynamic coefficients for the cases of the sharp-corner cylinder are relatively larger, and the coefficients on the round-corner cylinder are relatively smaller. The inertia and drag coefficients increase with the increase in the Kc and Re numbers. The present maximum inertia and drag coefficients, Cm = 2.68 and Cd = 3.65, are different from those in the previous studies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chaplin, J.R. Nonlinear forces on a horizontal cylinder beneath waves. J. Fluid Mech. 1984, 147, 449–464. [Google Scholar] [CrossRef]
- Wang, S.D.; Wei, G.; Du, H.; Wu, J.L.; Wang, X.L. Experimental investigation of the wave-flow structure of an oblique internal solitary wave and its force exerted on a slender body. Ocean Eng. 2020, 201, 107057. [Google Scholar] [CrossRef]
- Wang, S.; Du, H.; Wei, G.; Peng, P.; Xuan, P. Experimental modification of the internal solitary wave force exerted on a horizontal transverse cylinder due to wave-flow and vortex shedding. Ocean Eng. 2023, 269, 113513. [Google Scholar] [CrossRef]
- Feng, X. Analysis of higher harmonics in a focused water wave group by a nonlinear potential flow model. Ocean Eng. 2019, 193, 106581. [Google Scholar] [CrossRef]
- Feng, X.; Taylor, P.H.; Dai, S.; Day, A.H.; Willden, R.H.J.; Adcock, T.A.A. Experimental investigation of higher harmonic wave loads and moments on a vertical cylinder by a phase-manipulation method. Coast. Eng. 2020, 160, 103747. [Google Scholar] [CrossRef]
- Hu, J.; Lin, Y.H.; Maza, M. A semi-analytical theory for water waves interacting with a submerged/suspended circular cylinder patch. Ocean Eng. 2022, 247, 110667. [Google Scholar] [CrossRef]
- Tavassoli, A.; Kim, M.H. Interactions of fully nonlinear waves with submerged bodies by a 2D viscous NWT. In Proceedings of the International Ocean and Polar Engineering Conference, ISOPE-I-01-286, Stavanger, Norway, 17–22 June 2001. [Google Scholar]
- Teng, B.; Mao, H.F.; Lu, L. Viscous effects on wave forces on a submerged horizontal circular cylinder. China Ocean Eng. 2018, 32, 245–255. [Google Scholar] [CrossRef]
- Gu, F.; Huang, Y.; Zhang, D. Cavitation of multiscale vortices in circular cylinder wake at Re = 9500. J. Mar. Sci. Eng. 2021, 9, 1366. [Google Scholar] [CrossRef]
- Zhou, X.; Jiang, Q.; Wang, Y.; Chen, L.; Wang, S.; Wang, K. Numerical Simulation of Wave–Current Force Characteristics of Horizontal Floating Cylinder in Heave Motion. J. Mar. Sci. Eng. 2022, 10, 1884. [Google Scholar] [CrossRef]
- Zhou, X.; Jiang, Q.; Wang, K.; Wang, S. Analysis of Horizontal Cylinder Load under Different Conditions in Regards to Waves and Flows. J. Mar. Sci. Eng. 2024, 12, 1101. [Google Scholar] [CrossRef]
- Ding, W.; Sun, H.; Zhao, X.; Ai, C. Numerical investigation of an internal solitary wave interaction with tandem horizontal cylinders. Ocean Eng. 2022, 246, 110658. [Google Scholar] [CrossRef]
- Selvan, S.A.; Gayathri, R.; Behera, H.; Meylan, M.H. Surface wave scattering by multiple flexible fishing cage system. Phys. Fluids 2021, 33, 037119. [Google Scholar] [CrossRef]
- Kushwaha, A.K.; Behera, H.; Gupta, V.K. Wave scattering by a circular cylinder over a porous bed. Arch. Appl. Mech. 2024, 94, 555–570. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, H.; Li, K.; Cheng, L.; Huang, B.; Ren, Q. Experimental Investigation of Wave-Induced Forces on a Large Quasi-Elliptical Cylinder during Extreme Events. J. Mar. Sci. Eng. 2022, 10, 540. [Google Scholar] [CrossRef]
- Venugopal, V.; Varyani, K.S.; Barltrop, N.D.P. Wave force coefficients for horizontally submerged rectangular cylinders. Ocean Eng. 2006, 33, 1669–1704. [Google Scholar] [CrossRef]
- Liu, J.; Guo, A.; Li, H. Analytical solution for the linear wave diffraction by a uniform vertical cylinder with an arbitrary smooth cross-section. Ocean Eng. 2016, 126, 163–175. [Google Scholar] [CrossRef]
- Liu, J.; Guo, A. Wave force identification for a large-scale quasi-elliptical cylinder from monitored wave elevation. Ocean Eng. 2023, 271, 113769. [Google Scholar] [CrossRef]
- Han, H.; Guo, Y.; Huo, R. Semi-analytical solution of transverse vibration of cylinders with non-circular cross-section partially submerged in water. J. Mar. Sci. Eng. 2023, 11, 872. [Google Scholar] [CrossRef]
- Chatjigeorgiou, I.K.; Katsardi, V. Hydrodynamics and near trapping effects in arrays of multiple elliptical cylinders in waves. Ocean Eng. 2018, 157, 121–139. [Google Scholar] [CrossRef]
- Chatjigeorgiou, I.K. Three dimensional wave scattering by arrays of elliptical and circular cylinders. Ocean Eng. 2011, 38, 1480–1494. [Google Scholar] [CrossRef]
- Ai, C.; Ma, Y.; Yuan, C.; Dong, G. Semi-implicit non-hydrostatic model for 2D nonlinear wave interaction with a floating/suspended structure. Eur. J. Mech.-B/Fluids 2018, 72, 545–560. [Google Scholar] [CrossRef]
- Chen, X.; Liang, J.H.; Xu, G.; Chen, Q. A study on the interaction between circular or elliptical cross-section submerged floating tunnels and elevation internal solitary waves. Ocean Eng. 2023, 285, 115291. [Google Scholar] [CrossRef]
- Ding, W.; Sun, H.; Zhao, X.; Ai, C. Numerical study of the interaction between an internal solitary wave and a submerged extended cylinder using OpenFOAM. Ocean Eng. 2023, 274, 113985. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFoam®. Int. J. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Hur, D.S.; Mizutani, N.; Kim, D.S. Direct 3-D numerical simulation of wave forces on asymmetric structures. Coast. Eng. 2004, 51, 407–420. [Google Scholar] [CrossRef]
- Hieu, P.D.; Katsutoshi, T.; Ca, V.T. Numerical simulation of breaking waves using a two-phase flow model. Appl. Math. Model. 2004, 28, 983–1005. [Google Scholar] [CrossRef]
- Fenton, J.D. A fifth-order Stokes theory for steady waves. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 216–234. [Google Scholar] [CrossRef]
- Brigham, E.O.; Morrow, R.E. The fast Fourier transform. Inst. Electr. Electron. Eng. Spectr. 1967, 4, 63–70. [Google Scholar] [CrossRef]
- Morison, J.R.; Johnson, J.W.; Schaaf, S.A. The force exerted by surface waves on piles. J. Pet. Tec. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Bearman, P.W.; Graham, J.M.R.; Obasaju, E.D.; Drossopoulos, G.M. The influence of corner radius on the forces experienced by cylindrical bluff bodies in oscillatory flow. Appl. Ocean Res. 1984, 6, 83–89. [Google Scholar] [CrossRef]
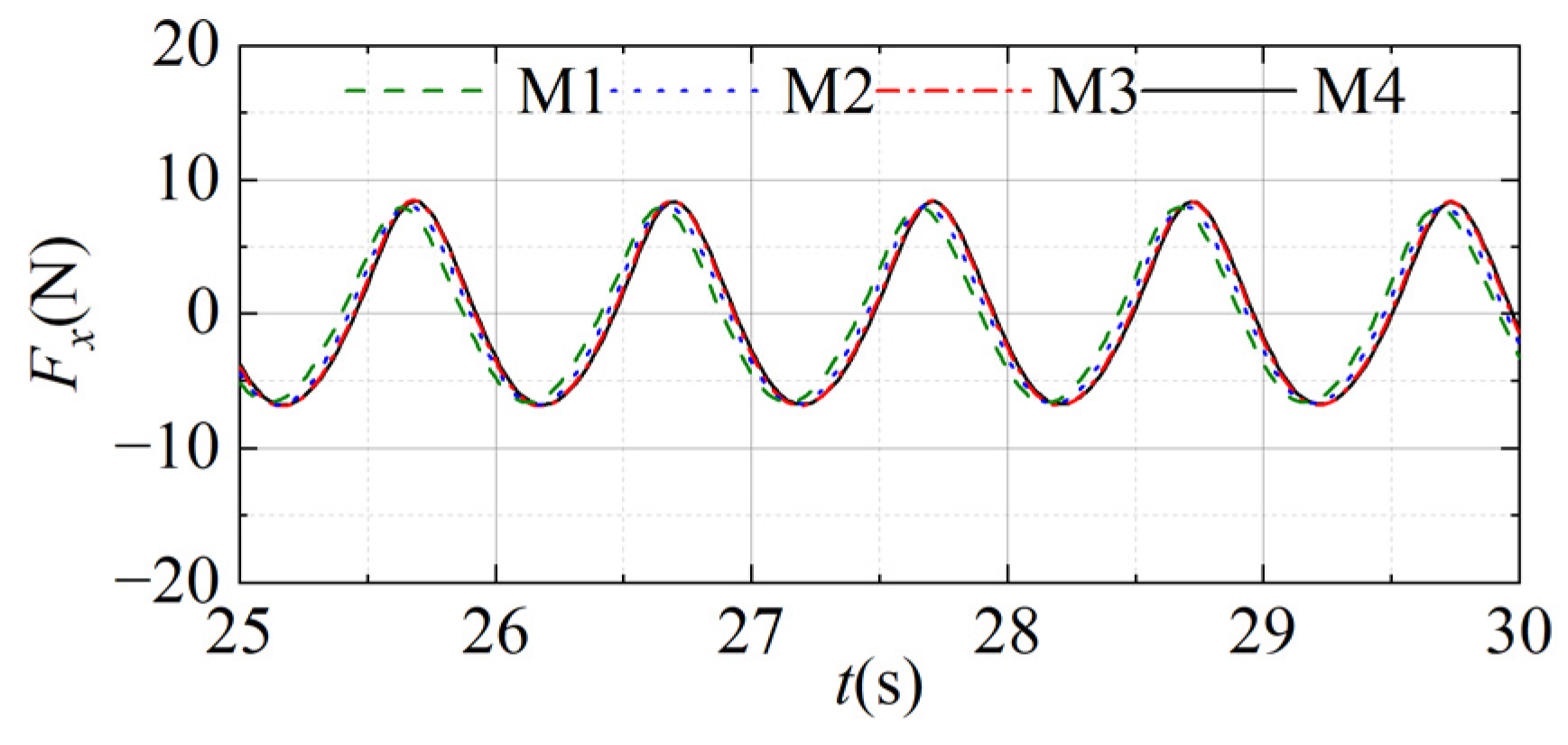




| Mesh Scheme | In a Wave Length | In a Wave Height | Along the Cylinder | In the Radial Direction |
|---|---|---|---|---|
| 1 | 50 | 10 | 40 | 6 |
| 2 | 75 | 15 | 56 | 8 |
| 3 | 100 | 20 | 72 | 14 |
| 4 | 120 | 24 | 96 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, H.; Zeng, J.; Wu, G.; Chen, H.; Zhang, S.; Yang, Y.; Yang, Q. Characteristics of Higher Harmonic Forces on Submerged Horizontal Cylinders with Sharp and Round Corners. J. Mar. Sci. Eng. 2024, 12, 1636. https://doi.org/10.3390/jmse12091636
Mao H, Zeng J, Wu G, Chen H, Zhang S, Yang Y, Yang Q. Characteristics of Higher Harmonic Forces on Submerged Horizontal Cylinders with Sharp and Round Corners. Journal of Marine Science and Engineering. 2024; 12(9):1636. https://doi.org/10.3390/jmse12091636
Chicago/Turabian StyleMao, Hongfei, Jinwen Zeng, Guanglin Wu, Hanqing Chen, Shuqin Zhang, Yuanting Yang, and Qinru Yang. 2024. "Characteristics of Higher Harmonic Forces on Submerged Horizontal Cylinders with Sharp and Round Corners" Journal of Marine Science and Engineering 12, no. 9: 1636. https://doi.org/10.3390/jmse12091636







