Influence of Bed Variations on Linear Wave Propagation beyond the Mild Slope Condition
Abstract
1. Introduction
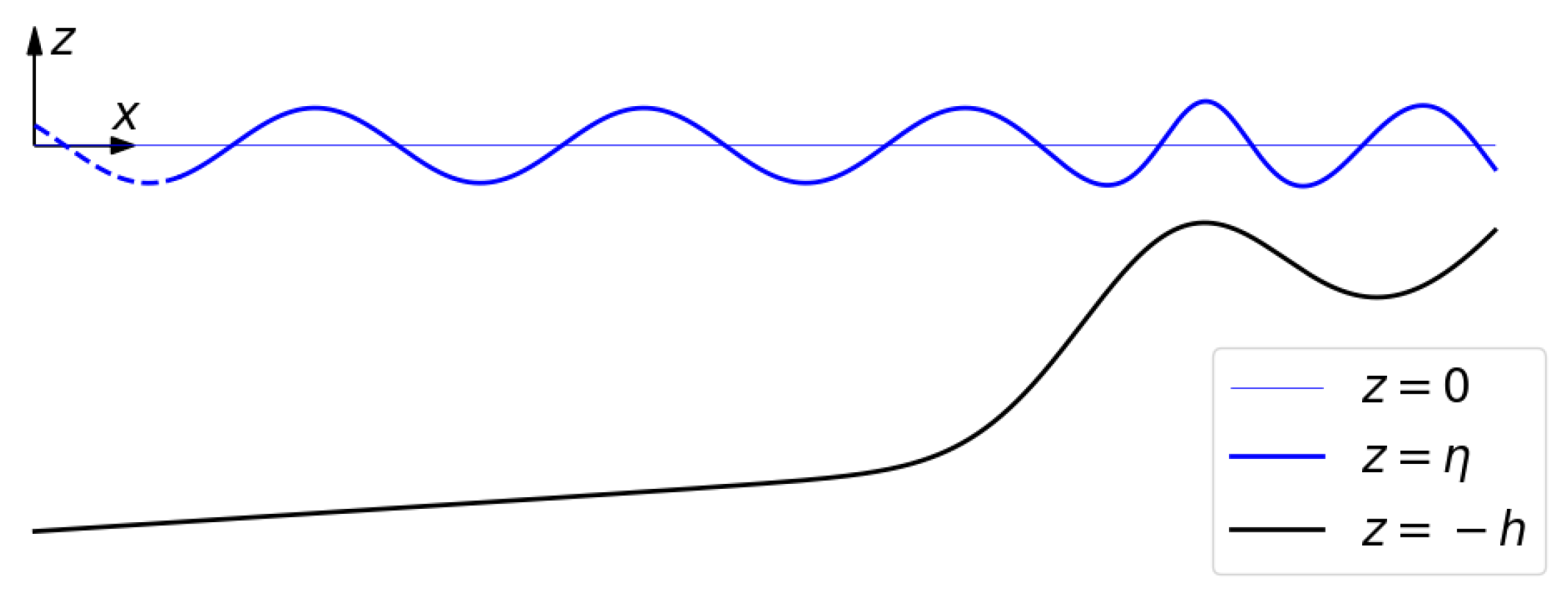
2. Governing Equations
2.1. Equations for Time-Harmonic Free-Surface Flows
2.2. The Imaginary Part: Vertical Profile of the Phase
3. The WKB Approximation
4. The Leading-Order Solution
4.1. Solution for the Equations
4.2. Spatial Derivatives
5. Solution to
5.1. The Vertical Profile of the Phase
5.2. Transmission and Reflections on a Ramp
6. Solution to
6.1. Equations for
6.2. Analytical solutions for
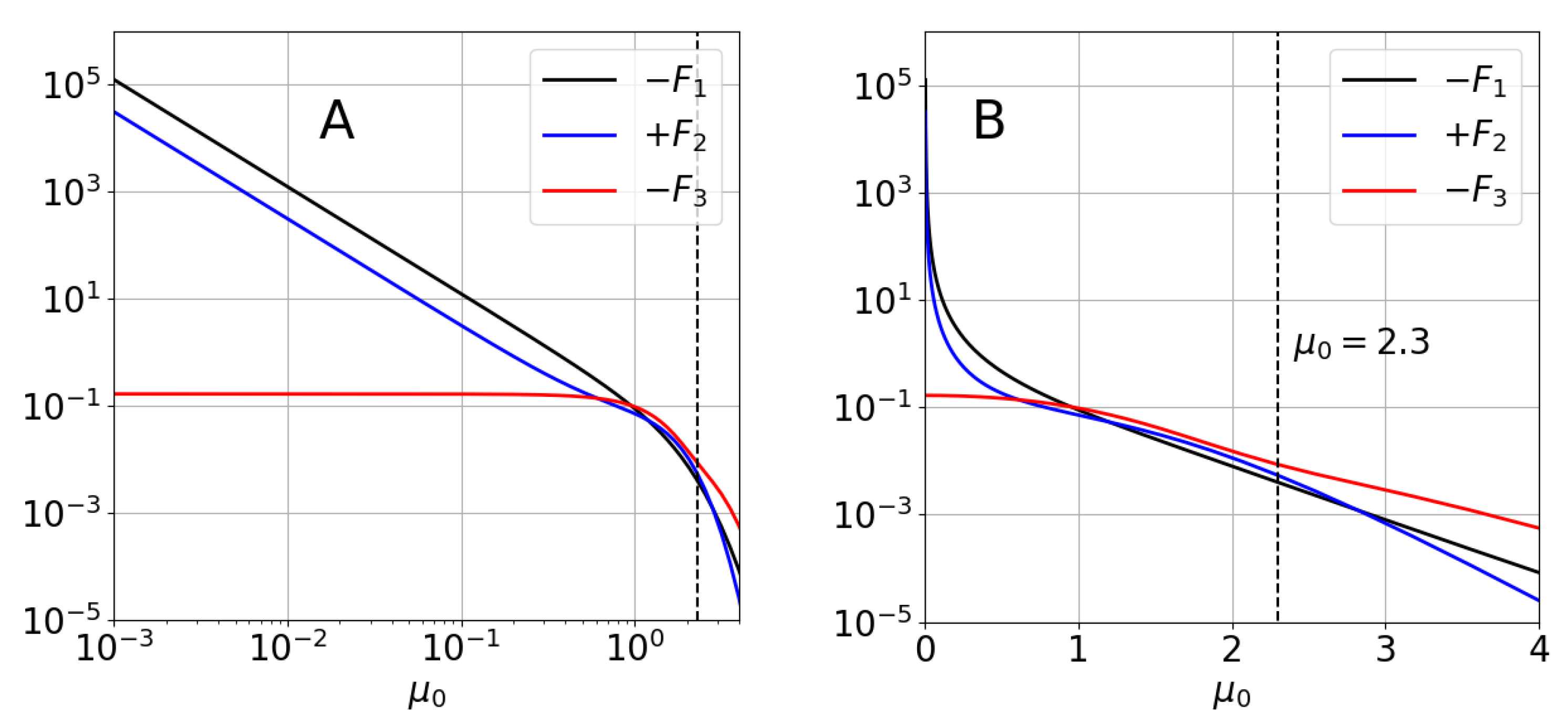
6.3. Numerical Solution for the General Case ()
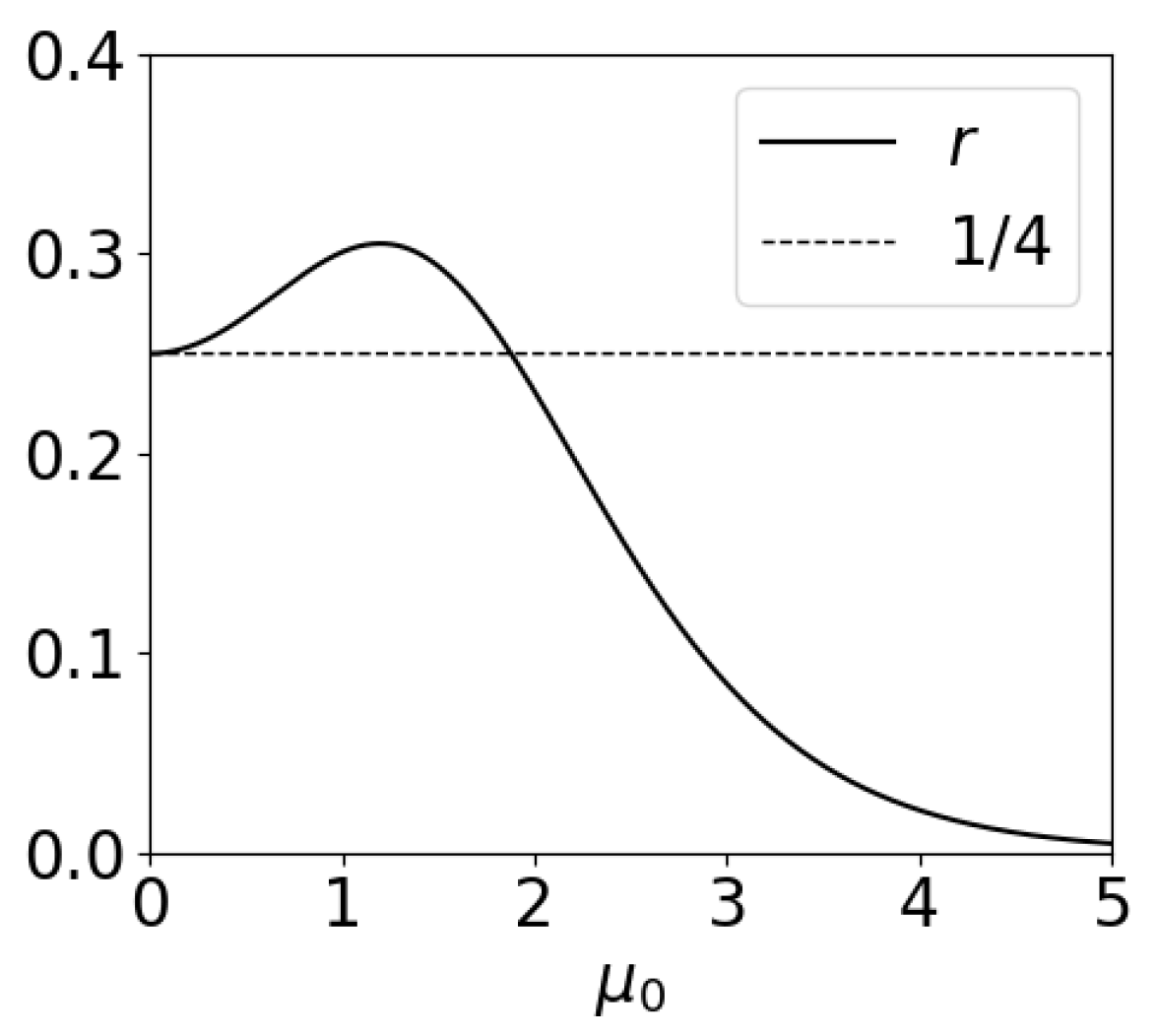
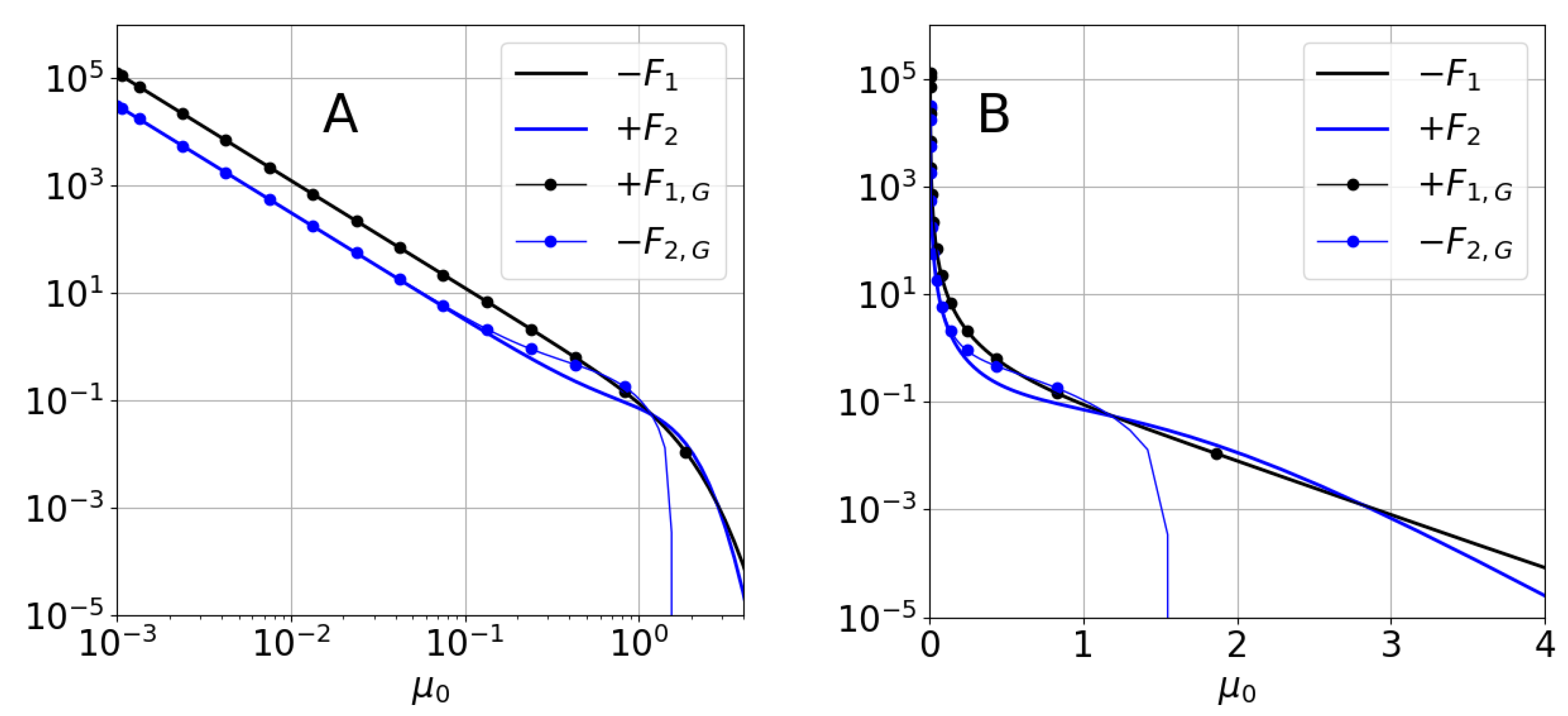
6.4. Comparison to the Expression by Ge et al. [29]
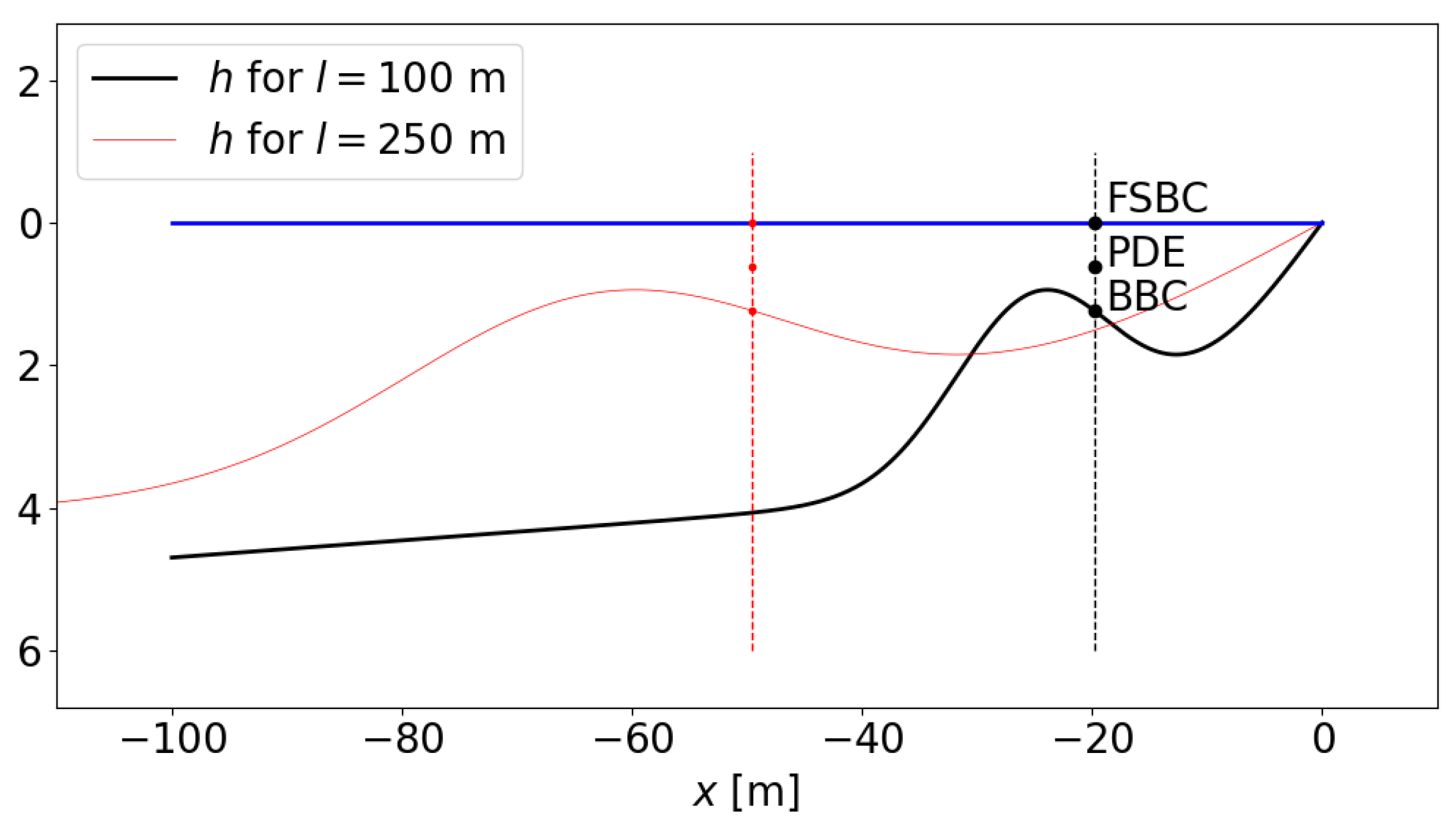
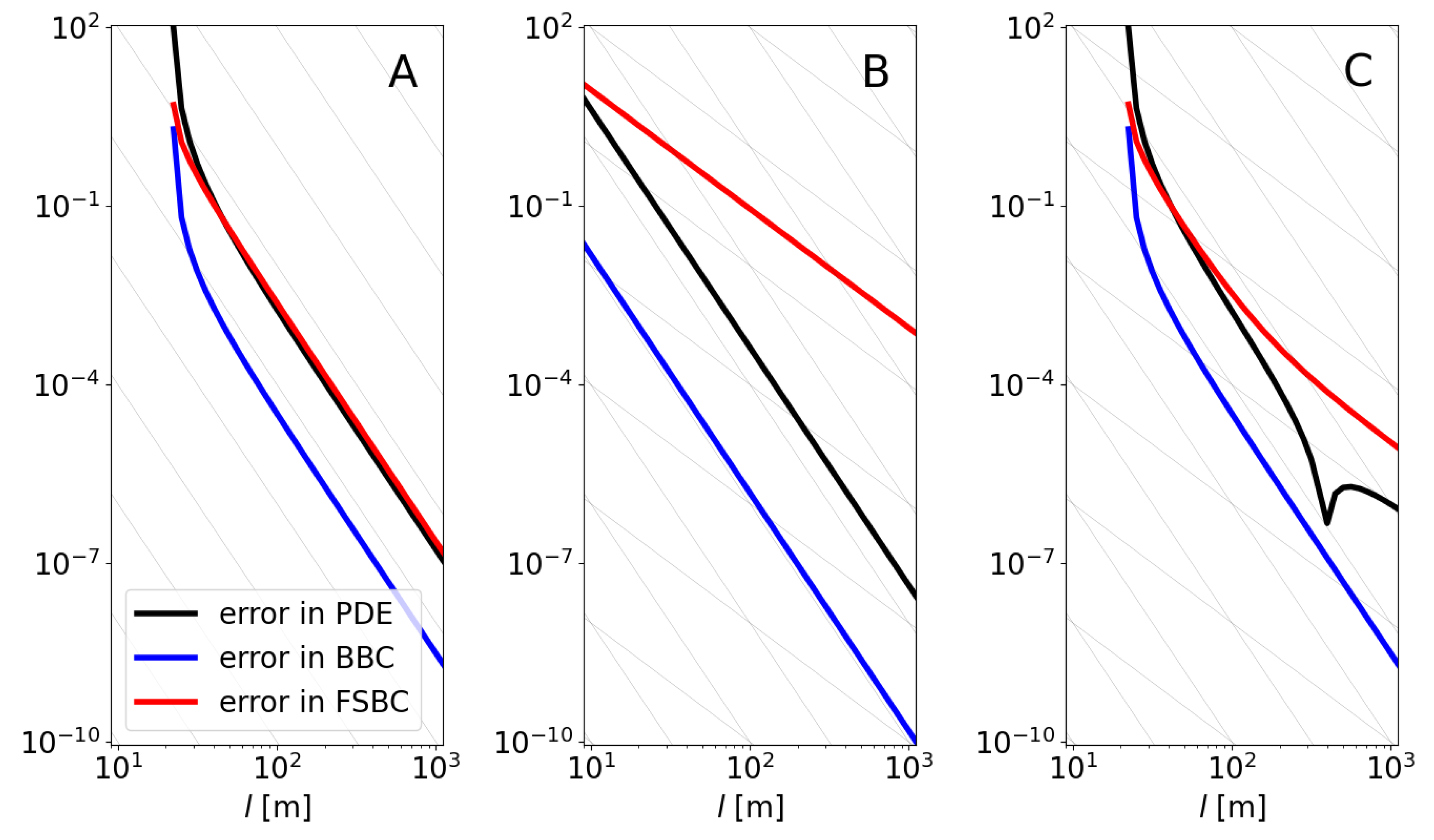
6.5. Numerical Checking of the Solution
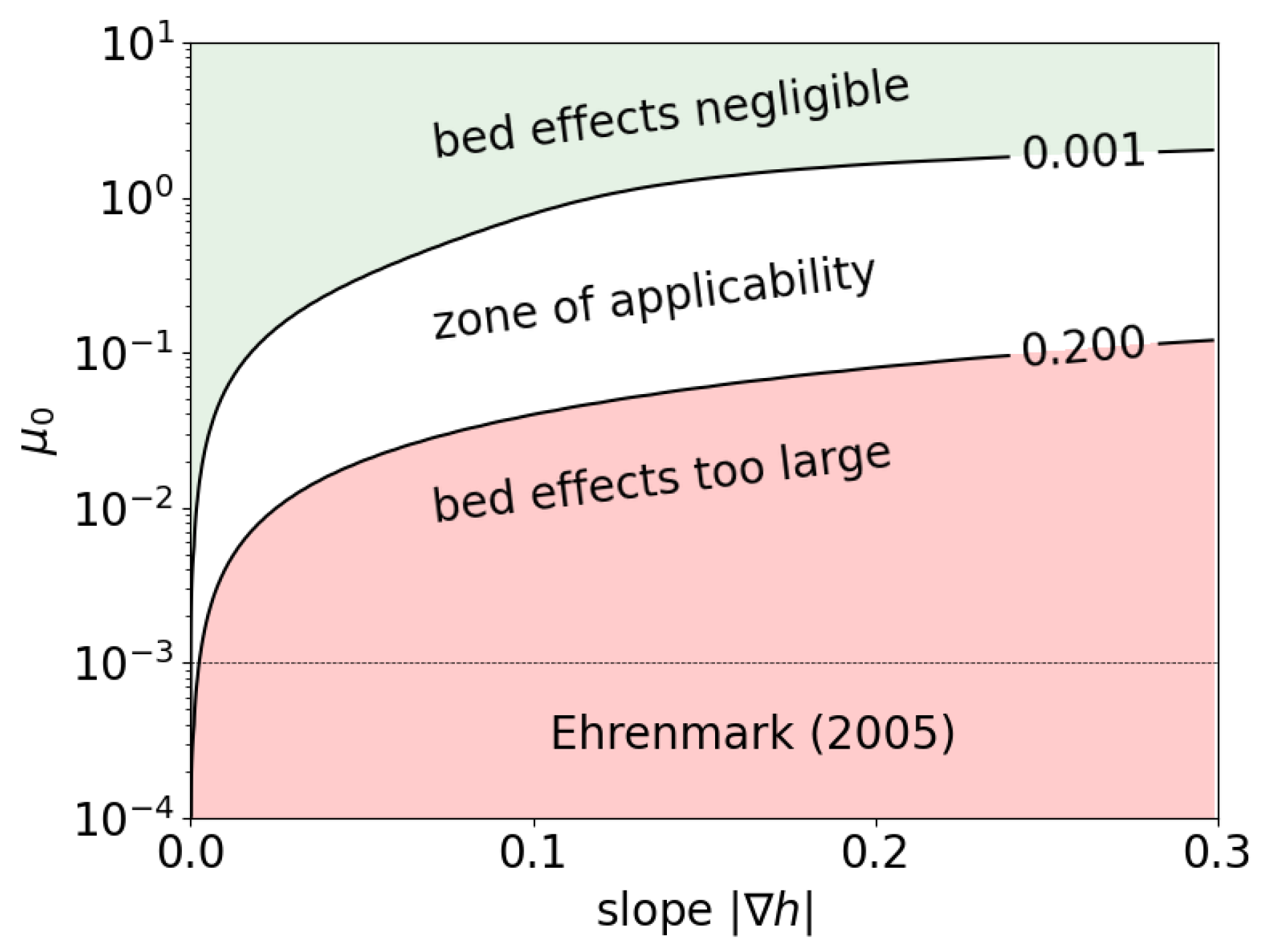
7. Two Cases of Application
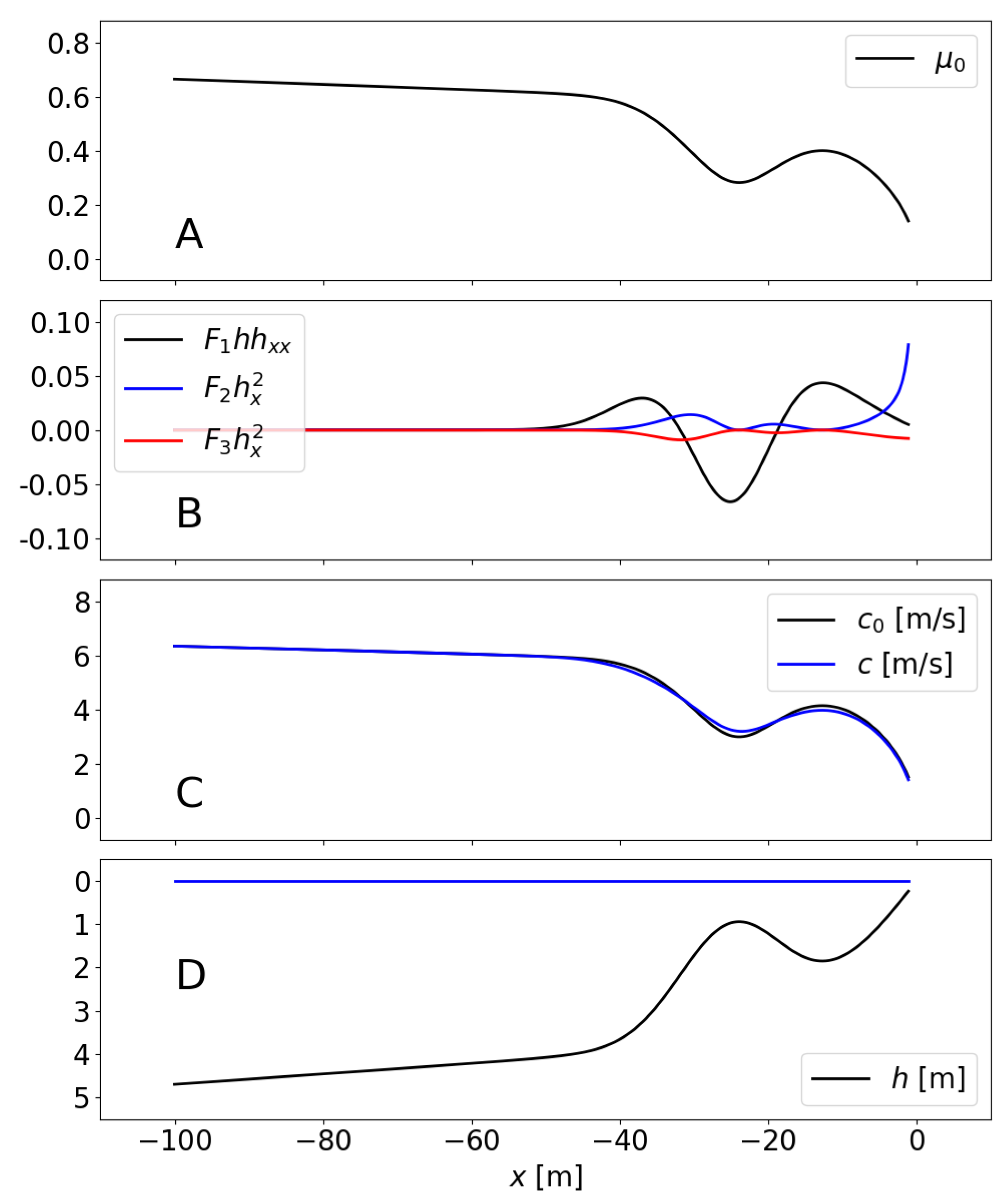
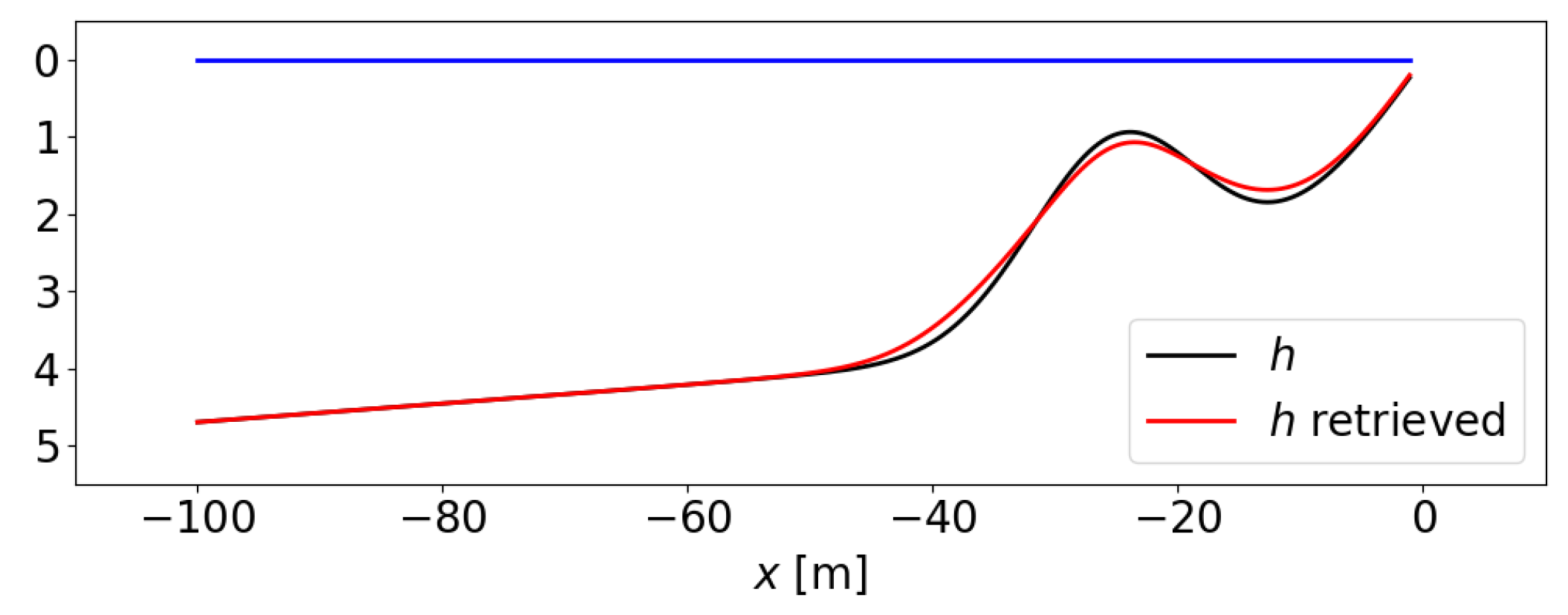
7.1. Nearshore Propagation and Depth Inversion Problem
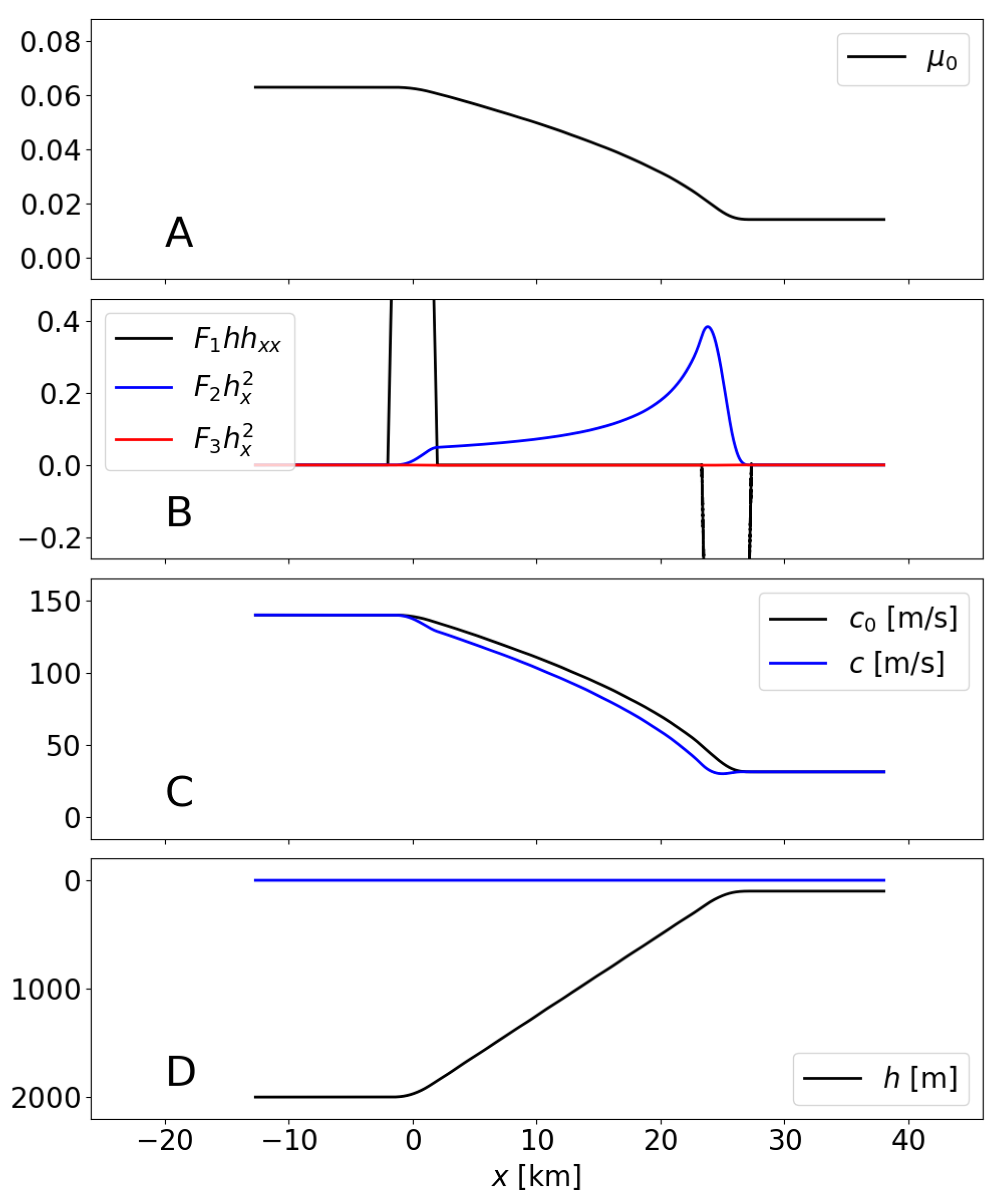
7.2. Tsunami Propagation over the Continental Slope
8. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BTEs | Boussinesq-type equations; |
| MSEs | Mild-slope equation; |
| SWEs | Shallow-water equations; |
| WKB | Wentzel, Kramers, and Brillouin (approach); |
| PDE | Partial differential equation; |
| BBC | Bottom boundary condition; |
| FSBC | Free-surface boundary condition. |
Appendix A. Expressions for α and β
Appendix B. Functions F1 and F2 for k1
References
- Mei, C.C. The Applied Dynamics of Ocean Surface Waves; World Scientific: Singapore, 1989. [Google Scholar]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific: Singapore, 1991. [Google Scholar]
- Svendsen, I.A. Introduction to Nearshore Hydrodynamics; Advanced Series on Ocean Engineering; World Scientific: Singapore, 2005. [Google Scholar]
- Kim, D.; Powers, T. Vertical integration of the Navier-Stokes equations for wave propagation in coastal waters. J. Fluid Mech. 2006, 566, 425–455. [Google Scholar]
- Chen, Q.; Kirby, J.T.; Dalrymple, R.A.; Kennedy, A.B.; Chawla, A. Boussinesq modeling of wave transformation, breaking, and runup. II: 2D. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 48–56. [Google Scholar] [CrossRef]
- Mendez, F.J.; Losada, I.J. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields. Coast. Eng. 2004, 51, 103–118. [Google Scholar] [CrossRef]
- Infantes, E.; Orfila, A.; Simarro, G.; Terrados, J.; Alomar, C.; Tintoré, J. Effect of a seagrass (Posidonia oceanica) meadow on wave propagation. Mar. Ecol. Prog. Ser. 2012, 456, 63–72. [Google Scholar] [CrossRef]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Performance evaluation of Wavewatch III in the Mediterranean Sea. Ocean Model. 2015, 90, 82–94. [Google Scholar] [CrossRef]
- Airy, G.B. Tides and waves. Encycl. Metrop. 1845, 5, 241–396. [Google Scholar]
- Burnside, W. On the modification of a train of waves as it advances into shallow water. Proc. Lond. Math. Soc. 1915, s2_14, 131–133. [Google Scholar] [CrossRef]
- Stokes, G.G. On the theory of oscillatory waves. Trans. Camb. Philos. Soc. 1847, 8, 441–455. [Google Scholar]
- Berkhoff, J.C.W. Computation of combined refraction-diffraction. In Proceedings of the 13th Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 June 1972; Volume 2, pp. 471–490. [Google Scholar]
- Berkhoff, J.C.W. Mathematical Models for Simple Harmonic Linear Waves: Wave Diffraction and Refraction. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 1976. [Google Scholar]
- Chamberlain, P.G.; Porter, D. The modified mild-slope equation. J. Fluid Mech. 1995, 291, 393–407. [Google Scholar] [CrossRef]
- Hsu, T.W.; Lin, T.Y.; Wen, C.C.; Ou, S.H. A complementary mild-slope equation derived using higher-order depth function for waves obliquely propagating on sloping bottom. Phys. Fluids 2006, 18, 087106. [Google Scholar] [CrossRef]
- Porter, R. An extended linear shallow-water equation. J. Fluid Mech. 2019, 876, 413–427. [Google Scholar] [CrossRef]
- Porter, D. The mild-slope equations: A unified theory. J. Fluid Mech. 2020, 887, A29. [Google Scholar] [CrossRef]
- Dingemans, M.W. Water Wave Propagation over Uneven Bottoms; World Scientific: Singapore, 1997. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Fluid Mechanics, 1st ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- Boussinesq, J. Théorie des vagues propagées le long d’un canal ou d’une mer peu profonde. Comptes Rendus L’AcadéMie Des Sci. 1872, 74, 891–897. [Google Scholar]
- Peregrine, D.H. Long waves on a beach. J. Fluid Mech. 1967, 27, 815–827. [Google Scholar] [CrossRef]
- Liu, P.L.F. Model equations for wave propagation from deep water to shallow water. In Advances in Coastal and Ocean Engineering; World Scientific: Singapore, 1994; Chapter 3; pp. 125–158. [Google Scholar]
- Wei, G.; Kirby, J.T.; Grilli, S.T.; Subramanya, R. A fully nonlinear Boussinesq model for surface waves. Part 1: Highly nonlinear unsteady waves. J. Fluid Mech. 1995, 294, 71–92. [Google Scholar] [CrossRef]
- Simarro, G.; Orfila, A.; Galan, A. Linear shoaling in Boussinesq-type wave propagation models. Coast. Eng. J. 2013, 80, 100–106. [Google Scholar] [CrossRef]
- Nwogu, O. Alternative form of Boussinesq equations for nearshore wave propagation. J. Waterw. Port Coastal Ocean Eng. 1993, 119, 618–638. [Google Scholar] [CrossRef]
- Booij, N. A note on the accuracy of the mild-slope equation. Coast. Eng. 1983, 7, 191–203. [Google Scholar] [CrossRef]
- Ehrenmark, U. An alternative dispersion equation for water waves over an inclined bed. J. Fluid Mech. 2005, 543. [Google Scholar] [CrossRef]
- Williams, P.; Ehrenmark, U. A note on the use of a new dispersion formula for wave transformation over Roseau’s curved beach profile. Wave Motion 2010, 47, 641–647. [Google Scholar] [CrossRef]
- Ge, H.; Liu, H.; Zhang, L. Accurate depth inversion method for coastal bathymetry: Introduction of water wave high-order dispersion relation. J. Mar. Sci. Eng. 2020, 8, 153. [Google Scholar] [CrossRef]
- Dingemans, M.W. Water Wave Propagation over Uneven Bottoms. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1994. [Google Scholar]
- Schäffer, H.A.; Madsen, P.A. Further enhancements of Boussinesq-type equations. Coast. Eng. 1995, 26, 1–14. [Google Scholar] [CrossRef]
- Yu, J.; Slinn, D. Effects of wave-current interaction on rip currents. J. Geophys. Res 2003, 108, 87. [Google Scholar] [CrossRef]
- Holman, R.; Bergsma, E.W.J. Updates to and performance of the cBathy algorithm for estimating nearshore bathymetry from remote sensing imagery. Remote Sens. 2021, 13, 3996. [Google Scholar] [CrossRef]
- Gawehn, M.; de Vries, S.; Aarninkhof, S. A self-adaptive method for mapping coastal bathymetry on-the-fly from wave field video. Remote Sens. 2021, 13, 4742. [Google Scholar] [CrossRef]
- Simarro, G.; Calvete, D. UBathy (v2.0): A software to obtain the bathymetry from video imagery. Remote. Sens. 2022, 14, 6139. [Google Scholar] [CrossRef]
| L in the Deep Zone [km] | |||||
|---|---|---|---|---|---|
| Slope [-] | 10 | 50 | 100 | 200 | 500 |
| — | |||||
| — | |||||
| — | |||||
| — | — | ||||
| — | — | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simarro, G. Influence of Bed Variations on Linear Wave Propagation beyond the Mild Slope Condition. J. Mar. Sci. Eng. 2024, 12, 1652. https://doi.org/10.3390/jmse12091652
Simarro G. Influence of Bed Variations on Linear Wave Propagation beyond the Mild Slope Condition. Journal of Marine Science and Engineering. 2024; 12(9):1652. https://doi.org/10.3390/jmse12091652
Chicago/Turabian StyleSimarro, Gonzalo. 2024. "Influence of Bed Variations on Linear Wave Propagation beyond the Mild Slope Condition" Journal of Marine Science and Engineering 12, no. 9: 1652. https://doi.org/10.3390/jmse12091652
APA StyleSimarro, G. (2024). Influence of Bed Variations on Linear Wave Propagation beyond the Mild Slope Condition. Journal of Marine Science and Engineering, 12(9), 1652. https://doi.org/10.3390/jmse12091652






