Coupled Motion Response Analysis for Dynamic Target Salvage under Wave Action
Abstract
1. Introduction
1.1. Theory of Hydrodynamic Interference of Multi-Floating Bodies
1.2. Numerical Simulation of Multi-Float Salvage System
1.3. Model Test of Multi-Floating Body Salvage System
2. Modelling and Numerical Simulation Methods
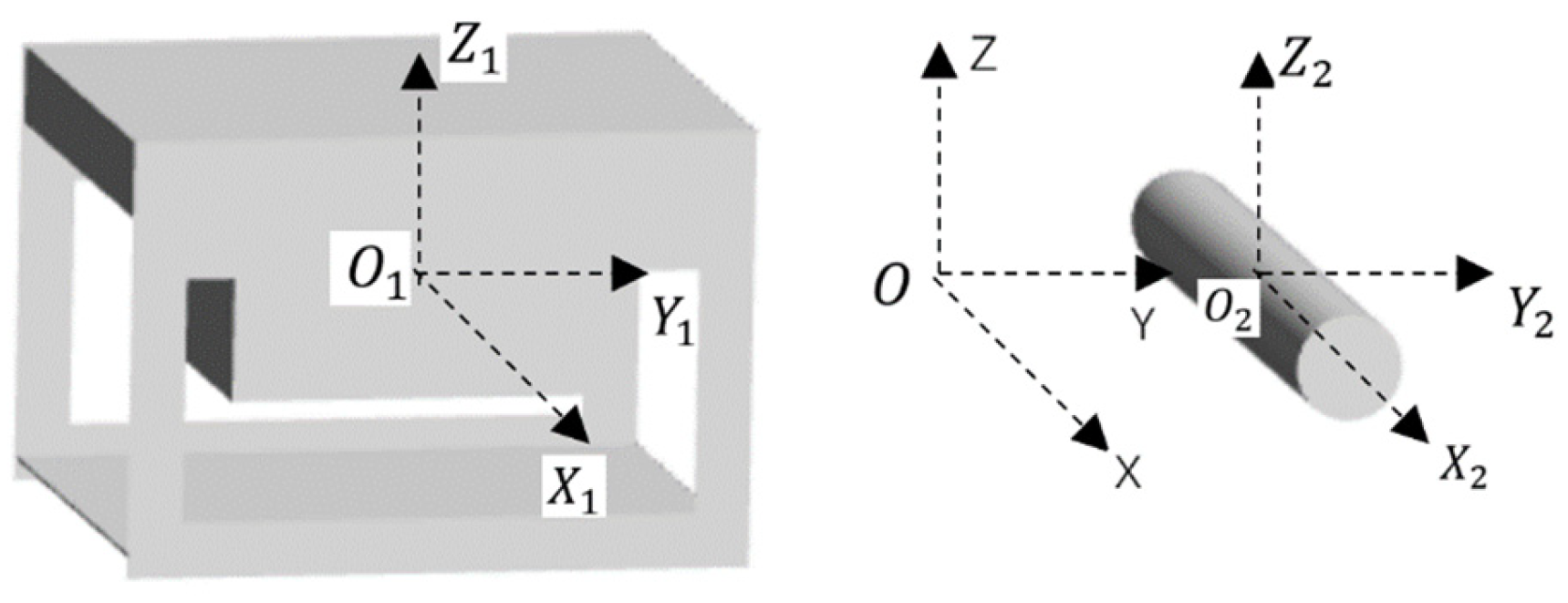
2.1. Floating Body Model
2.2. Theory
2.2.1. Governing Equation
2.2.2. Hydrodynamic Coefficient and Wave Force
2.2.3. Multi-Float Motion Response
2.2.4. Wave Mean Wave Mean Drift Force Drift Force
3. Numerical Implementation and Validation
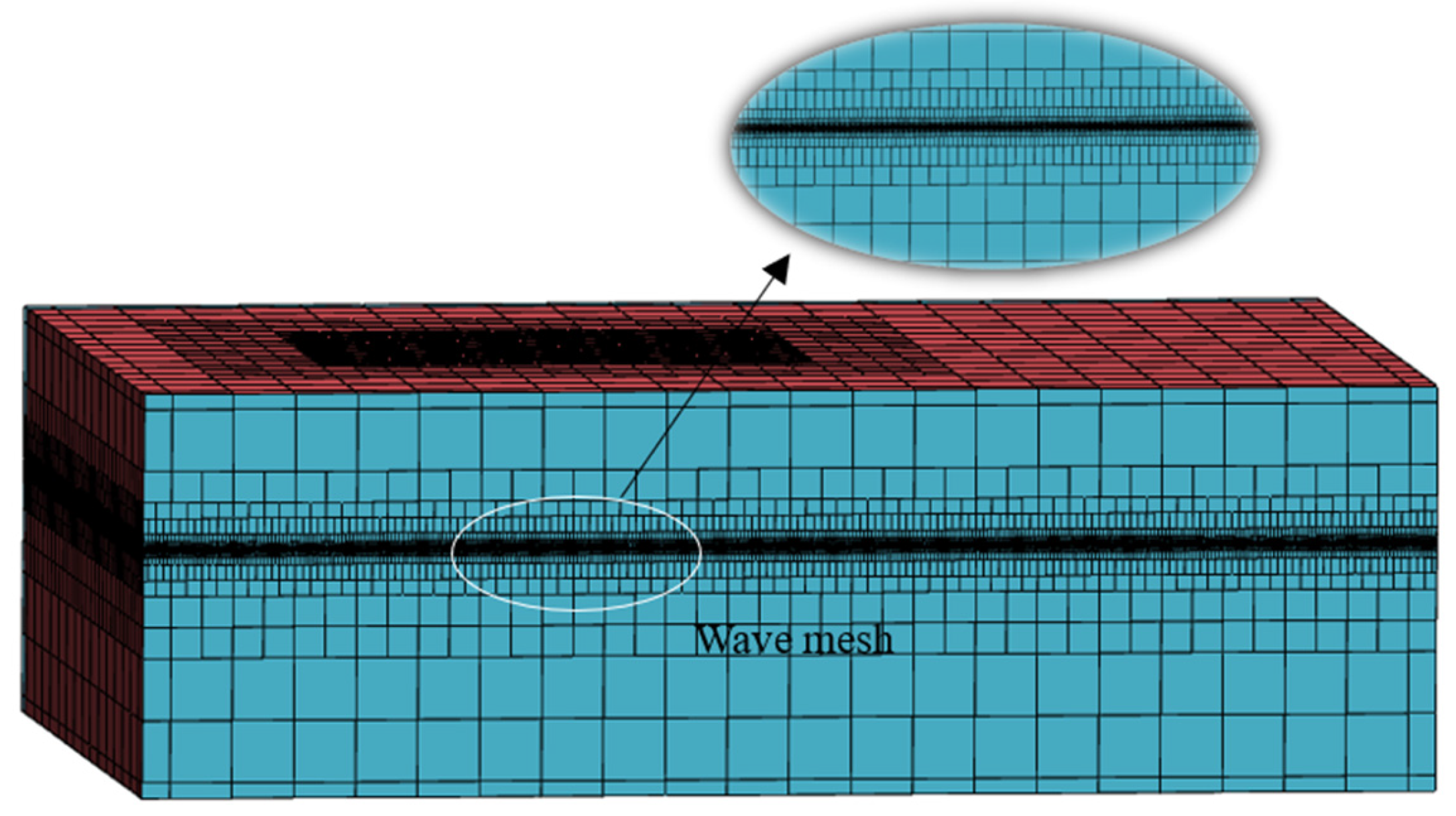
3.1. Numerical Simulation
3.2. Pool Testing and Validation
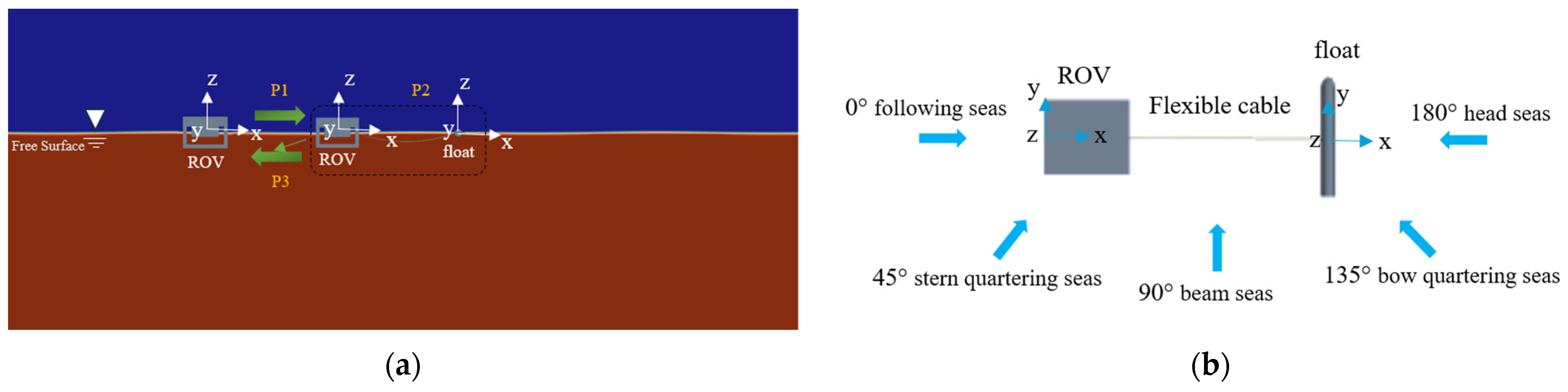
3.2.1. Experimental Equipment and Arrangement
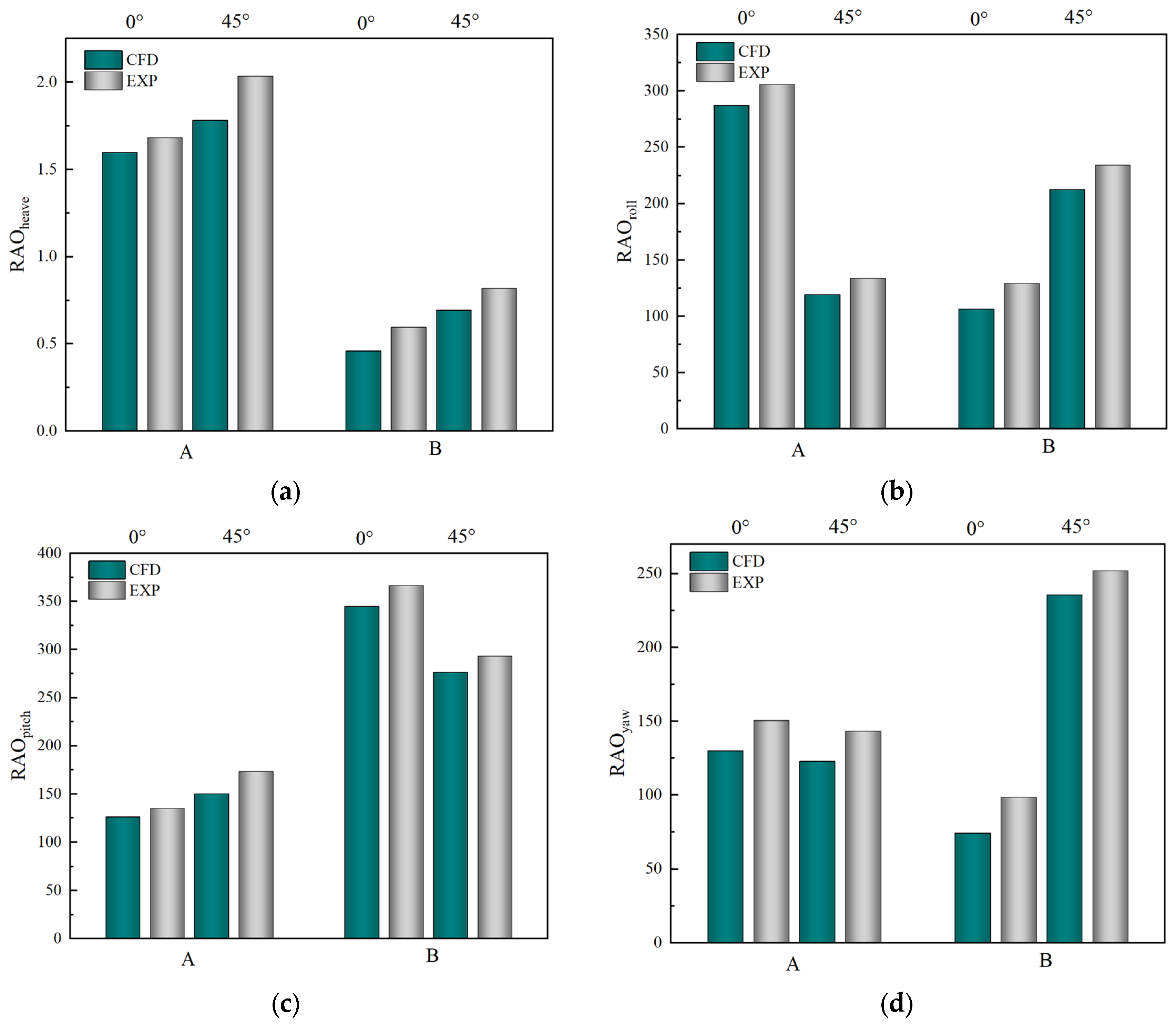
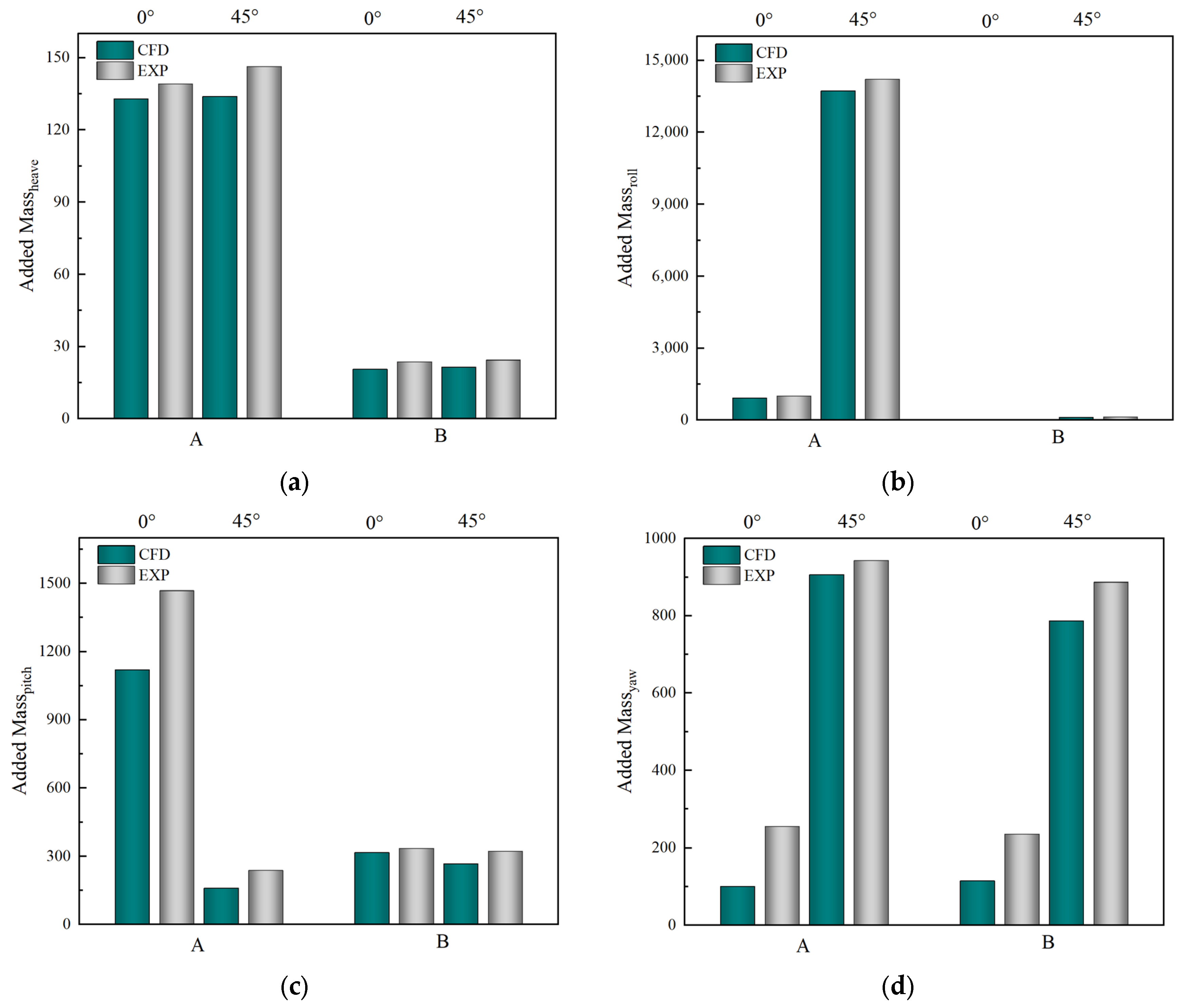
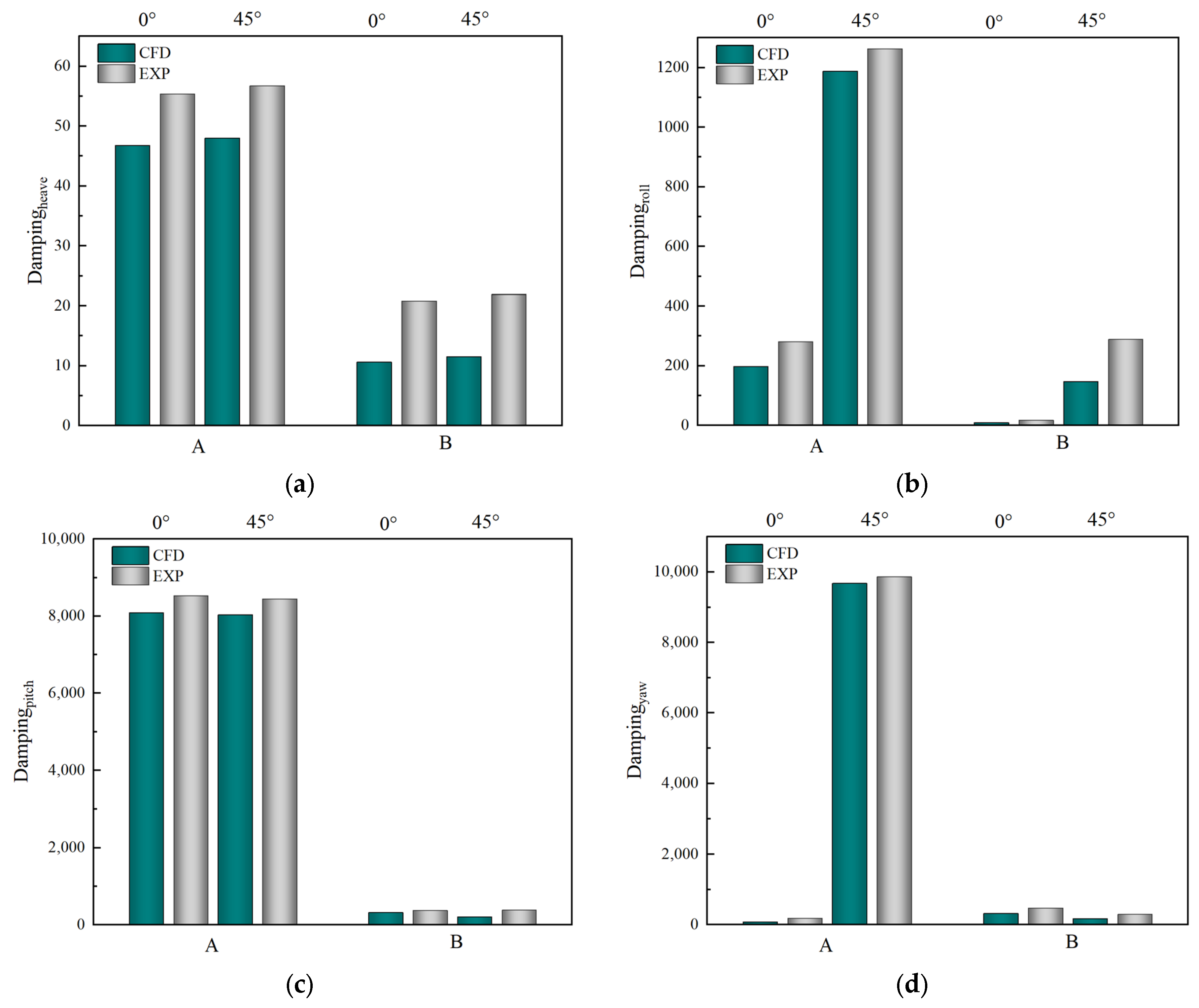
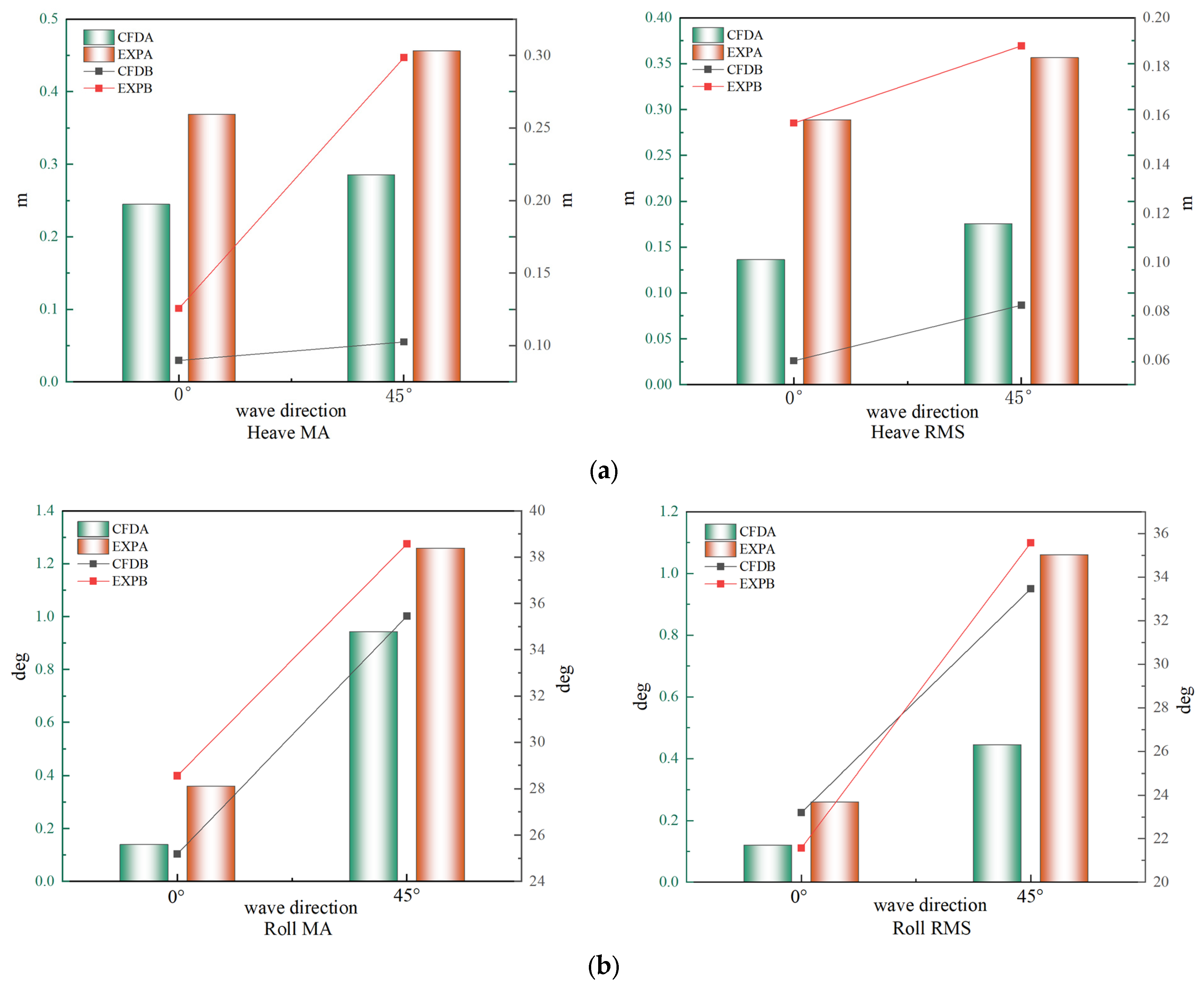
3.2.2. Analysis of Experimental Results
4. Results and Discussion
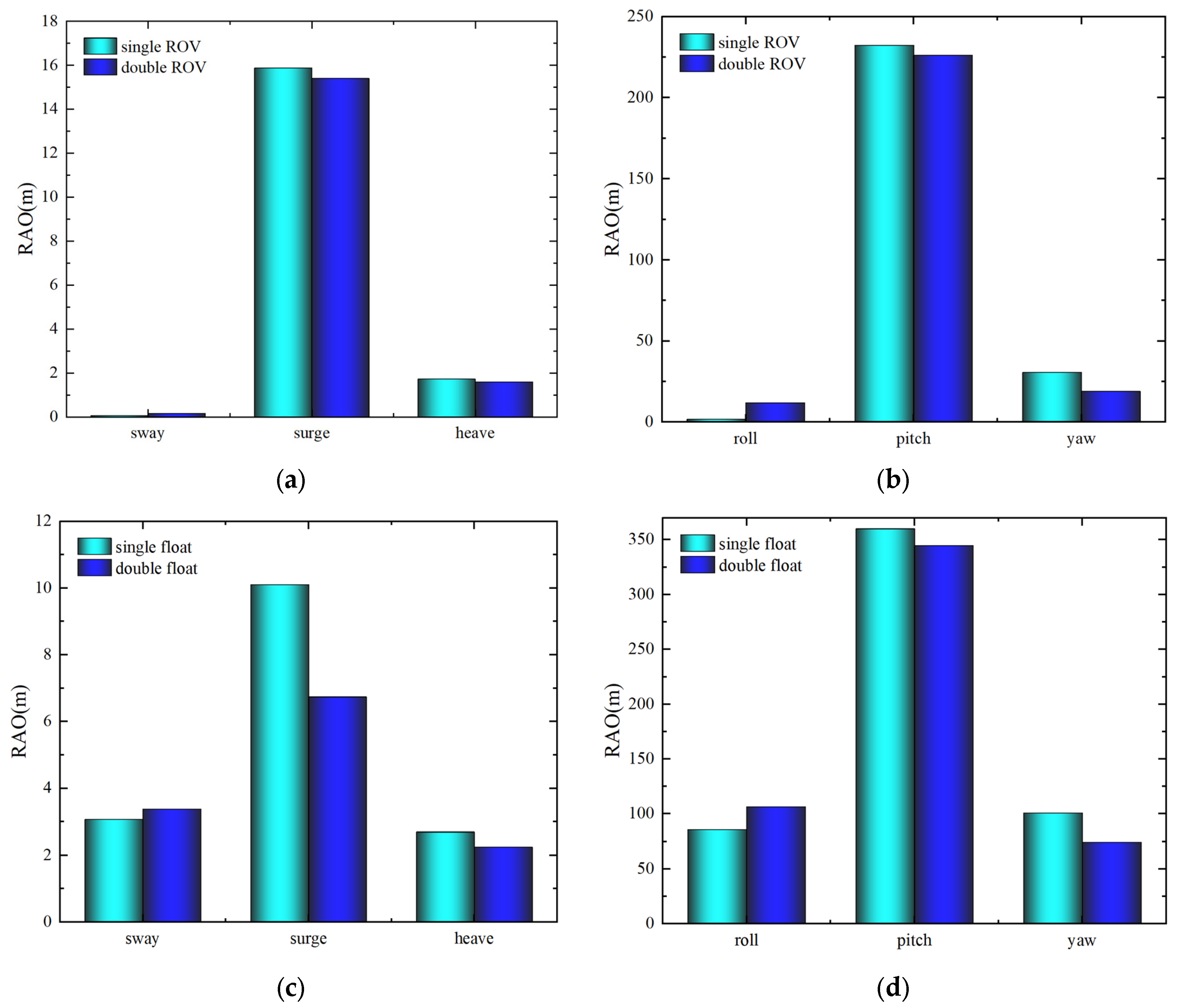
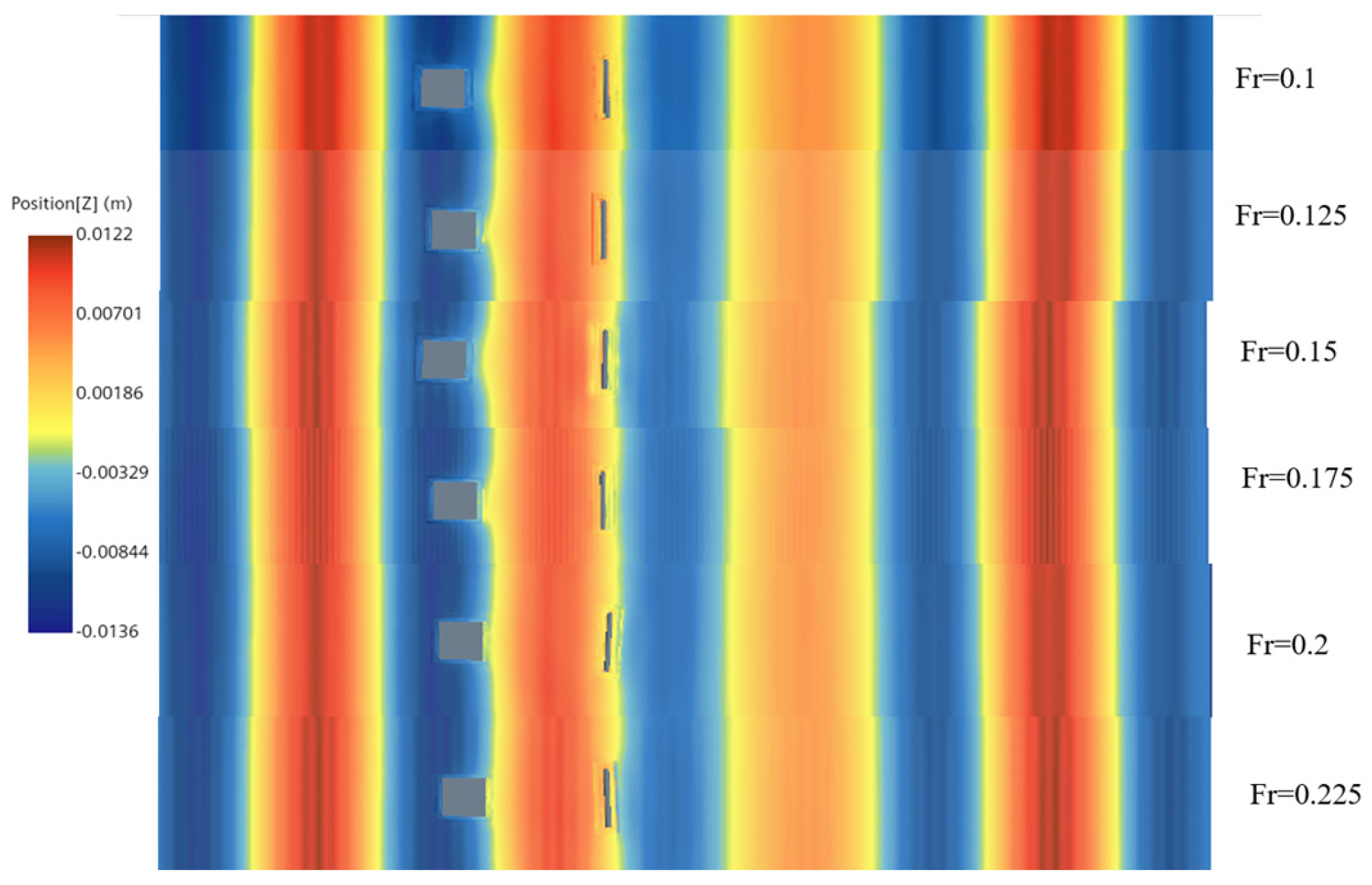
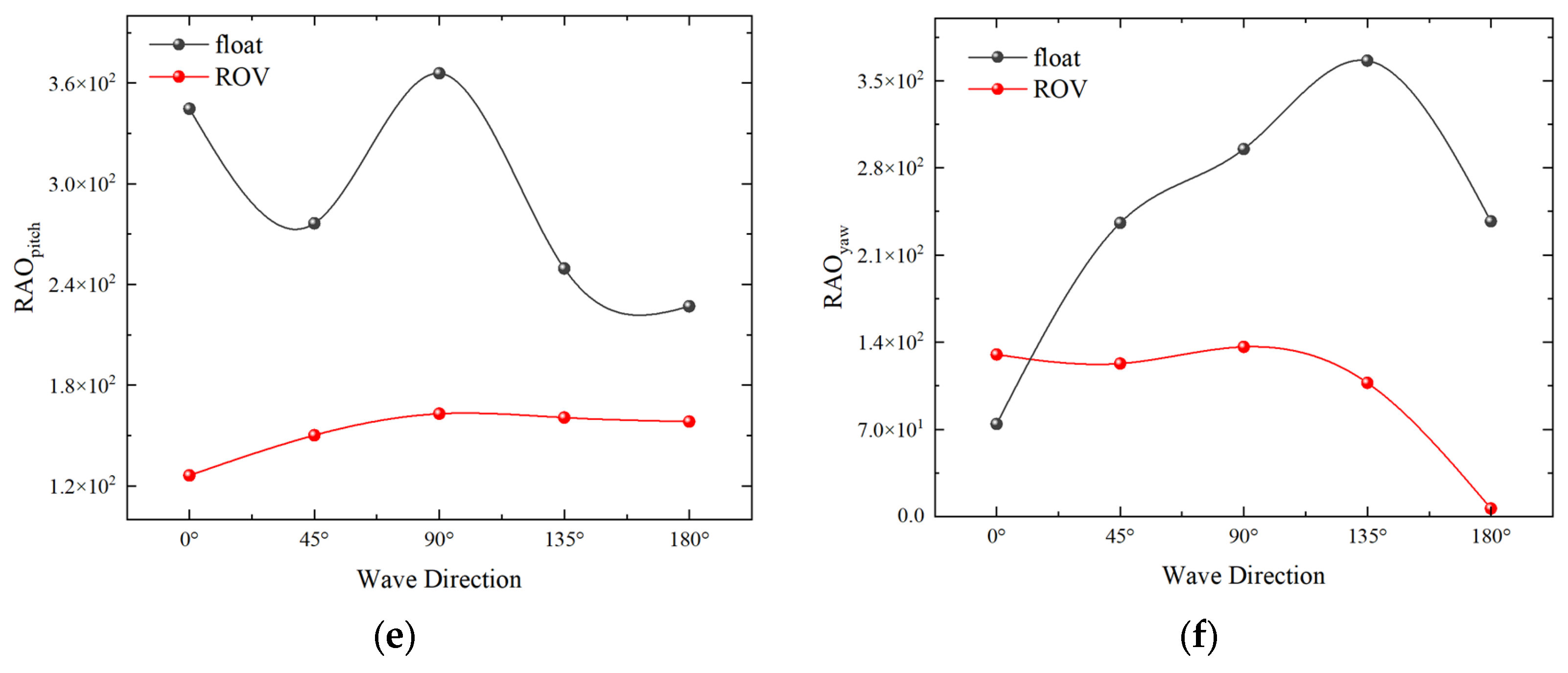
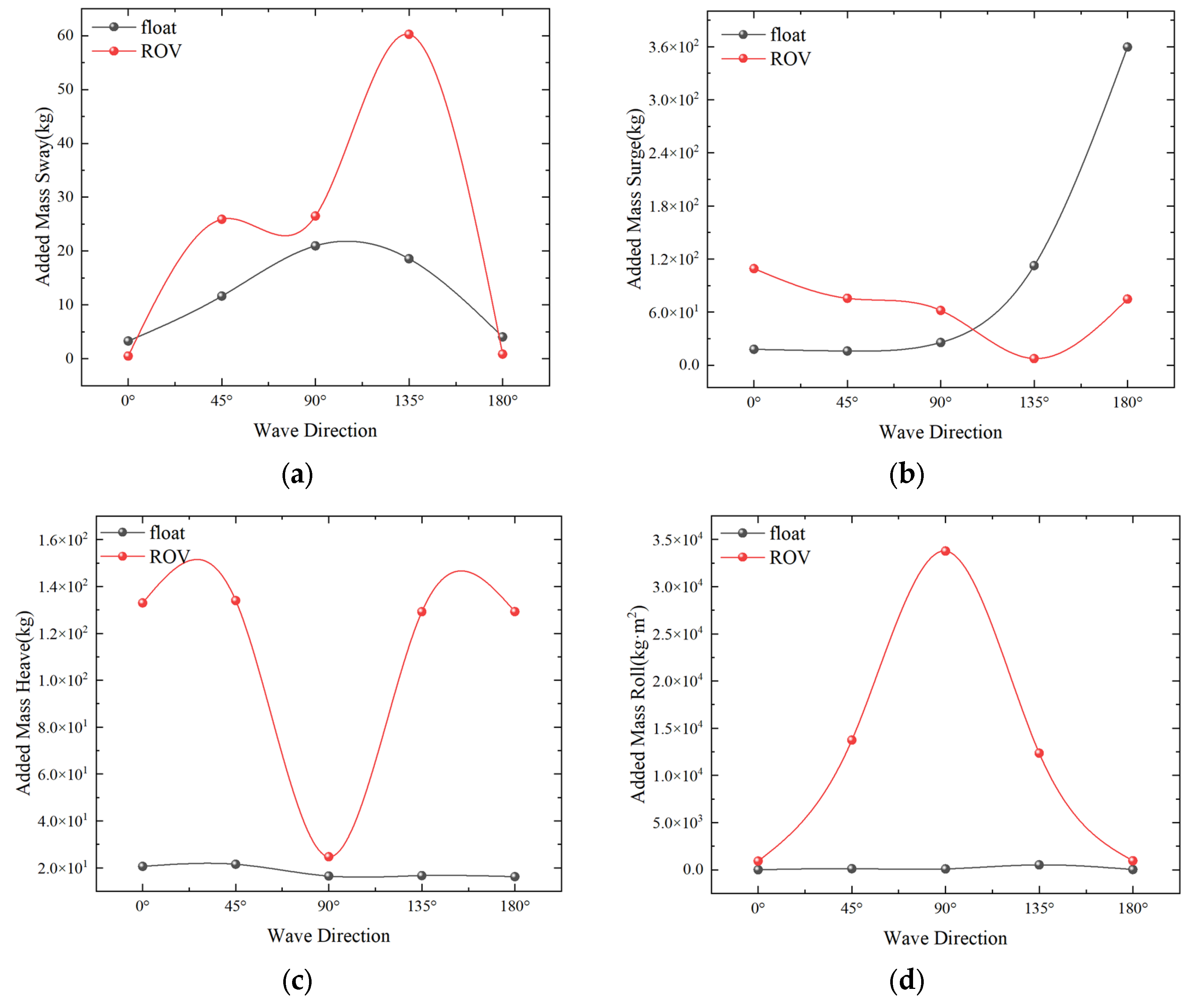
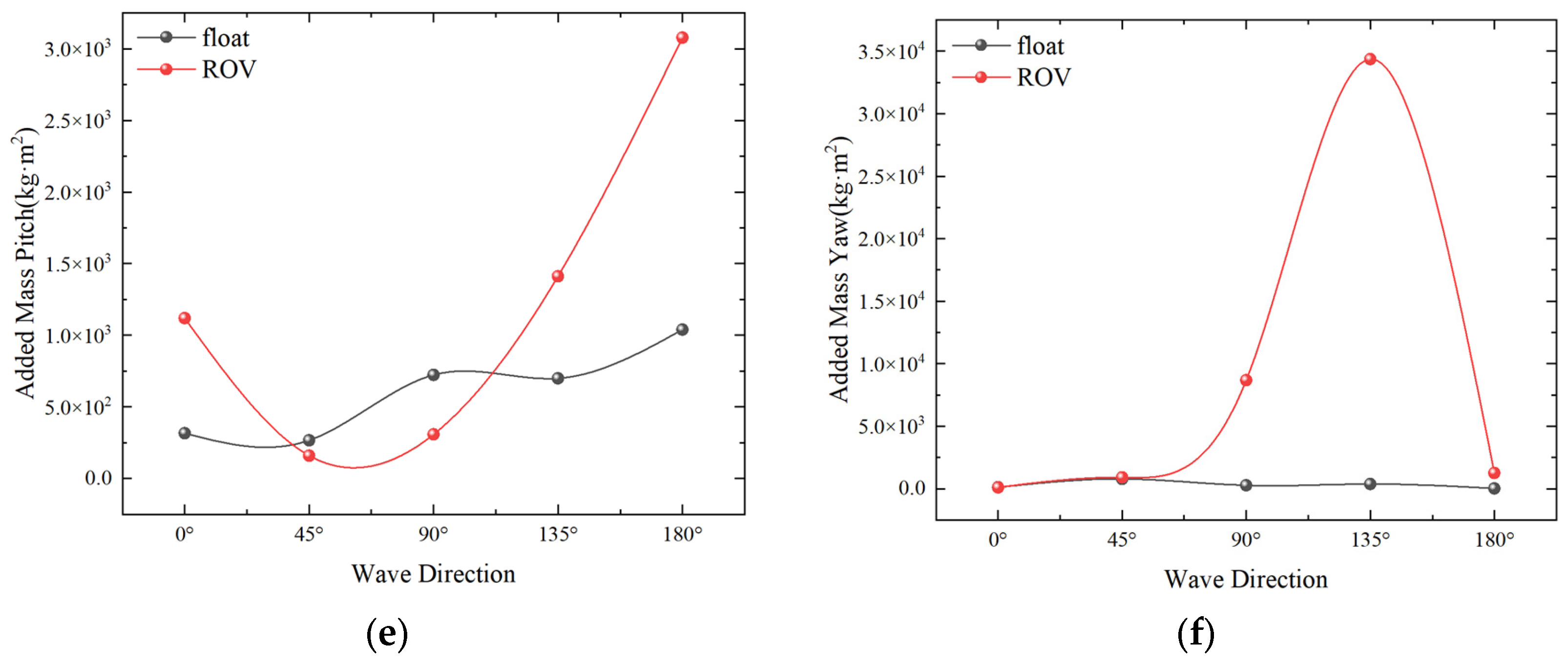
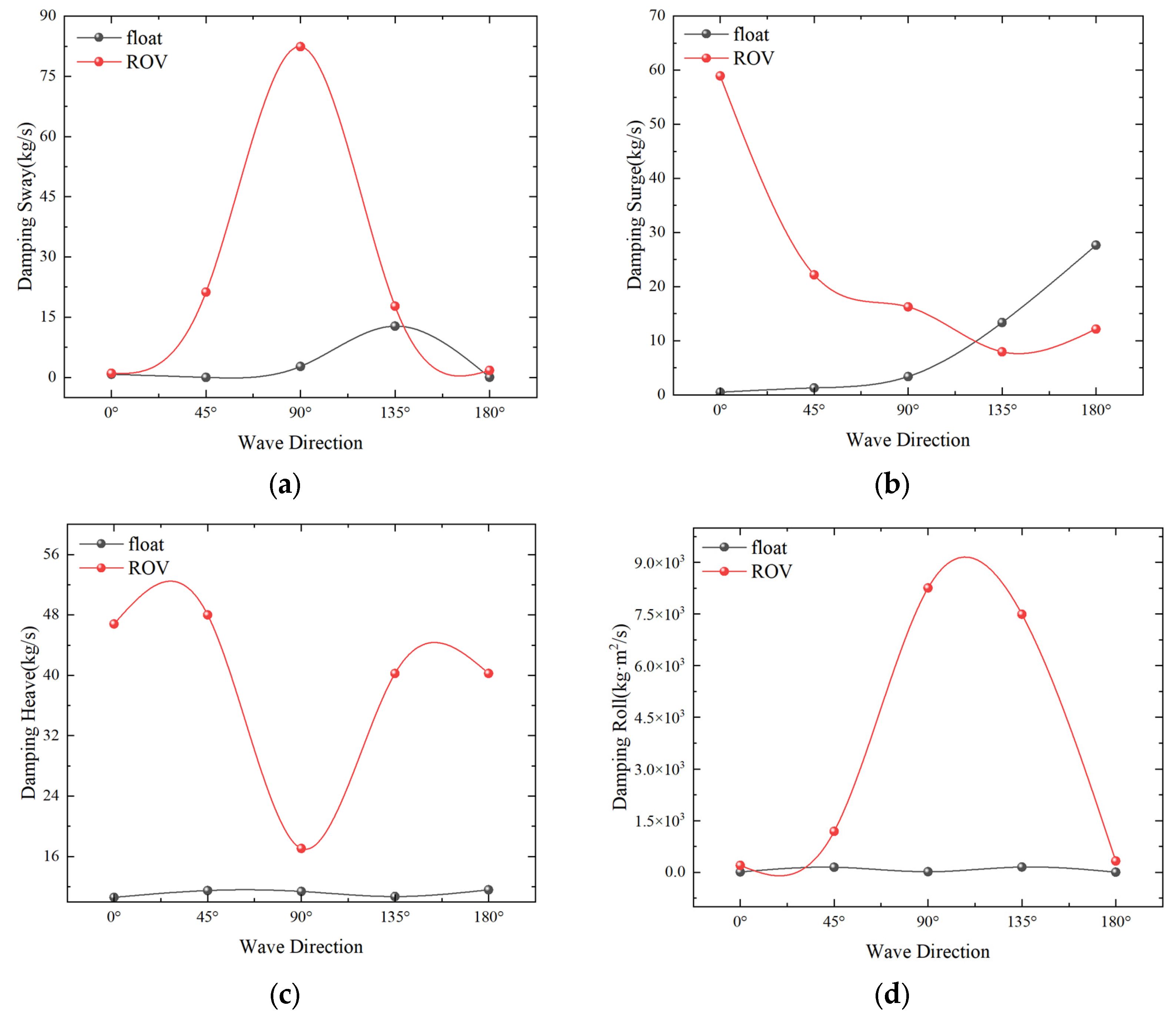
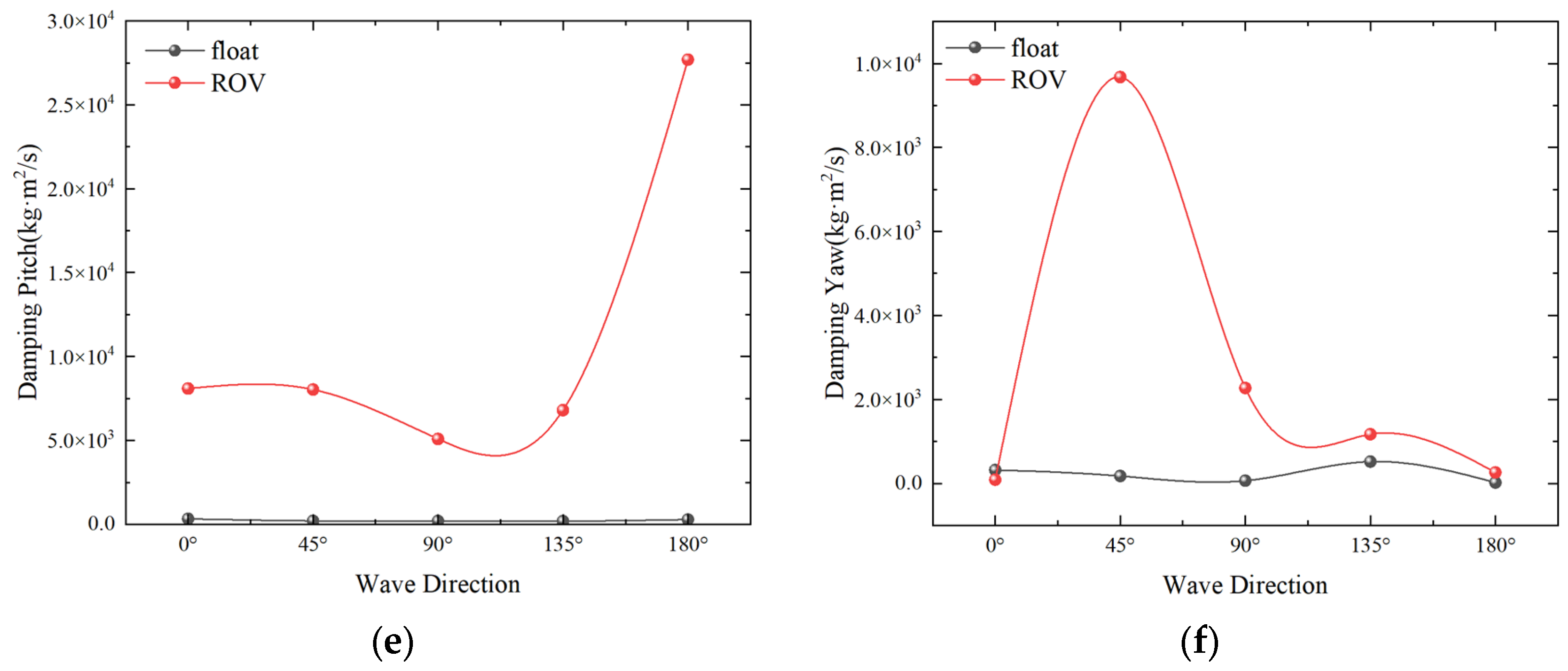
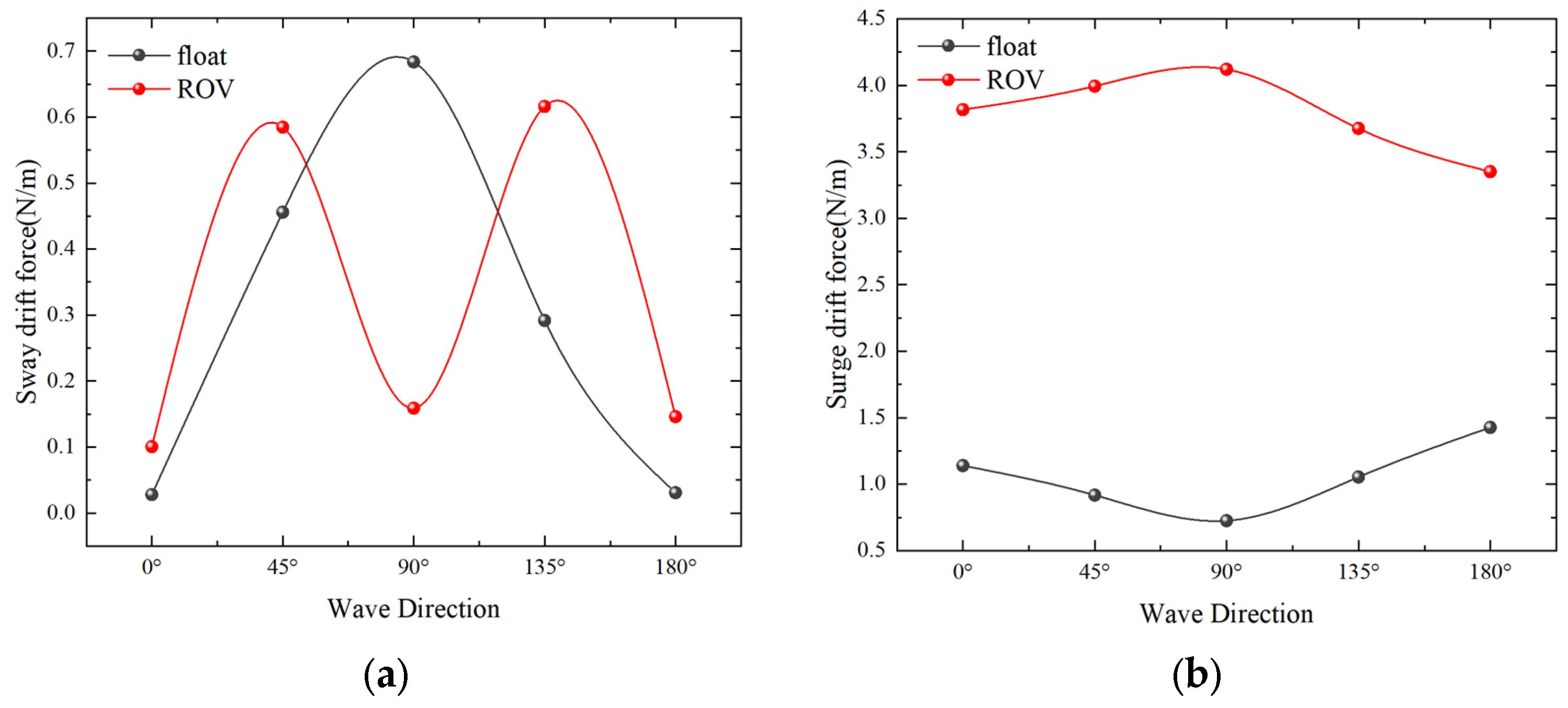
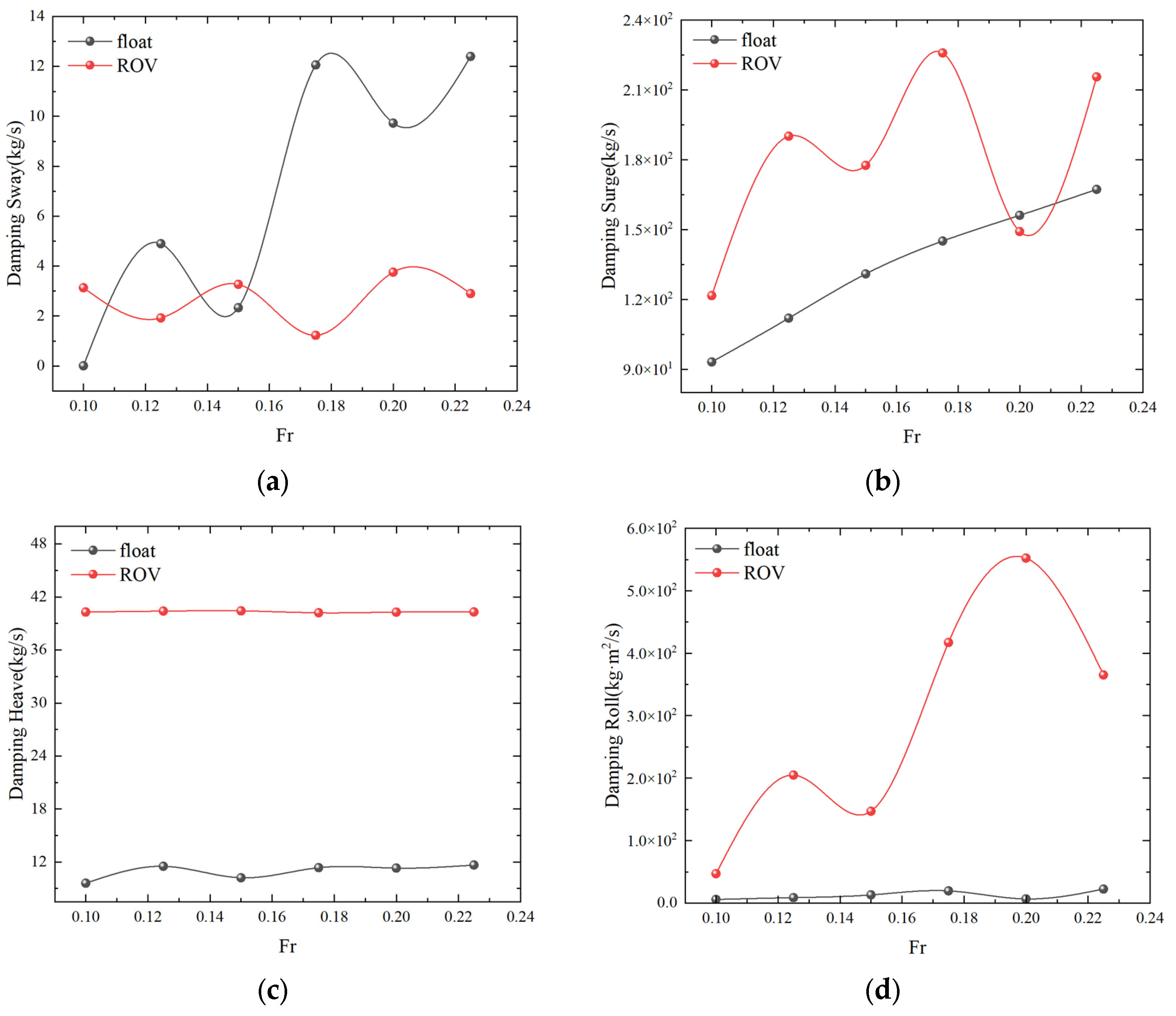
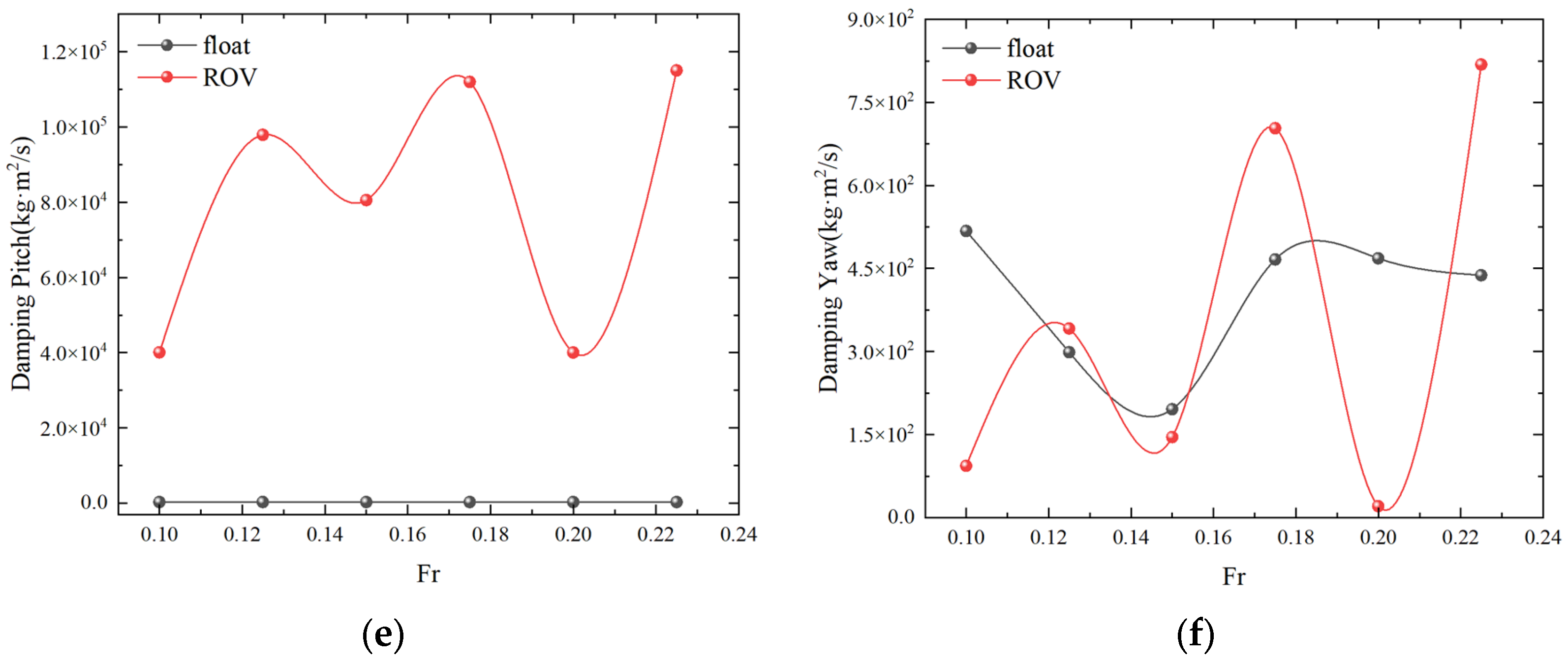
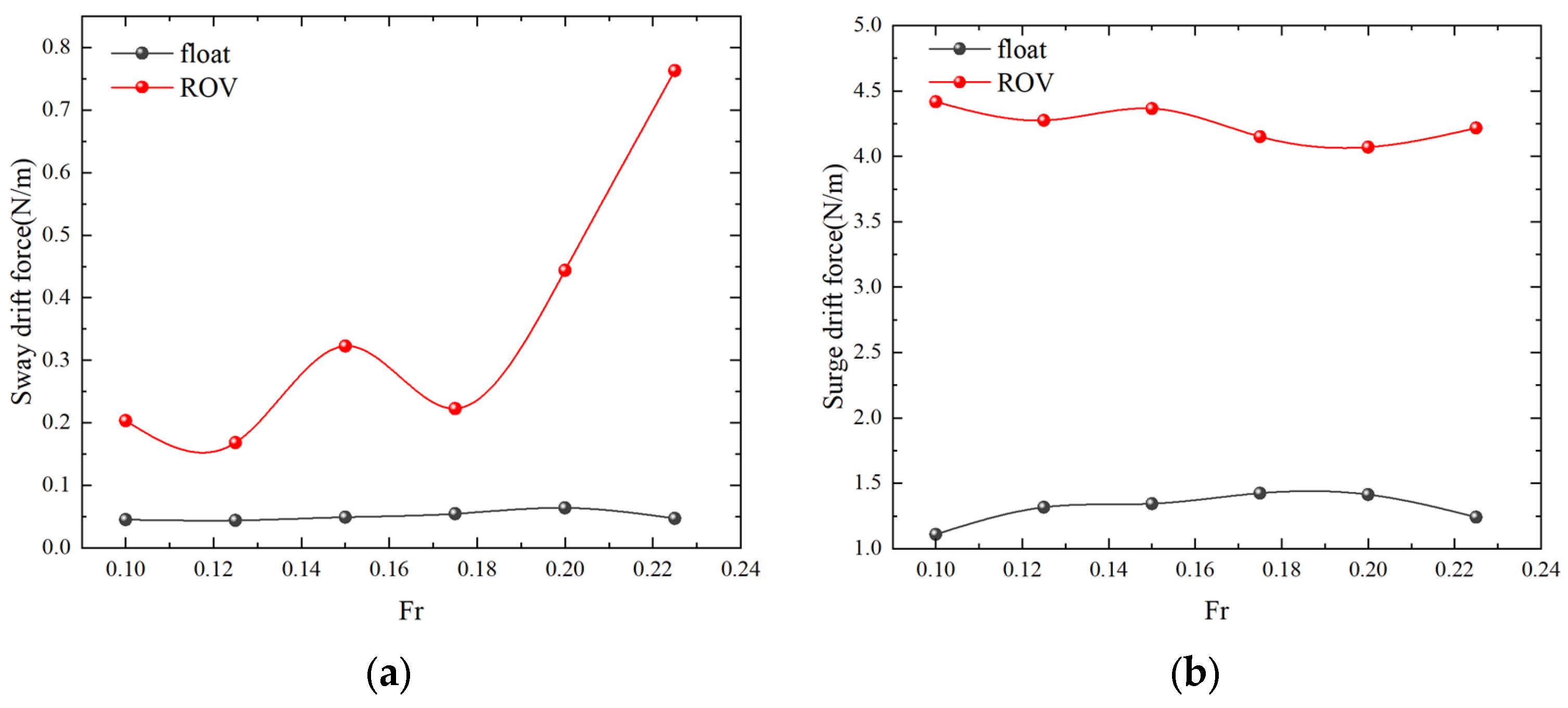
4.1. Numerical Simulation of Single-Float and Double-Float Coupling
4.2. Characteristics of Double Floating Body Berthing Motion
4.3. Characteristics of Double Floating Body Side-by-Side Motion
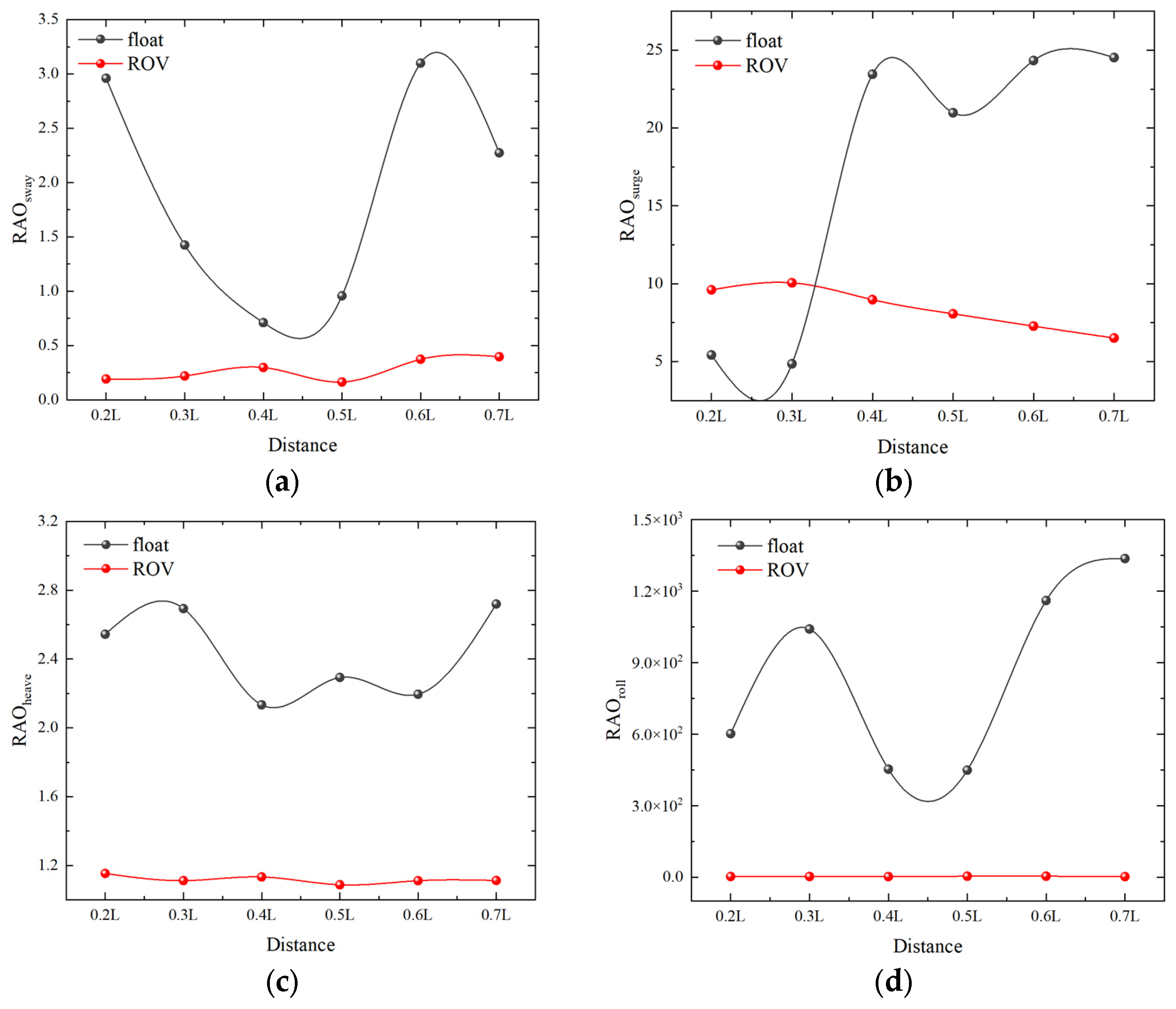
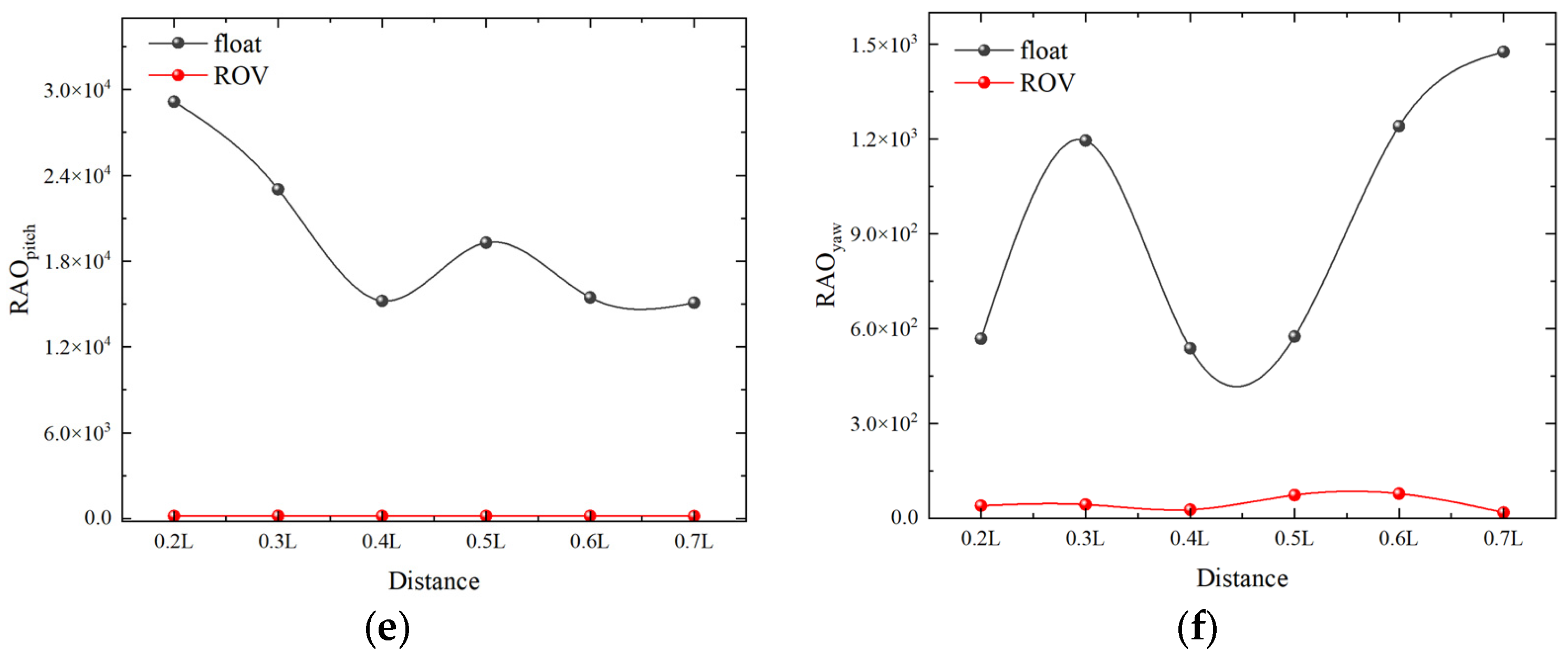
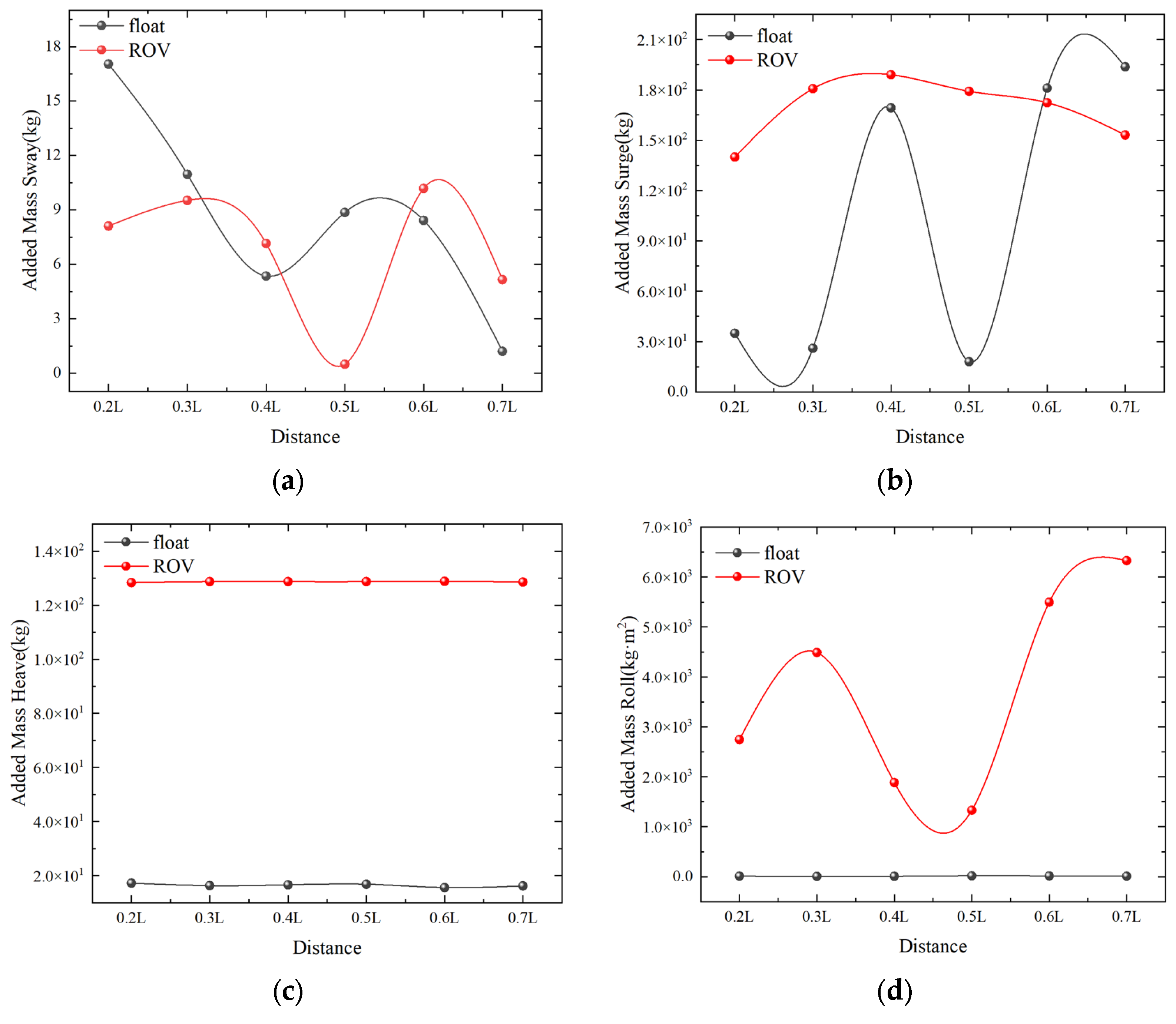
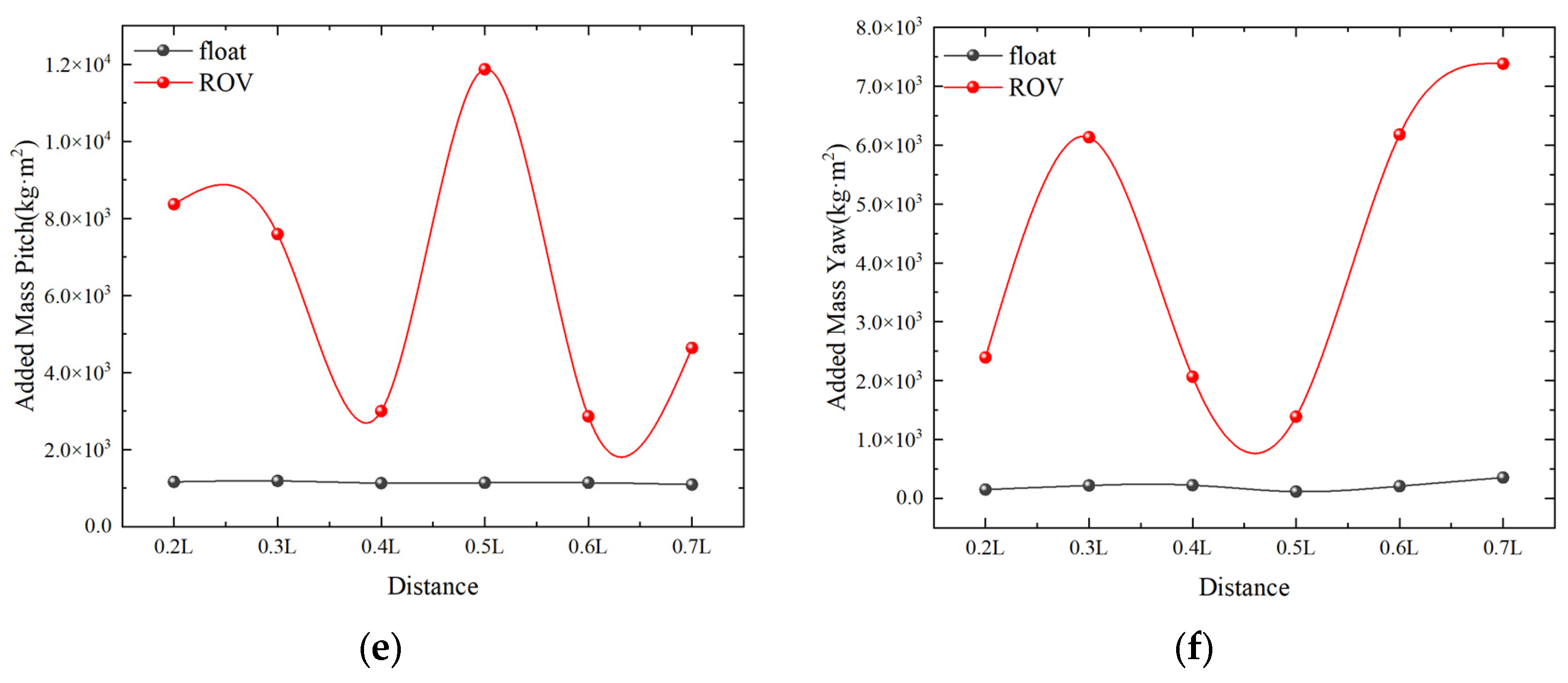
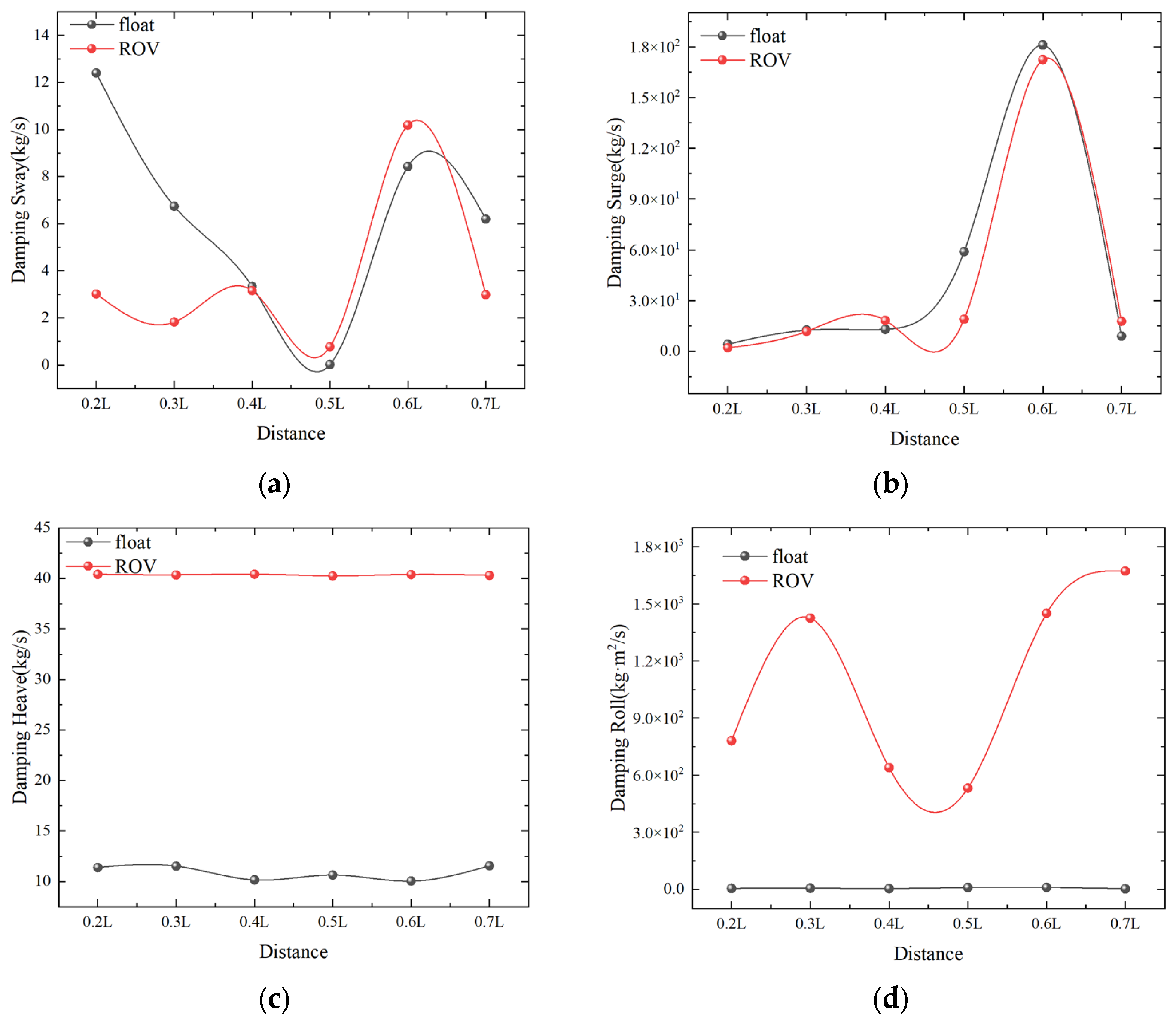
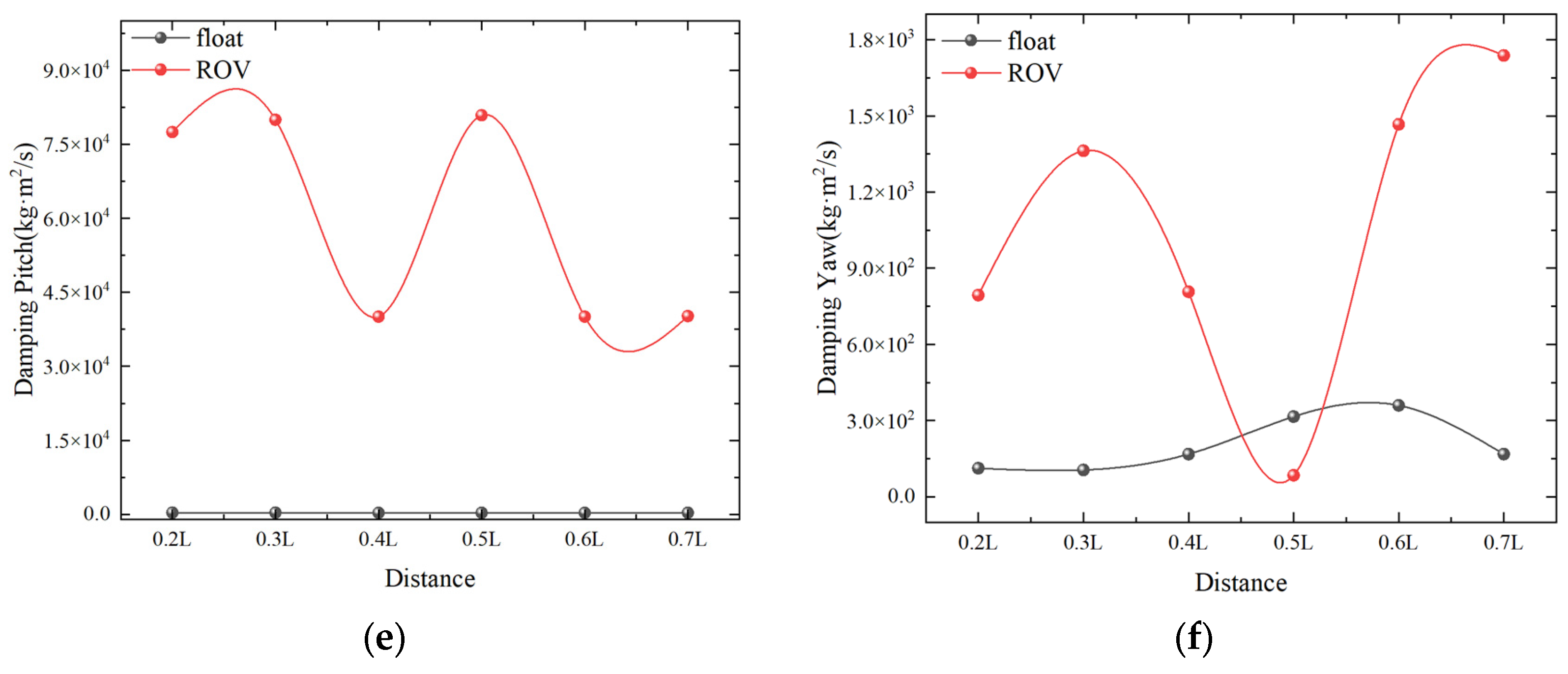
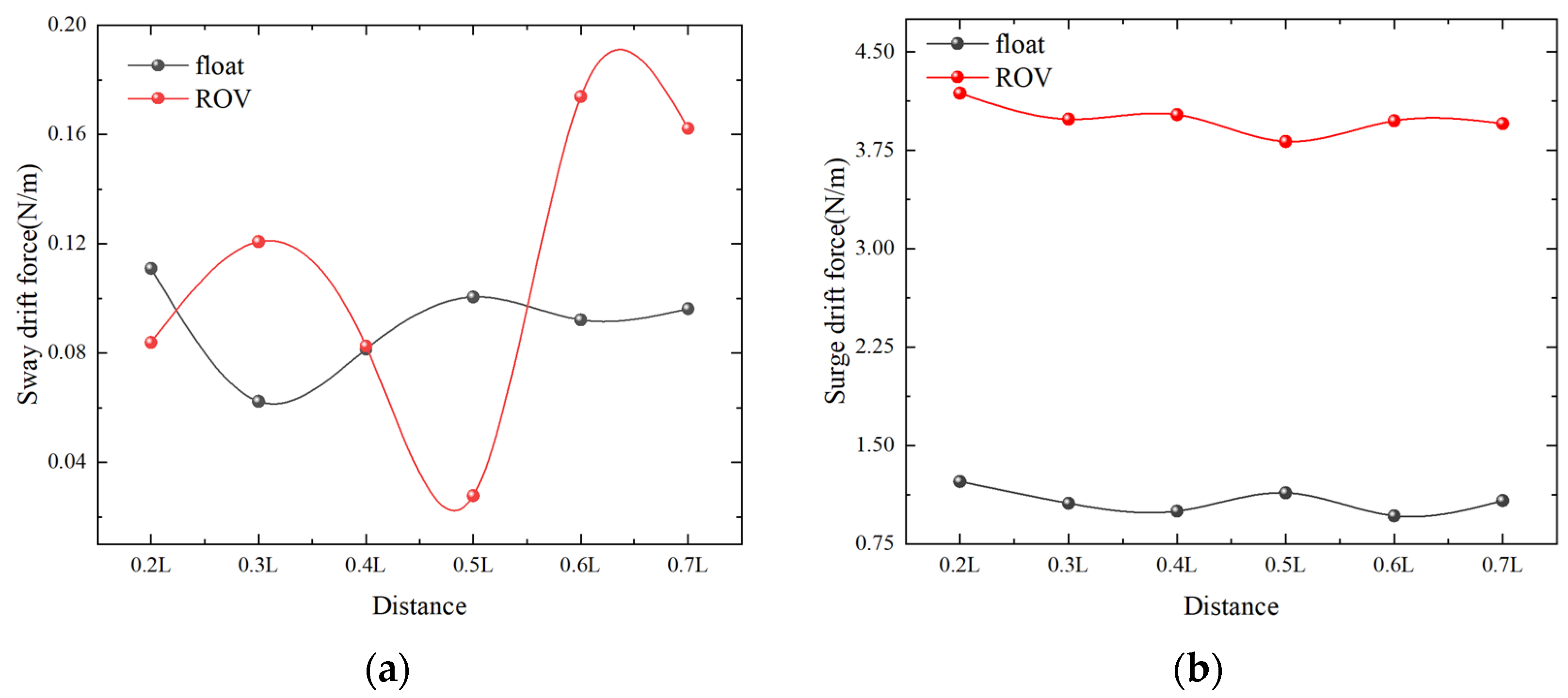
4.3.1. Effect of Spacing between Double Floats on Salvage Systems
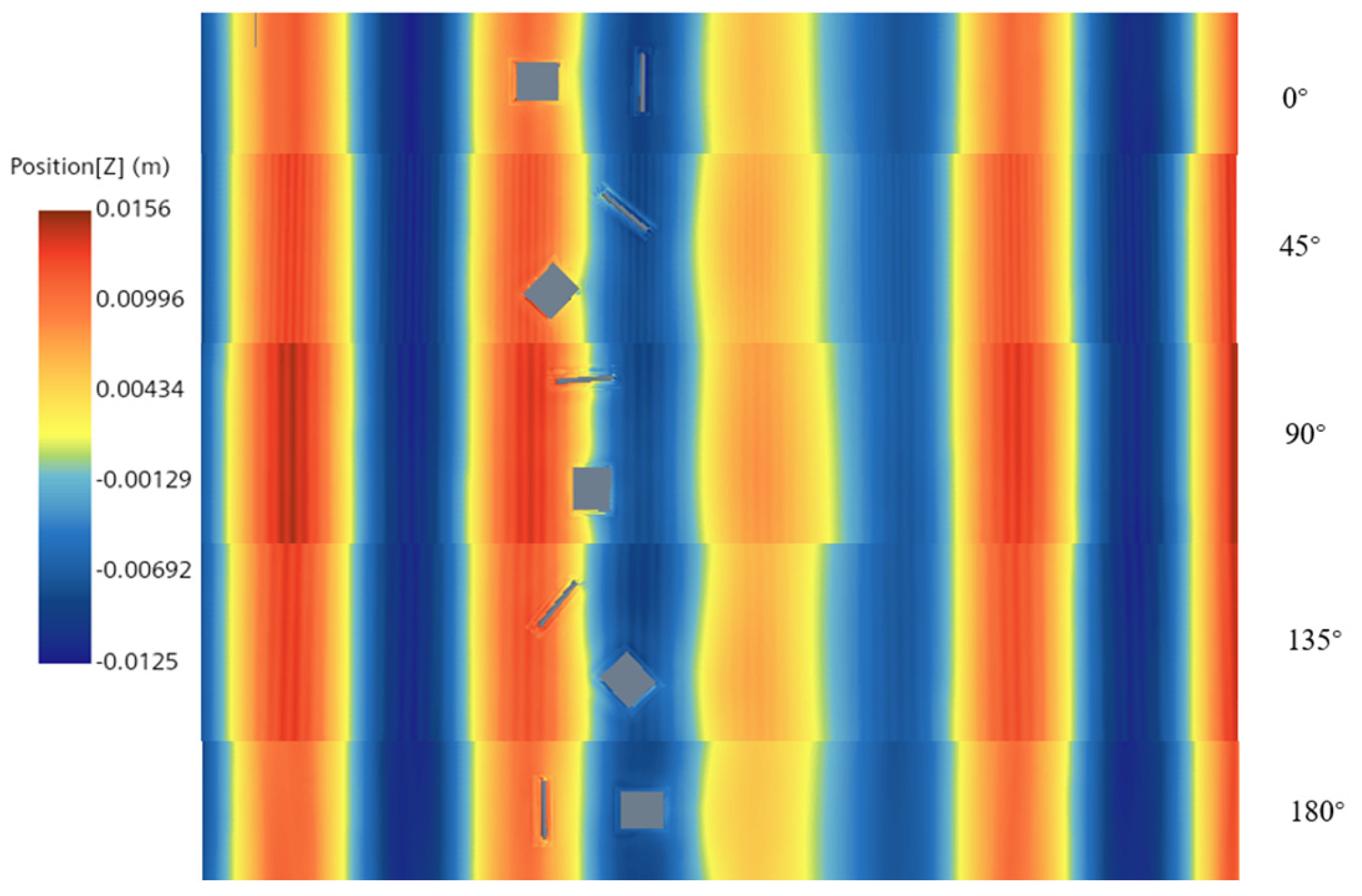
4.3.2. Effect of Wave Direction on Salvage Systems
4.4. Characteristics of Double Floating Body Towing Motion
5. Conclusions
- Numerical simulation of single-float and double-float coupling.
- 2.
- Characteristics of Double Floating Body Berthing Motion.
- 3.
- Characteristics of Double Floating Body Side-by-side Motion.
- 4.
- Characteristics of Double Floating Body Towing Motion.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.S. Research on Deep-Sea Wreckage Salvage System and Its Key Technology. Doctoral Dissertation, Harbin Engineering University, Harbin, China, 2019. [Google Scholar]
- Xiao, W.; Wanh, Y.; Liu, W.; Cheng, X.; Wang, D.; Zhang, L. Numerical Investigation of the Frequency-domain Coupled Hydrodynamics for Two Ships Advancing at Close Proximity in Waves. In Proceedings of the OCEANS 2018 MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Luo, X.C. Numerical Simulation and Experimental Study on the Problem of Coupled Action of FLNG Ship Motion and Liquid Tank Sloshing. Master’s Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]
- Xie, C.; Choi, Y.; Rongère, F.; Clément, A.H.; Delhommeau, G.; Babarit, A. Comparison of existing methods for the calculation of the infinite water depth free-surface Green function for the wave–structure interaction problem. Appl. Ocean Res. 2018, 81, 150–163. [Google Scholar] [CrossRef]
- Hong, L. Moving Pulsation Source Green’s Function Method and the Study of Resistance Increase of Sailing Ships in Waves. Doctoral Dissertation, Shanghai Jiao Tong University, Shanghai, China, 2017. [Google Scholar]
- Yang, J. Research on Three-Dimensional Time-Domain Nonlinear Wave Load Calculation Method. Doctoral Dissertation, China Shipbuilding Research Institute, Beijing, China, 2016. [Google Scholar]
- Kianejad, S.S.; Enshaei, H.; Duffy, J.; Ansarifard, N.; Ranmuthugala, D. Ship roll damping coefficient prediction using CFD. J. Ship Res. 2019, 63, 108–122. [Google Scholar] [CrossRef]
- Hong, Z.C. Hydrodynamic Performance Prediction and Optimisation of Ships Based on CFD Method. Doctoral Dissertation, Dalian University of Technology, Dalian, China, 2018. [Google Scholar]
- Yang, S.Y.; Zhang, H.S.; Wu, P.F. Theoretical solution and characterisation of second-order resonance for three-dimensional swaying motion of liquid tanks. Ocean Eng. 2015, 33, 71–79. [Google Scholar]
- Saripilli, J.R.; Sen, D. Sloshing-Coupled Ship Motion Algorithm for Estimation of Slosh-Induced Pressures: Keynote Contribution for the International Workshop on Wave Loads and Motions of Ships and Offshore Structures, Harbin, China, 5–7 November, 2017. J. Mar. Sci. Appl. 2018, 17, 312–329. [Google Scholar] [CrossRef]
- Yuan, C.P. Analysis of the Coupled Motion Response of Liquid Tank Sloshing and Ship under Irregular Wave Action. Master’s Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 2021. [Google Scholar]
- Xiao, K.L.; Chen, Z.G. Numerical simulation of time-domain coupled motions of multi-liquid tank wakes and aquaculture vessels. China Ship Res. 2020, 15, 136–144. [Google Scholar]
- Saghi, H. A parametric study on wave–floating storage tank interaction using coupled VOF-FDM method. J. Mar. Sci. Technol. 2019, 24, 454–465. [Google Scholar] [CrossRef]
- Yu, L.; Xue, M.A.; Zhu, A. Numerical investigation of sloshing in rectangular tank with permeable baffle. J. Mar. Sci. Eng. 2020, 8, 671. [Google Scholar] [CrossRef]
- Moradi, N.; Zhou, T.; Cheng, L. Effect of inlet configuration on wave resonance in the narrow gap of two fixed bodies in close proximity. Ocean Eng. 2015, 103, 88–102. [Google Scholar] [CrossRef]
- Gao, J.L.; Zang, J.; Chen, L.F.; Chen, Q.; Ding, H.Y.; Liu, Y.Y. On hydrodynamic characteristics of gap resonance between two fixed bodies in close proximity. Ocean Eng. 2019, 173, 28–44. [Google Scholar] [CrossRef]
- Gao, J.L.; He, Z.W.; Huang, X.H.; Liu, Q.; Zang, J.; Wang, G. Effects of free heave motion on wave resonance inside a narrow gap between two boxes under wave actions. Ocean Eng. 2021, 224, 108753. [Google Scholar] [CrossRef]
- Wu, Y.W.; Zhou, J.; Li, H.; Bi, Z. Numerical simulation of liquid tank sloshing with different shapes based on VOF method. Ship Sci. Technol. 2022, 44, 84–89. [Google Scholar]
- Saghi, R.; Hirdaris, S.; Saghi, H. The influence of flexible fluid structure interactions on sway induced tank sloshing dynamics. Eng. Anal. Bound. Elem. 2021, 131, 206–217. [Google Scholar] [CrossRef]
- Zhao, D.; Hu, Z.; Chen, G.; Lim, S.; Wang, S. Nonlinear sloshing in rectangular tanks under forced excitation. Int. J. Nav. Archit. Ocean Eng. 2018, 10, 545–565. [Google Scholar] [CrossRef]
- Ning, D.Z.; Su, P.; Zhang, S.W.; Li, X. Hydrodynamic characteristics of float-type sway-reducing structures in three-dimensional liquid tanks. J. Harbin Eng. Univ. 2019, 40, 154–161. [Google Scholar]
- Liu, Y.; Falzarano, J. A wall damping method to estimate the gap resonance in side-by-side offloading problems. Ocean Eng. 2019, 173, 510–518. [Google Scholar] [CrossRef]
- Zhao, W.; Milne, I.A.; Efthymiou, M.; Wolgamot, H.A.; Draper, S.; Taylor, P.; Taylor, R.E. Current practice and research directions in hydrodynamics for FLNG-side-by-side offloading. Ocean Eng. 2018, 158, 99–110. [Google Scholar] [CrossRef]
- Zhang, Z.K. Numerical Simulation of Multi-Floating Complex Structures under Wave Response. Master’s Thesis, Nanjing University of Science and Technology, Nanjing, China, 2018. [Google Scholar]
- Koop, A. Using CFD to determine scale effects on current loads of offshore vessels in side-by-side configuration. Ocean Eng. 2020, 195, 106707. [Google Scholar] [CrossRef]
- Jiang, C.; el Moctar, O.; Schellin, T.E. Mooring-Configurations Induced Decay Motions of a Buoy. J. Mar. Sci. Eng. 2021, 9, 350. [Google Scholar] [CrossRef]
- Saltari, F.; Pizzoli, M.; Coppotelli, G.; Gambioli, F.; Cooper, J.E.; Mastroddi, F. Experimental characterisation of sloshing tank dissipative behaviour in vertical harmonic excitation. J. Fluids Struct. 2022, 109, 103478. [Google Scholar] [CrossRef]
- Igbadumhe, J.-F.; Sallam, O.; Fürth, M.; Feng, R. Experimental Determination of Non-Linear Roll Damping of an FPSO Pure Roll Coupled with Liquid Sloshing in Two-Row Tanks. J. Mar. Sci. Eng. 2020, 8, 582. [Google Scholar] [CrossRef]
- Sanapala, V.S.; Sajish, S.D.; Velusamy, K.; Ravisankar, A.; Patnaik, B.S.V. An experimental investigation on the dynamics of liquid sloshing in a rectangular tank and its interaction with an internal vertical pole. J. Sound. Vib. 2019, 449, 43–63. [Google Scholar] [CrossRef]
- Liu, Y.L.; Teng, B. Variable amplitude coupling test of floatation tank motion and liquid tank sway. Ship Eng. 2022, 44, 71–74. [Google Scholar]
- Kawahashi, T.; Arai, M.; Wang, X. A study on the coupling effect between sloshing and motion of FLNG with partially filled tanks. J. Mar. Sci. Technol. 2019, 24, 917–929. [Google Scholar] [CrossRef]
- Song, X.; Liu, W.; Wu, H. Investigation on Load Characteristics of Hinged Connector for a Large Floating Structure Model under Wave Actions. J. Mar. Sci. Eng. 2023, 11, 786. [Google Scholar] [CrossRef]
- Song, N. Hydrodynamic Simulation Analysis and Experimental Research of Underwater Robot. Master’s Thesis, Dalian University of Technology, Dalian, China, 2020. [Google Scholar]
- Hao, J.; Ding, D.; Li, J.; Huang, J. The Wave Amplification Mechanism of Resonant Caisson. J. Mar. Sci. Eng. 2024, 12, 1038. [Google Scholar] [CrossRef]
- Zhou, W.; Cheng, Y.; Lin, Z. Numerical simulation of long-wave wave dissipation in near-water flat-plate array breakwaters. Ocean Eng. 2023, 268, 113377. [Google Scholar] [CrossRef]
- Malenica, Š.; Orozco, J.; Chen, X. In Some aspects of multibody interactions in seakeeping. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Seoul, Republic of Korea, 19–24 June 2005; ISOPE: Nanjing, China, 2005; p. ISOPE-I-05-250. [Google Scholar]
- Zhu, J.; Frerich, T.; Herrmann, A.S. CFD modeling and validation of heat transfer inside an autoclave based on a mesh independency study. J. Compos. Mater. 2021, 55, 2469–2487. [Google Scholar] [CrossRef]
- Chen, F. Hydrodynamic Characterisation of Small-Scale Broken Ice Coupled with Floating Platform in Wave Field. Master’s Thesis, Jiangsu University of Science and Technology, Zhenjiang, China, 2023. [Google Scholar]
- Xin, S.; Wang, Y.; Wang, L.; Zhu, X.; Chen, S.; Zhou, D. Dynamic analysis of the mooring system of a salvage barge: A coupled time-domain method considering seabed resistance during the off-bottom stage. Ocean Eng. 2023, 275, 114078. [Google Scholar] [CrossRef]
- Wang, G.Y.; Zhang, Q.; Zhao, Y.L. Analysis of velocity distribution of coastal currents under irregular waves. Ocean Eng. 2021, 39, 11–20. [Google Scholar]






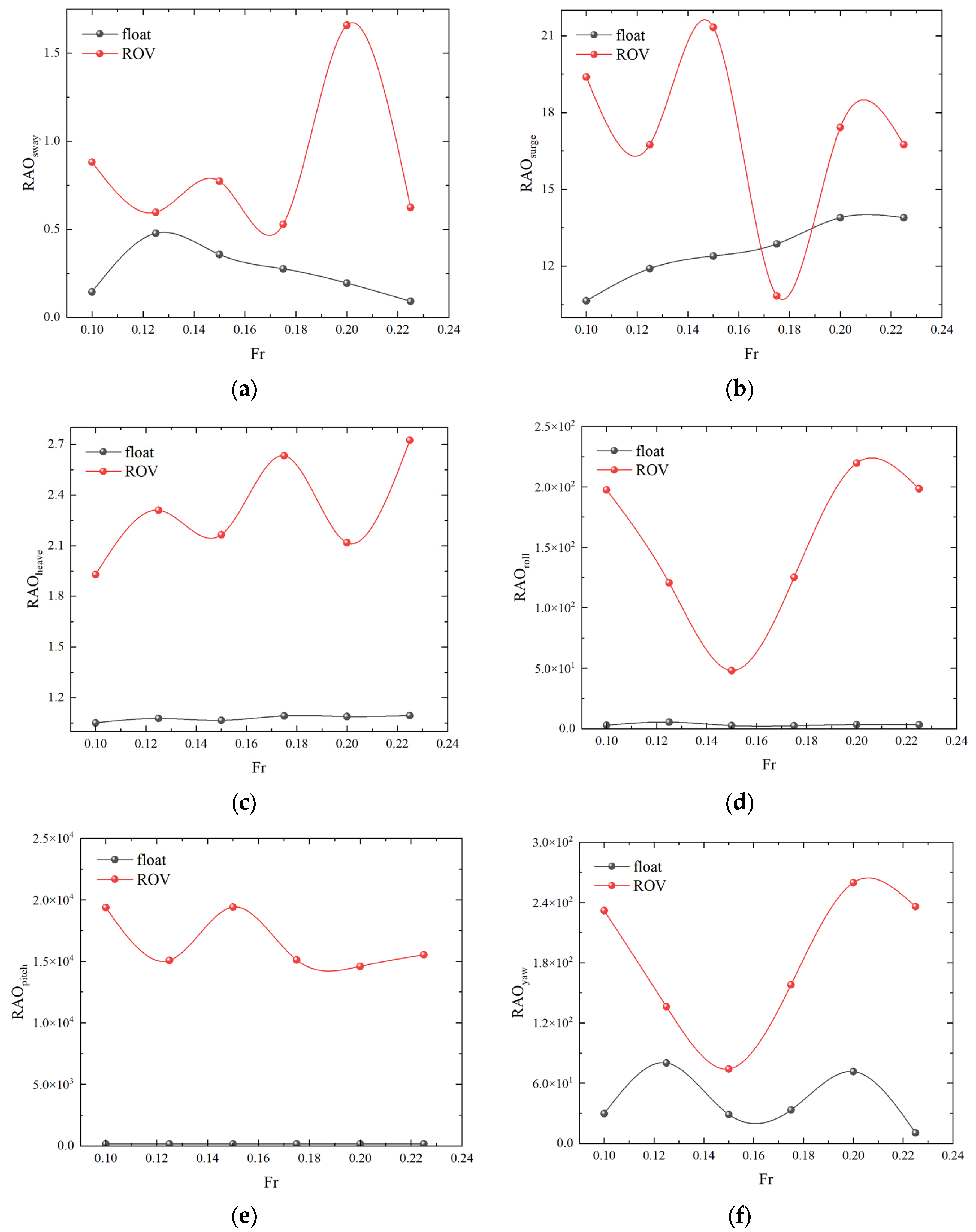
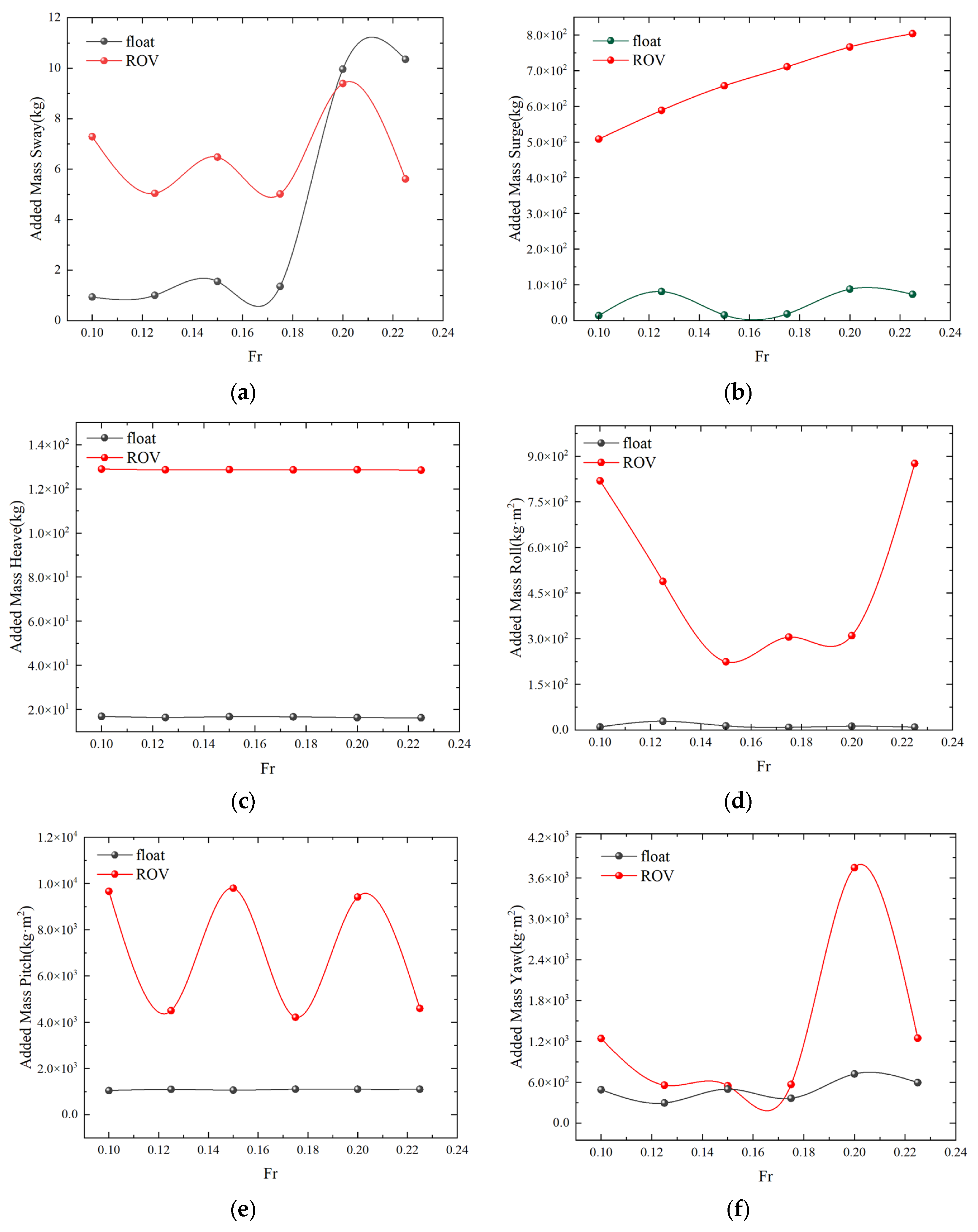
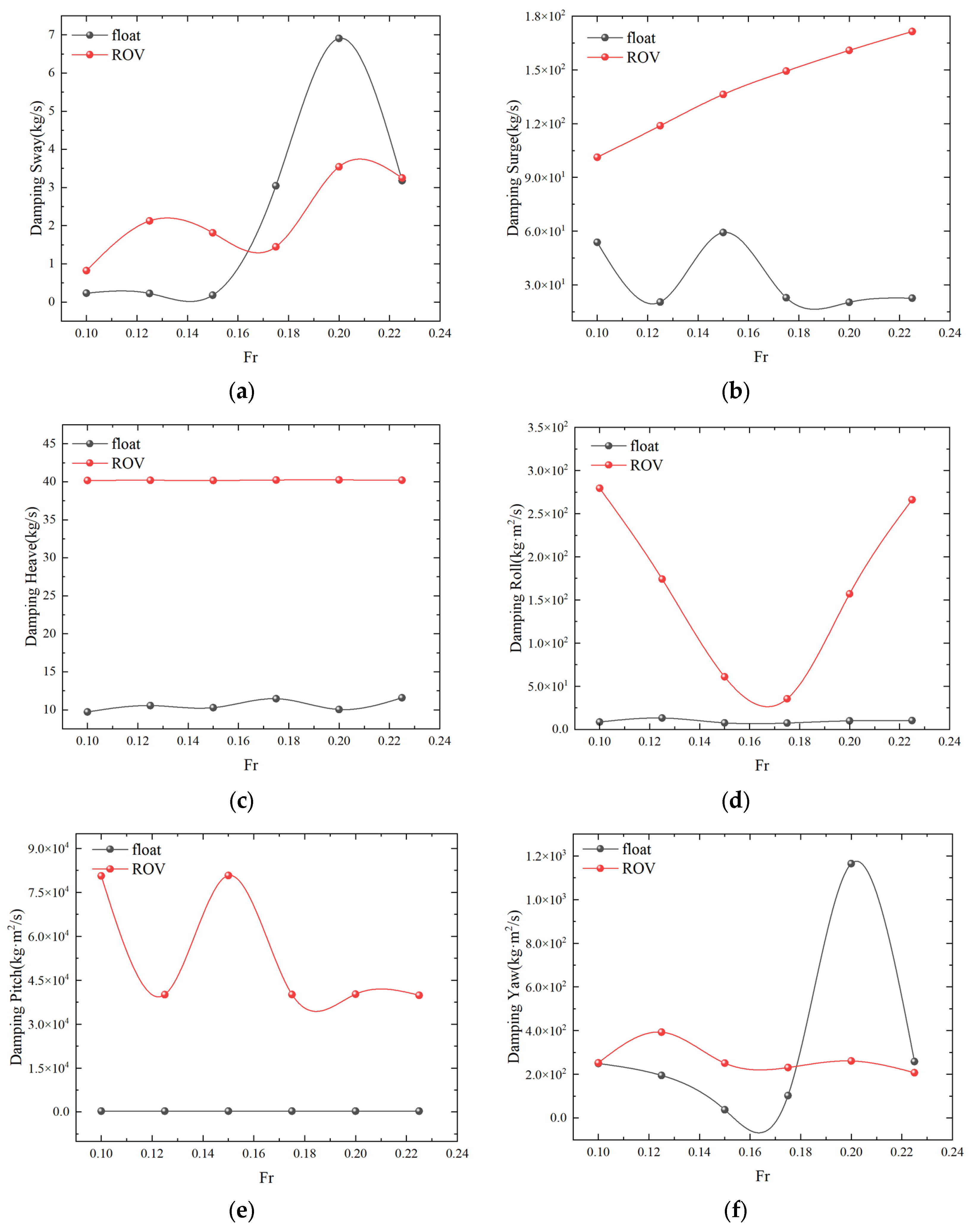
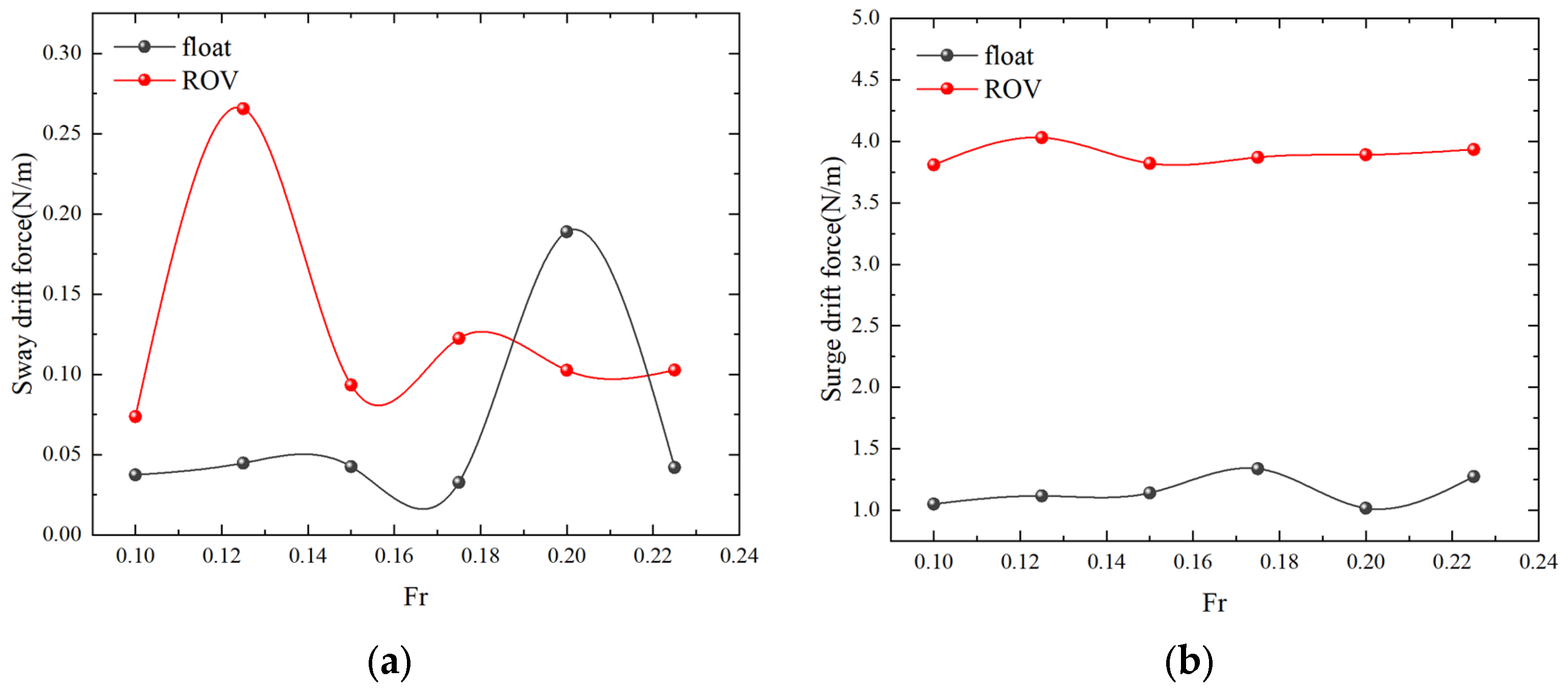
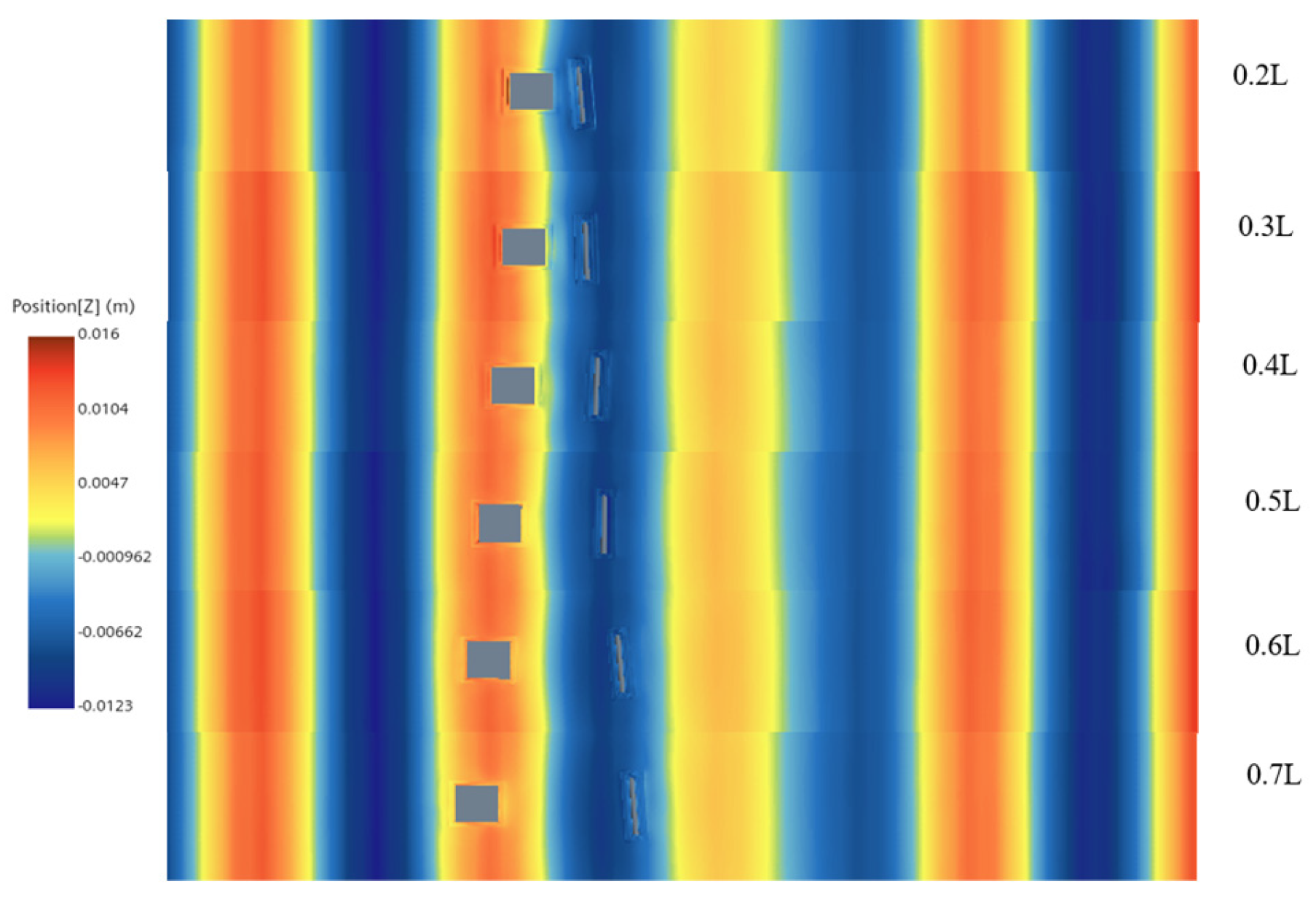

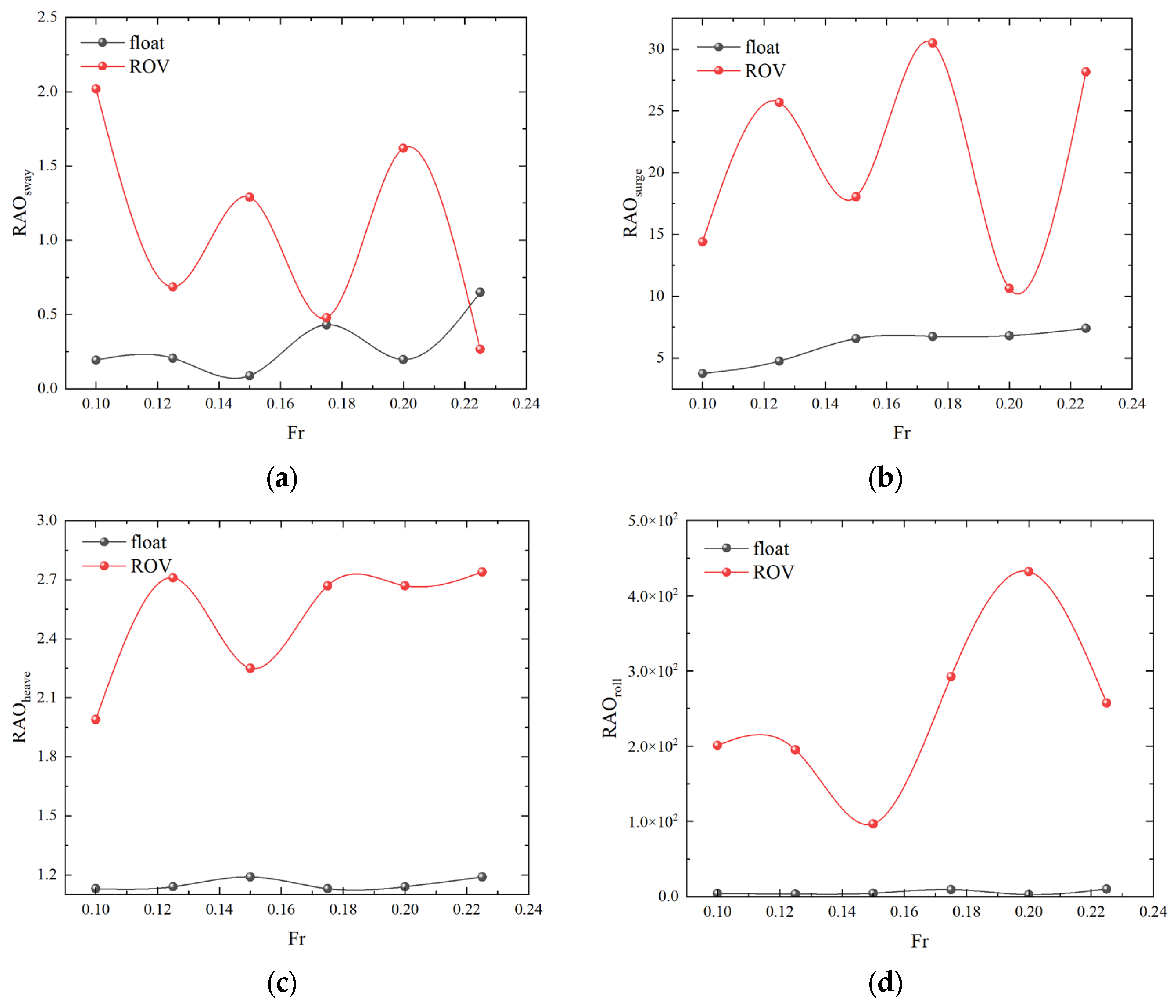
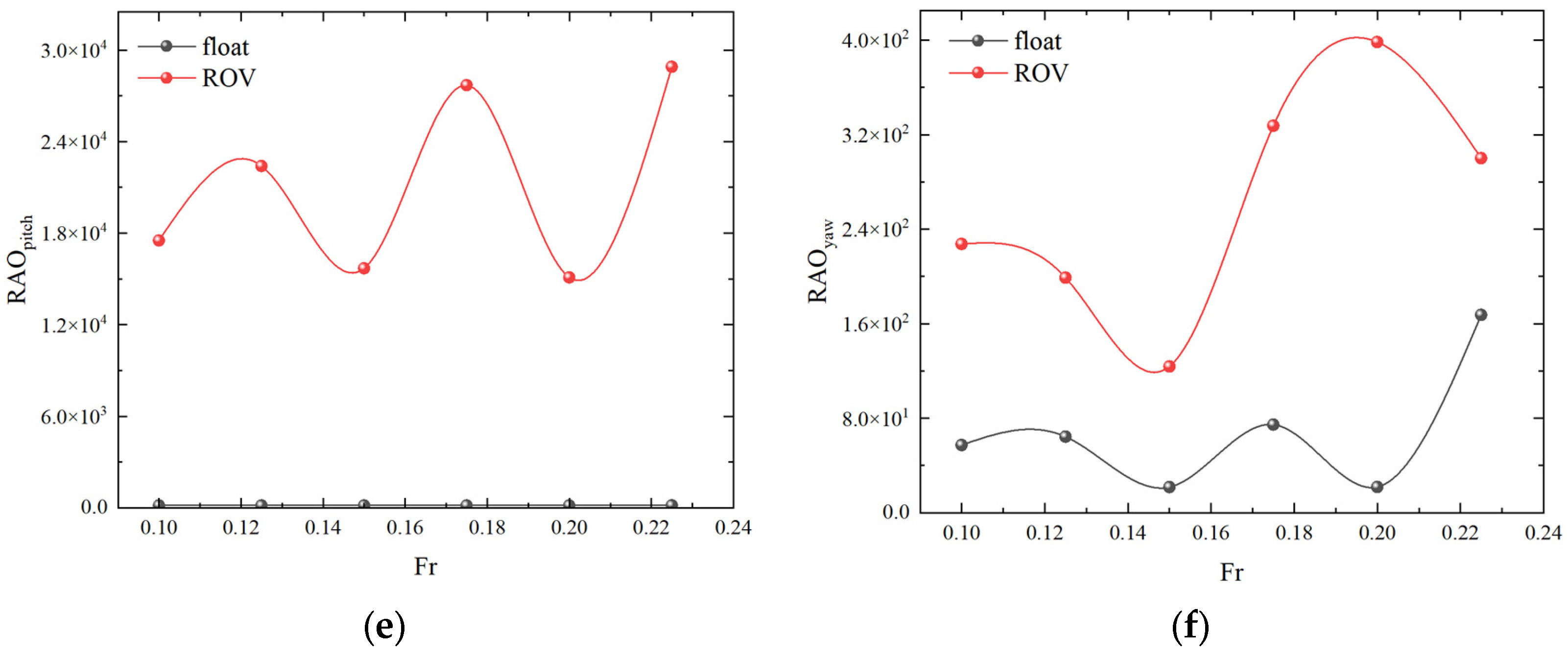
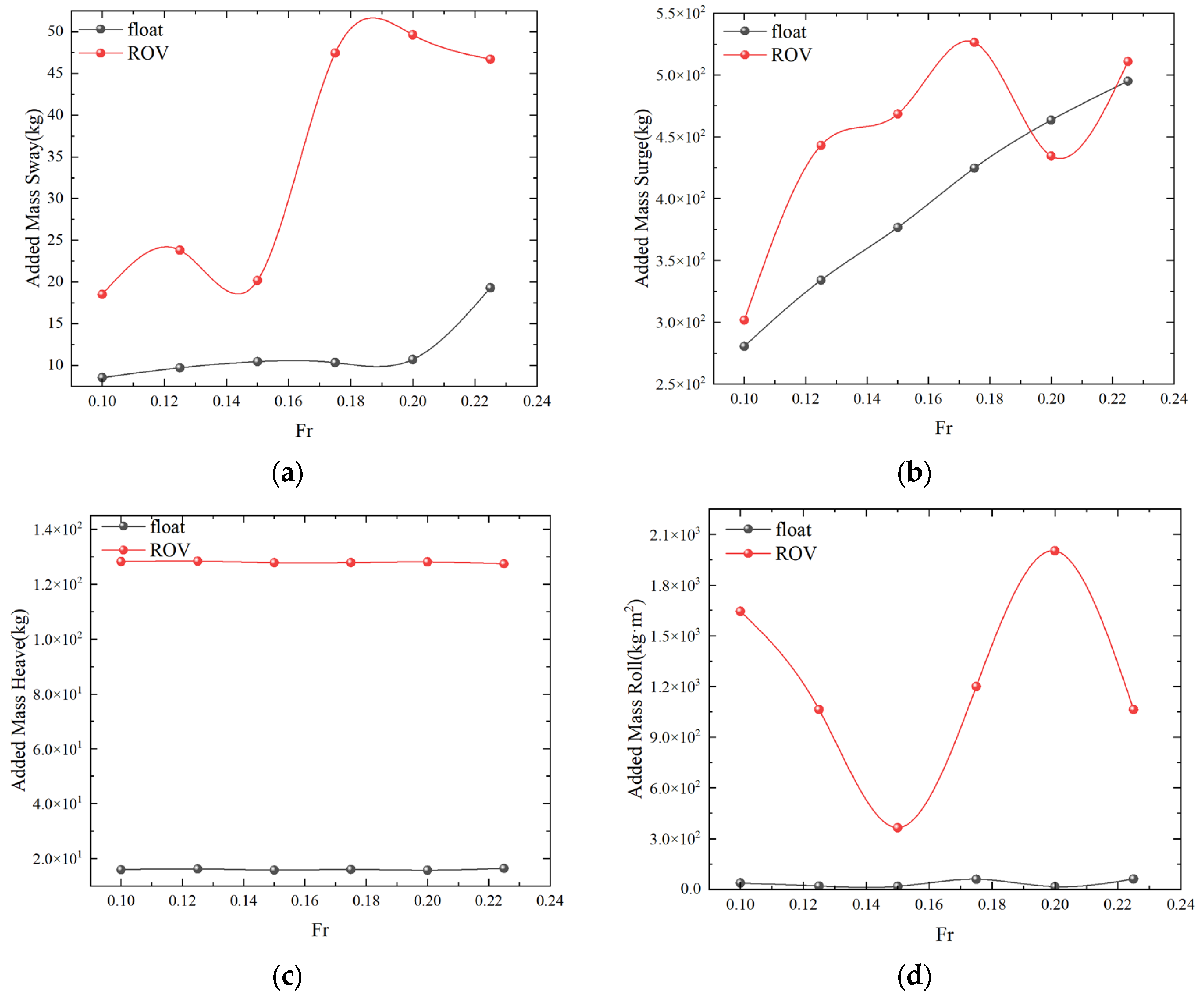
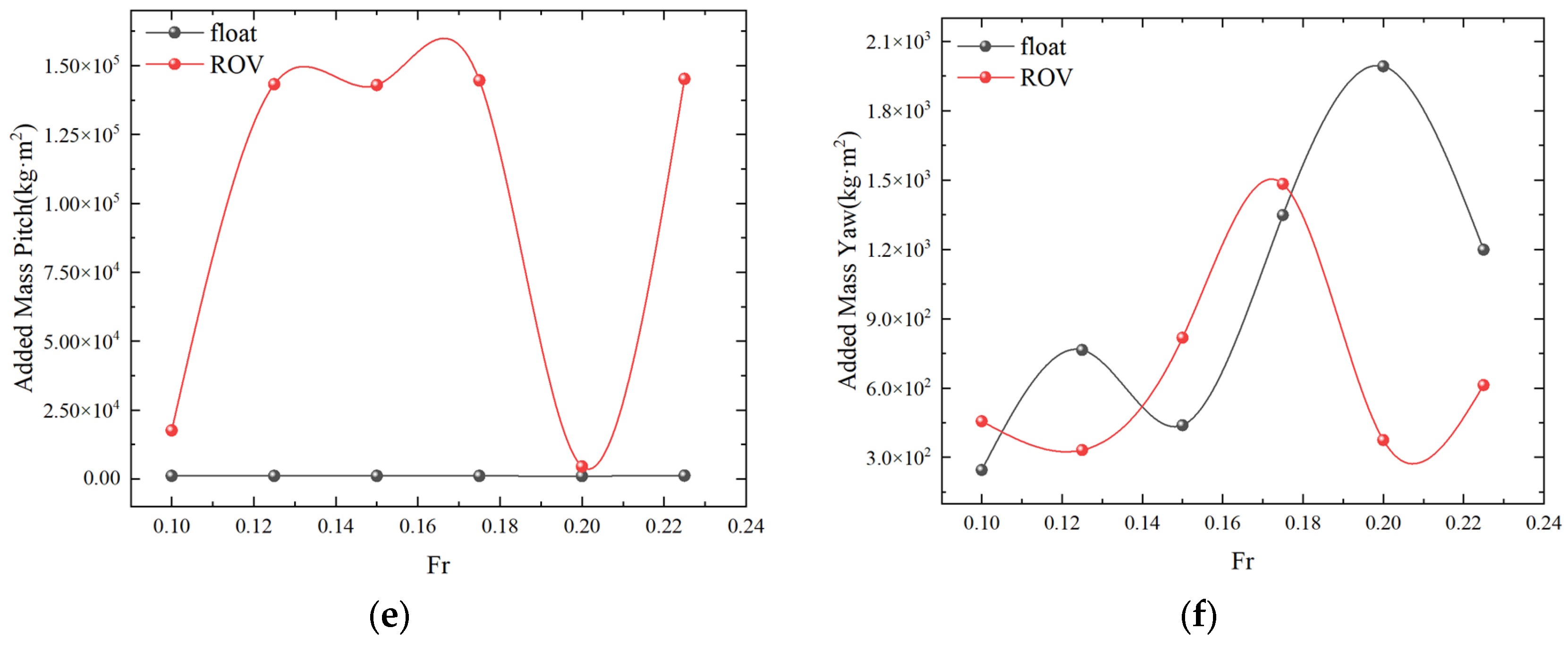

| Designation | Unit | Numerical Model |
|---|---|---|
| Molded length | La (m) | 0.86 |
| Molded breadth | Da (m) | 0.75 |
| Type high | Ha (m) | 0.60 |
| Draft | ha (m) | 0.40 |
| Weight | Ma (kg) | 94.91 |
| Center of gravity | CGa (m) | x = 0, y = 0, z = 0.168 |
| Moment of inertia | Ia (kg/m2) | x = 7.527, y = 8.366, z = 10.436 |
| Designation | Unit | Numerical Model |
|---|---|---|
| Molded length | Lb (m) | 1.2 |
| Diameter | Db (m) | 0.145 |
| Draft | hb (m) | 0.1 |
| Weight | Mb (kg) | 16.85 |
| Center of gravity | CGb (m) | x = 0, y = 0, z = 0.02 |
| Moment of inertia | Ib (kg/m2) | x = 2.42, y = 2.41, z = 0.07 |
| Grouping | Number of Grids | ROV Heave (m) | FLOAT Heave (m) | ROV Yaw (deg) | FLOAT Yaw (deg) |
|---|---|---|---|---|---|
| Rough | 3,714,646 | 0.2386 | 0.1043 | 1.1974 | 2.1831 |
| Medium | 4,851,752 | 0.2400 | 0.1055 | 1.2163 | 2.2255 |
| Fine | 6,173,772 | 0.2403 | 0.1063 | 1.2219 | 2.2409 |
| Working Conditions | 4DOFs | RAO | Added Mass | Damping | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CFD | EXP | CFD | EXP | CFD | EXP | ||||||||
| A | B | A | B | A | B | A | B | A | B | A | B | ||
| 0° | Heave | 1.60 | 0.46 | 1.68 | 0.60 | 133.00 | 20.60 | 139.20 | 23.60 | 46.80 | 10.60 | 55.38 | 20.78 |
| Roll | 286.92 | 106.46 | 305.98 | 129.06 | 916.61 | 6.21 | 1009.22 | 16.26 | 197.21 | 9.66 | 281.04 | 17.02 | |
| Pitch | 126.27 | 344.68 | 135.04 | 366.67 | 1120.00 | 316.49 | 1468.17 | 335.60 | 8090.00 | 323.10 | 8530.40 | 372.48 | |
| Yaw | 130.03 | 74.27 | 150.52 | 98.44 | 100.92 | 114.69 | 255.45 | 236.08 | 85.25 | 316.06 | 173.20 | 469.02 | |
| 45° | Heave | 1.78 | 0.70 | 2.04 | 0.82 | 134.00 | 21.50 | 146.40 | 24.40 | 48.00 | 11.50 | 56.72 | 21.90 |
| Roll | 119.14 | 212.37 | 133.77 | 234.34 | 13732.86 | 118.02 | 14213.03 | 133.13 | 1188.26 | 146.96 | 1263.29 | 288.30 | |
| Pitch | 150.16 | 276.36 | 173.36 | 293.36 | 159.90 | 267.47 | 237.78 | 322.54 | 8034.19 | 204.57 | 8444.43 | 380.92 | |
| Yaw | 122.78 | 235.71 | 143.23 | 252.06 | 906.45 | 787.14 | 942.99 | 886.75 | 9674.52 | 173.87 | 9862.07 | 291.25 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, G.; Chen, S.; Zhou, H.; Wan, F. Coupled Motion Response Analysis for Dynamic Target Salvage under Wave Action. J. Mar. Sci. Eng. 2024, 12, 1688. https://doi.org/10.3390/jmse12091688
Sun G, Chen S, Zhou H, Wan F. Coupled Motion Response Analysis for Dynamic Target Salvage under Wave Action. Journal of Marine Science and Engineering. 2024; 12(9):1688. https://doi.org/10.3390/jmse12091688
Chicago/Turabian StyleSun, Gang, Shengtao Chen, Hongkun Zhou, and Fei Wan. 2024. "Coupled Motion Response Analysis for Dynamic Target Salvage under Wave Action" Journal of Marine Science and Engineering 12, no. 9: 1688. https://doi.org/10.3390/jmse12091688
APA StyleSun, G., Chen, S., Zhou, H., & Wan, F. (2024). Coupled Motion Response Analysis for Dynamic Target Salvage under Wave Action. Journal of Marine Science and Engineering, 12(9), 1688. https://doi.org/10.3390/jmse12091688





