Prediction of Mooring Line Top-Tensions Incorporated with Identification of Lost Clump Weights
Abstract
:1. Introduction
2. Numerical Model
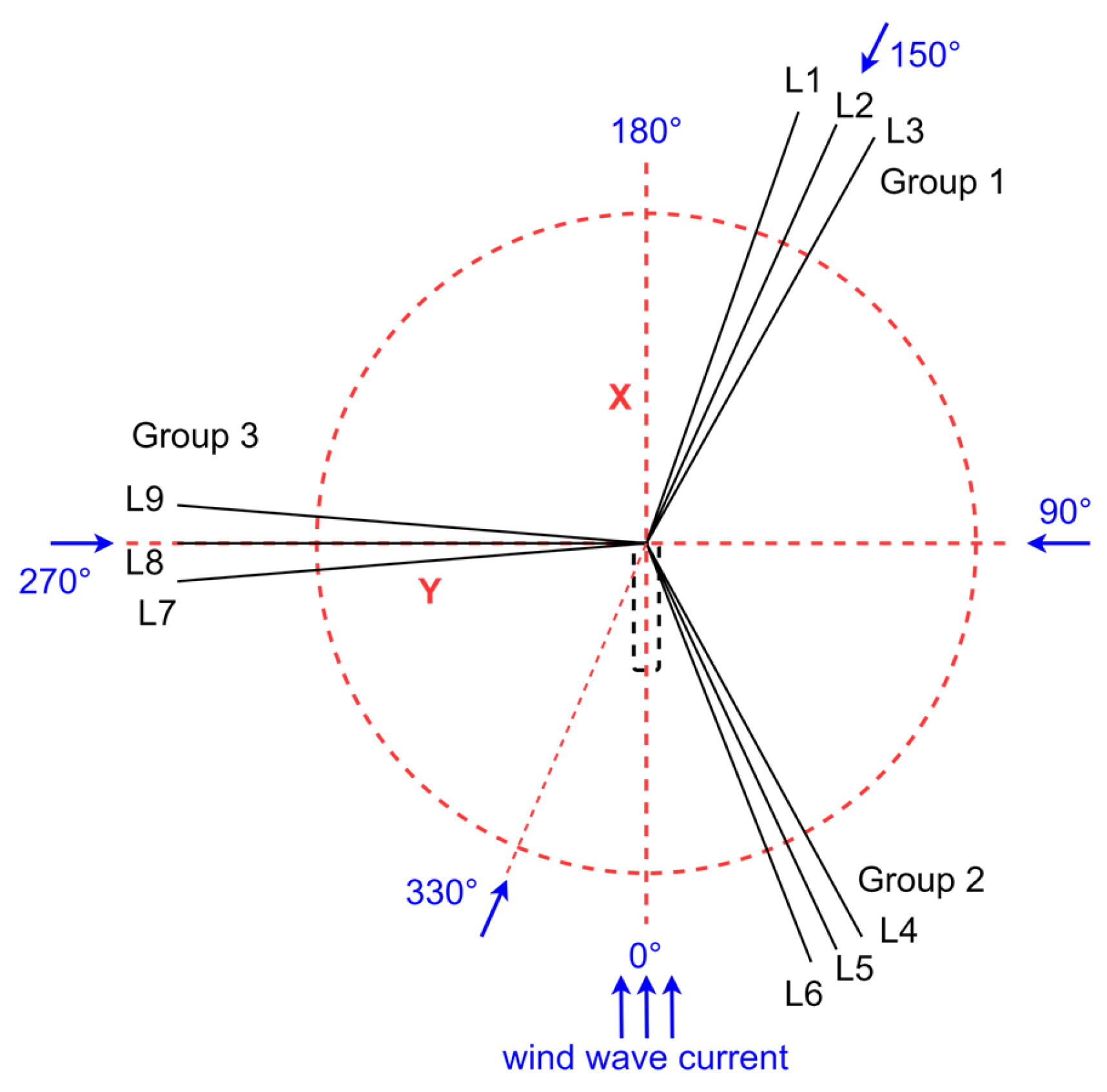
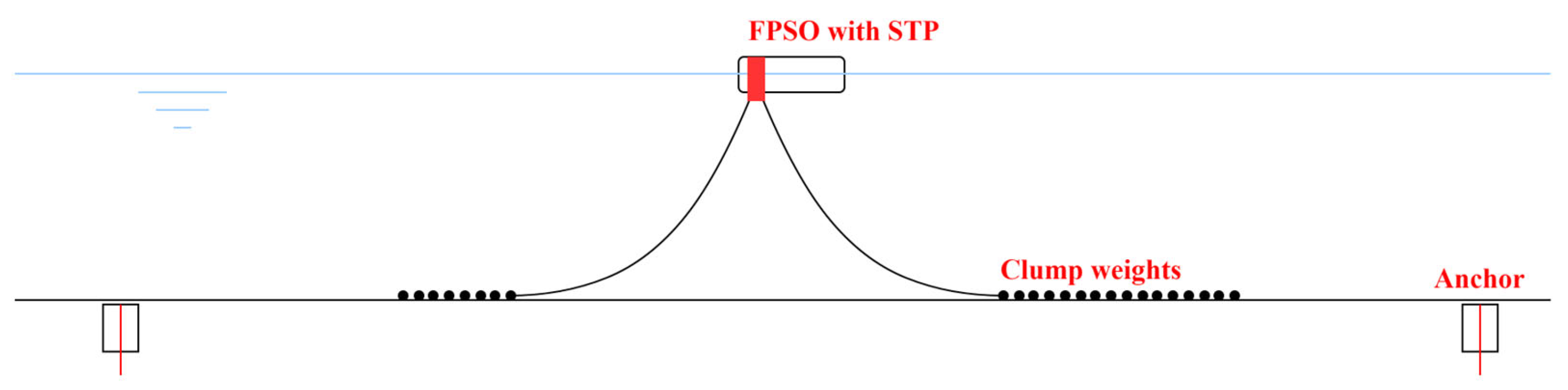
2.1. FPSO and Its Mooring System
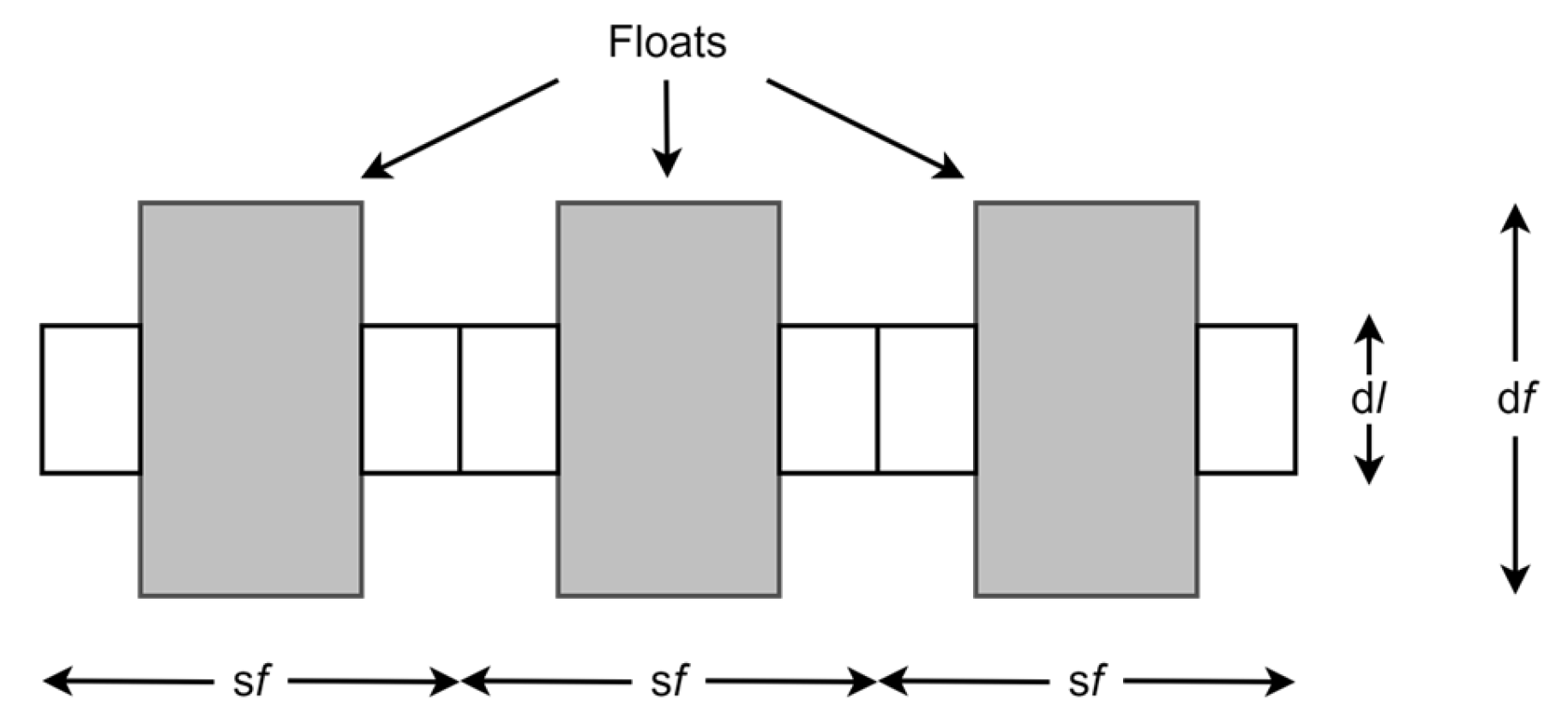
2.2. Simulation Method of Clump Weight Loss
3. Sensitivity Analyses of Clump Weight Loss
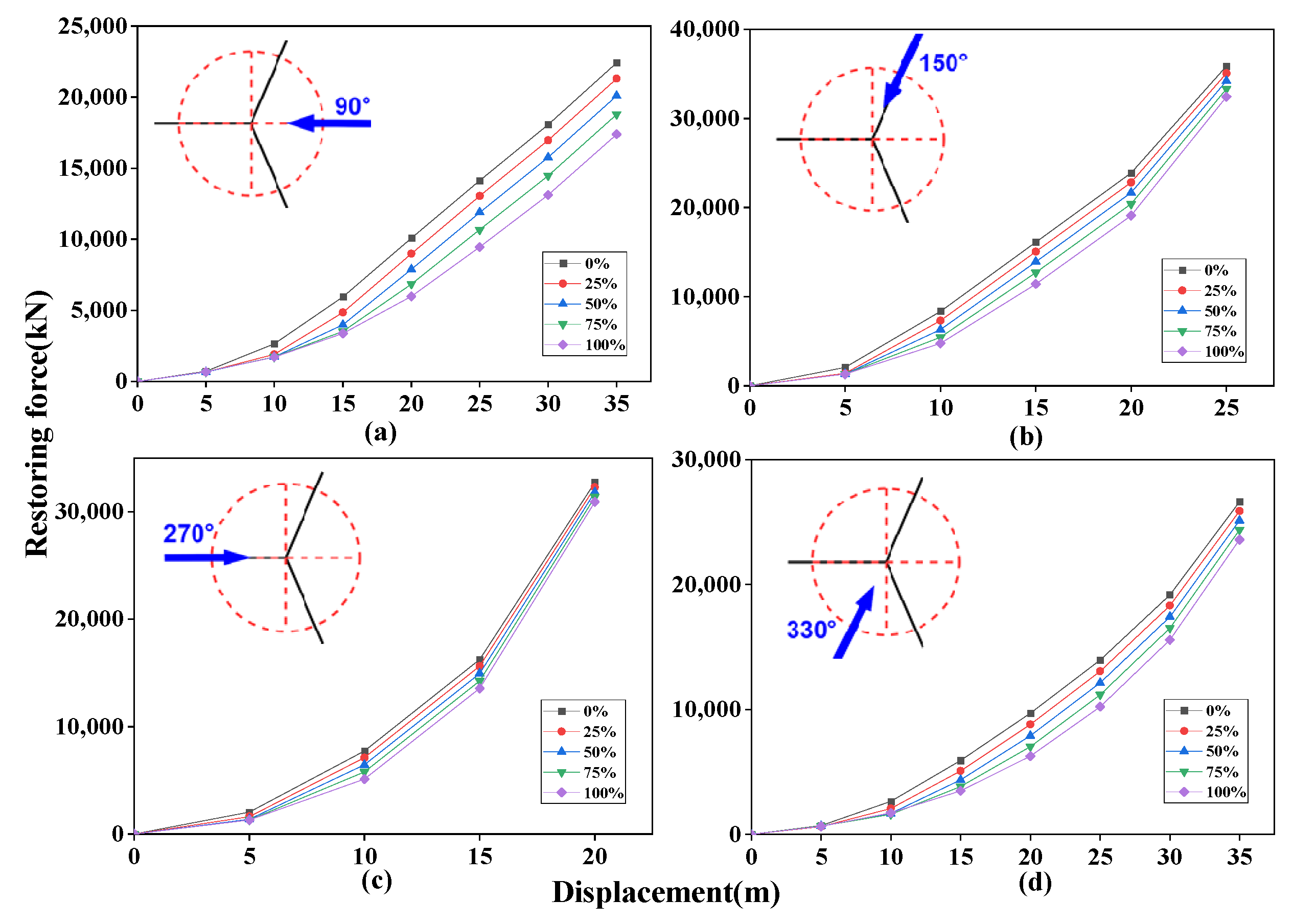
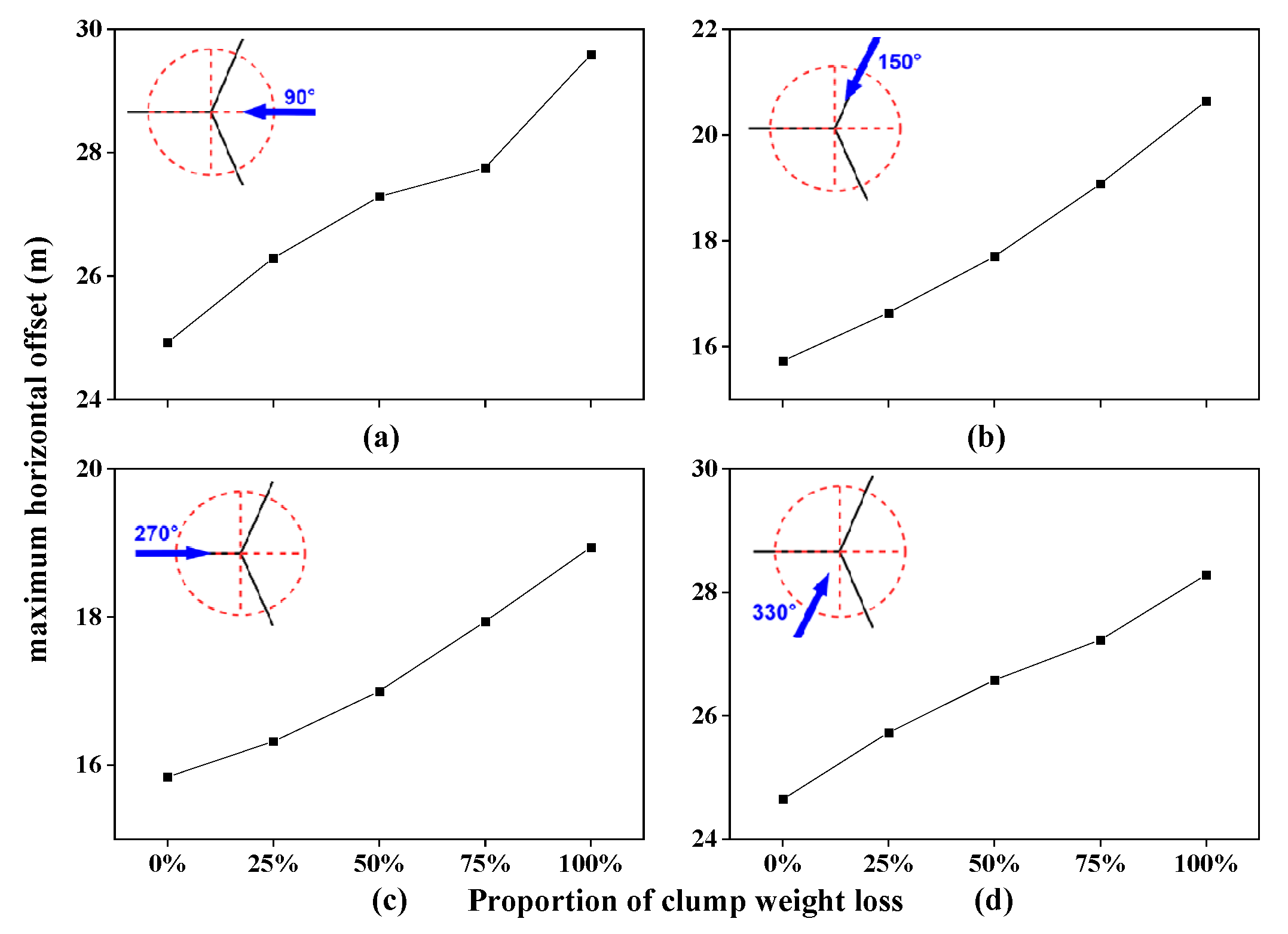
3.1. Static Analyses
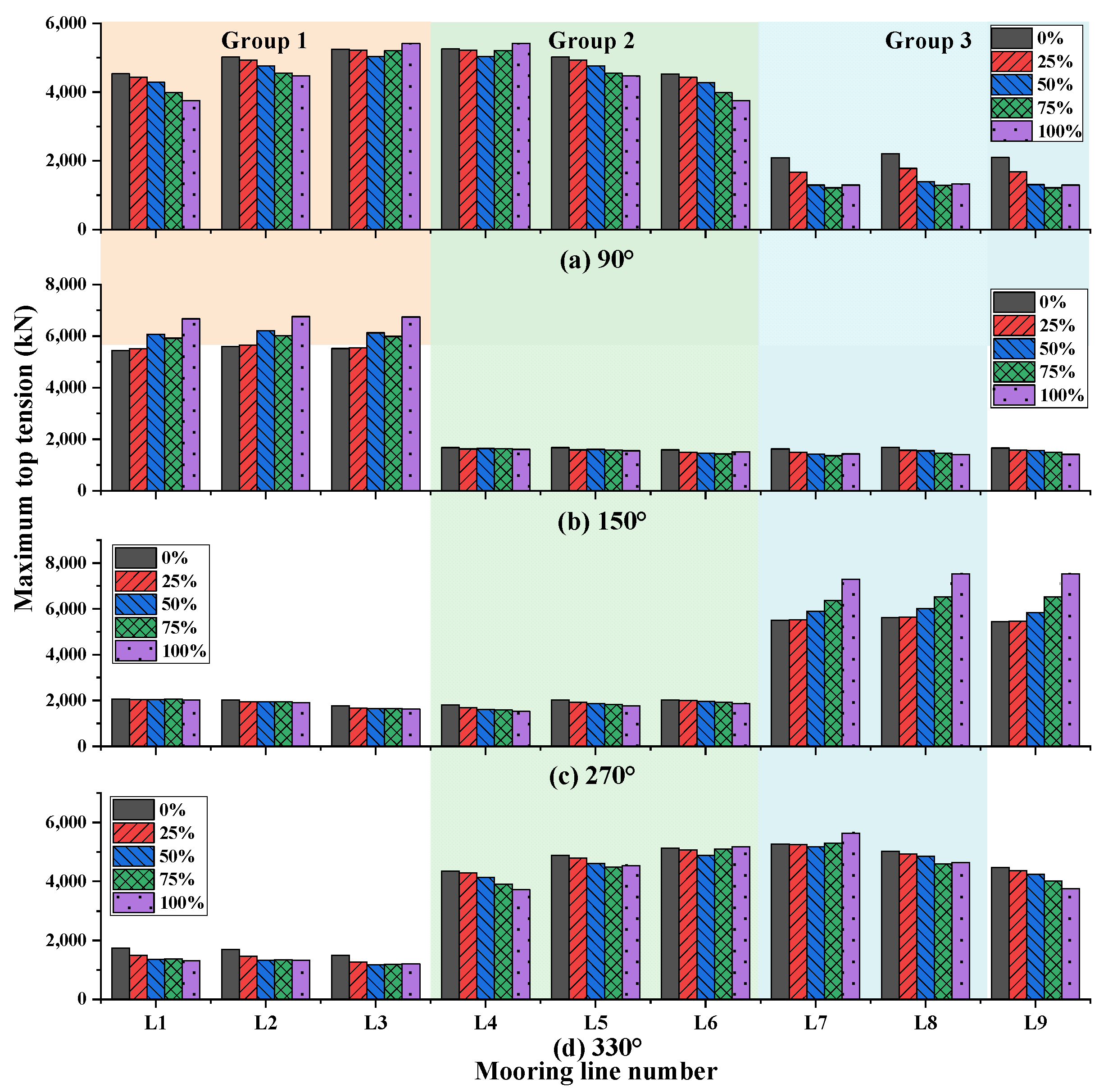
3.2. Dynamic Analyses
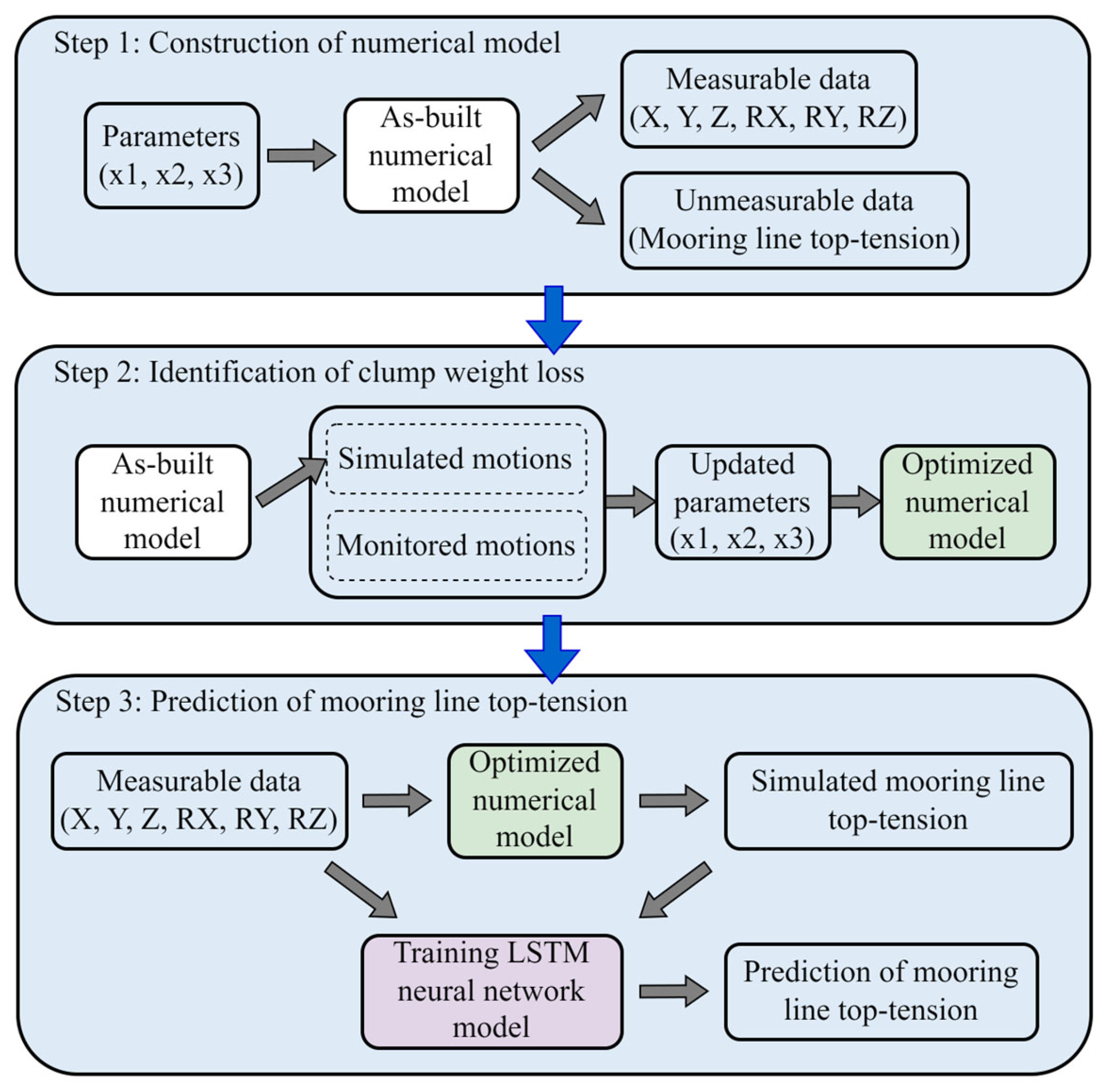
4. Inverse Analyses to Identify Loss of Clump Weight
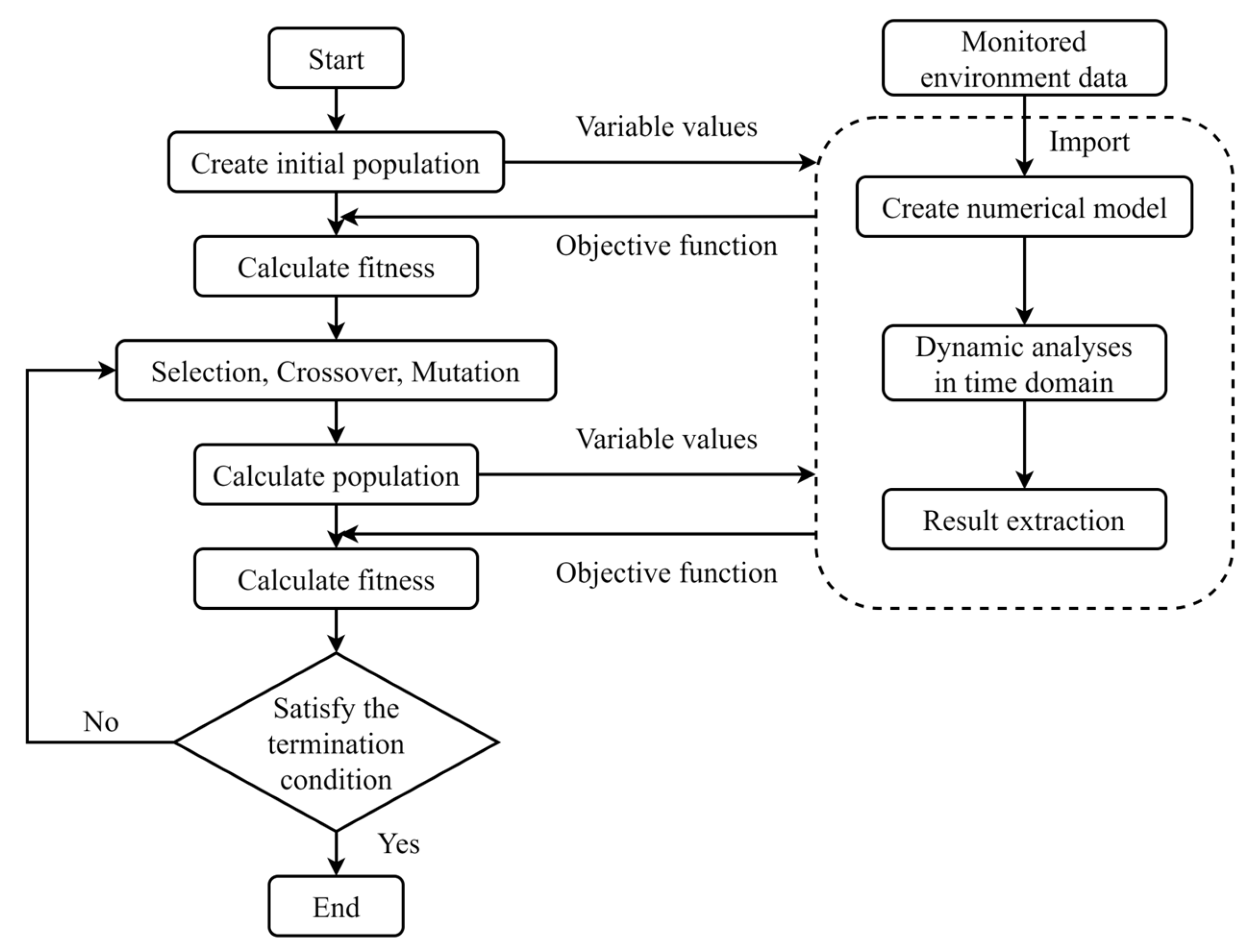
4.1. Method of the Mooring System Optimization Model
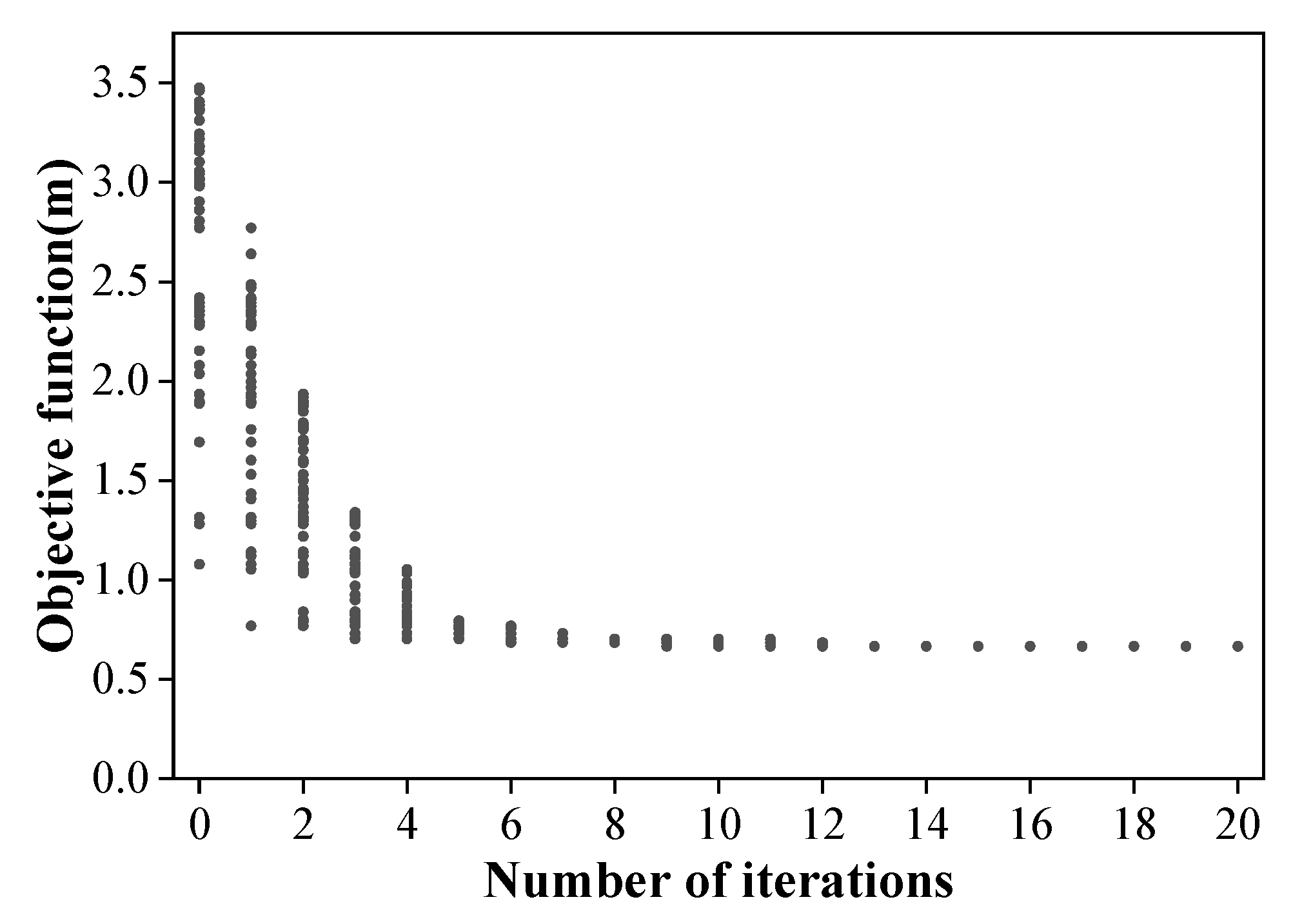
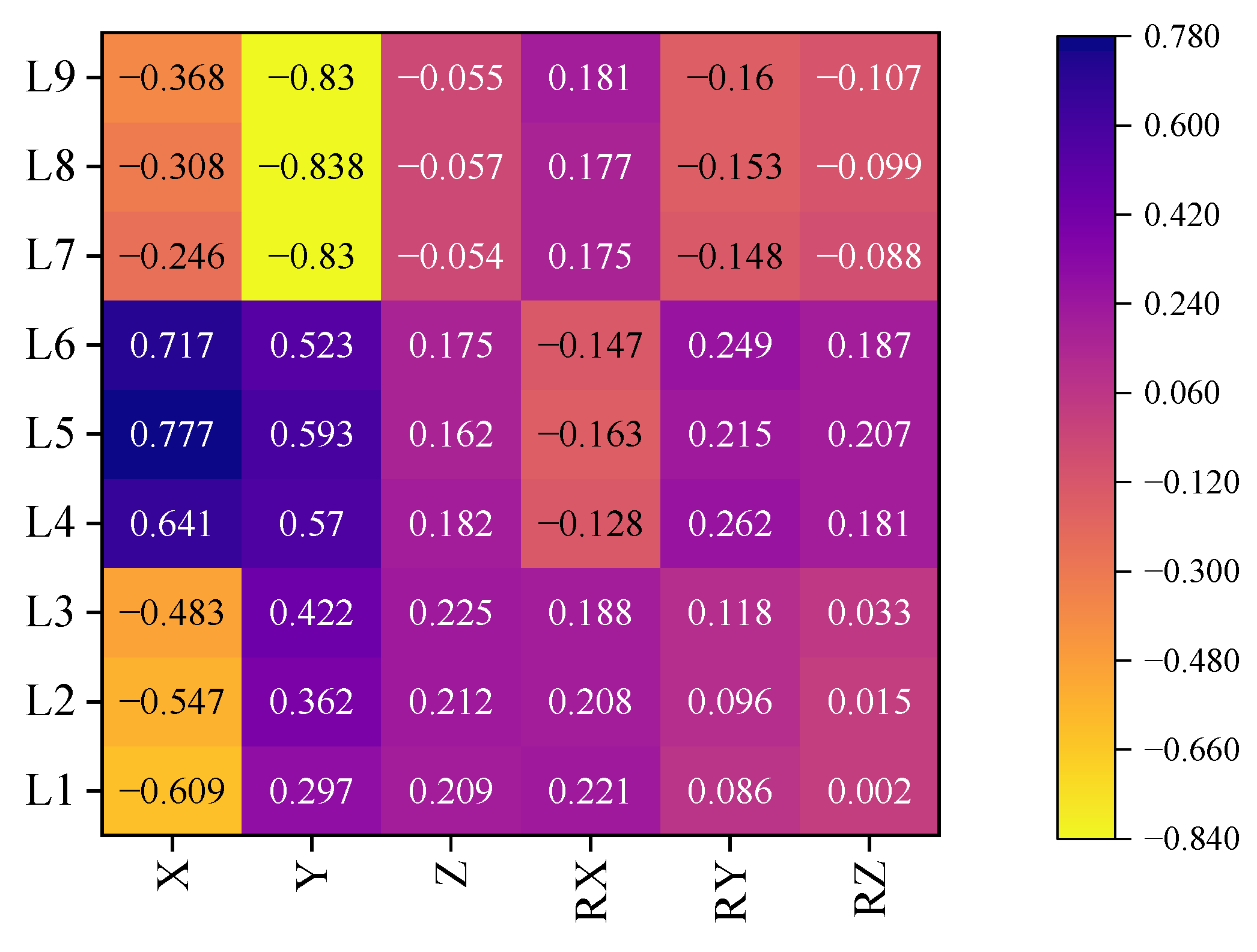
4.2. Parameter Identification and Model Optimization
5. Real-Time Prediction of Mooring Line Top-Tensions
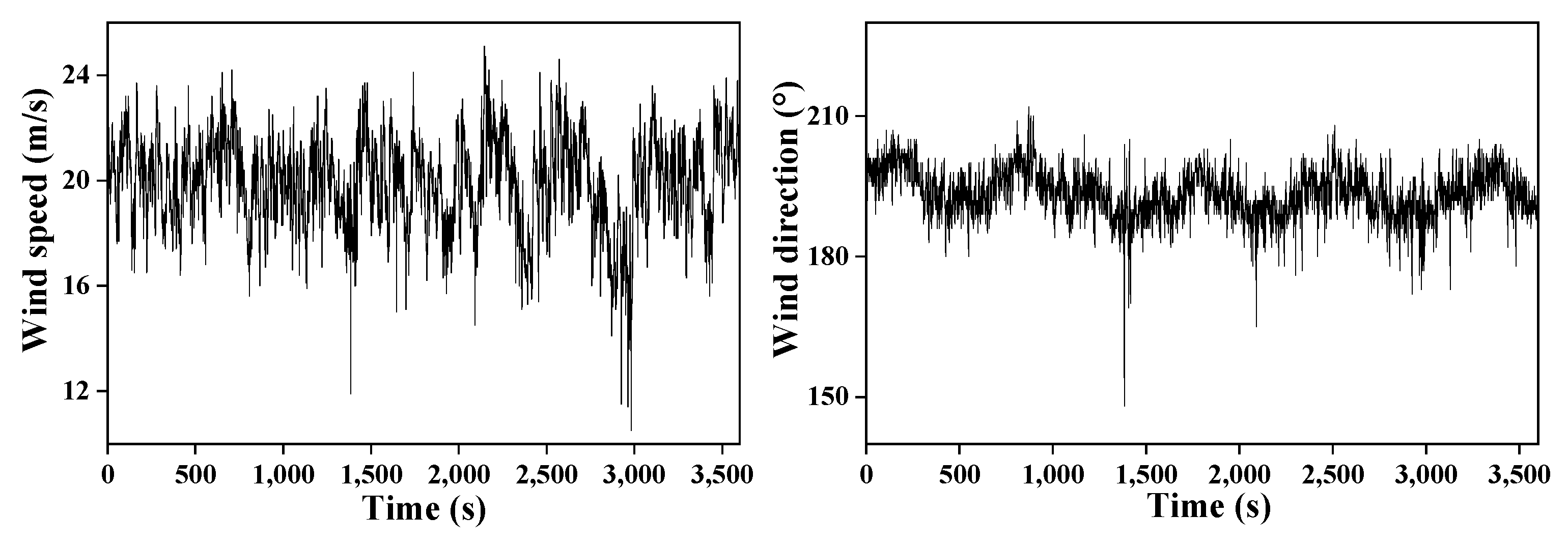
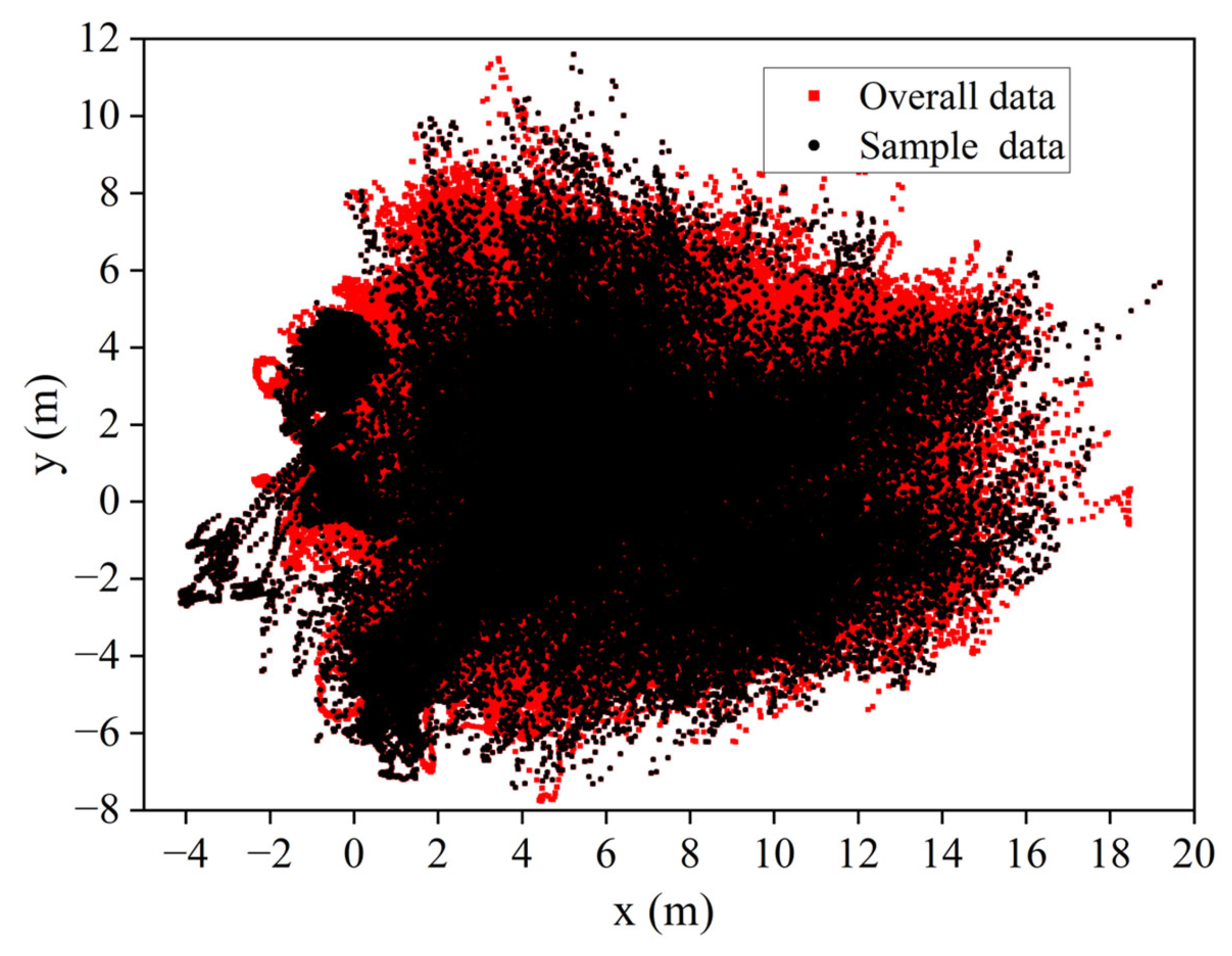
5.1. Data Pre-Processing
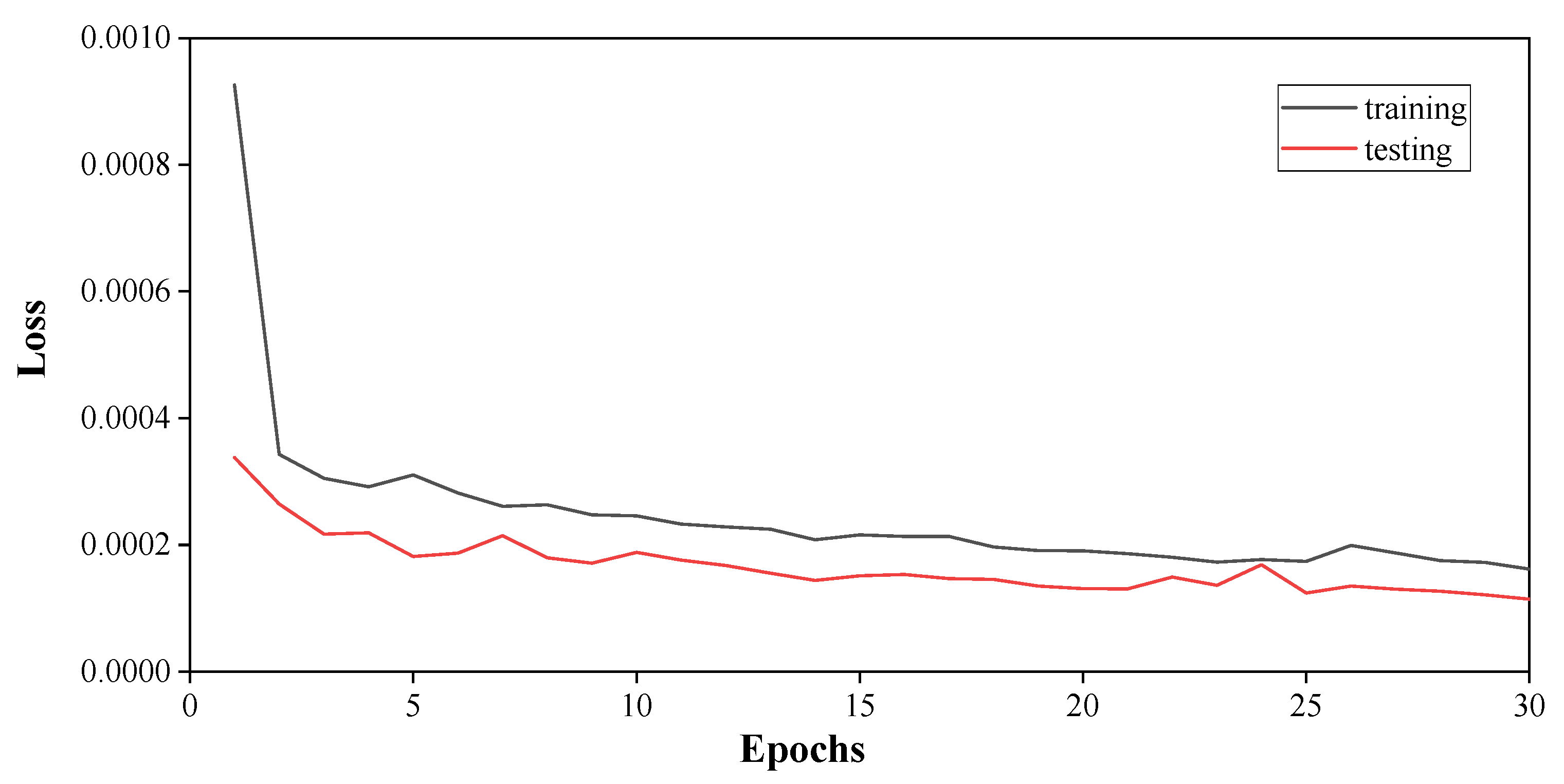
5.2. Prediction of Mooring Line Top-Tensions
6. Conclusions and Discussions
- (1)
- The measured motion data are used to identify the loss of clump weights since it affects the dynamic response of the FPSO and its mooring system. The mooring line components in the numerical model are modified accordingly. The relative error of the maximum horizontal displacement between the numerical results after modification and the measurement is reduced to less than 5%.
- (2)
- Correlation analysis shows that the mooring line top-tension is mostly related to surge and sway motions of the FPSO, so the horizontal motion trajectory of sample data should cover the overall data as much as possible to improve the prediction accuracy.
- (3)
- Through the developed LSTM neural network with a reasonable neural network structure, mooring line top-tensions can be predicted in real-time with a high accuracy by using the measured data of six DOF motions on-site as input.
- (4)
- The LSTM neural network developed in this work is trained with measured motion data from a whole month rather than simulated data, which improves the accuracy of the top-tension prediction of mooring lines.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaneko, T.; Wada, R.; Ozaki, M.; Inoue, T. Hybrid Model of a Physics-Based Model and Machine Learning for Real-Time Estimation of Unmeasurable Parts: Mapping from Measurable to Unmeasurable Variables. Ocean. Eng. 2022, 261, 112123. [Google Scholar] [CrossRef]
- Godoy Simoes, M.; Leonidas Merma Tiquilloca, J.; Mitio Morishita, H. Neural-Network-Based Prediction of Mooring Forces in Floating Production Storage and Offloading Systems. IEEE Trans. Ind. Appl. 2002, 38, 457–466. [Google Scholar] [CrossRef]
- de Pina, A.C.; de Pina, A.A.; Albrecht, C.H.; Leite Pires de Lima, B.S.; Jacob, B.P. ANN-Based Surrogate Models for the Analysis of Mooring Lines and Risers. Appl. Ocean. Res. 2013, 41, 76–86. [Google Scholar] [CrossRef]
- Kim, Y. Prediction of the Dynamic Response of a Slender Marine Structure under an Irregular Ocean Wave Using the NARX-Based Quadratic Volterra Series. Appl. Ocean. Res. 2015, 49, 42–56. [Google Scholar] [CrossRef]
- Yetkin, M.; Kim, Y. Time Series Prediction of Mooring Line Top Tension by the NARX and Volterra Model. Appl. Ocean. Res. 2019, 88, 170–186. [Google Scholar] [CrossRef]
- Qiao, D.; Li, P.; Ma, G.; Qi, X.; Yan, J.; Ning, D.; Li, B. Realtime Prediction of Dynamic Mooring Lines Responses with LSTM Neural Network Model. Ocean. Eng. 2021, 219, 108368. [Google Scholar] [CrossRef]
- Zhao, Y.; Dong, S.; Jiang, F.; Incecik, A. Mooring Tension Prediction Based on BP Neural Network for Semi-Submersible Platform. Ocean. Eng. 2021, 223, 108714. [Google Scholar] [CrossRef]
- Guarize, R.; Matos, N.A.F.; Sagrilo, L.V.S.; Lima, E.C.P. Neural Networks in the Dynamic Response Analysis of Slender Marine Structures. Appl. Ocean. Res. 2007, 29, 191–198. [Google Scholar] [CrossRef]
- Christiansen, N.H.; Torbergsen Voie, P.E.; Høgsberg, J.; Sødahl, N. Efficient Mooring Line Fatigue Analysis Using a Hybrid Method Time Domain Simulation Scheme. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; Volume 1. [Google Scholar]
- Ji, C.-Y.; Yuan, Z.-M.; Chen, M.-L. Study on a New Mooring System Integrating Catenary with Taut Mooring. China Ocean. Eng. 2011, 25, 427–440. [Google Scholar] [CrossRef]
- Yuan, Z.; Ji, C.; Chen, M.; Zhang, Y. Coupled Analysis of Floating Structures with a New Mooring System. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering—OMAE, Rotterdam, The Netherlands, 19–24 June 2011; Volume 6. [Google Scholar]
- Yuan, Z.M.; Incecik, A.; Ji, C. Numerical Study on a Hybrid Mooring System with Clump Weights and Buoys. Ocean. Eng. 2014, 88, 1–11. [Google Scholar] [CrossRef]
- Lee, K.; Chung, M.; Kim, S.; Shin, D.H. Damage Detection of Catenary Mooring Line Based on Recurrent Neural Networks. Ocean. Eng. 2021, 227, 108898. [Google Scholar] [CrossRef]
- Toromanovic, J.; Knutsson, S.; Mattsson, H.; Laue, J. Parameter Identification for an Embankment Dam Using Noisy Field Data. Proc. Inst. Civ. Eng. Geotech. Eng. 2020, 173, 519–534. [Google Scholar] [CrossRef]
- Maier, G.; Ardito, R.; Fedele, R. Inverse Analysis Problems in Structural Engineering of Concrete Dams; Computational Mechanics Tsinghua University Press & Springer: Beijing, China, 2004; pp. 97–107. [Google Scholar]
- Yu, Y.; Liu, X.; Wang, E.; Fang, K.; Huang, L. Dam Safety Evaluation Based on Multiple Linear Regression and Numerical Simulation. Rock. Mech. Rock. Eng. 2018, 51, 2451–2467. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning, Addison-Wesley, Reading, MA, 1989. NN Schraudolph J. 1989, 3, 9. [Google Scholar]
- Shafieefar, M.; Rezvani, A. Mooring Optimization of Floating Platforms Using a Genetic Algorithm. Ocean. Eng. 2007, 34, 1413–1421. [Google Scholar] [CrossRef]
- Xia, L.Y.; Zhi, L.; Chen, L.; Cheng, Y. Optimization Design and Calculation of Mooring System Parameters Based on Genetic Algorithm. In Proceedings of the 4th International Conference on Mechatronics and Mechanical Engineering (ICMME 2017), Lumpur, Malaysia, 28–30 November 2017; Volume 153. [Google Scholar]
- Pillai, A.C.; Thies, P.R.; Johanning, L. Mooring System Design Optimization Using a Surrogate Assisted Multi-Objective Genetic Algorithm. Eng. Optim. 2019, 51, 1370–1392. [Google Scholar] [CrossRef]
- BV-NR-493; Classification of Mooring Systems for Permanent and Mobile Offshore Units. Bureau Veritas: Calgary, AB, Canada, 2021.



| Parameters | Unit | Value |
|---|---|---|
| Significant wave height | m | 13.1 |
| Spectral peak period | s | 14.9 |
| Peak enhancement factor | / | 3.3 |
| 1 h mean wind velocity | m/s | 43.0 |
| Current velocity | m/s | 1.78 |
| Length/m | L1 | L2 | L3 | L4 | L5 |
| Initial model | 1014 | 1014 | 1014 | 1014 | 1014 |
| As-built model | 1021.5 | 1023.5 | 1023.3 | 1026.4 | 1016.6 |
| Length/m | L6 | L7 | L8 | L9 | |
| Initial model | 1014 | 623 | 623 | 623 | |
| As-built model | 1017.7 | 631.1 | 630.6 | 631.0 |
| Parameters | Unit | Value | |
|---|---|---|---|
| Wind | Mean speed | m/s | 20.0 |
| Mean direction | degree | 196.6 | |
| Wave | Hs | m | 5.33 |
| Tp | s | 10.84 | |
| Wave direction | degree | 70.5 | |
| Current | Surface speed | m/s | 0.38 |
| Surface direction | degree | 259.4 |
| Length/m | Group1-L2 | Group2-L5 | Group3-L8 | |||
|---|---|---|---|---|---|---|
| UCS2 | UCS3 | UCS2 | UCS3 | UCS2 | UCS3 | |
| As-built model | 90 | 15.1 | 90 | 15.2 | 42 | 15.5 |
| Updated model | 78 | 27.1 | 90 | 15.2 | 42 | 15.5 |
| Parameter | Unit | Sea State | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| Wind | Mean speed | m/s | 19.7 | 5.1 | 9.9 | 5.2 | 4.6 | 19.1 | 8.0 | 18.2 |
| Mean direction | ° | 197.6 | 324.4 | 338.8 | 213.0 | 280.1 | 196.0 | 65.0 | 241.1 | |
| Wave | Hs | m | 5.2 | 0.7 | 4.2 | 1.0 | 0.8 | 5.9 | 4.0 | 0.2 |
| Tp | s | 11.2 | 10.7 | 9.3 | 6.3 | 14.5 | 12.0 | 9.6 | 12.3 | |
| Direction | ° | 149.5 | 63.3 | 51.1 | 115.4 | 75.9 | 147.0 | 42.7 | 27.1 | |
| Current | Surface speed | m/s | 0.4 | 0.2 | 0.2 | 0.2 | 0.3 | 0.3 | 0.1 | 0.4 |
| Surface direction | ° | 268.3 | 359.1 | 323.6 | 5.3 | 2.3 | 267.5 | 367.9 | 321.3 | |
| Number of Neuron Nodes in Each Hidden Layer | RMSE | R2 | ||
|---|---|---|---|---|
| 1st | 2nd | 3rd | ||
| 32 | / | / | 0.0145 | 0.9012 |
| 64 | / | / | 0.0125 | 0.9268 |
| 128 | / | / | 0.0129 | 0.9220 |
| 256 | / | / | 0.0119 | 0.9333 |
| 256 | 32 | / | 0.0114 | 0.9397 |
| 256 | 64 | / | 0.0120 | 0.9326 |
| 256 | 128 | / | 0.0104 | 0.9492 |
| 256 | 256 | / | 0.0103 | 0.9503 |
| 256 | 256 | 32 | 0.0143 | 0.9037 |
| 256 | 256 | 64 | 0.0121 | 0.9314 |
| 256 | 256 | 128 | 0.0116 | 0.9375 |
| 256 | 256 | 256 | 0.0104 | 0.9497 |
| Sea State Number | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| RMSE | 23.24 | 2.47 | 8.39 | 13.2 | 4.31 | 25.79 | 6.83 | 10.96 |
| R2 | 0.94 | 0.51 | 0.87 | 0.92 | 0.52 | 0.86 | 0.90 | 0.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhong, Q.; Zhang, J.; Wang, X. Prediction of Mooring Line Top-Tensions Incorporated with Identification of Lost Clump Weights. J. Mar. Sci. Eng. 2025, 13, 631. https://doi.org/10.3390/jmse13040631
Li Y, Zhong Q, Zhang J, Wang X. Prediction of Mooring Line Top-Tensions Incorporated with Identification of Lost Clump Weights. Journal of Marine Science and Engineering. 2025; 13(4):631. https://doi.org/10.3390/jmse13040631
Chicago/Turabian StyleLi, Ying, Qiyuan Zhong, Jiamin Zhang, and Xiaomei Wang. 2025. "Prediction of Mooring Line Top-Tensions Incorporated with Identification of Lost Clump Weights" Journal of Marine Science and Engineering 13, no. 4: 631. https://doi.org/10.3390/jmse13040631
APA StyleLi, Y., Zhong, Q., Zhang, J., & Wang, X. (2025). Prediction of Mooring Line Top-Tensions Incorporated with Identification of Lost Clump Weights. Journal of Marine Science and Engineering, 13(4), 631. https://doi.org/10.3390/jmse13040631






