Analysis of the Main Influencing Factors of Marine Environment on the Nuclear Pressure Vessel of Floating Nuclear Power Plants
Abstract
1. Introduction
- Utilizing spectral analysis methods to examine the influence of marine environmental loads (such as hull deformation and six-degree-of-freedom inertial forces) on RPV fatigue damage and identifying the dominant damage factors.
- Applying the equivalent design wave method to analyze the stress distribution of RPVs under extreme sea conditions and identifying key stress factors.
- Proposing optimization strategies for FNPP operation to mitigate RPV fatigue damage and enhance structural safety based on the analytical results.
2. Marine Environment and Structural Model
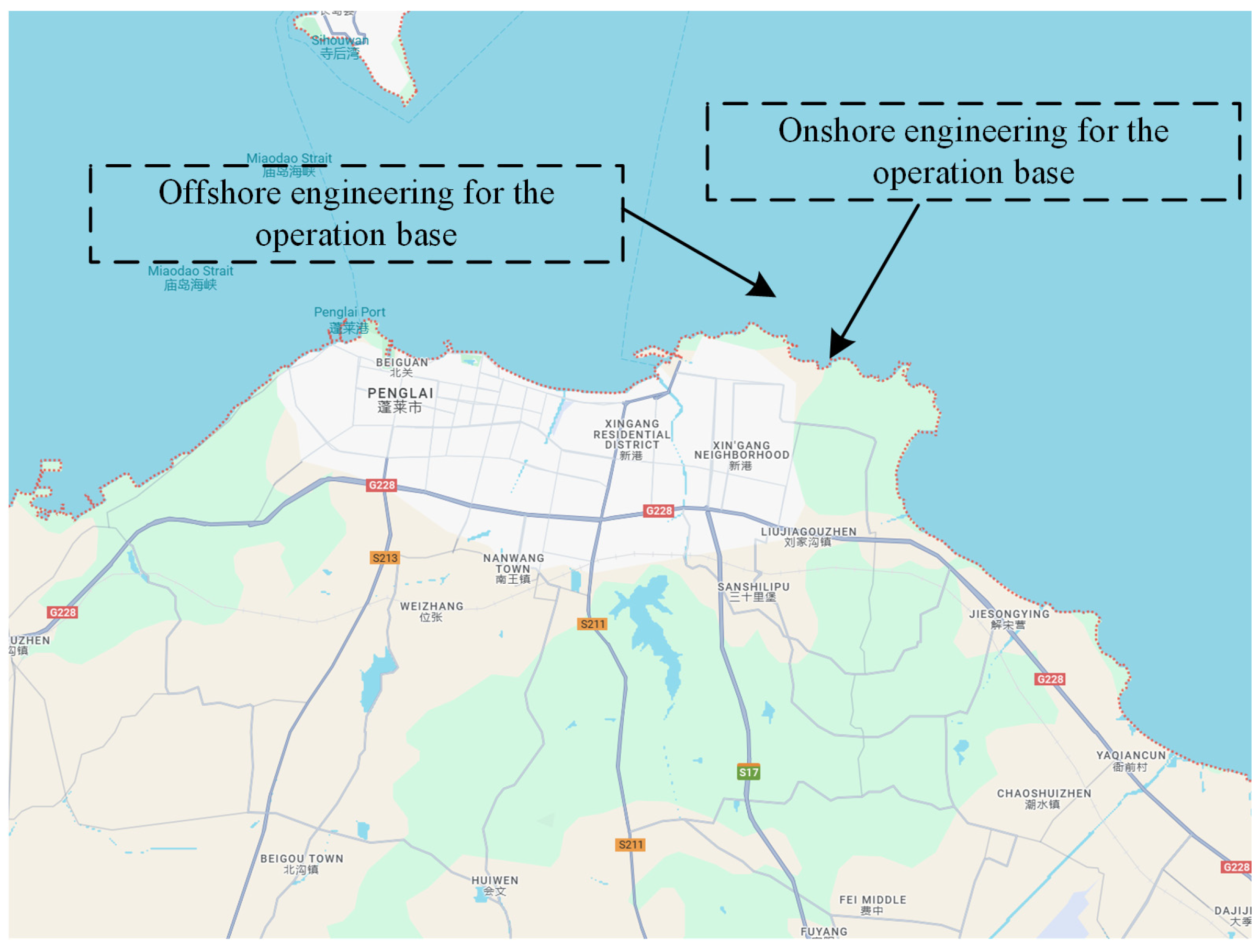
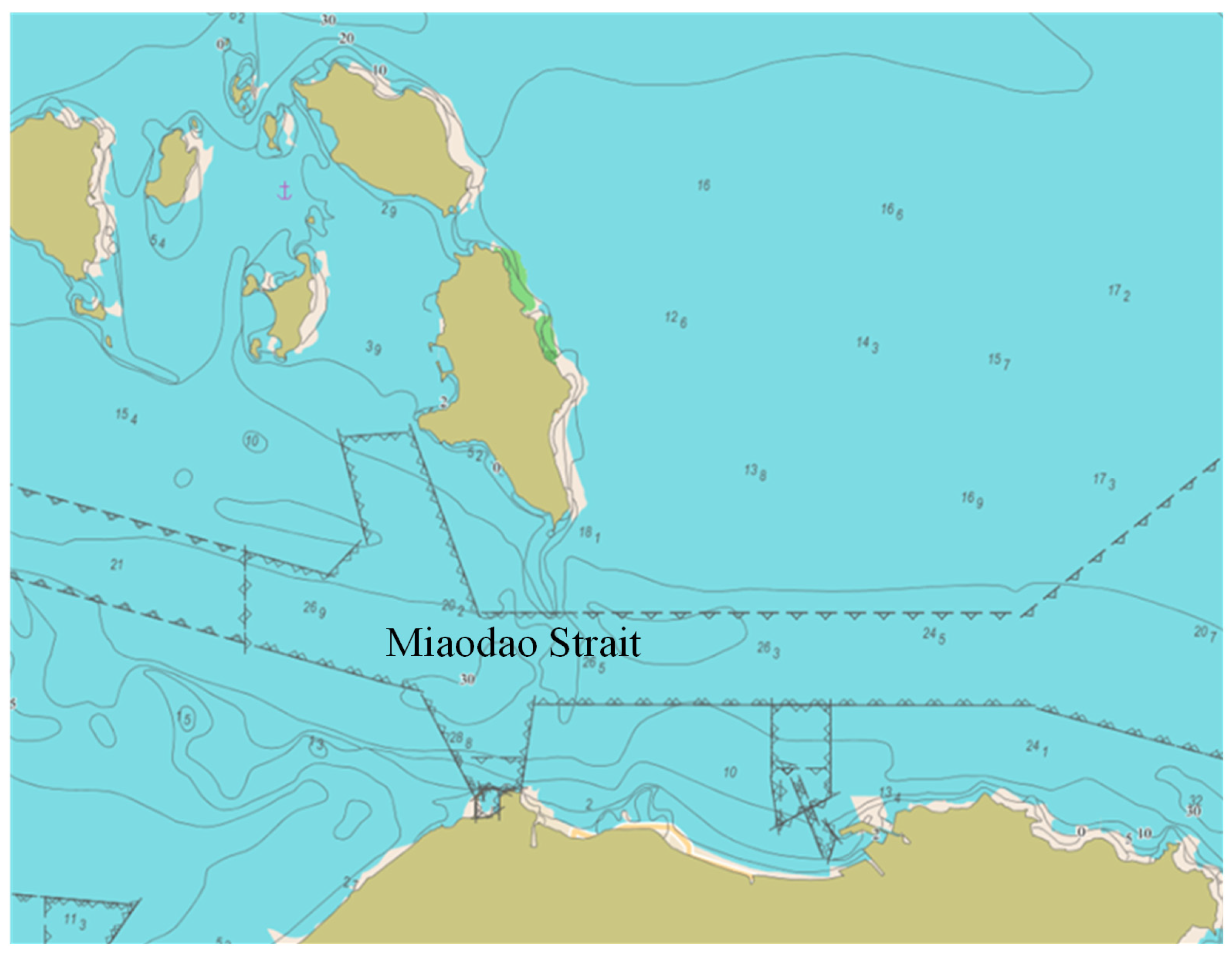
2.1. Operational Waters and Sea State Parameters
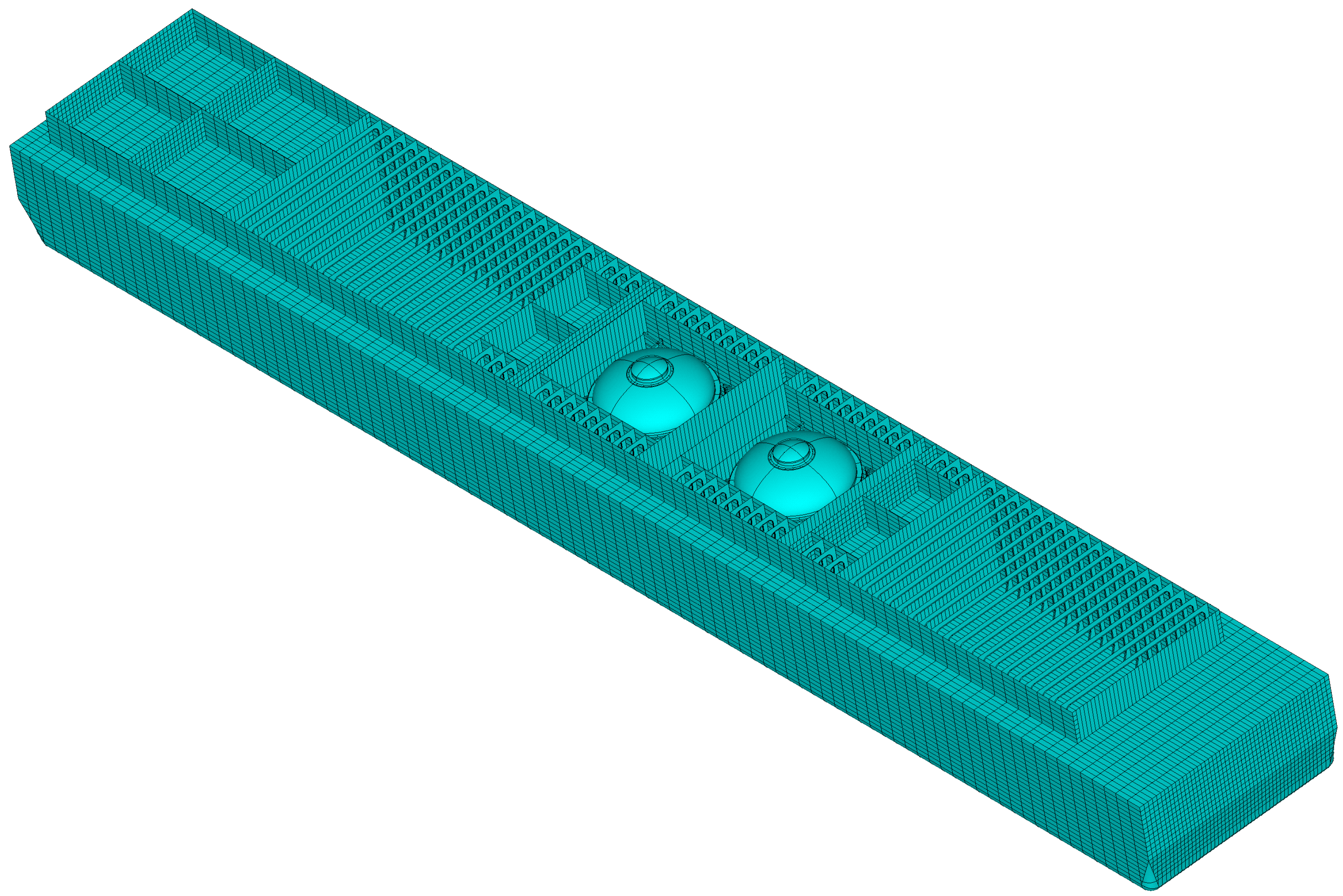
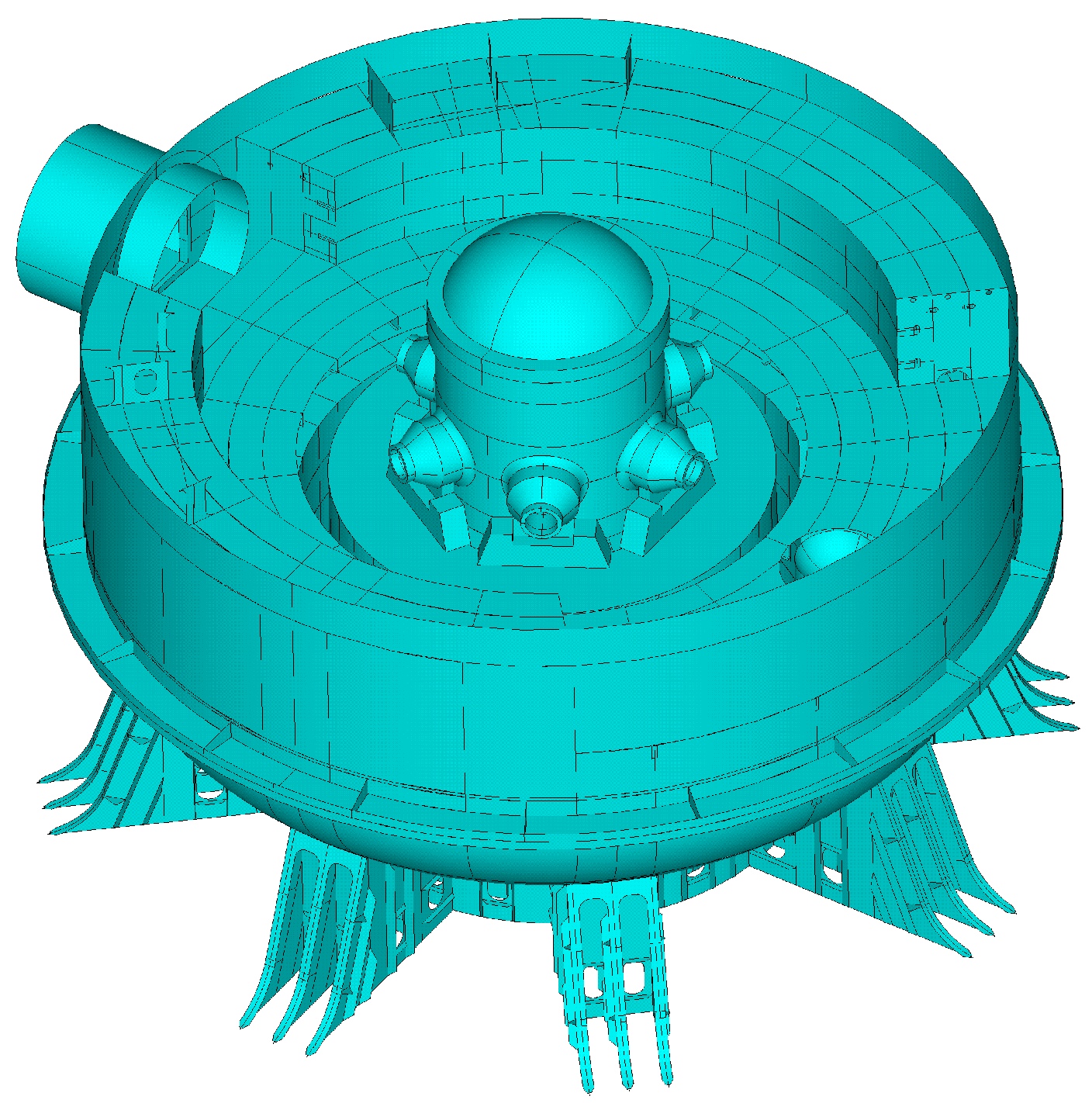
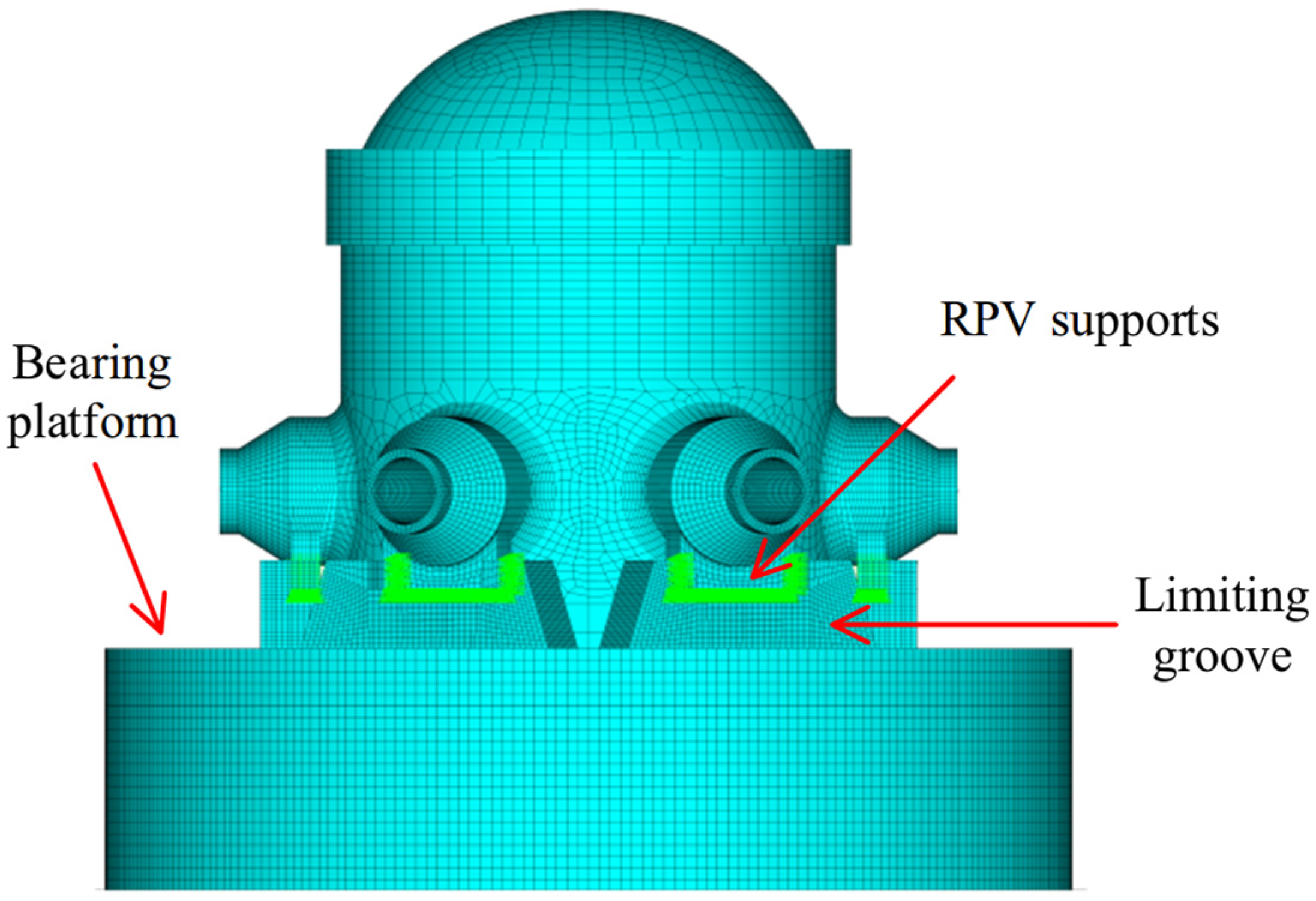
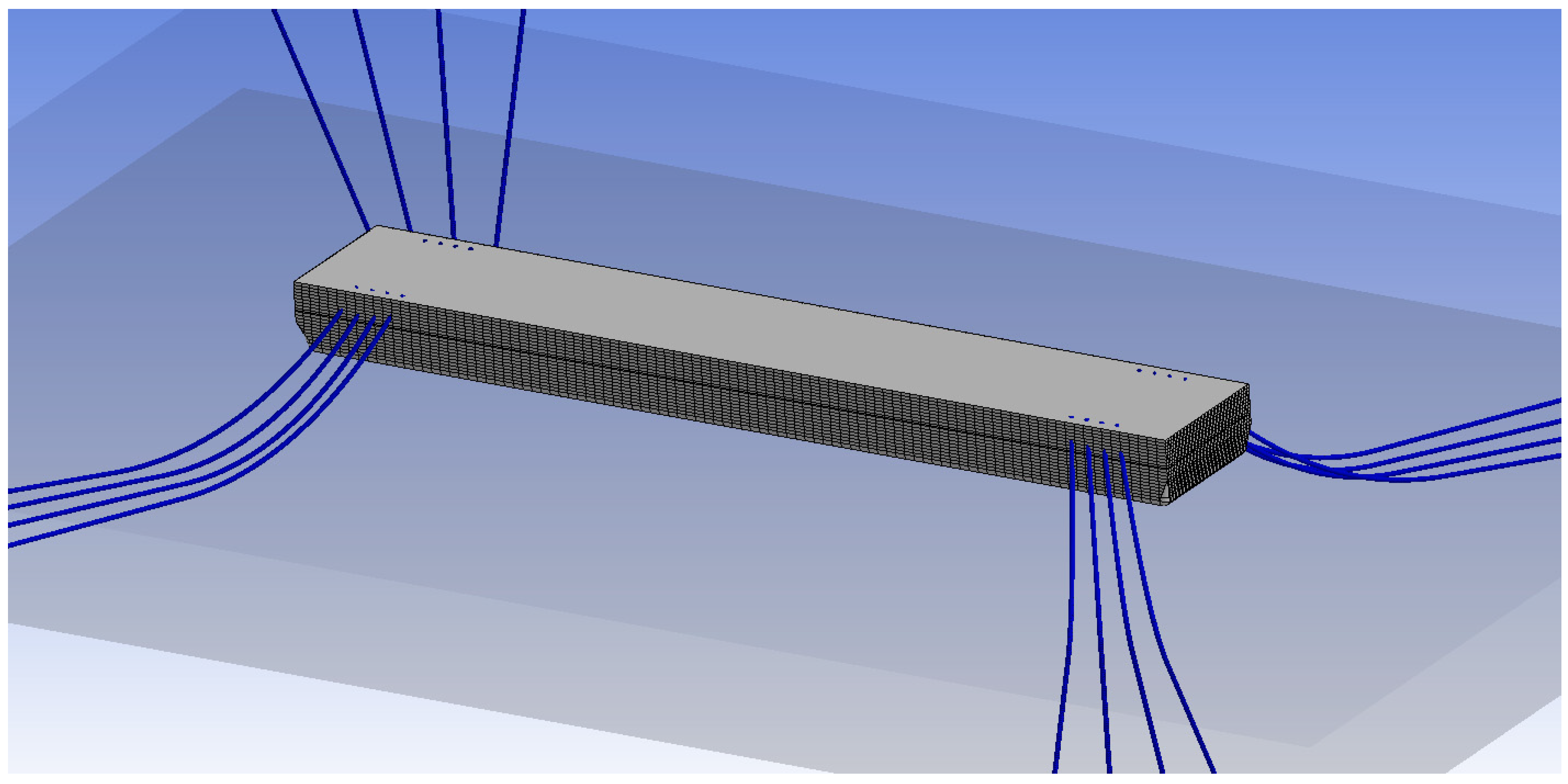
2.2. Structural Model
3. Structural Damage Analysis Induced by Various Inputs
3.1. Spectral Analysis Method
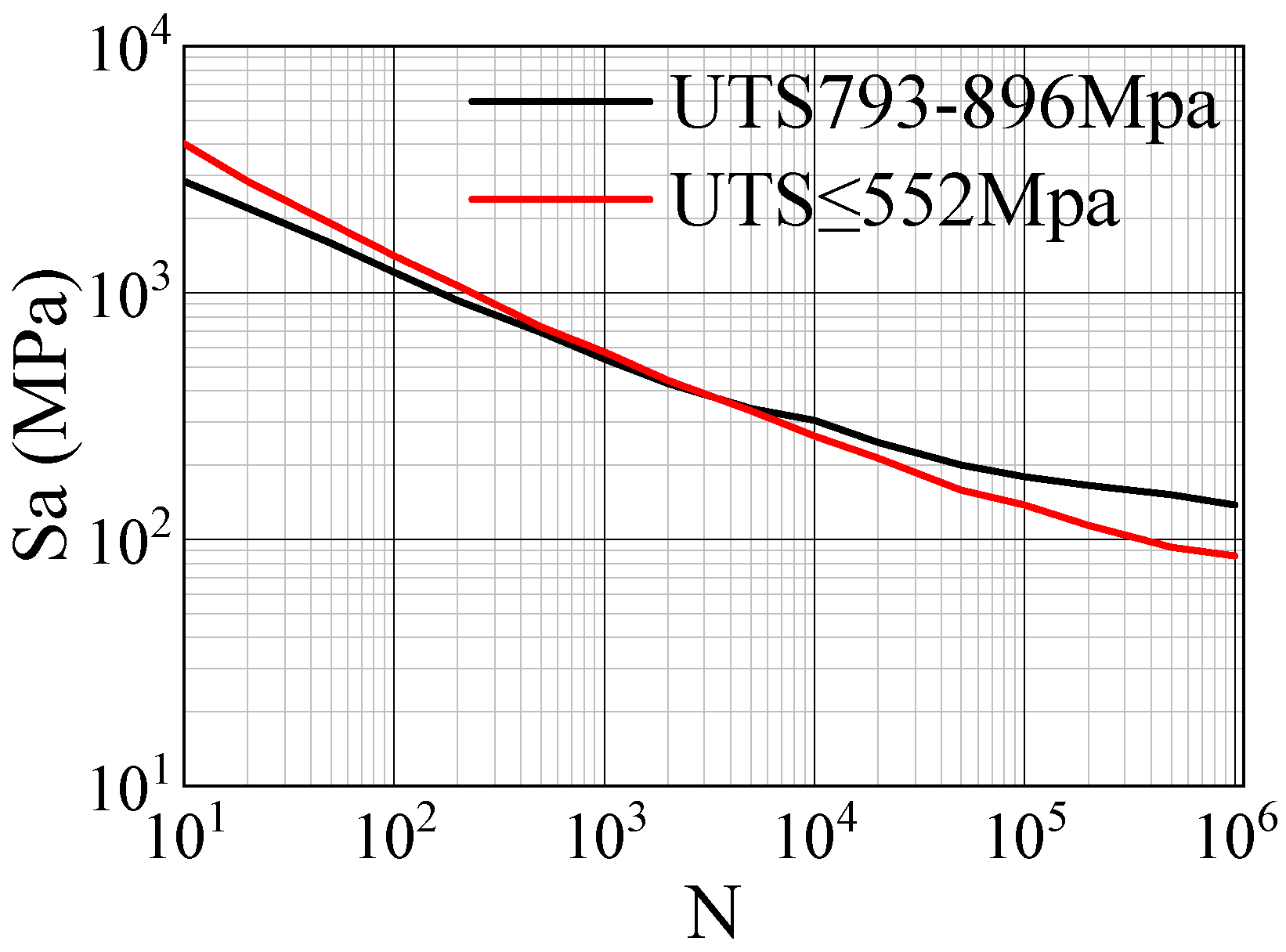
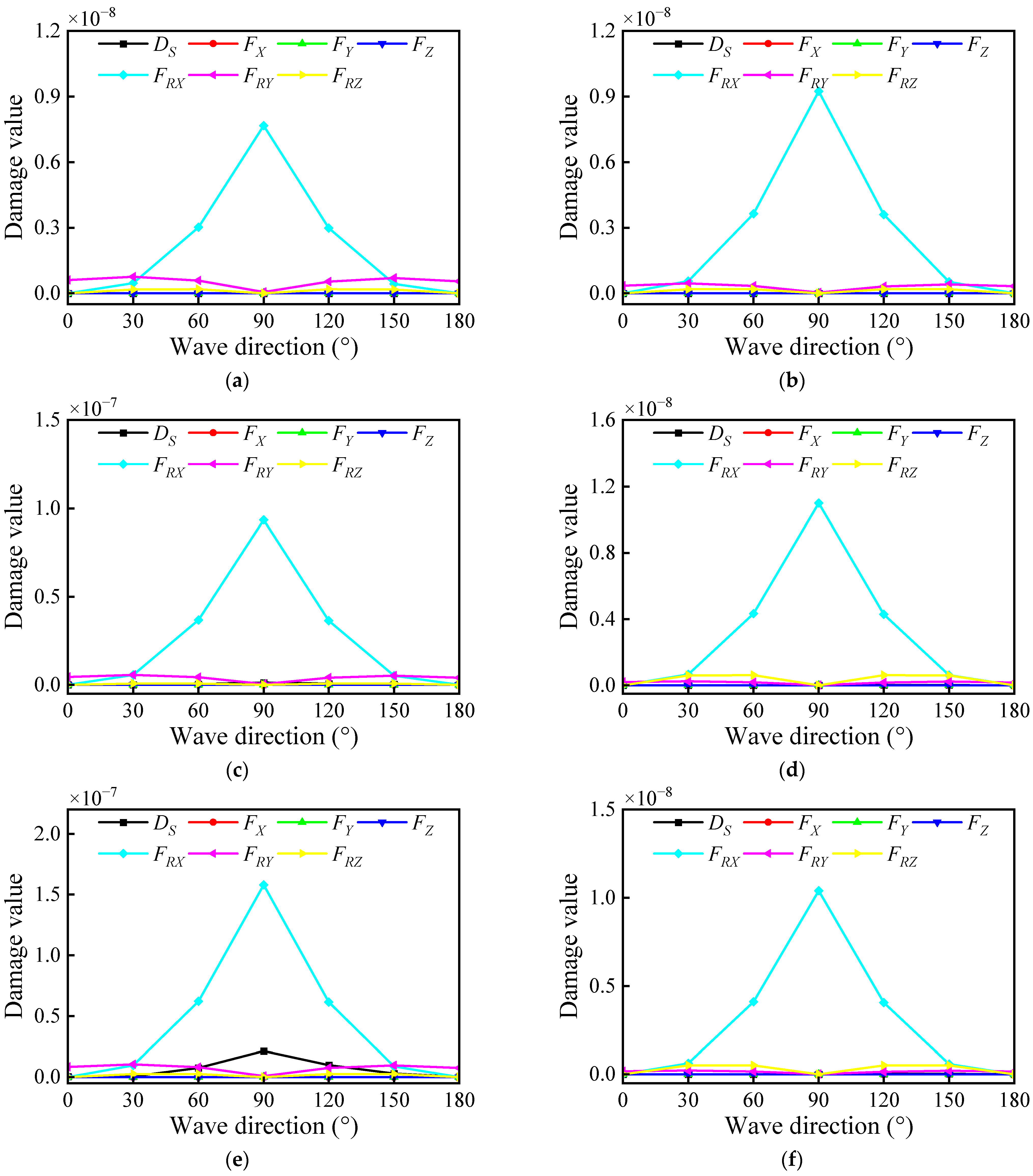
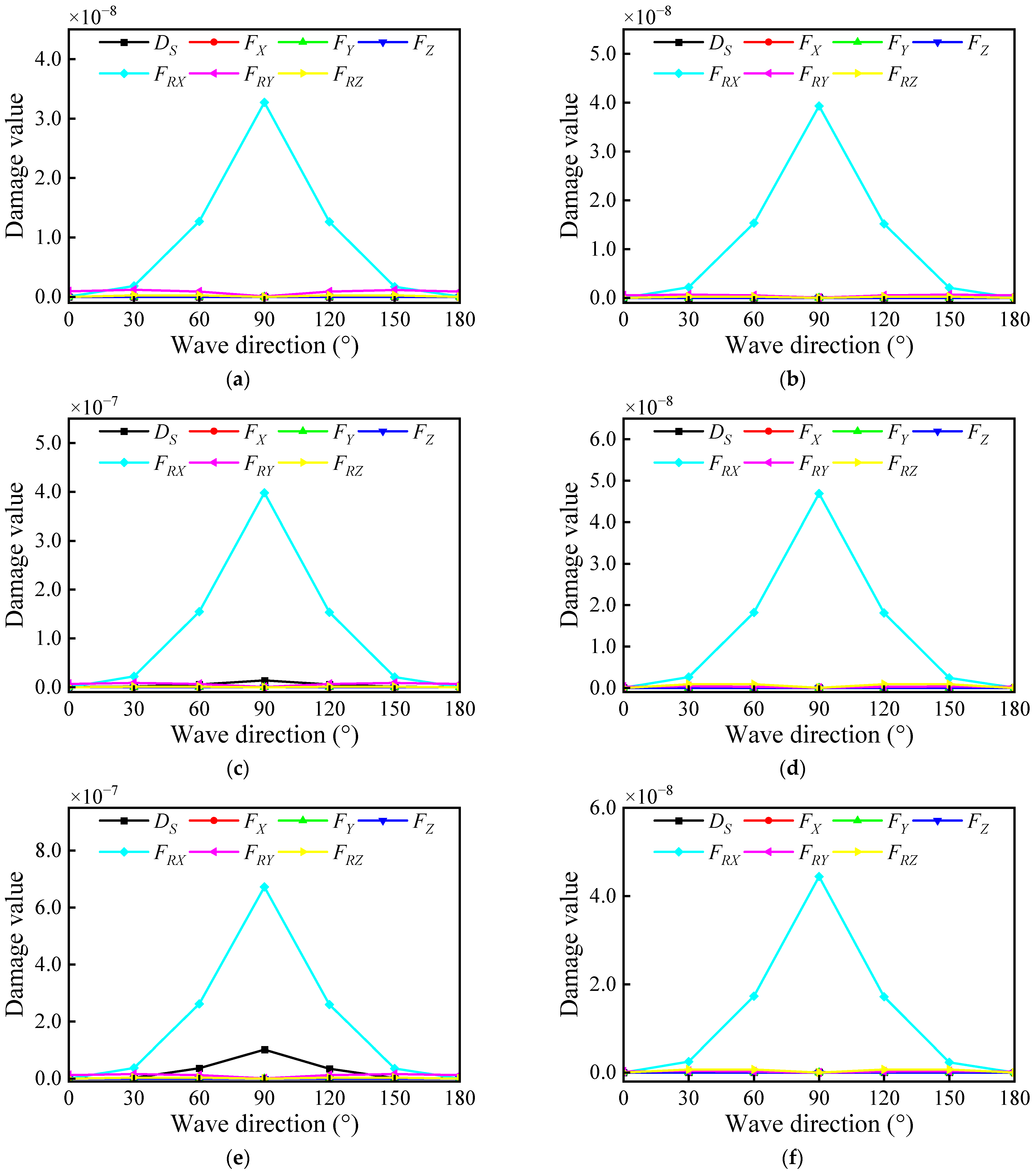
3.2. Structural Damage Evaluation
4. Structural Strength Analysis Under Various Inputs
4.1. Design Wave Method
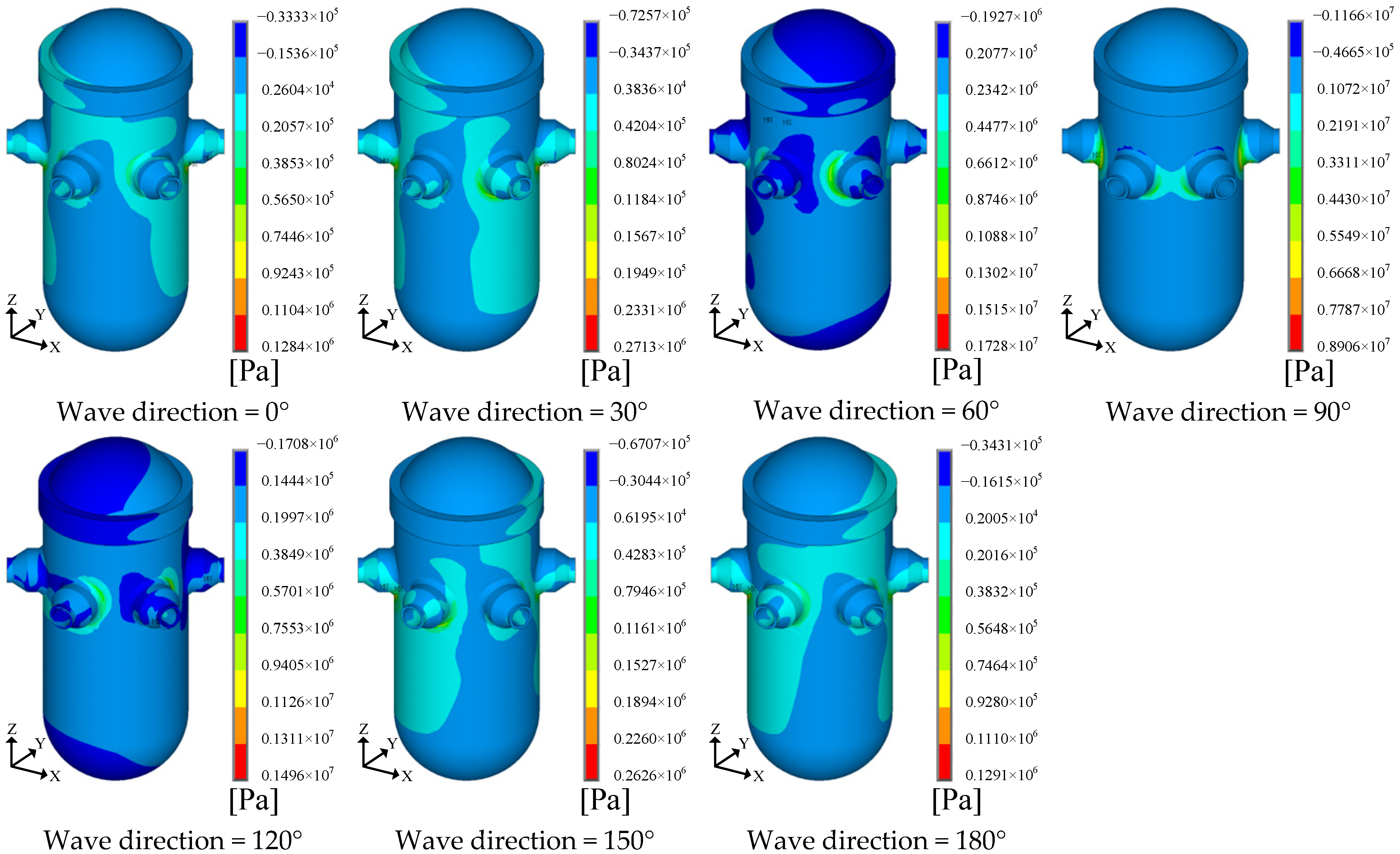
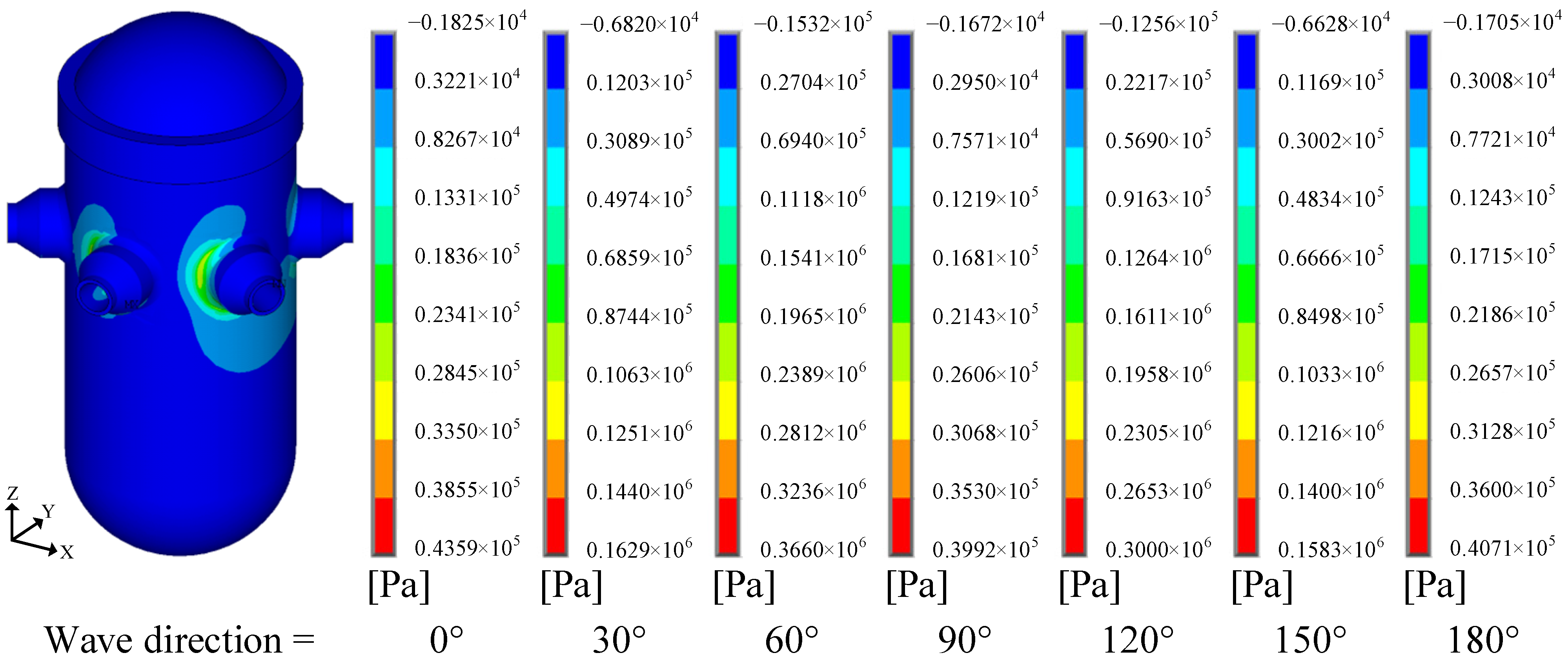
4.2. Structural Stress Distribution
5. Conclusions
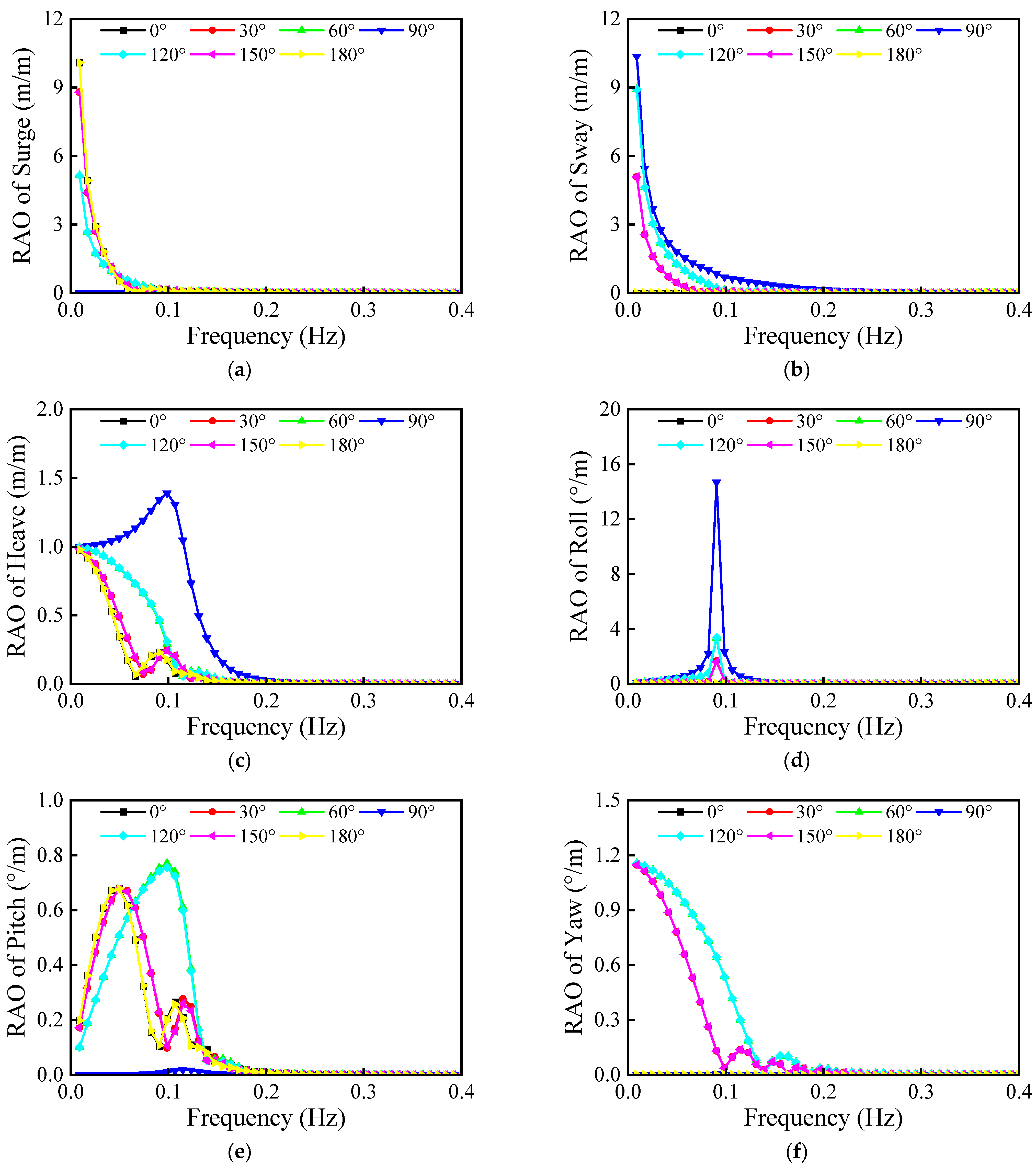
- Among the dynamic loads induced by the marine environment, roll inertial force had the most significant impact on RPV fatigue damage, followed by pitch inertial force, while the effects of translational inertial forces and hull deformation were relatively minor.
- The contribution of different dynamic loads to RPV fatigue damage varied significantly with wave direction. In beam seas, roll inertial force caused the highest fatigue damage. In head seas, pitch inertial force caused the highest fatigue damage.
- Under the 100-year return period extreme sea state, stress analysis based on the design wave method showed the following: The maximum stress occurred at the nozzle connection of the RPV. Rotational inertial forces induced significantly higher stresses than wave pressure and translational inertial forces, making them the dominant contributors to RPV structural strength.
- Unlike land-based nuclear power plants, the RPV in an FNPP must account for additional dynamic loads from the marine environment in strength and fatigue analyses. In addition to conventional thermal-pressure loads, hull deformation and inertial forces must be considered. Due to the large geometric scale of FNPPs, full-scale ship models must be used for hull deformation calculations, leading to high computational costs in RPV strength and fatigue analysis. To reduce computational expense, simplified models should be adopted, considering only the primary influencing factors.
- This study focused exclusively on the effects of the marine environment on the RPV structure, without considering thermal-pressure loads. Therefore, under a 100-year return period sea state, the calculated RPV stress was far below the yield strength of the material. Under typical sea conditions, the calculated fatigue damage of the RPV was also minimal, indicating an almost infinite fatigue life. This suggested that with the current structural design, the RPV did not face strength or fatigue failure issues when considering only marine environmental effects. In actual structural assessments, thermal-pressure loads must be incorporated, along with long-term operational conditions, for a more comprehensive evaluation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mcginty, F.C. Nuclear Power Plants and Maintainability. Hum. Factors 1965, 7, 355–361. [Google Scholar] [CrossRef] [PubMed]
- Vujić, J.; Bergmann, R.M.; Škoda, R.; Miletić, M. Small Modular Reactors: Simpler, Safer, Cheaper? Energy 2012, 45, 288–295. [Google Scholar] [CrossRef]
- Zhao, S.; Song, Y. A Development Overview of National and International Floating Nuclear Power Plant. Prog. Rep. China Nucl. Sci. Technol. 2017, 5, 93–98. [Google Scholar]
- Li, Q.; Song, D.; Zeng, W.; CHEN, Z.; Liu, J.; Wang, D.; Xiao, R. Overall Design and Verification of ACP100S Floating Nuclear Power Plant. Nucl. Power Eng. 2020, 41, 189–192. [Google Scholar]
- Collins, J.A. Failure of Materials in Mechanical Design: Analysis, Prediction, Prevention; John Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Li, Z.; Mao, W.; Ringsberg, J.W.; Johnson, E.; Storhaug, G. A Comparative Study of Fatigue Assessments of Container Ship Structures Using Various Direct Calculation Approaches. Ocean. Eng. 2014, 82, 65–74. [Google Scholar] [CrossRef]
- Garbatov, Y.; Ås, S.K.; Den Besten, H.; Haselbach, P.; Kahl, A.; Karr, D.; Kim, M.H.; Liu, J.; Lourenço de Souza, M.I.; Mao, W. Committee III. 2: Fatigue and Fracture. In Proceedings of the International Ship and Offshore Structures Congress, Vancouver, BC, Canada, 11–15 September 2022; p. D011S001R007. [Google Scholar]
- Mukhtar, A.; Khattak, M.A.; Rafique, A.F.; Zareen, N. Reactor Pressure Vessel (RPV) Design and Fabrication: A Literature Review. J. Adv. Res. Appl. Mech. 2016, 22, 1–12. [Google Scholar]
- Tachibana, Y.; Nakagawa, S.; Iyoku, T. Reactor Pressure Vessel Design of the High Temperature Engineering Test Reactor. Nucl. Eng. Des. 2004, 233, 103–112. [Google Scholar] [CrossRef]
- Törrönen, K.; Cullen, W.H. Effect of Light-Water Reactor Environments on Fatigue Crack Growth Rate in Reactor Pressure Vessel Steels; ASTM International: West Conshohocken, PA, USA, 1982. [Google Scholar] [CrossRef]
- Seifert, H.P.; Ritter, S. Stress Corrosion Cracking of Low-Alloy Reactor Pressure Vessel Steels under Boiling Water Reactor Conditions. J. Nucl. Mater. 2008, 372, 114–131. [Google Scholar] [CrossRef]
- DNV-CG-0129; Fatigue Assessment of Ship Structures. DNV AS: Høvik, Norway, 2021.
- ASME. Code Boiler and Pressure Vessel Code; ASME: New York, NY, USA, 2001. [Google Scholar]
- RCC-MR. Design and Manufacturing Rules for Fast Reactors. In AFCEN (June 1985), in Sell to AFNOR; AFNOR: Paris, France, 1985. [Google Scholar]
- Ma, F.; Li, H.; Zhang, M.; Qu, X. A Quasi Time-Domain Method for Fatigue Analysis of Reactor Pressure Vessels in Floating Nuclear Power Plants in Marine Environments. J. Mar. Sci. Eng. 2024, 12, 2085. [Google Scholar] [CrossRef]
- Yuan, J.; Ma, F.; Zhang, M.; Shen, K.; Tang, J. The Time-Domain Design Stress Method for Fatigue Analysis of the Reactor Pressure Vessel in Floating Nuclear Power Plants. J. Mar. Sci. Eng. 2025, 13, 235. [Google Scholar] [CrossRef]
- Shen, K.; Ma, F.; Yuan, J.; Zhang, M. A Damage Combination Method for Fatigue Analysis of Pressure Equipment in Floating Nuclear Power Plants. J. Mar. Sci. Eng. 2025, 13, 236. [Google Scholar] [CrossRef]
- Veritas, D.N. Hull Structural Design Ships with Length 100 Metres and Above. In DNV Rules for Classification of Ships; DNV: Byrum, Norway, 2009. [Google Scholar]
- Phelps, B.P. Determination of Wave Loads for Ship Structural Analysis; Aeronautical and Maritime Research Laboratory: Melbourne, Australia, 1997. [Google Scholar]
- You, Z. Unified Approach for Estimation of Return Ocean Wave Height. Oceanol. Limnol. Sin. 2022, 53, 1015–1025. [Google Scholar]




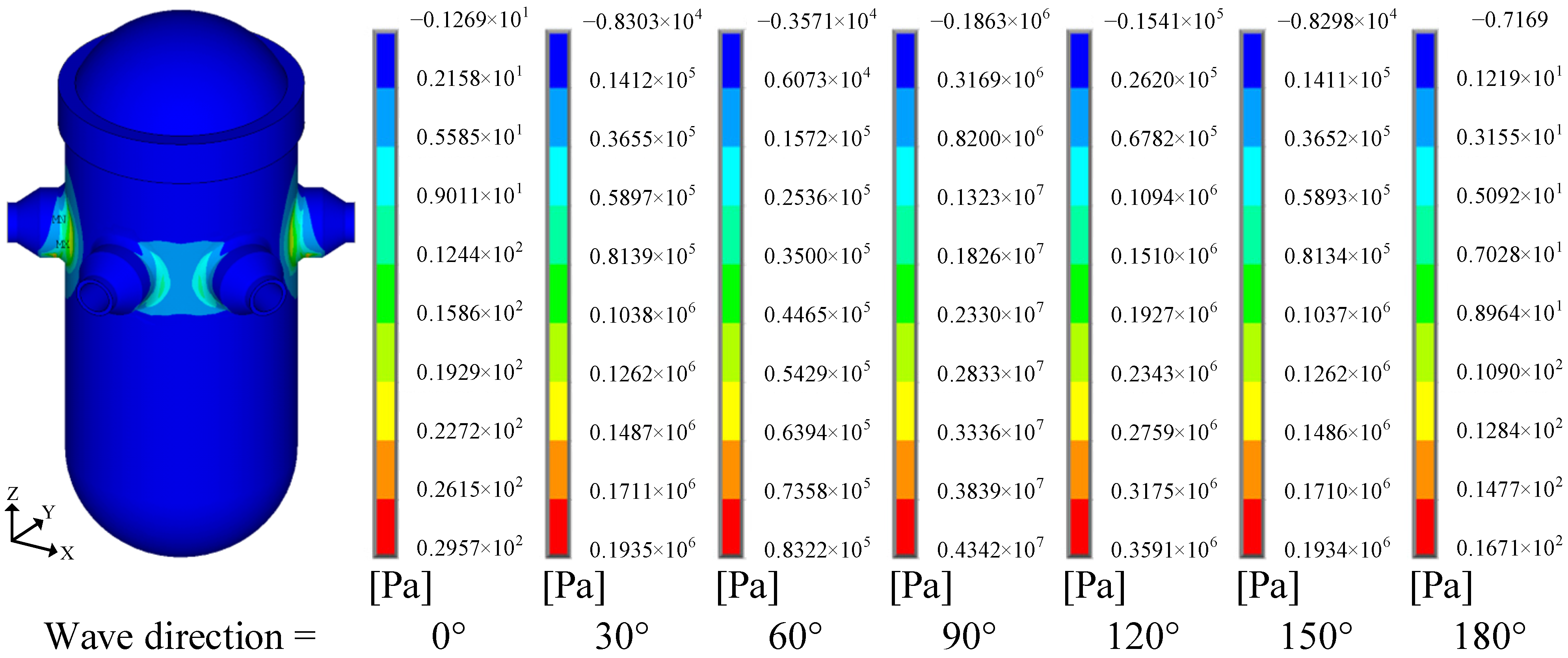

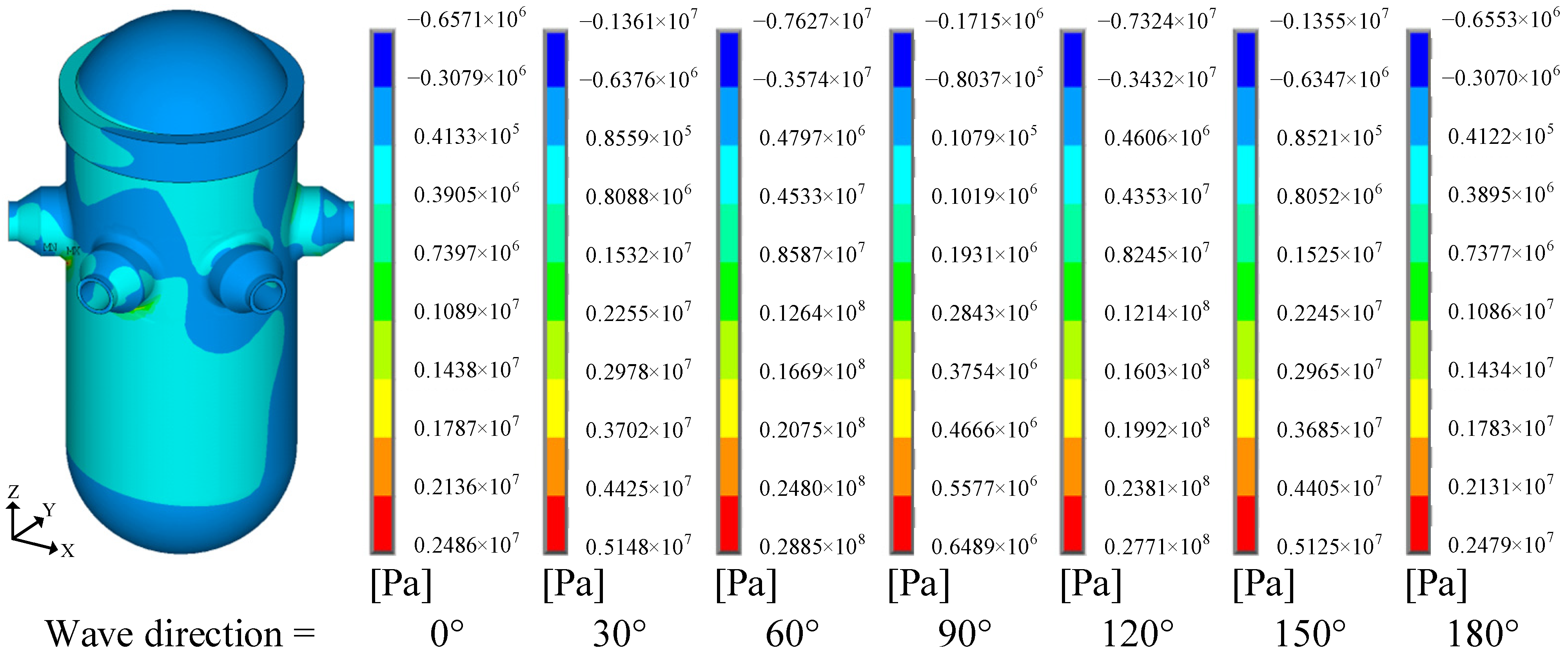
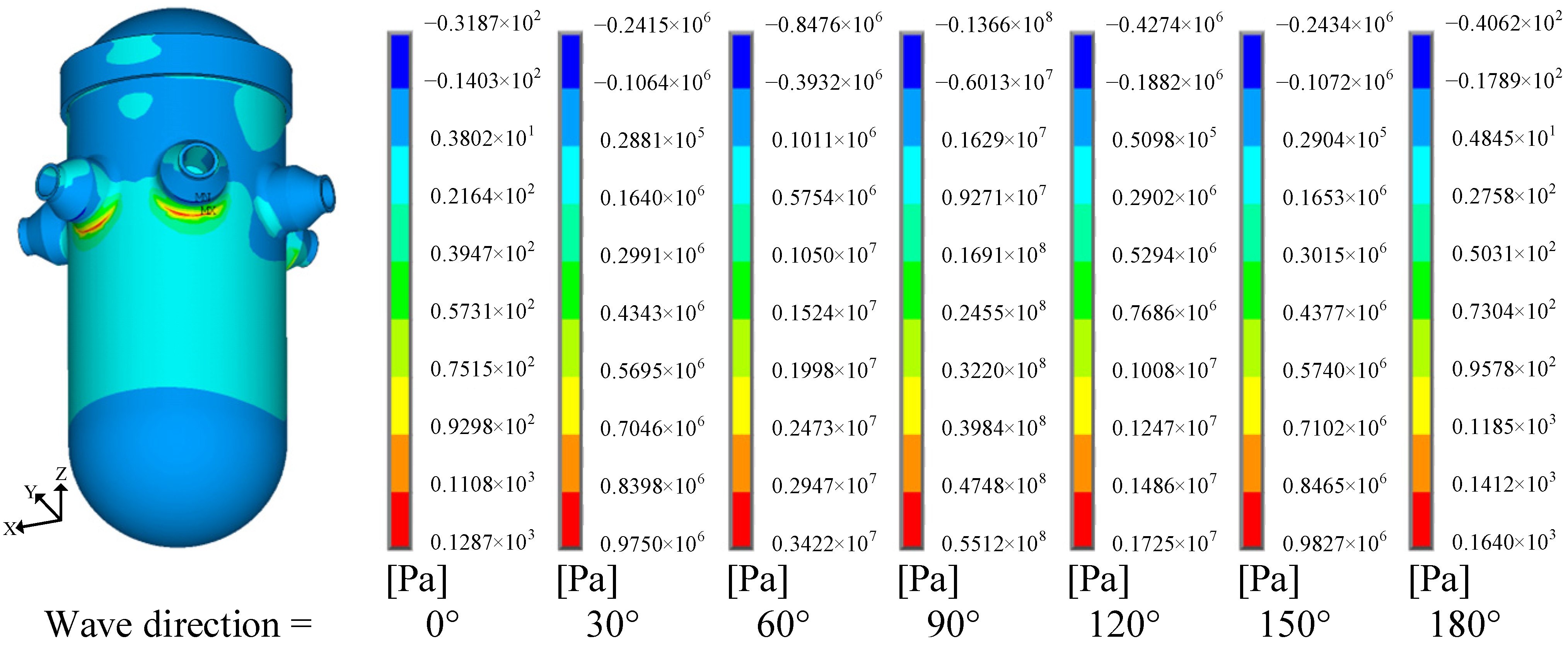
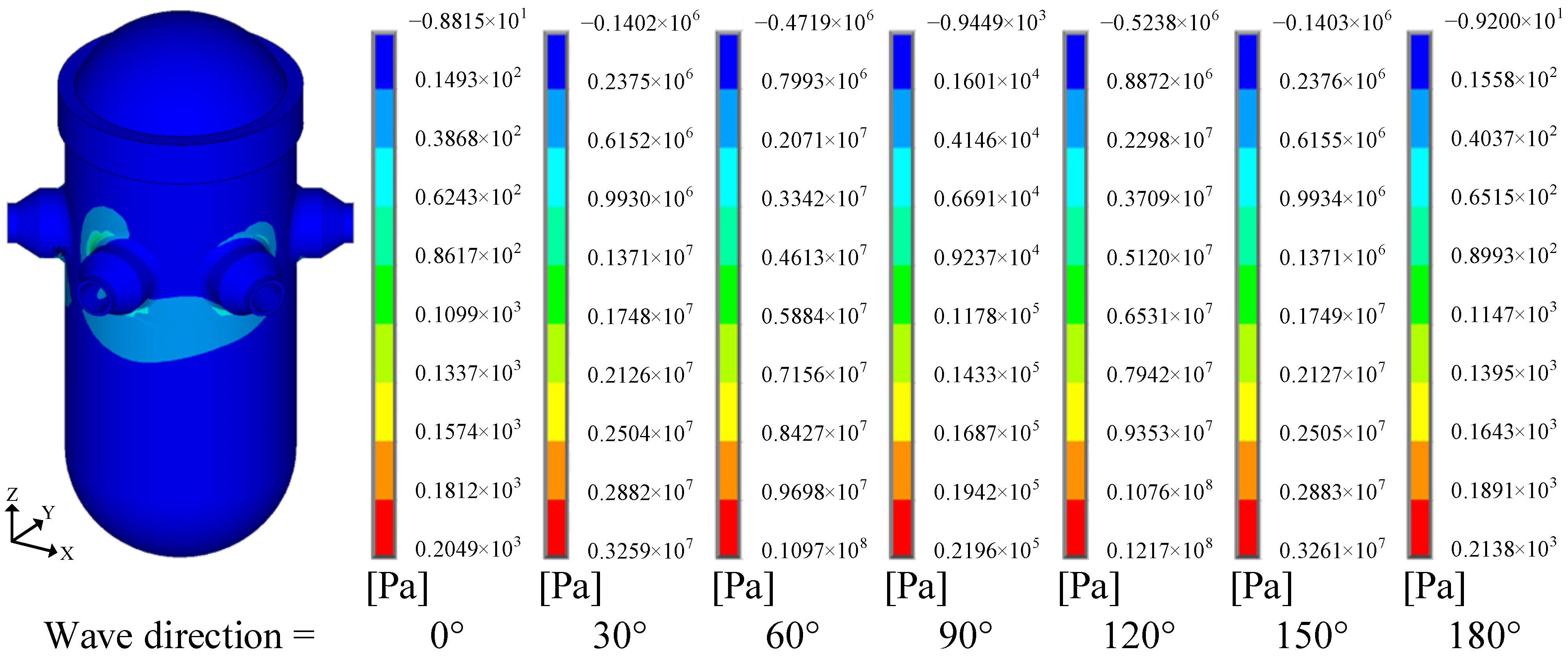
| Return Period | Hs (m) | Hmax (m) | Tz (s) | Ts (s) |
|---|---|---|---|---|
| 1 year | 3.7 | 6.4 | 6.4 | 7.3 |
| 10 years | 4.3 | 7.5 | 6.9 | 7.9 |
| 50 years | 4.6 | 8.0 | 7.3 | 8.3 |
| 100 years | 4.8 | 8.4 | 7.4 | 8.4 |
| 500 years | 5.2 | 9.0 | 7.8 | 8.9 |
| Wave Direction (°) | ·N·m) | ·N) |
|---|---|---|
| 0 | 12.89 | 6.19 |
| 30 | 18.96 | 5.42 |
| 60 | 26.74 | 4.32 |
| 90 | 3.17 | 0.56 |
| 120 | 25.50 | 4.13 |
| 150 | 18.98 | 5.43 |
| 180 | 13.06 | 6.21 |
| Wave Direction (°) | Wave Height (m) | Period (s) | Phase (°) |
|---|---|---|---|
| 0 | 4.2 | 16.3 | 172.9 |
| 30 | 7.0 | 15.0 | 168.8 |
| 60 | 12.4 | 9.0 | 128.7 |
| 90 | 11.2 | 9.0 | −74.7 |
| 120 | 12.4 | 9.5 | 135.2 |
| 150 | 7.0 | 15.0 | 170.7 |
| 180 | 4.2 | 16.3 | 174.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, F.; Zhang, M.; Qu, X. Analysis of the Main Influencing Factors of Marine Environment on the Nuclear Pressure Vessel of Floating Nuclear Power Plants. J. Mar. Sci. Eng. 2025, 13, 795. https://doi.org/10.3390/jmse13040795
Ma F, Zhang M, Qu X. Analysis of the Main Influencing Factors of Marine Environment on the Nuclear Pressure Vessel of Floating Nuclear Power Plants. Journal of Marine Science and Engineering. 2025; 13(4):795. https://doi.org/10.3390/jmse13040795
Chicago/Turabian StyleMa, Fuxuan, Meng Zhang, and Xianqiang Qu. 2025. "Analysis of the Main Influencing Factors of Marine Environment on the Nuclear Pressure Vessel of Floating Nuclear Power Plants" Journal of Marine Science and Engineering 13, no. 4: 795. https://doi.org/10.3390/jmse13040795
APA StyleMa, F., Zhang, M., & Qu, X. (2025). Analysis of the Main Influencing Factors of Marine Environment on the Nuclear Pressure Vessel of Floating Nuclear Power Plants. Journal of Marine Science and Engineering, 13(4), 795. https://doi.org/10.3390/jmse13040795






