Marine Gravity Field Modeling Using SWOT Altimetry Data in South China Sea

Abstract

The Surface Water and Ocean Topography (SWOT) satellite delivers an unprecedented spatial resolution, offering new opportunities for advanced marine gravity field modeling. This study investigates the application of SWOT observational data by computing deflections of the vertical (DOVs) using the eight-directional geoid gradient method, followed by gravity field inversion through the inverse Vening–Meinesz (IVM) formula. Experimental results in the South China Sea region demonstrate that SWOT DOVs, based on 19 observation cycles, achieved accuracies of 0.86 arcseconds for the east–west component $\eta$ and 0.77 arcseconds for the north–south component $\xi$. The marine gravity field inversion accuracy reached 4.97 mGal, comparable to the multi-source altimetry-derived model SIO_v32.1. Further analysis reveals that the primary contributions of SWOT DOVs are observed within the 3.5–20 km wavelength band, with cross-track systematic errors identified as the key factor influencing both DOV calculations and gravity anomaly inversion. Additionally, extending the SWOT observation period enhances DOV accuracy, particularly for the $\eta$. These findings highlight the potential of SWOT data in advancing high-resolution marine gravity field modeling.

1. Introduction

The marine gravity field serves as a foundational dataset in geophysics, with extensive applications in studies on the Earth’s shape and internal structure, seafloor topography inversion, and marine resource exploration, among other critical areas [1]. The most direct and effective method for obtaining marine gravity data is shipborne gravity measurement, which delivers high-precision gravity observations. However, the vast expanse of the oceans severely limits its spatial coverage. In contrast, satellite altimetry-derived sea surface height (SSH) offers a viable alternative for inverting gravity anomalies [2,3,4]. Coupled with its near-global and uniform coverage, satellite altimetry has emerged as a primary and indispensable technique for constructing the marine gravity field [5].

The primary methods for marine gravity field inversion based on multi-altimetry data include the inverse Stokes method, the inverse Vening–Meinesz (IVM) method [6], the Laplace method [7], and the least squares collocation (LSC) method. The inverse Stokes method is suitable for recovering marine gravity from geoid height data [8]. The LSC method, which is based on statistical theory, requires the construction of an accurate prior covariance matrix between deflections of the vertical (DOVs) and gravity anomalies, limiting its broader application [9]. Theoretically, due to the differential calculations involved, DOVs exhibit reduced long-wavelength radial orbital errors [10] and contain richer short-wavelength signals, making the IVM and Laplace methods the preferred approaches for gravity recovery [11,12].

Traditional satellite altimetry, represented by pulse-limited radar altimetry, is characterized by a relatively large orbital spacing. Consequently, it typically requires the integration of data from multiple satellites and Geodetic Mission (GM) data to enhance the density of altimetry measurements [13]. However, systematic biases exist between different altimetry satellites [14], and GM data necessitate time-varying corrections for sea surface variations [9,15,16], which introduce inherent errors. In contrast to pulse-limited radar, synthetic aperture radar (SAR) and laser-based altimeters offer advantages in recovering the short-wavelength components of the marine gravity field. Nevertheless, studies on CryoSat-2 and ICESat-2 have demonstrated that despite their higher along-track spatial resolution, their effective wavelength remains around 20 km due to the influence of short-wavelength ocean signals [15,17]. As a result, current global marine gravity field models constructed from data acquired by pulse-limited radar altimeters, SAR altimeters, and others, such as the DTU17 model [18] released by the Technical University of Denmark (DTU) and the SIO_v32.1 model [15] released by the Scripps Institution of Oceanography (SIO), still have a spatial resolution greater than 10 km, even though their grid resolution is $1^{\prime }\times 1^{\prime }$.

In December 2022, the Surface Water and Ocean Topography (SWOT) Mission was successfully launched, providing new opportunities to address a range of scientific challenges [19]. Equipped with the Ka-band Radar Interferometer (KaRIn), SWOT delivers two-dimensional ocean altimetry data with resolutions better than 2 km. Currently, SWOT data have been applied in various fields, particularly in ocean gravity inversion studies. Yu et al. demonstrated that the IVM exhibited greater robustness compared to the inverse Stokes method when utilizing SWOT data [4]. Ma et al. significantly enhanced the accuracy of their results by 45% through the cross-cycle calibration and multi-cycle collinear adjustment of single-cycle simulated data [20]. Additionally, Wan et al. explored the impacts of environmental errors inherent to interferometric radar altimetry on gravity field recovery [21]. Moreover, Wang et al. evaluated the capability of SWOT Level 2 KaRIn Beta data to recover high-frequency ocean gravity signals [22].

The core objective of this study is to utilize nearly one year of observational data from the SWOT satellite for marine gravity field inversion. Firstly, the eight-directional geoid gradient method is employed to compute the DOVs for the South China Sea. The research evaluates how this approach contributes to improving the precision and spatial resolution of the DOV model. Subsequently, based on the SWOT DOV model, the IVM method is applied to invert a gravity field model for the South China Sea. This study conducts a comprehensive analysis of the computational accuracy of various SWOT DOV components and assesses the impact of their incremental signals on gravity anomaly inversion using the IVM method. Additionally, the research explores the influence of SWOT data from different cycle lengths on the inversion of both DOV and gravity anomalies, providing insights into the temporal variability in and optimization of SWOT data for marine gravity field recovery.

2. Study Area and Dataset

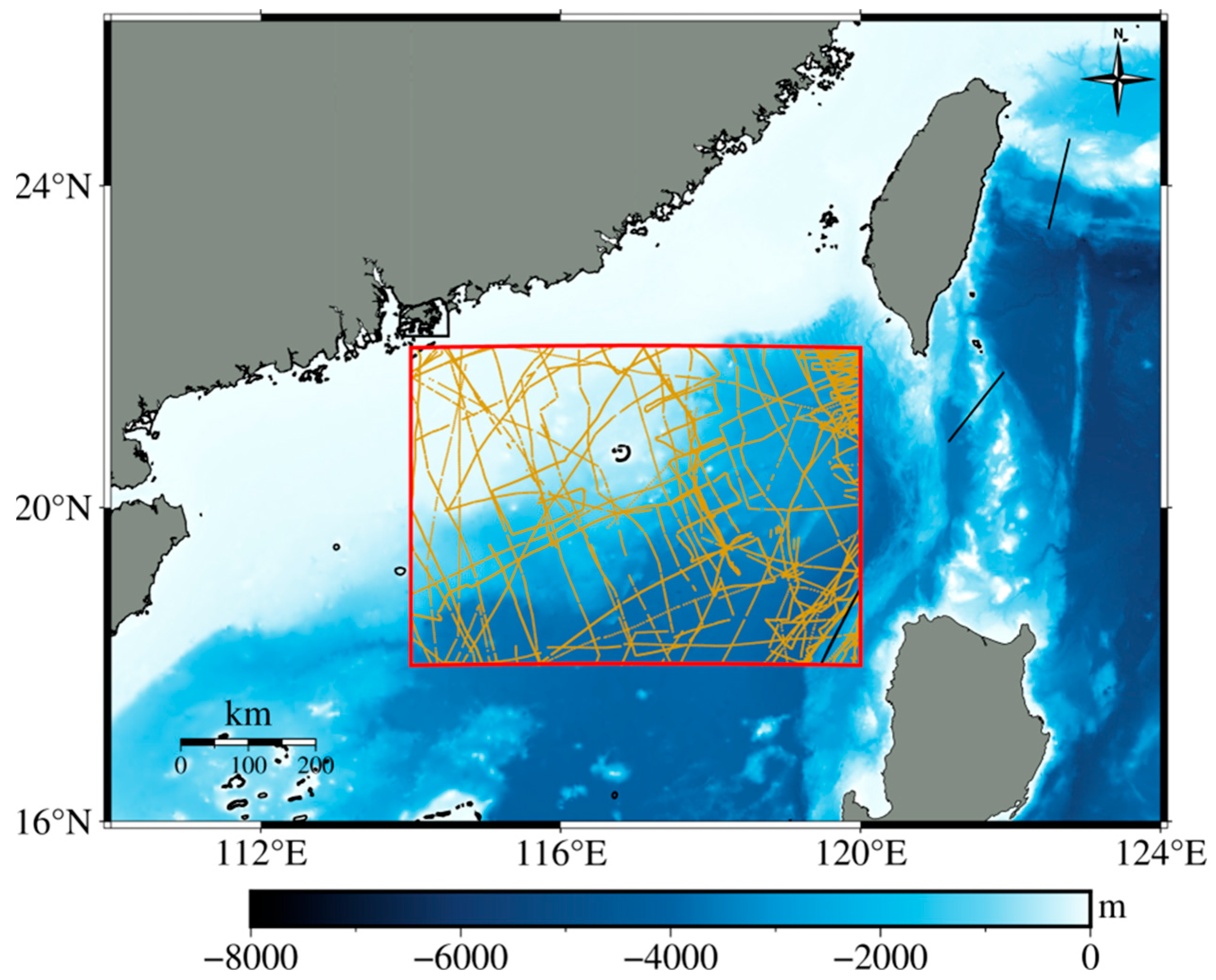
2.1. Study Area

The study area is in the South China Sea (18° N~22° N, 114° E~120° E), as shown in Figure 1. This area is characterized by a notable topographic diversity, where the continental shelf dominates the western sector, while the Manila Trench on the eastern side exhibits dramatic seabed changes. Moreover, the South China Sea is renowned for its complex marine dynamic environment, significantly influenced by tides, ocean currents, and other dynamic factors, which profoundly impact altimetry data’s accuracy and interpretation. This region’s unique topographic and dynamic features make it an ideal candidate for studying the application of SWOT satellite data in enhancing marine gravity field modeling and vertical deflection analysis.

2.2. Dataset in Study Area

2.2.1. Shipborne Gravity Data

The shipborne gravity data within the experimental region were obtained from the National Oceanic and Atmospheric Administration (NOAA), comprising a total of 41,472 gravity points. During actual measurement processes, shipborne gravimeters are influenced by various factors such as sea waves and changes in sailing speed. Additionally, their observation data can be affected by disturbances like vertical acceleration, cross-coupling effects, and the Eötvös effect. Therefore, to improve the accuracy of the measurement data, it is necessary to use a reference gravity field model to correct long-wavelength errors in marine gravimeters, including zero drift, reference field inconsistencies, horizontal deviations, and base station connection errors [23]. The systematic deviations that may exist between the reference gravity field model and the shipborne gravity anomaly data can be expressed as

$$\left\{\begin{array}{l}\delta g_e=a_0+a_1{\sin }^2\phi \\ \phi ={\phi }_0+\Delta \varphi \\ {\sin }^2\phi =(1-\cos 2\phi )/2\end{array}\right.$$

(1)

where $\delta g_e$ represents the deviation between the reference gravity field model and the shipborne gravity anomaly data; $a_0$ and $a_1$ denote the fitting parameters; and φ is the latitude of the survey vessel. Assuming the measurement vessel maintains a constant velocity v along the meridian direction, with the initial latitude denoted as ${\phi }_0$, the change in latitude at any given time can be expressed as

$$\Delta \phi =vt/R$$

(2)

where R represents the mean radius of the Earth, and t represents the ship’s sailing time. Therefore, by utilizing the Maclaurin series expansion of a second-order cosine function [24], Equation (1) can be transformed into a quadratic polynomial in terms of time:

$$\delta g_e=k_0+k_{1}t+k_2{t}^2$$

(3)

In Equation (3), $k_0$, $k_1$, $k_2$ represent the parameters to be fitted. Additionally, the observation platform may exhibit horizontal deviations. Under the assumption that the measurement vessel’s speed and heading remain constant, a constant offset can be introduced to correct for these deviations. Furthermore, systematic errors arising from differences in reference baselines across different routes and the zero drift of the marine gravimeter can also be rectified using constant offsets. Considering the aforementioned factors, the correction for shipborne gravity anomaly data can be calculated using the following formula:

$$\delta g_i=a_i+b_i{t}_i+c_i{t}_i^2$$

(4)

In Equation (4), i represents the route number, and $a_i$, $b_i$, and $c_i$ denote the parameters to be fitted. $\delta g_i$ represents the difference between the reference gravity field and the shipborne gravity anomaly at the observation point. For each route, a set of parameters is determined, and Equation (4) is used to correct the gravity anomaly observations for that specific route. Finally, using the reference gravity anomaly model as the benchmark, shipborne gravity points with differences exceeding three times the mean error are eliminated.

Systematic corrections were applied to the discrepancies between the shipborne gravity anomaly data and the XGM2019e gravity field model (truncated to degree 2190) [25]. The statistical results of the discrepancies are presented in

Table 1. Statistics of shipborne gravity data before and after systematic correction (unit: mGal).

Shipborne Gravity Anomaly	Min	Max	Mean	STD
Before correction	−25.72	26.88	2.77	8.83
After correction	−20.43	23.51	0.00	4.90

. The results show that the standard deviation (STD) between the corrected shipborne gravity anomalies and the XGM2019e model’s gravity anomalies decreased by 3.93 mGal, and the mean value approached 0 mGal. These findings validate the effectiveness of the correction method, ensuring consistency between the shipborne gravity data and the XGM2019e model.

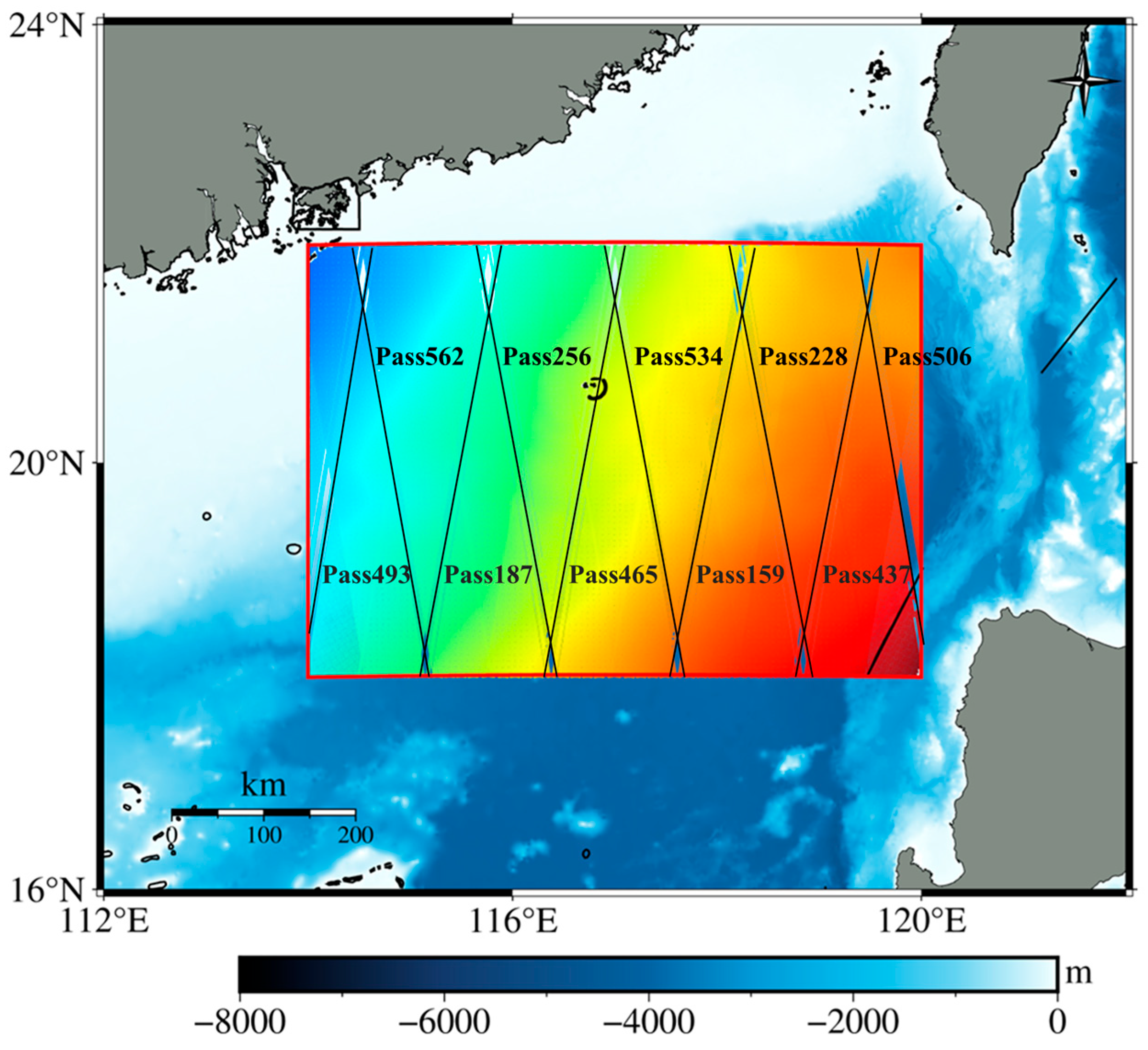
2.2.2. SWOT Altimetry Data

The experiment utilized SWOT altimetry data obtained from the SWOT Exper_L2_LR_SSH dataset distributed by Archiving, Validation, and Interpretation of Satellite Oceanographic Data (AVISO), The dataset was accessed and downloaded using the FTP protocol, ftp://ftp-access.aviso.altimetry.fr/, (accessed on 1 March 2025). This dataset covers 10 tracks (Pass 159/187/228/256/437/465/493/506/534/562) over the study area, as shown in Figure 2. The observation time window for the SWOT altimetry data spans from November 2023 to December 2024 (Cycle 007–025), with a total observation period of approximately one year. In terms of data processing, the PCI0 version was used for cycles 007–022. This algorithm primarily relies on pre-calibrated parameters obtained during the in-orbit calibration phase. Starting from Cycle 023, the data were processed using the PCI2 version (distributed by AVSIO, available from Cycle 023 onwards). The PCI2 version optimized the inter-satellite phase correction model, effectively suppressing stripe noise caused by jitter in the dual-platform interferometric baseline, significantly improving the data quality.

To obtain the sea surface height (SSH), the sea surface height anomaly (SSHA) measured by KaRIn $ssha\_karin$ is combined with the mean sea surface (MSS) and the cross-calibration correction value $R_{cross}$:

$$H_{\mathrm{corr}}=ssha\_karin+MSS+R_{cross}$$

(5)

Here, $R_{cross}$ adopts the cross-calibration correction parameters (height_cor_xover) provided within the Exper_L2_LR_SSH dataset. After obtaining the SSH, unreliable data must be filtered out based on specific editing criteria. To ensure the reliability and applicability of the altimetry data, the following screening strategies were implemented:

• ancillary_surface_classification_flag = 0. Only ocean data were selected;
• distance_to_coast > 2000 m. Nearshore altimetry data are susceptible to influences such as topography, sea state variations, and abnormal radar echo patterns, which can degrade the measurement accuracy. Therefore, data within 2000 m of the coastline were excluded to minimize the impact of coastal interference on the calculations;
• Significant Wave Height (SWH) < 6 m. Under high sea state conditions (SWH > 6 m), the quality of altimetry data can be significantly compromised, leading to increased measurement errors. Thus, data with an SWH greater than 6 m were filtered out to reduce the uncertainties caused by intense sea state variations [26];
• ssha_karin_qual = 0. This flag serves as a critical filtering parameter to effectively exclude poor-quality data from the wide swath edges and center, ensuring the overall quality and reliability of the altimetry data.

2.2.3. SIO Model

The SIO series of marine gravity field models have been updated to version 32.1 [15]. SIO_V32.1 is derived from satellite altimetry data, including Geosat, ERS-1, Jason-1, Jason-2, Cryosat LRM, Cryosat SAR, Sentinel-3A/B, and the Ka-band altimeter SARAL/AltiKa. To enhance the model’s accuracy, specific retracking processes were applied to the coastal waveforms of Jason-1/2, Envisat, AltiKa, and Cryosat-LRM. These products are released in 1′ × 1′ grid formats, including DOV models (east_32.1 and north_32.1), gravity anomaly models (grav_32.1), and vertical gravity gradient models (curv_32.1), which can be downloaded from https://topex.ucsd.edu/pub/global_grav_1min/ (accessed on 1 March 2025).

2.2.4. Mean Sea Surface Model

The CNES_CLS_22 mean sea surface (MSS) model was jointly developed by the Centre national d’études spatiales (CNES) and Collecte Localisation Satellites (CLS). It incorporates high-precision Exact Repeat Mission (ERM) data and high-coverage GM data, such as CryoSat-2 and SARAL/AltiKa. It employs specialized filtering and correction techniques to optimize the data quality and reduce the impacts of ocean variability and noise. Advanced data processing methods, including local least squares collocation and variable cross-covariance models, are used to achieve precise measurements of short wavelengths (<30 km). The model’s accuracy has improved by 40% compared to its predecessors, reaching centimeter-level precision [27].

2.2.5. Mean Dynamic Topography Model

The MDT_CNES_CLS_22 mean dynamic topography (MDT) model [28] is a high-resolution global MDT model. It integrates multi-year satellite altimetry data, gravity satellite data (GRACE, GOCE), drift buoy observations, high-frequency radar, and temperature–salinity profile data to provide an enhanced MDT solution.

3. Method

Following the preprocessing steps detailed in Section 2.2, the SWOT altimetry data can be effectively employed to derive the SSH. However, the computation of DOVs from SWOT data deviates substantially from traditional satellite altimetry methods. To address this, we adopt the eight-directional geoid gradient method for calculating SWOT DOVs. These derived DOVs are subsequently utilized in the inversion of the marine gravity field through the IVM method. All computational procedures are conducted within the Remove–Compute–Restore (RCR) framework. Specifically, the contribution of the XGM2019e global gravity model up to degree and order 2190 is initially removed, the residual component is computed, and the full signal is then restored by re-incorporating the model’s contribution.

3.1. Calculation DOV Based on Eight-Directional Geoid Gradient

When processing SWOT SSH data, it is necessary to first calculate the average value of all cycle data for the same pass to effectively mitigate the effects of temporal sea surface variability. Notably, the SWOT satellite’s interferometric altimetry introduces inherent instrument errors (such as baseline errors and phase errors) that can cause systematic tilt biases in the cross-track direction (i.e., perpendicular to the satellite’s flight trajectory). This cross-track tilt error significantly impacts the accuracy of subsequent gravity inversion results. Therefore, systematic correction is essential in data processing. The specific steps are as follows:

Frist, since the SWOT utilizes KaRIn technology, systematic errors such as baseline errors and roll angle errors affect data along the cross-track direction. To mitigate these biases, a smooth MSS model (CNES_CLS_22) is employed as the reference surface to correct the tilt in the SWOT-derived SSH. The discrepancies between the two are modeled using the following equation:

$$\Delta l_i+v_i=f\cdot d_i+q$$

(6)

where $\Delta l_i$ represents the difference between the original SWOT MSS and the MSS model. $d_i$ denotes the distance from the nadir track, $v_i$ is the residual error, and f and q are coefficients used to correct the bias and tilt in the SSH along the cross-track direction. The coefficients f and q are estimated using the least squares method. These coefficients are then applied to correct the respective cross-track data, resulting in the complete H_{MSS_SWOT}.

Then, the SWOT geoid $N_{\mathrm{SWOT}}$ is obtained by subtracting the mdt_CNES_CLS_22 MDT model from H_{MSS_SWOT}. Using the 2190-degree geoid from the XGM2019e model as the reference field, the long-wavelength marine geoid signal is subtracted from the SWOT MSS to obtain the residual SWOT geoid:

$$N_{\mathrm{res}}=N_{\mathrm{SWOT}}-N_{\mathrm{XGM}2019\mathrm{e}}$$

(7)

Due to the limitations of orbit spacing, traditional altimetry data can only be used to calculate the geoid gradient along the track direction. This means that the DOV component can only be inferred from the geoid gradient along the track direction. As a result, with an increasing satellite orbit inclination, the accuracy of the north–south component ($\xi$) of the DOV gradually improves, while the accuracy of the east–west component ($\eta$) of the DOV gradually decreases, leading to a significant disparity in the precision of these two components. However, SWOT, with its unique two-dimensional wide-swath observation capability, extends beyond the traditional along-track and cross-track directions to include six additional tilt directions, as illustrated in Figure 3. The residual geoid gradients ${\epsilon }_i,i=1,2,3\dots ,8$ and their respective azimuth angles ${\alpha }_i,i=1,2,3\dots ,8$ are calculated for each of the eight directions relative to the flow point.

Therefore, at each calculation point of the ascending and descending tracks, a system of equations based on the residual geoid gradients from eight directions can be established:

$$\left[\begin{array}{l}{\epsilon }_1\\ ⋮\\ {\epsilon }_8\end{array}\right]+\left[\begin{array}{l}{v}_1\\ ⋮\\ v_8\end{array}\right]=\left[\begin{array}{l}\cos {\alpha }_1,\sin {\alpha }_1\\ ⋮\\ \cos {\alpha }_8,\sin {\alpha }_8\end{array}\right]\left[\begin{array}{l}\xi \\ \eta \end{array}\right]$$

(8)

where $v_i$ represents the correction term, and the azimuth angle ${\alpha }_i$ can be calculated using the positional data of adjacent points:

$$\alpha =\arctan \left({\displaystyle \frac{\cos {\phi }_q\sin \left({\lambda }_q-{\lambda }_p\right)}{\cos {\phi }_p\sin {\phi }_q-\sin {\phi }_p\cos {\phi }_q\cos \left({\lambda }_q-{\lambda }_p\right)}}\right)$$

(9)

where φ and λ denote latitude and longitude, respectively.

By setting

$$L=\left[\begin{array}{l}{\epsilon }_1\\ ⋮\\ {\epsilon }_8\end{array}\right],V=\left[\begin{array}{l}{v}_1\\ ⋮\\ v_8\end{array}\right],A=\left[\begin{array}{l}\cos {\alpha }_1,\sin {\alpha }_1\\ ⋮\\ \cos {\alpha }_8,\sin {\alpha }_8\end{array}\right],X=\left[\begin{array}{l}\xi \\ \eta \end{array}\right]$$

(10)

It is important to note that the eight vectors ($\cos {\alpha }_i,\sin {\alpha }_i$) in matrix A are uniformly distributed within the regular grid with a resolution of 2 km (see Figure 3), ensuring that matrix A is not ill conditioned. Using the least squares method to solve the system of equations, we can obtain the residual DOV components:

$$X={\left(A^{T}PA\right)}^{-1}{A}^{T}PL$$

(11)

Finally, the XGM2019e model is used to recover the 2190-degree signal and obtain the SWOT DOV.

3.2. Inverse Vening–Meinesz (IVM) Method

In 1998, Hwang derived the spectral representation formula of the IVM, which converts the DOV into gravity anomalies and geoid heights, based on the spherical harmonic expansion of the disturbing potential and its functional relationships [10]. The mathematical expression of the IVM formula is as follows:

$$\Delta g(p)={\displaystyle \frac{{\gamma }_0}{4\pi }}{\displaystyle {\iint }_{\sigma }{H}^{\prime }({\xi }_q\cos {\alpha }_{qp}+{\eta }_q\sin {\alpha }_{qp})}d{\sigma }_q$$

(12)

where ${\gamma }_0$ represents normal gravity, p is the computation point, q is the flow point, and ${\alpha }_{qp}$ denotes the azimuth angle from point q to point p. ${\xi }_q$ and ${\eta }_q$ represent the DOVs in point q, respectively. $H^{\prime }$ represents the derivative of the integration kernel function, defined as

$$H^{\prime }={\displaystyle \frac{dH}{d{\psi }_{pq}}}=-{\displaystyle \frac{\cos \frac{{\psi }_{pq}}{2}}{2{\sin }^2\frac{{\psi }_{pq}}{2}}}+{\displaystyle \frac{\cos \frac{{\psi }_{pq}}{2}\left(3+2\sin \frac{{\psi }_{pq}}{2}\right)}{2\sin \frac{{\psi }_{pq}}{2}\left(1+\sin \frac{{\psi }_{pq}}{2}\right)}}$$

(13)

$$\cos {\psi }_{pq}=\sin {\phi }_p\sin {\phi }_q+\cos {\phi }_p\cos {\phi }_q\cos ({\lambda }_q-{\lambda }_p)$$

(14)

where ψ_pq represents the spherical distance between points p and q. To facilitate computation, Equation (12) is transformed into a discrete form of numerical integration, and the one-dimensional fast Fourier transform (FFT) [29] is utilized to solve the integral problem rapidly and efficiently:

$$\begin{array}{c}\mathsf{\Delta }{g}_{{\varphi }_p}\left({\lambda }_p\right)={\displaystyle \frac{\overline{\gamma }\mathsf{\Delta }\varphi \mathsf{\Delta }\lambda }{4\pi }}{\displaystyle \sum _{{\varphi }_q={\varphi }_1}^{{\varphi }_n}}{\displaystyle \sum _{{\lambda }_q={\lambda }_1}^{{\lambda }_n}}{H}^{\prime }\left(\mathsf{\Delta }{\lambda }_{qp}\right)\left({\xi }_{\cos }\cos {\alpha }_{qp}+{\eta }_{\cos }\sin {\alpha }_{qp}\right)\\ \hspace{1em}={\displaystyle \frac{\overline{\gamma }\mathsf{\Delta }\varphi \mathsf{\Delta }\lambda }{4\pi }}{F}_1^{-1}\{{\displaystyle \sum _{{\varphi }_q={\varphi }_1}^{{\varphi }_n}}\left[F_1\left(H^{\prime }\left(\mathsf{\Delta }{\lambda }_{qp}\right)\cos {\alpha }_{qp}\right)\right]F_1\left({\xi }_{\cos }\right)\\ +\left[F_1\left(H^{\prime }\left(\mathsf{\Delta }{\lambda }_{qp}\right)\sin {\alpha }_{qp}\right)\right]F_1\left({\eta }_{\cos }\right)\}\end{array}$$

(15)

where ${\xi }_{\cos }={\xi }_q\cos {\phi }_q$, ${\eta }_{\cos }={\eta }_q\cos {\phi }_q$. Δφ and Δλ represent the grid spacing for latitude and longitude, respectively. F₁ denotes the one-dimensional Fourier transform, and F₁⁻¹ denotes the one-dimensional inverse Fourier transform.

If the spherical distance ψ_pq in the kernel function equals zero, it will cause the kernel function to become singular. The region where the kernel function becomes singular is referred to as the inner zone. In this case, the formula for calculating the gravity anomaly is as follows:

$$\mathsf{\Delta }g={\displaystyle \frac{s_0\overline{\gamma }}{2}}\left({\xi }_y+{\eta }_x\right)={\displaystyle \frac{\overline{\gamma }}{2}}\sqrt{{\displaystyle \frac{\mathsf{\Delta }x\mathsf{\Delta }y}{\pi }}}({\displaystyle \frac{\partial \xi }{\partial y}}+{\displaystyle \frac{\partial \eta }{\partial x}})$$

(16)

where $S_0$ represents the radius of the inner zone, $\Delta x=R\Delta \lambda \cos \phi$, and $\Delta y=R\Delta \phi$. ξ_y, η_x denote the rate of change of the north–south component of the DOV along the y-axis and the east–west component of the DOV along the x-axis, respectively. These are expressed as

$$\left\{\begin{array}{l}{\xi }_x(i)={\displaystyle \frac{1}{2R\mathsf{\Delta }\phi }}[\xi (i+1)-\xi (i-1)]\\ {\eta }_y(i)={\displaystyle \frac{1}{2R\mathsf{\Delta }\lambda \cos \phi }}[\eta (i+1)-\eta (i-1)]\end{array}\right.$$

(17)

4. Results and Analysis

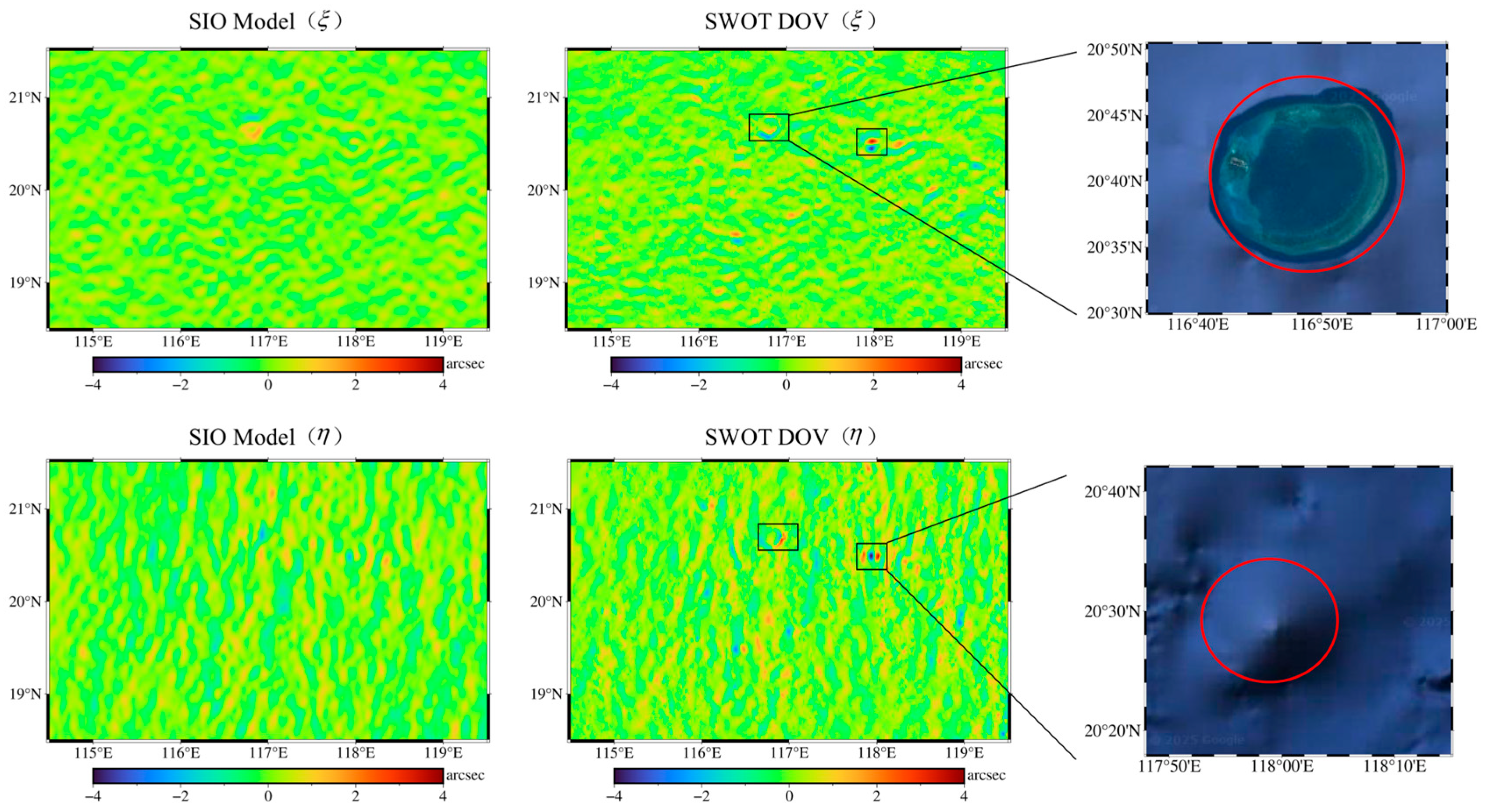
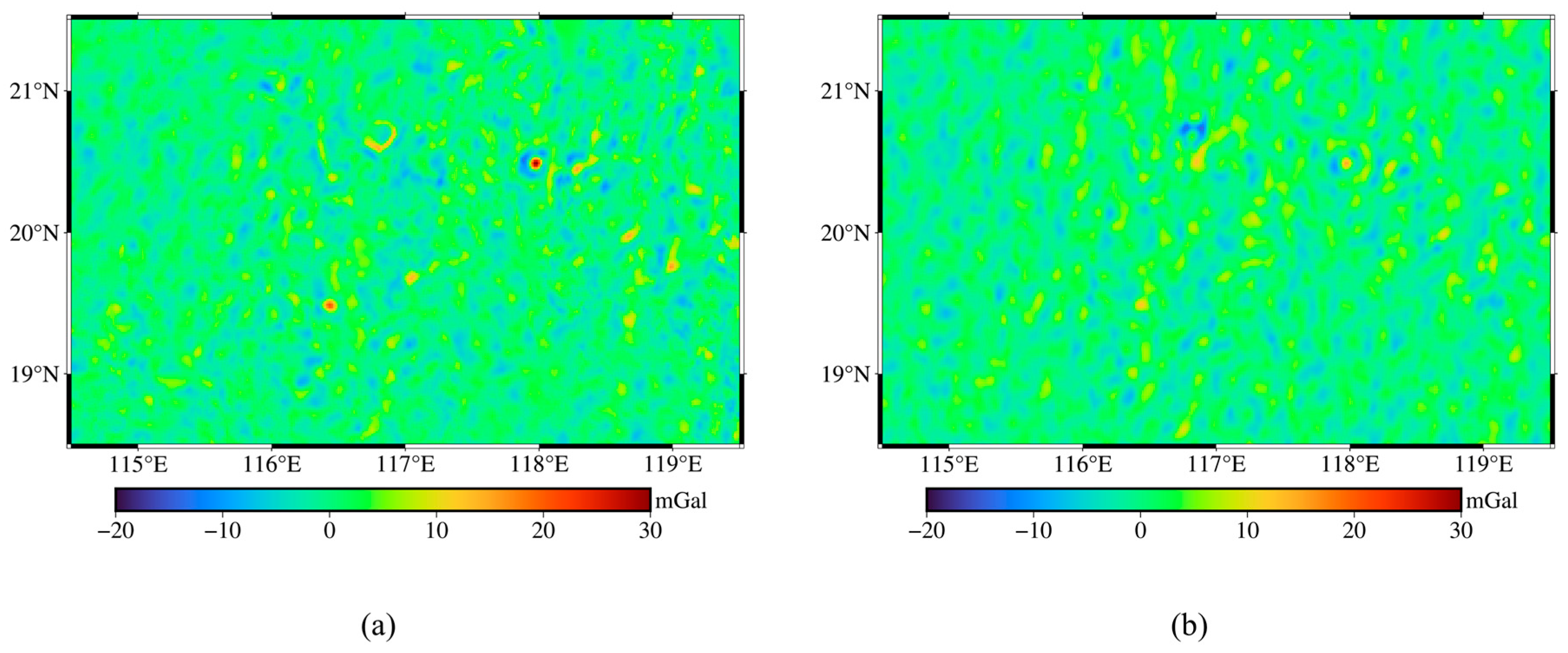
4.1. Results of the SWOT DOV Calculation

The residual DOV components are shown in Figure 4 From the figure, it can be observed that, within the experimental region, both the $\xi$ and $\eta$ components of the SWOT DOV exhibit distinct features near seamounts and the Dongsha Atoll (a typical geomorphic structure formed by coral reefs surrounding a lagoon, characterized by a ring or horseshoe shape, usually lacking a central island; see the black-boxed area in Figure 4). In contrast, the SIO model, due to its resolution limitations, is significantly less capable of capturing the details of seafloor topography compared to the SWOT data. This demonstrates that the SWOT satellite possesses high-resolution ocean altimetry capabilities, enabling it to accurately capture the perturbation effects of complex seafloor topography on the ocean gravity field. Traditional altimeters, constrained by their spatial resolution, often struggle to accurately invert the fine structures of DOVs.

To quantitatively assess the accuracy of SWOT-derived DOVs, a forward modeling of DOVs was carried out using the Vening–Meinesz integral formula based on shipborne gravity data within the study area. First, the gravity anomalies up to degree and order 2190 were calculated using the XGM2019e gravity field model and subsequently removed from the shipborne gravity anomaly data in the study area, yielding residual gravity anomalies. These residual gravity anomalies were then gridded. Following this, the Vening–Meinesz integral formula was applied to compute the residual DOVs at the shipborne measurement points through forward modeling:

$$\left\{\begin{array}{l}\xi ={\displaystyle \frac{1}{4\pi r\gamma }}{\displaystyle {\iint }_s\Delta }{g}^{\prime }{\displaystyle \frac{\partial S(r,\psi ,r^{\prime })}{\partial \psi }}cos\alpha ds\\ \eta ={\displaystyle \frac{1}{4\pi r\gamma }}{\displaystyle {\iint }_s\Delta }{g}^{\prime }{\displaystyle \frac{\partial S(r,\psi ,r^{\prime })}{\partial \psi }}sin\alpha ds\end{array}\right.$$

(18)

where r and $r^{\prime }$ represents the radial distance in the computation point and flow point. $\gamma$ is the normal gravity in the computation point. $\Delta g^{\prime }$ represent the free-air gravity anomaly in the flow point. $S(r,\psi ,r^{\prime })$ represents the kernel function, and its derivative with respect to $\psi$ is calculated using the following formula:

$${\displaystyle \frac{\partial }{\partial \psi }}S(r,\psi ,r^{\prime })=\left[\begin{array}{l}-{\displaystyle \frac{2r}{L^3}}-{\displaystyle \frac{3}{rL}}+{\displaystyle \frac{5}{r^2}}+{\displaystyle \frac{3}{r^2}}ln{\displaystyle \frac{r-r^{\prime }cos\psi +L}{2r}}\\ -{\displaystyle \frac{3r^{\prime }(L+r)cos\psi }{r^{2}L(r-r^{\prime }cos\psi +L)}}\end{array}\right]r^{\prime }sin\psi$$

(19)

$$L=\sqrt{r^2+{r^{\prime }}^2+2r{r}^{\prime }\cos \psi }$$

(20)

The SWOT DOV was interpolated to the shipborne measurement locations, and their differences from the DOV derived from the forward modeling of shipborne gravity anomalies are shown in Figure 5. Observations reveal that most of the deviations are less than 1 arcsecond. Statistical data in

Table 2. Statistics of the DOV components between the SWOT and SIO models (unit: arcseconds).

Model	DOV	Max	Min	Mean	RMS	STD
SWOT	$\xi$	2.94	−3.56	0.04	0.77	0.77
	$\eta$	3.75	−4.09	−0.01	0.86	0.86
SIO	$\xi$	2.96	−3.54	0.07	0.76	0.76
	$\eta$	3.66	−4.34	−0.02	0.87	0.87

show that the precision of the calculated SWOT DOV reaches 0.77 arcseconds ($\xi$) and 0.86 arcseconds ($\eta$), respectively, with a difference of less than 0.1 arcseconds between the two. It is noteworthy that in the South China Sea, the $\eta$ component error of traditional altimetry satellites is typically one to two times that of the $\xi$ component. Therefore, the improved precision of the $\eta$ component in SWOT highlights the superiority of its altimetry mode.

Additionally, the SIO model was introduced for comparison. As a multi-source altimetry fusion product, the SIO model not only incorporates traditional altimeter data but also integrates new altimetry data such as the Ka-band altimeter (Altika) and synthetic aperture radar altimeters (CryoSat-2, Sentinel-3A/B), thus representing a higher precision level of historical satellite altimetry data. The comparison results with the SIO model indicate that the precision of SWOT based on 19 repeat cycles (approximately 1 year) is comparable to that of the SIO model. However, it should be noted that this comparison does not directly prove that the precision of the SWOT DOV is lower than that of the SIO model. The reason lies in the shipborne gravity data having a sampling interval greater than 2 km and the potential loss of high-frequency signals during the gridding and forward modeling process. Despite this, the results still reflect, to some extent, the precision level of the SWOT DOV, providing an important reference for evaluating its actual performance.

To further analyze the differences between the SWOT DOV and the SIO model, a Power Spectral Density (PSD) analysis was conducted to compare their PSD values across different wavelength ranges. A higher PSD value indicates stronger signals within that band. The results are shown in Figure 6. In the short wavelength range of 3.5–20 km, the SWOT DOV exhibits a significant enhancement in signals, primarily due to the high spatial resolution of its wide-swath radar interferometry technology, which enables it to capture small to medium-scale sea surface height signals that are often missed due to sparse tracks and an insufficient cross-track resolution. In the medium wavelength range of 20–50 km, the PSD values of both models are similar. This is because the SIO model assimilates various Ka-band and SAR altimetry data, such as Altika (with a cross-track resolution of 80 km), CryoSat-2 (with a cross-track resolution of 7–10 km), and Sentinel-3A/B (with a cross-track resolution of 104 km), which fill in the signals within this band. In summary, the differences between SWOT and the SIO model are primarily reflected in the short-wavelength signals (3.5–20 km).

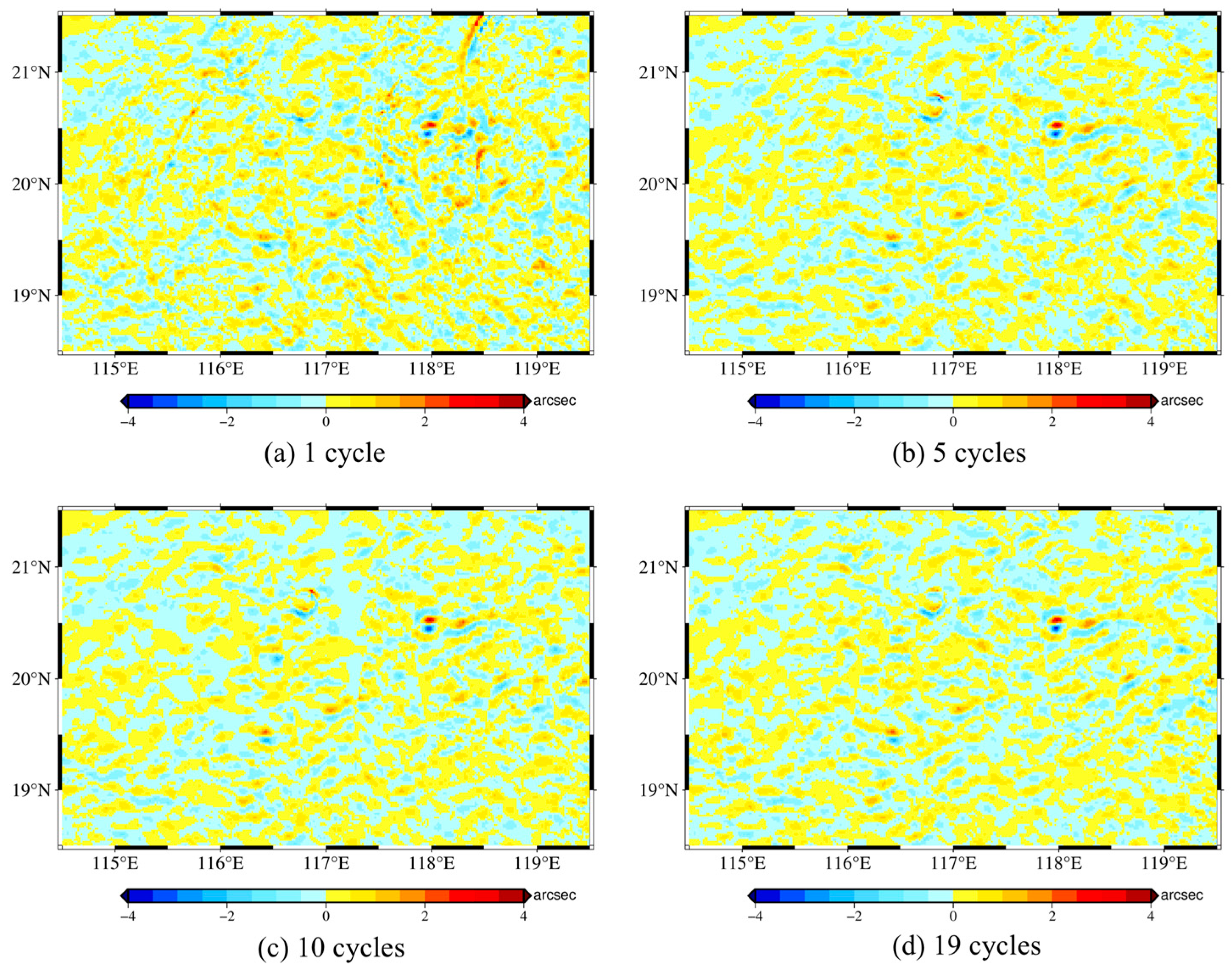
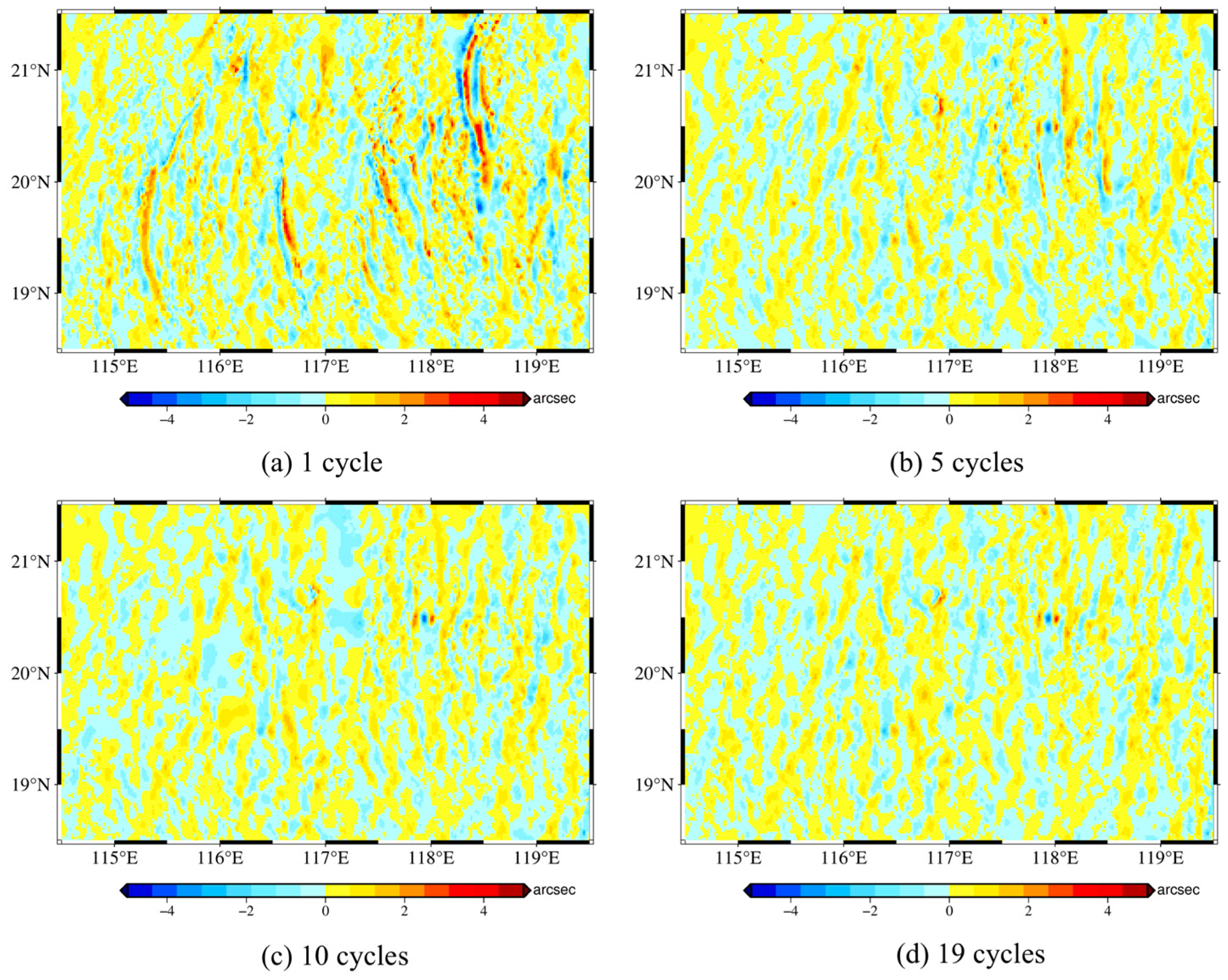
4.2. Impact on the Accuracy of IVM Method Using SWOT DOV

The gravity anomalies derived from the SWOT DOV using the IVM method are shown in Figure 7a. For comparison, Figure 7b presents the results from the SIO marine gravity field model grav_32.1 after the removal of spherical harmonic degree 2190. It can be observed that the gravity anomaly model obtained from SWOT inversion exhibits finer details and a higher correlation with the topography, particularly in the Dongsha Atoll region.

Further comparison with 21,940 shipborne gravity anomaly observations reveals that the RMS of the SWOT-derived gravity anomalies is 4.97 mGal, slightly higher than the 4.78 mGal of the SIO model (grav_32.1). This discrepancy can be attributed to two factors. First, the resolution of the optimal mean sea surface (MSS) grid constructed from conventional nadir altimetry (MSS_CNES_CLS2022) is still insufficient to fully meet the resolution requirements of SWOT. Second, high-frequency noise in SWOT DOV data has influenced the accuracy of gravity anomaly inversion using the IVM method.

To investigate the impact of high-frequency signals in the SWOT DOV on the IVM method, Gaussian filtering was applied to the components of the DOVs. Since the resolution of the Expert_L2_LR_SSH product is 2 km, the grid resolution was fixed at 1′ × 1′, representing the highest available resolution. Four experimental groups were designed: The first group used unfiltered DOV grids. The second group applied a Gaussian filter with a radius of 10 km to the ξ component, while the η component remained unchanged. The third group applied a Gaussian filter with a radius of 10 km to the η component, while leaving the ξ component unchanged. And the fourth group applied a Gaussian filter with a radius of 10 km to both components of the DOVs. The 10 km Gaussian filtering radius was specifically chosen to target the wavelength band where SWOT altimetry signals exhibit their dominant spectral energy. As shown in Figure 8, the signals within the 10 km wavelength band in the DOVs were attenuated after filtering.

The results of the comparison with 21,940 shipborne gravity anomaly measurements within the modeling area are shown in

Table 3. Results of gravity anomaly inversion using the IVM method from filtering different DOV components in four sets of experiments (Unit: mGal).

Group	Max	Min	Mean	STD
Group 1	23.99	−23.66	0.65	4.97
Group 2	23.45	−23.40	0.65	4.95
Group 3	23.77	−23.22	0.65	4.92
Group 4	23.23	−22.95	0.66	4.90

. It can be observed that, at a 1′ resolution, the signals within the 10 km wavelength band of the η component have a significant impact on the accuracy of IVM gravity anomaly inversion. Compared to the unfiltered data, applying a Gaussian filter with a 10 km radius to both components of the DOVs improves the overall accuracy of the gravity anomaly by approximately 0.07 mGal. The primary contribution to this improvement comes from the filtering of the η component, while a smaller contribution is attributed to the ξ component.

Figure 9 shows the PSD of the gravity anomalies derived from the four experimental groups. The results demonstrate that filtering only the η component leads to a more significant reduction in the PSD of the gravity anomalies compared to filtering only the ξ component. However, the reduction in PSD is far less pronounced than when both components are filtered simultaneously. This indicates that, in the inversion within this region, the contribution of the ξ component within the 10 km wavelength band is greater than that of the η component. Nevertheless, as shown in Table 3, removing the contributions of both the ξ and η components within 10 km wavelength band still significantly improves the accuracy of the gravity anomaly inversion. This suggests that, within the 10 km wavelength band, the noise in the DOVs has a more significant impact on the accuracy of the IVM method than the genuine signals.

5. Discussion

Studies based on SWOT simulated data indicate that increasing the number of SWOT observation cycles helps improve the accuracy of DOV calculations. To analyze the actual impact of the number of cycles on the calculation of SWOT DOVs, data from 1, 5, 10, and 19 cycles were used to compute the SWOT DOVs.

Figure 10 and Figure 11 display the residual DOV components calculated from different numbers of cycles. It can be observed that the DOV components computed from a single cycle exhibit multiple north–south-oriented arc-shaped anomalies, with this phenomenon being particularly pronounced in the $\eta$ component. These anomalies may be related to mesoscale turbulence captured by SWOT. In ocean dynamics, mesoscale turbulent motions cause spatiotemporal variations in sea surface height, thereby influencing the DOVs computed by SWOT. As the number of observation cycles increases, these anomalies gradually weaken and eventually disappear. Specifically, the $\xi$ component converges closely with the 19-cycle result after accumulating 5 cycles, whereas the $\eta$ component requires an accumulation up to the 10th cycle to approximate the 19-cycle result.

Quantitative comparison with shipborne measurement data (see

Table 4. Accuracy of the DOV components of SWOT under different cycles (unit: arcseconds).

Period	DOV	Max	Min	Mean	STD
1 cycle	$\xi$	9.00	−8.98	−0.04	0.83
	$\eta$	4.56	−4.57	−0.01	1.07
5 cycles	$\xi$	8.86	−8.73	−0.02	0.77
	$\eta$	3.84	−4.18	−0.02	0.91
10 cycles	$\xi$	9.03	−9.31	−0.02	0.77
	$\eta$	3.92	−4.03	−0.01	0.89
19 cycles	$\xi$	8.80	−8.82	−0.02	0.77
	$\eta$	3.75	−4.09	−0.01	0.86

) further validates the aforementioned results. Statistical analysis shows that the STD of the bias in the ξ component from single-cycle data is 0.83 arcseconds, which is 0.06 arcseconds higher than the result from 19 cycles. The difference in the η component is even more pronounced, with an STD discrepancy of 0.21 arcseconds between single-cycle and 19-cycle data. As the number of observation cycles increases, the ξ component stabilizes to its optimal accuracy (STD: 0.77 arcseconds) after only 5 cycles, while the η component requires a gradual accumulation up to 19 cycles to improve to 0.86 arcseconds. Moreover, the rate of improvement in accuracy for the η component significantly slows down after 10 cycles. These results indicate that increasing the number of observation cycles exhibits a significant directional disparity in enhancing the accuracy of DOV calculations. For SWOT DOV computation, the core challenge lies in mitigating instrument errors in the cross-track direction. Simply increasing the number of observation cycles can partially reduce but cannot entirely eliminate these errors.

The residual gravity anomalies inverted from DOVs of different cycles are shown in Figure 12. It can be observed that the error distribution pattern of gravity anomalies is similar to that of the η component. When using only single-cycle altimetry data, the inverted gravity anomalies exhibit obvious arc-shaped artifacts. After applying five cycles of SWOT data, these arc-shaped artifacts are weakened and mainly concentrated around 118–119° E. With 10 cycles of SWOT data, the arc-shaped artifacts essentially disappear. This suggests that the key to improving the accuracy of the gravity field lies in error compensation for cross-track data, consistent with the conclusions drawn earlier.

6. Conclusions

This study calculates the SWOT DOV components using the eight-directional geoid gradient method based on SWOT observational data and subsequently inverts the gravity field model in the South China Sea region using the IVM method. Based on the experimental results, a systematic analysis is conducted on the inversion accuracy, the impact of observation periods on the DOV solutions, and the influence of high-frequency SWOT DOV signals on gravity anomaly inversion via the IVM method. The conclusions are as follows:

(1)

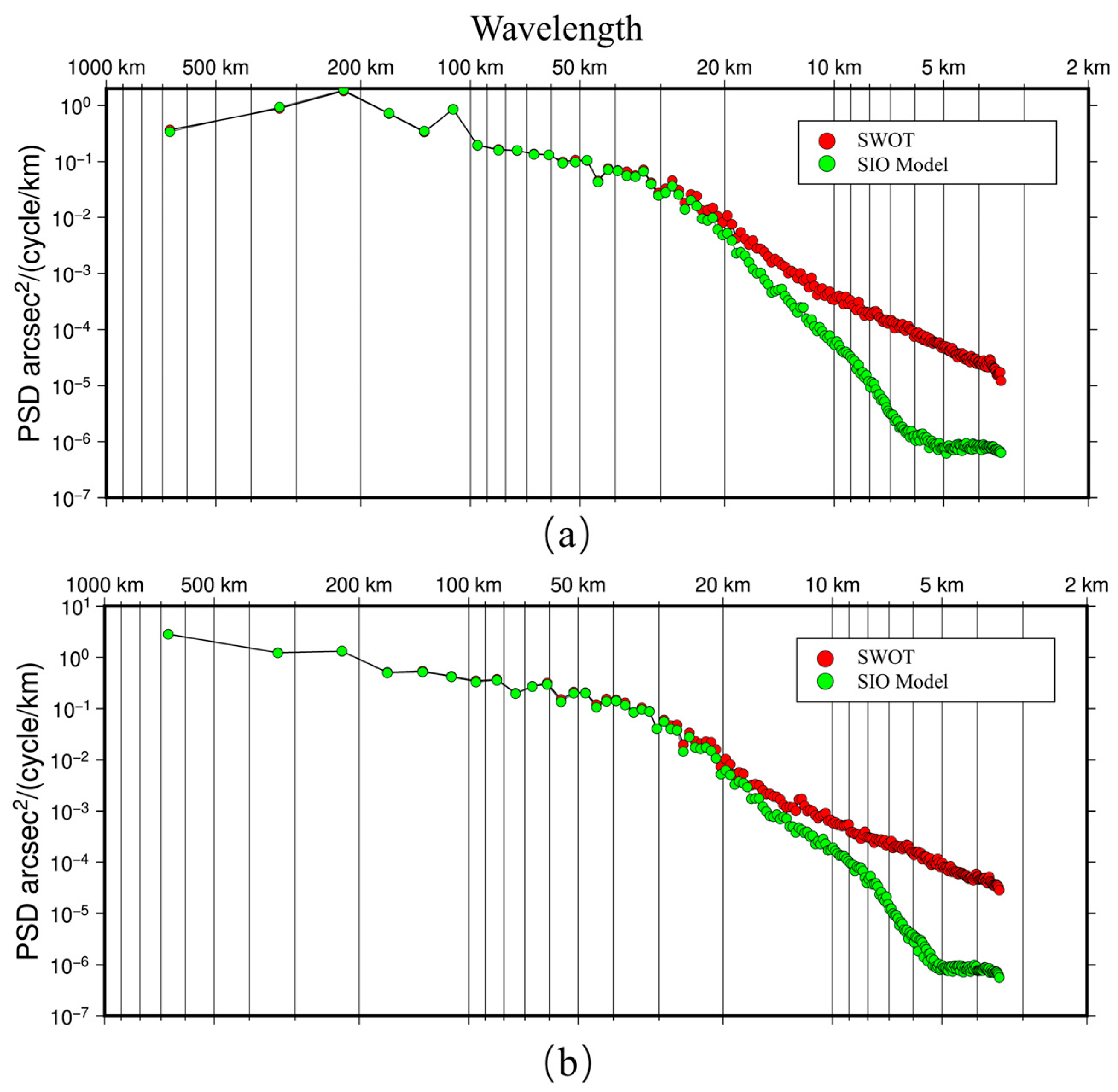
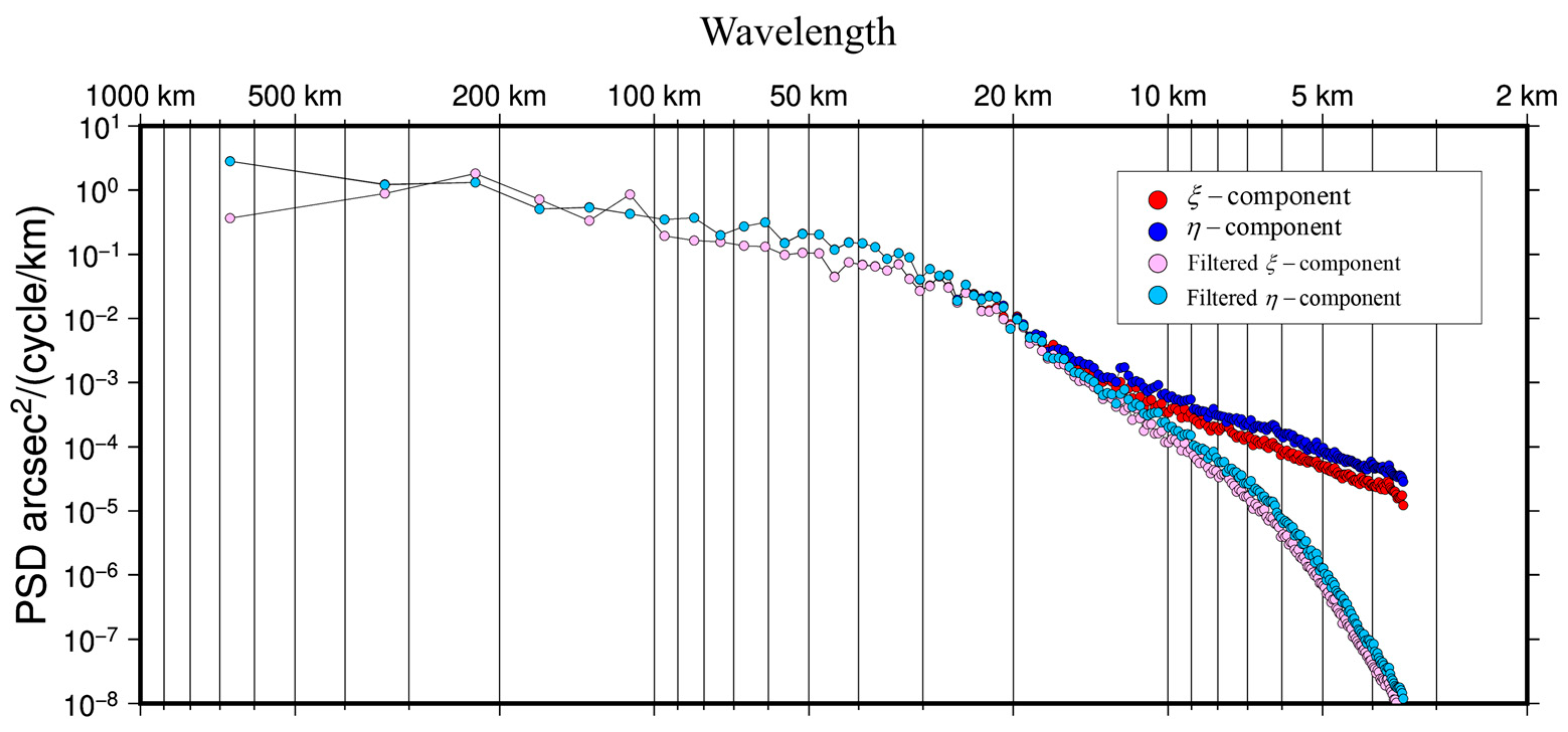
The DOVs derived from SWOT data can precisely characterize seafloor topographic features. Compared with shipborne gravity data, the differences between the η and ξ components of DOVs derived from nearly one year of SWOT data are significantly smaller than those from traditional altimetry satellites. The accuracy of these components is comparable to the multi-source altimetry fusion model SIO_v32.1. PSD analysis indicates that, compared to the SIO model, SWOT shows spectral gains primarily in the short-wavelength range of 3.5–20 km, demonstrating that SWOT’s wide-swath interferometric mode effectively captures medium to small-scale sea surface height signals;

(2)

Increasing the SWOT observation period improves the accuracy of DOVs, but the efficiency of the improvement varies directionally. Specifically, the ξ component reaches a stable and satisfactory accuracy with fewer observation cycles, whereas the η component requires the accumulation of more observation cycles to achieve a comparable accuracy. This directional difference indicates that cross-track errors caused by factors such as baseline roll and phase drift are critical limitations affecting the accuracy of the η component. Although the impact of these errors can be partially mitigated by an increasing data accumulation, they cannot be completely eliminated, suggesting the necessity for developing targeted correction algorithms;

(3)

The SWOT DOV gains are mainly concentrated within the 3.5–20 km wavelength band, but high-frequency signals in this band are prone to amplification by noise during the inversion of gravity anomalies using the IVM method. Through an analysis involving four filtering experiments, it is found that applying a 10 km Gaussian low-pass filter to DOV components improves the gravity anomaly inversion accuracy, with noise in the η component having a more pronounced impact. Further PSD analysis confirms that within this band, the interference from noise surpasses the actual DOV signals, particularly in the η component.