Numerical Study on the Influence of Rudder Fillets on Submarine Wake Field and Noise Characteristics
Abstract
1. Introduction
2. Models
2.1. Submarine Model
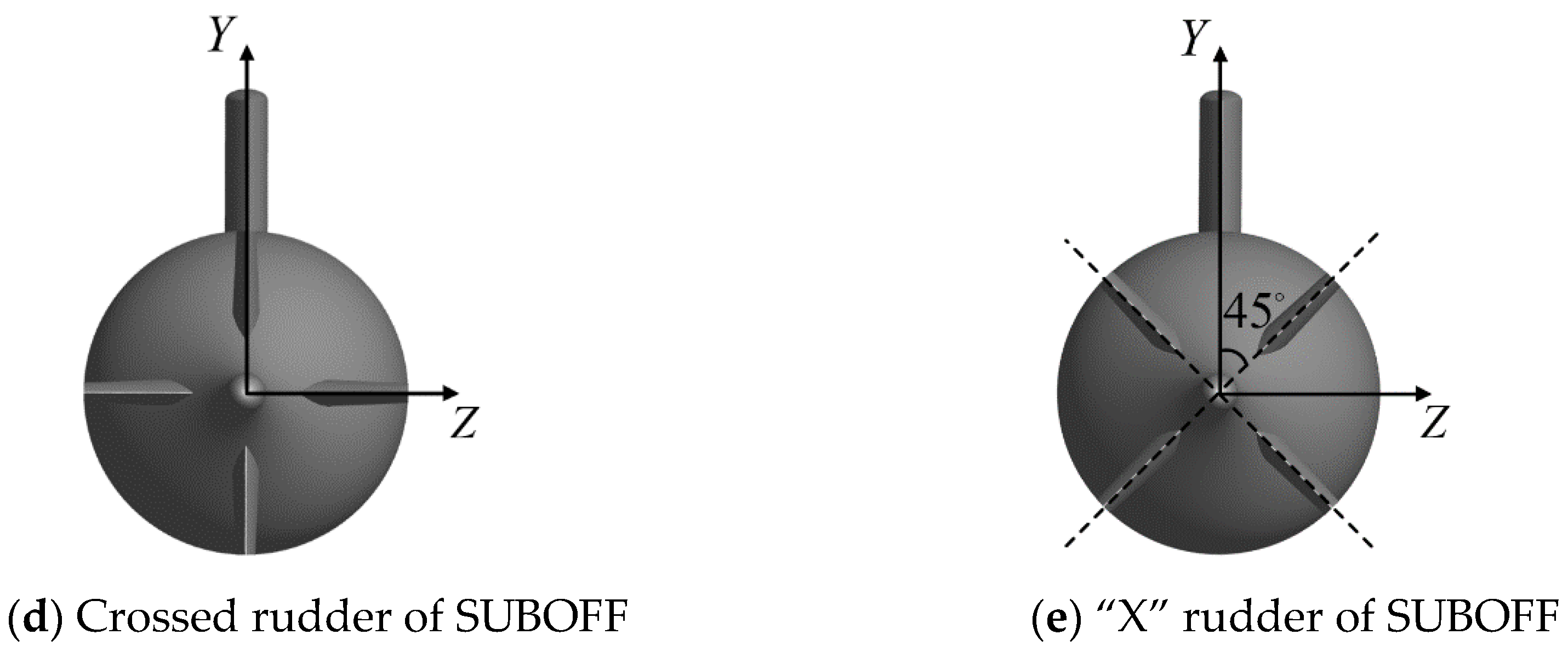
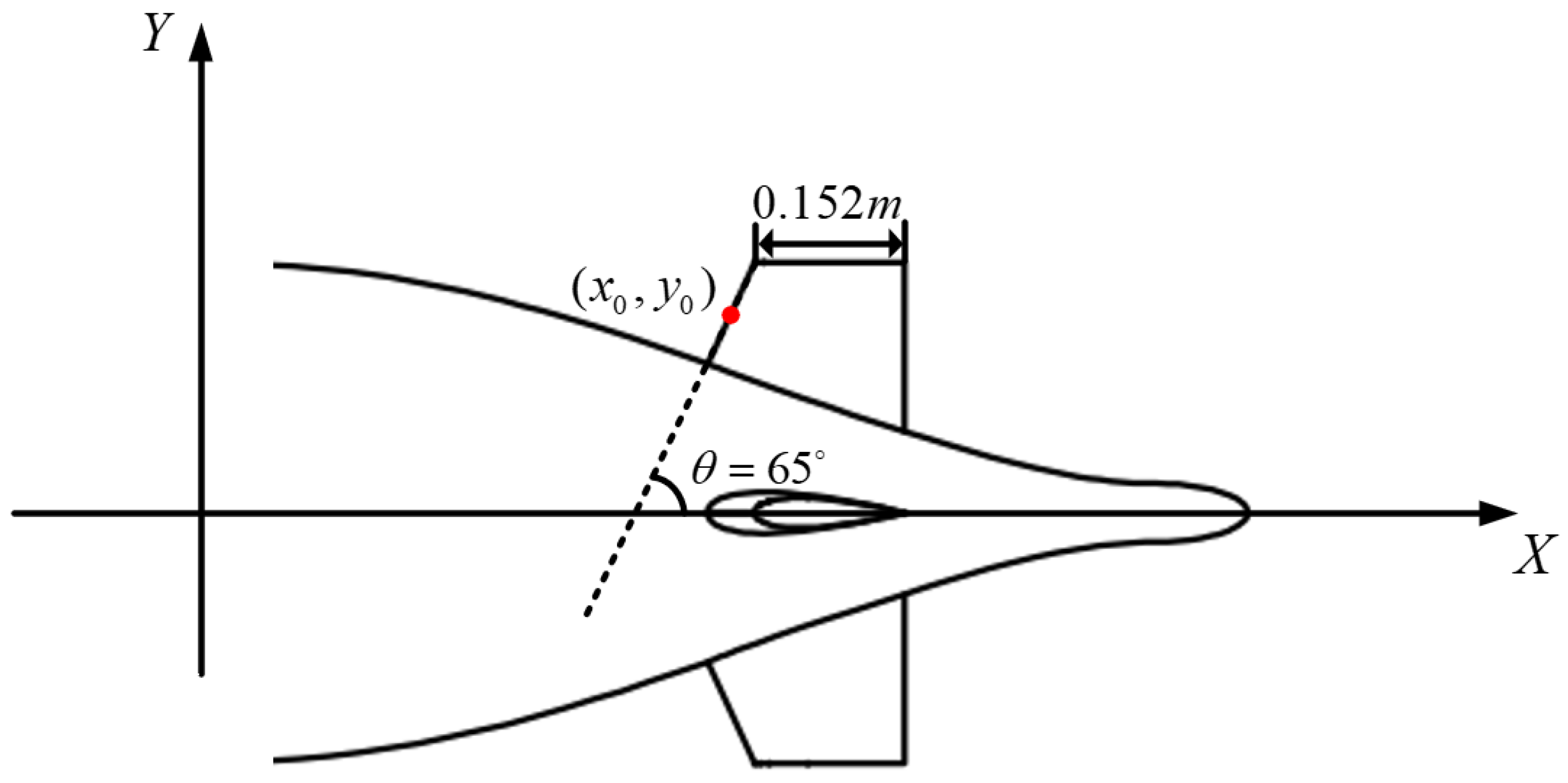
2.2. Design of the Stern Rudder with Fillets
3. Numerical Methods
3.1. Fluid Motion Control Equations
3.2. IDDES
3.3. The FW-H Equation
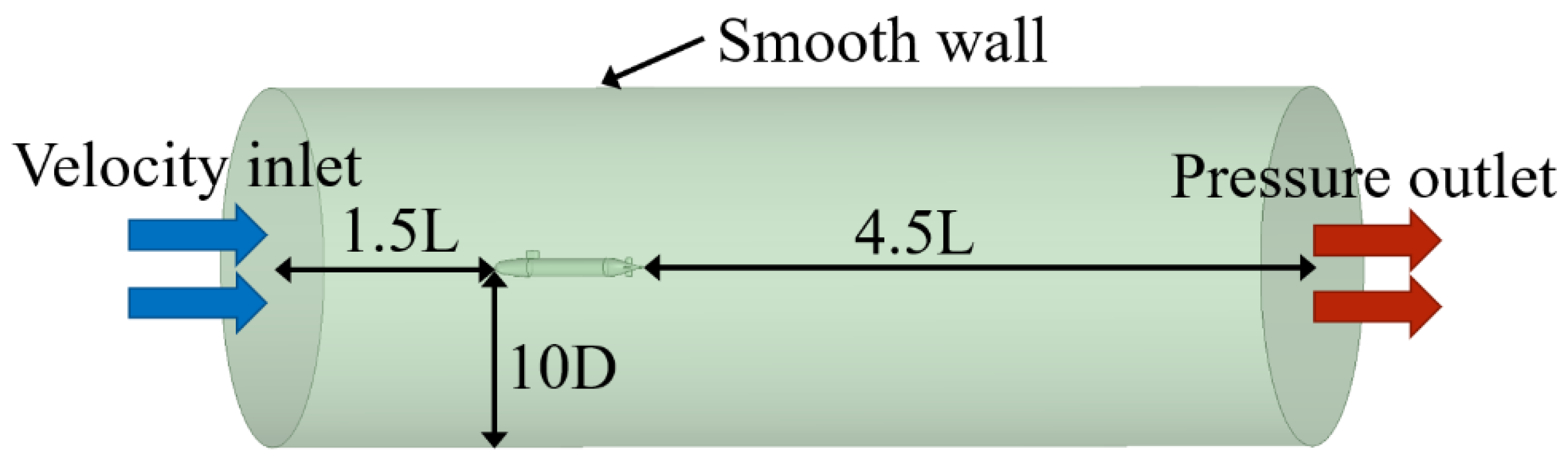
3.4. Computational Domain and Boundary Conditions
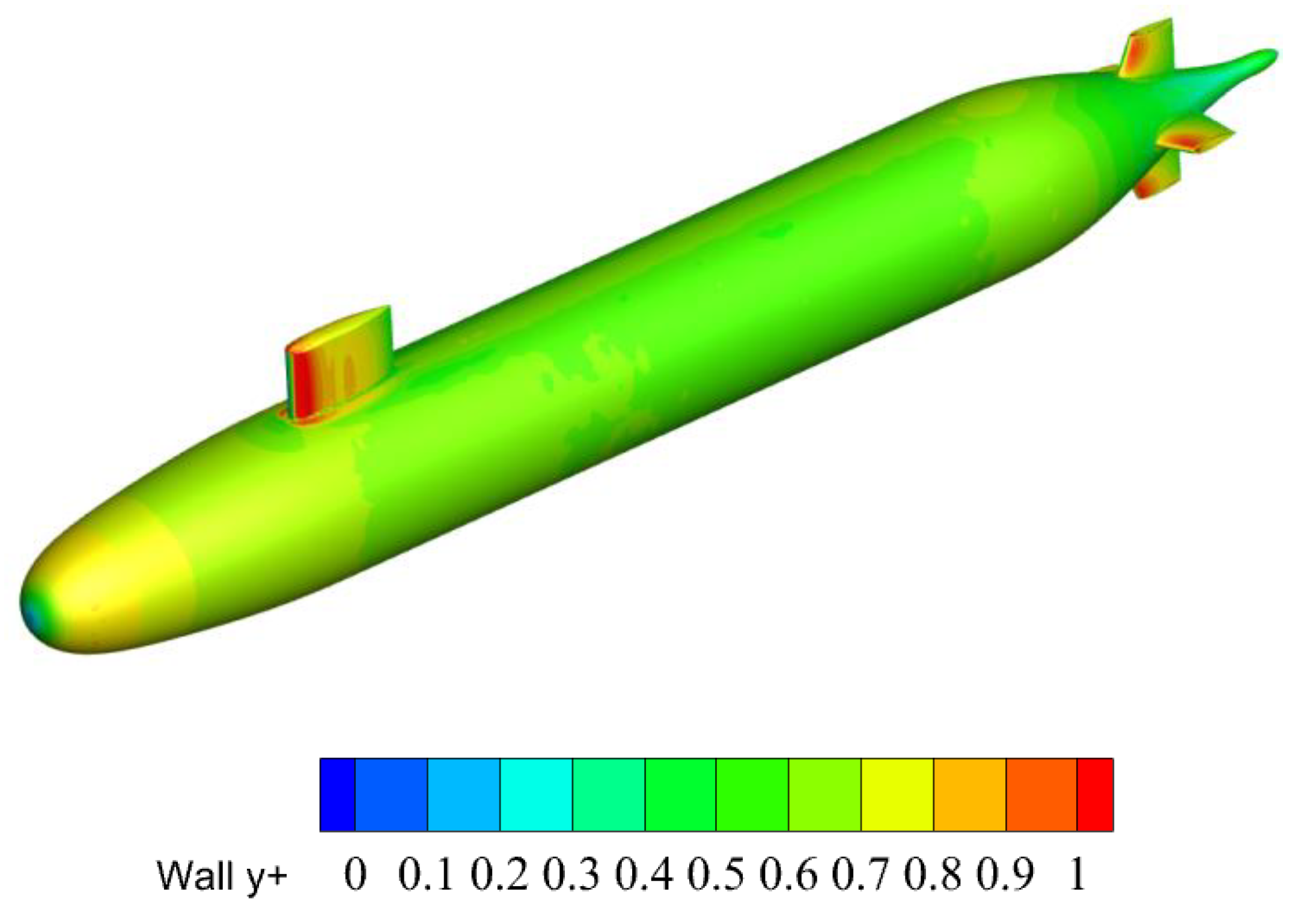
3.5. Grid Independence Verification
3.6. Numerical Validation
4. Results and Discussion
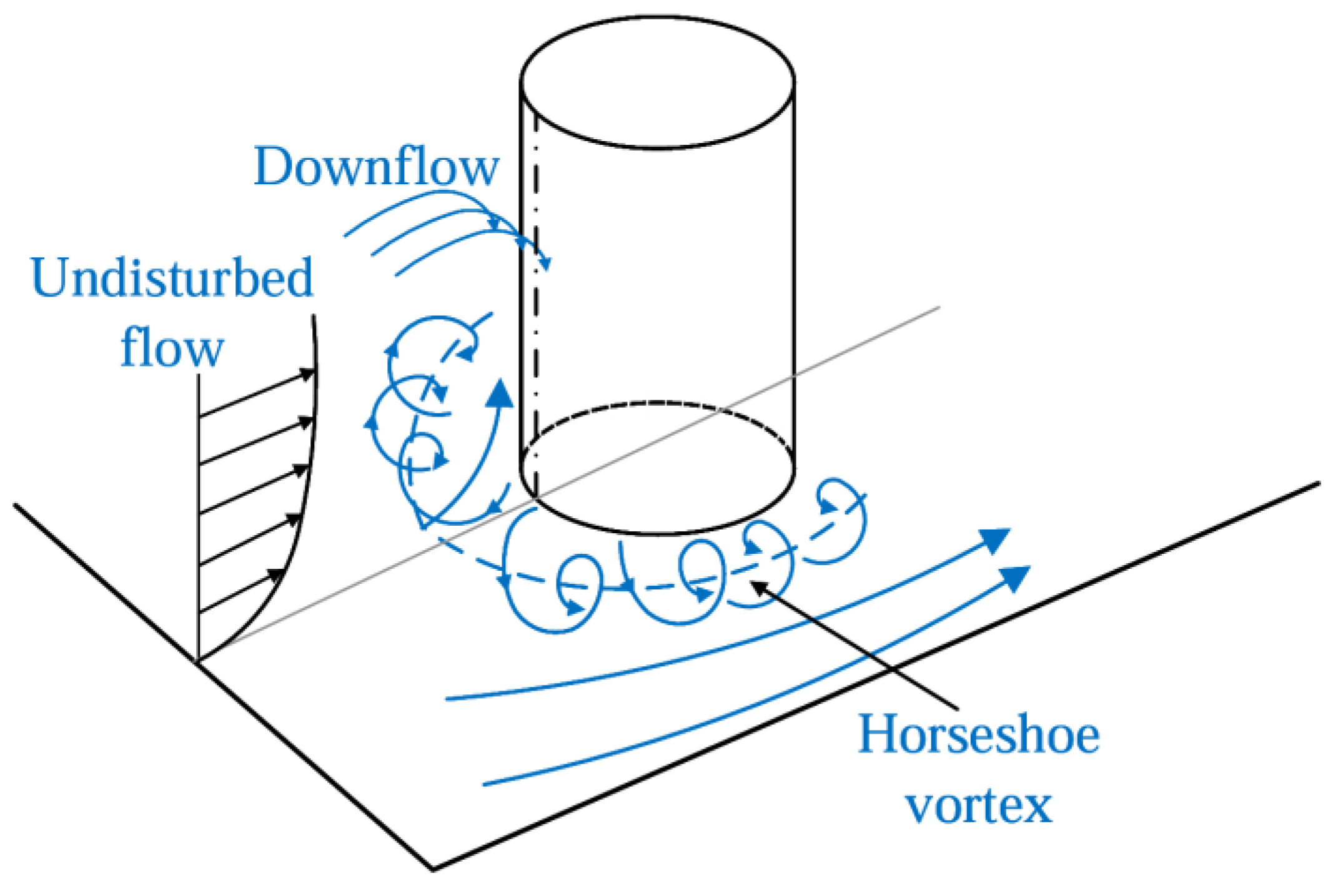
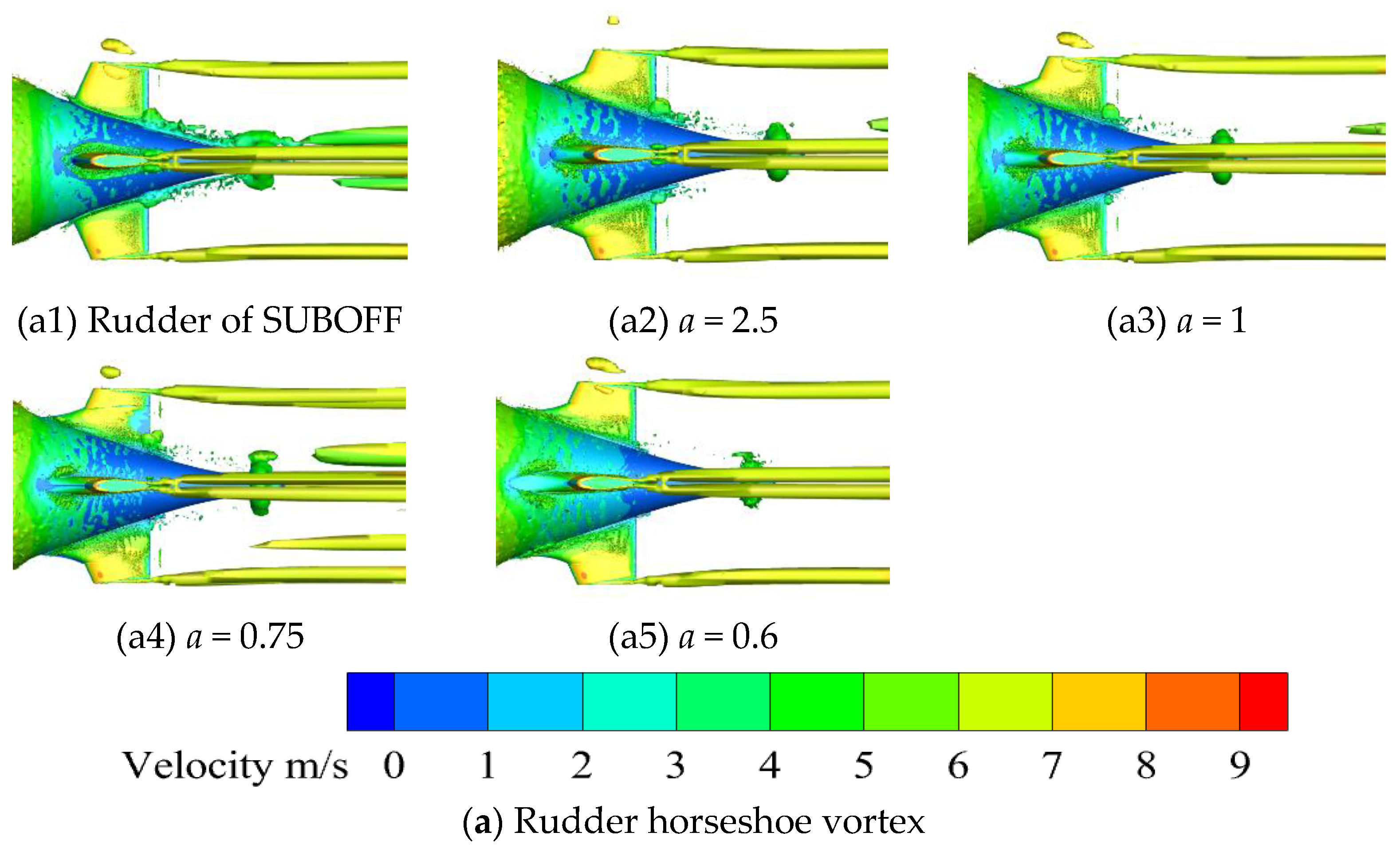
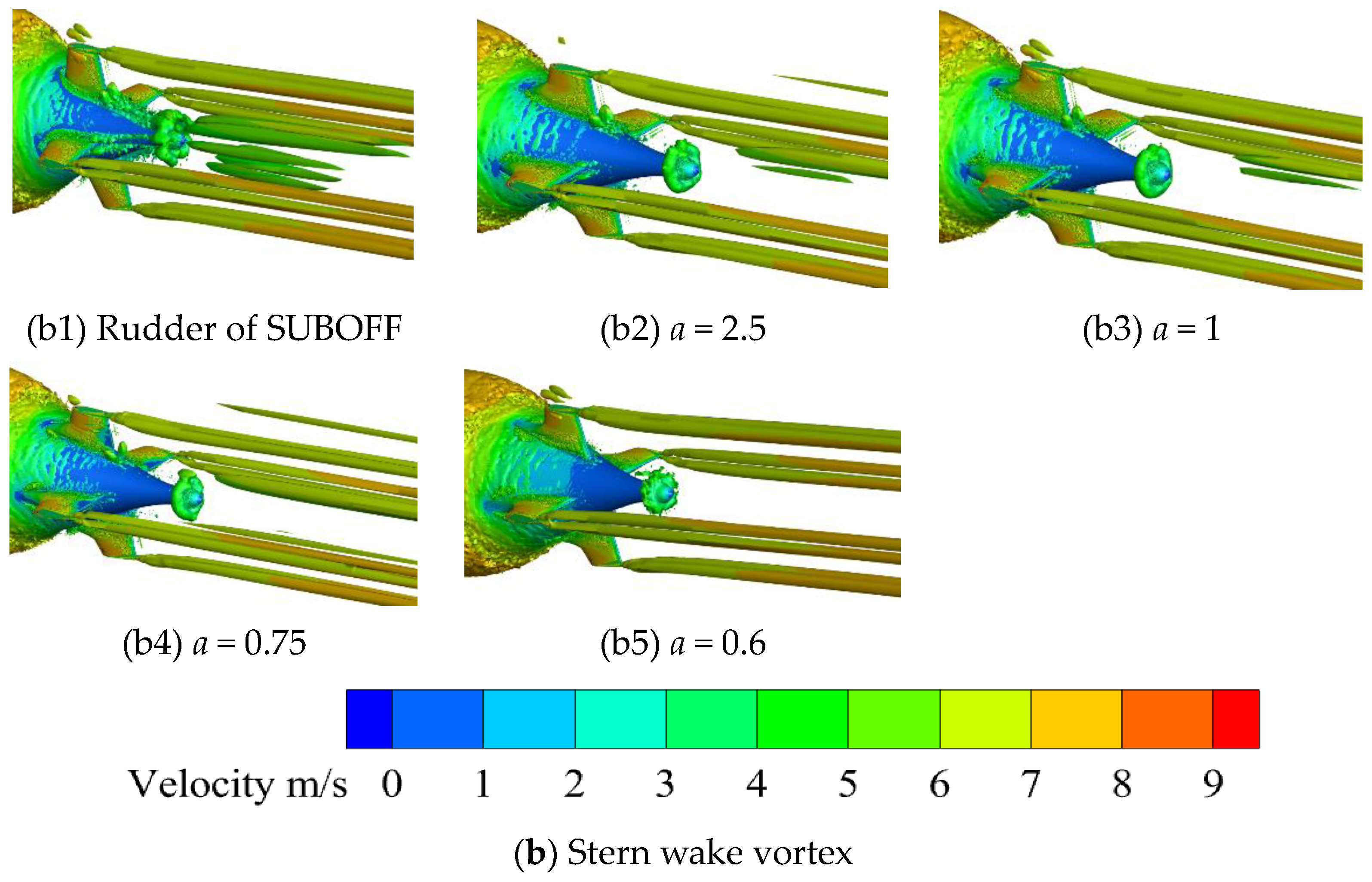
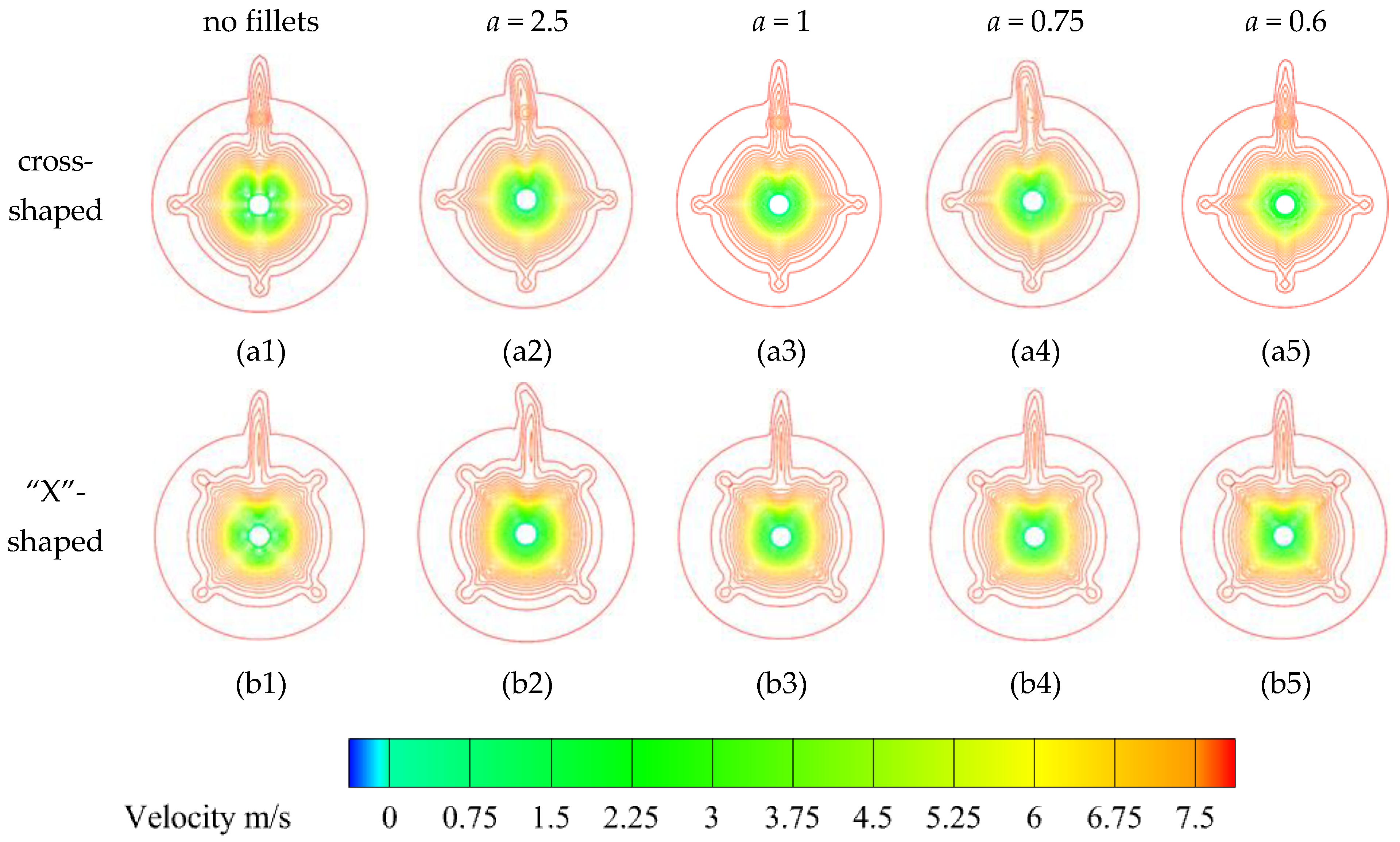
4.1. Effect of Rudders on Submarine Stern Vortices
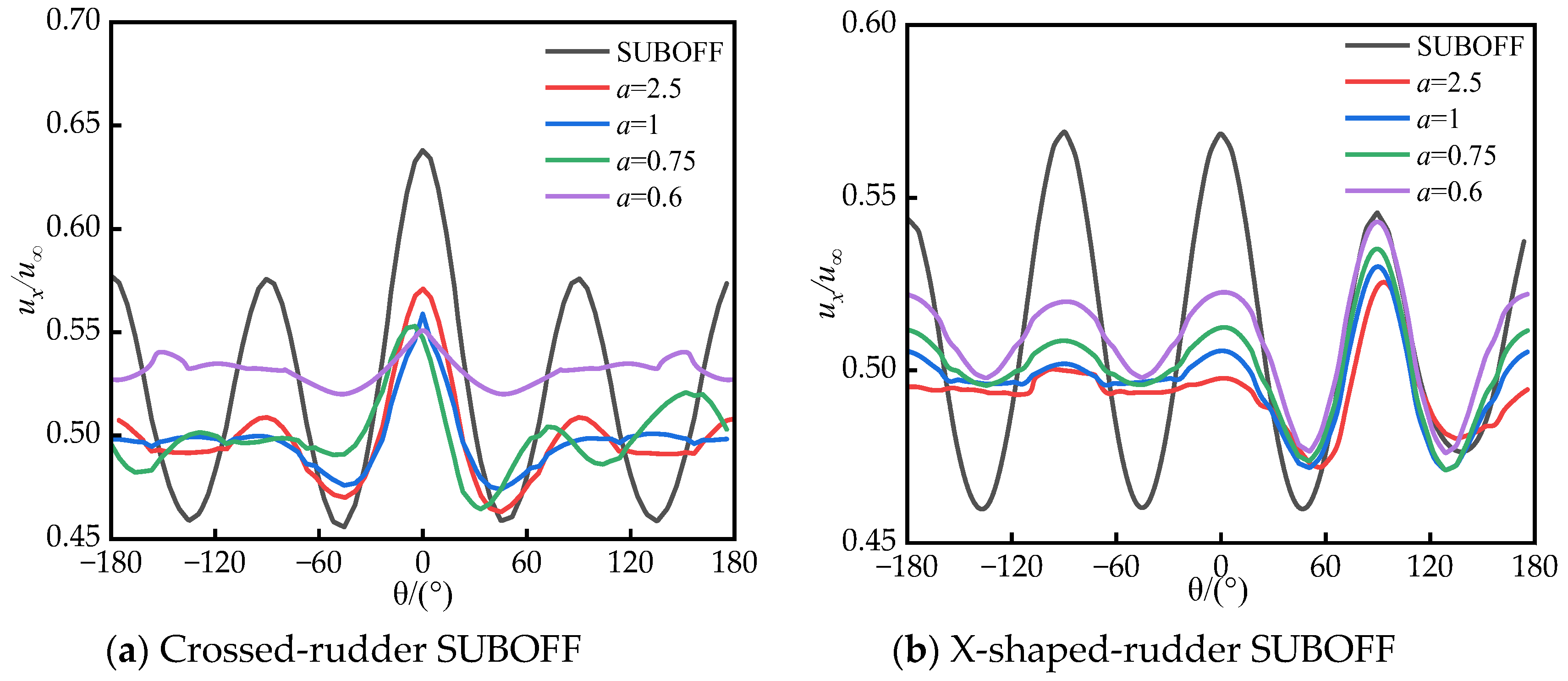
4.2. Effect of Rudder Distribution and Structure on Submarine Velocity Field
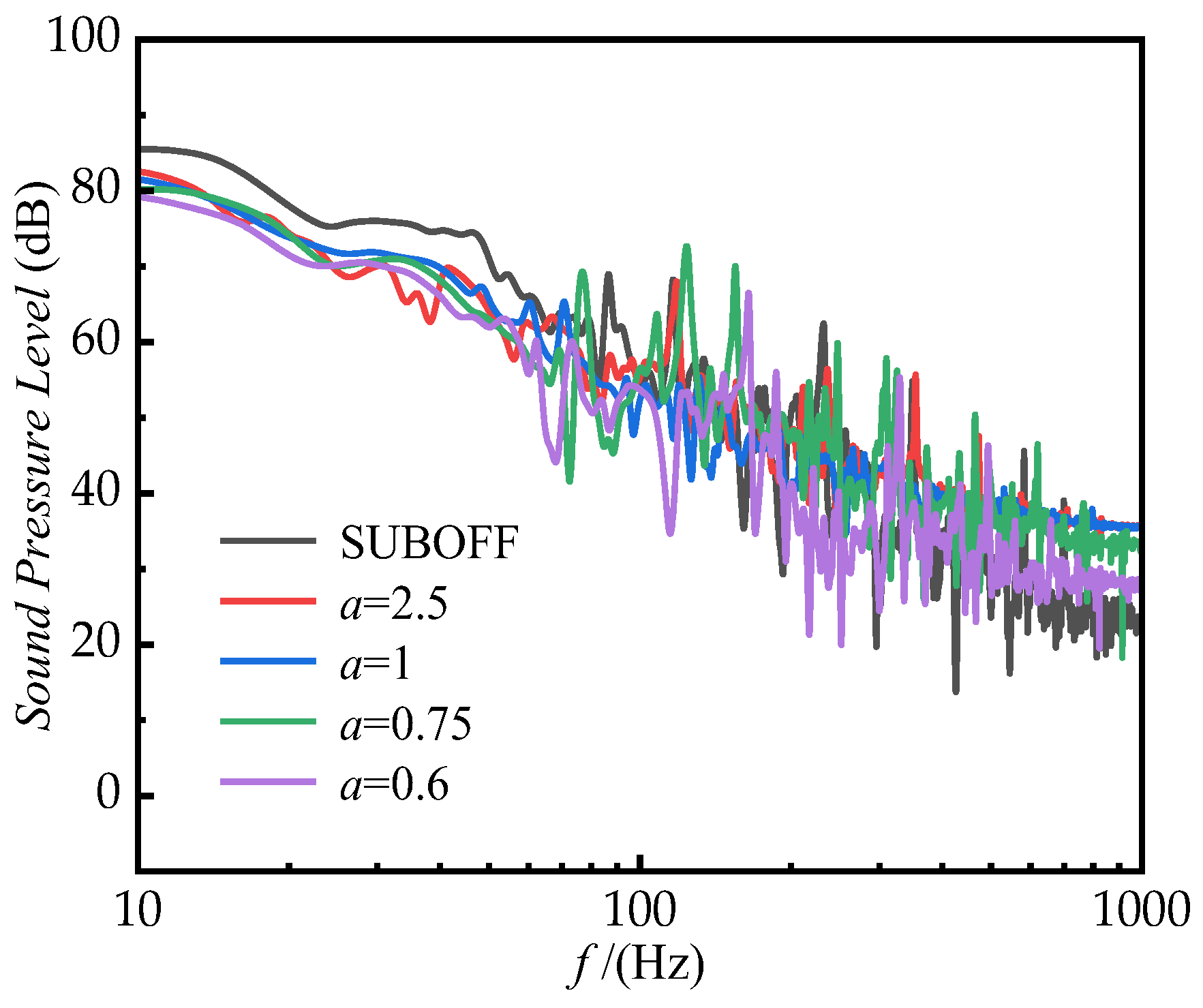
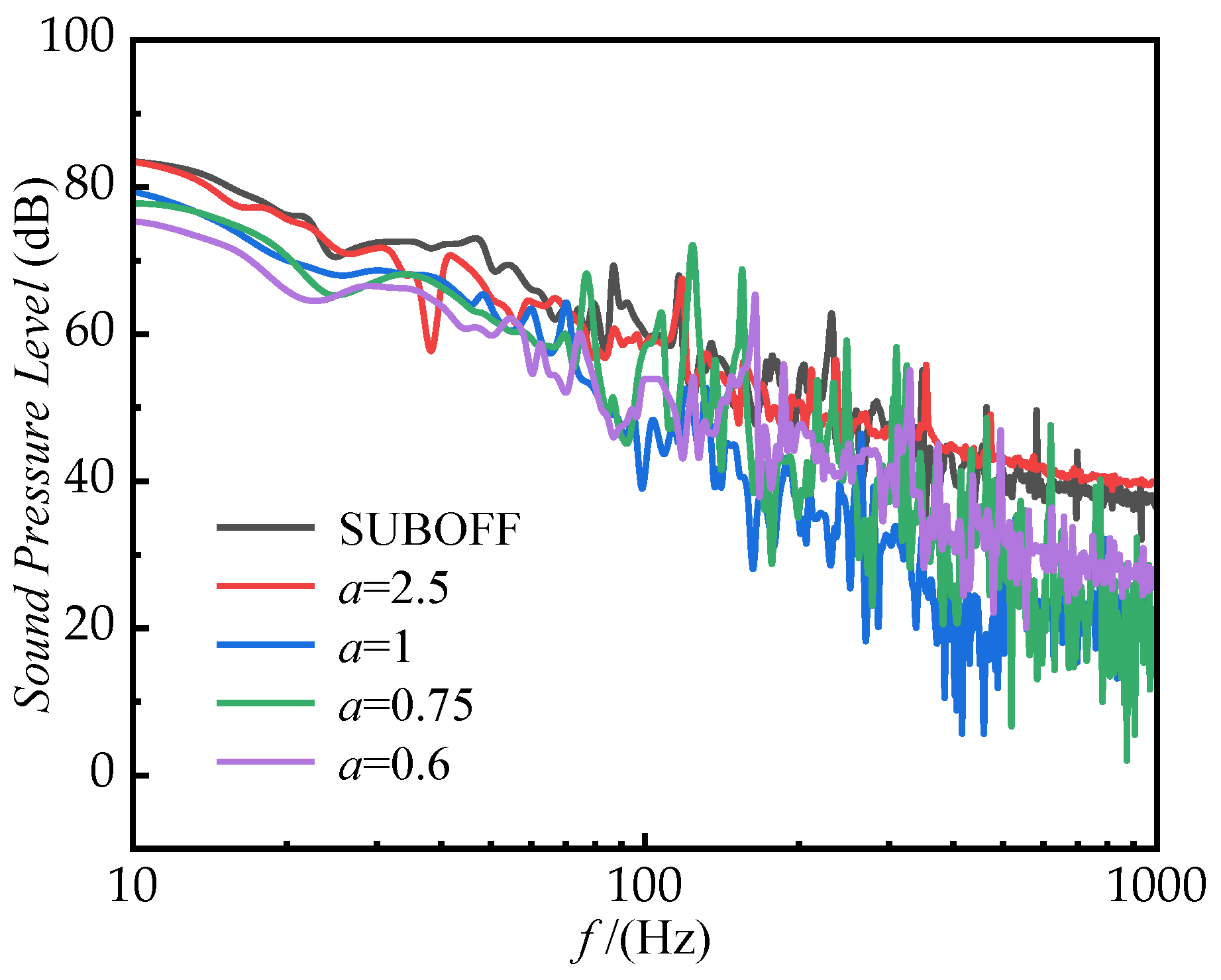
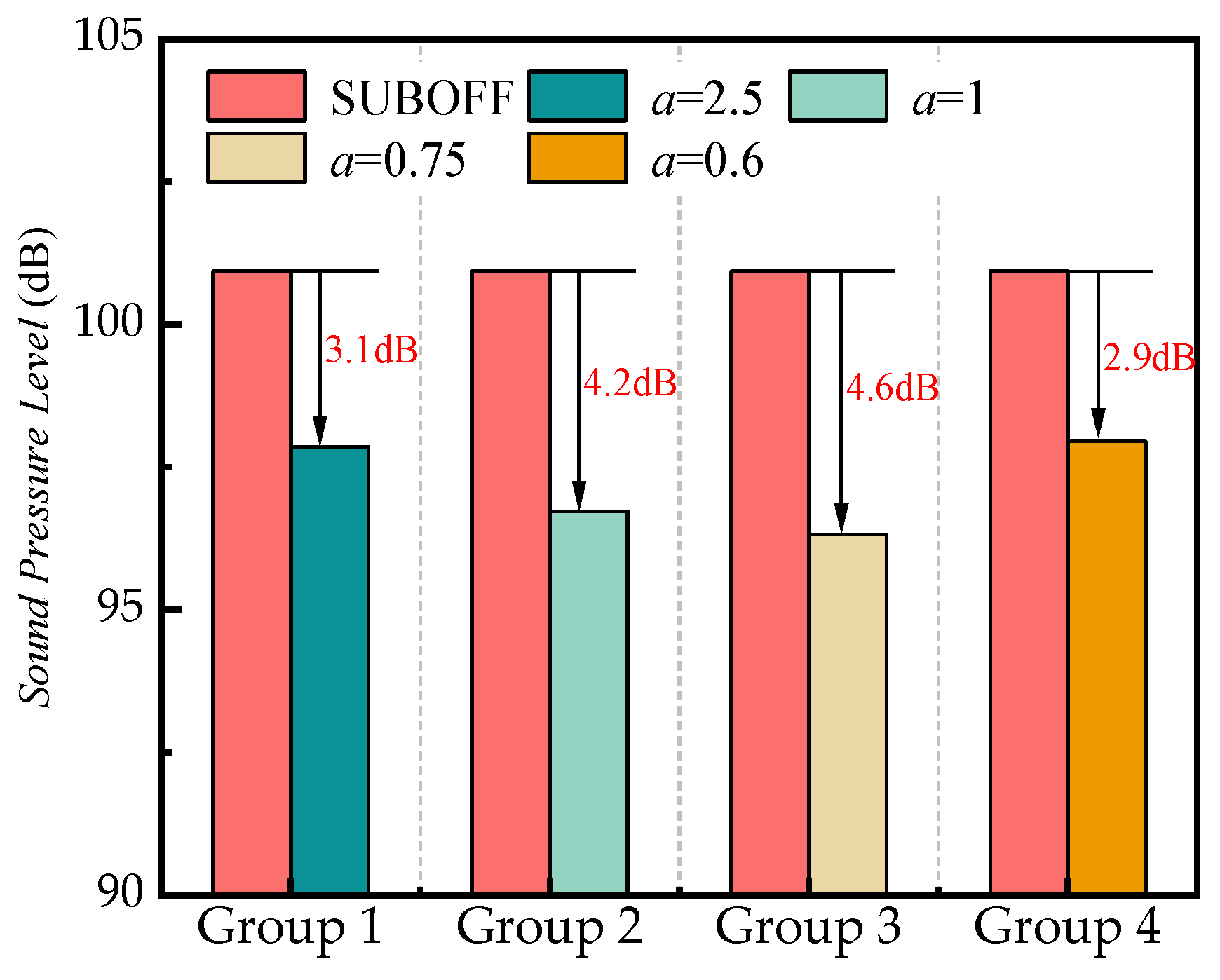
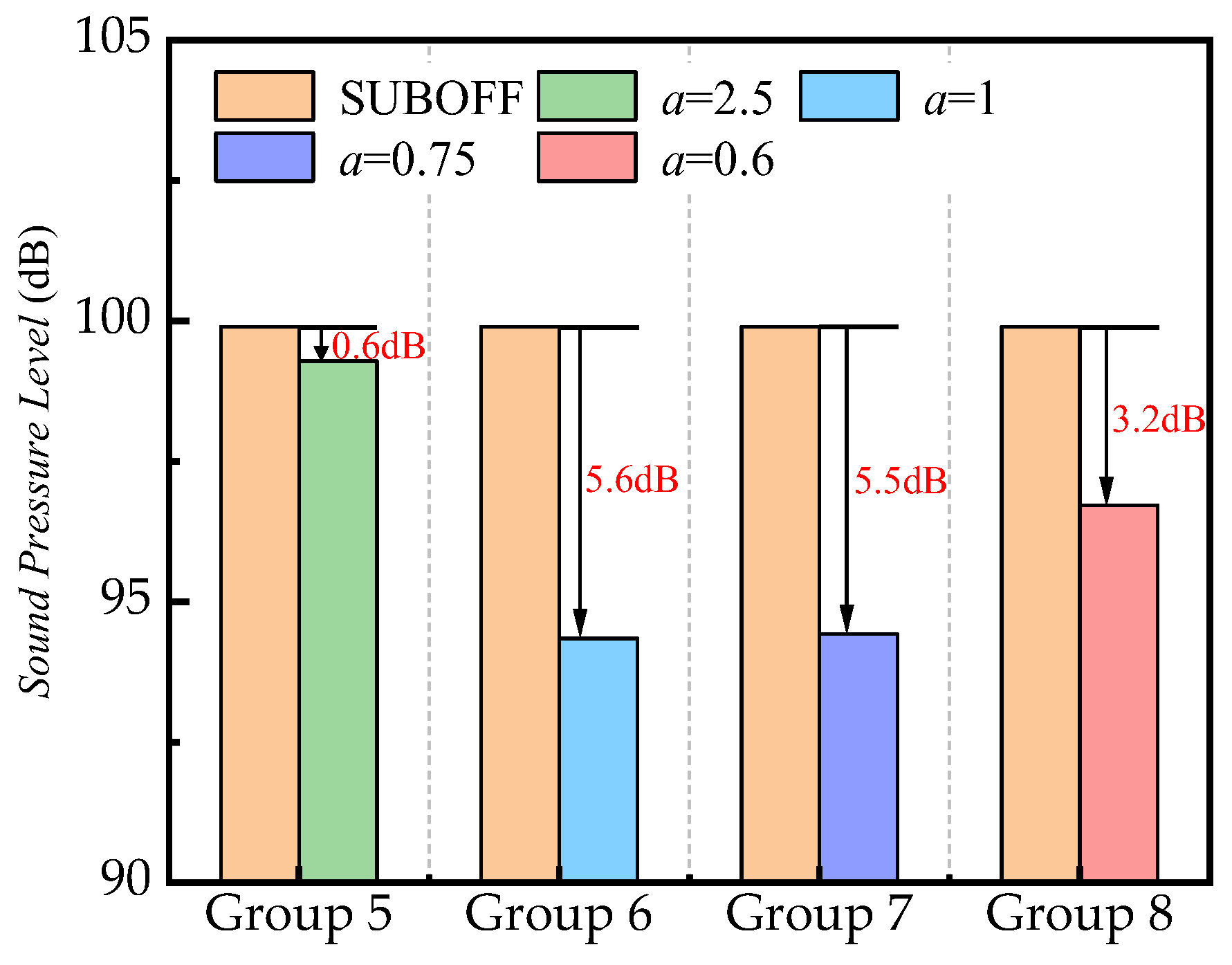
4.3. Effect of Rudder Fillets on Submarine Hydrodynamic Noise
5. Conclusions
- (1)
- In this paper, a general line equation for corner filling is derived based on the parabolic equation, which constructs corner-filling-type lines that can be used for most submarine attachments.
- (2)
- Using the IDDES model and comparing the simulation and test results, the drag force’s relative error is only 2.7%, at maximum, at different speeds. The distribution of the pressure coefficient along the upper surface of the SUBOFF submarine is highly consistent with the test results, indicating that the results computed by the IDDES model have high realism and reliability.
- (3)
- For both crossed-rudder and “X”-rudder submarines, increasing the fillet disrupts the horseshoe vortex structure, effectively suppressing its adverse effects (e.g., flow separation and turbulence generation) and improving the wake flow field. Notably, the “X” rudder demonstrates superior performance over the crossed rudder in reducing low-speed regions on the propeller plane, further optimizing wake uniformity.
- (4)
- Larger fillets enhance the suppression of the horseshoe vortex, leading to improved velocity field homogeneity across the submarine propeller plane. Specifically, the circumferential velocity peak-to-valley difference at the propeller plane is reduced by 25.20% to 49.34%, highlighting the critical role of fillets in flow stabilization.
- (5)
- For the crossed rudder and “X” rudder, the addition of a fillet at their leading edges can achieve the effect of noise reduction. Respectively, the submarine hydrodynamic noise can be reduced by up to 4.6 dB and 5.6 dB.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | |
| p | pressure (Pa) |
| u,v,w | velocity components (m/s) |
| L | SUBOFF body length (m) |
| D | maximum body diameter of SUBOFF (m) |
| Cp | pressure coefficient |
| LDES | DES length scale (m) |
| Q | Q-criterion for vortex identification (s−2) |
| Re | Reynolds number |
| y+ | dimensionless wall distance |
| k | turbulent kinetic energy (m2/s2) |
| Greek | |
| density (kg/m3) | |
| θ | azimuth angle (Degree) |
| τtrub | Reynolds stress tensor (Pa) |
| µ | viscosity (Pa.s) |
| ε | turbulent dissipation rate (1/s) |
| ω | specific turbulence dissipation rate (1/s) |
| Subscript | |
| t | turbulence |
| w | wall |
| i | inlet |
| o | outlet |
| ref | reference |
| Abbreviations | |
| CFD | computational fluid dynamic |
| RANS | Reynolds-averaged Naiver–Stokes |
| LES | large eddy simulation |
| GID | grid-induced separation |
| DES | Detached Eddy Simulation |
| DDES | Delayed Detached Eddy Simulation |
| IDDES | Improved Delayed Detached Eddy Simulation |
| SST | Shear Stress Transport |
| FW-H | FfowcsWilliams–Hawkings |
References
- Xiao, X.; Liang, Q.; Ke, L.; Hu, Y.; Zhang, L. Effects of X Rudder Area on the Horizontal Mechanical Properties and Wake Flow Field of Submarines. J. Phys. Conf. Ser. 2021, 2095, 012089. [Google Scholar] [CrossRef]
- Zhou, G.L.; Ou, Y.P.; Gao, X.P.; Liu, R.J. Submarine Maneuverability Prediction Research Status and Prospects. Shipbuild. China 2018, 59, 203–214. [Google Scholar]
- Cao, Z.J.; Xiao, C.R.; Li, S.Q.; Liang, Q.F. Comparative Stability Analysis of “X” Rudder and Crossed Rudder Submarines. Ship Sci. Technol. 2021, 43, 51–55. [Google Scholar]
- Jiao, Y.C. Layout optimization of submarine X rudder. J. Ordnance Equip. Eng. 2018, 39, 40–44+71. [Google Scholar]
- Toxopeus, S.; Kuin, R.; Kerkvliet, M.; Hoeijmakers, H.; Nienhuis, B. Improvement of resistance and wake field of an underwater vehicle by optimising the fin-body junction flow with CFD. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Yeo, S.-J.; Hong, S.-Y.; Song, J.-H.; Seol, H.-S. Analysis of the effect of vortex reduction structures on submarine tonal noise via frequency-domain method employing thickness noise source. Ocean Eng. 2022, 257, 111640. [Google Scholar] [CrossRef]
- Rahmani, M.; Gavzan, I.J.; Manshadi, M.D. Experimental investigation of the effect of sail geometry on the flow around the SUBOFF submarine model inspired by the dolphin’s dorsal fin. Ships Offshore Struct. 2023, 19, 769–778. [Google Scholar] [CrossRef]
- Wang, X.; Huang, Q.; Pan, G. Numerical research on the influence of sail leading edge shapes on the hydrodynamic noise of a submarine. Appl. Ocean Res. 2021, 117, 102935. [Google Scholar] [CrossRef]
- Li, M.J.; Wang, M.X.; Wang, L.; Liu, Z.H. Numerical simulation and experimental study of noise-reducing stern fillets of underwater navigational body. J. Ship Mech. 2016, 20, 1345–1354. [Google Scholar]
- Jin, Z.; Wang, P.; Xia, H.; Ding, Y.; Han, P. Validation of Numerical Simulation on the Flow Field of Submarine with Various Types of stern appendages. In Proceedings of the OCEANS 2018 MTS/IEEE Charleston, Charleston, SC, USA, 22–25 October 2018. [Google Scholar]
- Dai, J.C. Characterization of Propeller Radiated Noise and Hydroelastic Vibration. Master’s Thesis, Dalian University of Technology, Dalian, China, 2022. [Google Scholar]
- Alin, N.; Fureby, C.; Svennberg, U.; Sandberg, W.; Ramamurti, R.; Bensow, R. Eddy Simulation of the Transient Flow around a Submarine during Maneuver. In Proceedings of the 45th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 8–11 January 2007; pp. 17082–17099. [Google Scholar]
- Liu, Z.H.; Xiong, Y. Control of submarine horseshoe vortices by vortex-reducing rectifiers and its comparison with the effect of auxiliary wings. J. Ship Mech. 2011, 15, 1102–1109. [Google Scholar]
- Muscari, R.; Di Mascio, A.; Verzicco, R. Modeling of vortex dynamics in the wake of a marine propeller. Comput. Fluids 2013, 73, 65–79. [Google Scholar] [CrossRef]
- Chen, H.; Yuan, X.X.; Bi, L.; Hua, R.H.; Si, F.F.; Tang, Z.G. Separate flow simulation based on a hybrid RANS/LES approach. Acta Aeronaut. ET Astronaut. Sin. 2020, 41, 177–188. [Google Scholar]
- Liu, J.H.; Li, G.H.; Wang, F.X. Tilt-transition state rotor-wing aerodynamic interference characteristics. Acta Aeronaut. Astronaut. Sin. 2022, 43, 208–219. [Google Scholar]
- Groves, N.C.; Huang, T.T.; Chang, M.S. Geometric Characteristics of DARPA SUBOFF Models; David Taylor Research Center: Washington, DC, USA, 1989. [Google Scholar]
- Panton, R.L. Incompressible Flow; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 1998. [Google Scholar]
- Hinze, J.O. Turbulence; McGraw-Hill Publishing Co: New York, NY, USA, 1975. [Google Scholar]
- Wilcox, D.C. Reassessment of the Scale-Determining Equation for Advanced Turbulence Models. AIAA J. 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Cui, G.X.; Xu, C.X.; Huang, W.X. Turbulence Simulation and Theory; Tsinghua University Press: Beijing, China, 2017. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A New Version of Detached-Eddy Simulation, Resistant to Ambiguous Grid Densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A Hybrid RANS-LES Approach with Delayed DES and Wall-Modelled LES Capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Ffowcs Williams, J.E.; Hawkings, D.L. Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Philos. Trans. R. Soc. A 1969, 264, 321–342. [Google Scholar]
- Park, S. CFD Study of Submarine Hydrodynamics near the Free Surface in Snorkel Conditions. Water 2025, 17, 734. [Google Scholar] [CrossRef]
- Lositaño, I.C.M.; Danao, L.A.M. Steady wind performance of a 5 kW three-bladed H-rotor Darrieus Vertical Axis Wind Turbine (VAWT) with cambered tubercle leading edge (TLE) blades. Energy 2019, 175, 278–291. [Google Scholar] [CrossRef]
- Huang, T.; Liu, H.L. Measurement of flows over an axisymmetric body with various appendages in a wind tunnel: The DARPA SUBOFF experimental program. Fluid Dyn. 1994, 5, 321. [Google Scholar]
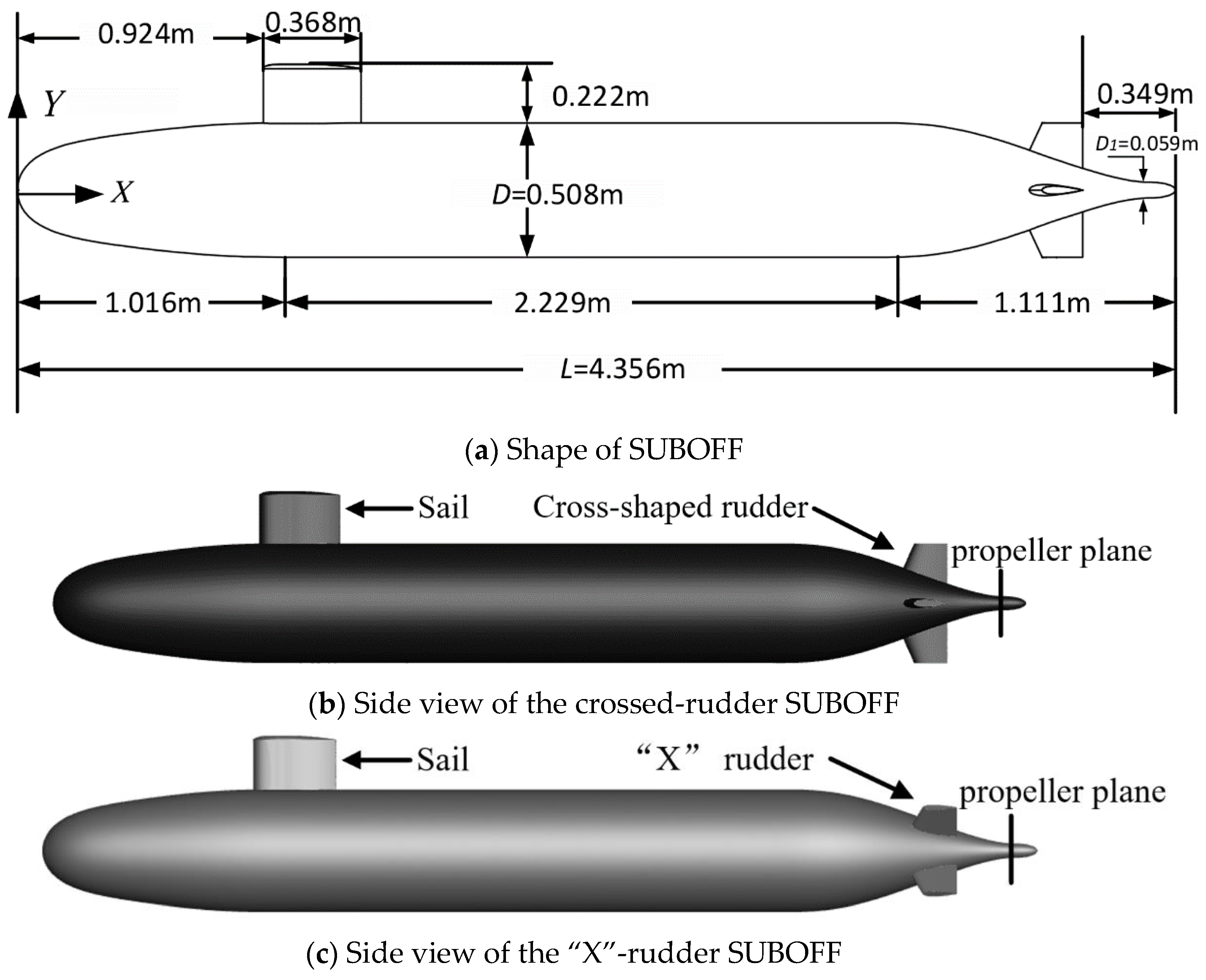







| Parameters | Value (m) |
|---|---|
| Total body length | 4.356 |
| Maximum body diameter | 0.508 |
| Forebody length | 1.016 |
| Parallel middle body length | 2.229 |
| Afterbody length | 1.111 |
| Total sail length | 0.368 |
| Total sail height | 0.222 |
| SUBOFF propeller plane diameter | 0.059 |
| Distance between the leading edge of the sail and the SUBOFF bow | 0.924 |
| Distance between the tail fin trailing edge and the SUBOFF stern | 0.349 |
| Parameter | Setting Situation |
|---|---|
| Computational domain material | Liquid water |
| Inlet | Velocity inlet (7.161 m/s) |
| Outlet | Pressure outlet |
| Computational domain wall | Smooth wall |
| SUBOFF wall | No-slip wall |
| Parameters | Setting Situation |
|---|---|
| Turbulence model (transient calculation) | IDDES |
| Acoustical model | FW-H |
| y+ | 0.9 < y+ < 1 |
| Pressure–velocity coupling scheme | SIMPLE |
| Momentum | Second-order upwind |
| Turbulent kinetic energy | Second-order upwind |
| Turbulent dissipation rate | Second-order upwind |
| Transient formulation | Second-order implicit |
| Reference sound pressure | 1 × 10−6 Pa |
| Sound source | SUBOFF model surface |
| Type of sound source | Wall |
| Convergence criteria (drag detection) | Drag change < 0.1% over 100 consecutive iterations |
| Maximum number of iterations/time step | 20 |
| Maximum analysis frequency | 1000 Hz |
| Transient calculation time step | 5 × 10−4 s |
| Under relaxation factor | Pressure: 0.3 Momentum: 0.7 Turbulent kinetic energy: 0.8 Turbulent dissipation rate: 0.8 |
| Grid | Number of Grids (×104) | Force (N) | Nodes (×104) | GCI (%) | Skewness |
|---|---|---|---|---|---|
| Grid A | 242.5 | 105.4 | 464.0 | 11.32 | 0.66 |
| Grid B | 545.2 | 104.3 | 739.9 | 7.61 | 0.61 |
| Grid C | 850.0 | 103.0 | 1305.8 | 4.84 | 0.55 |
| Grid D | 1192.1 | 102.5 | 2072.6 | 1.22 | 0.62 |
| Grid E | 1406.9 | 102.4 | 2879.2 | 1.15 | 0.56 |
| Grid F | 1721.5 | 102.4 | 3564.5 | 1.14 | 0.57 |
| Speed (m/s) | Experimental Value (N) | Calculated Value (N) | Relative Error (%) |
|---|---|---|---|
| 3.051 | 102.3 | 102.6 | 0.3 |
| 5.144 | 283.8 | 289.1 | 1.8 |
| 6.096 | 389.2 | 396.8 | 1.9 |
| 7.161 | 526.6 | 529.0 | 0.4 |
| 8.231 | 675.6 | 693.8 | 2.7 |
| 9.152 | 821.1 | 840.9 | 2.4 |
| ΔUx | Reduced Magnitude (%) | ||
|---|---|---|---|
| Cross-Shaped | “X”-Shaped | ||
| SUBOFF | 0.18234 | 0.10993 | 39.71 |
| a = 2.5 | 0.10789 | 0.05466 | 49.34 |
| a = 1 | 0.07688 | 0.05078 | 33.95 |
| a = 0.75 | 0.07049 | 0.04891 | 30.61 |
| a = 0.6 | 0.05175 | 0.03871 | 25.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Chen, E.; Liu, X.; Yang, A. Numerical Study on the Influence of Rudder Fillets on Submarine Wake Field and Noise Characteristics. J. Mar. Sci. Eng. 2025, 13, 830. https://doi.org/10.3390/jmse13050830
Yuan H, Chen E, Liu X, Yang A. Numerical Study on the Influence of Rudder Fillets on Submarine Wake Field and Noise Characteristics. Journal of Marine Science and Engineering. 2025; 13(5):830. https://doi.org/10.3390/jmse13050830
Chicago/Turabian StyleYuan, Hao, Eryun Chen, Xingsheng Liu, and Ailing Yang. 2025. "Numerical Study on the Influence of Rudder Fillets on Submarine Wake Field and Noise Characteristics" Journal of Marine Science and Engineering 13, no. 5: 830. https://doi.org/10.3390/jmse13050830
APA StyleYuan, H., Chen, E., Liu, X., & Yang, A. (2025). Numerical Study on the Influence of Rudder Fillets on Submarine Wake Field and Noise Characteristics. Journal of Marine Science and Engineering, 13(5), 830. https://doi.org/10.3390/jmse13050830





