Hydrodynamic Modeling of a Reef-Fringed Pocket Beach Using a Phase-Resolved Non-Hydrostatic Model
Abstract
1. Introduction
2. Methods
2.1. Study Site and Field Observations
2.2. Numerical Model Description
2.3. Model Set-Up
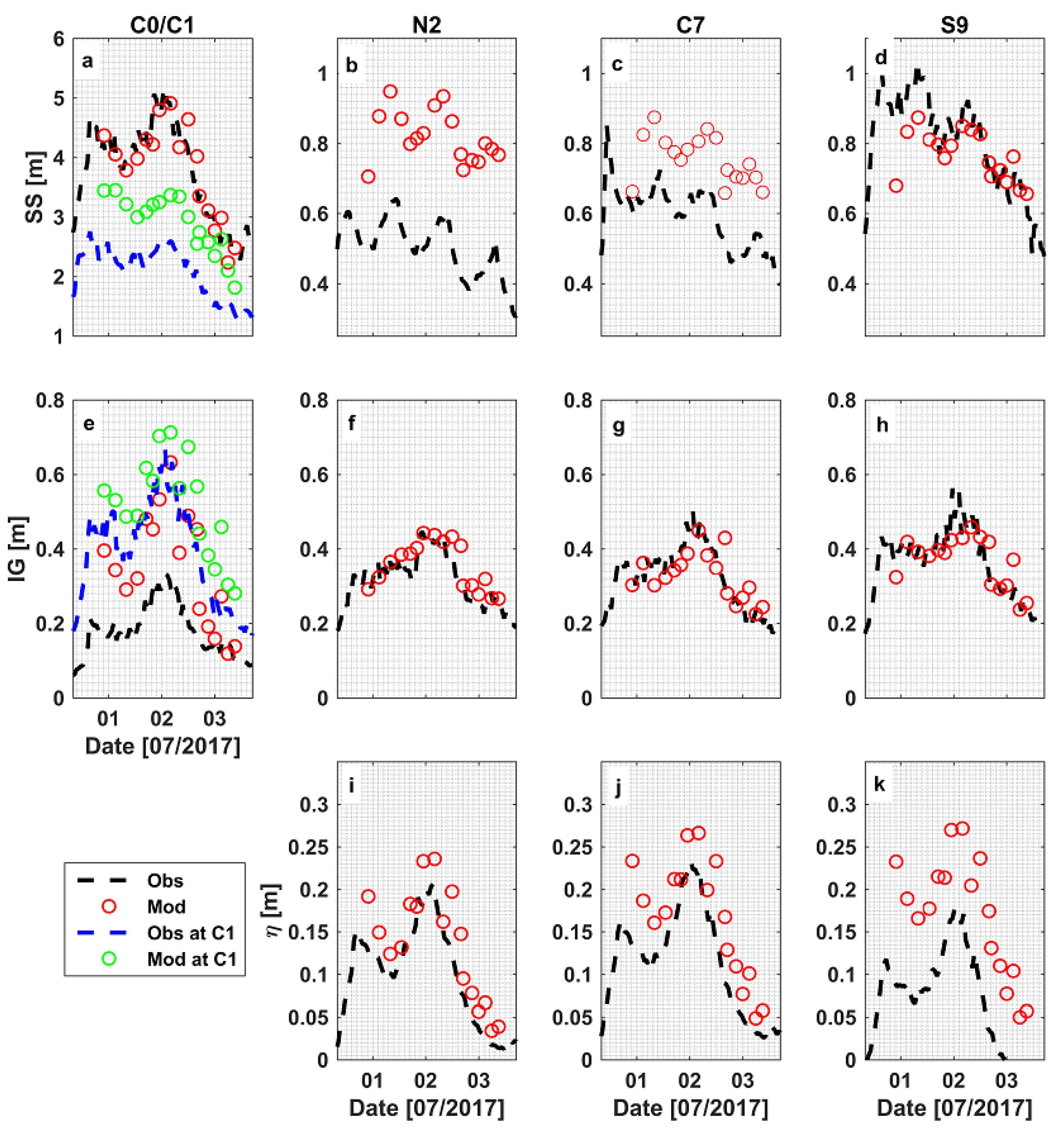
2.4. Model Performance
3. Results
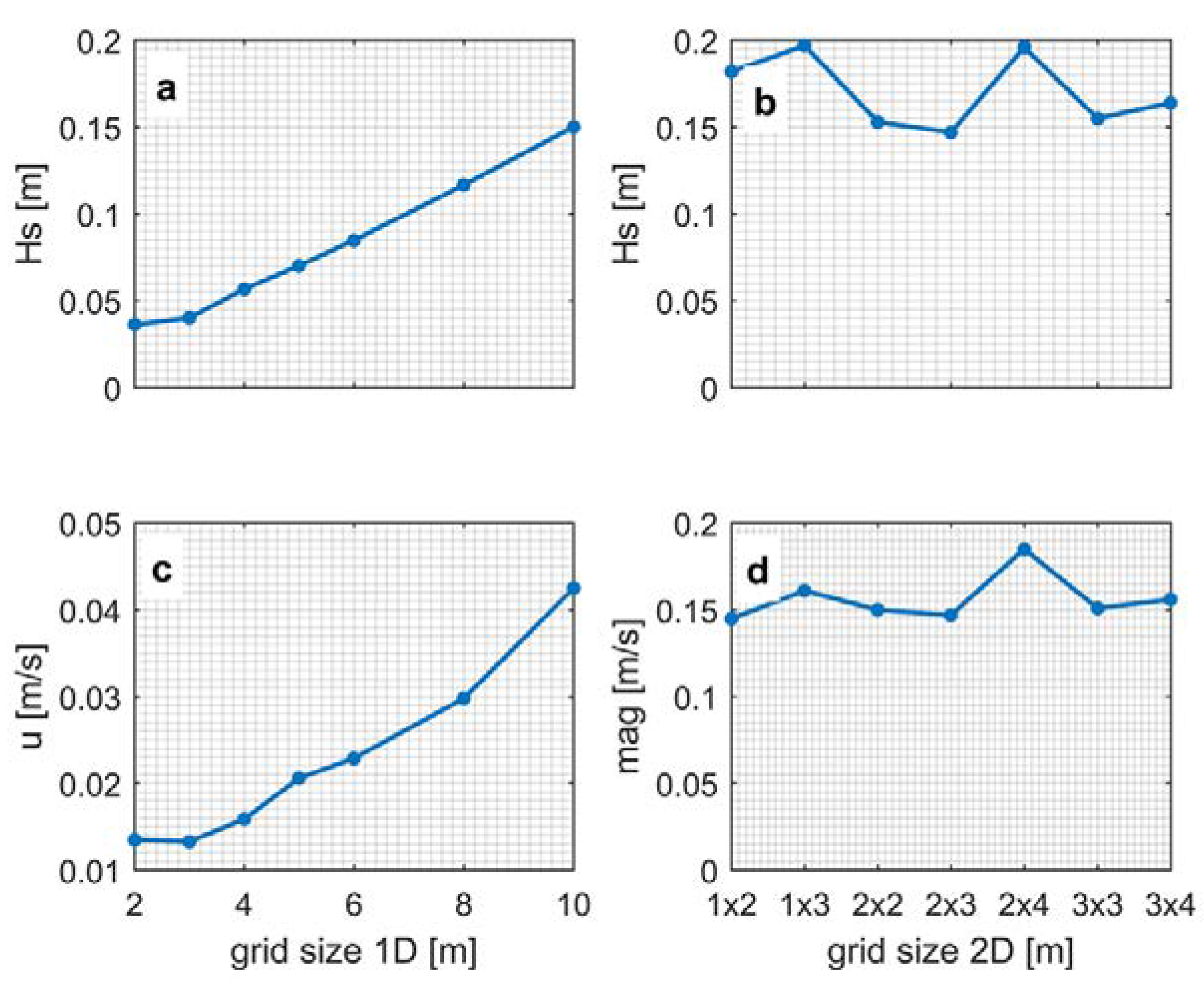
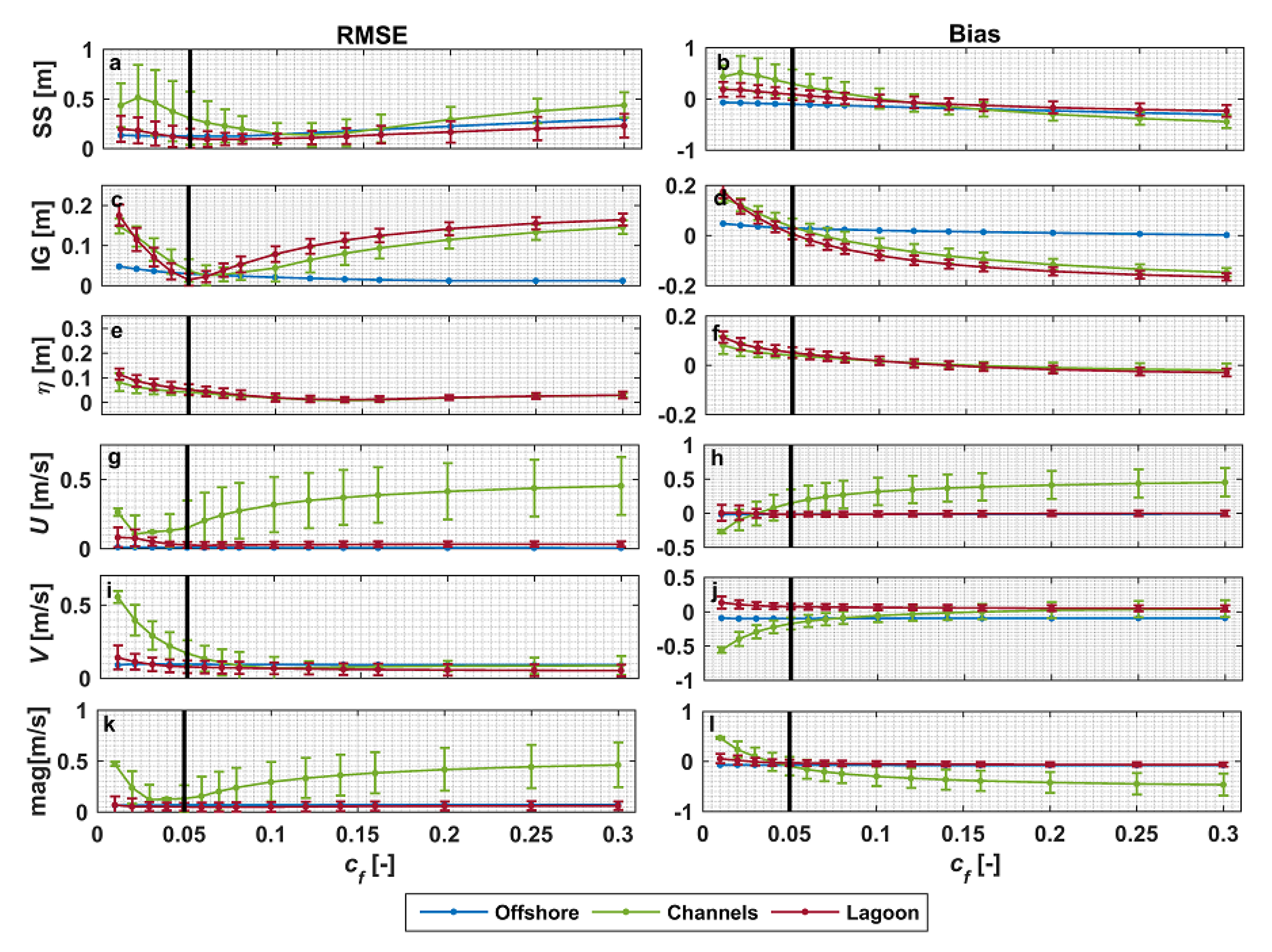
3.1. Model Calibration
3.2. Model Application
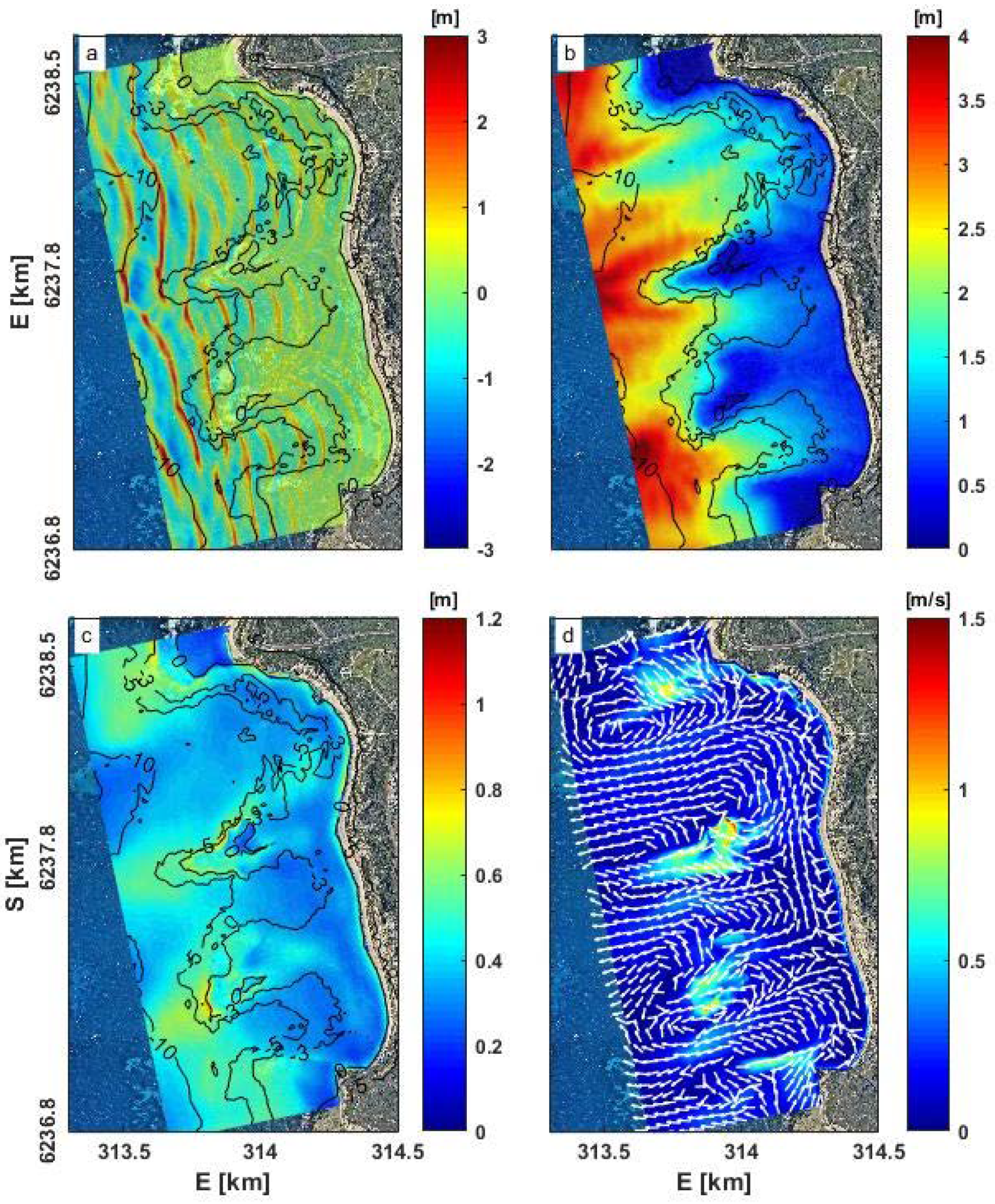
3.2.1. Wave Height and Setup
3.2.2. Depth-Averaged Currents
3.3. General Circulation Dynamics
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Buckley, M.; Lowe, R.; Hansen, J. Evaluation of nearshore wave models in steep reef environments. Theor. Comput. Obs. Oceanogr. 2014, 64, 847–862. [Google Scholar] [CrossRef]
- Drost, E.J.F.; Cuttler, M.V.W.; Lowe, R.J.; Hansen, J.E. Predicting the hydrodynamic response of a coastal reef-lagoon system to a tropical cyclone using phase-averaged and surfbeat-resolving wave models. Coast. Eng. 2019, 152, 103525. [Google Scholar] [CrossRef]
- Monismith, S.G. Hydrodynamics of Coral Reefs. Annu. Rev. Fluid Mech. 2007, 39, 37–55. [Google Scholar] [CrossRef]
- Lowe, R.J.; Falter, J.L. Oceanic Forcing of Coral Reefs. Annu. Rev. Mar. Sci. 2015, 7, 43–66. [Google Scholar] [CrossRef] [PubMed]
- Winter, G.; Castelle, B.; Lowe, R.J.; Hansen, J.E.; McCall, R. When is flow re-entrainment important for the flushing time in coastal reef systems? Cont. Shelf Res. 2020, 206, 104194. [Google Scholar] [CrossRef]
- Sheremet, A.; Kaihatu, J.M.; Su, S.F.; Smith, E.R.; Smith, J.M. Modeling of nonlinear wave propagation over fringing reefs. Coast. Eng. 2011, 58, 1125–1137. [Google Scholar] [CrossRef]
- Filipot, J.-F.; Cheung, K.F. Spectral wave modeling in fringing reef environments. Coast. Eng. 2012, 67, 67–79. [Google Scholar] [CrossRef]
- Roelvink, D.; McCall, R.; Mehvar, S.; Nederhoff, K.; Dastgheib, A. Improving predictions of swash dynamics in XBeach: The role of groupiness and incident-band runup. Coast. Eng. 2018, 134, 103–123. [Google Scholar] [CrossRef]
- Van Dongeren, A.; Lowe, R.; Pomeroy, A.; Trang, D.M.; Roelvink, D.; Symonds, G.; Ranasinghe, R. Numerical modeling of low-frequency wave dynamics over a fringing coral reef. Coast. Eng. 2013, 73, 178–190. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.S. Efficient computation of surf zone waves using the nonlinear shallow water equations with non-hydrostatic pressure. Coast. Eng. 2008, 55, 780–790. [Google Scholar] [CrossRef]
- Jeschke, A.; Pedersen, G.; Vater, S.; Behrens, J. Depth-averaged Non-hydrostatic Extension for Shallow Water Equations with Quadratic Vertical Pressure Profile: Equivalence to Boussinesq-type Equations. Int. J. Numer. Methods Fluids 2017, 84, 569–583. [Google Scholar] [CrossRef]
- Kazolea, M.; Ricchiuto, M. On wave breaking for Boussinesq-type models. Ocean. Model. 2018, 123, 16–39. [Google Scholar] [CrossRef]
- Madsen, P.A.; Bingham, H.B.; Liu, H. A new Boussinesq method for fully nonlinear waves from shallow to deep water. J. Fluid Mech. 2002, 462, 1–30. [Google Scholar] [CrossRef]
- Pomeroy, A.; Lowe, R.; Symonds, G.; Van Dongeren, A.; Moore, C.C.C. The dynamics of infragravity wave transformation over a fringing reef. J. Geophys. Res. Ocean. 2012, 117. [Google Scholar] [CrossRef]
- Lashley, C.H.; Roelvink, D.; van Dongeren, A.; Buckley, M.L.; Lowe, R.J. Nonhydrostatic and surfbeat model predictions of extreme wave run-up in fringing reef environments. Coast. Eng. 2018, 137, 11–27. [Google Scholar] [CrossRef]
- Quataert, E.; Storlazzi, C.; van Rooijen, A.; Cheriton, O.; van Dongeren, A. The influence of coral reefs and climate change on wave-driven flooding of tropical coastlines. Geophys. Res. Lett. 2015, 42, 6407–6415. [Google Scholar] [CrossRef]
- Ma, G.; Shi, F.; Kirby, J.T. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean. Model. 2012, 43, 22–35. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Lynett, P. Nearshore Wave Modeling with High-Order Boussinesq-Type Equations. J. Waterw. Port. Coast. Ocean. Eng. 2006, 132, 348–357. [Google Scholar] [CrossRef]
- Brocchini, M. A reasoned overview on Boussinesq-type models: The interplay between physics, mathematics and numerics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20130496. [Google Scholar] [CrossRef]
- Masselink, G.; Tuck, M.; McCall, R.; van Dongeren, A.; Ford, M.; Kench, P. Physical and Numerical Modeling of Infragravity Wave Generation and Transformation on Coral Reef Platforms. J. Geophys. Res. Ocean. 2019, 124, 1410–1433. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, C.; Zheng, J.; Tong, C.; Wang, P.; Chen, S. Modelling Wave Breaking across Coral Reefs Using a Non-Hydrostatic Model. J. Coast. Res. 2018, 85, 501–505. [Google Scholar] [CrossRef]
- Wei, Z.; Jia, Y. Non-hydrostatic finite element model for coastal wave processes. Coast. Eng. 2014, 92, 31–47. [Google Scholar] [CrossRef]
- Roeber, V.; Cheung, K.F. Boussinesq-type model for energetic breaking waves in fringing reef environments. Coast. Eng. 2012, 70, 1–20. [Google Scholar] [CrossRef]
- Rijnsdorp, D.P.; Ruessink, G.; Zijlema, M. Infragravity-wave dynamics in a barred coastal region, a numerical study. J. Geophys. Res. Ocean. 2015, 120, 4068–4089. [Google Scholar] [CrossRef]
- Nicolae Lerma, A.; Pedreros, R.; Robinet, A.; Sénéchal, N. Simulating wave setup and runup during storm conditions on a complex barred beach. Coast. Eng. 2017, 123, 29–41. [Google Scholar] [CrossRef]
- Torres-Freyermuth, A.; Mariño-Tapia, I.; Coronado, C.; Salles, P.; Medellín, G.; Pedrozo-Acuña, A.; Silva, R.; Candela, J.; Iglesias-Prieto, R. Wave-induced extreme water levels in the Puerto Morelos fringing reef lagoon. Nat. Hazards Earth Syst. Sci. 2012, 12, 3765–3773. [Google Scholar] [CrossRef]
- Sous, D.; Dodet, G.; Bouchette, F.; Tissier, M. Momentum Balance Across a Barrier Reef. J. Geophys. Res. Ocean. 2020, 125, e2019JC015503. [Google Scholar] [CrossRef]
- Risandi, J.; Hansen, J.E.; Lowe, R.J.; Rijnsdorp, D.P. Shoreline Variability at a Reef-Fringed Pocket Beach. Front. Mar. Sci. 2020, 7. [Google Scholar] [CrossRef]
- Mory, M.; Hamm, L. Wave height, setup and currents around a detached breakwater submitted to regular or random wave forcing. Coast. Eng. 1997, 31, 77–96. [Google Scholar] [CrossRef]
- Beetham, E.; Kench, P.S.; O’ Callaghan, J.; Popinet, S. Wave transformation and shoreline water level on Funafuti Atoll, Tuvalu. J. Geophys. Res. Ocean. 2016, 121, 311–326. [Google Scholar] [CrossRef]
- Rijnsdorp, D.P.; Smit, P.B.; Zijlema, M.; Reniers, A.J.H.M. Efficient non-hydrostatic modelling of 3D wave-induced currents using a subgrid approach. Ocean. Model. 2017, 116, 118–133. [Google Scholar] [CrossRef]
- Feddersen, F.; Clark, D.B.; Guza, R.T. Modeling surf zone tracer plumes: 1. Waves, mean currents, and low-frequency eddies. J. Geophys. Res. Ocean. 2011, 116, C11027. [Google Scholar] [CrossRef]
- Smit, P.; Zijlema, M.; Stelling, G. Depth-induced wave breaking in a non-hydrostatic, near-shore wave model. Coast. Eng. 2013, 76, 1–16. [Google Scholar] [CrossRef]
- Lowe, R.J.; Falter, J.L.; Monismith, S.G.; Atkinson, M.J. A numerical study of circulation in a coastal reef-lagoon system. J. Geophys. Res. Ocean. 2009, 114, C06022. [Google Scholar] [CrossRef]
- Willmott, C.J. Statistics for the evaluation and comparison of models. J. Geophys. Res. Ocean. 1985, 90, 8995–9005. [Google Scholar] [CrossRef]
- Hansen, J.E.; Raubenheimer, B.; List, J.H.; Elgar, S. Modeled alongshore circulation and force balances onshore of a submarine canyon. J. Geophys. Res. Ocean. 2015, 120, 1887–1903. [Google Scholar] [CrossRef]
- Pearson, S.; Storlazzi, C.; van Dongeren, A.; Tissier, M.; Reniers, A. A Bayesian-Based System to Assess Wave-Driven Flooding Hazards on Coral Reef-Lined Coasts. J. Geophys. Res. Ocean. 2017, 122, 10099–10117. [Google Scholar] [CrossRef]
- Lowe, R.J.; Shavit, U.; Falter, J.L.; Koseff, J.R.; Monismith, S.G. Modeling flow in coral communities with and without waves: A synthesis of porous media and canopy flow approaches. Limnol. Oceanogr. 2008, 53, 2668–2680. [Google Scholar] [CrossRef]
- Rosman, J.H.; Hench, J.L. A framework for understanding drag parameterizations for coral reefs. J. Geophys. Res. Ocean. 2011, 116, C08025. [Google Scholar] [CrossRef]
- Péquignet, A.C.N.; Becker, J.M.; Merrifield, M.A. Energy transfer between wind waves and low-frequency oscillations on a fringing reef, Ipan, Guam. J. Geophys. Res. Ocean. 2014, 119, 6709–6724. [Google Scholar] [CrossRef]
- Gomes, E.R.; Mulligan, R.P.; Brodie, K.L.; McNinch, J.E. Bathymetric control on the spatial distribution of wave breaking in the surf zone of a natural beach. Coast. Eng. 2016, 116, 180–194. [Google Scholar] [CrossRef]
- Fringer, O.B.; Dawson, C.N.; He, R.; Ralston, D.K.; Zhang, Y.J. The future of coastal and estuarine modeling: Findings from a workshop. Ocean. Model. 2019, 143, 101458. [Google Scholar] [CrossRef]
- Henderson, S.M.; Bowen, A.J. Simulations of dissipative, shore-oblique infragravity waves. J. Phys. Oceanogr. 2003, 33, 1722–1732. [Google Scholar] [CrossRef][Green Version]
- de Bakker, A.T.M.; Tissier, M.F.S.; Ruessink, B.G. Shoreline dissipation of infragravity waves. Cont. Shelf Res. 2014, 72, 73–82. [Google Scholar] [CrossRef]
- Feddersen, F.; Guza, R.T.; Elgar, S.; Herbers, T.H.C. Alongshore momentum balances in the nearshore. J. Geophys. Res. Ocean. 1998, 103, 15667–15676. [Google Scholar] [CrossRef]
- van Rooijen, A.A.; McCall, R.T.; van Thiel de Vries, J.S.M.; van Dongeren, A.R.; Reniers, A.J.H.M.; Roelvink, J.A. Modeling the effect of wave-vegetation interaction on wave setup. J. Geophys. Res. Ocean. 2016, 121, 4341–4359. [Google Scholar] [CrossRef]
- Pomeroy, A.W.M.; Lowe, R.J.; Ghisalberti, M.; Storlazzi, C.; Symonds, G.; Roelvink, D. Sediment transport in the presence of large reef bottom roughness. J. Geophys. Res. Ocean. 2017, 122, 1347–1368. [Google Scholar] [CrossRef]








| Site Label | Instrument Type | Approximate Depth (m) | Sampling Frequency (Hz) | Location |
|---|---|---|---|---|
| Northern area | ||||
| N1 | RBR Solo | 3.5 | 2 | Lagoon |
| N2 | RBR Solo | 2.5 | 2 | Lagoon |
| Central area | ||||
| C0 | AWAC/RBR | 21.3 | 1 | Offshore |
| C1 | RDI Workhorse | 7.9 | 1 | Channel |
| C2 | RBR Solo | 4.7 | 1 | Channel |
| C3 | RBR Solo | 4.0 | 2 | Channel |
| C4 | RDI Workhorse | 4.0 | 1 | Lagoon |
| C5 | RBR Solo | 2.1 | 2 | Lagoon |
| C6 | Nortek Aquadopp | 3.4 | 1 | Lagoon |
| C7 | RBR Solo | 3.0 | 2 | Lagoon |
| C8 | RBR Solo | 2.6 | 2 | Lagoon |
| Southern area | ||||
| S0 | AWAC/RBR | 19.0 | 1 | Offshore |
| S1 | RDI Workhorse | 7.6 | 1 | Channel |
| S2 | RBR Solo | 5.5 | 2 | Channel |
| S3 | RBR Solo | 3.6 | 2 | Channel |
| S4 | RBR Solo | 2.9 | 2 | Lagoon |
| S5 | RBR Solo | 2.9 | 2 | Lagoon |
| S6 | Nortek Aquadopp | 2.1 | 1 | Lagoon |
| S7 | Nortek Vector | 3.3 | 2 | Lagoon |
| S8 | RBR Solo | 2.3 | 2 | Lagoon |
| S9 | Nortek Vector | 2.5 | 2 | Lagoon |
| S10 | Nortek Aquadopp | 2.3 | 1 | Lagoon |
| Sensor Location | SS Wave Heights | IG Wave Heights | Setup | Current Magnitude | Current Direction | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WS [-] | RMSE [m] | Bias [m] | WS [-] | RMSE [m] | Bias [m] | WS [-] | RMSE [m] | Bias [m] | WS [-] | RMSE [m/s] | Bias [m/s] | WS [-] | RMSE [°] | Bias [°] | |
| North | |||||||||||||||
| N2 | 0.79 | 0.13 | 0.11 | 0.85 | 0.06 | 0.04 | 0.84 | 0.05 | 0.04 | N/A | N/A | N/A | N/A | N/A | N/A |
| N3 | 0.29 | 0.23 | 0.23 | 0.88 | 0.03 | 0.02 | 0.89 | 0.04 | 0.04 | N/A | N/A | N/A | N/A | N/A | N/A |
| Central | |||||||||||||||
| C0 | 0.92 | 0.29 | −0.02 | 0.62 | 0.08 | 0.06 | N/A | N/A | N/A | 0.47 | 0.09 | −0.07 | 0.52 | 132.85 | −65.91 |
| C1 | 0.55 | 0.61 | 0.59 | 0.83 | 0.08 | 0.07 | N/A | N/A | N/A | 0.66 | 0.16 | −0.06 | 0.25 | 45.23 | −43.77 |
| C2 | 0.34 | 0.37 | 0.36 | 0.9 | 0.04 | 0.03 | 0.88 | 0.04 | 0.04 | N/A | N/A | N/A | N/A | N/A | N/A |
| C3 | 0.3 | 0.21 | 0.21 | 0.87 | 0.03 | 0.00 | 0.85 | 0.05 | 0.05 | N/A | N/A | N/A | N/A | N/A | N/A |
| C4 | 0.85 | 0.06 | −0.04 | 0.86 | 0.03 | −0.01 | N/A | N/A | N/A | 0.54 | 0.04 | 0.00 | 0.25 | 66.41 | −58.91 |
| C5 | 0.27 | 0.26 | 0.25 | 0.87 | 0.04 | 0.00 | 0.86 | 0.05 | 0.05 | N/A | N/A | N/A | N/A | N/A | N/A |
| C6 | 0.29 | 0.21 | 0.20 | 0.84 | 0.04 | 0.00 | 0.88 | 0.05 | 0.04 | 0.32 | 0.03 | 0.02 | 0.78 | 131.8 | 130.55 |
| C7 | 0.49 | 0.13 | 0.13 | 0.84 | 0.04 | −0.01 | 0.85 | 0.05 | 0.05 | N/A | N/A | N/A | N/A | N/A | N/A |
| C8 | 0.77 | 0.06 | 0.05 | 0.82 | 0.04 | −0.01 | 0.77 | 0.07 | 0.07 | N/A | N/A | N/A | N/A | N/A | N/A |
| South | |||||||||||||||
| S0 | 0.96 | 0.23 | −0.04 | 0.73 | 0.09 | 0.08 | N/A | N/A | N/A | 0.46 | 0.08 | −0.07 | 0.44 | 128.55 | −105.02 |
| S1 | 0.64 | 0.58 | 0.55 | 0.77 | 0.12 | 0.10 | 0.38 | 0.06 | 0.05 | 0.61 | 0.33 | −0.30 | 0.14 | 23.64 | −23.42 |
| S2 | 0.85 | 0.13 | −0.05 | 0.87 | 0.04 | 0.02 | 0.83 | 0.05 | 0.05 | N/A | N/A | N/A | N/A | N/A | N/A |
| S3 | 0.85 | 0.08 | 0.00 | 0.86 | 0.04 | 0.01 | 0.78 | 0.07 | 0.06 | N/A | N/A | N/A | N/A | N/A | N/A |
| S4 | 0.68 | 0.08 | 0.04 | 0.81 | 0.06 | 0.04 | 0.84 | 0.05 | 0.05 | N/A | N/A | N/A | N/A | N/A | N/A |
| S5 | 0.82 | 0.06 | 0.01 | 0.83 | 0.05 | 0.02 | 0.79 | 0.06 | 0.06 | N/A | N/A | N/A | N/A | N/A | N/A |
| S6 | 0.71 | 0.06 | −0.01 | 0.85 | 0.04 | −0.01 | 0.87 | 0.05 | 0.04 | 0.39 | 0.11 | −0.09 | 0.57 | 103.49 | 40.19 |
| S7 | 0.77 | 0.07 | −0.03 | 0.82 | 0.05 | −0.01 | N/A | N/A | N/A | 0.29 | 0.06 | −0.05 | 0.22 | 83.93 | 78.43 |
| S8 | 0.8 | 0.06 | −0.01 | 0.84 | 0.05 | −0.01 | 0.76 | 0.07 | 0.07 | N/A | N/A | N/A | N/A | N/A | N/A |
| S9 | 0.8 | 0.06 | −0.02 | 0.84 | 0.04 | −0.01 | 0.62 | 0.11 | 0.10 | 0.43 | 0.04 | −0.03 | 0.11 | 89.28 | 88.47 |
| S10 | 0.35 | 0.18 | 0.18 | 0.72 | 0.05 | −0.02 | 0.76 | 0.07 | 0.07 | 0.35 | 0.02 | 0.02 | 0.42 | 73.29 | −62.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Risandi, J.; Rijnsdorp, D.P.; Hansen, J.E.; Lowe, R.J. Hydrodynamic Modeling of a Reef-Fringed Pocket Beach Using a Phase-Resolved Non-Hydrostatic Model. J. Mar. Sci. Eng. 2020, 8, 877. https://doi.org/10.3390/jmse8110877
Risandi J, Rijnsdorp DP, Hansen JE, Lowe RJ. Hydrodynamic Modeling of a Reef-Fringed Pocket Beach Using a Phase-Resolved Non-Hydrostatic Model. Journal of Marine Science and Engineering. 2020; 8(11):877. https://doi.org/10.3390/jmse8110877
Chicago/Turabian StyleRisandi, Johan, Dirk P. Rijnsdorp, Jeff E. Hansen, and Ryan J. Lowe. 2020. "Hydrodynamic Modeling of a Reef-Fringed Pocket Beach Using a Phase-Resolved Non-Hydrostatic Model" Journal of Marine Science and Engineering 8, no. 11: 877. https://doi.org/10.3390/jmse8110877
APA StyleRisandi, J., Rijnsdorp, D. P., Hansen, J. E., & Lowe, R. J. (2020). Hydrodynamic Modeling of a Reef-Fringed Pocket Beach Using a Phase-Resolved Non-Hydrostatic Model. Journal of Marine Science and Engineering, 8(11), 877. https://doi.org/10.3390/jmse8110877





