Photogrammetry: Linking the World across the Water Surface

Abstract

Three-dimensional (3D) surveying and modelling of the underwater environment is challenging; however, it becomes even more arduous when the scene or asset to measure extends from above to underwater through the water surface. While this is topic of high interest for a number of different application fields (engineering, geology, archeology), few solutions are available, usually expensive and with no guarantee of obtaining homogenous accuracy and resolution in the two media. This paper focuses on a procedure to survey and link the above and the underwater worlds based on photogrammetry. The two parts of the asset, above and underwater, are separately surveyed and then linked through two possible analytical procedures: (1) independent model adjustment or (2) relative orientation constraints. In the first case, rigid pre-calibrated rods are installed across the waterline on the object to be surveyed; in the second approach, a synchronized stereo-camera rig, with a camera in water and the other above the water, is employed. The theoretical foundation for the two approaches is provided and their effectiveness is proved through two challenging case studies: (1) the 3D survey of the leak of the Costa Concordia shipwreck and (2) 3D modelling of Grotta Giusti, a complex semi-submerged cave environment in Italy.

1. Introduction

Measuring natural and man-made structures in three dimensions (3D) across the water surface is a very challenging task, yet necessary for a large number of applications ranging from marine infrastructures, civil engineering, cultural heritage, biology, civil protection, forensics, and many others.

While on land, 3D surveying techniques are routinely applied with success, meeting different accuracy requirements, underwater, because of physical characteristics and complexity of operations related to water medium, systematic mapping has been achieved only partially and with more relaxed accuracy requirements if compared to land measurements. While on land a large variety of traditional surveying techniques can be used and exchanged to carry out similar 3D measurement tasks, most often, underwater, few solutions, if any, are available.

Underwater, radio signals do not transmit well, thus eliminating the possibility to exploit the ubiquity of global navigation satellite system(GNSS) positioning sensors and techniques; depending on water turbidity, active and passive optical techniques such as laser scanning and photogrammetry could not be feasible, while acoustic systems may not reach necessary accuracy and resolution.

For this reason, 3D surveys of subsea environments require an extensive analysis of the project requirements, often finding a trade-off between required tolerances and costs to reduce the technical complexity of measurement tasks and operations.

Whenever environmental conditions allow for the use of available optical and acoustic techniques, and, depending on the application fields (e.g., archaeological reconnaissance, mapping, subsea metrology, high precision structural monitoring), underwater surveys can be accomplished from different platforms ranging from airplane and helicopters to vessels on the water surface, divers, submarines, remotely operated vehicles (ROV), autonomous underwater vehicles (AUV).

A very peculiar and special 3D surveying case concerns the 3D modelling of objects that are partially emerged and partially submerged. This pertains for example to objects of different nature like those shown in Figure 1.

Currently, high resolution 3D measurement techniques available as commercial industrial solutions rely on a combination of optical and acoustic methods such as LIDAR and multi beam echo sounder (MBES) mounted onboard surface vessels or static optical and acoustic scanning devices (such as respectively tripod mounted SL1 Deep sea time of flight - ToF laser scanner and the BV5000) [7,8]. Static scanning devices are capable of better metrological performances but require significantly higher acquisition time and efforts to displace the devices around the object to be surveyed. A high-resolution through-water laser scanning solution has been proposed by [9] under the constraint of static, flat, and wave-less water surface.

This paper deals with high precision photogrammetry-based techniques to perform 3D measurements of objects that are partially submerged in water under the assumption that the asset, structure, or environment to be measured itself is a rigid body (it does not undergo any deformation during the surveying). The presented approaches do not require any acoustic, nor GNSS or inertial navigation system (INS) based positioning systems, underwater or above the water, and use (low-cost) passive sensors to photogrammetrically determine both the submerged and emerged parts of the object in 3D and with color information. The methods also work in case the object is not still, as for example in case of floating objects such as pontoons, ships, and floating wind turbines. Two different procedures based on photogrammetry are presented:

• Using rigid pre-calibrated rods installed across the waterline on the object to be surveyed;
• Using a synchronized underwater stereo-camera rig.

Figure 2 shows a simulated scenario where a boat, damaged in the underwater parts of the hull, need to be repaired. The boat would require to be docked for surveying and inspecting the damaged parts to then proceed to their replacement and repairing.

The photogrammetric methods here presented would allow to significantly reduce the overall time and related costs with a much more efficient damage assessment and repairing operations. Method 1 was presented by the authors in [10] and applied for maritime engineering as well as archaeology applications [11]. The second method was utilized by the authors for the 3D survey of a semi submerged cave system [12], but technical details about the technique have not been provided thus far. In the following, the manuscript provides a complete overview of the photogrammetric methods and principles used by the two techniques, by providing unpublished technical details and results. Two relevant applications are presented and used to highlight the main benefits and drawbacks of the two methods: the semi submerged gash of Costa Concordia shipwreck surveyed using method one, and the case of the semi submerged cave system in Italy, Grotta Giusti surveyed using method two. The accuracy assessment as well as comparative analyses will be provided for the two above mentioned case studies.

The novelties of the current can be summarized:

• The theoretical framework for two different possible approaches has been unified;
• The processing of the Costa Concordia survey has been updated and refined, following a fully automatic pipeline which merges the advantages of state-of-the-art structure from motion (SfM) – multi view stereo (MVS) procedures with the rigorousness of photogrammetry; moreover, the results of the newly implemented independent model adjustment to link the part below the water with the part above the water are reported for the first time;
• Details of the relative orientation procedure for joining the above and underwater surveys of the ‘Grotta Giusti’ semi-submerged cave system based on a synchronized stereo camera are reported and discussed.

2. Materials and Methods

2.1. Overview of the Two Methods

The methods here presented assume that the object to be surveyed can be considered a rigid body thus not undergoing any significant shape deformation during the period of the 3D survey.

For both methods the 3D survey of the object entails a three-step procedure consisting of:

• An underwater photogrammetry survey of the submerged part;
• An above the water photogrammetric survey of the emerged part;
• An optimized analytical process to link the two photogrammetric coordinate systems together for a seamless 3D model generation.

At the end of the first two steps, two independent photogrammetric models are derived, one for the emerged and one for the submerged part of the asset. Here, independent means that each photogrammetric model is defined in its own datum or, in other words, has its own coordinates system. The merging of the two parts, or the transformation in a common reference system, is carried out using linking devices (Figure 2) consisting, respectively, of:

(1)

A number of pre-calibrated rigid rods as shown in Figure 2a attached to the object to be surveyed showing target plates below and above the water;

(2)

A synchronized stereo camera rig (Figure 2b) used with a camera underwater and the other one above the water.

The mathematical methods behind the two delineated approaches is here after detailed.

2.2. Method 1 Precalibrated Linking Targets

Method 1 is based on rigid rods firmly attached to the partially submerged object and visible both above and underwater. They serve as hinge or joint between the two independent photogrammetric models. Each rod presents at least one target plate above and one target plate below the water, each of them featuring a minimum of three coded targets. Before being attached and after being removed from the object, the rods are calibrated, so that the relative position between the targets on the different plates is measured. The plates of each rod visible either above or underwater allow the computation of a similarity transformation1 for bringing each rod in the coordinate system of the two separated photogrammetric models. Here, it should be noted that, while the rods are roto-translated in the photogrammetric coordinate systems, their scale is preserved and ‘transferred’ to the photogrammetric models. Once all the rods are roto-translated in both the photogrammetric coordinate systems, they constitute the common elements to compute a further transformation and merge the two photogrammetric models in a common coordinate system.

A minimum configuration would require one plate with three targets above the water and one plate below the water. Theoretically, a single rod would then be sufficient, but the solution would be weak. At least three rods well distributed over the surveyed area are advised.

While here we are considering a simplified linking target consisting in a straight rod, in case of objects with rounded shapes, the targets should be accordingly designed. For example, two rods connected with a joint can be fitted to the shape of the asset, provided that the joint is properly tightened to maintain its calibrated structure throughout the survey.

From a theoretical/mathematic point of view, to converge to the final solution where the two originally independent photogrammetric models are merged in a unique coordinate system, the procedure can be summarized in three sequential steps:

• Each single linking target is roto-translated, one at time, through a rigid similarity transformation and the target coordinates of the rod plates are determined in each of the two photogrammetric models (Figure 3a,b);
• The two photogrammetric models of the above and underwater parts are oriented in the same coordinate system, choosing one of the them as reference;
• In the last step, a refinement of the alignment is performed by re-computing simultaneously the similarity transformations for the models and the coordinates of all the target plates on the rods (Figure 3c).

The first two steps produce a coarse alignment between the two photogrammetric models above and underwater. The alignment is then refined through the last step, which recalls the semi-analytical or independent model aerial triangulation method [13], where photogrammetric stereo models are firstly relatively oriented and then transformed in the absolute datum defined by ground control points (GCPs).

The implemented free-network independent models adjustment estimates the optimal reference system for the two photogrammetric models, minimizing the mean variance of the target 3D coordinates. Each observation, i.e., the target coordinates known in each photogrammetric model, contributes to the final result according to the estimated uncertainty derived from the photogrammetric processing. This implies that the final errors of the transformation depend on the quality of the observations themselves. Assuming that no outliers are present, this last step improves the alignment, leading to smaller uncertainties. Not many iterations are usually required to converge to the optimal solution and the complexity of the problem is not high. Therefore, the computational time of the independent model adjustment is not significantly greater than the coarse alignment step.

2.2.1. Coarse Alignment between the Two Photogrammetric Models

This is a very common problem in all the disciplines of surveying, i.e., the transformation of the point coordinates from a coordinate system $C{S}^a$ to another coordinate system $C{S}^b$. If a set of points are known in both the coordinate systems, the mathematical relation or transformation can be computed and applied to transform point coordinates from one system to the other. The transformation parameters2 are calculated as solution of a system of equations where point coordinates in one system are regarded as observation vector and the transformation parameters are regarded as unknown vector.

Let $C{S}^a=\left\{0^a, X^a,Y^a,Z^a\right\}$ and $C{S}^b=\left\{0^b,x^b,y^b,z^b\right\}$ define two spatial Cartesian coordinate systems:

• $C{S}^a$ being the target, global, reference, or higher-order coordinate system, i.e., the final coordinate system where the coordinates of the points must be known;
• $C{S}^b$ being the local or lower-order coordinate system, i.e., the initial coordinate system where the coordinates of the points have been measured.

Equation (1) provides the transformation between $C{S}^a$ and $C{S}^b$, i.e., the transformation to obtain the coordinates of points originally known in system $C{S}^b$ in the target system $C{S}^a$:

$${\left[\begin{array}{c}{X}_P\\ Y_P\\ Z_P\end{array}\right]}^a={\left[\begin{array}{c}{X}_{0^b}\\ Y_{0^b}\\ Z_{0^b}\end{array}\right]}^a+\Lambda {\mathit{R}}_b^a\cdot {\left[\begin{array}{c}{x}_P\\ y_P\\ z_P\end{array}\right]}^b$$

(1)

where

• ${\left[\begin{array}{c}{X}_P\\ Y_P\\ Z_P\end{array}\right]}^a=\mathit{P}\left(X^a,Y^a,Z^a\right)$ are the coordinates of a generic point P in the target system $C{S}^a$ (here the apex indicates the system where the coordinates are defined);
• ${\left[\begin{array}{c}{X}_{0^b}\\ Y_{0^b}\\ Z_{0^b}\end{array}\right]}^a$ are the coordinates of the origin $0^b$ of system $C{S}^b$ known into system $C{S}^a$;
• $\Lambda =\left[\begin{array}{ccc}{\lambda }_1& 0& 0\\ 0& {\lambda }_2& 0\\ 0& 0& {\lambda }_3\end{array}\right]$ is the diagonal matrix containing the scale factors in the three directions; usually ${\lambda }_1={\lambda }_2={\lambda }_3=\lambda$, i.e., an isotropic scale factor exists between the two systems so that $\Lambda$ reduces to:

  $$\Lambda =\left[\begin{array}{ccc}\lambda & 0& 0\\ 0& \lambda & 0\\ 0& 0& \lambda \end{array}\right]$$

  (2)
• ${\mathit{R}}_b^a$ is the 3 × 3 rotation matrix from system $C{S}^b$ to system $C{S}^a$:

  $${\mathit{R}}_b^a={\left[\begin{array}{ccc}\mathrm{c}\phi \mathrm{c}\kappa & -\mathrm{c}\phi \mathrm{s}\kappa & \mathrm{s}\phi \\ \mathrm{c}\omega \mathrm{s}\kappa +\mathrm{s}\omega \mathrm{s}\phi \mathrm{c}\kappa & \mathrm{c}\omega \mathrm{c}\kappa -\mathrm{s}\omega \mathrm{s}\phi \mathrm{s}\kappa & -\mathrm{s}\omega \mathrm{c}\phi \\ \mathrm{s}\omega \mathrm{s}\kappa -\mathrm{c}\omega \mathrm{s}\phi \mathrm{c}\kappa & \mathrm{s}\omega \mathrm{c}\kappa +\mathrm{c}\omega \mathrm{s}\phi \mathrm{s}\kappa & \mathrm{c}\omega \mathrm{c}\phi \end{array}\right]}_b^a$$

  (3)

  where $\mathrm{c}=\cos (·)$ and $\mathrm{s}=\sin (·)$ and $\omega ,\phi ,\kappa$ are the three rotation angles between the two coordinate systems. It is noteworthy that the rotation matrix ${\mathit{R}}_b^a$ contains the sequential rotations that, applied to the axes of target system $C{S}^a$, transform system $C{S}^a$ to be parallel with system $C{S}^b$:

  $${\mathit{R}}_b^a={\mathit{R}}_{X^a}\left\{{\omega }_b^a\right\}·{\mathit{R}}_{Y^a}\left\{{\phi }_b^a\right\}·R_{Z^a}\left\{{\kappa }_b^a\right\}$$

  (4)
• ${\left[\begin{array}{c}{x}_P\\ y_P\\ z_P\end{array}\right]}^b=\mathit{P}\left(x^b,y^b,z^b\right)$ are the coordinates of point P in system $C{S}^b$.

The inverse transformation which permits to compute the coordinates of points originally known in the target system $C{S}^a$ into the system $C{S}^b$ is given by:

$${\left[\begin{array}{c}{x}_P\\ y_P\\ z_P\end{array}\right]}^b= {\Lambda }^{-1}{\mathit{R}}_a^b\cdot {\left[\begin{array}{c}{X}_P-X_{0^b}\\ Y_P-Y_{0^b}\\ Z_P-Z_{0^b}\end{array}\right]}^a$$

(5)

where

$${\mathit{R}}_a^b={\left({\mathit{R}}_b^a\right)}^{-1}={\left({\mathit{R}}_b^a\right)}^T$$

(6)

An equivalent but more concise form of the similarity transformation is achieved with the so-called 4 × 4 homogeneous transformation matrix:

$${\left[\begin{array}{c}\begin{array}{c}{X}_P\\ Y_P\\ Z_P\end{array}\\ 1\end{array}\right]}^a={\mathit{T}}_b^a\cdot {\left[\begin{array}{c}\begin{array}{c}{x}_P\\ y_P\\ z_P\end{array}\\ 1\end{array}\right]}^b= \left[\begin{array}{cc}\Lambda {\mathit{R}}_b^a& {\mathit{t}}_b^a\\ \mathbf{0}& 1\end{array}\right]\cdot {\left[\begin{array}{c}\begin{array}{c}{x}_P\\ y_P\\ z_P\end{array}\\ 1\end{array}\right]}^b$$

(7)

where:

• ${\left[\begin{array}{c}\begin{array}{c}{X}_P\\ Y_P\\ Z_P\end{array}\\ 1\end{array}\right]}^a$ and ${\left[\begin{array}{c}\begin{array}{c}{x}_P\\ y_P\\ z_P\end{array}\\ 1\end{array}\right]}^b$ are the homogeneous coordinates of point P with respect to system ${\mathrm{CS}}^a$ and system ${\mathrm{CS}}^{\mathrm{b}}$, respectively;
• the transformation matrix is given by:

  $$\left[\begin{array}{cc}\Lambda {\mathit{R}}_b^a& {\mathit{t}}_b^a\\ \mathbf{0}& 1\end{array}\right]={\left[\begin{array}{cc}\begin{array}{cc}\begin{array}{c}\begin{array}{c}\lambda ·r_{11}\\ r_{21 }\end{array}\\ \begin{array}{c}{r}_{31 }\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{c}{r}_{12 }\\ \lambda ·r_{22}\end{array}\\ \begin{array}{c}{r}_{32 }\\ 0\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\begin{array}{c}{r}_{13 }\\ r_{23 }\end{array}\\ \begin{array}{c}\lambda ·r_{33}\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{c}{X}_{0^b}^a\\ Y_{0^b}^a\end{array}\\ \begin{array}{c}{Z}_{0^b}^a\\ 1\end{array}\end{array}\end{array}\end{array}\right]}_b^a$$

  (8)

  being $r_{ij, \{\begin{array}{c}i=1:3\\ j=1:3\end{array}}$ the elements of the rotation matrix (3) ${\mathit{R}}_b^a$.

For the generic case of a 3D transformation, the minimum number of points that would provide the solution for the seven unknown parameters are, for example, two complete (all the three coordinates are known in both the systems) 3D points and a third point with one of the coordinates known in the two systems. To avoid singularities in the computation, the simplest solution is to provide two 3D points not lying on the same axis of the coordinate system and the third point not aligned to the others. However, in general, more than the minimum of common points is used in order to increase the reliability of the computed transformation parameters. When the number of observations is larger than the number of unknown parameters (seven) the problem reduces to an estimation process, where the “best” solution for the unknowns are to be inferred from observations.

The most commonly used method in modern surveying for the estimation of parameters is the least squares (LS) approach. An adjustment problem requires the definition of the mathematical model, a combination of (i) a functional model, which relates the parameters to be estimated to the observations, and (ii) a stochastic model, which is a statistical description that defines the random fluctuations in the measurements and, consequently, the parameters. In Appendix A, the full derivation of the LS approach for the case of interest is reported.

The first step of the developed procedure requires that a similarity transformation is computed to roto-translate each individual rod in both the photogrammetric models, above and underwater, separately. In other words, considering one of photogrammetric models as the reference coordinate system (i.e., system $C{S}^a$ in Figure 1 and Equation (1)) and taking one rod at time (which constitutes system $C{S}^b$ in Figure 1 and Equation (1)), an LS adjustment process is performed for computing the transformation parameters that transform the rod into the photogrammetric coordinate system. This procedure is repeated for all the rods with the first photogrammetric model and, similarly, with the second photogrammetric model. Thus, if, for example, four rods are employed, 4 × 2 separate adjustment processes are to be computed.

At the end of this analytical procedure, the coordinates of the targets on the rods are known in both the two distinct photogrammetric models (up and down). It is worth to note that, after this set of transformations, in the photogrammetric model of the emerged part also the targets in water are known and, analogously, in the submerged model the targets in air are estimated. That means that now the two separate photogrammetric models have enough common points through which a further transformation can be computed, choosing one model as reference coordinate system.

2.2.2. Refinement of the Alignment through Independent Models Adjustment

The final step of the outlined procedure consists in refining the coarse alignment between the two photogrammetric models achieved in the last phase. This is performed through a procedure inspired by the adjustment of independent models employed in aerial triangulation.

A variety of approaches have been proposed in literature to solve the problem [14]; nevertheless, the mathematics behind the independent models method essentially recalls the formalism introduced for the computation of a similarity transformation. The definition provided by Krauss [13] is exceptionally explicative, i.e., a chain of spatial similarity transformations, where the transformation parameters of each independent model, which in turn provide the exterior orientation parameters, and the coordinates of all the tie points are simultaneously computed in the ground coordinate system. Additionally, in the case of block adjustment by independent models, the problem is non-linear and the linearization procedure is to be followed (Appendix B).

2.3. Method 2 Precalibrated Stereo Camera

Method 2 is based on the use of a synchronized stereo camera rig consisting of two cameras each placed in an underwater housing firmly mounted on a rigid pole (Figure 4). The stereo camera rig allows to fully survey simultaneously the semi submerged object without the need of external scale bars nor the measurement of distances between signalized points on its surface. A system calibration is required to estimate the interior orientation plus lens distortion parameters of each camera when used both under and above the water and to estimate the relative orientation between the two cameras [15]. This procedure has been exploited for photogrammetric applications both above and underwater [15,16].

The relative orientation between two cameras viewing the same scene is the procedure of finding the five degrees of freedom of one camera relative to the other (one degree of freedom is considered known or fixed). Assuming that the cameras are pre-calibrated, their relative orientation can be estimated by observing at least five homologous points between the two cameras to solve for the five unknowns by means of the co-planarity equations or by determining the absolute orientation (six degrees of freedom) relative to an external reference frame for both cameras independently. Then, a roto-translation is computed to make coincident the external reference frame with one of the two camera reference systems (the left one in general).

In the following equations, the letters G, R, and L, indicate, respectively, the Global, Right camera, and Left camera reference frames. The superscripts specify the reference frame where the quantity is defined, e.g., $P_{}^G$ is the position vector of a generic point P known in the global frame, ${\mathrm{R}}_{\mathrm{G}}^{\mathrm{R}}$ is the rotation matrix from the global to the right camera frame, and ${\mathrm{O}}_{\mathrm{R}}^{\mathrm{G}}$ represents the origin of right camera frame expressed in the global reference frame. According to this notation, the coordinates of the point $P_{}^G$ known in the global frame can be expressed in the right camera reference frame as function of the exterior orientation parameters of the right camera:

$$P^R={\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]}^R=R_G^R·{\left[\begin{array}{c}X-X_{oR}\\ Y-Y_{oR}\\ Z-Z_{oR}\end{array}\right]}^G=R_G^R·\left(P^G-O_R^G\right)$$

(9)

$$R_G^R=\left[\begin{array}{ccc}\mathrm{c}\phi \mathrm{c}k& \mathrm{c}\omega \mathrm{s}k+\mathrm{s}\omega \mathrm{s}\phi \mathrm{c}k& \mathrm{s}\omega \mathrm{s}k-\mathrm{c}\omega \mathrm{s}\phi \mathrm{c}k\\ -\mathrm{c}\phi \mathrm{s}k& \mathrm{c}\omega \mathrm{c}k-\mathrm{s}\omega \mathrm{s}\phi \mathrm{s}k& \mathrm{s}\omega \mathrm{c}k+\mathrm{c}\omega \mathrm{s}\phi \mathrm{s}k\\ \mathrm{s}\phi & -\mathrm{s}\omega \mathrm{c}\phi & \mathrm{c}\omega \mathrm{c}\phi \end{array}\right]$$

(10)

$$O_R^G={\left[\begin{array}{c}{X}_{oR}\\ Y_{oR}\\ Z_{oR}\end{array}\right]}^G$$

(11)

where (10)3 and (11) are, respectively, the rotation matrix containing the orientation angles and the position vector of the right camera perspective center in the global frame. To perform a relative orientation between the two cameras is equivalent to re-orienting the global reference system to be coincident with the left camera frame. This transformation is expressed as:

$$P^R={\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]}^R=R_L^R·{\left[\begin{array}{c}X-X_{oR}\\ Y-Y_{oR}\\ Z-Z_{oR}\end{array}\right]}^L=R_L^R·\left(P^L-O_R^L\right)$$

(12)

$$R_L^R=R_G^R·{\left(R_G^L\right)}^{\mathrm{T}}$$

(13)

$$O_R^L=R_G^L·\left(O_R^G-O_L^G\right)$$

(14)

where (13) and (14) are, respectively, the rotation matrix (i.e., orientation angles or boresight angles) and coordinates of the right camera in the left camera reference frame. In other words, Equation (14) represents the components of the baseline (or lever arm) between the two cameras in the reference system centered on the left camera. From the above transformation, the exterior orientation parameters of the chosen refence camera become null and the exterior orientation of the second camera relative to the first is obtained. This procedure is convenient when the exterior orientation of the two cameras is known, for example from a bundle adjustment process. Typically, a self-calibration with coded targets is performed to recover the interior orientation parameters of the two cameras and as a result of the bundle adjustment, the exterior orientations of the cameras are determined. For a stereo-triangulation camera system, which is composed of two cameras fixed to each other, the relative orientation in theory should be the same for each camera pose. Thermal influences and mechanical instability of the frame to which the cameras are fixed might also have a significant contribution to relative orientation differences between several distinct stereo camera poses. In practice, the presence of errors in the image measurements or an inappropriate mathematical model (i.e., missing parameters to correct lens distortions) results in different relative orientations for each camera pose. Because several camera poses are generally used in a self-calibration procedure, most probable values for the relative orientation (three positions and three orientation angles of the second camera with respect to the first camera) can be obtained either through simple averaging with statistical removal of outliers (i.e., median filter) or through a more rigorous approach using relative orientation constraints in a simultaneous bundle adjustment [16,17].

In method two, the photogrammetric survey of the semi submerged object is carried out after the stereo camera rig calibration following the procure descried above. Let $C{S}^a=\left\{0^a, X^a,Y^a,Z^a\right\}$ and 〖$C{S}^b=\left\{0^b,x^b,y^b,z^b\right\}$ be the two spatial Cartesian coordinate systems respectively above and below the water. The linking between the two $CS$ can be performed in a way very similar to what was described in method one, but this time exploiting the stereo camera relative orientation as link between the above the water and below the water worlds.

The survey is then accomplished in three steps: the stereo camera is used to acquire the above the water and underwater parts by carrying out two separate image acquisitions with the stereo camera once completely (i) above the water and (ii) completely underwater; (iii) a third image acquisition step with the stereo camera rig placed across the water surface so that one camera acquires the part of the object below the water and the other camera the part above the water. This last step completes the procedure allowing to photogrammetrically link together the two separate surveys carried out below and above the water, exploiting the relative orientation of the two cameras measured from calibration. Theoretically, a single image pair acquired with the stereo camera placed across the water surface would suffice to provide the link between the above and below the water coordinate systems. From simple geometric considerations redundant and more spatially distributed stereo camera positions are necessary and an average transformation can be computed.

Alternatively, using the transformation parameters computed with Equations (9)–(14), for each camera position computed below the water, it is possible to compute the camera position above the water (or vice versa). This process produces the correspondent positions of the cameras in the other medium which can be used to estimate a similarity transformation between the expected positions from the relative orientation and the one from the image orientation step. Additionally, a constrained bundle adjustment can be run to adjust the camera positions so that they comply with the relative orientation.

3. Results

3.1. Case Study 1: Photogrammetric Survey of Semi-Submerged Object Using Linking Targets on Pre-Calibrated Rods. The Case Study of Costa Concordia Shipwreck

On the 12th of January 2012, the 290 m long Italian cruise ship Costa Concordia partially sank off the coast of Isola del Giglio after she struck her port side on a reef known as Le Scole (Figure 5a). After the collision, the ship, without steering control or propulsive power, ran aground close to the Giglio Porto harbor entrance, leaning with the starboard side against the seafloor with a final inclination angle of about 70 degrees (Figure 5b). An investigation to measure the dimensions and determine the characteristics of the leak produced by the collision of the ship with the rocks was required, posing non-trivial problems: (i) after the grounding, the leak was situated on the above-the-water side of the stranded ship and extended at the current waterline 6 m above and 4 m below the sea surface circa: to achieve a complete inspection of the ship’s area interested by the impact a complete survey both above and below the water was necessary; (ii) the leak was positioned on the ship’s side facing toward the open sea hence not visible from the shoreline: it was not possible either to measure the ship directly from the coast or to signalize and measure control points on the object with topographic methods; (iii) the area to be surveyed had an elongated shape of approximately 60 m long and 10 m high.

The project’s requirement to have both submerged and emerged parts with the same accuracy did not allow to integrate different techniques, e.g., optical methods (laser scanning, photogrammetry) for the upper part and acoustic equipment for the underwater area due to the limits of currently available technologies. Moreover, the collision against the rocks caused the ship steel plates to be heavily deformed, with further small cracks potentially occluded, hence, not visible from a sea-level point-of-view. Therefore, an integrated and unified photogrammetric survey of both parts was assumed to be the most feasible solution in order to satisfy the stringently inspection needs. Method one described in Section 2.2, consisting in two separate photogrammetric surveys carried out in the two different media (one in air above the sea level and one in water below the sea level) using linking targets, was then applied.

The lack of ground control elements required a carefully planning and strict acquisition protocol. It is well known that photogrammetric networks formed by bundle of rays may be distorted and twisted in areas free of control points [13] and that it is more evident for image triangulation of elongated strips where systematic errors accumulate and can cause a twist of the model [20].

Indeed, in absence of external control points deformation and twist of photogrammetric model can occur in presence of systematic errors not correctly modelled. In such a case, the unmodelled errors propagate in the solution, causing the typical dome shape shown in recent publications [20,21,22,23]. The bundle adjustment process can highlight the shape of such deformation, but it is not able to accurately estimate the magnitude, usually tending to an underestimation. Only a strong camera network geometry can mitigate the unwanted and uncontrollable effect and provide more reliable results. Camera calibration both in air and water was a crucial step to reduce systematic errors. The images were acquired with a digital single lens reflex (DSLR) camera (Nikon D300) equipped with a 35 mm for the above-the-water survey and a 24 mm lens underwater. When used in water, the camera was sealed in a waterproof housing with a dome port. Details on the calibration in air and in water can be found in [10].

Targeting operation was performed before the photogrammetric survey: 500 white magnetic circular targets (30 mm diameter and of 4 mm thick) and five 3 m long rods were evenly distributed over the surveyed area. Three rods had two plates below the waterline and one above (OD-E, OD-H, OD-D, where OD stands for orientation device, Figure 6c–e). The remaining two rods were fixed in the opposite way with one plate below and two above the sea level (OD-F, OD-G, Figure 6a,b,e).

Two scale bars were attached underwater, one horizontally (SB-C) and one vertically (SB-A), while another scale bar was fixed above the waterline (SB-B) (Figure 6e).

To strengthen the connection between the surveys above and below the sea surface, the tidal effect was considered (Figure 7): a 25 cm wide part of the hull was submerged when the tide reached its maximum and was emerged with the minimum tidal value. The in-air surveys were executed at different times of the day (morning and evening) and repeated in different days to have the common part of the hull both in underwater and dry conditions.

The photogrammetric survey of the emerged part of the ship was carried out using different boats (pilot boat, rubber boat) having different heights above the sea level and at different distances, measured through a laser distance meter, from the ship (from 6 up to almost 12 m). The camera network comprising all the different acquisitions for the above-the-water part is shown in Figure 8.

In total, 200 images were acquired with a ground sample distance (GSD, i.e., the image resolution on the object) ranging from 0.9 mm to 1.9 mm (Figure 8). The underwater survey was carried out in the late afternoon when sun was low enough on the horizon to limit reflections on the sea and ship surface, adequate lighting underwater was assured by using a strobe. The underwater shots were taken according to a photogrammetric aerial-like strip scheme with additional stations with convergent and rolled images:

-

Four strips were realized at different planned depths (namely −1.5 m, −2 m, −3 m, and −4 m) in different days. In Figure 9 the separate strips at different depths are displayed in different colors;

-

The shots were taken to assure a forward overlap of circa 80% (50 cm distance along strip) and a sidelap of circa 40% between two adjacent strips

-

A mean distance of circa 3 m was maintained from the hull in order to assure the necessary GSD and a sufficient contrast on the hull surface according to the average visibility ascertained after a preliminary underwater reconnaissance.

About 800 images were acquired with a mean GSD of 0.7 mm. To improve the accuracy of the photogrammetric network every five images, convergent and rotated photographs were included [20].

The two surveys were first elaborated separately through a fully automatic procedure comprising the following steps4:

• Automatic image orientation and triangulation using structure from motion (SfM) tools.
• Filtering and regularization of automatic extracted tie points: a filtering and regularization procedure of tie points from SfM algorithms was developed and tested in several applications and presented in previous papers [20,22]. The leading principle of the procedure is to regularize the distribution of tie points in object space, while preserving connectivity and high multiplicity between observations. A regular volumetric grid (voxelization) is generated, and the side length of each voxel is set equal to a fixed percentage of the image footprint and decided in order to guarantee a redundant number of observations in each image. The 3D tie points that are inside each voxel are collected in a subset. A score is assigned to each point on the basis of the following properties listed in ascending order of importance: (i) point’s proximity to the barycenter of the considered voxel, (ii) point’s visibility on more than two images, (iii) intersecting angle, (iv) point’s visibility on images belonging to different blocks or strips. The 3D tie points with the highest score in each cell are kept. The results of the filtering are shown in Figure 10 and summarized in

  Table 1. Filtering of the sparse tie point clouds of above and underwater photogrammetric models.

  	Original Tie Points	Filtered Tie Points	Percentage Reduction
  Above the Water
  Number of three-dimensional (3D) Point	151,824	5689	96%
  Number of Image Observations	940,636	56,473	94%
  Average Number of Tie Points Per Image		282
  Underwater
  Number of 3D Point	420,328	11,313	97%
  Number of Image Observations	1070,626	53,263	95%
  Average Number of Tie Points Per Image		67

  and

  Table 2. Characteristics of filtered sparse tie point clouds above and under-the-water photogrammetric models.

  	Number of Intersecting Optical Rays	Number of Strips	Intersection Angle
  Above the water
  Mean	10	2	41°
  Standard deviation	7	1	19°
  Max	32	4	90°
  Underwater
  Mean	5	2	28°
  Standard deviation	4	1	15°
  Max	38	4	89°

  .
• Photogrammetric bundle adjustment using the filtered tie points as image observations: different versions of self-calibrating bundle adjustment were run, separately for the emerged and submerged models. All the strips were processed following both (a) a free network adjustment with a-posteriori scaling (using both the scale bars and the visible parts of the rods) and (b) using the same reference distances as constraints in the adjustment process. For the above-the-water mode, a further test was considered, using only the closest strips carried out in the evening, hence with very similar lighting conditions and almost simultaneous with the underwater surveys and the known distances as constraints. The combination providing the best independent model adjustment was selected, i.e., the constrained adjustment with only the closest strips for the above-the-water model and constrained adjustment with all the strips for the underwater model. Their results are summarized in

  Table 3. Statistics of the selected different bundle adjustment processes for the above and underwater survey.

  			Above-the-Water	Underwater
  Object Space	sXYZ Precision vector length [m]	Mean	0.0026	0.0027
  		Stdv	0.0008	0.0010
  		Max	0.0051	0.0060
  Image Space	Root mean square reprojection Error [Pixel]	Mean	0.336	0.449
  		Stdv	0.137	0.134
  		Max	0.826	1.129
  	Max residual error [Pixel]	Mean	0.523	0.741
  		Stdv	0.226	0.234
  		Max	1.287	1.683

  .
• Dense image matching: the exterior, interior orientation and additional parameters obtained from the photogrammetric bundle adjustment of the two surveys were used for the generation of separate high dense point clouds (Figure 11).
• Mesh generation and editing: The two high dense point clouds were finally triangulated using the Poisson algorithm [34] implemented in CloudCompare [33]. The optimization procedure described in [35] was used to find the optimum compromise between resolution and usability of the generation of meshes useful for successive analyses, such as highlighting of cracks, calculation of the water flood through the leak, etc. [10].

At the end of the third step, i.e., after the photogrammetric bundle adjustment, the two separate photogrammetric models (above and underwater) were aligned through the procedure described in Section 2.2. The transformation computed was then used to merge the dense point clouds and meshes derived from steps 4 and 5:

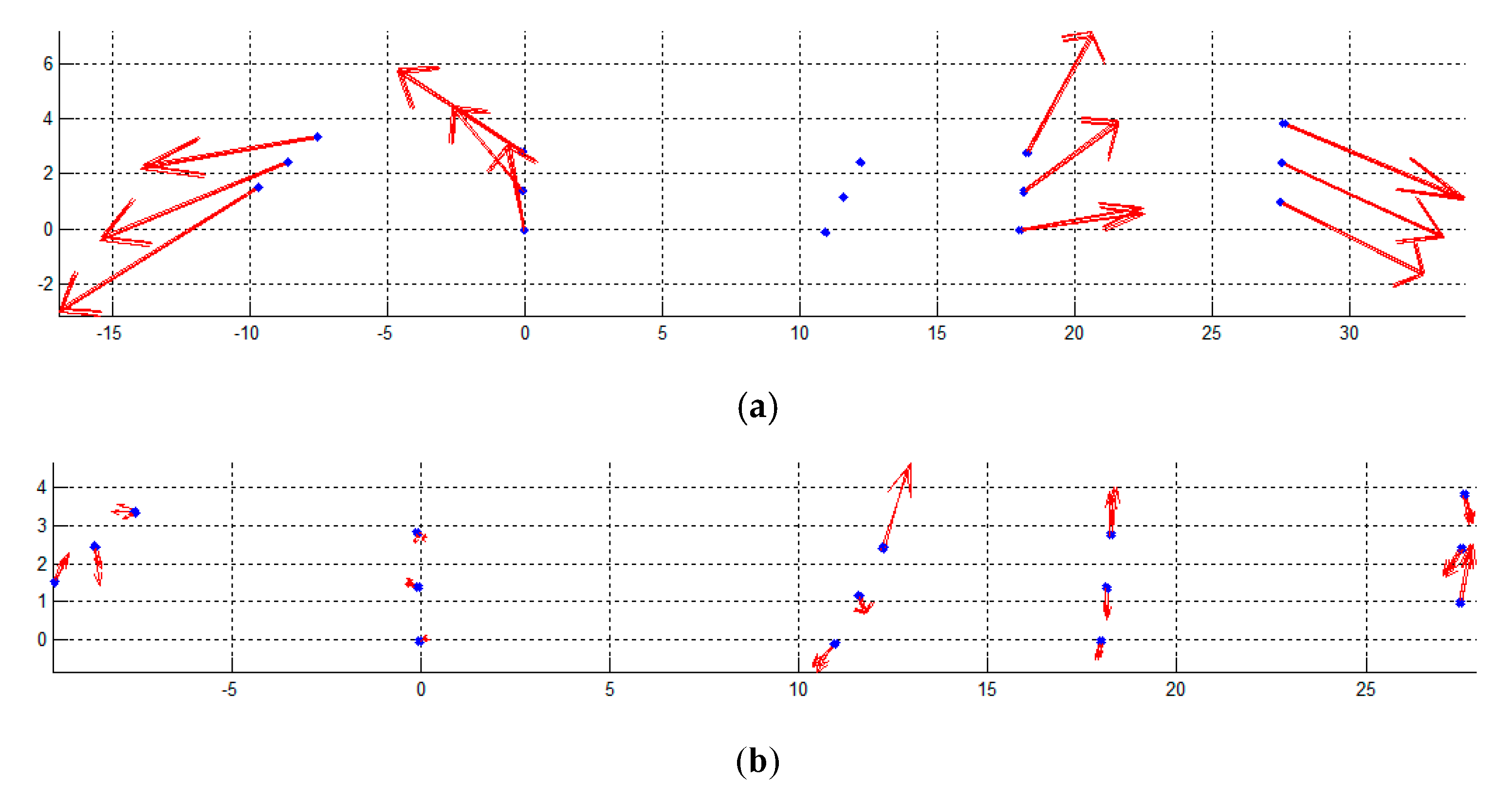
• Coarse alignment of two photogrammetric models: the first step of the coarse rigid transformation was carried out by mounting each single rod separately on the above and underwater photogrammetric models (Figure 12). Each transformation from the rod to both above and underwater independent models was computed without scale factor for preserving the higher accuracy scale of the rods. Two of the four targets of OD-H plate above the water were soiled by the fuel floating around the ship, making it not possible to compute the transformation to bring OD-H in the above-the-water photogrammetric model. After this step, the 3D coordinates of all the OD targets, except OD-H, were known in the both the photogrammetric models and were used to compute the similarity transformation for their assembling. Figure 13a shows the graphical results of the transformation, computed with 48 common points and without scale factor. Both the residual vectors, from the underwater reference system to the above the water reference system, and residual distribution are reported. The statistics are summarized in

  Table 4. Results of the transformations between underwater and the above the water coordinate systems.

  RMSE X [m]	RMSE Y [m]	RMSE Z [m]	RMSE Length [m]	RMSE Mean (Magnitude) [m]	Max Residual [m]
  Coarse Alignment
  0.0051	0.003	0.0164	0.0174	0.0159	0.0269
  Independent Models Adjustment
  0.003	0.0008	0.0011	0.0014	0.0011	0.0037

  , which shows that the mean difference (in terms of root mean square error, RMSE) between the two models is of 0.016 m with a maximum of 0.027 m.
• Refinement of the alignment through independent model adjustment: the coordinates and transformation parameters computed in the previous step were used as approximations for the independent model free-network adjustment, where the scale factors of the rods were used as constraints. The results are shown in Figure 13b and Table 4. The spatial residuals from the comparison shown that, with respect to the coarse rigid transformation are reduced by a factor of about 10.

The computed transformation was used to merge the two photogrammetric models (Figure 14 and Figure 15).

3.2. Case Study 2: Photogrammetric Survey of Semi-Submerged Environment Using a Synchronized Underwater Stereo-Camera Rig. The Case Study of Grotta Giusti

This application deals with the virtualization of Grotta Giusti, an underground semi-submerged cave system in central Italy. It is the European biggest cave filled with warm water and is currently part of a thermal resort. Differently from the previous application where high accuracy was the leading parameter for the surveying and modelling, in this case the main motivation was to create a virtual model of an environment accessible only partially and to few visitors (recreational divers, http://www.grottagiustidiving.com/). A more in-depth project description is discussed in [12], while here, we will focus on the developed approach to survey the semi-submersed areas of the cave relying on a stereo camera system (method 2 Section 2.3).

The cave, which has the characteristic of a fault, alternates parts completely submerged with crystal clear thermal water with areas that are dry and parts that are partially filled with water.

The entrance chamber for the diving experience, called ‘Lago del Limbo’, is a semi submerged environment of about 20 × 8 × 17 m, with a maximum water depth of about 10 m. The chamber was surveyed with a stereo rig and with a DSLR camera. The stereo rig featured a two GoPro Hero4 Black Edition in their underwater pressure housings (Figure 16a), two underwater lights (Figure 16b) on the handles and two red laser pointers. The GoPro stereo rig was preliminary calibrated (Figure 16b and Figure 17), using rods and calibration devices previously measured in laboratory [10]. The GoPro cameras were set in video mode and an automatic software synchronization algorithm was developed. The synchronization is based on the automatic localization in the recorded streams of common events, i.e., flashing lights visible in the videos and sounds audible in the audio channels [36,37]. The fisheye lens model was used as mathematical basis for the image projection when the GoPro was used above the water, while due to total internal reflection [38] a pinhole was adopted when the camera was used below the water.

The calibrated baseline from the calibration above the water resulted equal to 336.07 ± 0.33 mm, the calibration underwater resulted 335.9 ± 0.54 mm5. The difference is likely due to thermal influences. The higher standard deviation is instead most likely caused by the uncompensated refractive effects of water [38].

The laser pointers were collimated to intersect at the calibrated working distance of about 50 cm. Their position and orientations with respect to the two cameras were also computed during the calibration stage providing an additional scaling information that can be used as a cross check. The calibrated stereo rig was used under and above-the-water to provide 3D scaled photogrammetric measurements of the two separate environments of the cave. Two strips above and five strips underwater with about 60–80% overlap were acquired. For the strip acquired across the water, images had to be masked in the area were the water surface was visible causing false tie point matchings due to reflections and refractive effects. The process was accomplished using a simple rectangular mask automatically built on the basis of simple geometrical assumptions. Once the single strips underwater and above the water were oriented and scaled using the a priori knowledge on the relative orientation, the procedure described in Section 2.3 was adopted to join the submerged and emerged parts of the cave, relying on the use of the stereo system as link across the water level. The camera positions above the water were computed using the relative orientation applied to the positions computed underwater.

Before the survey, the rods (Figure 18) were installed across the water level to assess the accuracy of the method. A similarity transformation was performed to rigidly align each rod to the corresponding one in photogrammetric reference system, as explained in Section 2.2.

The root mean square error (RMSE) of residuals of all five rods reached sub-centimeter accuracy in linking the above and below water 3D data (Figure 19). The high residuals on the rod named OD_C-D were due to instability in the fixing of the rod to the cave wall which was noted during the survey.

Figure 20 shows the 3D visualization above and below water after the merging of the two photogrammetric models.

The rest of the chamber (parts far away from the water level, such as the ceiling) was photogrammetrically surveyed with a Nikon D750 in a NiMAR waterproof housing, coupled with a more powerful strobe unit. The final virtual model is accessible at this link: http://3dom.fbk.eu/repository/grottagiusti/.

4. Discussions and Conclusions

The paper has presented an approach, fully based on photogrammetry, to survey semi submerged assets. While they can be also floating, the only restriction is that the objects do not undergo any deformation (rigid body assumption). The proposed method entails a three-step procedure, i.e., the separate survey of the (i) above and (ii) underwater parts and (iii) a process to link the two separate models, transforming them in a common reference system. Two different approaches have been developed to solve the last step: (1) an independent model adjustment is computed using a number of pre-calibrated rigid rods or (2) a calibrated relative orientation constraint is adopted through the use of synchronized stereo camera rig with a camera above and the other underwater.

The theoretical framework and mathematical details have been provided and the feasibility of two methods proved through two different case studies. In particular, the accuracy potential of method 1 has been proved in a very challenging application, i.e., the 3D survey of the Costa Concordia leak. The effectiveness of method (2) has been demonstrated in the 3D modelling of a complex semi-submerged cave environment.

Method 1 proved to be a very accurate and reliable method with redundant control provided by different pre calibrated linking devices. Although it has the disadvantage of requiring the fixation of the linking targets on the object to be surveyed, for the Costa Concordia this was accomplished using neodymium magnets which assured a good stability over different days (in other experimentation suction caps were used for fiberglass boats). Nevertheless, one of the linking devices was probably touched by workers participating in other simultaneous operations or by the strength of sea waves. The presence of natural points or targets around the target plates allowed to discover the motion and properly separate the processing in different days. For this reason, it is suggestable to perform the two surveys, underwater and above the water, at short delays between each other.

Method 2 proved to be a very flexible method not requiring any target on the object. The use of a stereo camera rig mounting GoPro action cameras proved not only to be lightweight and easy to use but also represented a very low-cost method. This method requires the stereo camera rig to be calibrated and the final accuracy results are therefore expected to rely on the mechanical stability of the rig system. For more accurate scaling, redundancy and control over the final solution, linking devices across the water or scale bars above and below the water are suggested.

While the two methods can be considered interchangeable and can be employed separately, an integrated approach would be advisable. The accuracy of method 2 is highly correlated to the baseline between the two cameras: while a long baseline would reduce the measurement uncertainty, it might negatively affect the portability of the system, also risking to compromise its stability. Another crucial aspect is the stereo-rig calibration, which has to be repeated each time the system is dismantled, for example, to download the images, charge the battery, etc. On the other hand, as reported in both the case studies, the linking rods can move during the survey. Consequently, high redundancy is essential, but, at the same time, can critically increase the time for the targeting operation. The combined use of the two approaches would represent a more robust solution for applications where often it is very hard, if not impossible, to obtain an independent accuracy check. This aspect will need further investigation, with a specifically designed experimentation to analyze the simultaneous adjustment using relative constraints from the stereo camera rig in combination with an independent model adjustment of the linking devices.