Wind-Induced Currents in the Gulf of California from Extreme Events and Their Impact on Tidal Energy Devices
Abstract
:1. Introduction
2. Methodology
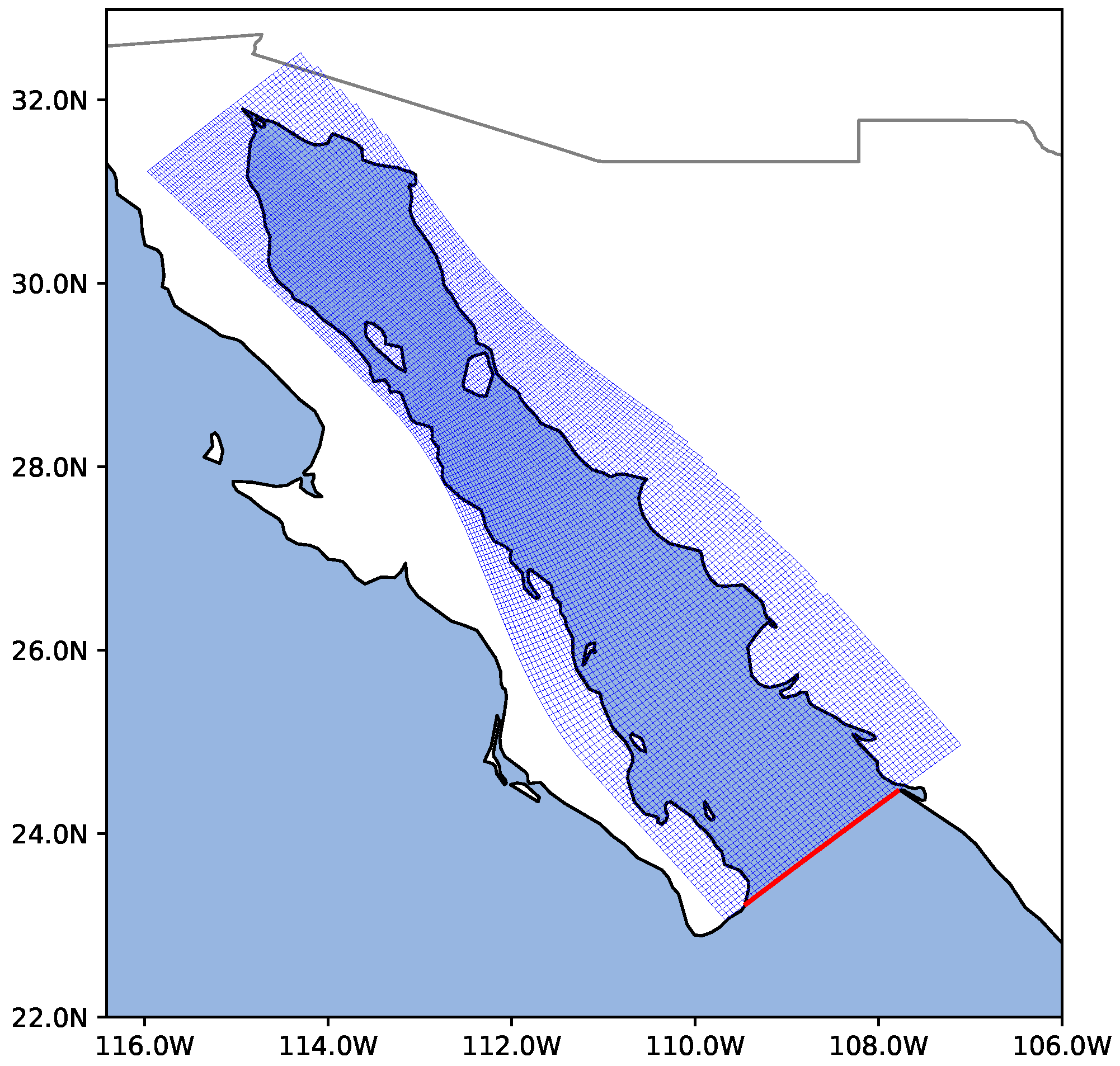
2.1. The Model
- the vertical accelerations are neglected in the momentum equations;
- the momentum conservation equation in the vertical is replaced by a balance equation for the pressure field, and;
- the vertical velocities are computed from the continuity equation.
2.2. The Wind Forcing
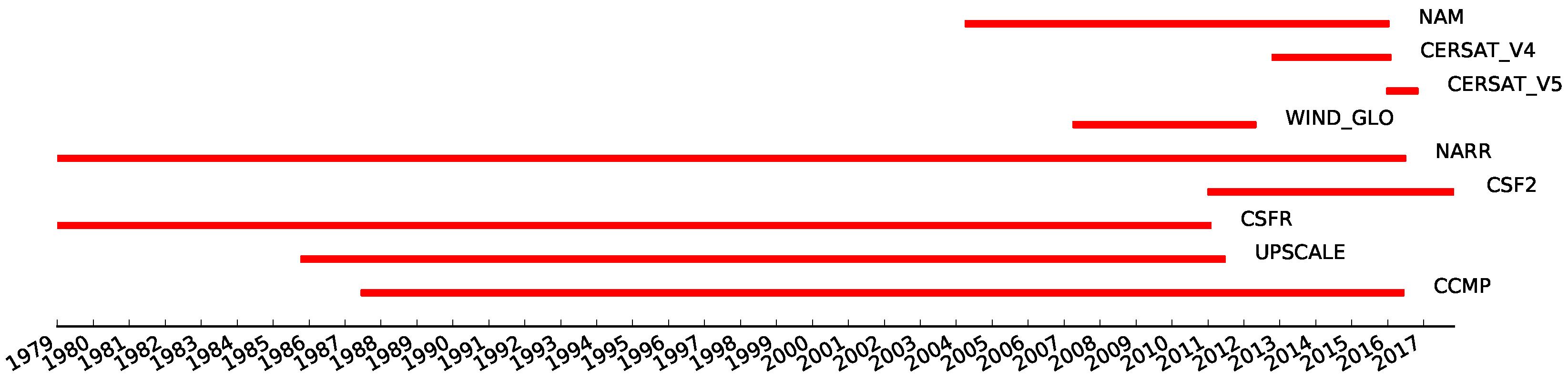
2.3. Surface Wind Climatology
2.3.1. UK on PRACE—Weather-Resolving Simulations of Climate for globAL Environmental Risk (UPSCALE) Dataset
2.3.2. North American Mesoscale Forecast System (NAM)
2.3.3. North American Regional Analysis (NARR)
2.3.4. Cross-Calibrated Multi-Platform (CCMP)
2.3.5. Climate Forecast System Reanalysis (CFSR)
2.3.6. Centre ERS d’Archivage et de Traitement (CERSAT)
2.3.7. Global Ocean (GLO)
2.4. Wind Data Processing
- interpolate the data to a common latitude-longitude grid with grid-spacing, using linear interpolation;
- evaluate the angle of the wind, , for each gridpoint, relative to the mean and its standard deviation , and select the data satisfying the condition:
- from this subset of datasets, select the data with wind speeds, v, satisfying the condition:where, as before, and are the standard deviation and mean of the wind speed across all datasets selected by criteria one, respectively; and
- average the remaining sources.
2.5. Tidal Forcing
3. Verification
3.1. Sea Surface Height
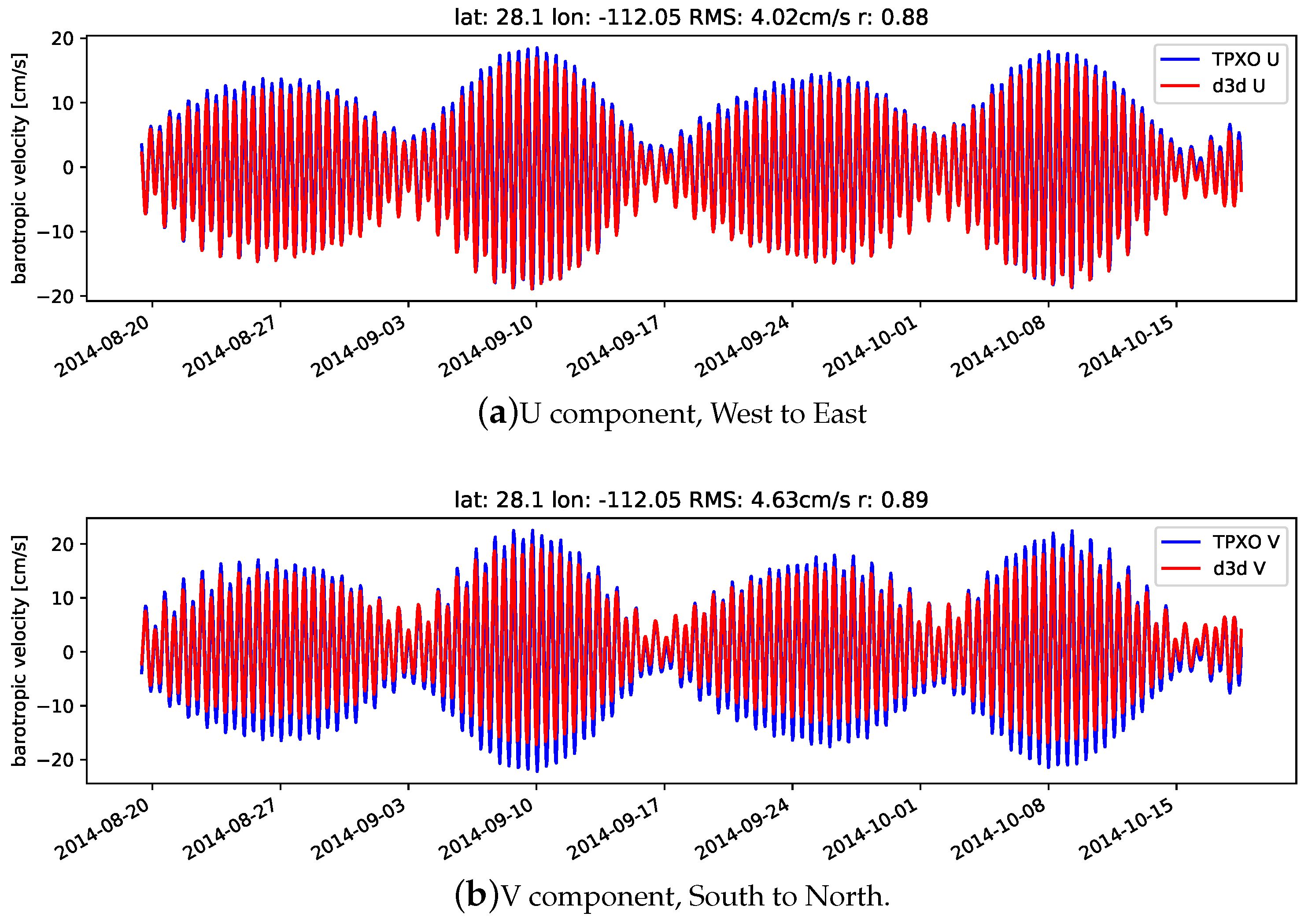
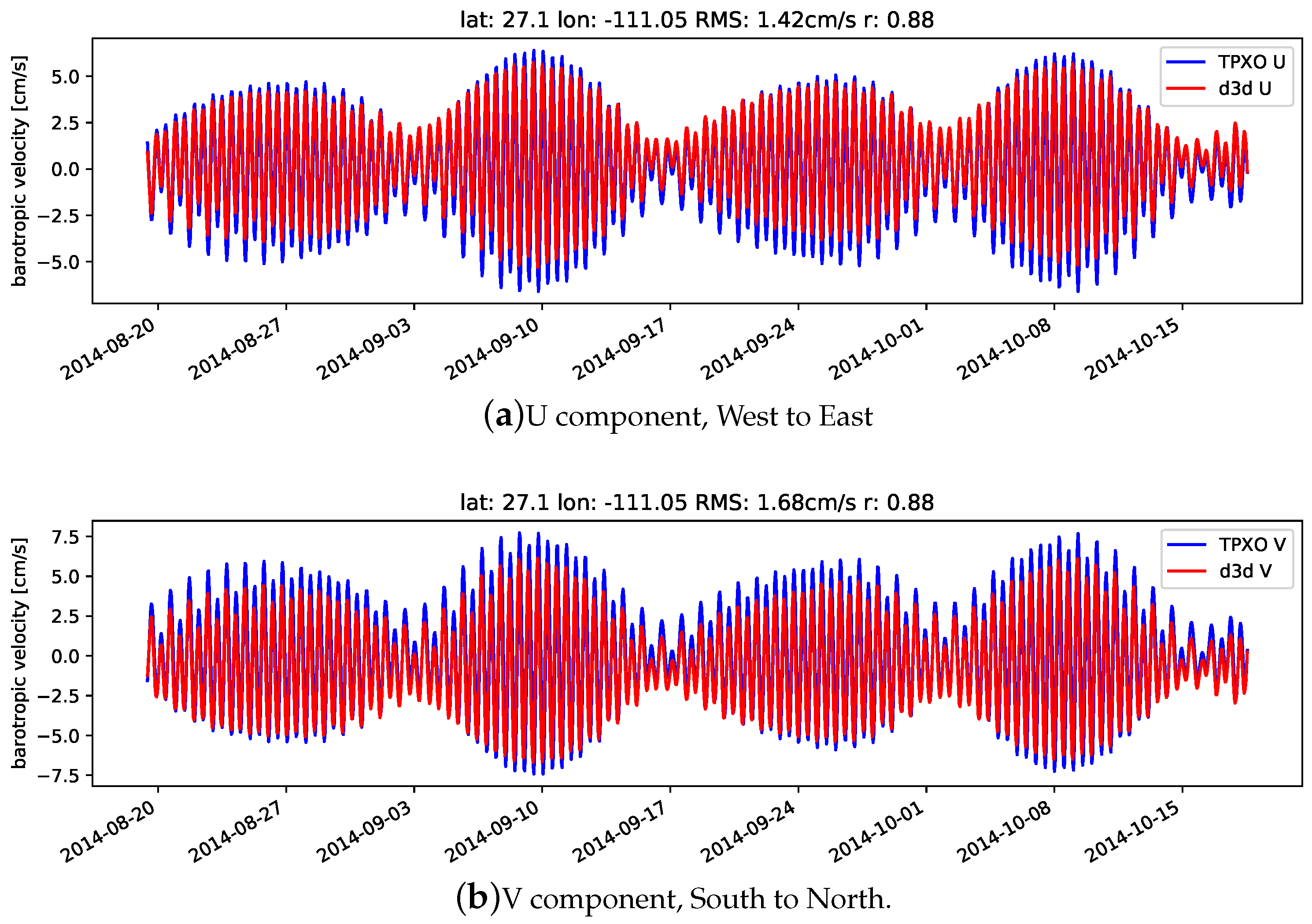
3.2. Currents
4. Results
4.1. Convergence of the Wind Forcing with Vertical Resolution
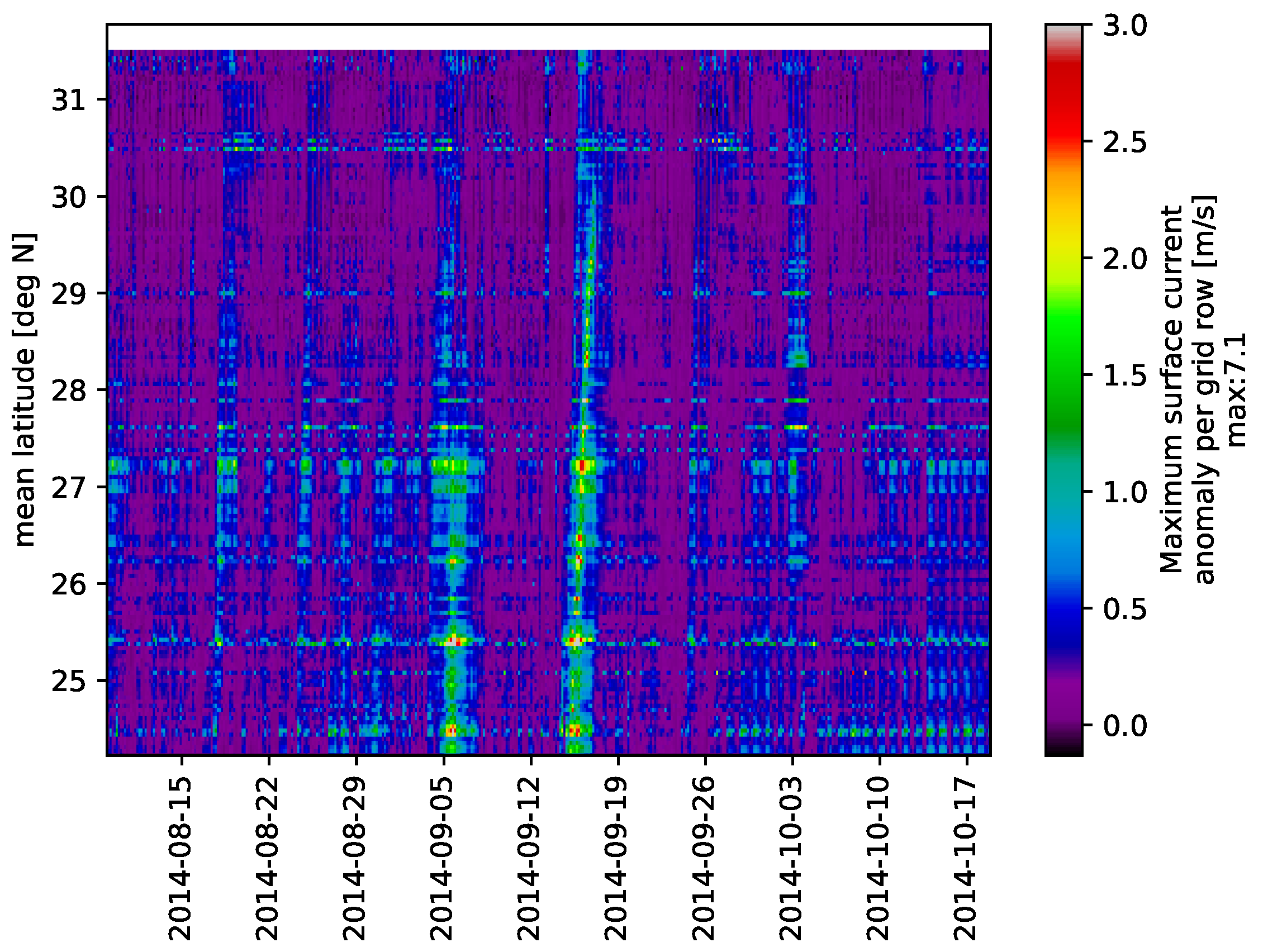
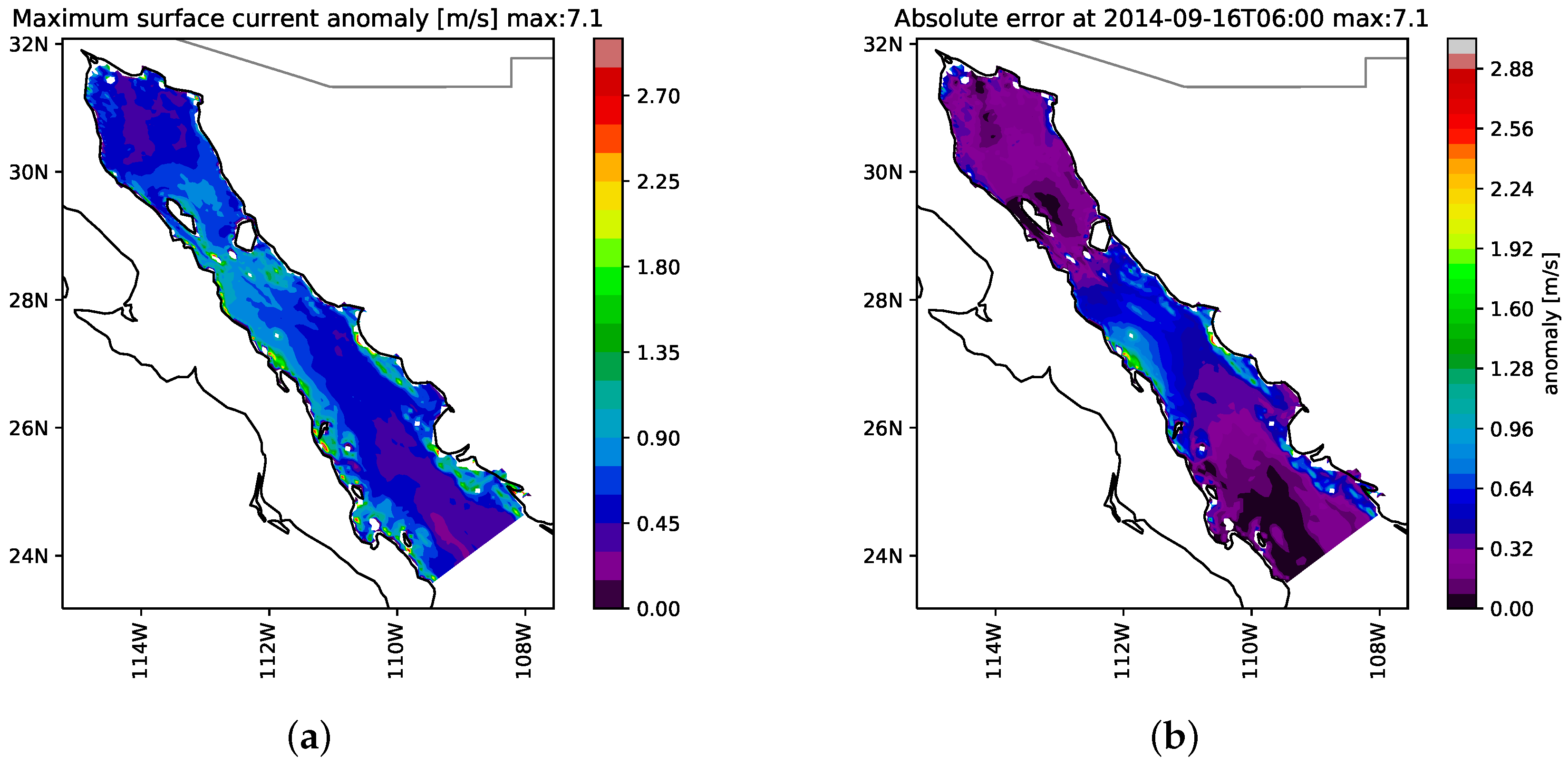
4.2. Maximum Anomaly in Surface Currents
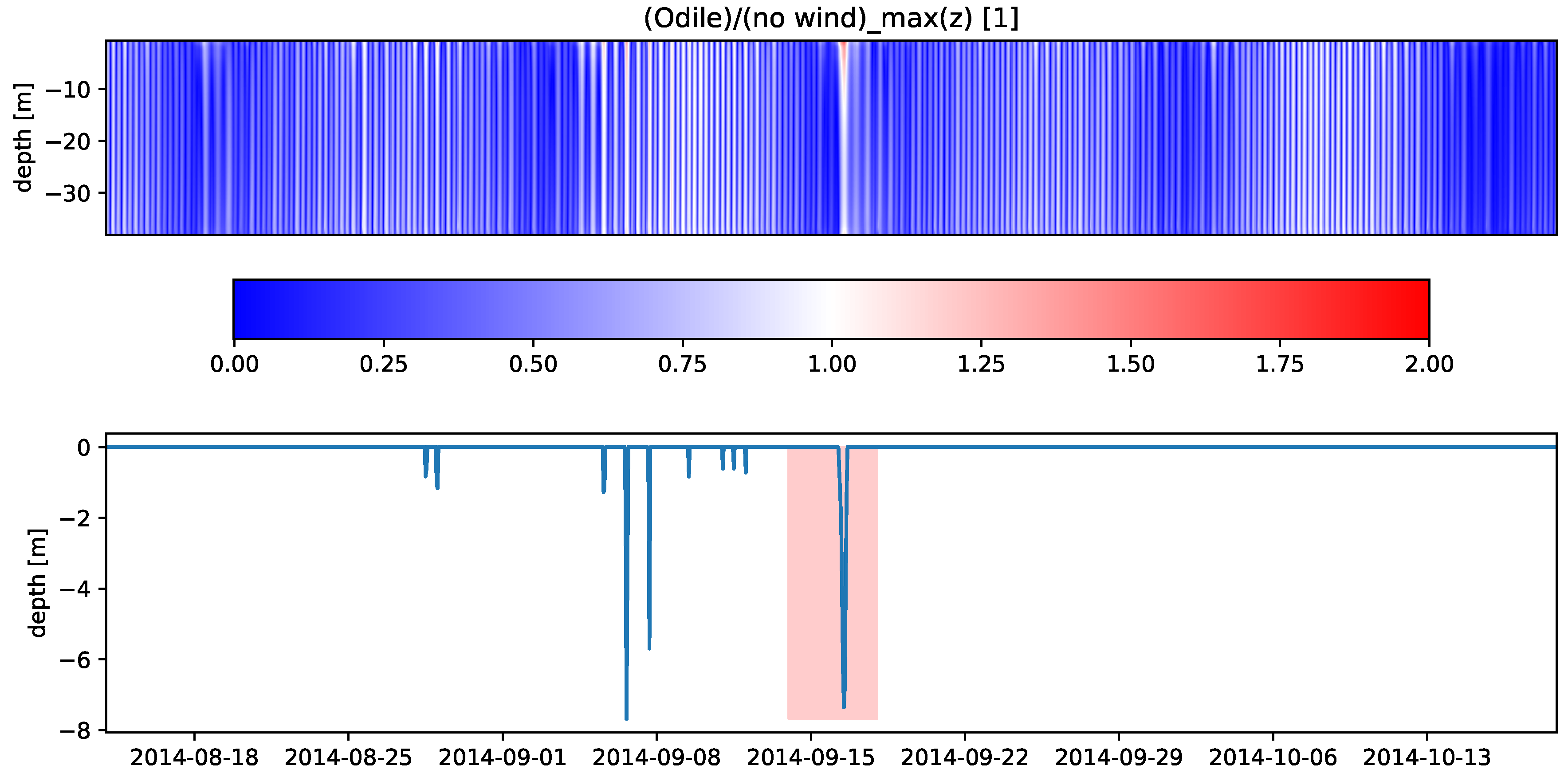
4.2.1. Comparison Odile—No Wind
4.2.2. Wind Climatology Induced Surface Current Anomaly
4.3. Safe Depth
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sinden, G.E. Renewable Electricity Generation: Resource Characteristics and Implications of Wind, Wave and Tidal Stream Power in the UK; Technical Report; UK Department of Energy and Climate Change: London, UK, 2007.
- Roberts, A.; Thomas, B.; Sewell, P.; Khan, Z.; Balmain, S.; Gillman, J. Current tidal power technologies and their suitability for applications in coastal and marine areas. J. Ocean Eng. Mar. Energy 2016, 2, 227–245. [Google Scholar] [CrossRef] [Green Version]
- Cresswell, N.; Ingram, G.; Dominy, R. The impact of diffuser augmentation on a tidal stream turbine. Ocean Eng. 2015, 108, 155–163. [Google Scholar] [CrossRef] [Green Version]
- Segura, E.; Morales, R.; Somolinos, J. Cost Assessment Methodology and Economic Viability of Tidal Energy Projects. Energies 2017, 10, 1806. [Google Scholar] [CrossRef] [Green Version]
- Haas, K.A.; Fritz, H.M.; French, S.P.; Smith, B.T.; Neary, V. Assessment of Energy Production Potential from Tidal Streams in the United States; Technical Report; Georgia Tech Research Corporation: Atlanta, GA, USA, 2011. [Google Scholar]
- Rose, S.; Jaramillo, P.; Small, M.J.; Grossmann, I.; Apt, J. Quantifying the hurricane risk to offshore wind turbines. Proc. Natl. Acad. Sci. USA 2012, 109, 3247–3252. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Black, W.J.; Dickey, T.D. Observations and analyses of upper ocean responses to tropical storms and hurricanes in the vicinity of Bermuda. J. Geophys. Res. 2008, 113, C08009. [Google Scholar] [CrossRef] [Green Version]
- Hiriart Le Bert, G. Potencial energético del Alto Golfo de California. Boletín de la Sociedad Geológica Mexicana 2009, 61, 143–146. [Google Scholar] [CrossRef]
- Carbajal, N.; Backhaus, J.O. Simulation of tides, residual flow and energy budget in the Gulf of California. Oceanol. Acta 1998, 21, 429–446. [Google Scholar] [CrossRef] [Green Version]
- Romero-Vadillo, E.; Zaytsev, O.; Morales-Pérez, R. Tropical cyclone statistics in the Northeastern Pacific. Atmósfera 2007, 20, 197–213. [Google Scholar]
- Cangialosi, J.P.; Kimberlain, T.B. Hurricane Odile (EP152014); Technical Report; National Hurricane Center: Miami, FL, USA, 2015. [Google Scholar]
- Stelling, G.S. On the Construction of Computational Methods for Shallow Water Flow Problems. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1983. [Google Scholar]
- Lavín, M.F.; Marinone, S.G. An Overview of the Physical Oceanography of the Gulf of California. In Nonlinear Processes in Geophysical Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2003; pp. 173–204. [Google Scholar] [CrossRef] [Green Version]
- Phillips, N.A. A Coordinate System having some special advantages for numerical forecasting. J. Meteorol. 1957, 14, 184–185. [Google Scholar] [CrossRef] [Green Version]
- Deltares. Delft3D-FLOW User Manual Version 3.15: Simulation of Multi-Dimensional Hydrodynamic Flows and Transport Phenomena, Including Sediments; Technical Report; Deltares: Delft, The Netherlands, 2018. [Google Scholar]
- Bryant, K.; Akbar, M. An Exploration of Wind Stress Calculation Techniques in Hurricane Storm Surge Modeling. J. Mar. Sci. Eng. 2016, 4, 58. [Google Scholar] [CrossRef]
- Akbar, M.; Kanjanda, S.; Musinguzi, A. Effect of Bottom Friction, Wind Drag Coefficient, and Meteorological Forcing in Hindcast of Hurricane Rita Storm Surge Using SWAN +ADCIRC Model. J. Mar. Sci. Eng. 2017, 5, 38. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.K.; Liu, C.X.; Li, Q.; Dai, G.F.; Song, Q.T.; Lv, W.H. Typhoon air-sea drag coefficient in coastal regions. J. Geophys. Res. Oceans 2015, 120, 716–727. [Google Scholar] [CrossRef]
- Bordoni, S.; Ciesielski, P.E.; Johnson, R.H.; McNoldy, B.D.; Stevens, B. The low-level circulation of the North American Monsoon as revealed by QuikSCAT. Geophys. Res. Lett. 2004, 31, L10109. [Google Scholar] [CrossRef] [Green Version]
- Badan-Dangon, A.; Dorman, C.E.; Merrifield, M.A.; Winant, C.D. The lower atmosphere over the Gulf of California. J. Geophys. Res. 1991, 96, 16877. [Google Scholar] [CrossRef]
- Douglas, M.W. The Summertime Low-Level Jet over the Gulf of California. Mon. Weather Rev. 1995, 123, 2334–2347. [Google Scholar] [CrossRef] [Green Version]
- Mizielinski, M.S.; Roberts, M.J.; Vidale, P.L.; Schiemann, R.; Demory, M.E.; Strachan, J.; Edwards, T.; Stephens, A.; Lawrence, B.N.; Pritchard, M.; et al. High-resolution global climate modelling: The UPSCALE project, a large-simulation campaign. Geosci. Mod. Dev. 2014, 7, 1629–1640. [Google Scholar] [CrossRef] [Green Version]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- Walters, D.N.; Best, M.J.; Bushell, A.C.; Copsey, D.; Edwards, J.M.; Falloon, P.D.; Harris, C.M.; Lock, A.P.; Manners, J.C.; Morcrette, C.J.; et al. The Met Office Unified Model Global Atmosphere 3.0/3.1 and JULES Global Land 3.0/3.1 configurations. Geosci. Mod. Dev. 2011, 4, 919–941. [Google Scholar] [CrossRef] [Green Version]
- Black, T.L. The New NMC Mesoscale Eta Model: Description and Forecast Examples. Weather Forecast. 1994, 9, 265–278. [Google Scholar] [CrossRef] [Green Version]
- Mesinger, F.; DiMego, G.; Kalnay, E.; Mitchell, K.; Shafran, P.C.; Ebisuzaki, W.; Jović, D.; Woollen, J.; Rogers, E.; Berbery, E.H.; et al. North American Regional Reanalysis. Bull. Am. Meteorol. Soc. 2006, 87, 343–360. [Google Scholar] [CrossRef] [Green Version]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP–DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Atlas, R.; Hoffman, R.N.; Bloom, S.C.; Jusem, J.C.; Ardizzone, J. A Multiyear Global Surface Wind Velocity Dataset Using SSM/I Wind Observations. Bull. Am. Meteorol. Soc. 1996, 77, 869–882. [Google Scholar] [CrossRef] [Green Version]
- Atlas, R.; Hoffman, R.N.; Ardizzone, J.; Leidner, S.M.; Jusem, J.C.; Smith, D.K.; Gombos, D. A Cross-calibrated, Multiplatform Ocean Surface Wind Velocity Product for Meteorological and Oceanographic Applications. Bull. Am. Meteorol. Soc. 2011, 92, 157–174. [Google Scholar] [CrossRef]
- Hoffman, R.N.; Leidner, S.M.; Henderson, J.M.; Atlas, R.; Ardizzone, J.V.; Bloom, S.C. A Two-Dimensional Variational Analysis Method for NSCAT Ambiguity Removal: Methodology, Sensitivity, and Tuning. J. Atmos. Ocean. Technol. 2003, 20, 585–605. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP Climate Forecast System Reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef]
- Bentamy, A.; Fillon, D.C. Gridded surface wind fields from Metop/ASCAT measurements. Int. J. Remote Sens. 2011, 33, 1729–1754. [Google Scholar] [CrossRef] [Green Version]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef] [Green Version]
- Marinone, S.; González, J.; Figueroa, J. Prediction of currents and sea surface elevation in the Gulf of California from tidal to seasonal scales. Environ. Mod. Softw. 2009, 24, 140–143. [Google Scholar] [CrossRef]
- FES2014 Was Produced by Noveltis, Legos and CLS and Distributed by Aviso+, with Support from CNES. Available online: https://www.aviso.altimetry.fr/ (accessed on 2 August 2019).
- Khare, V.; Khare, C.; Nema, S.; Baredar, P. Tidal Energy Systems: Design, Optimization and Control; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Chen, L.; Lam, W.H. A review of survivability and remedial actions of tidal current turbines. Renew. Sustain. Energy Rev. 2015, 43, 891–900. [Google Scholar] [CrossRef] [Green Version]







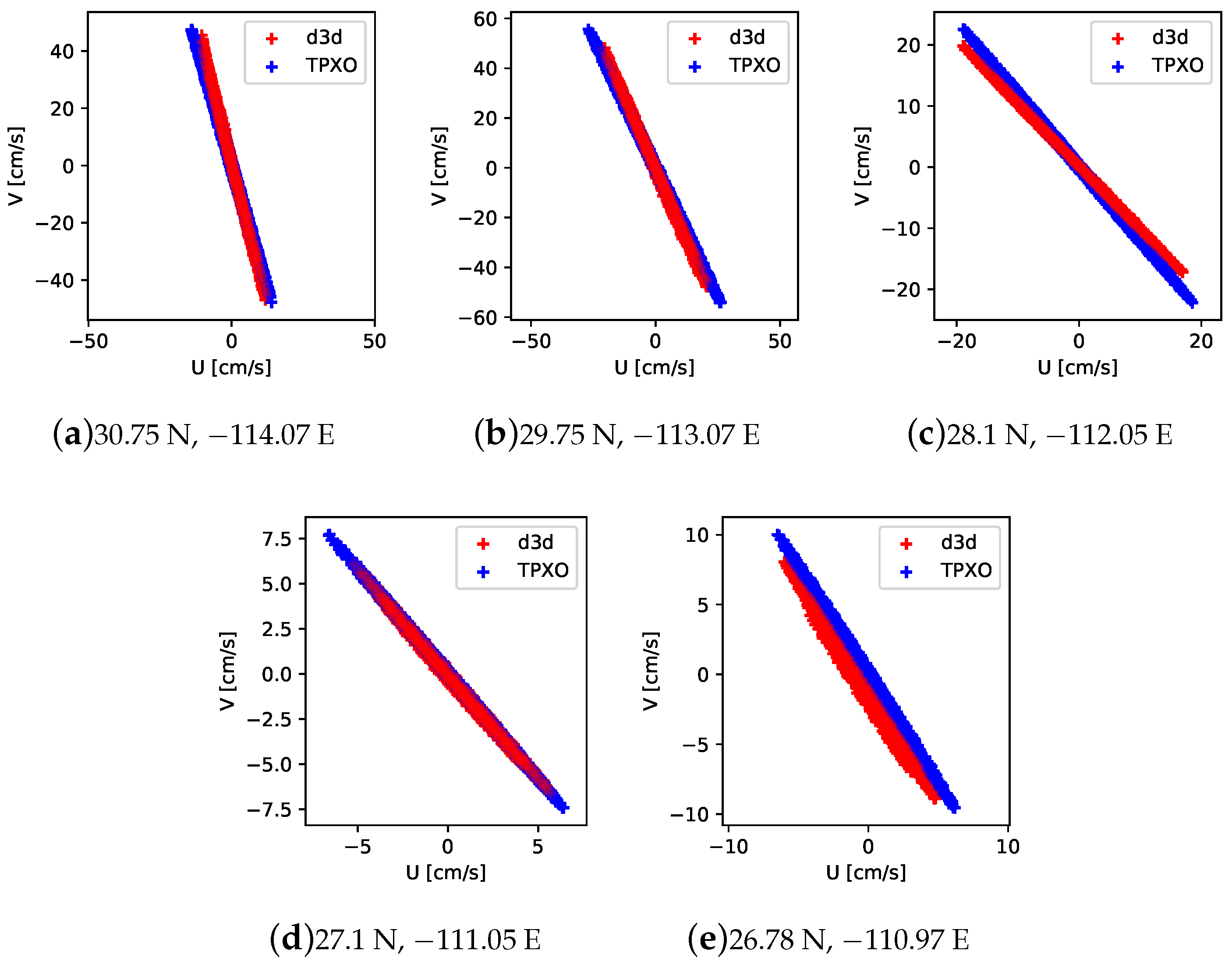







| Latitude | Longitude | RMS GulfCal-d3d [m] | RMS FES-d3d [m] | r GulfCal-d3d | r FES-d3d |
|---|---|---|---|---|---|
| 30.73 | −114.07 | 0.23 | 1.14 | 0.986 | 0.309 |
| 28.10 | −112.04 | 0.14 | 0.06 | 0.919 | 0.959 |
| 26.36 | −110.67 | 0.13 | 0.04 | 0.977 | 0.988 |
| 24.65 | −109.42 | 0.13 | 0.04 | 0.990 | 0.996 |
| Vertical Level | run 1 | run 2 | … | run 7 | run 8 | run 9 | run 10 |
|---|---|---|---|---|---|---|---|
| 34 | … | 0.010 | |||||
| 33 | … | 0.016 | 0.010 | ||||
| 32 | … | 0.031 | 0.016 | 0.020 | |||
| 31 | … | 0.063 | 0.031 | 0.031 | 0.040 | ||
| 30 | … | 0.063 | 0.063 | 0.062 | 0.080 | ||
| 29 | … | 0.125 | 0.125 | 0.125 | 0.160 | ||
| 28 | … | 0.250 | 0.250 | 0.250 | 0.320 | ||
| 27 | … | 0.500 | 0.500 | 0.500 | 0.640 | ||
| 26 | 2.0 | … | 1.000 | 1.000 | 1.000 | 1.280 | |
| 25 | 4.0 | 2.0 | … | 2.000 | 2.000 | 2.000 | 1.440 |
| 24 | 4.0 | 4.0 | … | 4.000 | 4.000 | 4.000 | 4.000 |
| … | … | … | … | … | … | … | … |
| 1 | 4.0 | 4.0 | … | 4.000 | 4.000 | 4.000 | 4.000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gross, M.; Magar, V. Wind-Induced Currents in the Gulf of California from Extreme Events and Their Impact on Tidal Energy Devices. J. Mar. Sci. Eng. 2020, 8, 80. https://doi.org/10.3390/jmse8020080
Gross M, Magar V. Wind-Induced Currents in the Gulf of California from Extreme Events and Their Impact on Tidal Energy Devices. Journal of Marine Science and Engineering. 2020; 8(2):80. https://doi.org/10.3390/jmse8020080
Chicago/Turabian StyleGross, Markus, and Vanesa Magar. 2020. "Wind-Induced Currents in the Gulf of California from Extreme Events and Their Impact on Tidal Energy Devices" Journal of Marine Science and Engineering 8, no. 2: 80. https://doi.org/10.3390/jmse8020080
APA StyleGross, M., & Magar, V. (2020). Wind-Induced Currents in the Gulf of California from Extreme Events and Their Impact on Tidal Energy Devices. Journal of Marine Science and Engineering, 8(2), 80. https://doi.org/10.3390/jmse8020080






