Hydrodynamic Response of a Combined Wind–Wave Marine Energy Structure
Abstract
:1. Introduction
2. Theoretical Background Used for the Development of the Numerical Mode
2.1. Potential Flow Theory
2.2. Viscous Load Modeling
2.2.1. Morison Equation (Cylinders of the Semisubmersible Platform)
2.2.2. Heave Mode Viscous Load Effects on the WEC
2.3. Equation of Motion of the Combined Structure
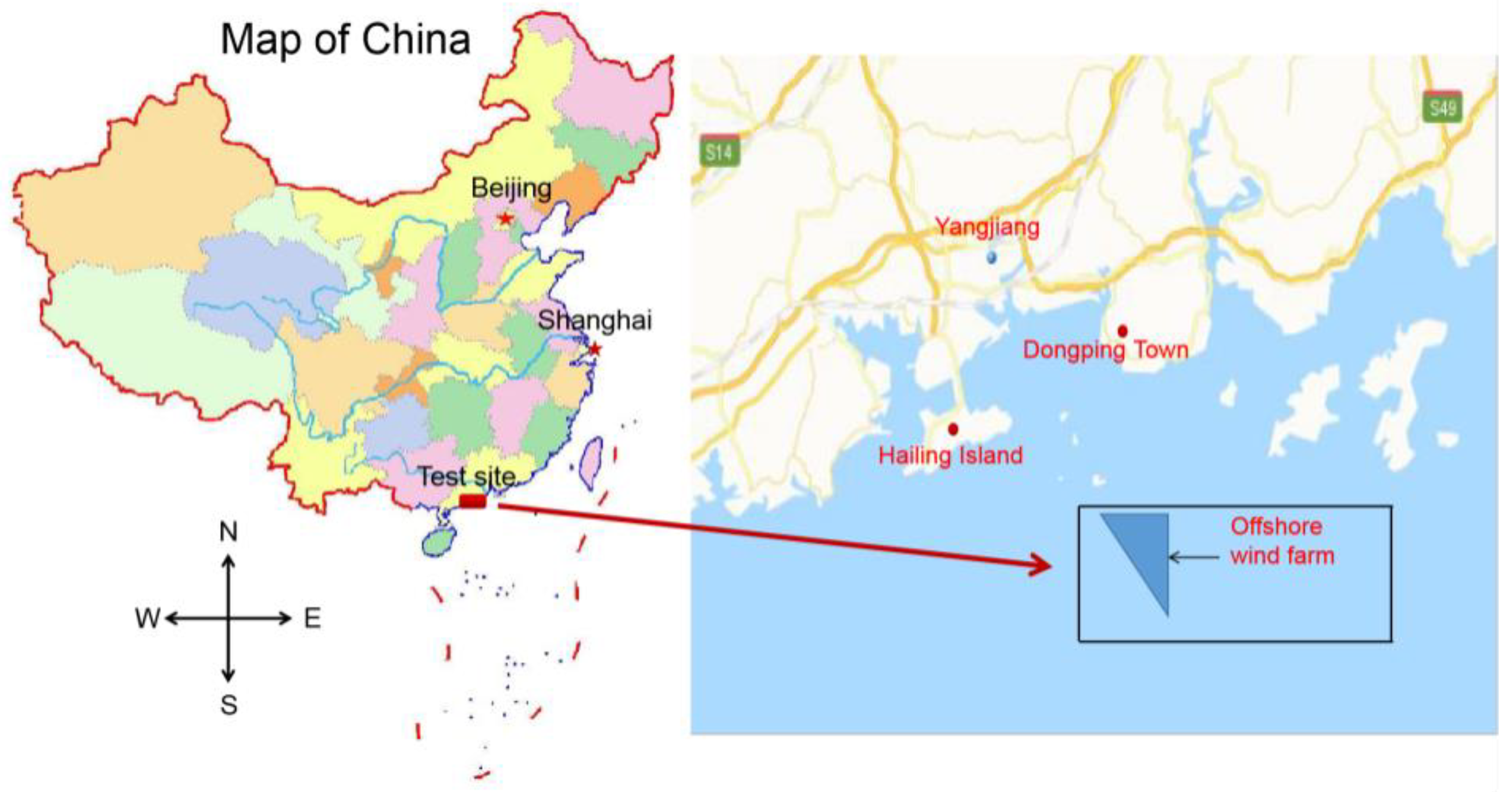
3. Characteristics of the Combined Structure
3.1. Design Parameters of the 5-MW Semisubmersible Wind Turbine and of the WEC
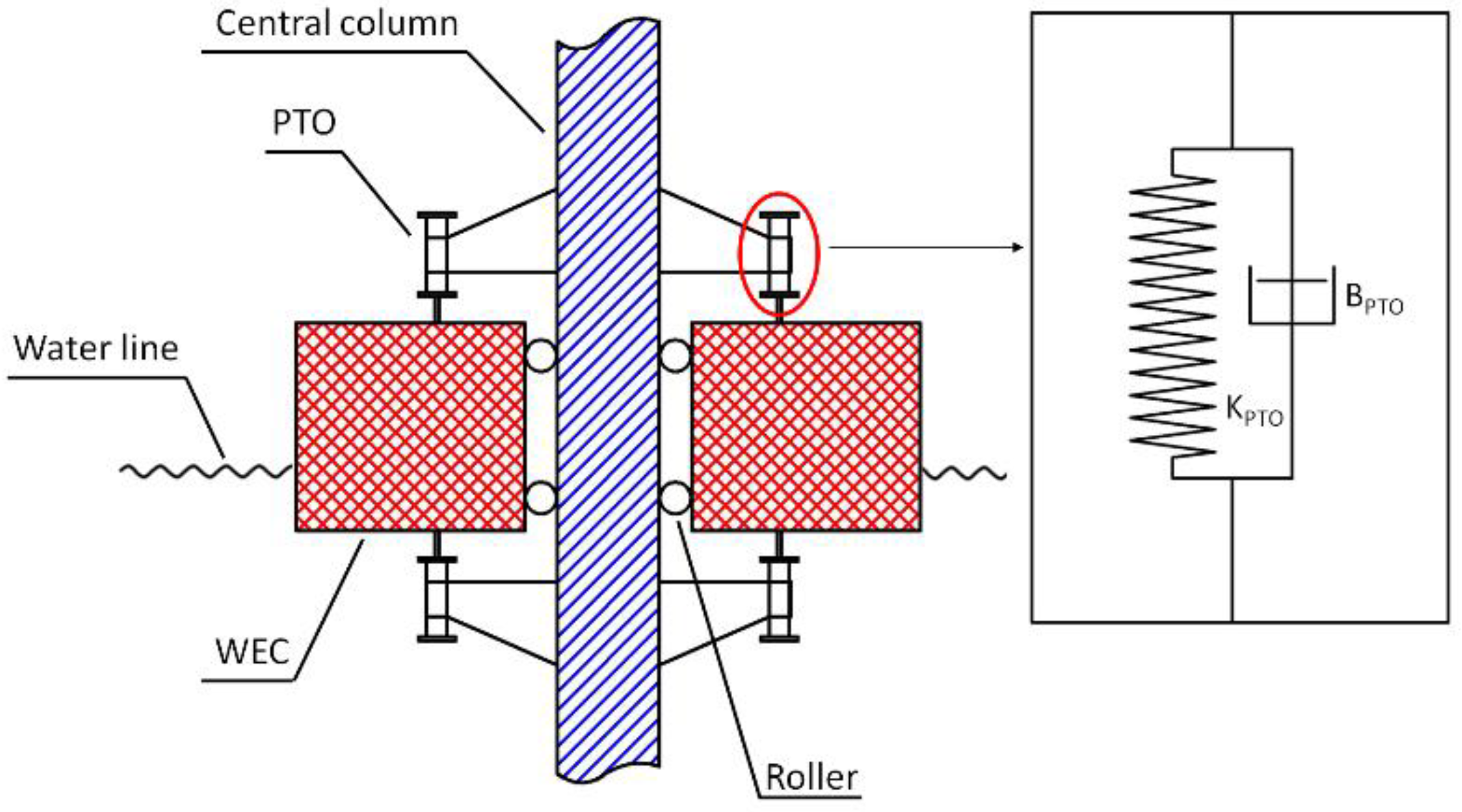
3.2. Power-Take-Off (PTO) System
4. Results and Discussion
4.1. Model Parameters Best Selection
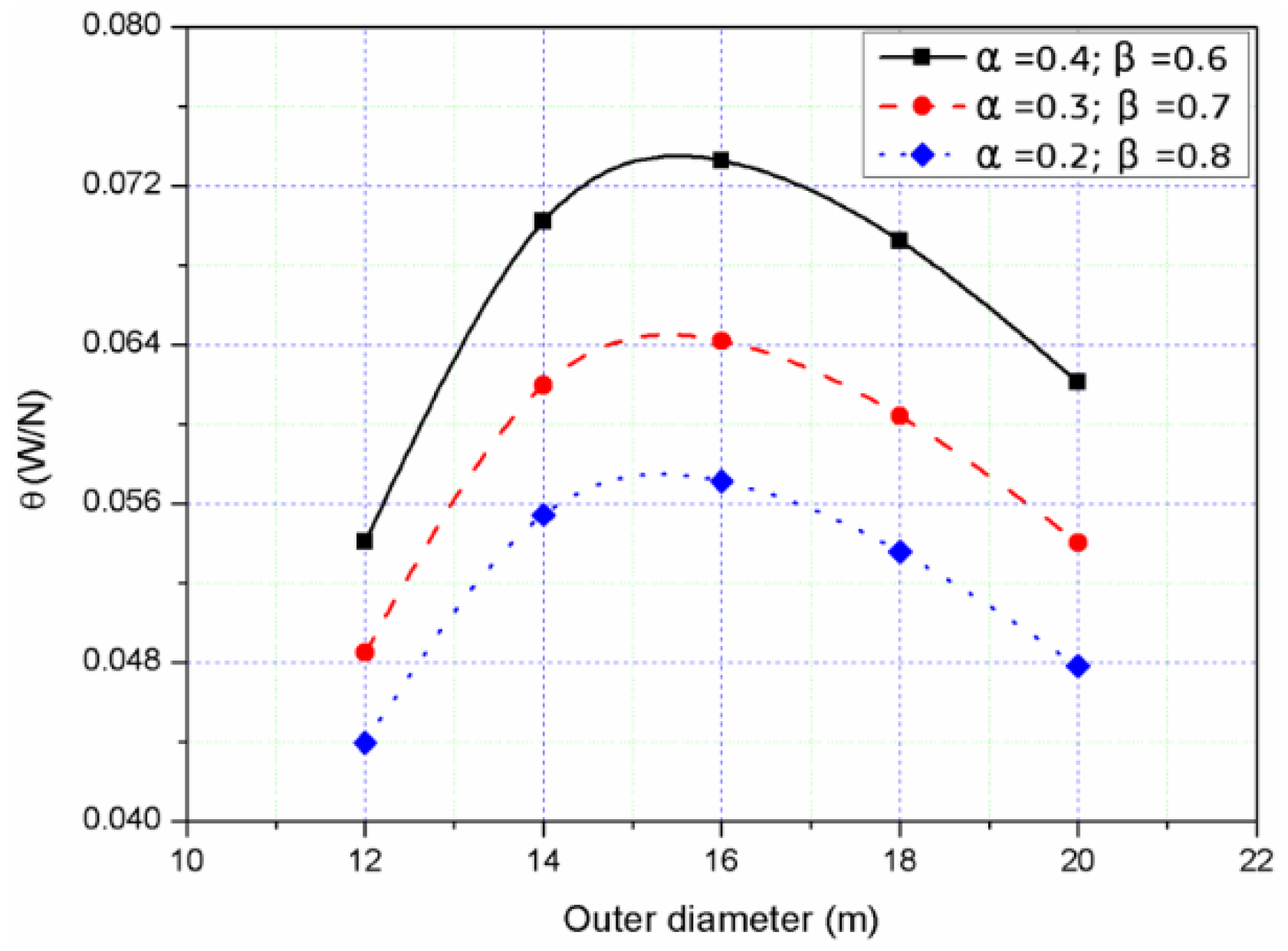
4.1.1. Preliminary Determination of Structural Design Parameters of the WEC
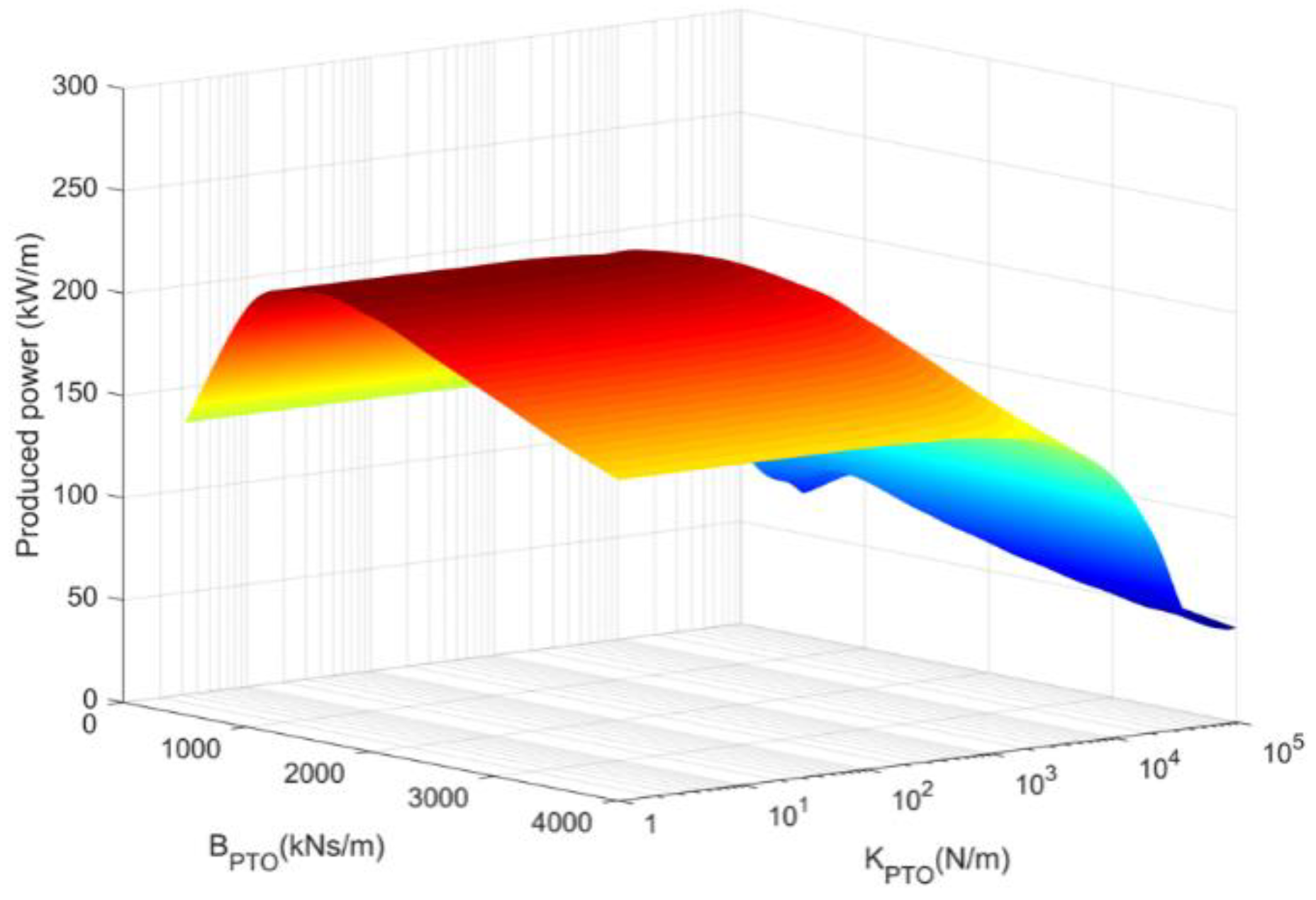
4.1.2. Determination of Rational BPTO and KPTO Parameters
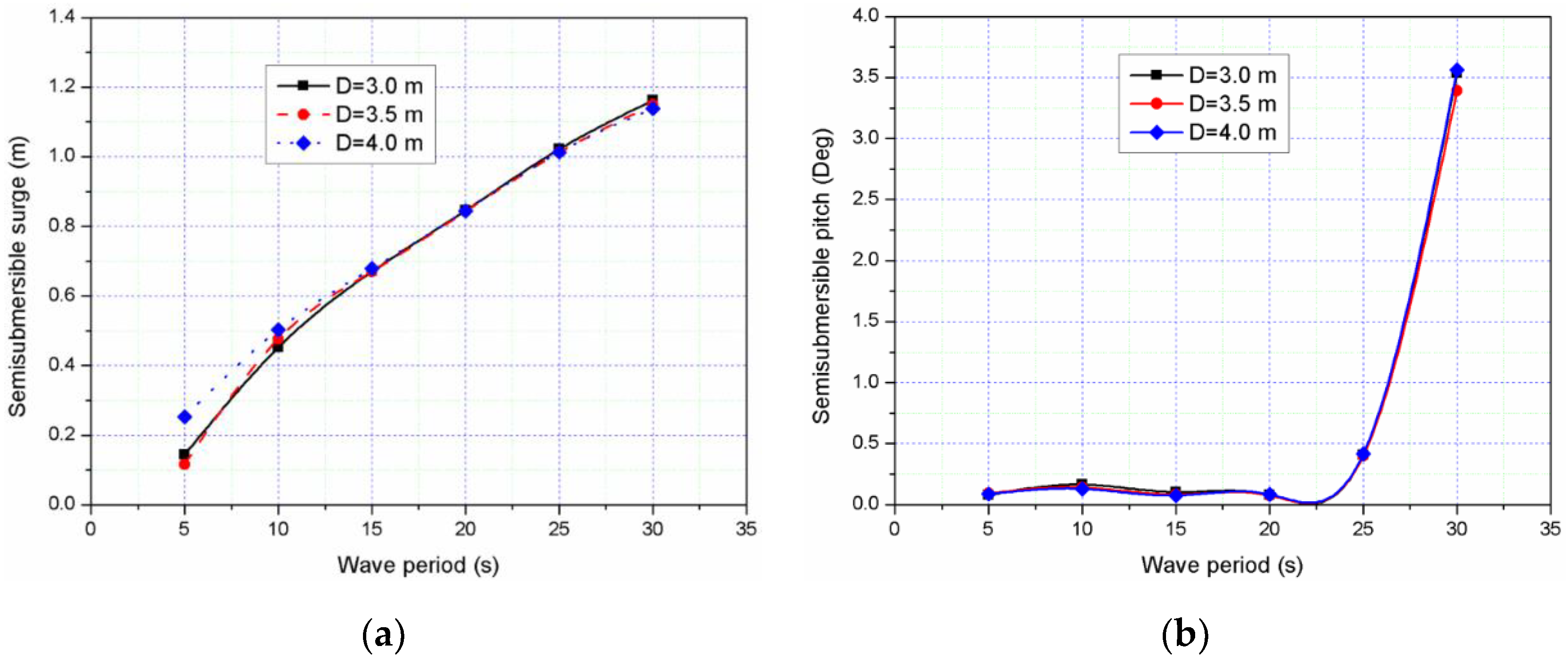
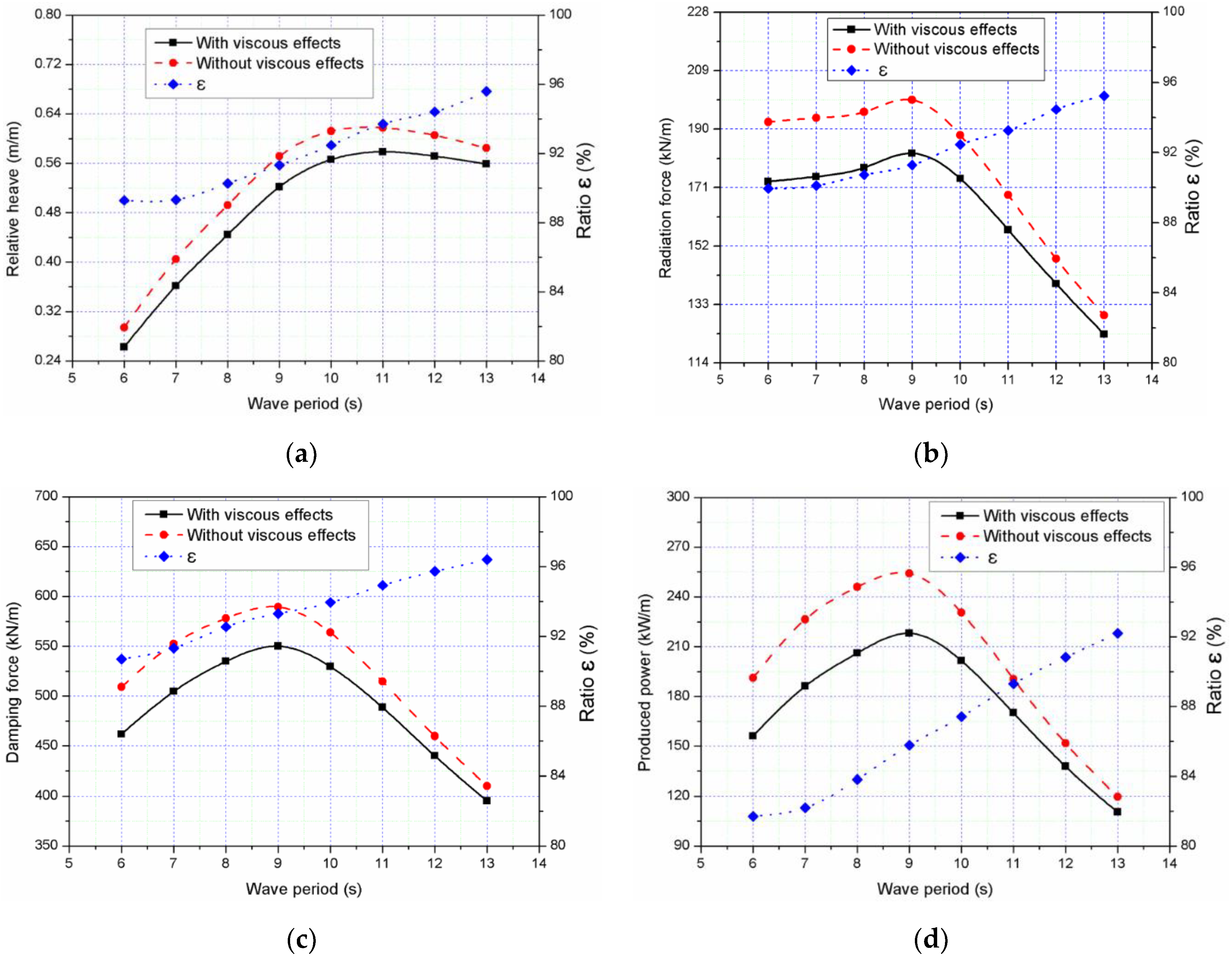
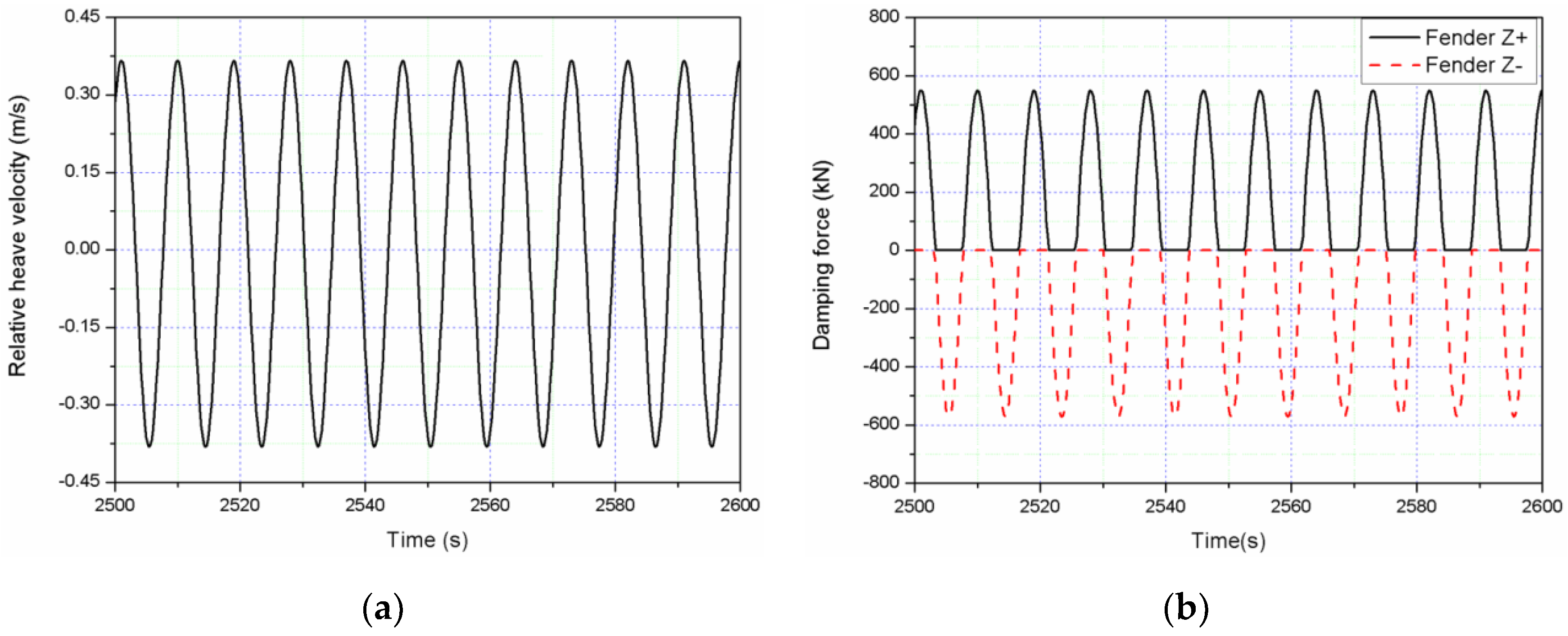
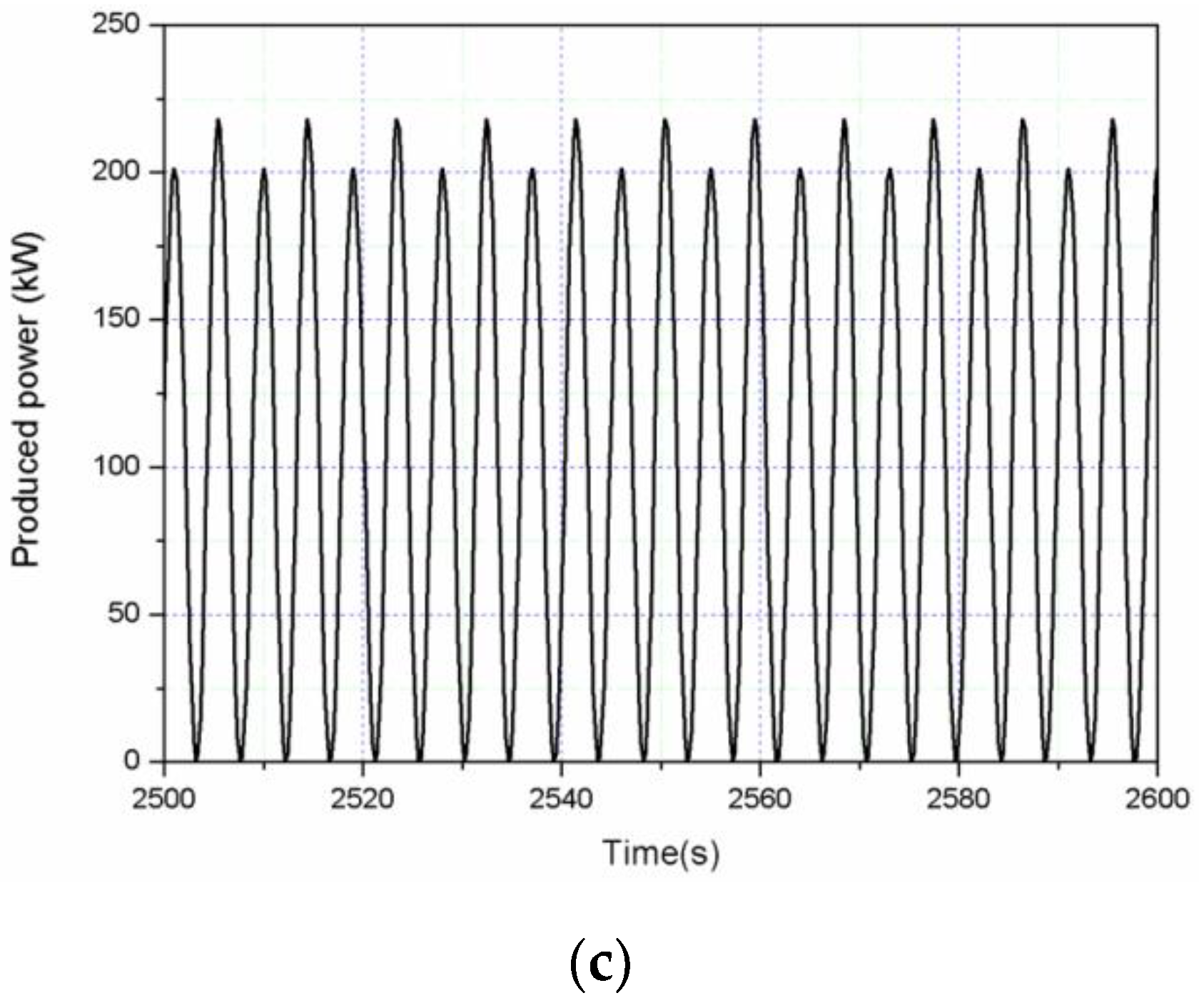
4.2. Viscous Effects on the Heave Motion of the WEC
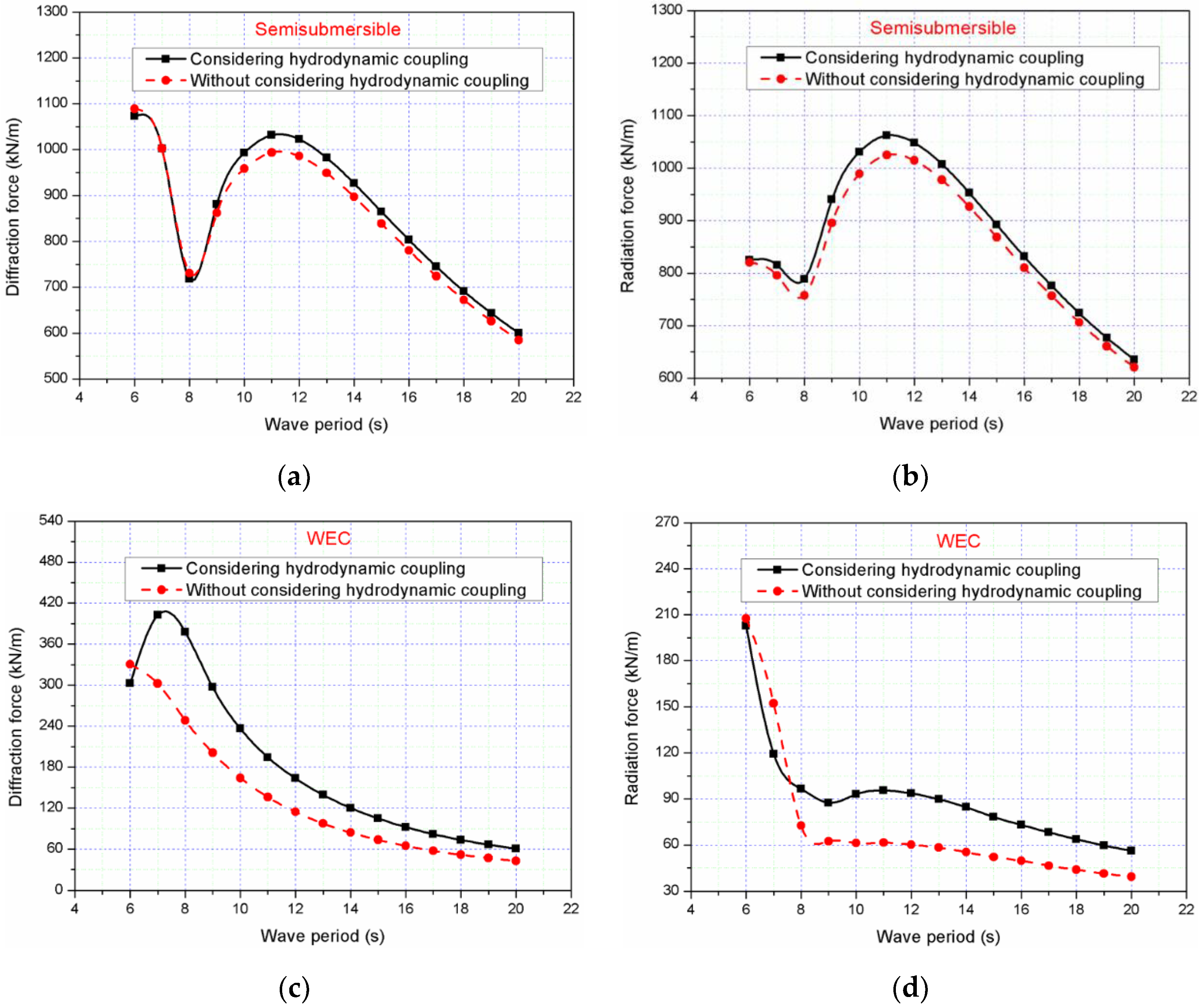
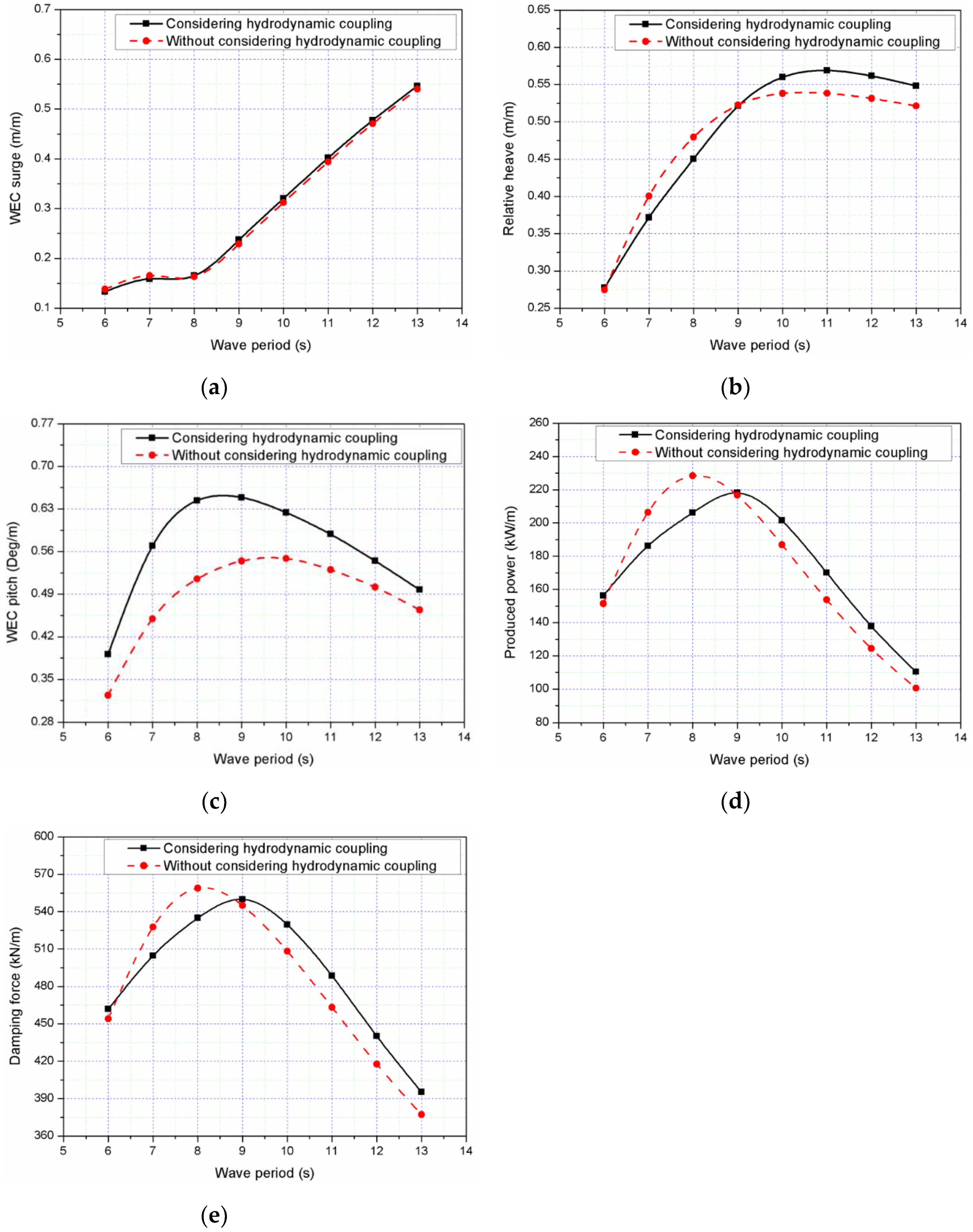
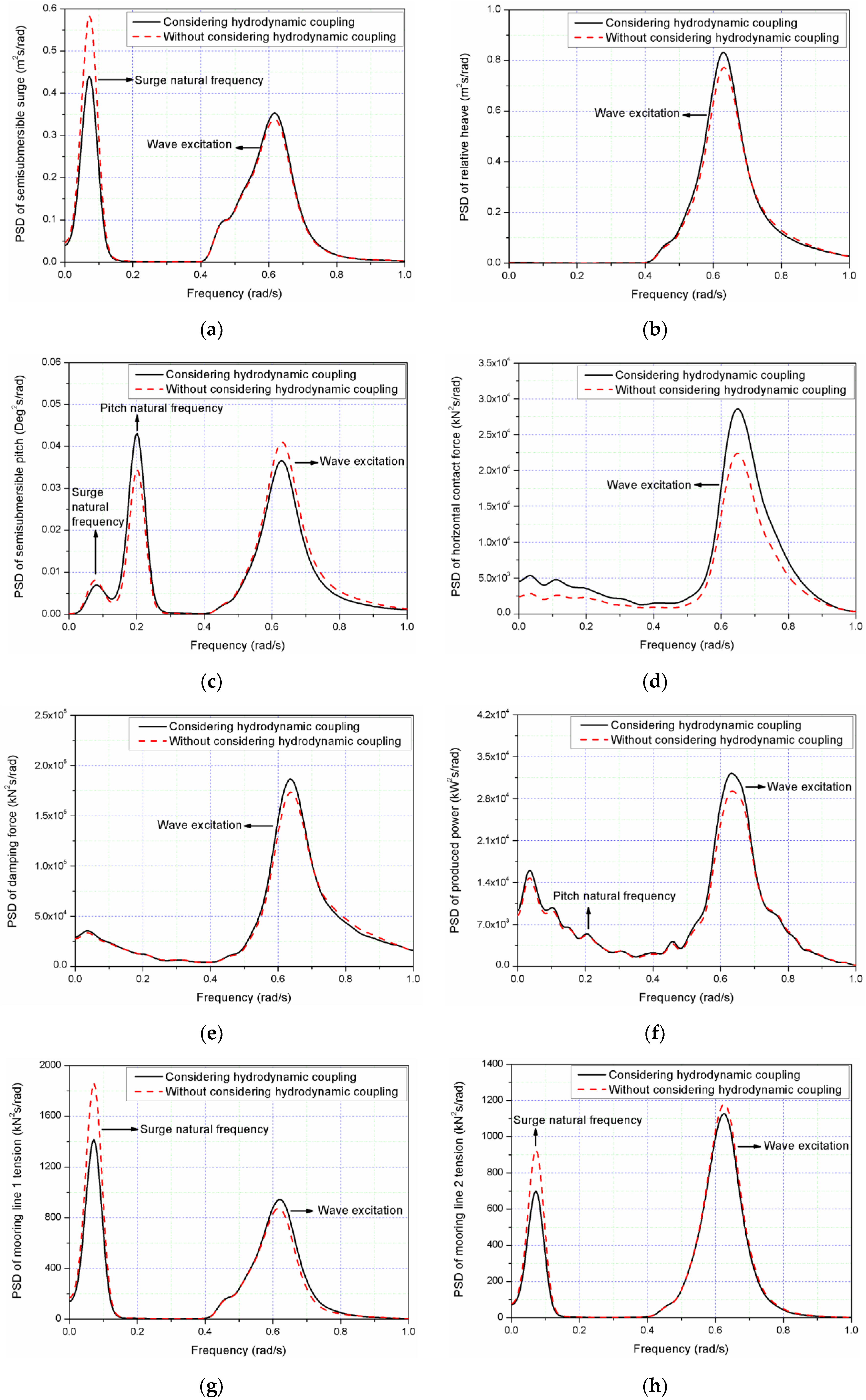
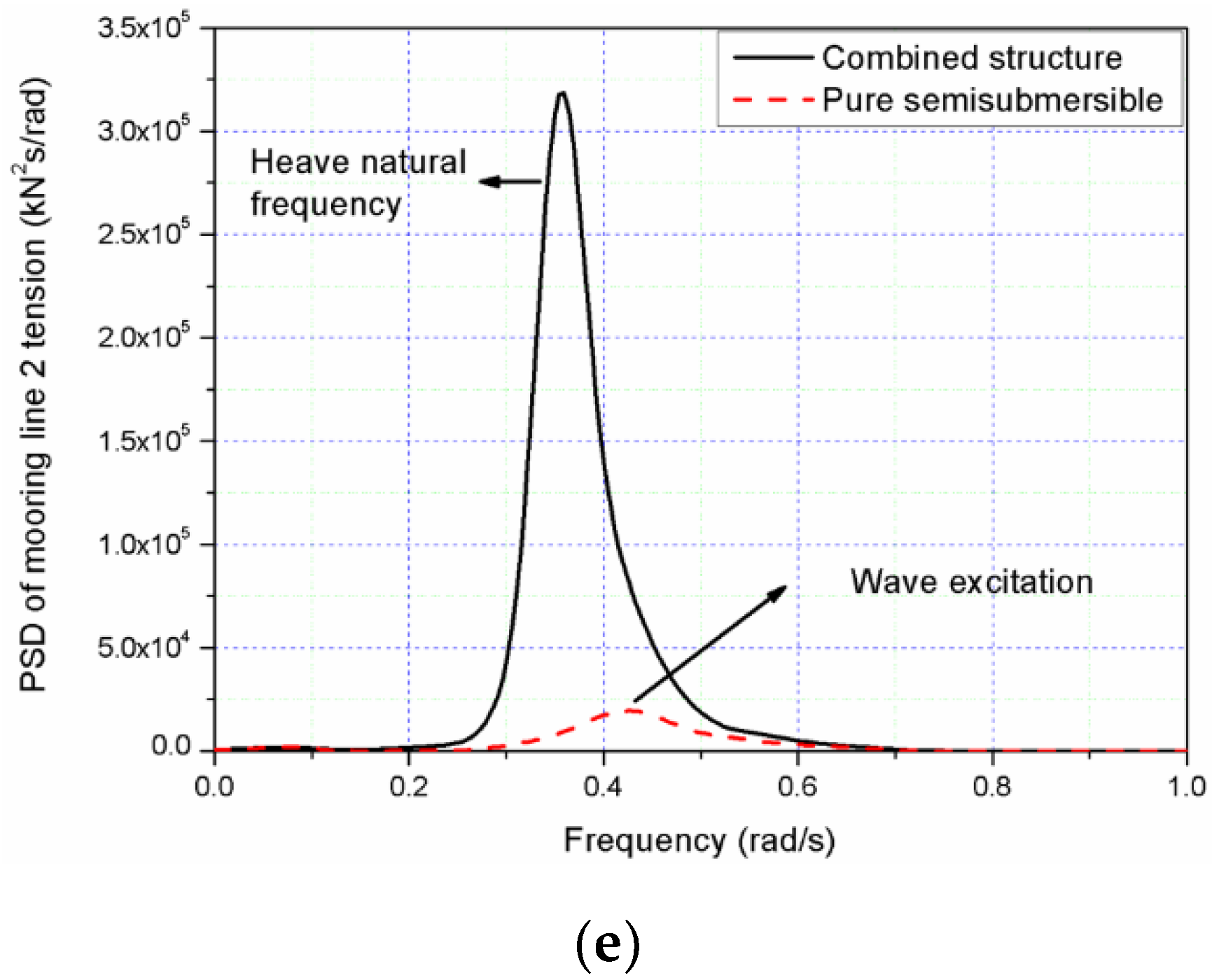
4.3. The Hydrodynamic Coupling Effect on the Combined Structure
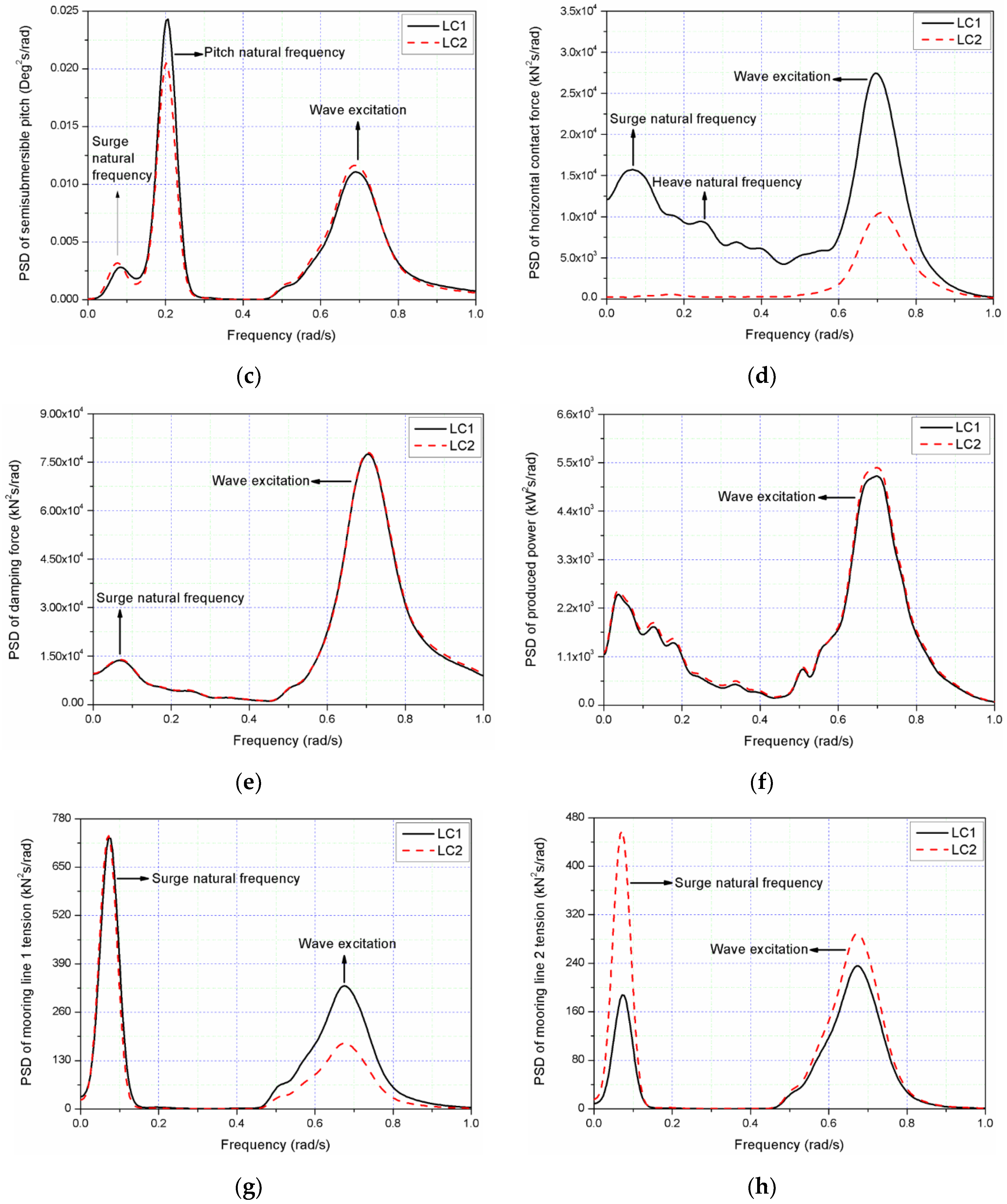
4.4. Dynamic Responses of the Combined Structure under Different Type Environmental Conditions
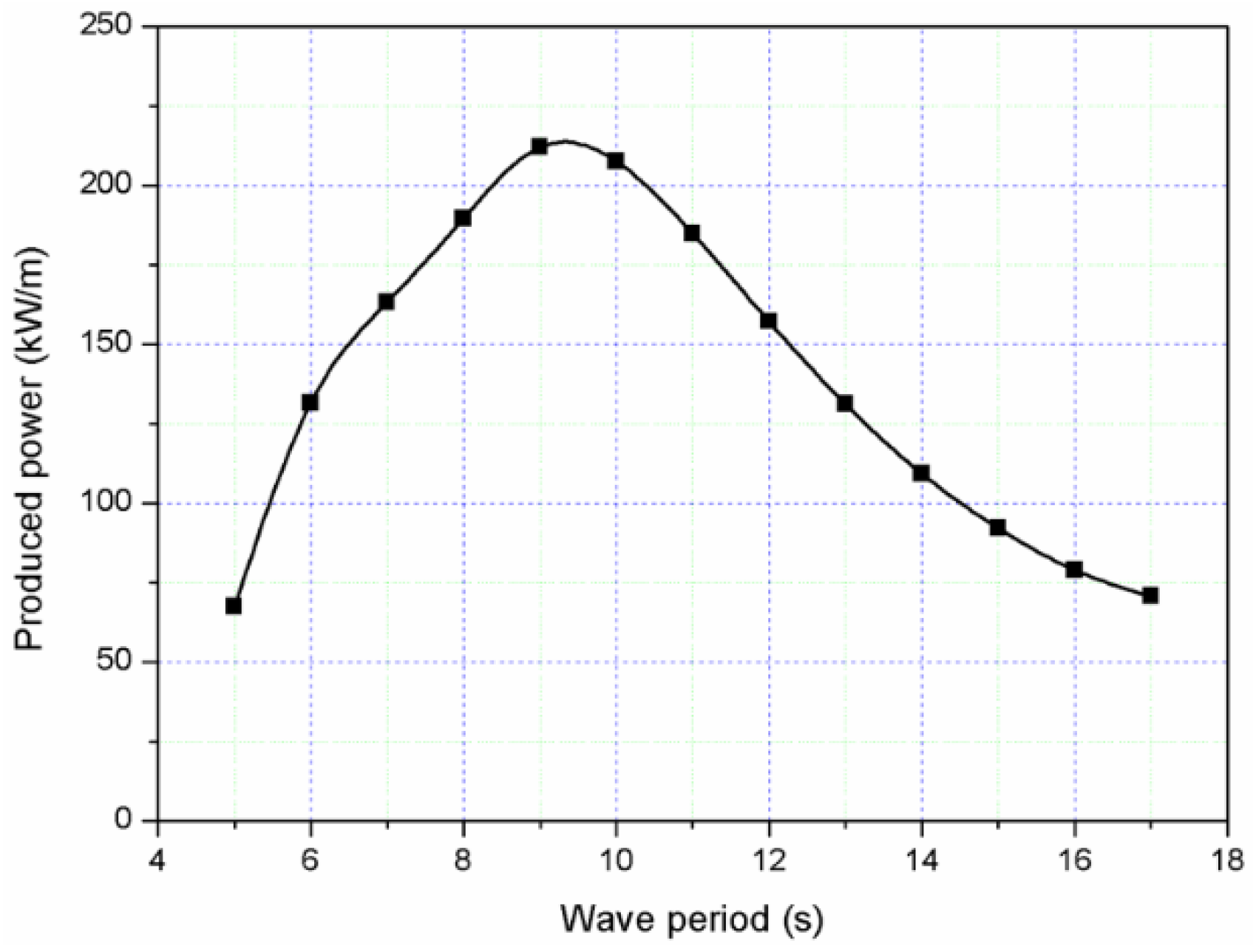
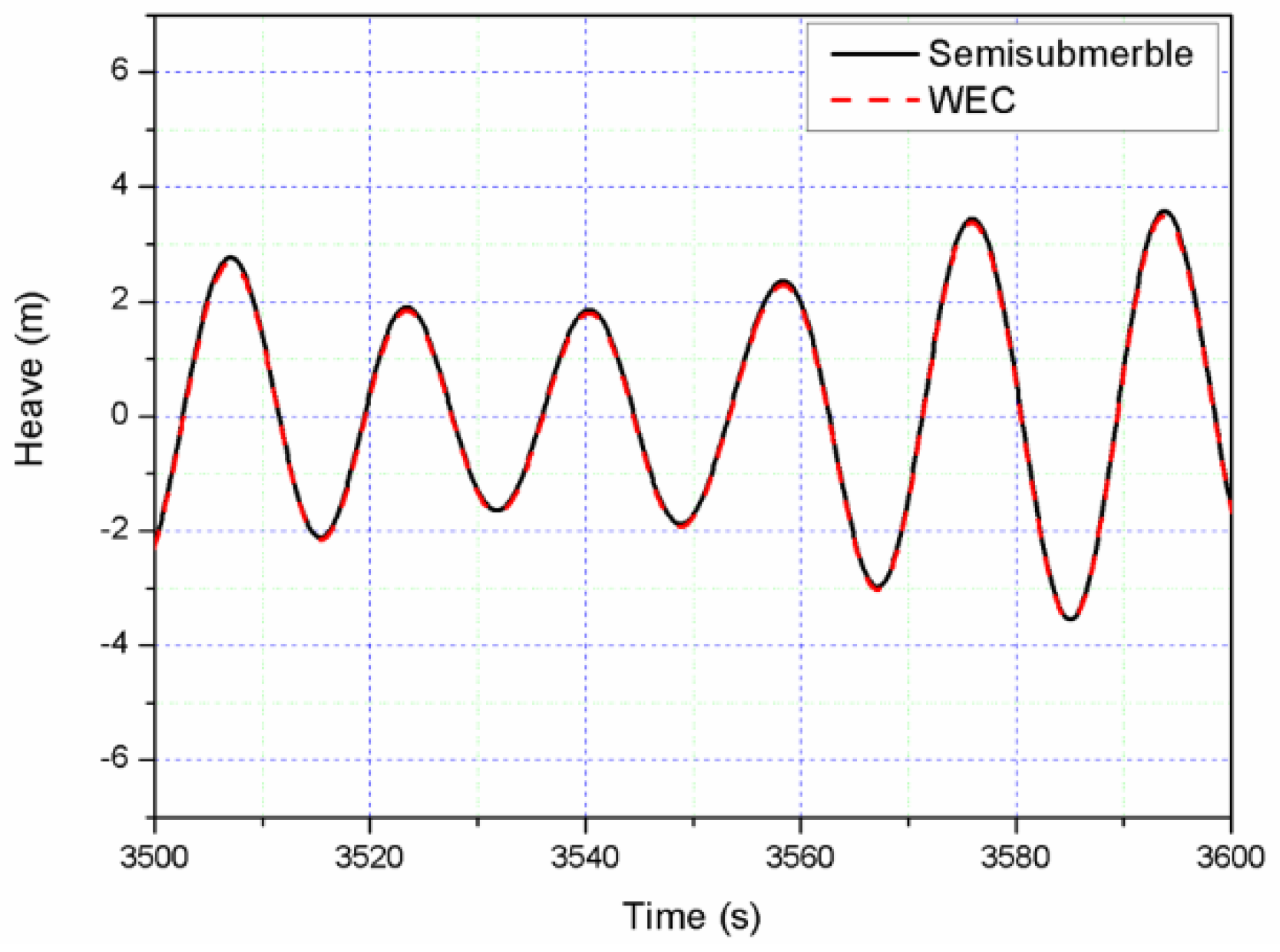
4.4.1. Regular Waves
4.4.2. Irregular Wave and Wind Conditions
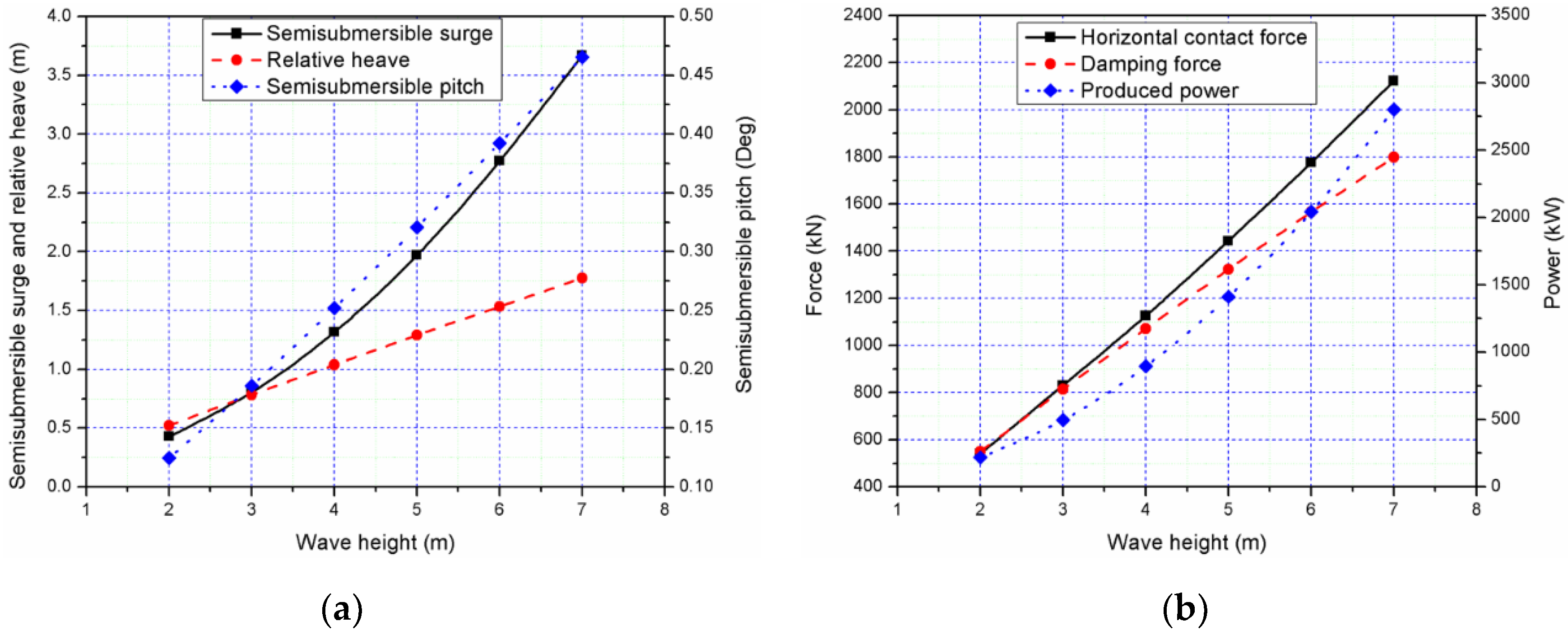
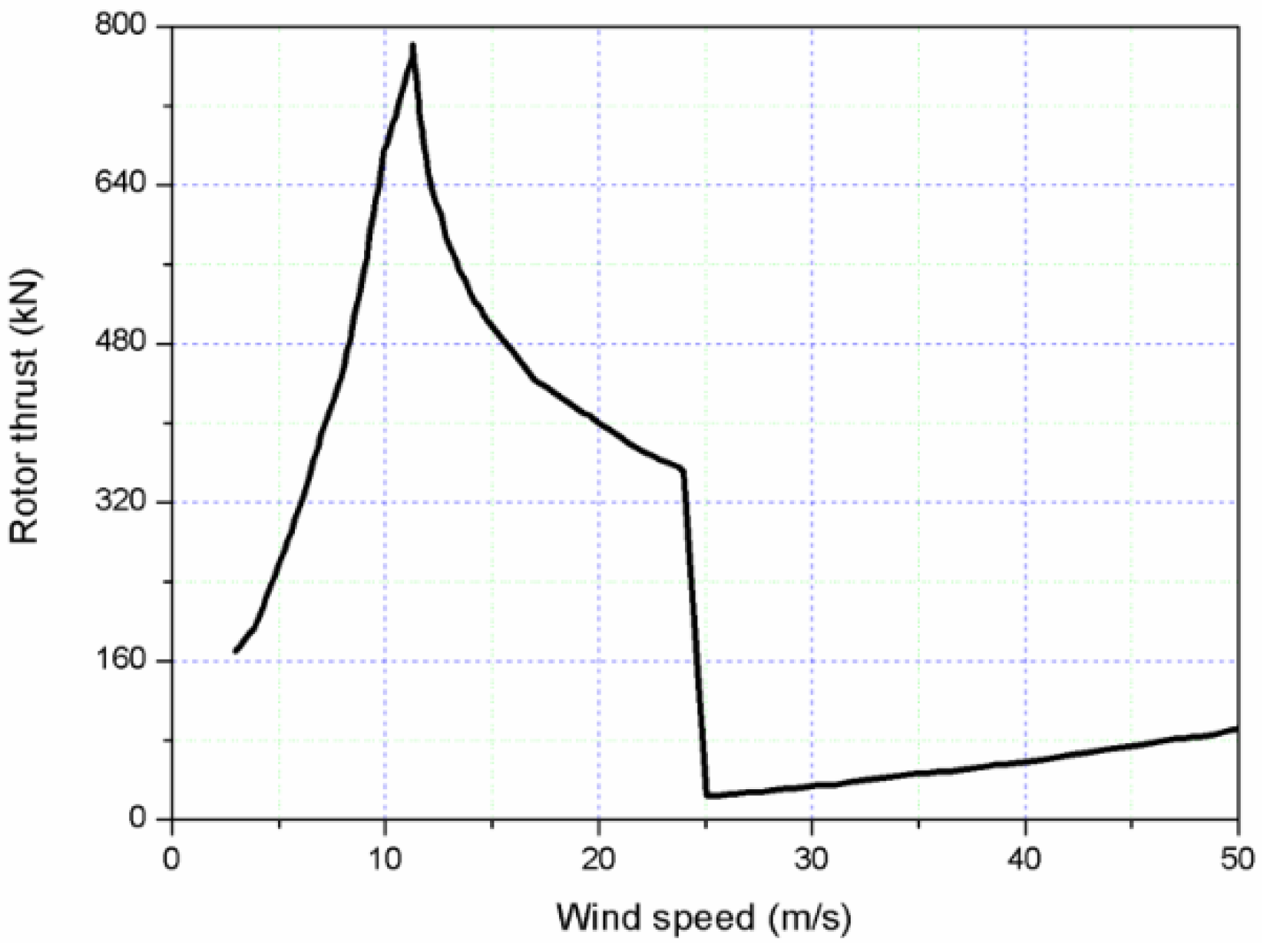
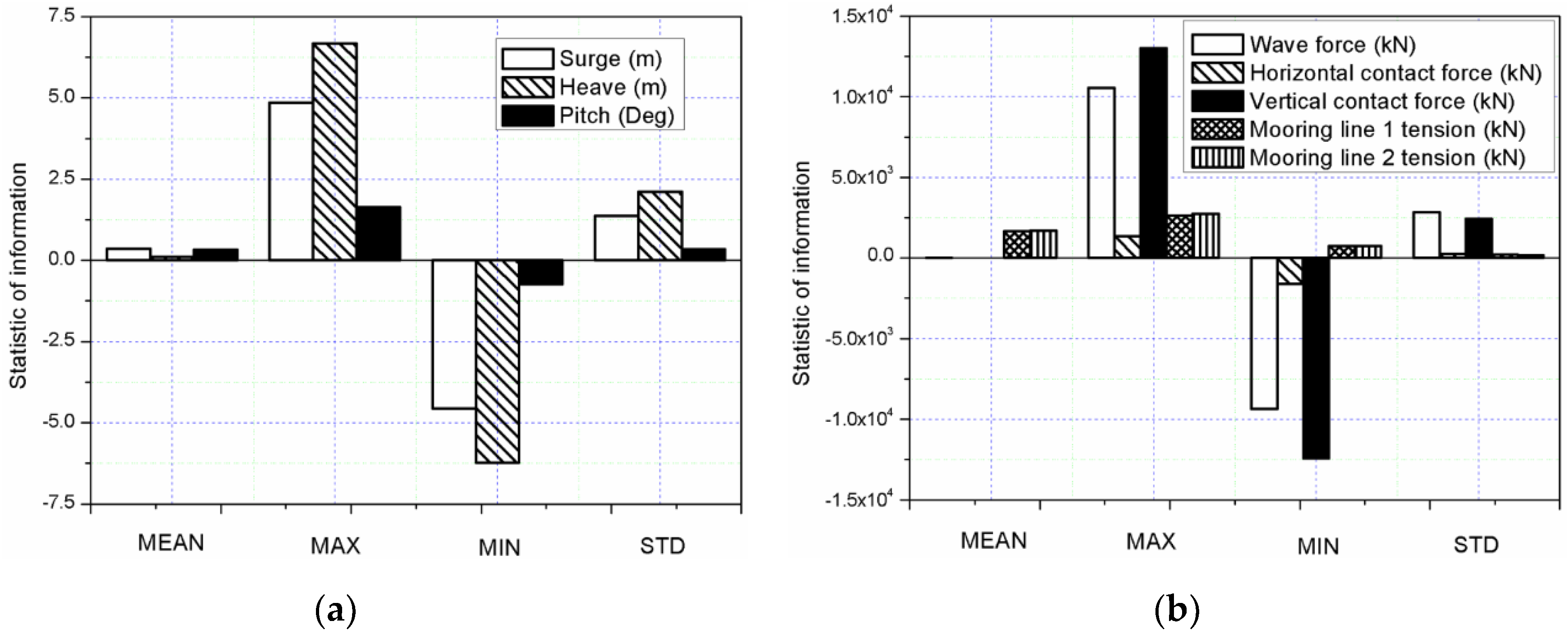
4.5. Dynamic Responses of the Combined Structure in Extreme Sea Conditions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Wind Energy Association. Offshore Wind in Europe Key Trends and Statistics 2019; Wind Europe: Brussels, Belgium, 2020. [Google Scholar]
- Cai, S.K. Grid parity speeds up the development of offshore wind power industry—the practitioner mission of offshore wind power in the next five years. South Energy Constr. 2019, 2, 7–15. [Google Scholar]
- Marina Platform. Available online: https://www.msp-platform.eu/projects/marina-platform (accessed on 3 April 2020).
- Peiffer, A.; Roddier, D.; Aubault, A. Design of a point absorber inside the WindFloat structure. In Proceedings of the 30th International Conference on Ocean, Offshore and Arctic Engineering (OMAE), Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Aubault, A.; Alves, M.; Sarmento, A.; Roddier, D.; Peiffer, A. Modeling of an oscillating water column on the floating foundation WindFloat. In Proceedings of the 30th International Conference on Ocean, Offshore and Arctic Engineering (OMAE), Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Muliawan, M.J.; Karimirad, M.; Moan, T. Dynamic response and power performance of a combined spar-type floating wind turbine and coaxial floating wave energy converter. Renew. Energy 2013, 50, 47–57. [Google Scholar] [CrossRef]
- Muliawan, M.J.; Karimirad, M.; Gao, Z.; Moan, T. Extreme responses of a combined spar-type floating wind turbine and floating wave energy converter (STC) system with survival modes. Ocean Eng. 2013, 65, 71–82. [Google Scholar] [CrossRef]
- Wan, L.; Gao, Z.; Moan, T. Experimental and numerical study of hydrodynamic responses on a combined wind and wave concept in survival modes. Coast. Eng. 2015, 104, 151–169. [Google Scholar] [CrossRef] [Green Version]
- Wan, L.; Gao, Z.; Moan, T.; Lugni, C. Experimental and numerical comparisons of a combined wind and wave energy converter concept under operational conditions. Renew. Energy 2016, 93, 87–100. [Google Scholar] [CrossRef]
- Wan, L.; Gao, Z.; Moan, T.; Lugni, C. Comparative experimental study of the survivability of a combined wind and wave energy converter in two testing facilities. Ocean Eng. 2016, 111, 82–94. [Google Scholar] [CrossRef] [Green Version]
- Michailides, C.; Gao, Z.; Moan, T. Experimental study of the functionality of a semisubmersible wind turbine combined with flap-type Wave Energy Converters. Renew. Energy 2016, 93, 675–690. [Google Scholar] [CrossRef]
- Michailides, C.; Gao, Z.; Moan, T. Experimental and numerical study of the response of the offshore combined wind/wave energy concept SFC in extreme environmental conditions. Mar. Struct. 2016, 50, 35–54. [Google Scholar] [CrossRef]
- Michailides, C.; Luan, C.Y.; Gao, Z.; Moan, T. Effect of flap type wave energy converters on the response of a semi-submersible wind turbine in operational conditions. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering (OMAE), San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Ren, N.X.; Ma, Z.; Fan, T.H.; Zhai, G.J.; Ou, J.P. Experimental and numerical study of hydrodynamic responses of a new combined monopile wind turbine and a heave-type wave energy converter under typical operational conditions. Ocean Eng. 2018, 159, 1–8. [Google Scholar] [CrossRef]
- Luan, C.; Gao, Z.; Moan, T. Design and analysis of a braceless steel 5-MW semi-submersible wind turbine. In Proceedings of the ASME 2016 35st International Conference on Ocean, Offshore and Arctic Engineering (OMAE 2016), Busan, Korea, 19–24 June 2016. [Google Scholar]
- Yang, S.H.; Wang, Y.Q.; He, H.Z.; Zhang, J.; Chen, H. Dynamic properties and energy conversion efficiency of a floating multi-body wave energy converter. China Ocean Eng. 2018, 32, 347–357. [Google Scholar] [CrossRef]
- Wavebob. Available online: http://www.wavebob.com (accessed on 3 April 2020).
- ANSYS, A.W., Inc. AQWA Manual Release 15.0; ANSYS A.W., Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Li, Y.C.; Teng, B. The Effect of Waves on Marine Buildings, 3rd ed.; Ocean Publication: Beijing, China, 2015; pp. 270–273. [Google Scholar]
- Van Rijn, L.C. Principles of Fluid Flow and Surface Waves in Rivers, Estuaries, Seas and Oceans, 3rd ed.; Aqua Publications: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Morison, J.R.; Johnson, J.W.; Schaaf, S.A. The force exerted by surface waves on piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Gao, W.; Dong, L.; Huang, J. ANSYS AQWA Software Introduction and Improvement, 1st ed.; China Water Resources and Hydropower Press: Beijing, China, 2018. [Google Scholar]
- Cao, H.; Tang, Y.G.; Tao, H.C.; Qin, Y. Design and frequency domain analysis of semi-submersible floating foundation for offshore wind turbine. Ocean Eng. 2013, 31, 61–67. [Google Scholar]
- Bai, J.; Li, Y.; Qu, Z.S.; Tang, Y.G. Optimization design of heave suppression structure for new cylindrical FPSO. Ocean Eng. 2020, 38, 20–29. [Google Scholar]
- Wang, Y.P.; Shi, W.; Zhang, L.X.; Michailides, C.; Zhou, L. Hydrodynamic analysis of a floating hybrid renewable energy system. In Proceedings of the 30th International Society of Offshore and Polar Engineers, Shanghai, China, 14–19 June 2020. [Google Scholar]
- Fang, M.C.; Kim, C.H. Hydrodynamically coupled motions of two ships advancing in oblique waves. J. Ship Res. 1986, 30, 159–171. [Google Scholar]
- Oortmerssen, G.V. Hydrodynamic interaction between two structures, floating in waves. In Proceedings of the 2nd International Conference on Behaviour of Offshore Structures, BOSS’79, London, UK, 28–31 August 1979. [Google Scholar]
- Zhao, Z.X.; Li, X.; Wang, W.H.; Shi, W. Analysis of dynamic characteristics of an ultra-large semi-submersible floating wind turbine. Mar. Sci. Eng. 2019, 7, 169. [Google Scholar] [CrossRef] [Green Version]
- Tom, N.M. Design and Control of a Floating Wave-Energy Converter Utilizing a Permanent Magnet linear Generator. Ph.D. Thesis, UC Berkeley, Berkeley, CA, USA, 2013. [Google Scholar]
- Falnes, J. A review of wave-energy extraction. Mar. Struct. 2007, 20, 185–201. [Google Scholar] [CrossRef]
- Gao, Z.; Moan, T.; Wan, L.; Michailides, C. Comparative numerical and experimental study of two combined wind and wave energy concepts. J. Ocean Eng. Sci. 2016, 1, 36–51. [Google Scholar] [CrossRef] [Green Version]
- Ren, N.X.; Zhu, Y.; Ma, Z.; Wu, H.B. Comparative study of hydrodynamic responses of two combined wind turbine and wave energy converter systems under typical operational sea cases. In Proceedings of the 37th International Conference on Ocean, Offshore and Arctic Engineering (OMAE), Madrid, Spain, 17–22 June 2018. [Google Scholar]







| Parameters | Values | |
|---|---|---|
| Wind turbine (NREL 5 MW) | Rotor-Nacelle-Assembly | 350 t |
| Hub height | 90 m | |
| Tower mass | 347.46 t | |
| semisubmersible platform | Semisubmersible mass | 9738 t |
| Diameter of the central column | 6.5 m | |
| Diameter of the three side columns | 6.5 m | |
| Operating draft | 30 m | |
| Water displacement | 10,298 m3 | |
| Water depth | 200 m | |
| WEC device | Outer/Inner diameter | 16 m/8 m |
| Height/Draft | 8 m/3.5 m | |
| Mass | 463.5 t | |
| Water displacement | 452.2 m3 | |
| Center of mass | (0, 0, −1 m) |
| Sea States | Wave Type | Wave Height Hs (m) | Wave Period Tp (s) | Wind Speed Uwind (m/s) |
|---|---|---|---|---|
| LC 1 | Irregular | 2.0 | 9 | 0 |
| LC 2 | Irregular | 2.0 | 9 | 17 |
| LC 3 | Irregular | 3.0 | 10 | 24 |
| LC 4 | Irregular | 8.6 | 15 | 31.2 |
| Surge | Heave | Pitch |
|---|---|---|
| 0.07545 | 0.2543 | 0.2108 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, L.; Michailides, C.; Wan, L.; Shi, W. Hydrodynamic Response of a Combined Wind–Wave Marine Energy Structure. J. Mar. Sci. Eng. 2020, 8, 253. https://doi.org/10.3390/jmse8040253
Wang Y, Zhang L, Michailides C, Wan L, Shi W. Hydrodynamic Response of a Combined Wind–Wave Marine Energy Structure. Journal of Marine Science and Engineering. 2020; 8(4):253. https://doi.org/10.3390/jmse8040253
Chicago/Turabian StyleWang, Yapo, Lixian Zhang, Constantine Michailides, Ling Wan, and Wei Shi. 2020. "Hydrodynamic Response of a Combined Wind–Wave Marine Energy Structure" Journal of Marine Science and Engineering 8, no. 4: 253. https://doi.org/10.3390/jmse8040253
APA StyleWang, Y., Zhang, L., Michailides, C., Wan, L., & Shi, W. (2020). Hydrodynamic Response of a Combined Wind–Wave Marine Energy Structure. Journal of Marine Science and Engineering, 8(4), 253. https://doi.org/10.3390/jmse8040253







