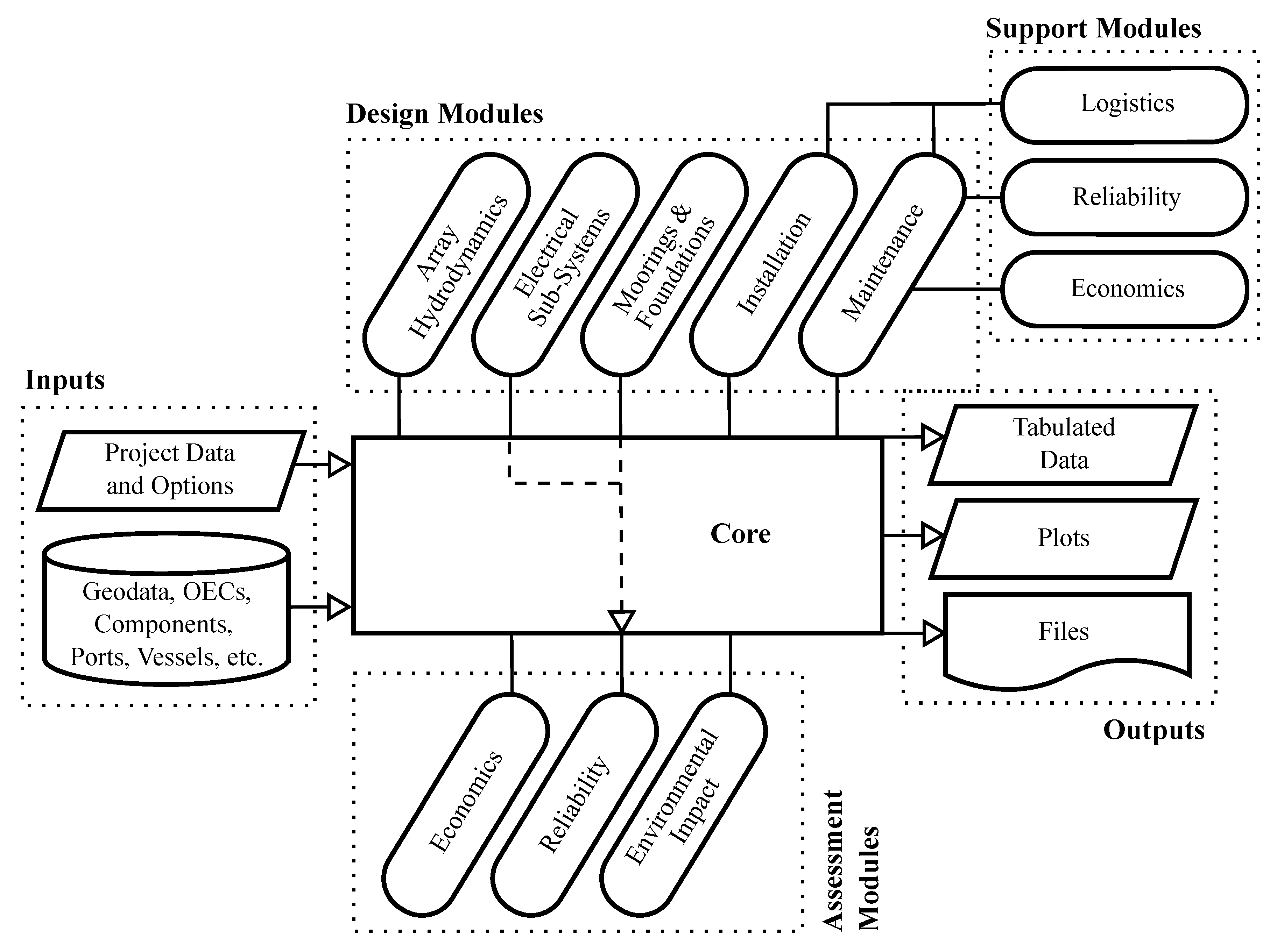
Figure 2 shows all the stages of the algorithm used in DTOcean, which will be discussed in the following subsections. Each stage is repeated for a number of representative velocity fields (RVFs), with each having an associated probability of occurrence. The selection of RVFs and calculation of the probabilities is described in
Appendix A. DTOcean uses a regular two-dimensional computational grid to store field data, as shown in
Figure 3, which contains bathymetric data, depth averaged tidal velocities and turbulence intensities. Where data are required at positions which do not intersect with a node of the computation grid (such as the location of TECs), values are interpolated linearly.
2.2.2. Hub Height Adjustment
In the next stage of the calculation, the values of velocity and turbulence intensity within the 2D flow field are adjusted to account for the vertical position of the TEC rotors within the water column. The vertical profile of a tidally driven channel is complex and variable, both in terms of velocity and turbulence [
29]. Accurately modelling such dynamic processes is extremely computationally expensive, thus, at the cost of some accuracy in velocity values and wake prediction, reduced order assumptions are used. As in [
30], the velocity magnitude at height
z above the sea bed,
, can be estimated using a power law expression such as
where
is the depth averaged velocity.
, known as the bed roughness coefficient, and
are calibrated to best represent the underlying physics. DTOcean’s original method for predicting
, given in [
28], significantly underestimated its value, thus fixed values of
and
, as suggested in [
31], were adopted for the present study.
As the TEC rotor operates over a range of depths, the difference in velocities between the top and bottom of the rotor is taken. Equation (
3) can be written
Subsequently, the velocity over the rotor,
is defined
where
and
and
are the values of
w for the vertical limits of the rotor. Note that this approximation improves upon methods that do not consider variation of velocity in the water column, but does not attempt the power weighted approach (“method of bins”) prescribed in [
32]. Nonetheless, at the scale of problem investigated here, using the power law given by Equation (
3), the errors in power production will be slightly under-estimated in comparison, which is deemed acceptable for a study of this nature. As with [
32], the variation of velocity across the horizontal plane of the rotor is not considered in the calculation of
.
To adjust the given turbulence intensity for the depth of the rotor consider that, under the assumption of homogeneous isotropic turbulence, the turbulence intensity,
I, is given by
where
k is the turbulence kinetic energy. If
k is also assumed to be uniform throughout the water column, it can be shown that
where
is the turbulence intensity over the TEC rotor and
is the turbulence intensity associated with the depth averaged velocity.
2.2.4. Wake Interactions
The next, and most complex, step in the energy extraction calculation is determining the velocities coincident with the TEC rotors subject to interactions with the wakes of other TECs. The approach taken in DTOcean to solve this problem follows a similar approach to the classic ‘Jensen’ model [
11], where superposition of parametrically defined wakes is used to determine the velocity deficits for arrays of wind turbines. Where Jensen used an analytical model to determine the induction factor (as defined in momentum theory), which is then used to determine the velocity of the wake, the approach in DTOcean is to directly access the velocities and turbulence kinetic energies within the wake of each TEC rotor using a database of normalised CFD simulations. In a further improvement to the Jensen model, the TEC wakes are assumed to develop along the streamlines emanating from each TEC rotor, rather than along the perpendicular to the rotor plane. Additionally, scaling of the modelled wakes can be used to account for blockage and rotor yaw angle. This process is illustrated in
Figure 4a. Note that the process has been improved from that used in the original DTOcean software, as will be discussed further below.
As detailed in [
28] (Section 3.3.3.4), a database of 2-dimensional CFD simulations (calculated using OpenFOAM [
33]) was developed for use with DTOcean’s hydrodynamics module. The length scales (in the
x and
y planes) of the simulations are normalised by the rotor diameter, while the velocity scale is normalised by the local velocity upstream of the TEC. Subsequently, the remaining parameters affecting the development of the TEC wakes are the rotor’s thrust coefficient,
, and the turbulence intensity of the incoming flow. The output field values are the scaling factor of the input velocity and the turbulence kinetic energy.
Beyond scaling the CFD simulations by the diameter of the TEC rotor being simulated, additional scaling can be undertaken to account for the effects of blockage and rotor yaw angle, as developed in [
28]. Through numerical investigation, using the CFD TEC model (see [
28]), it was determined that the
x-axis of the CFD simulations should be scaled by a factor of
, where
B is the blockage ratio for the flow being investigated. DTOcean determines
B through a combination of a user defined factor,
, over the range
, and an additional factor determined as follows.
The distance of each TEC rotor relative to the streamlines of the other rotors (denoted
) is calculated as shown in
Figure 5. Subsequently, the first row of TECs (
) can be determined (i.e., those TEC rotors with no perpendicular interceptor with the streamlines of other rotors). Next, the area of a vertical transect across the deployment area coincident to the first row of TECs,
A, is calculated. Finally, the blockage over the transect,
, and the final blockage ratio,
B, are given by
where
D is the TEC rotor diameter and
is the yaw angle of rotor
i. To account for the yaw angle of the rotor, the
y-axis of the CFD simulations is also scaled, using a factor of
.
The next stage is to update the velocity and turbulence intensity incident to each TEC rotor (subscript
r is dropped), i.e.,
where
and
are the velocity magnitude and turbulence intensity for rotor
i. The superscript 0 refers to the undisturbed state of the flow, while superscript
m refers to the modified flow in the presence of the TECs.
and
are coefficients of the undisturbed velocity and turbulence intensity, for each rotor
i, that are to be determined. By using Equation (
4), Equation (
7) can alternatively be written in terms of the turbulence kinetic energy and
as follows
where
is the turbulence kinetic energy at rotor
i and
is the coefficient to be determined.
Reading from the database of CFD simulations can be described by the function
where the subscript
refers to the value of the parameter at the position of rotor
i subject to the influence of rotor
j. Here,
maps the CFD solution onto the streamline emanating from rotor
j and where
does not exist (such as for TECs in the first row),
is set to unity and
.
Once all coefficients
and
are known, they are superimposed. Several engineering approaches, as detailed in [
34], exist to superimpose the velocity deficits predicted by Jensen style analytical wake models. In the original DTOcean code the ‘quadratic summation’ or ‘residual sum of squares’ (RSS) approach was used to superimpose the velocities, while the wake with maximum turbulence kinetic energy was used to directly calculate
(using Equation (
4)). It was discovered in this work, however, that the function
f can return a value greater than one, which exceeds the valid range of values for use in RSS approaches. Because of this, the current work uses the basic ‘dominating wake’ approach, where the wake with the greatest velocity deficit is chosen, i.e.
Additionally, rather than use an alternative method to superimpose the turbulence kinetic energy, the value for the same dominant wake is used. If
then
As seen in
Figure 4a, at this stage the unmodified DTOcean code would calculate
and
and move onto the next stage of the energy extraction calculation. In the Jensen model, the values of
would be calculated for each row of downstream rotors in an iterative manner, to capture the compound affect of the wakes. Due to the non-uniform flow fields in tidal current energy simulations, identifying which TECs lie upstream of others is not straightforward, so the present work proposes to iterate
all of the coefficients until convergence. Rewriting Equations (
6) and (
8) as
where the superscript
l represents the index of the iteration step, and combining Equations (
9)–(
12) as a single function
presents the problem in an iterative form. If
and
represent the coefficients for all
rotors then let
for
and define the residual of the coefficient of velocity to be
. Finally, the iterations are considered converged if
is less than a chosen value (
was used herein). The complete process is illustrated in
Figure 4b.
The value of using the proposed iterative solution over the original method in DTOcean is made clear by
Figure 6. It can be seen that the mean value of
for the initial iteration (analogous to the original DTOcean method) can both over- and under-estimate the converged value, and that the error can be significant across a range of values of
.