Hydroelastic Response of a Flexible Submerged Porous Plate for Wave Energy Absorption
Abstract
:1. Introduction
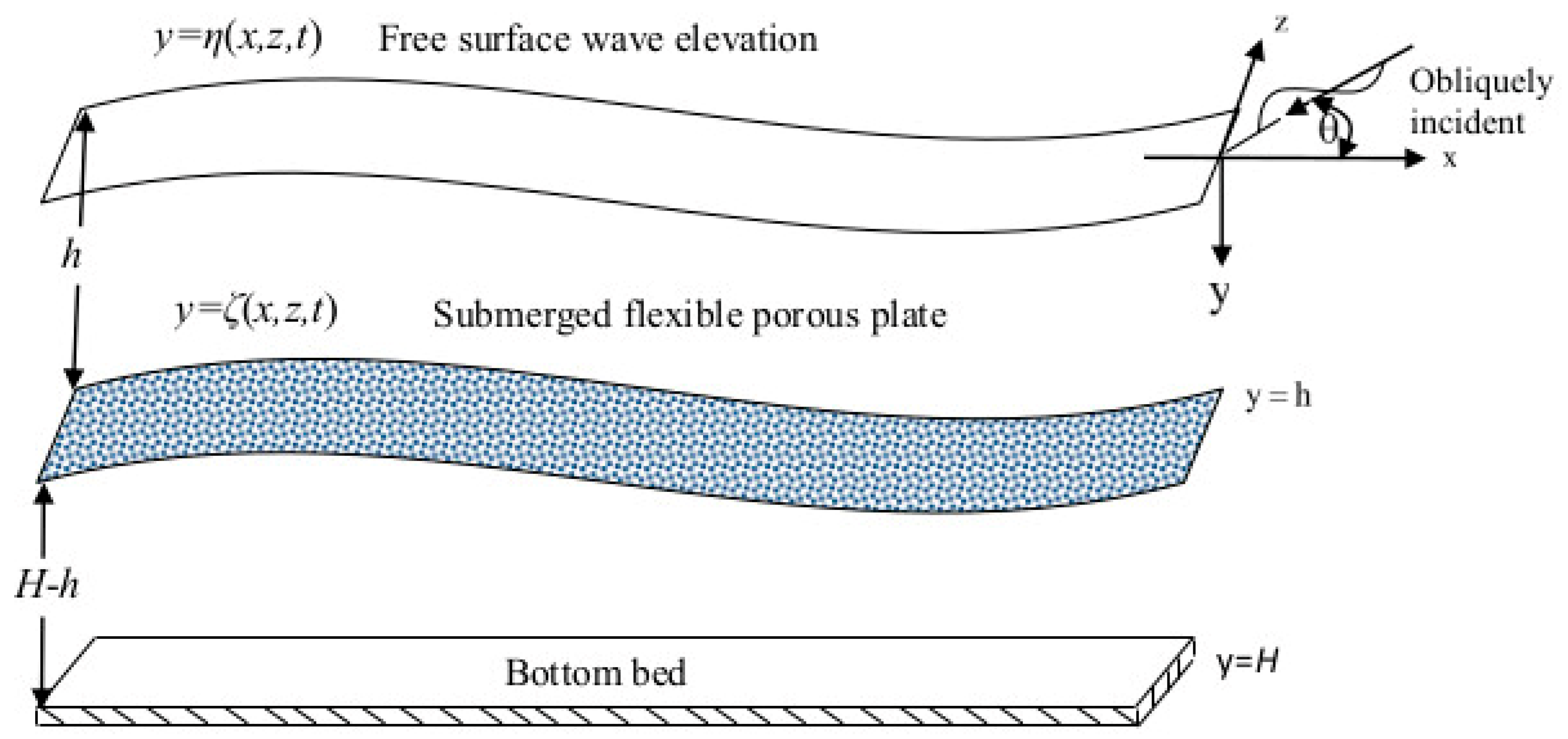
2. Mathematical Model
3. Expansion Formulae in FD and ID
3.1. Integral and Series form of Green’s Function Based on Reduced Wave Equation
3.2. Expansion Formulae for Wavemaker Problem Using Green’s Function under Oblique Waves
4. Usefulness of the Expansion Formula under the Action of Oblique Waves in FD
4.1. Governing Equation and Boundary Conditions
4.2. Solution Technique
4.3. Determination of Unknown Coefficients
4.4. Comparison Results and Hydroelastic Response
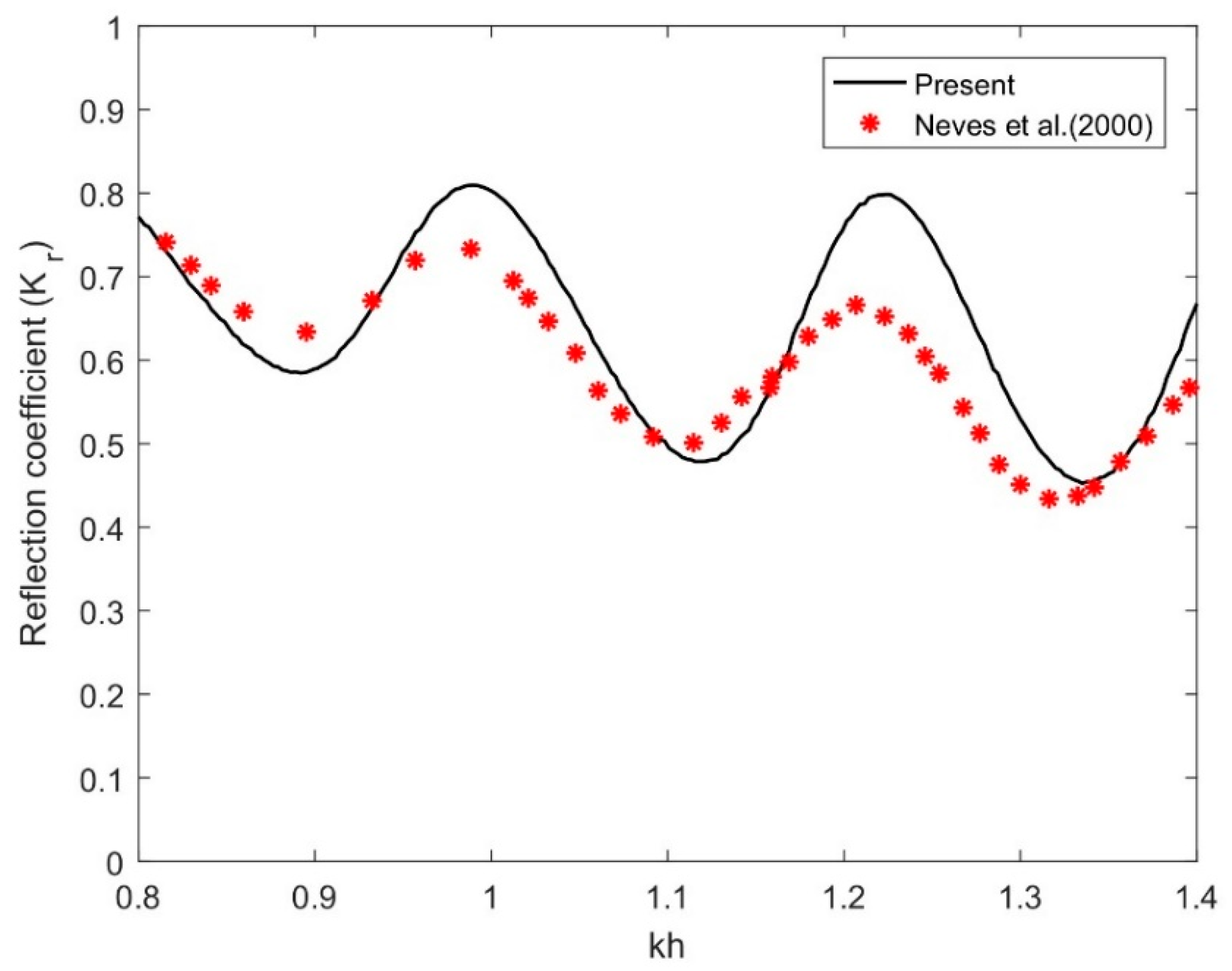
4.4.1. Comparison with Experimental and Analytical Results
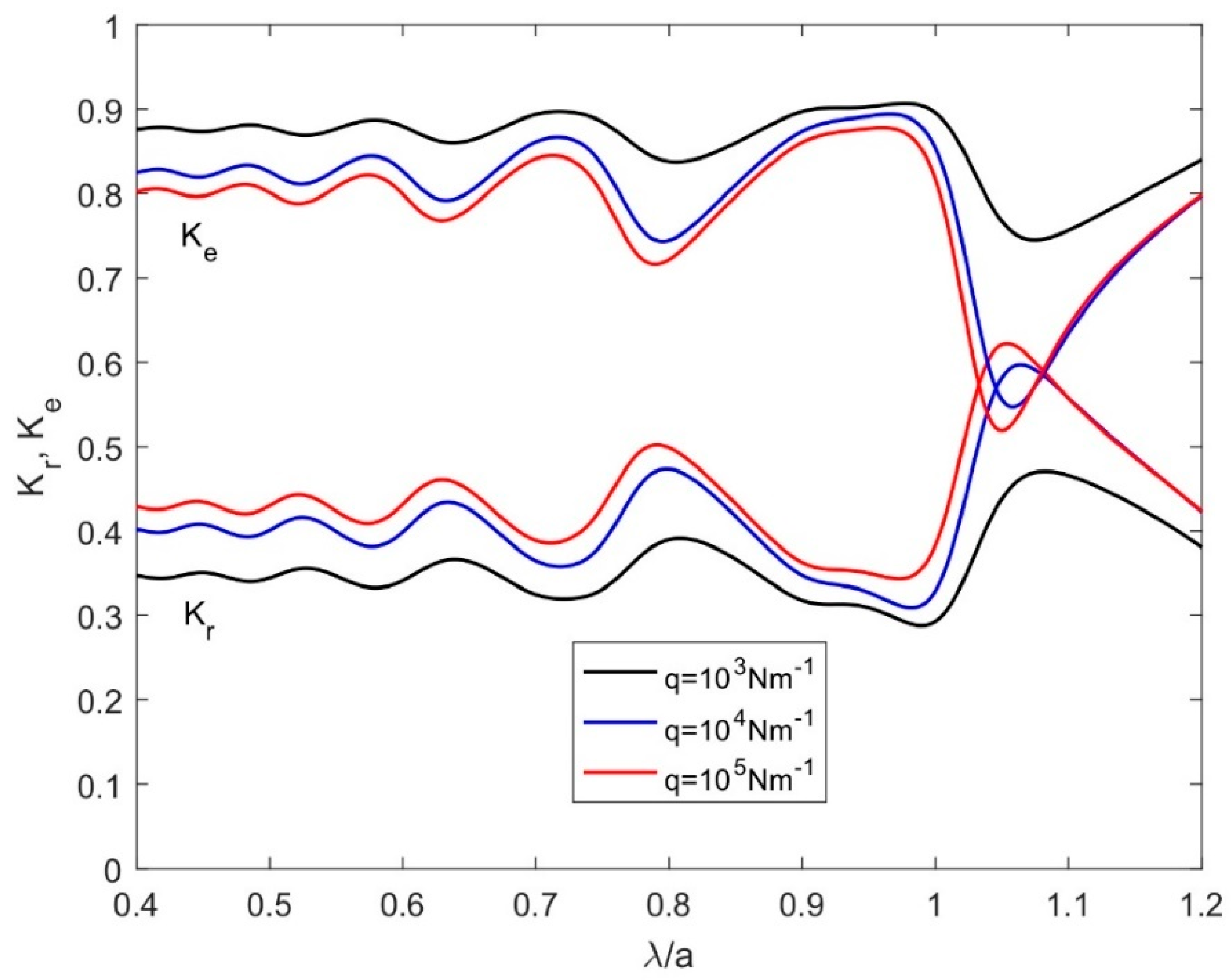
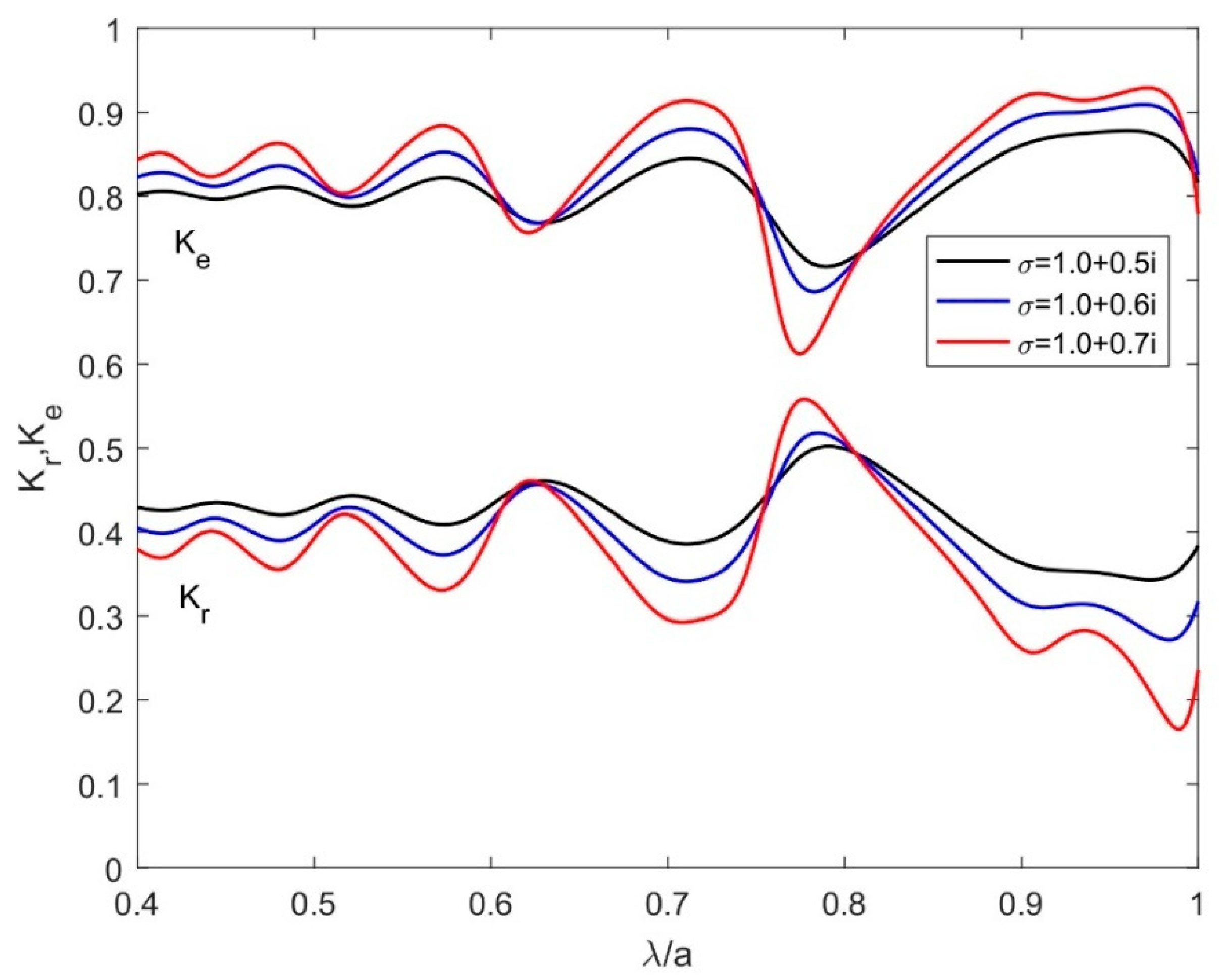
4.4.2. Effect of Design Parameters on the Hydroelastic Response of a Moored Submerged Horizontal Flexible Plate
5. Conclusions
- Under oblique waves, the Green’s functions, expansion formulae, and expansion form for the wavemaker problem is derived here in FD and ID which are communicated for the first time.
- The derived Green’s function can facilitate the analysis of the thin and thick flexible plate, and applications to wavemaker problems over boundary integral equation formulations associated with real physical problems in BEM analysis.
- The basic limitations of the present approach are (i) relevant boundary conditions must be linear (maybe of higher-order), (ii) structural boundaries must be at constant of co-ordinates (ends of the structure must be at fixed locations), (iii) the coefficients associated with the equations must uncomplicated, and (iv) after all, the solution must be a series of solutions. Therefore, the MEFEM approach can be used for the rectangular and circular shaped flexible plate and membrane type structures.
- For numerical correctness and convergence of the series solution, in the computation is confined.
- Comparison results show that the present results based on the analytical solution are supported by the published experimental data and as well as analytical results.
- The analysis of the reflection and the dissipation coefficients indicated that the absorption of wave energy over a flexible plate is remarkable for the suitable value of the oblique angle of the incident wave and mooring stiffness.
- The study demonstrates that plate displacement reduces with an increase in oblique angle, suitable positing, and appropriate choice of porous-effect parameter.
- As a result, the present formulation can be further generalized to develop a wave energy converter (WEC)-type attachment for wave energy extraction.
Author Contributions
Funding
Conflicts of Interest
Abbreviations List
| BVP | Boundary Value Problem |
| FD | Finite Depth |
| ID | Infinite Depth |
| MEFEM | Matched eigenfunction expansion method |
| WEC | Wave Energy Converter |
| BEM | Boundary Element Method |
Appendix A. Shallow Water Equations
References
- Cho, I.H.; Koh, H.J.; Kim, J.R.; Kim, M.H. Wave scattering by dual submerged horizontal porous plates. Ocean Eng. 2013, 73, 149–158. [Google Scholar] [CrossRef]
- Guo, Y.C.; Mohapatra, S.C.; Guedes Soares, C. Wave energy dissipation of a submerged horizontal flexible porous membrane under oblique wave interaction. Appl. Ocean Res. 2020, 94, 101948. [Google Scholar] [CrossRef]
- Zheng, S.; Meylan, M.H.; Zhu, G.; Greaves, D.; Iglesias, G. Hydroelastic interaction between water waves and an array of circular floating porous elastic plates. J. Fluid Mech. 2020. [Google Scholar] [CrossRef]
- Zheng, S.; Meylan, M.H.; Fan, L.; Greaves, D.; Iglesias, G. Wave scattering by a floating porous elastic plate of arbitrary shape: A semi–analytical study. J. Fluids Struct. 2020, 92, 102827. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Sahoo, T.; Guedes Soares, C. Surface gravity wave interaction with a submerged horizontal flexible porous plate. Appl. Ocean Res. 2018, 78, 61–74. [Google Scholar] [CrossRef]
- Li, Z.F.; Wu, G.X.; Shi, Y.Y. Interaction of uniform current with a circular cylinder submerged below an ice sheet. Appl. Ocean Res. 2019, 86, 310–319. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Wan, Z.; Fang, Y. Wave reflection by a vertical wall with a horizontal submerged porous plate. Ocean Eng. 1998, 25, 767–779. [Google Scholar] [CrossRef]
- Neves, M.G.; Losada, I.J.; Losada, M.A. Short-wave and wave group scattering by submerged porous plate. J. Eng. Mech. 2000, 126, 1048–1056. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.J.; Li, Y.C. A new analytical solution for wave scattering by a submerged horizontal porous plate with finite thickness. Ocean Eng. 2012, 42, 83–92. [Google Scholar] [CrossRef]
- Evans, D.V.; Peter, M.A. Asymptotic reflection of linear water waves by submerged horizontal porous plates. J. Eng. Math. 2011, 69, 135–154. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Li, Y.C.; Teng, B. Wave interaction with a perforated wall breakwater with a submerged horizontal porous plate. Ocean Eng. 2007, 34, 2364–2373. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y. An alternate analytical solution for water-wave motion over a submerged horizontal porous plate. J. Eng. Math. 2011, 69, 385–400. [Google Scholar] [CrossRef]
- Cho, I.H.; Kim, M.H. Transmission of oblique incident waves by a submerged horizontal porous plate. Ocean Eng. 2013, 61, 56–65. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Sahoo, T.; Guedes Soares, C. Surface gravity wave interaction with submerged horizontal flexible structures. J. Hydrodyn. Ser. B 2018, 30, 481–498. [Google Scholar] [CrossRef]
- Das, D.; Mandal, B.N. Oblique wave scattering by a circular cylinder submerged beneath an ice-cover. Int. J. Eng. Sci. 2006, 44, 166–179. [Google Scholar] [CrossRef]
- Sturova, V. Radiation of waves by a cylinder submerged in water with ice floe or polynya. J. Fluid Mech. 2015, 784, 373–395. [Google Scholar] [CrossRef]
- Tkacheva, L.A. Oscillations of a cylindrical body submerged in a fluid with ice cover. J. Appl. Mech. Tech. Phys. 2015, 56, 1084–1095. [Google Scholar] [CrossRef]
- Guo, Y.C.; Mohapatra, S.C.; Guedes Soares, C. Review of developments in porous membranes and net-type structures for breakwaters and fish cages. Ocean Eng. 2020, 200, 107027. [Google Scholar] [CrossRef]
- Losada, I.J.; Silva, R.; Losada, M.A. 3-D non-breaking regular wave interaction with submerged breakwaters. Coast. Eng. 1996, 28, 229–248. [Google Scholar] [CrossRef]
- Losada, I.J.; Silva, R.; Losada, M.A. Interaction of non-breaking directional random waves with submerged breakwaters. Coast. Eng. 1996, 28, 249–266. [Google Scholar] [CrossRef]
- Losada, I.J.; Petterson, M.D.; Losada, M.A. Harmonic generation past a submerged porous step. Coast. Eng. 1997, 31, 281–304. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.C.; Teng, B.; Dong, S. Wave motion over a submerged breakwater with an upper horizontal porous plate and a lower horizontal solid plate. Ocean Eng. 2008, 35, 1588–1596. [Google Scholar] [CrossRef]
- Cho, I.H.; Kim, M.H. Wave absorbing system using inclined perforated plates. J. Fluid Mech. 2008, 608, 1–20. [Google Scholar] [CrossRef]
- Yueh, C.Y.; Chuang, S.H. Wave scattering by a submerged porous plate wave absorber. In Proceedings of the 19th International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 July 2009. [Google Scholar]
- Liu, Y.; Li, H.J. Wave reflection and transmission by porous breakwaters: A new analytical solution. Coast. Eng. 2013, 78, 46–52. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Sahoo, T. Oblique wave diffraction by a flexible floating structure in th epresence of a submerged flexible structure. Geophys. Astrophys. Fluid Dyn. 2014, 108, 615–638. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Ghoshal, R.; Sahoo, T. Effect of compression on wave diffraction by a floating elastic plate. J. Fluids Struct. 2013, 36, 124–135. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Guedes Soares, C. Effect of submerged horizontal flexible membrane on moored floating elastic plate. In Maritime Technology and Engineering 3; Guedes Soares, C., Santos, T.A., Eds.; Taylor & Francis Group: London, UK, 2016; pp. 1181–1188. [Google Scholar]
- Mohapatra, S.C.; Guedes Soares, C. Interaction of ocean waves with floating and submerged horizontal flexible structures in three-dimensions. Appl. Ocean Res. 2019, 83, 136–154. [Google Scholar] [CrossRef]


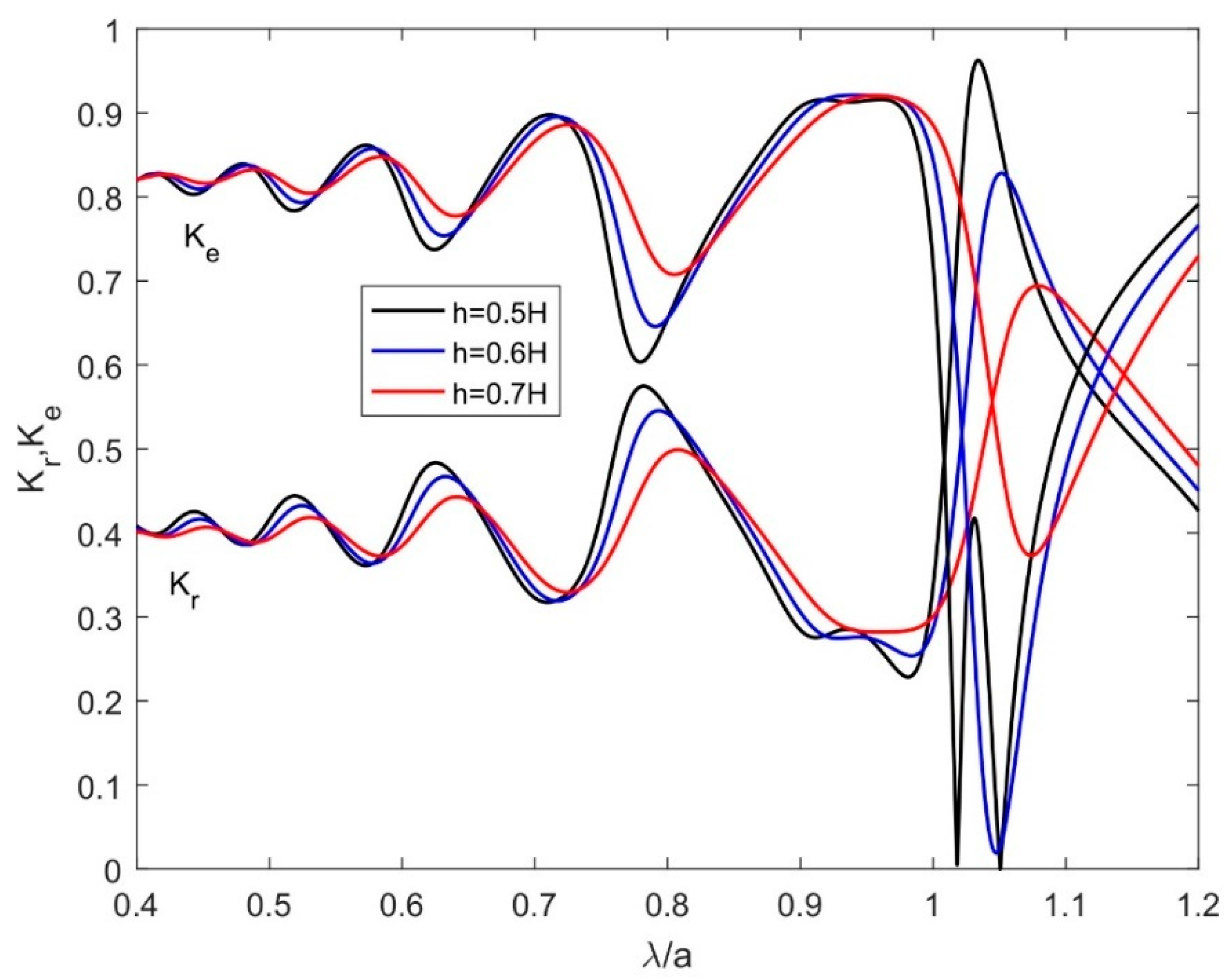



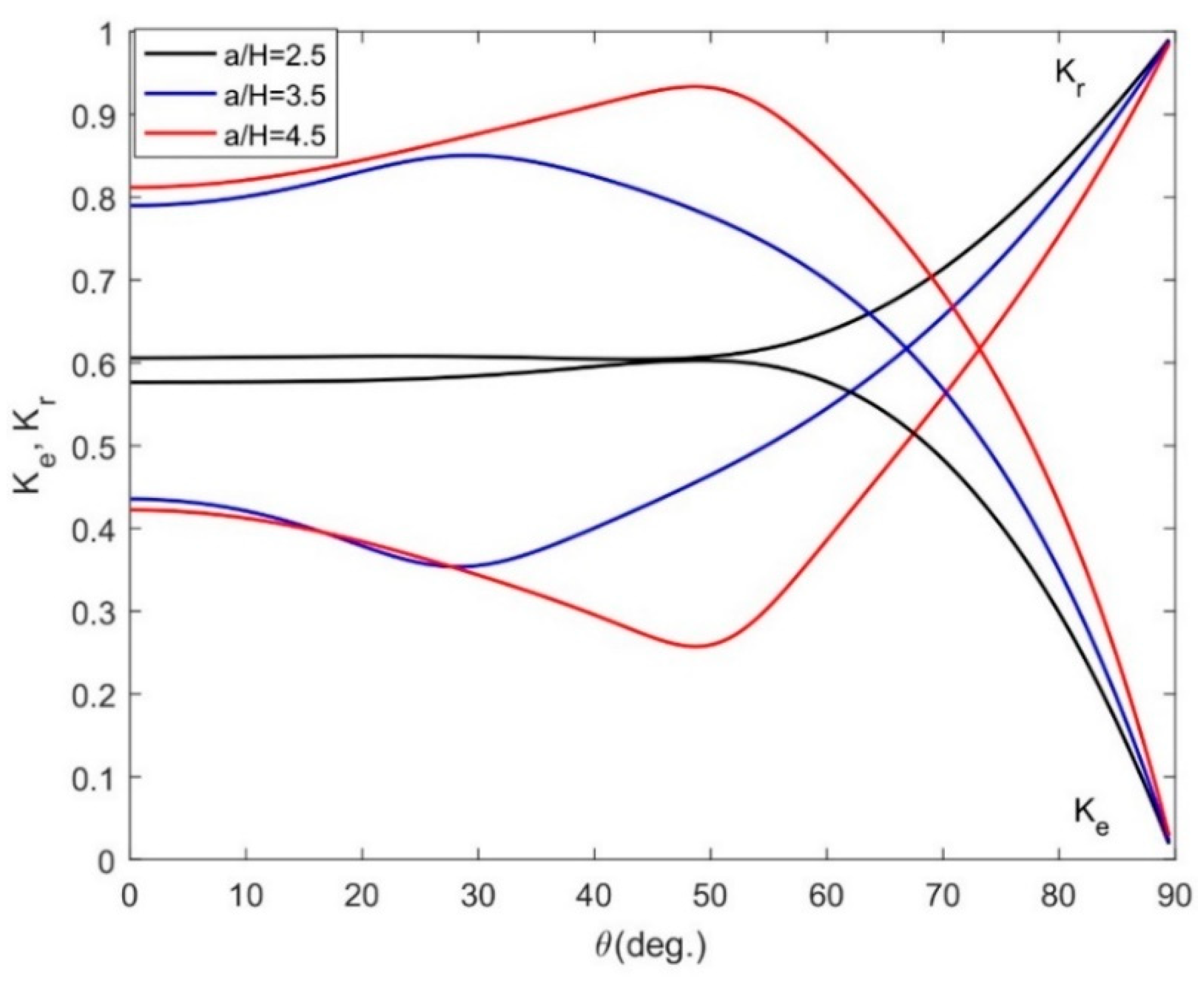
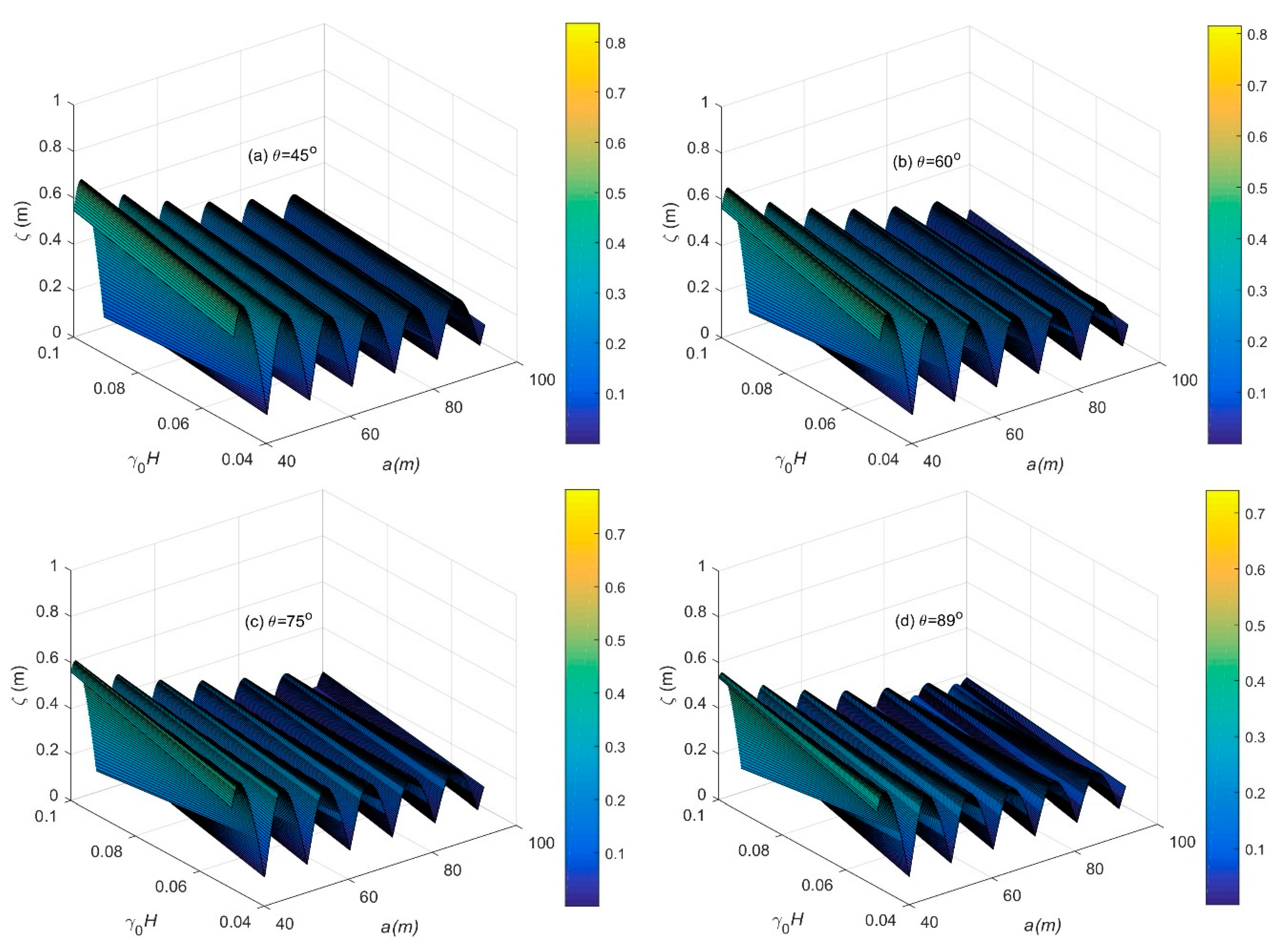

| Parameters | Kr (Reflection Coefficient) | Ke (Dissipation Coefficient) | |
|---|---|---|---|
| q = 102 Nm−1 | 3 | 0.3726 | 0.8588 |
| 5 | 0.3467 | 0.8774 | |
| 8 | 0.3467 | 0.8774 | |
| q = 103 Nm−1 | 3 | 0.3737 | 0.8569 |
| 5 | 0.3470 | 0.8761 | |
| 8 | 0.3470 | 0.8761 | |
| q = 104 Nm−1 | 3 | 0.4310 | 0.8013 |
| 5 | 0.4028 | 0.8245 | |
| 8 | 0.4028 | 0.8245 | |
| 1 + 0.6i | 3 | 0.3519 | 0.8738 |
| 5 | 0.3259 | 0.8915 | |
| 8 | 0.3259 | 0.8915 | |
| 1 + 0.8i | 3 | 0.3128 | 0.8998 |
| 5 | 0.2873 | 0.9153 | |
| 8 | 0.2873 | 0.9153 | |
| 30° | 3 | 0.4089 | 0.8301 |
| 5 | 0.3839 | 0.8498 | |
| 8 | 0.3839 | 0.8498 | |
| 45° | 3 | 0.3910 | 0.8446 |
| 5 | 0.3653 | 0.8639 | |
| 8 | 0.3653 | 0.8639 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohapatra, S.C.; Guedes Soares, C. Hydroelastic Response of a Flexible Submerged Porous Plate for Wave Energy Absorption. J. Mar. Sci. Eng. 2020, 8, 698. https://doi.org/10.3390/jmse8090698
Mohapatra SC, Guedes Soares C. Hydroelastic Response of a Flexible Submerged Porous Plate for Wave Energy Absorption. Journal of Marine Science and Engineering. 2020; 8(9):698. https://doi.org/10.3390/jmse8090698
Chicago/Turabian StyleMohapatra, Sarat Chandra, and C. Guedes Soares. 2020. "Hydroelastic Response of a Flexible Submerged Porous Plate for Wave Energy Absorption" Journal of Marine Science and Engineering 8, no. 9: 698. https://doi.org/10.3390/jmse8090698






