A User-Oriented Local Coastal Flooding Early Warning System Using Metamodelling Techniques
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description: Physical Setting, User Practices and Needs
2.2. Methodology
- •
- Define the indicators (Ij, with j = 1:N) (Section 2.3);
- •
- Set up the process-based model that will be used to build the learning dataset for the metamodels (Section 2.4);
- •
- Build (and validate) the metamodels Yi = fi(X) (with i = 1:M) that are needed to estimate the indicators Ij (j = 1:N) (Section 2.5);
- •
- Implement the post-processing of the metamodel outputs (including the computation of Zk indicators) to estimate the indicators Ij (Section 2.6); and
- •
- Deploy the FEWS, which downloads the forecasted conditions X and returns the indicators Ij (j = 1:N) for the next 6 tides (Section 2.7).
2.3. Indicators and Classes
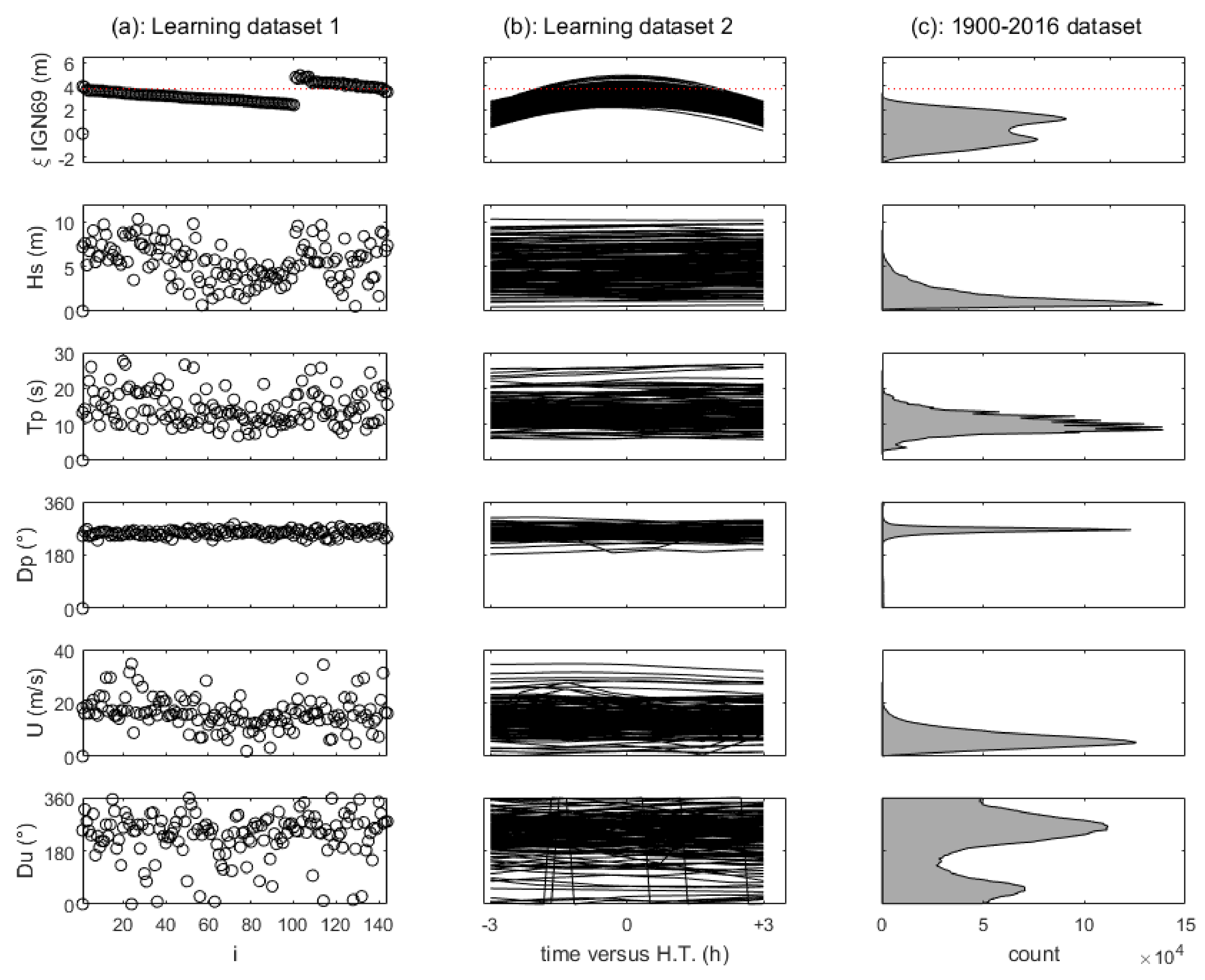
2.4. Process-Based Model Setup and Validation
2.5. Metamodels
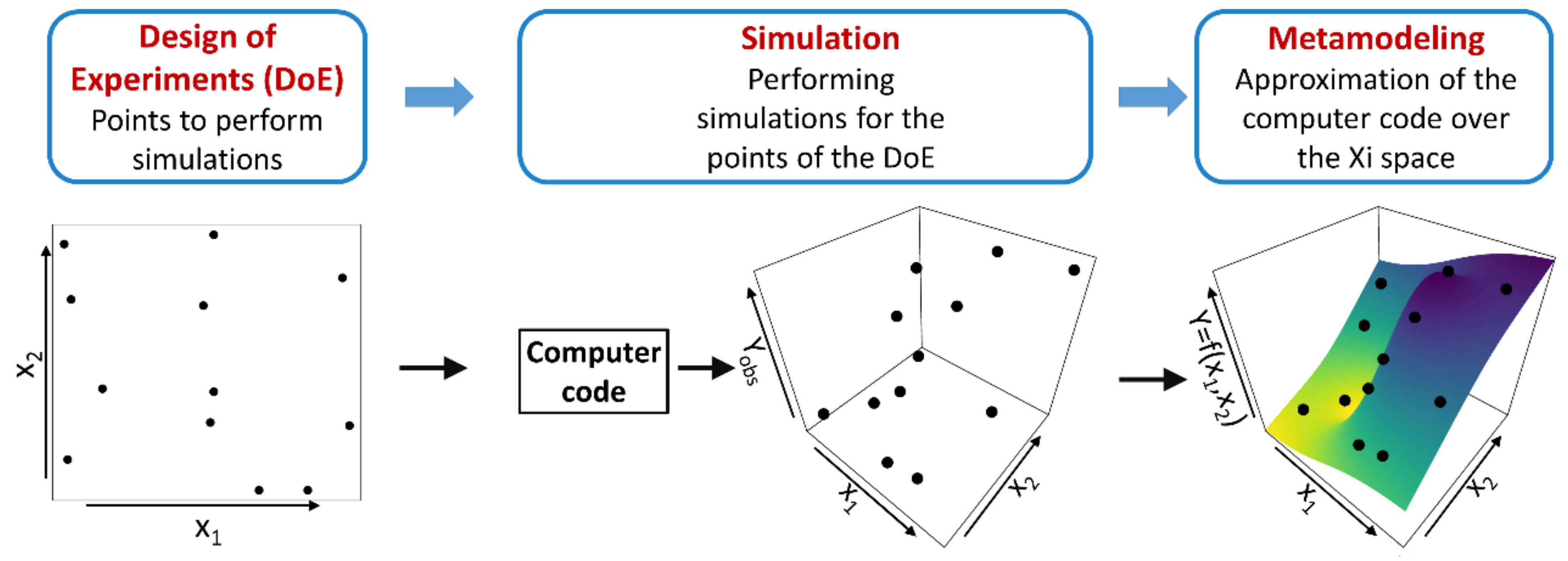
2.5.1. Principles of Metamodelling
2.5.2. Design of Experiments
2.5.3. Metamodelling Technique
2.6. Requirements, Combination Rules of the Metamodel-Based Predictions, Optimisation, and Validation Procedure
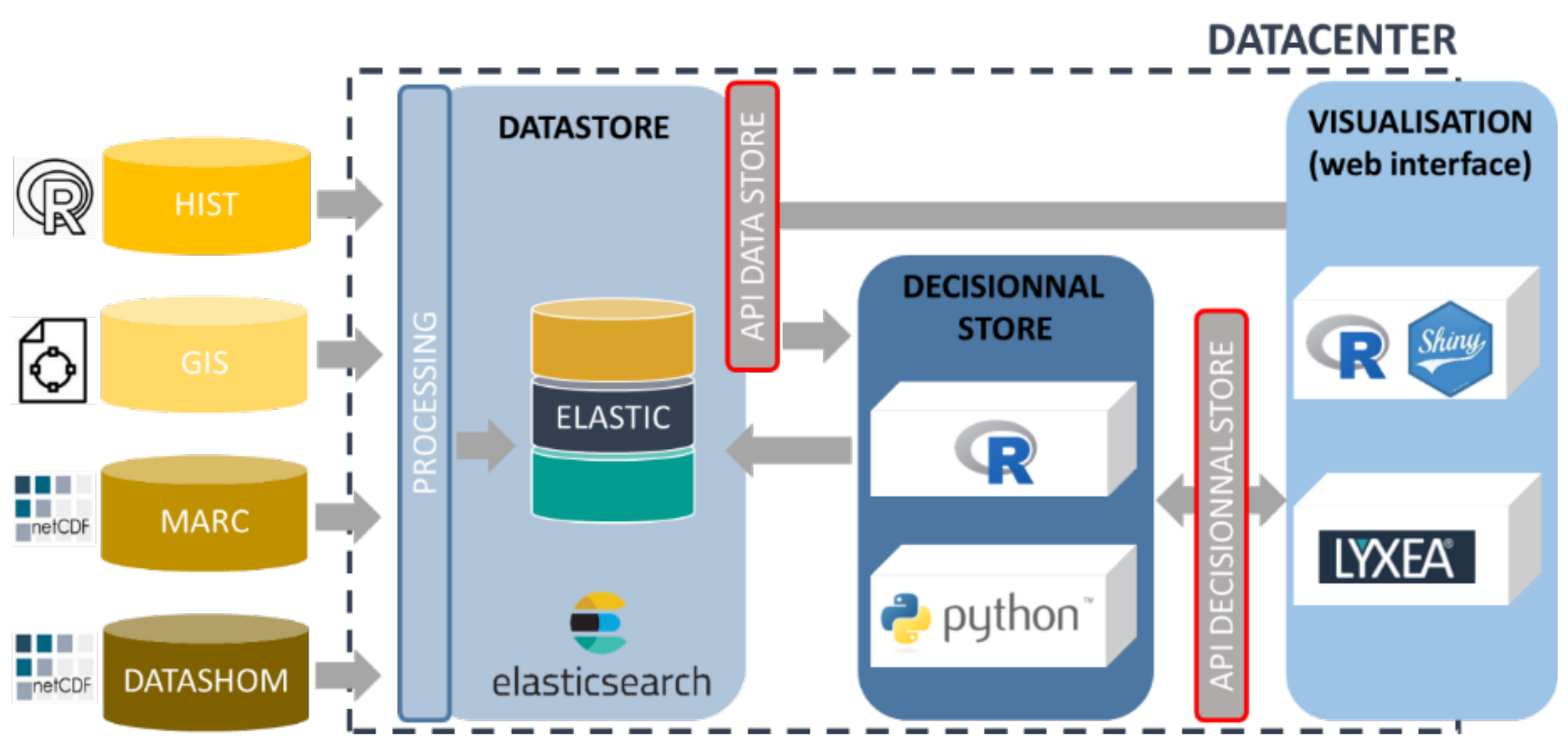
2.7. Implementation in an FEWS
3. Results
3.1. Grid Experiment and Numerical Modelling Results: Preliminary Analysis
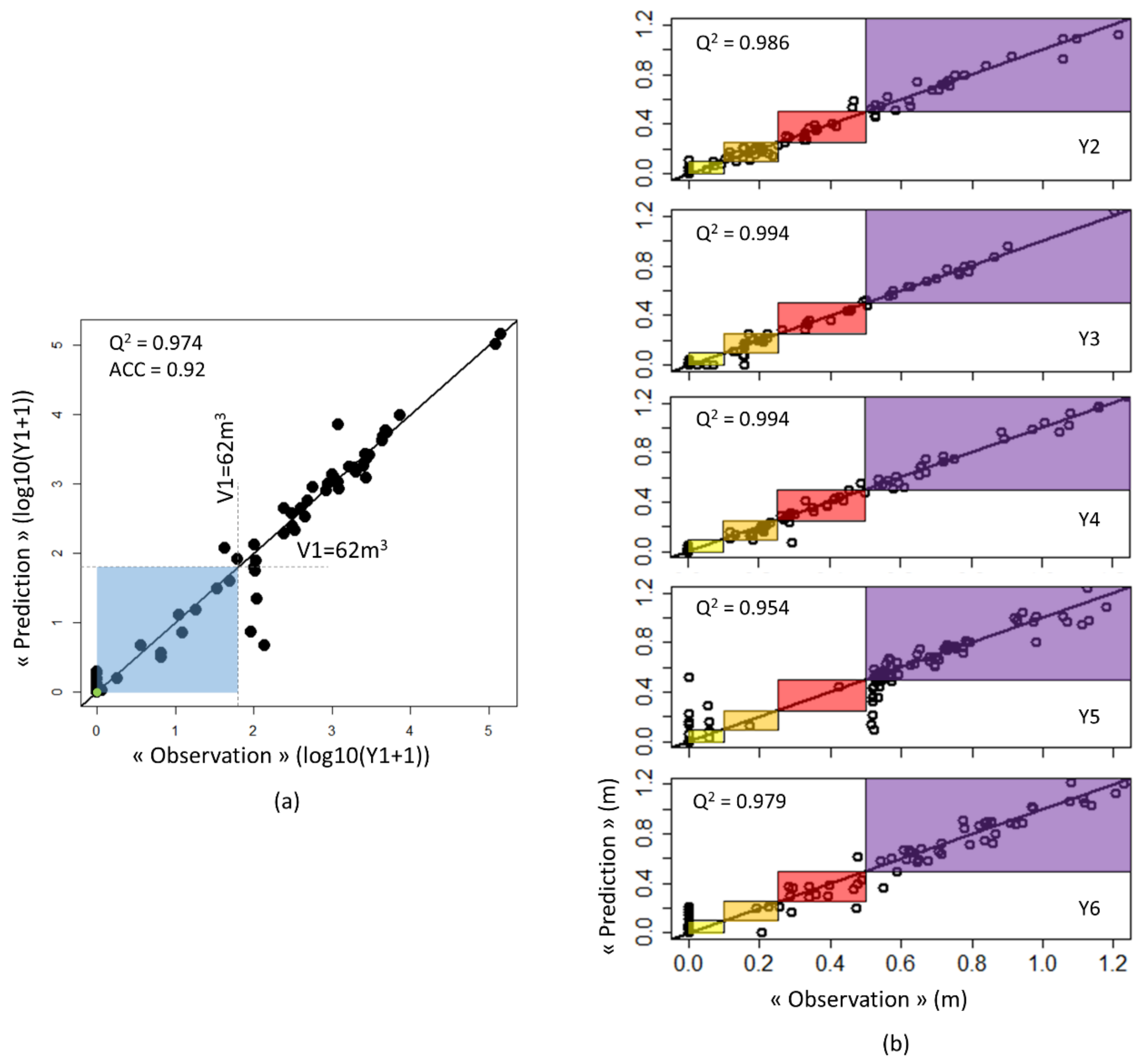
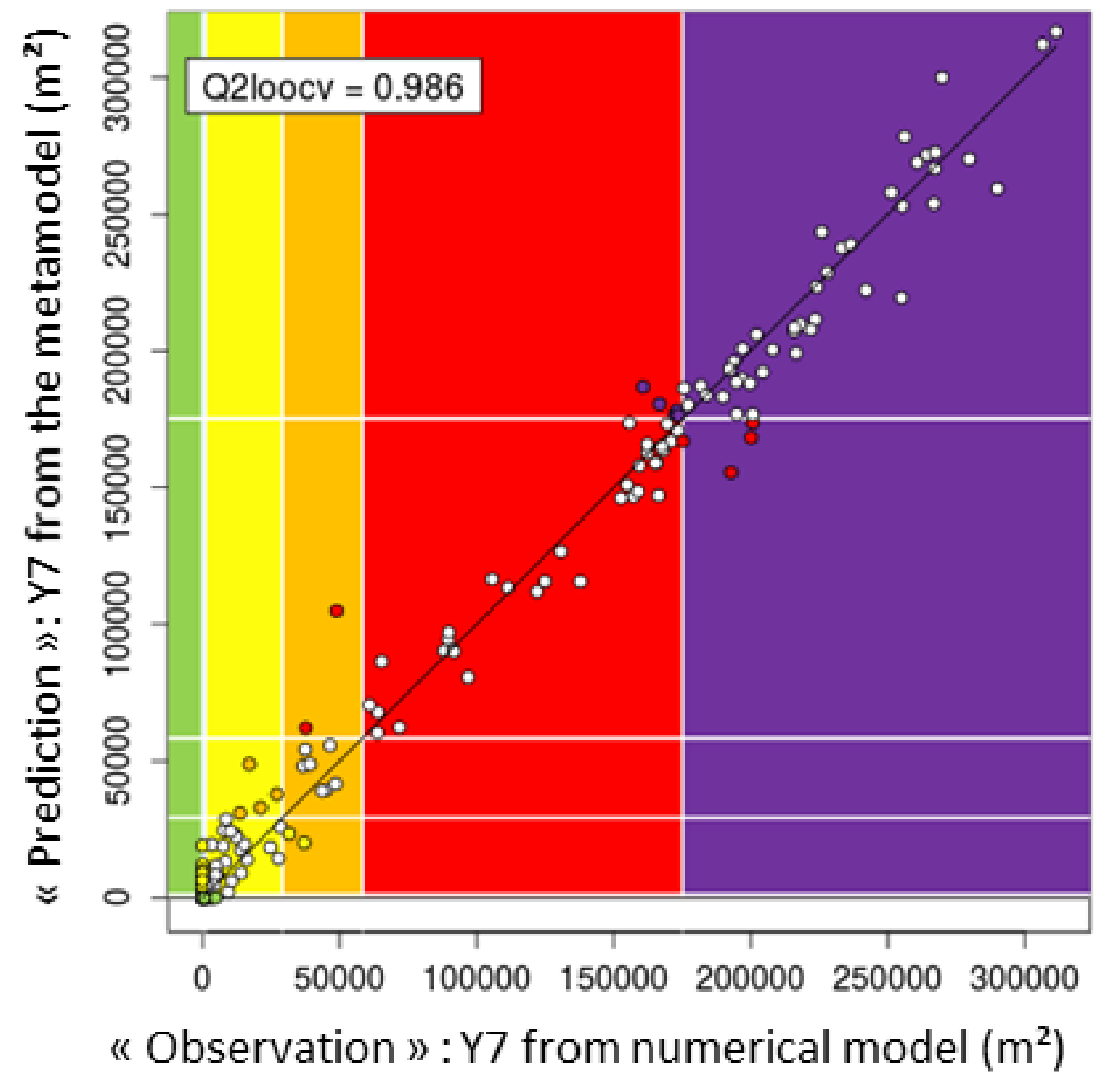
3.2. Metamodel Cross-Validation
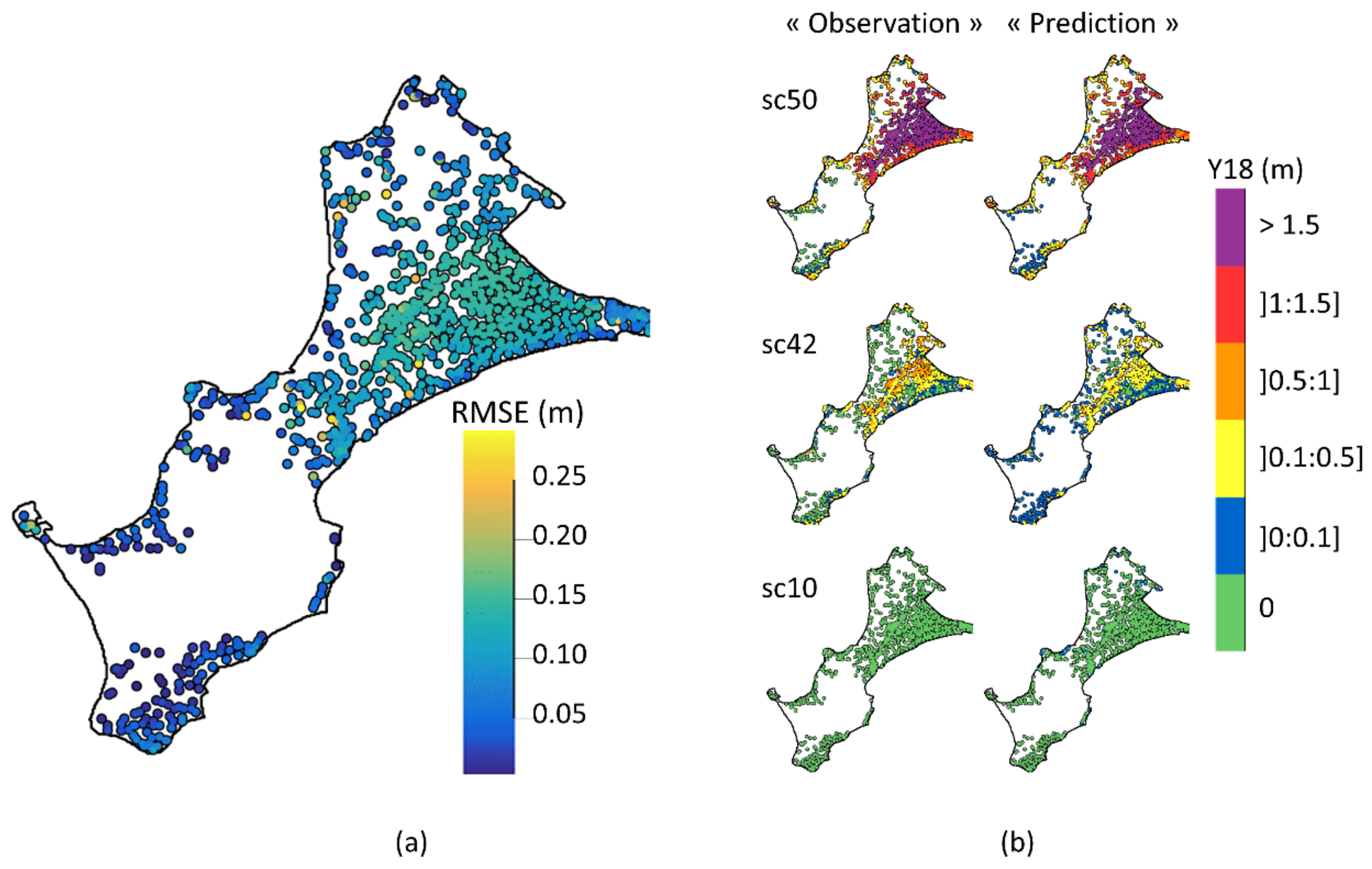
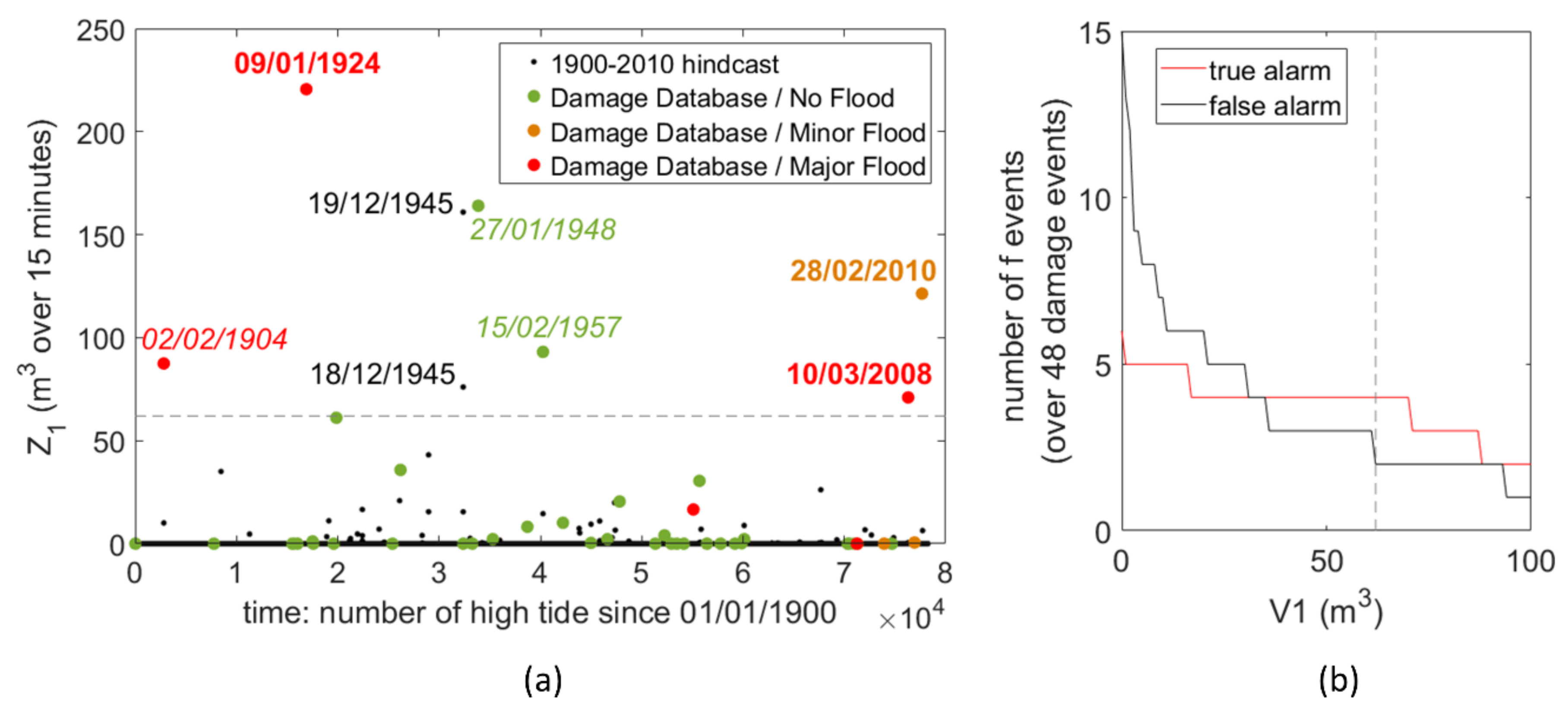
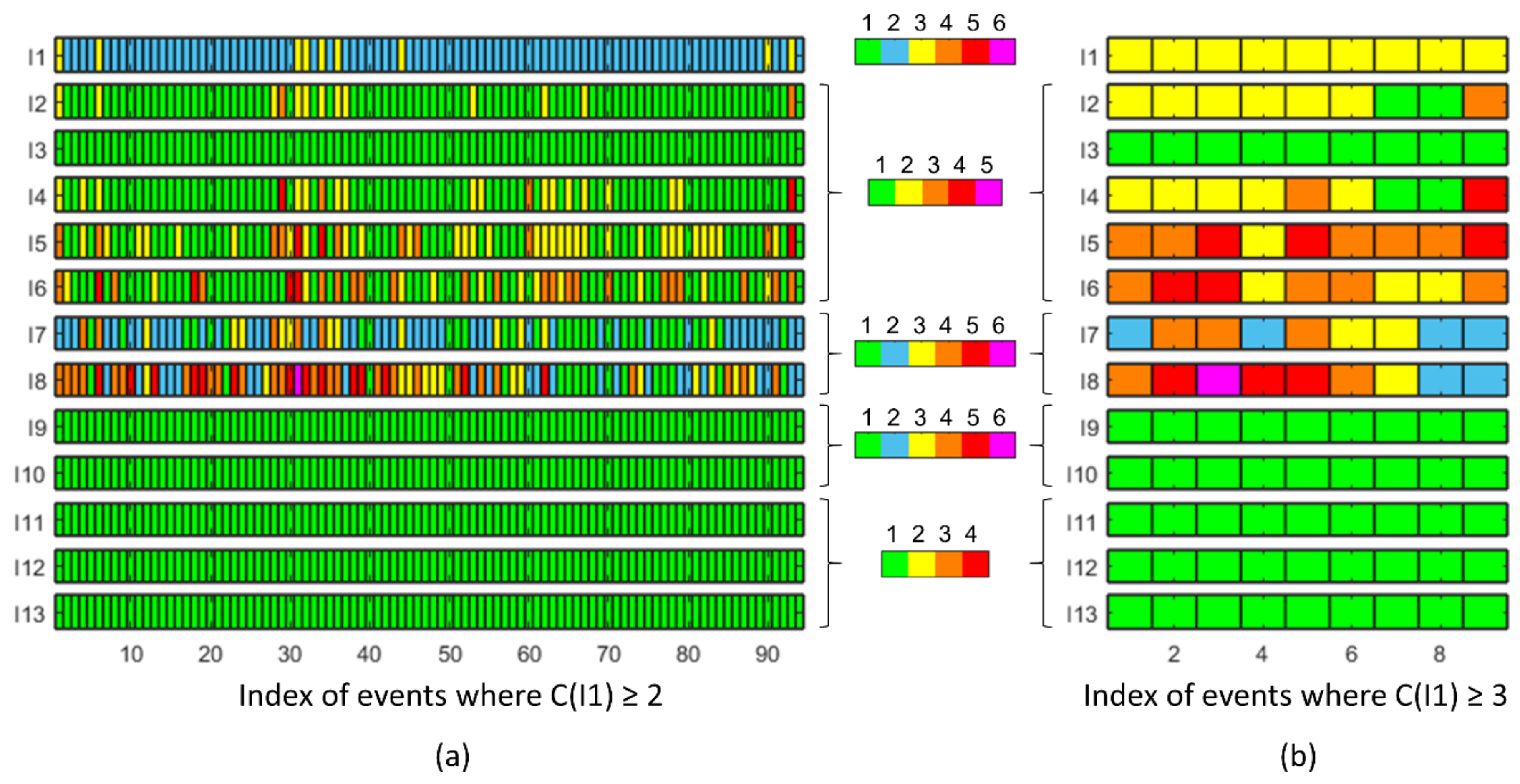
3.3. Indicator Predictions: Raw Results, Optimisation, Hindcast, and Reinforced Hindcast
3.4. FEWS: Operational Use of the FEWS and First Feedbacks
4. Discussion and Recommendations
4.1. Discussion
4.2. Recommendations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Acronyms and Abbreviations
| ACO-Gp | Ant colony-based algorithm for the structural optimisation of Gaussian process models with scalar and/or functional inputs |
| CRAN | Comprehensive R Archive Network |
| DDTM56 | Direction Départementale des Territoires et de la Mer (translation: Departmental Directorate of Territories and the Sea) of French department 56 (Morbihan) |
| DEM | Digital elevation model |
| DGPS | Differential Global Positioning System |
| DHI | Danish Hydraulic Institute |
| FEWS | Forecast and early warning system |
| GP | Gaussian process |
| HT | High tide |
| HPC | High-performance computing |
| IGN | Institut National de l’Information Géographique et Forestière (translation: National Institute of Geographic and Forestry Information) |
| LOO | Leave one out |
| LOPS | Laboratoire d’Océanographie Physique et Spatiale (translation: Physical and Space Oceanography Laboratory) |
| MARC | Modélisation et Analyse pour la Recherche Côtière (translation: Modelling and Analysis for Coastal Research) |
| MEDDTL | Ministère de l’Écologie, du Développement Durable des Transports et du Logement (translation: Ministry of Ecology, Sustainable Development, Transport and Housing) |
| MIKE21 | software package for the 2D modelling of hydrodynamics, waves, sediment dynamics, water quality and ecology; for more details, see https://www.mikepoweredbydhi.com/products/mike-21-3, accessed on 25 July 2021 |
| PCA | Principal component analysis |
| RF | Random forest |
| RGE | Référentiel à grande echelle (translation: large-scale reference system) |
| TELEMAC2D | module of the TELEMAC system for solving the Saint-Venant equations using The finite-element or finite-volume method and a computational mesh of triangular elements; for more details, see http://www.opentelemac.org, accessed on 25 July 2021 |
| SDIS56 | Service Départemental d’Incendie et de Secours (translation: Departmental Fire and Rescue Service) of French department 56 (Morbihan) |
| SHOM | Service Hydrographique et Océanographique de la Marine (translation: French Navy Hydrographic and Oceanographic Service) |
| SWASH | Simulating Waves till Shore. SWASH is a general-purpose numerical tool for simulating unsteady, non-hydrostatic, free-surface, rotational flow and transport phenomena in coastal waters driven by waves, tides, buoyancy and wind forces. It provides a general basis for describing wave transformations from deep water to a beach, port, or harbour, complex changes to rapidly varied flows, and density-driven flows in coastal seas, estuaries, lakes and rivers. For more details, see https://swash.sourceforge.io/, accessed on 25 July 2021 |
| VISOV | Volontaires Internationaux et Soutien Opérationnel Virtuel (translation: International Volunteers and Virtual Operational Support) |
| VOST | Virtual Operations Support Team |
| VVS | Vigilance Vague Submersion (translation: wave-flood warning) |
| WW3 | WAVEWATCH III®, a community wave modelling framework that includes the latest scientific advancements in the field of wind-wave modelling and dynamics |
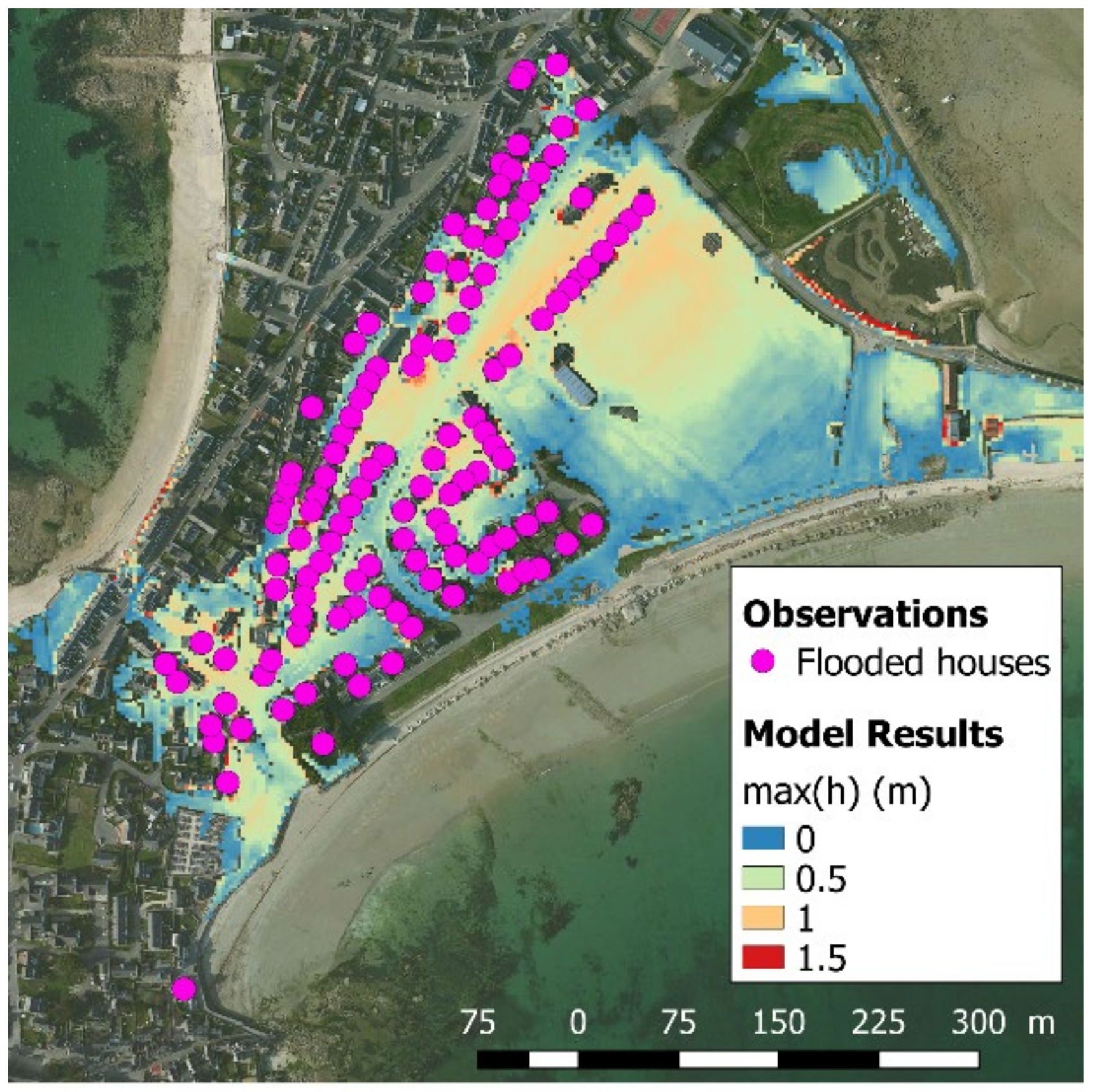
Appendix A. The Flood Event on 10 March 2008 (Observations and Model Results)
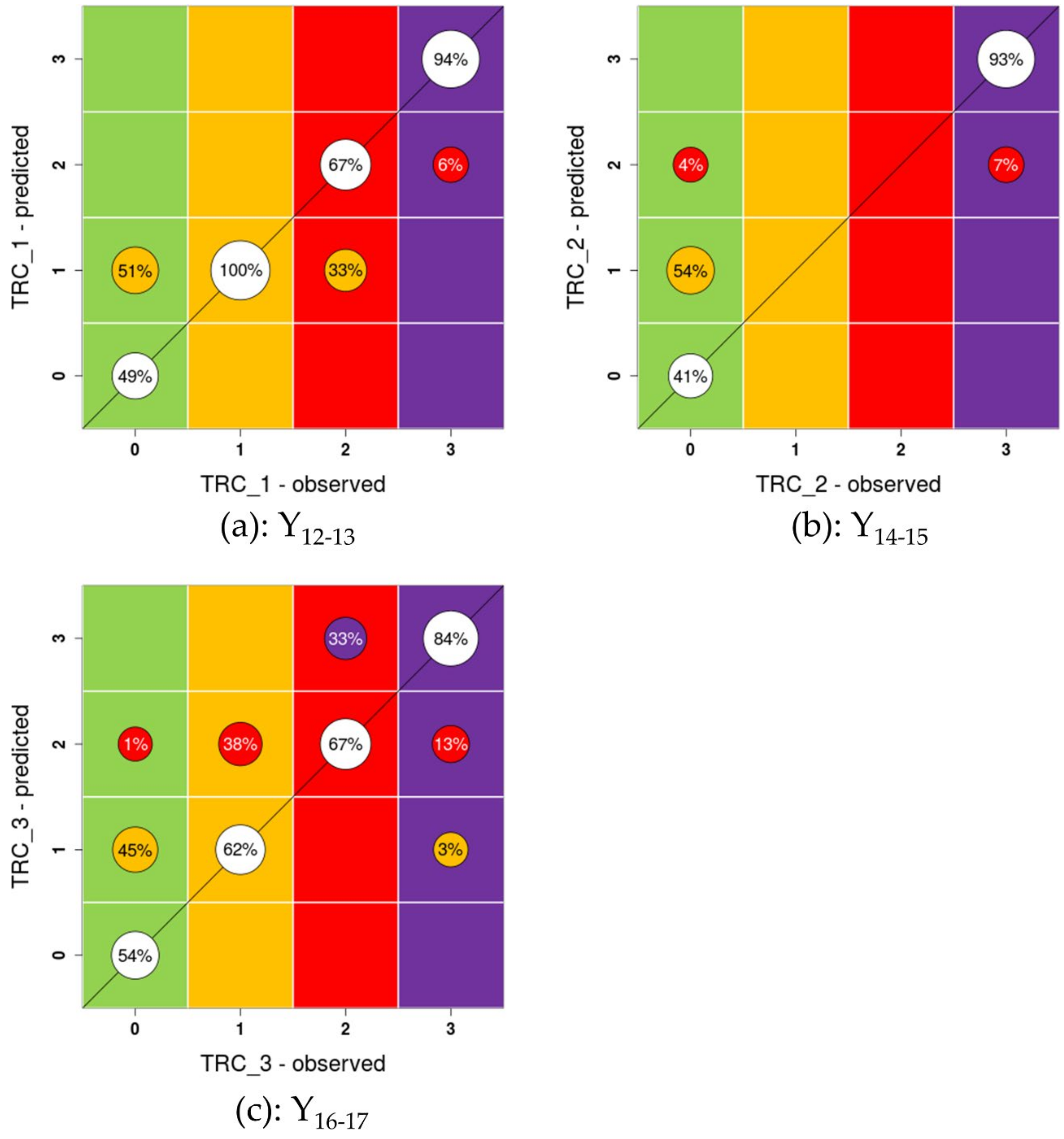
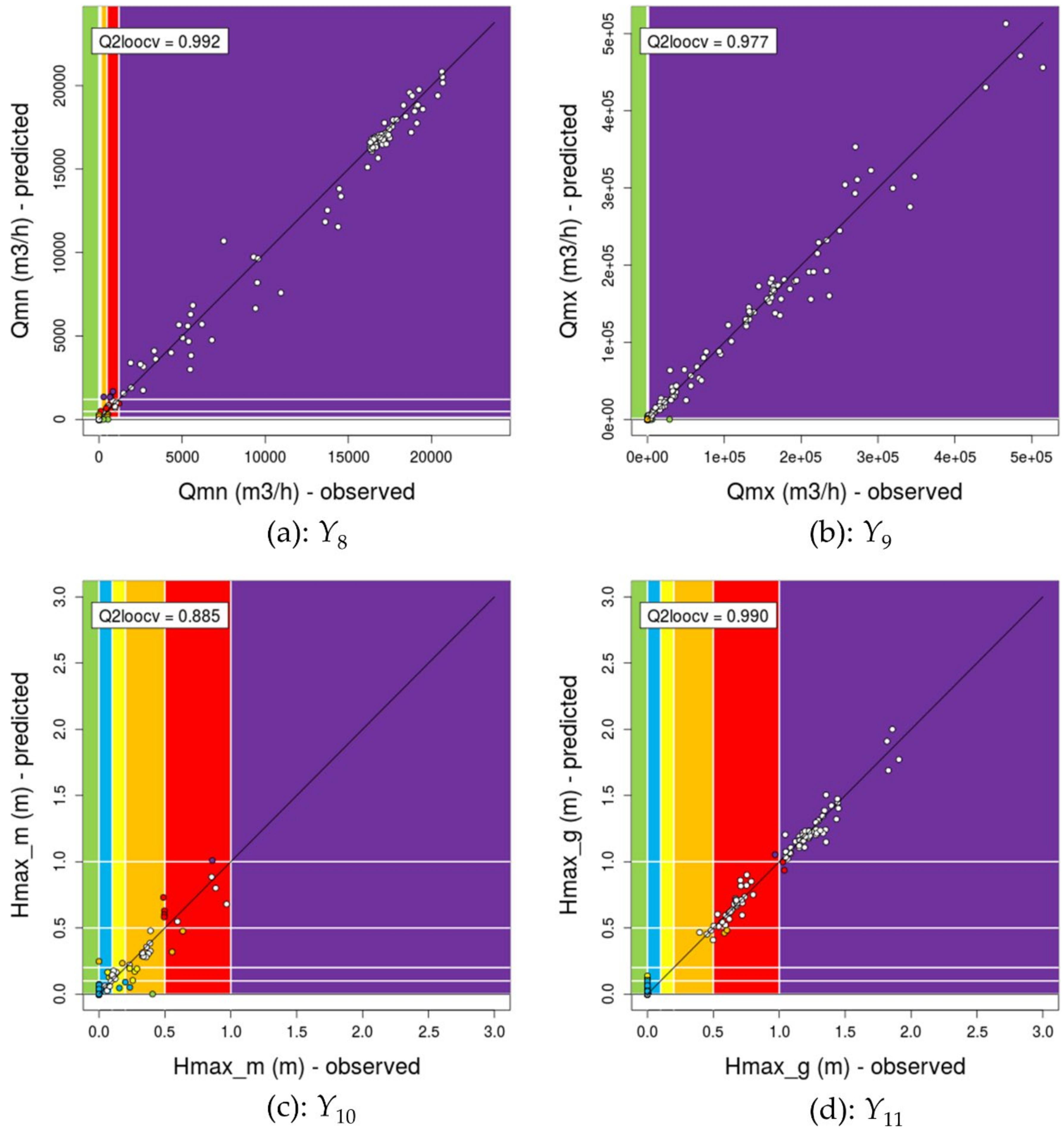
Appendix B. Cross-Validation Plots for Metamodels Y8 to Y13
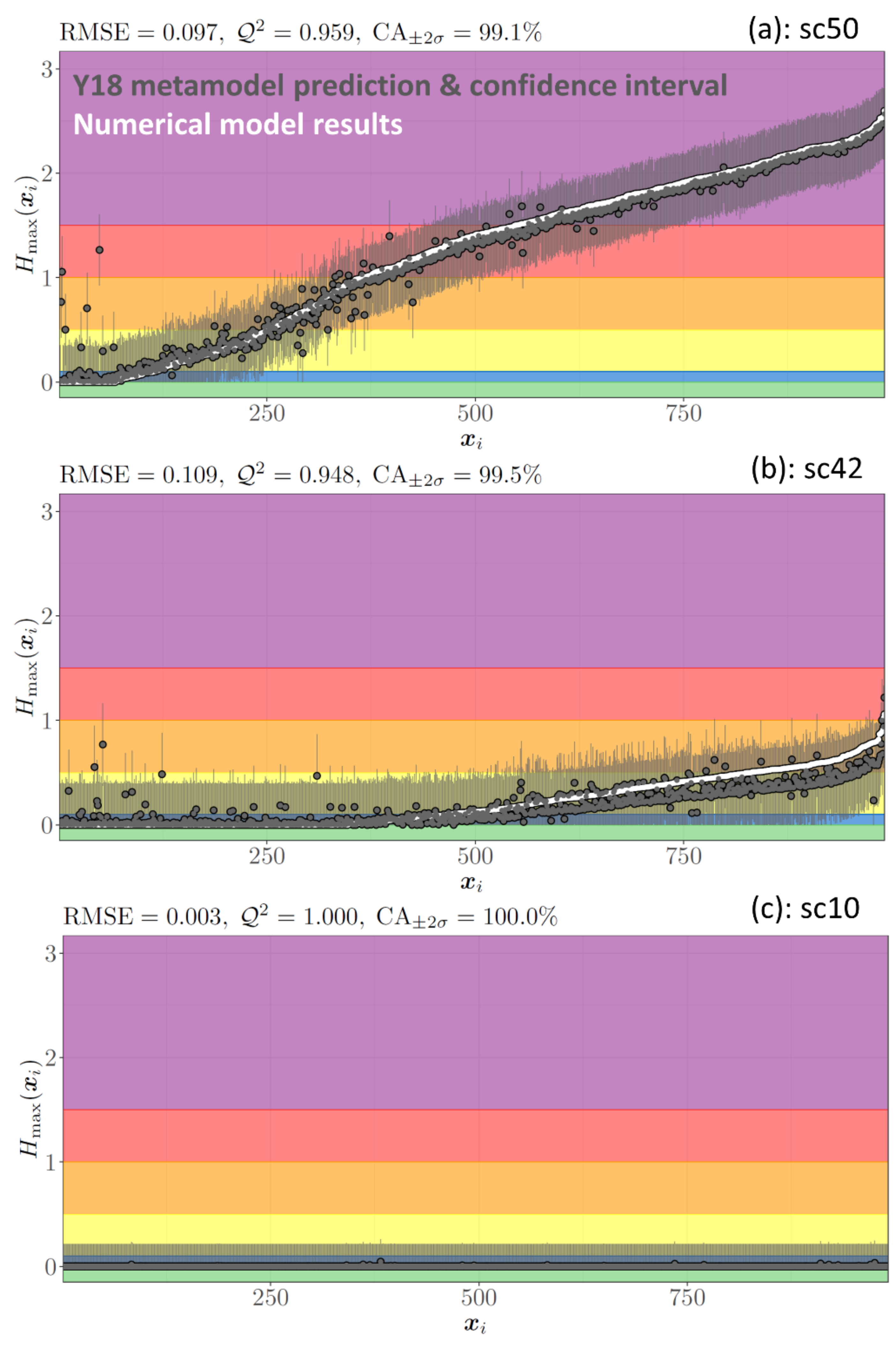
Appendix C. Cross-Validation Plots for Metamodel YI8
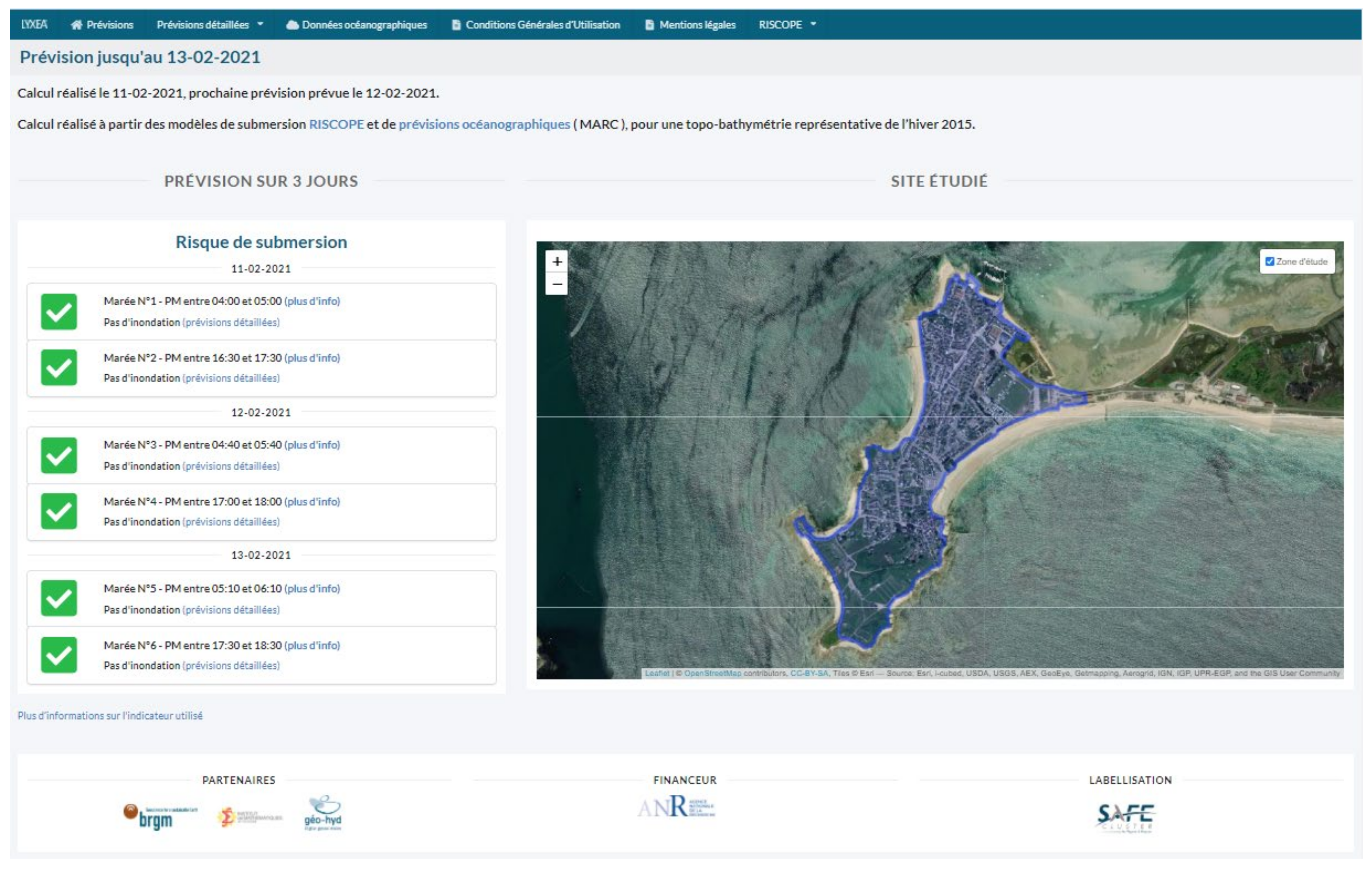
Appendix D. Screen Captures of the FEWS User Interface

References
- McGranahan, G.; Balk, D.; Anderson, B. The rising tide: Assessing the risks of climate change and human settlements in low elevation coastal zones. Environ. Urban. 2007, 19, 17–37. [Google Scholar] [CrossRef]
- Oppenheimer, M.; Glavovic, B.C.; Hinkel, J.; van de Wal, R.; Magnan, A.K.; Abd-Elgawad, A.; Cai, R.; Cifuentes-Jara, M.; DeConto, R.M.; Ghosh, T.; et al. Sea Level Rise and Implications for Low-Lying Islands, Coasts and Communities. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.-O., Roberts, D.C., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., et al., Eds.; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Jongman, B. Effective adaptation to rising flood risk. Nat. Commun. 2018, 9, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Le Roy, S.; Pedreros, R.; André, C.; Paris, F.; Lecacheux, S.; Marche, F.; Vinchon, C. Coastal flooding of urban areas by overtopping: Dynamic modelling application to the Johanna storm (2008) in Gâvres (France). Nat. Hazards Earth Syst. Sci. 2015, 15, 2497–2510. [Google Scholar] [CrossRef] [Green Version]
- Idier, D.; Pedreros, R.; Rohmer, J.; Le Cozannet, G. The Effect of Stochasticity of Waves on Coastal Flood and Its Variations with Sea-level Rise. J. Mar. Sci. Eng. 2020, 8, 798. [Google Scholar] [CrossRef]
- Idier, D.; Rohmer, J.; Pedreros, R.; Le Roy, S.; Lambert, J.; Louisor, J.; Le Cozannet, G.; Le Cornec, E. Coastal flood: A composite method for past events characterisation providing insights in past, present and future hazards—joining historical, statistical and modelling approaches. Nat. Hazards 2020, 101, 465–501. [Google Scholar] [CrossRef] [Green Version]
- Doong, D.-J.; Chuang, L.Z.-H.; Wu, L.-C.; Fan, Y.-M.; Kao, C.C.; Wang, J.-H. Development of an operational coastal flooding early warning system. Nat. Hazards Earth Syst. Sci. 2012, 12, 379–390. [Google Scholar] [CrossRef]
- Tromble, E.; Kolar, R.; Dresback, K.; Hong, Y.; Vieux, B.; Luettich, R.; Gourley, J.; Kelleher, K.; Van Cooten, S. Aspects of Coupled Hydrologic-Hydrodynamic Modeling for Coastal Flood Inundation. In Proceedings of the Eleventh International Conference on Estuarine and Coastal Modeling, Seattle, WA, USA, 4–6 November 2009; pp. 724–743. [Google Scholar]
- Stansby, P.; Chini, N.; Apsley, D.; Borthwick, A.G.L.; Bricheno, L.M.; Horrillo-Caraballo, J.M.; McCabe, M.; Reeve, D.E.; Rogers, B.; Saulter, A.; et al. An integrated model system for coastal flood prediction with a case history for Walcott, UK, on 9 November 2007. J. Flood Risk Manag. 2013, 6, 229–252. [Google Scholar] [CrossRef] [Green Version]
- Stokes, K.; Poate, T.; Masselink, G.; King, E.; Saulter, A.; Ely, N. Forecasting coastal overtopping at engineered and naturally defended coastlines. Coast. Eng. 2020, 164, 103827. [Google Scholar] [CrossRef]
- Merrifield, M.A.; Johnson, M.; Guza, R.T.; Fiedler, J.W.; Young, A.P.; Henderson, C.S.; Lange, A.M.Z.; O’Reilly, W.C.; Ludka, B.C.; Okihiro, M.; et al. An early warning system for wave-driven coastal flooding at Imperial Beach, CA. Nat. Hazards 2021, 108, 2591–2612. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.-W. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef] [Green Version]
- Fotovatikhah, F.; Herrera, M.; Shamshirband, S.; Chau, K.-W.; Ardabili, S.F.; Piran, J. Survey of computational intelligence as basis to big flood management: Challenges, research directions and future work. Eng. Appl. Comput. Fluid Mech. 2018, 12, 411–437. [Google Scholar] [CrossRef] [Green Version]
- Kaya, C.M.; Tayfur, G.; Gungor, O. Predicting flood plain inundation for natural channels having no upstream gauged stations. J. Water Clim. Chang. 2017, 10, 360–372. [Google Scholar] [CrossRef]
- Dong, S.; Yu, T.; Farahmand, H.; Mostafavi, A. A hybrid deep learning model for predictive flood warning and situation awareness using channel network sensors data. Comput. Civ. Infrastruct. Eng. 2020, 36, 402–420. [Google Scholar] [CrossRef]
- Dai, W.; Tang, Y.; Zhang, Z.; Cai, Z. Ensemble Learning Technology for Coastal Flood Forecasting in Internet-of-Things-Enabled Smart City. Int. J. Comput. Intell Syst 2021, 14, 166. [Google Scholar] [CrossRef]
- Rohmer, J.; Idier, D. A meta-modelling strategy to identify the critical offshore conditions for coastal flooding. Nat. Hazards Earth Syst. Sci. 2012, 12, 2943–2955. [Google Scholar] [CrossRef]
- Jia, G.; Taflanidis, A.A. Kriging metamodeling for approximation of high-dimensional wave and surge responses in real-time storm/hurricane risk assessment. Comput. Methods Appl. Mech. Eng. 2013, 261–262, 24–38. [Google Scholar] [CrossRef]
- Simpson, T.; Poplinski, J.; Koch, P.N.; Allen, J. Metamodels for Computer-based Engineering Design: Survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef] [Green Version]
- Basher, R. Global early warning systems for natural hazards: Systematic and people centred. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2006, 364, 2167–2182. [Google Scholar] [CrossRef]
- Rohmer, J.; Idier, D.; Pedreros, R. A nuanced quantile random forest approach for fast prediction of a stochastic marine flooding simulator applied to a macrotidal coastal site. Stoch. Environ. Res. Risk Assess. 2020, 34, 867–890. [Google Scholar] [CrossRef]
- Betancourt, J.; Bachoc, F.; Klein, T.; Idier, D.; Pedreros, R.; Rohmer, J. Gaussian process metamodeling of functional-input code for coastal flood hazard assessment. Reliab. Eng. Syst. Saf. 2020, 198, 106870. [Google Scholar] [CrossRef] [Green Version]
- López-Lopera, A.F.; Idier, D.; Rohmer, J.; Bachoc, F. Multioutput Gaussian processes with functional data: A study on coastal flood hazard assessment. arXiv. 2020. Available online: https://arxiv.org/abs/2007.14052 (accessed on 25 July 2021).
- Idier, D.; Aurouet, A.; Bachoc, F.; Baills, A.; Betancourt, J.; Durand, J.; Mouche, R.; Rohmer, J.; Gamboa, F.; Klein, T.; et al. Toward a User-Based, Robust and Fast Running Method for Coastal Flooding Forecast, Early Warning, and Risk Prevention. J. Coast. Res. 2020, 95, 1111–1116. [Google Scholar] [CrossRef]
- Cariolet, J.M. Inondation des Côtes Basses et Risques Associés en Bretagne: Vers une Redéfinition des Processus Hydrodynamiques Liés aux Conditions Météo-Océaniques et des Paramètres Morphosédimentaires. Océan, Atmosphère. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2011. [Google Scholar]
- Pedreros, R.; Idier, D.; Le Roy, S.; David, A.; Schaeffer, C.; Durand, J.; Desmazes, F. Infragravity Waves in a Complex Macro-tidal Environment: High Frequency Hydrodynamic Measurements and Modelling. J. Coast. Res. 2020, 95, 1235–1239. [Google Scholar] [CrossRef]
- Haiden, T.; Janousek, M.; Vitart, F.; Ben-Bouallegue, Z.; Ferranti, L.; Prates, F. Evaluation of ECMWF Forecasts, Including the 2021 Upgrade. Available online: https://www.ecmwf.int/en/elibrary/20142-evaluation-ecmwf-forecasts-including-2021-upgrade (accessed on 8 October 2021).
- Kramer, M.; Terheiden, K.; Wieprecht, S. Safety criteria for the trafficability of inundated roads in urban floodings. Int. J. Disaster Risk Reduct. 2016, 17, 77–84. [Google Scholar] [CrossRef] [Green Version]
- Jonkman, S.; Penningrowsell, E.C. Human Instability in Flood Flows1. JAWRA J. Am. Water Resour. Assoc. 2008, 44, 1208–1218. [Google Scholar] [CrossRef]
- MEDDTL. Guide Méthodologique Plans de Prévention des Risques Littoraux, 2014. Available online: https://www.ecologie.gouv.fr/sites/default/files/Guide%20PPRL%20-%20version%20finale%20mai%202014.pdf (accessed on 25 July 2021).
- Gallien, T.W.; Kalligeris, N.; Delisle, M.-P.C.; Tang, B.-X.; Lucey, J.T.D.; Winters, M.A. Coastal Flood Modeling Challenges in Defended Urban Backshores. Geosciences 2018, 8, 450. [Google Scholar] [CrossRef] [Green Version]
- Van der Meer, J.W.; Allsop, N.W.H.; Bruce, T.; De Rouck, J.; Kortenhaus, A.; Pullen, T.; Schüttrumpf, H.; Troch, P.; Zanuttigh, B. Manual on Wave Overtopping of Sea Defences and Related Structures. An Overtopping Manual Largely Based on European Research, but for Worldwide Application. EurOtop. 2018. Available online: www.overtopping-manual.com (accessed on 12 October 2020).
- Grilli, A.R.; Westcott, G.; Grilli, S.T.; Spaulding, M.L.; Shi, F.; Kirby, J.T. Assessing Coastal Hazard from Extreme Storms with a Phase Resolving Wave Model: Case Study of Narragansett, RI, USA. Coast. Eng. 2020, 160, 103735. [Google Scholar] [CrossRef]
- Nicolae-Lerma, A.; Bulteau, T.; Elineau, S.; Paris, F.; Durand, P.; Anselme, B.; Pedreros, R. High-resolution marine flood modelling coupling overflow and overtopping processes: Framing the hazard based on historical and statistical approaches. Nat. Hazards Earth Syst. Sci. 2018, 18, 207–229. [Google Scholar] [CrossRef] [Green Version]
- SWASH Team. Swash User Manual, Swash Version 6.01, TU Delft. 2019. Available online: http://www.tudelft.nl/swash (accessed on 25 July 2021).
- Ardhuin, F.; Rogers, W.E.; Babanin, A.V.; Filipot, J.; Magne, R.; Roland, A.; Van der Westhuysen, A.; Queffeulou, P.; Lefevre, J.; Aouf, L.; et al. Semiempirical dissipation source functions for ocean waves. Part I: Definition, calibration, and validation. J. Phys. Oceanogr. 2010, 40, 917–941. [Google Scholar] [CrossRef] [Green Version]
- Le Maître, O.P.; Knio, O.M. Spectral Methods for Uncertainty Quantification: With Applications to Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-90-481-3520-2. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning (Adaptive Computation and Machine Learning); The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-0-387-84858-7. [Google Scholar]
- Wasserman, L. All of Nonparametric Statistics; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 10 0387251456. [Google Scholar]
- Gouldby, B.; Méndez, F.J.; Guanche, Y.; Rueda, A.; Mínguez, R. A methodology for deriving extreme nearshore sea conditions for structural design and flood risk analysis. Coast Eng. 2014, 88, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Tharwat, A. Linear vs. quadratic discriminant analysis classifier: A tutorial. Int. J. Appl. Pattern Recognit. 2016, 3, 145–180. [Google Scholar] [CrossRef]
- Perrin, T.; Roustant, O.; Rohmer, J.; Alata, O.; Naulin, J.; Idier, D.; Pedreros, R.; Moncoulon, D.; Tinard, P. Functional principal component analysis for global sensitivity analysis of model with spatial output. Reliab. Eng. Syst. Saf. 2021, 211, 107522. [Google Scholar] [CrossRef]
- Rohmer, J.; Lecacheux, S.; Pedreros, R.; Quetelard, H.; Bonnardot, F.; Idier, D. Dynamic parameter sensitivity in numerical modelling of cyclone-induced waves: A multi-look approach using advanced meta-modelling techniques. Nat. Hazards 2016, 84, 1765–1792. [Google Scholar] [CrossRef]
- Li, M.; Wang, R.-Q.; Jia, G. Efficient dimension reduction and surrogate-based sensitivity analysis for expensive models with high-dimensional outputs. Reliab. Eng. Syst. Saf. 2020, 195, 106725. [Google Scholar] [CrossRef]
- Al Kajbaf, A.; Bensi, M. Application of surrogate models in estimation of storm surge:A comparative assessment. Appl. Soft Comput. 2020, 91, 106184. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- De Boor, C. A Practical Guide to Splines. Applied Mathematical Sciences; Springer: New York, NY, USA, 1978; p. 348. [Google Scholar]
- Jolliffe, I. Principal Component Analysis; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Antoniadis, A.; Helbert, C.; Prieur, C.; Viry, L. Spatio-temporal metamodeling for West African monsoon. Environmetrics 2012, 23, 24–36. [Google Scholar] [CrossRef] [Green Version]
- Muehlenstaedt, T.; Fruth, J.; Roustant, O. Computer experiments with functional inputs and scalar outputs by a norm-based approach. Stat. Comput. 2016, 27, 1083–1097. [Google Scholar] [CrossRef] [Green Version]
- Nanty, S.; Helbert, C.; Marrel, A.; Pérot, N.; Prieur, C. Sampling, Metamodeling, and Sensitivity Analysis of Numerical Simulators with Functional Stochastic Inputs. SIAM/ASA J. Uncertain. Quantif. 2016, 4, 636–659. [Google Scholar] [CrossRef]
- Betancourt, J.; Bachoc, F.; Klein, T.; Gamboa, F. Ant Colony Based Model Selection for Functional-Input Gaussian Process Regression. 2020. Available online: https://hal.archives-ouvertes.fr/hal-02532713v2 (accessed on 25 July 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria. Available online: https://www.R-project.org/ (accessed on 25 July 2021).
- Betancourt, J.; Bachoc, F.; Klein, T.R. Package Manual: Gaussian Process Regression for Scalar and Functional Inputs with funGp-The In-Depth Tour. RISCOPE Project. 2020. Available online: https://hal.archives-ouvertes.fr/hal-02536624 (accessed on 25 July 2021).
- Stein, M.L. Prediction and inference for truncated spatial data. J. Comput. Graph. Stat. 1992, 1, 91–110. [Google Scholar]
- Gormley, C.; Tong, Z. Elasticsearch: The Definitive Guide: A Distributed Real-Time Search and Analytics Engine; O’Reilly Media: Sebastopol, CA, USA, 2015; ISBN 9781449358525. [Google Scholar]
- Chang, W.; Cheng, J.; Allaire, J.; Xie, Y.; McPherson, J. Shiny: Web Application Framework for R. R Package Version 1.5.0. 2020. Available online: https://CRAN.R-project.org/package=shiny (accessed on 25 July 2021).
- Le Cornec, E.; Le Bris, E.; Van Lierde, M. Atlas des Risques Littoraux sur le Département du Morbihan. Phase 1: Recensement et Conséquences des Tempêtes et Coups de Vent Majeurs; Rapport d’étude GEOS-DHI; Direction Départementales des Territoires et de la Mer du Morbihan: Vannes, France, 2012. [Google Scholar]
- Vanhatalo, J.; Vehtari, A. Sparse log Gaussian processes via MCMC for spatial epidemiology. Proc. Mach. Learn. Res. 2007, 1, 73–89. [Google Scholar]
- López-Lopera, A.F.; Bachoc, F.; Durrande, N.; Roustant, O. Finite-dimensional Gaussian approximation with linear inequality constraints. SIAM/ASA J. Uncertain. Quantif. 2018, 6, 1224–1255. [Google Scholar] [CrossRef]
- Bachoc, F.; Suvorikova, A.; Ginsbourger, D.; Loubes, J.-M.; Spokoiny, V. Gaussian processes with multidimensional distribution inputs via optimal transport and Hilbertian embedding. Electron. J. Stat. 2020, 14, 2742–2772. [Google Scholar] [CrossRef]
- Liu, X.; Guillas, S. Dimension reduction for Gaussian process emulation: An application to the influence of bathymetry on tsunami heights. SIAM/ASA J. Uncertain. Quantif. 2017, 5, 787–812. [Google Scholar] [CrossRef]
- Jonkman, S.N.; Kok, M.; Vrijling, J.K. Flood Risk Assessment in the Netherlands: A Case Study for Dike Ring South Holland. Risk Anal. 2008, 28, 1357–1374. [Google Scholar] [CrossRef]
- Kwadijk, J.C.J.; Haasnoot, M.; Mulder, J.P.M.; Hoogvliet, M.M.C.; Jeuken, A.B.M.; van der Krogt, R.A.A.; van Oostrom, N.G.C.; Schelfhout, H.A.; van Velzen, E.H.; van Waveren, H.; et al. Using adaptation tipping points to prepare for climate change and sea level rise: A case study in the Netherlands. Wiley Interdiscip. Rev. Clim. Chang. 2010, 1, 729–740. [Google Scholar] [CrossRef]
- Mel, R.A.; Viero, D.P.; Carniello, L.; D’Alpaos, L. Optimal floodgate operation for river flood management: The case study of Padova (Italy). J. Hydrol. Reg. Stud. 2020, 30, 100702. [Google Scholar] [CrossRef]
- Harley, M.D.; Kinsela, M.A.; Sánchez-García, E.; Vos, K. Shoreline change mapping using crowd-sourced smartphone images. Coast. Eng. 2019, 150, 175–189. [Google Scholar] [CrossRef]
- Silvertown, J. A new dawn for citizen science. Trends Ecol. Evol. 2009, 24, 467–471. [Google Scholar] [CrossRef]
- Roger, E.; Tegart, P.; Dowsett, R.; Kinsela, M.A.; Harley, M.D.; Ortac, G. Maximising the potential for citizen science in New South Wales. Aust. Zoöl. 2020, 40, 449–461. [Google Scholar] [CrossRef]
- Liu, S.B. Crisis Crowdsourcing Framework: Designing Strategic Configurations of Crowdsourcing for the Emergency Management Domain. Comput. Support. Cooperative Work. (CSCW) 2014, 23, 389–443. [Google Scholar] [CrossRef]
- Kankanamge, N.; Yigitcanlar, T.; Goonetilleke, A. Kamruzzaman Can volunteer crowdsourcing reduce disaster risk? A systematic review of the literature. Int. J. Disaster Risk Reduct. 2019, 35, 101097. [Google Scholar] [CrossRef]
- Bates, P.D.; Dawson, R.J.; Hall, J.W.; Horritt, M.S.; Nicholls, R.J.; Wicks, J.; Hassan, M.A.A.M. Simplified two-dimensional numerical modelling of coastal flooding and example applications. Coast. Eng. 2005, 52, 793–810. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Haigh, I.D.; Ozsoy, O.; Wadey, M.P.; Nicholls, R.; Gallop, S.L.; Wahl, T.; Brown, J. An improved database of coastal flooding in the United Kingdom from 1915 to 2016. Sci. Data 2017, 4, 170100. [Google Scholar] [CrossRef] [Green Version]
- Tavares, A.O.; Barros, J.L.; Freire, P.; Santos, P.P.; Perdiz, L.; Fortunato, A.B. A coastal flooding database from 1980 to 2018 for the continental Portuguese coastal zone. Appl. Geogr. 2021, 135, 102534. [Google Scholar] [CrossRef]
- Azzimonti, D.; Ginsbourger, D.; Chevalier, C.; Bect, J.; Richet, Y. Adaptive design of experiments for conservative estimation of excursion sets. Technometrics 2021, 63, 13–26. [Google Scholar] [CrossRef] [Green Version]
- Boudière, E.; Maisondieu, C.; Ardhuin, F.; Accensi, M.; Pineau-Guillou, L.; Lepesqueur, J. A suitable metocean hindcast database for the design of Marine energy converters. Int. J. Mar. Energy 2013, 3–4, e40–e52. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Balmaseda, M.; Balsamo, G.; Engelen, R.; Simmons, A.J.; Thépaut, J.-N. Toward a consistent reanalysis of the climate system. Bull. Am. Meteor. Soc. 2014, 95, 1235–1248. [Google Scholar] [CrossRef]

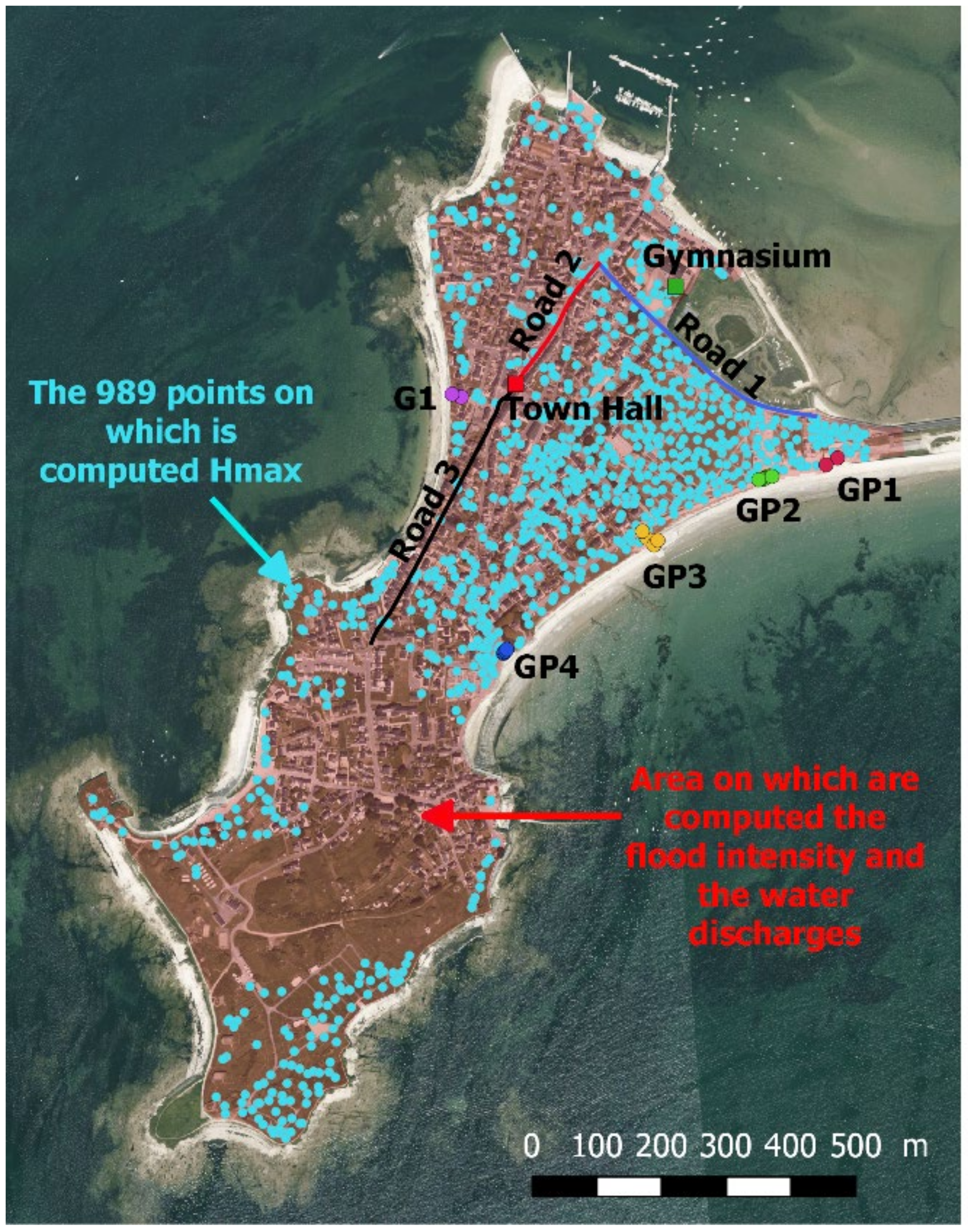


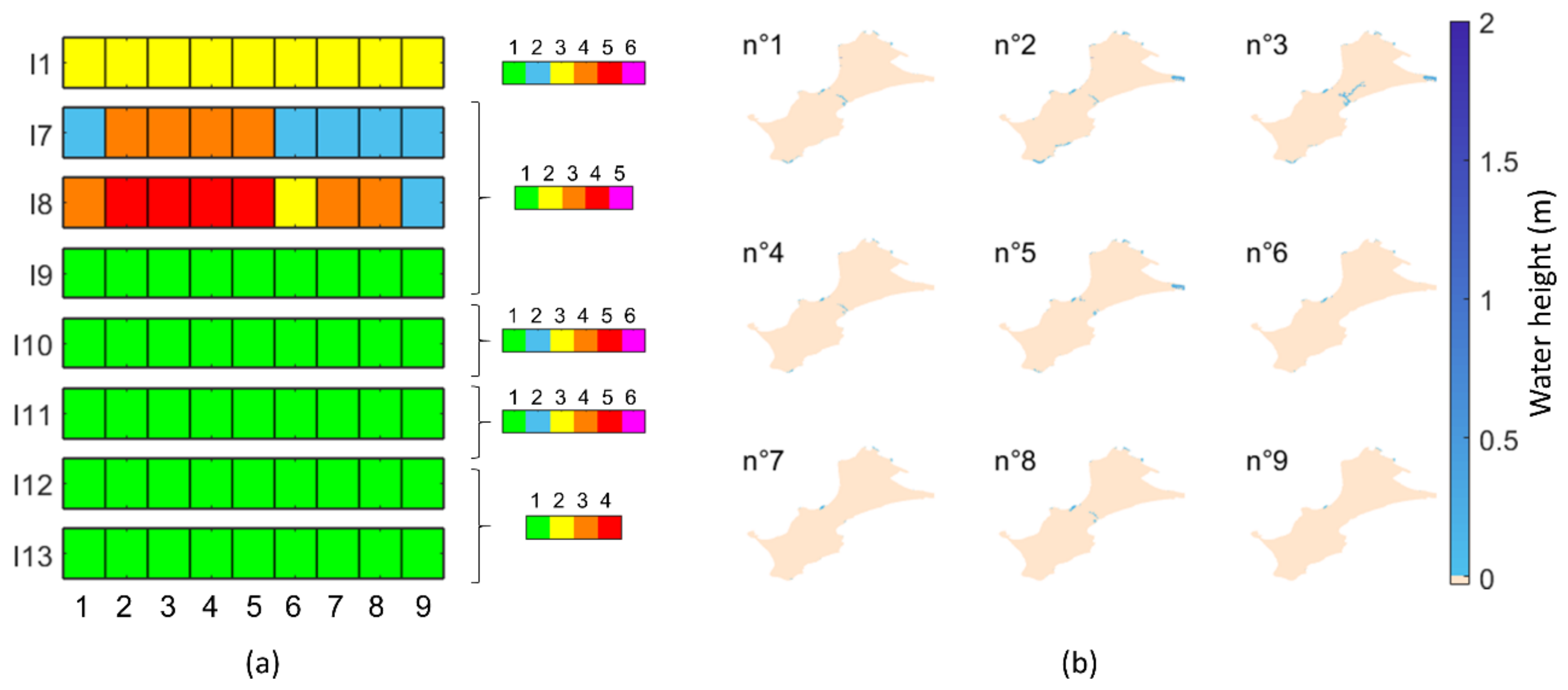
| Needs | Indicator Ij | j |
|---|---|---|
| Flood intensity | 1 |
| Human risk at survey point GP1 | 2 |
| Human risk at survey point GP2 | 3 | |
| Human risk at survey point GP3 | 4 | |
| Human risk at survey point GP4 | 5 | |
| Human risk at survey point G1 | 6 | |
| Mean water discharge | 7 |
| Maximal water discharge | 8 | |
| Water height in front of the town hall | 9 |
| Water height in front of the gymnasium | 10 | |
| Practicability of road portion 1 | 11 |
| Practicability of road portion 2 | 12 | |
| Practicability of road portion 3 | 13 | |
| Water height in hundreds of pre-selected locations | 14 |
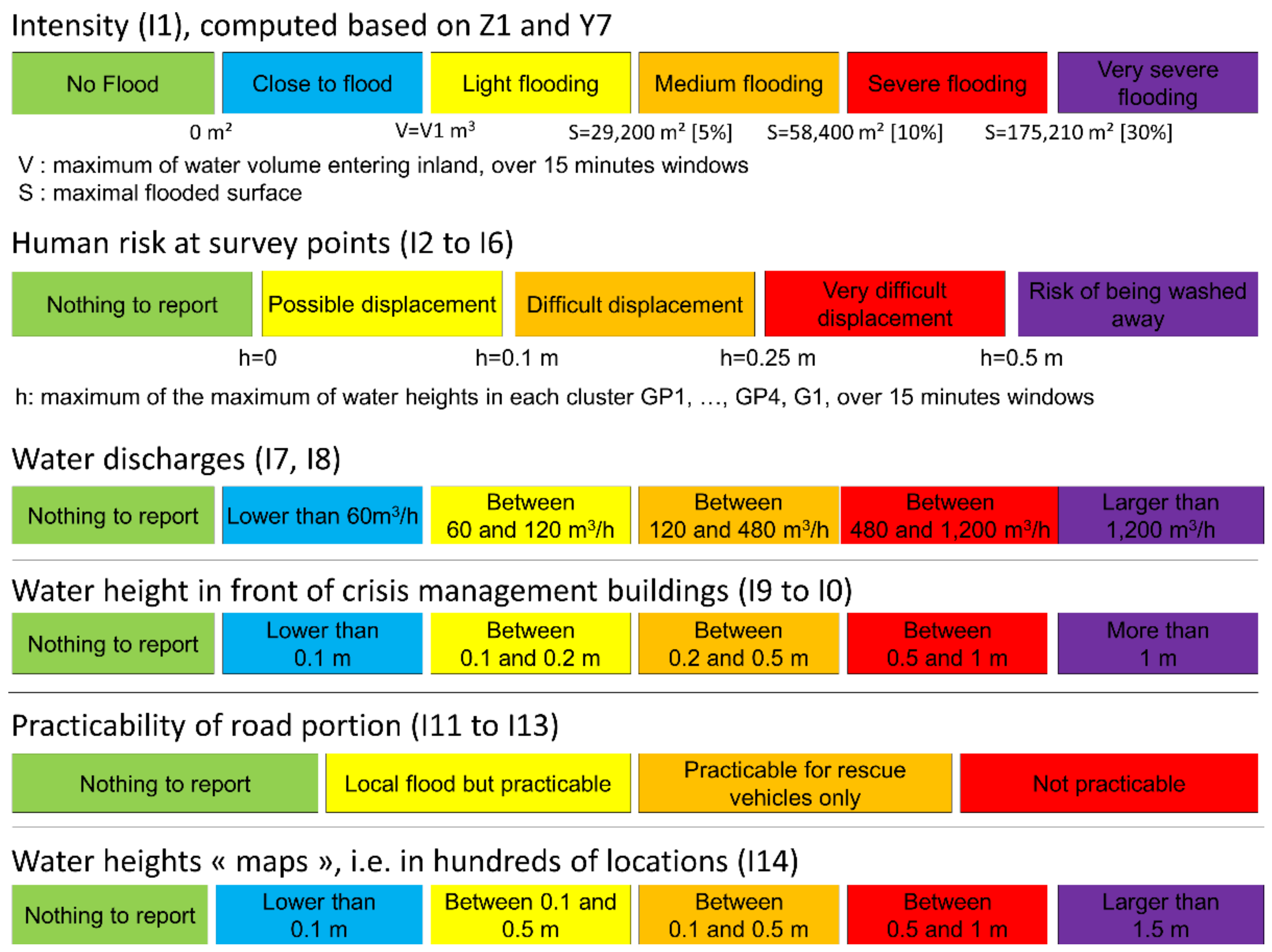
| I | Significance of Yi | Unit | Input | Zk = f(Yi) | No. j of the Indicator Ij for Which | |
|---|---|---|---|---|---|---|
| Zi Is the Main Input | Zi Is a Secondary Input | |||||
| 1 | Volume of water entering inland over 15 min | m3 | S | Z1 = Maxt(Y1) | N.C. | 1 to 13 |
| 2 | Maximal water height over the cluster of points GP1, GP2, GP3, GP4, and G1 over 15 min | m | S | Z2 = Maxt(Y2) | 2 | |
| 3 | Z3 = Maxt(Y3) | 3 | ||||
| 4 | Z4 = Maxt(Y4) | 4 | ||||
| 5 | Z5 = Maxt(Y5) | 5 | ||||
| 6 | Z6 = Maxt(Y6) | 6 | ||||
| 7 | Maximal flooded surface | m2 | F | Z7 = Y7 | 1 | 10, 11, 13 |
| 8 | Mean (Y8) and maximal (Y9) water discharge entering inland | m3/h | F | Z8 = Y8 | 7 | |
| 9 | Z9 = Y9 | 8 | ||||
| 10 | Maximal water height over the event in front of the town hall (Y10) and the gymnasium (Y10) | m | F | Z10 = Y10 | 9 | |
| 11 | Z11 = Y11 | 10 | ||||
| 12 | For each road, Section 1, Section 2 and Section 3: total head (as defined in [29]) for the entire road (Y12,14,16) and the highest track of the road (Y13,15,17) | m | F | For k = 12,13,14Zk(Yk = 0) = 0, elseZk(Yk+1 < hE11) = 1Zk(hE1 < Yk+1 &#; hE2) = 2Zk (hE2 < Yk+1) = 3 | 11 | |
| 13 | ||||||
| 14 | 12 | |||||
| 15 | ||||||
| 16 | 13 | |||||
| 17 | ||||||
| 18 | Maximal water height in NP locations (NP = 989) | m | F | Z15 (n = 1:NP) = Y18 (n = 1:NP) | 14 | |
| Date | I1 Prediction with X=, N Days in Advance (1 to 3) | I1 from the Numerical Modelling with X=, One Day in Advance | VVS Warnings | Observations [Town Hall Information; Photos] → Evaluation of I1 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Xmarc | Xdatashom | Xmarc | Xdatashom | |||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 1 | |||
| 29 September 2019 | 2 | 2 | 2 | 1 | 1 | 2 | 2 | 1 | NTR | [NTR; wave overtopping on the tombolo but outside the study area *] → 1 to 2 |
| 30 September 2019 | 2 | 2 | 2 | 1 | 1 | 1 | 2 | 1 | NTR | |
| 14 January 2020 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | Orange | [NTR; water level close to the coastal defence crests at GP4 *] → 1 to 2 |
| 10 February 2020 | 2 | 2 | 2 | 1 | 1 | 1 | 2 | 1 | Orange | |
| 11 March 2020 | 2 | 2 | 2 | 1 | 1 | 1 | 2 | 1 | NTR | [NTR; No photo] → 1 to 2 |
| 9 April 2020 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | NTR | [NTR; No photo] → 1 to 2 |
| 17 October 2020 | 2 | 1 | 1 | 1 | 1 | 1 | NTR | [NTR; No photo] → 1 to 2 | ||
| 15 November 2020 | 2 | 2 | 1 | 1 | 2 | 1 | NTR | [NTR; No photo] → 1 to 2 | ||
| 16 December 2020 | 2 | 2 | 2 | 1 | 1 | 1 | 2 | 2 | NTR | [NTR; No photo] → 1 to 2 |
| 30 January 2021 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | Orange | [small overtopping/overflow on the tombolo, but outside the study area; small overtopping *] → 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Idier, D.; Aurouet, A.; Bachoc, F.; Baills, A.; Betancourt, J.; Gamboa, F.; Klein, T.; López-Lopera, A.F.; Pedreros, R.; Rohmer, J.; et al. A User-Oriented Local Coastal Flooding Early Warning System Using Metamodelling Techniques. J. Mar. Sci. Eng. 2021, 9, 1191. https://doi.org/10.3390/jmse9111191
Idier D, Aurouet A, Bachoc F, Baills A, Betancourt J, Gamboa F, Klein T, López-Lopera AF, Pedreros R, Rohmer J, et al. A User-Oriented Local Coastal Flooding Early Warning System Using Metamodelling Techniques. Journal of Marine Science and Engineering. 2021; 9(11):1191. https://doi.org/10.3390/jmse9111191
Chicago/Turabian StyleIdier, Déborah, Axel Aurouet, François Bachoc, Audrey Baills, José Betancourt, Fabrice Gamboa, Thierry Klein, Andrés F. López-Lopera, Rodrigo Pedreros, Jérémy Rohmer, and et al. 2021. "A User-Oriented Local Coastal Flooding Early Warning System Using Metamodelling Techniques" Journal of Marine Science and Engineering 9, no. 11: 1191. https://doi.org/10.3390/jmse9111191
APA StyleIdier, D., Aurouet, A., Bachoc, F., Baills, A., Betancourt, J., Gamboa, F., Klein, T., López-Lopera, A. F., Pedreros, R., Rohmer, J., & Thibault, A. (2021). A User-Oriented Local Coastal Flooding Early Warning System Using Metamodelling Techniques. Journal of Marine Science and Engineering, 9(11), 1191. https://doi.org/10.3390/jmse9111191