Transient Responses Evaluation of FPSO with Different Failure Scenarios of Mooring Lines
Abstract
:1. Introduction
2. Governing Equations and Formulation
2.1. Mooring Line Model
2.2. Hydrodynamic Model of FPSO
2.2.1. Wave Force Calculation
2.2.2. Wind Force Calculation
2.2.3. Current Force Calculation
2.2.4. Coupled Analysis of FPSO and Mooring Lines
2.2.5. Simulation of Mooring Line Breakage at a Certain Time
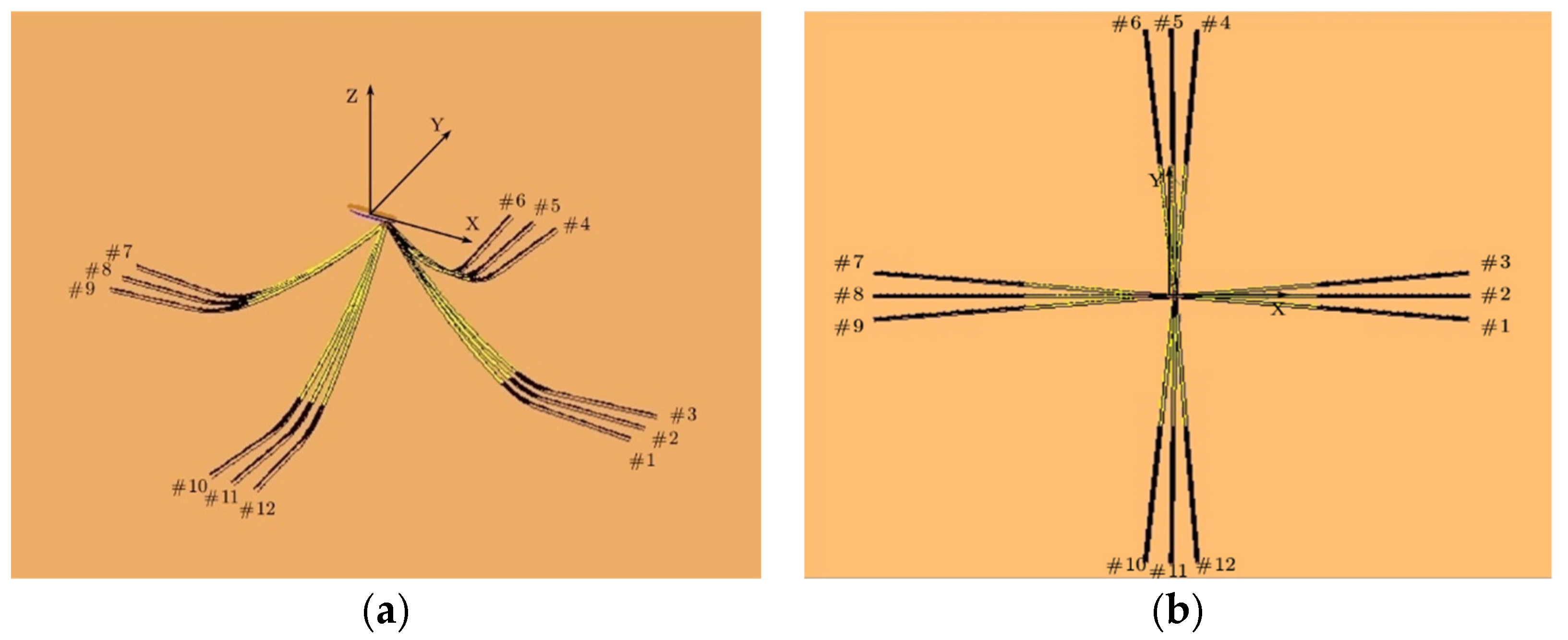
3. FPSO and Mooring System Arrangement
3.1. Description of FPSO and Mooring System
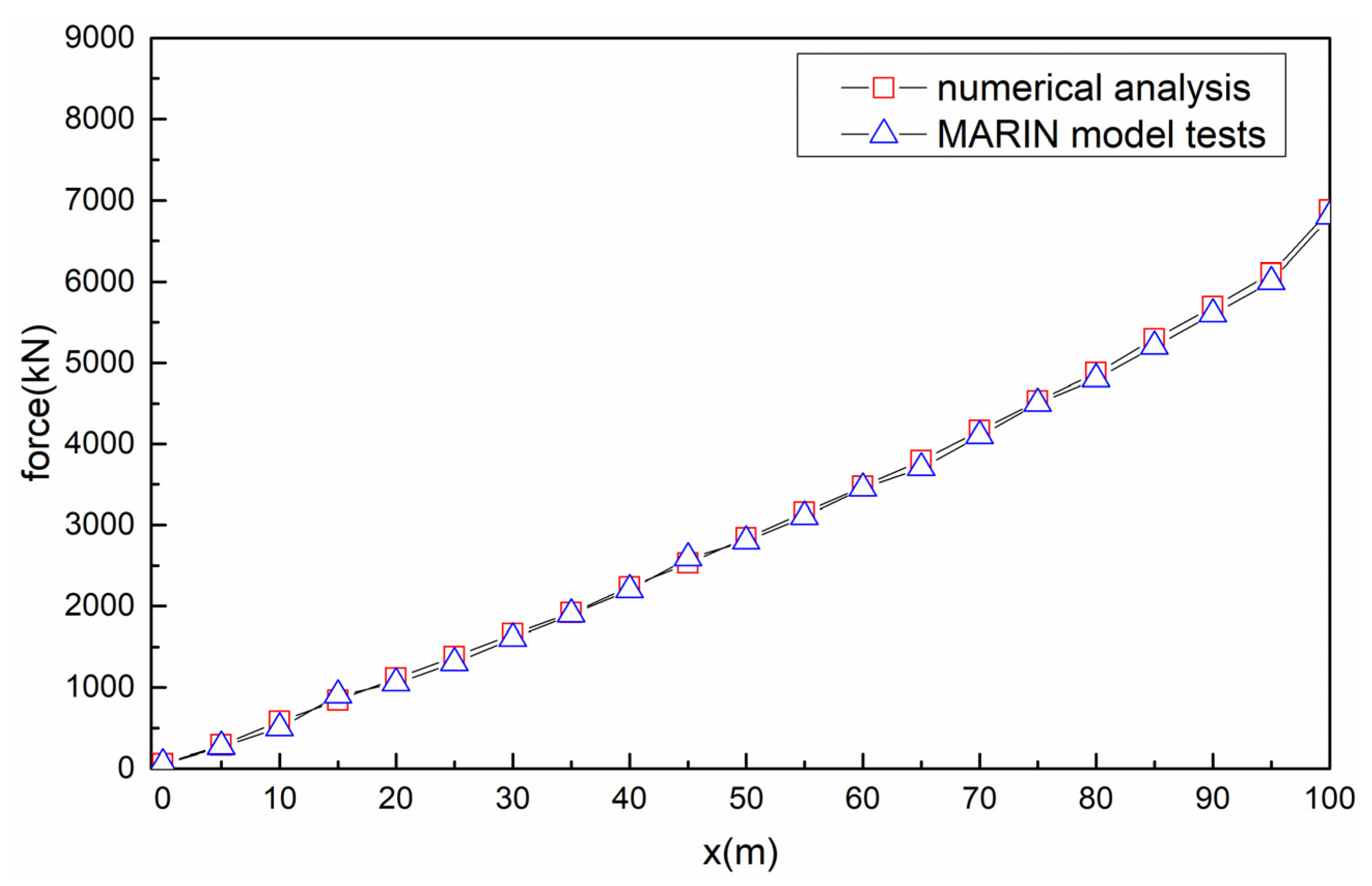
3.2. Motion Responses Calculation Model Verification
4. Environmental Condition and Mooring Line Broken Cases
5. Analysis of FPSO System with Broken Mooring Lines
5.1. Static Analysis
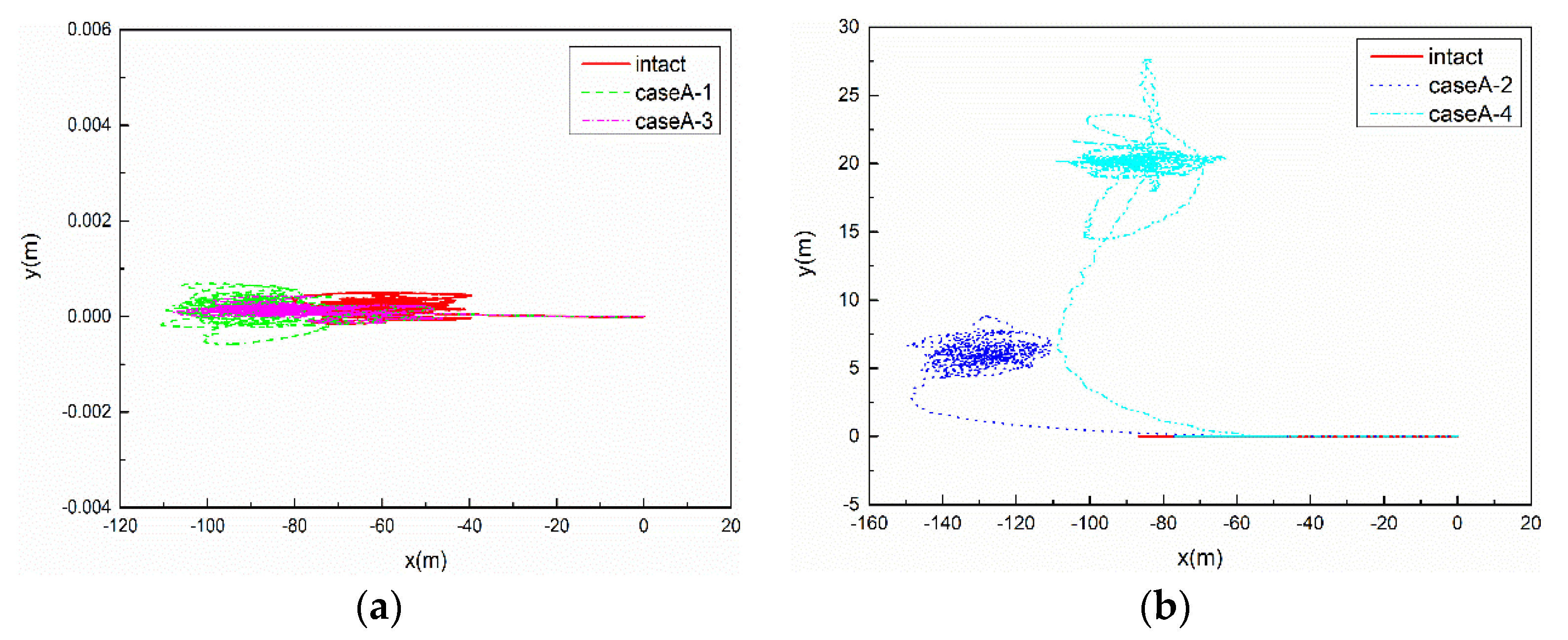
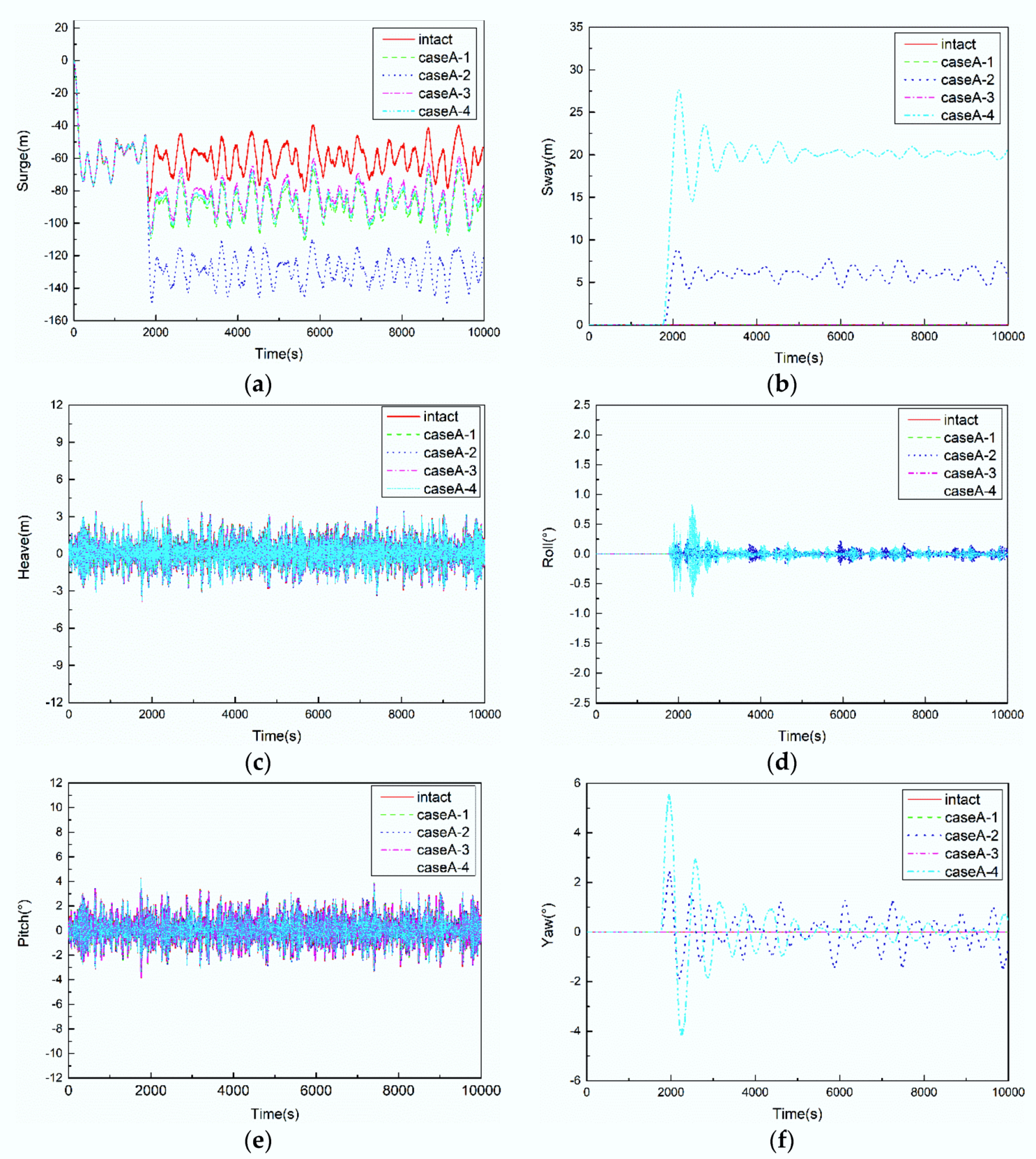
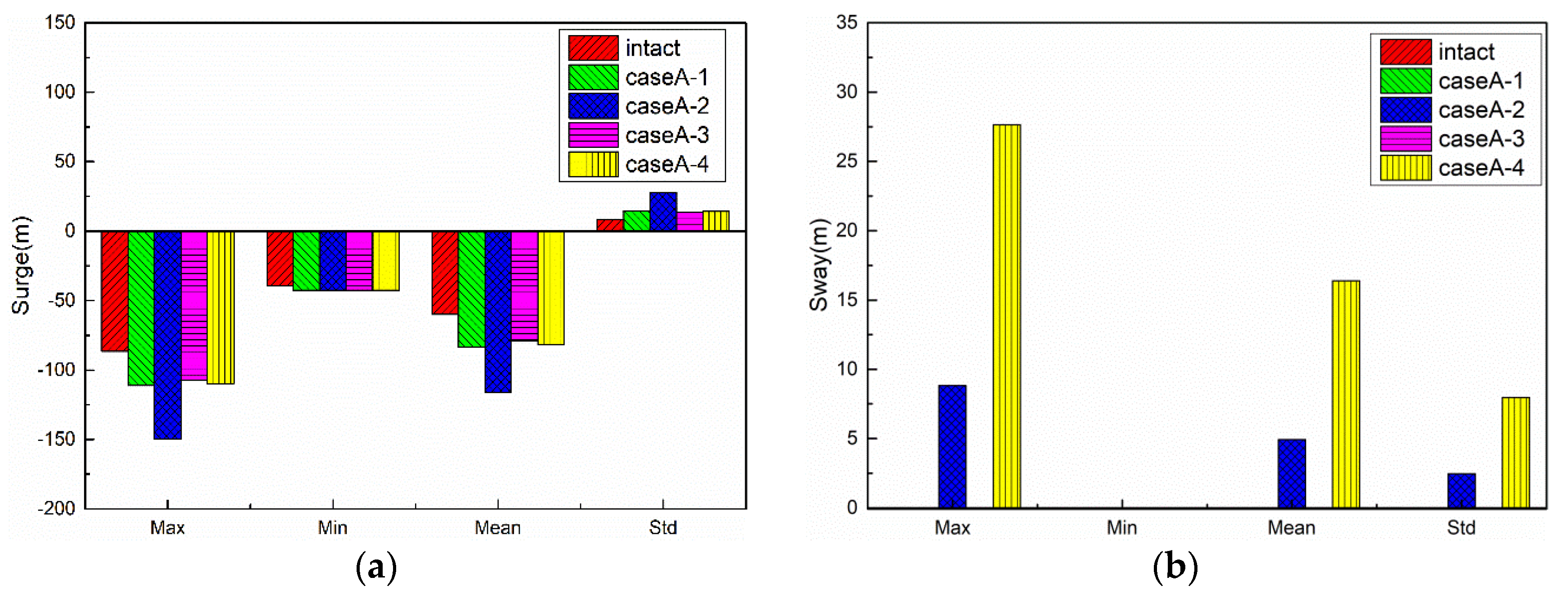
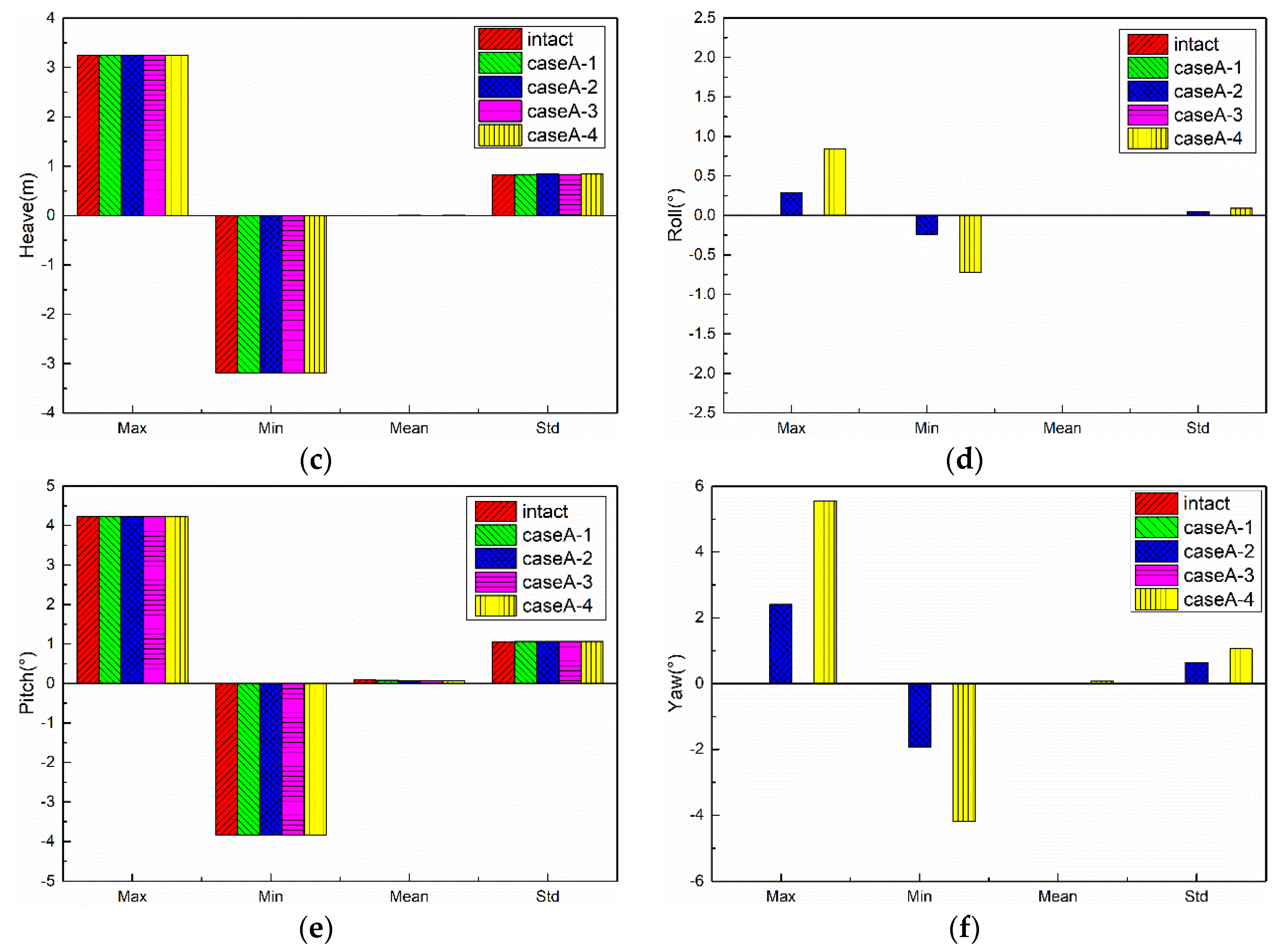
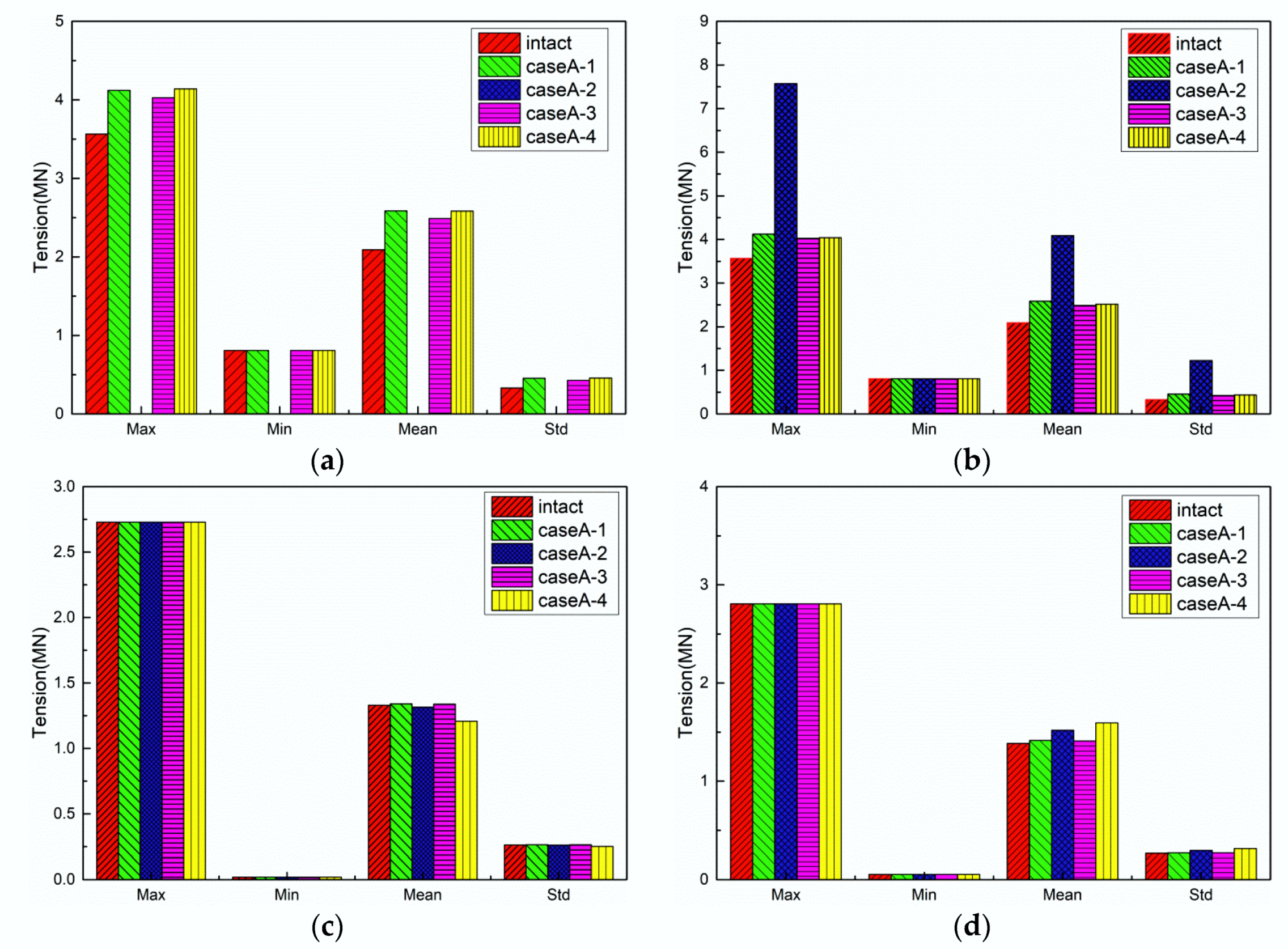
5.2. Results of CaseA
5.2.1. Motion Responses of FPSO
5.2.2. Mooring Line Tension
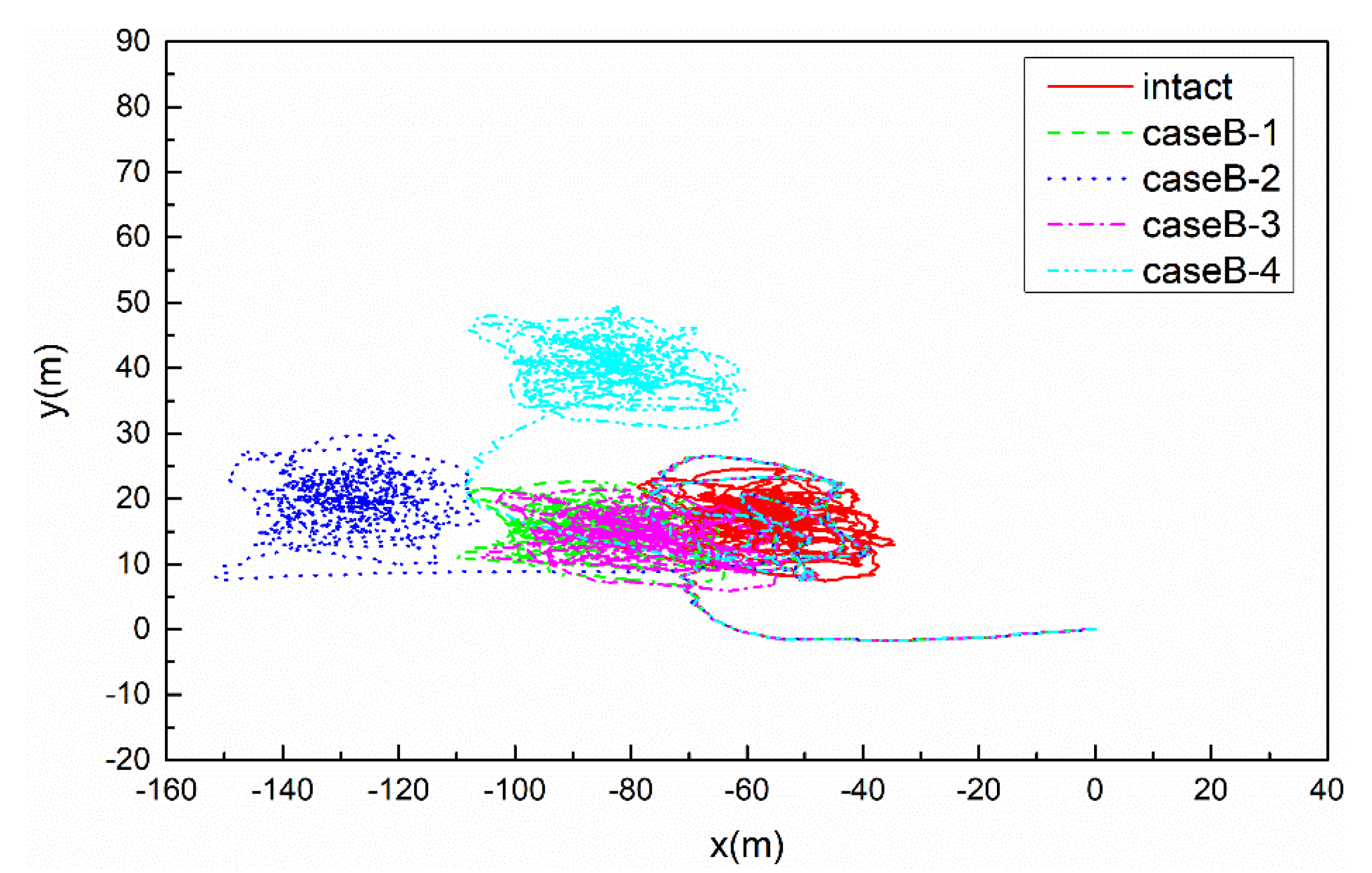
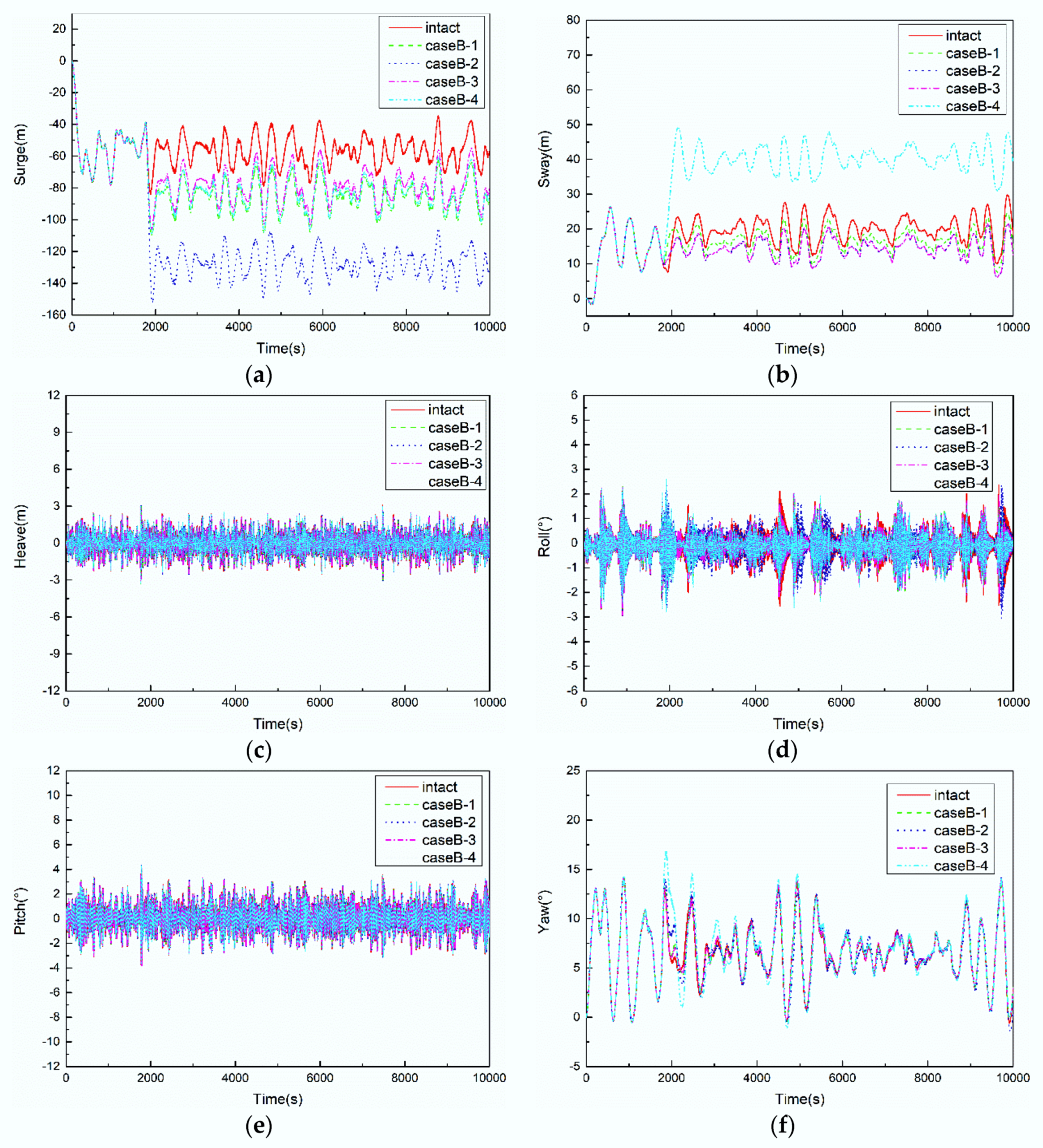
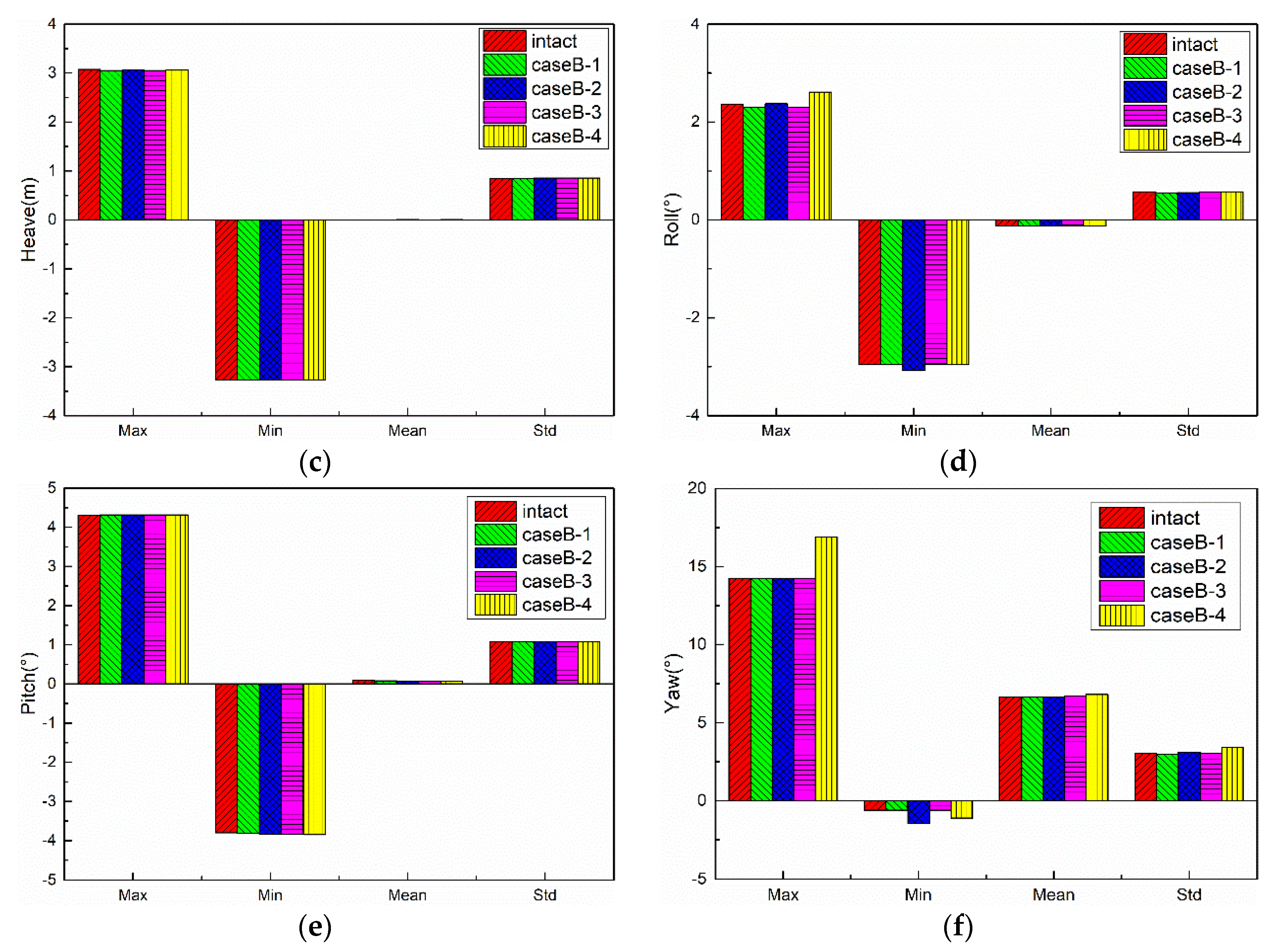
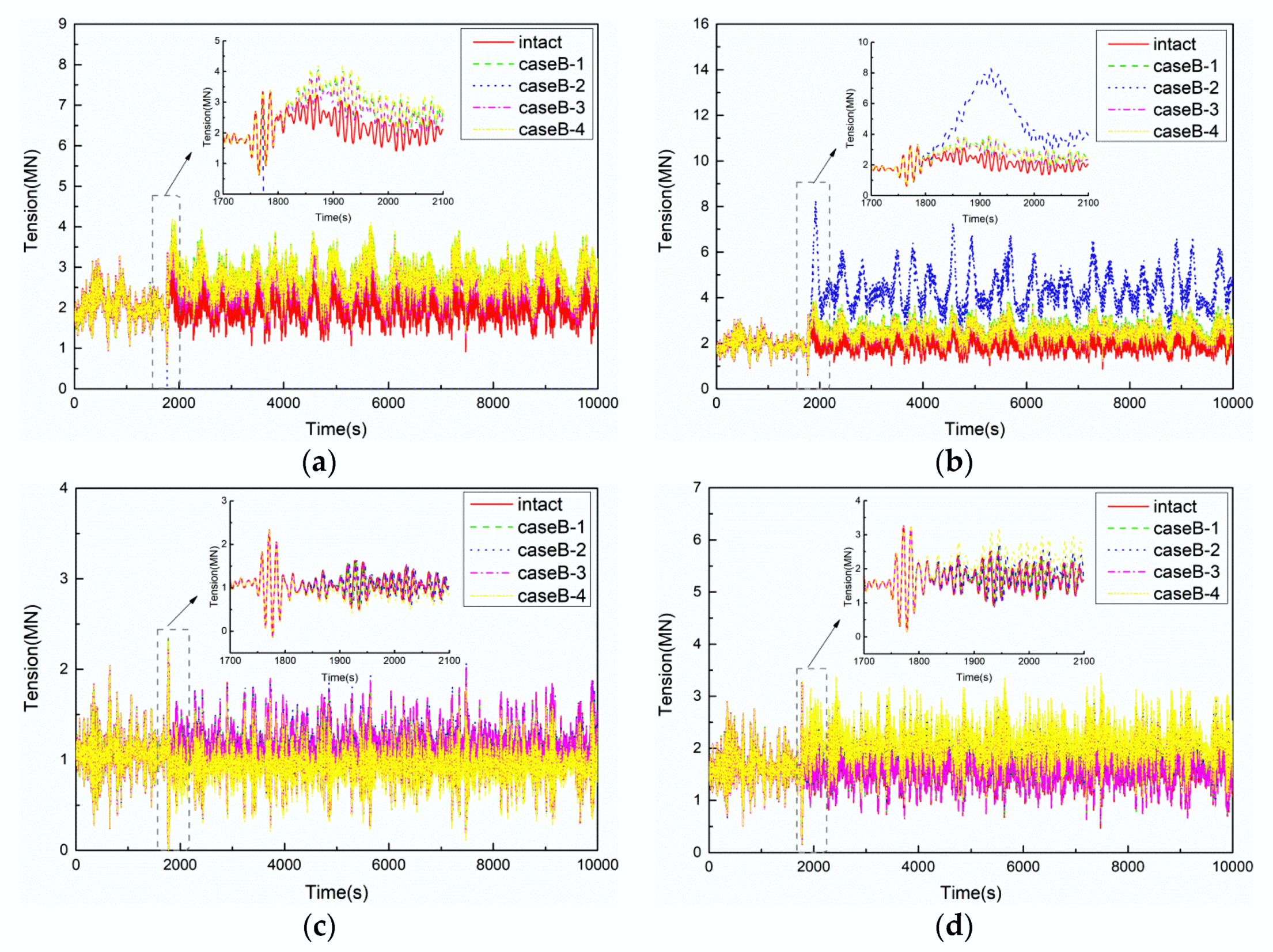
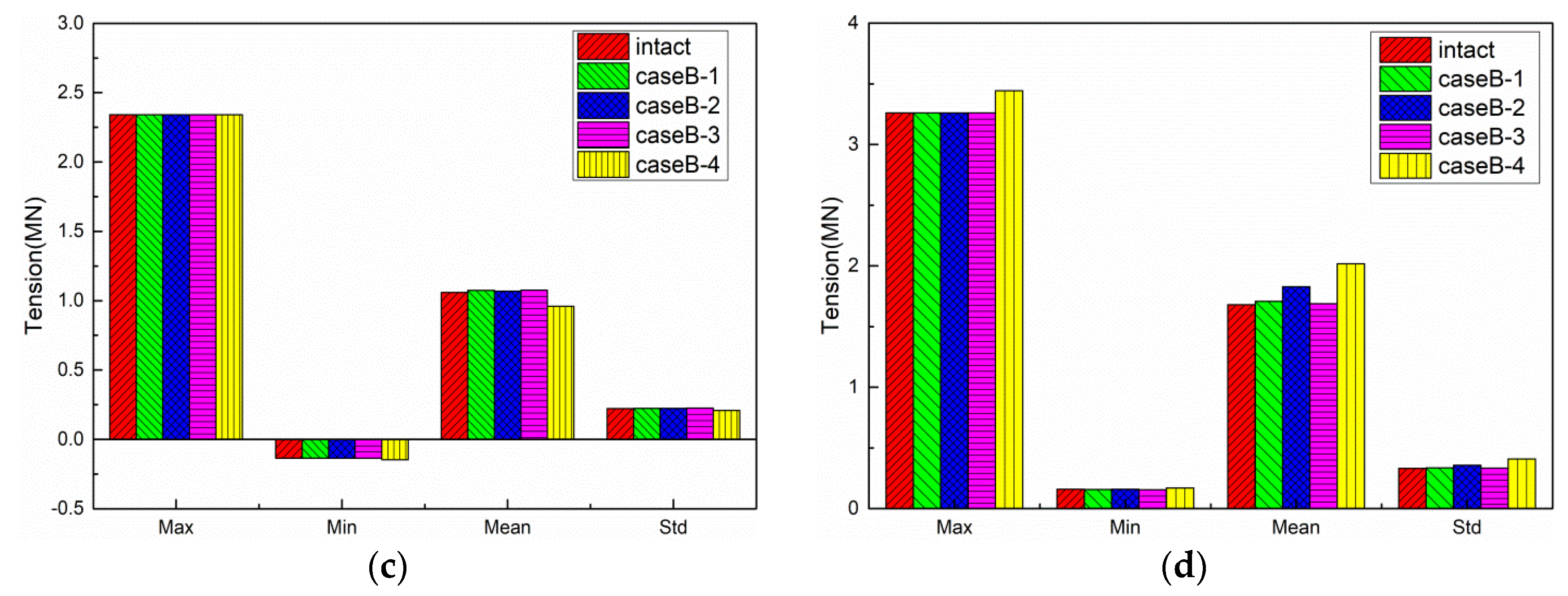
5.3. Results of CaseB
5.3.1. Motion Responses of FPSO
5.3.2. Mooring Line Tension
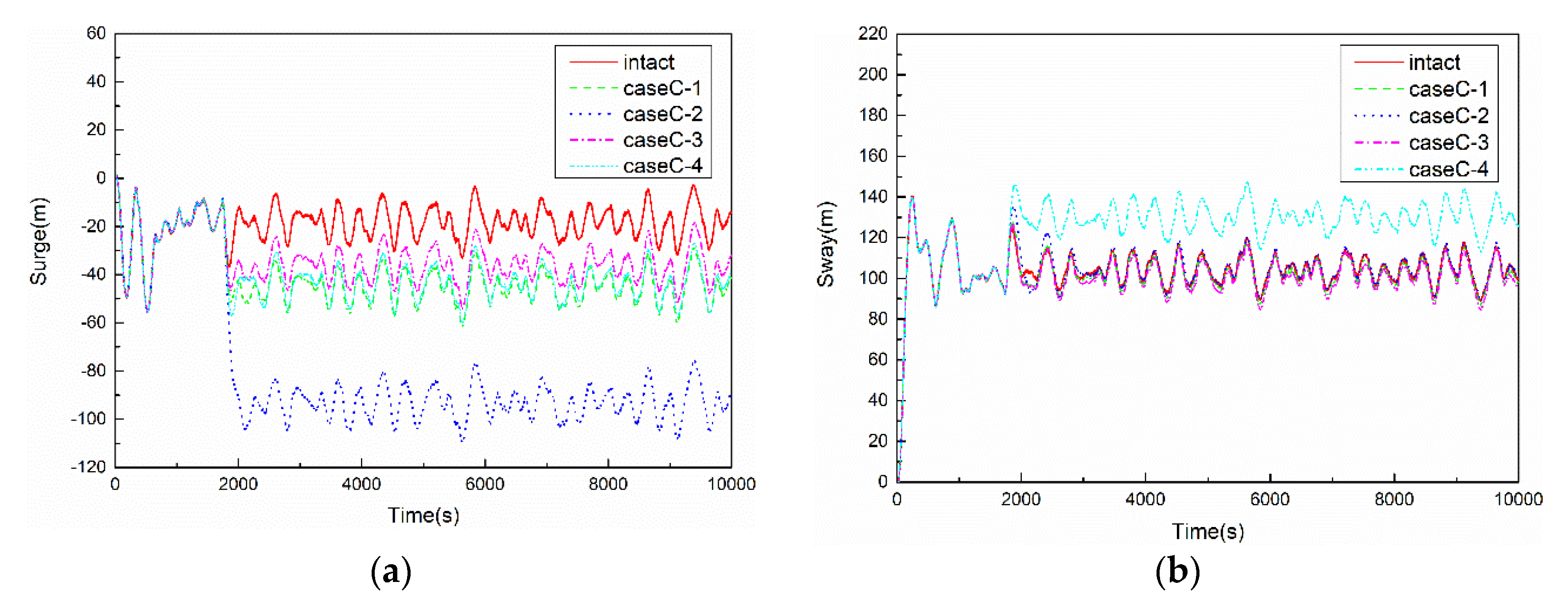
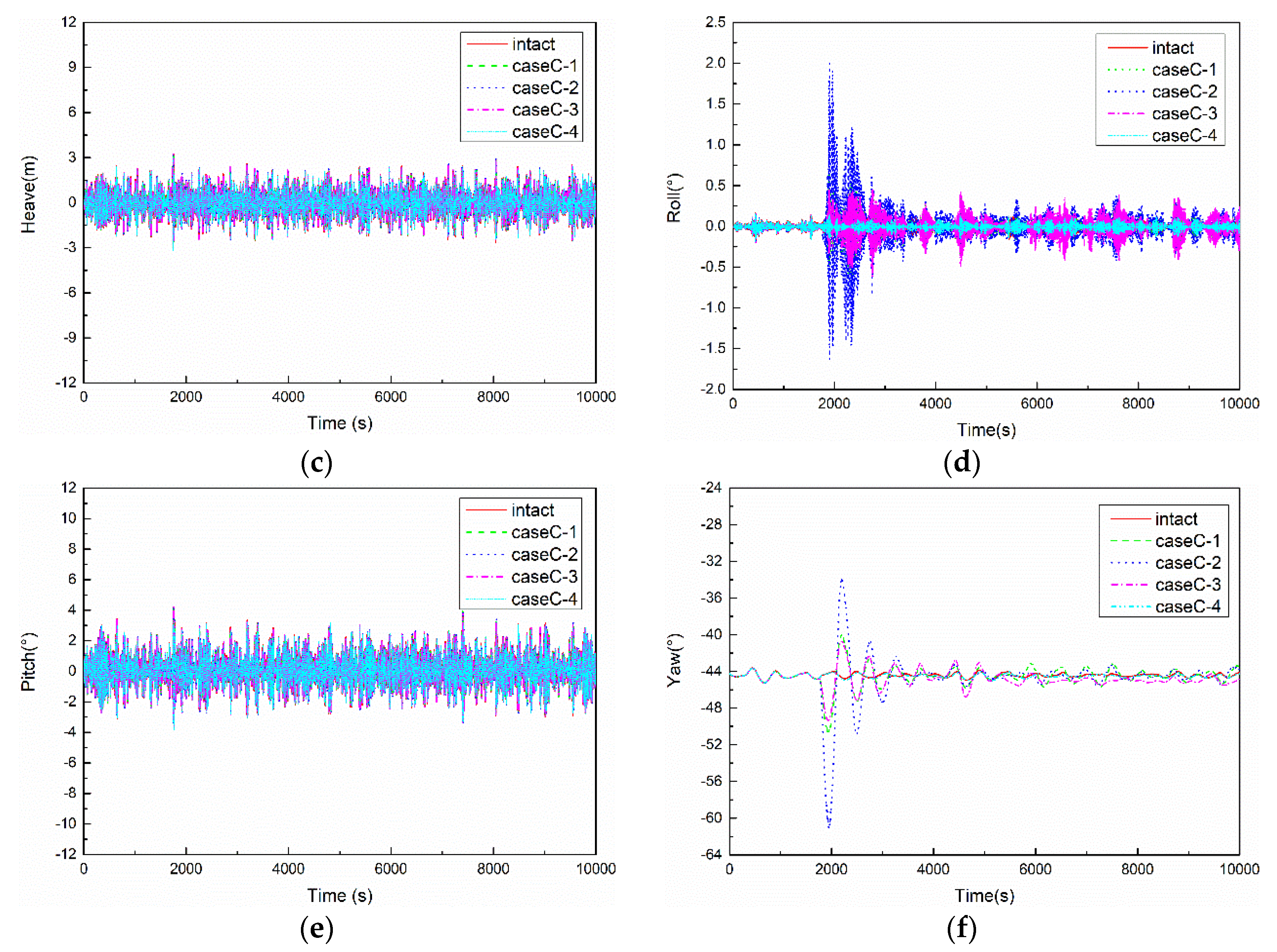
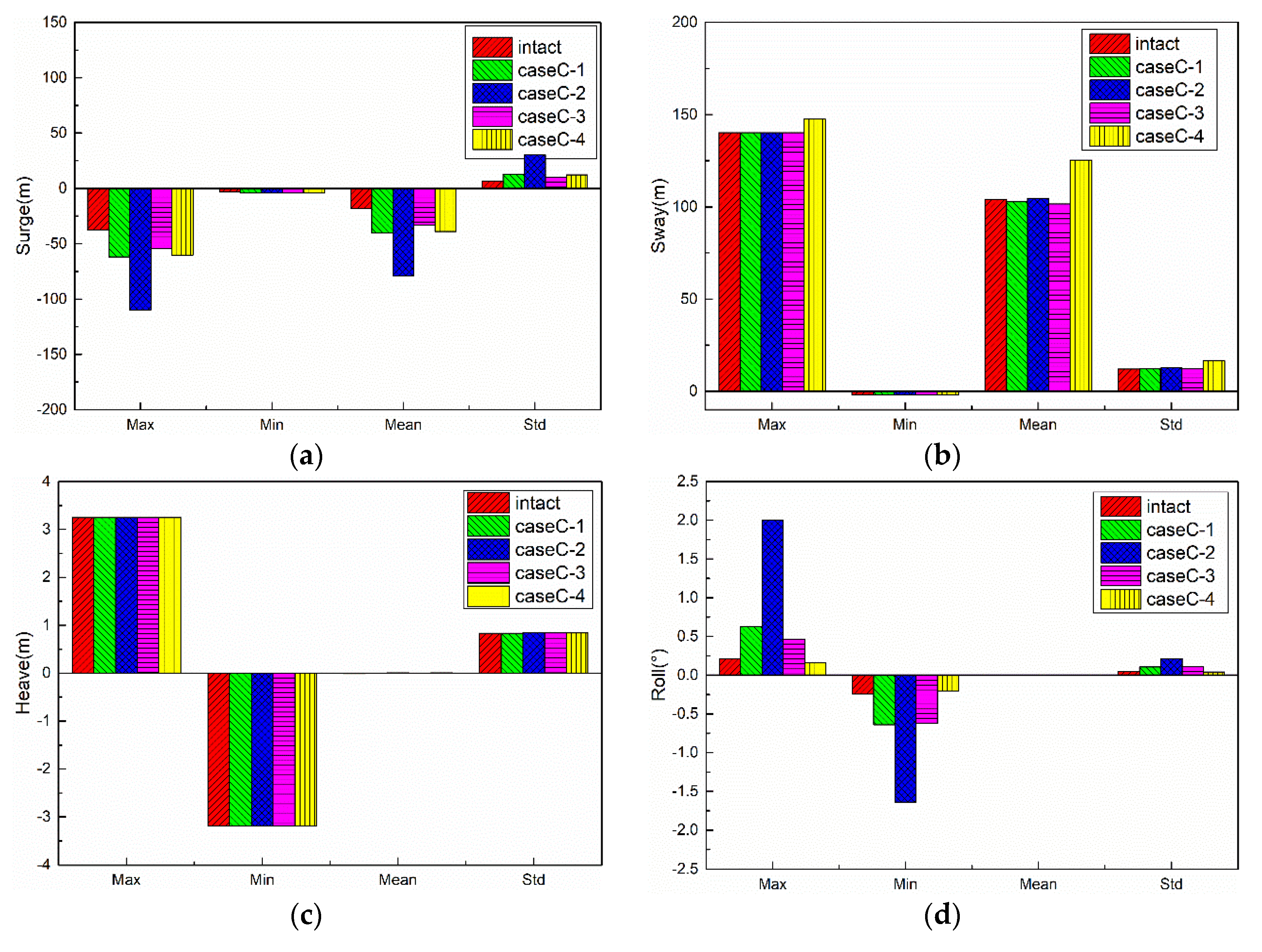
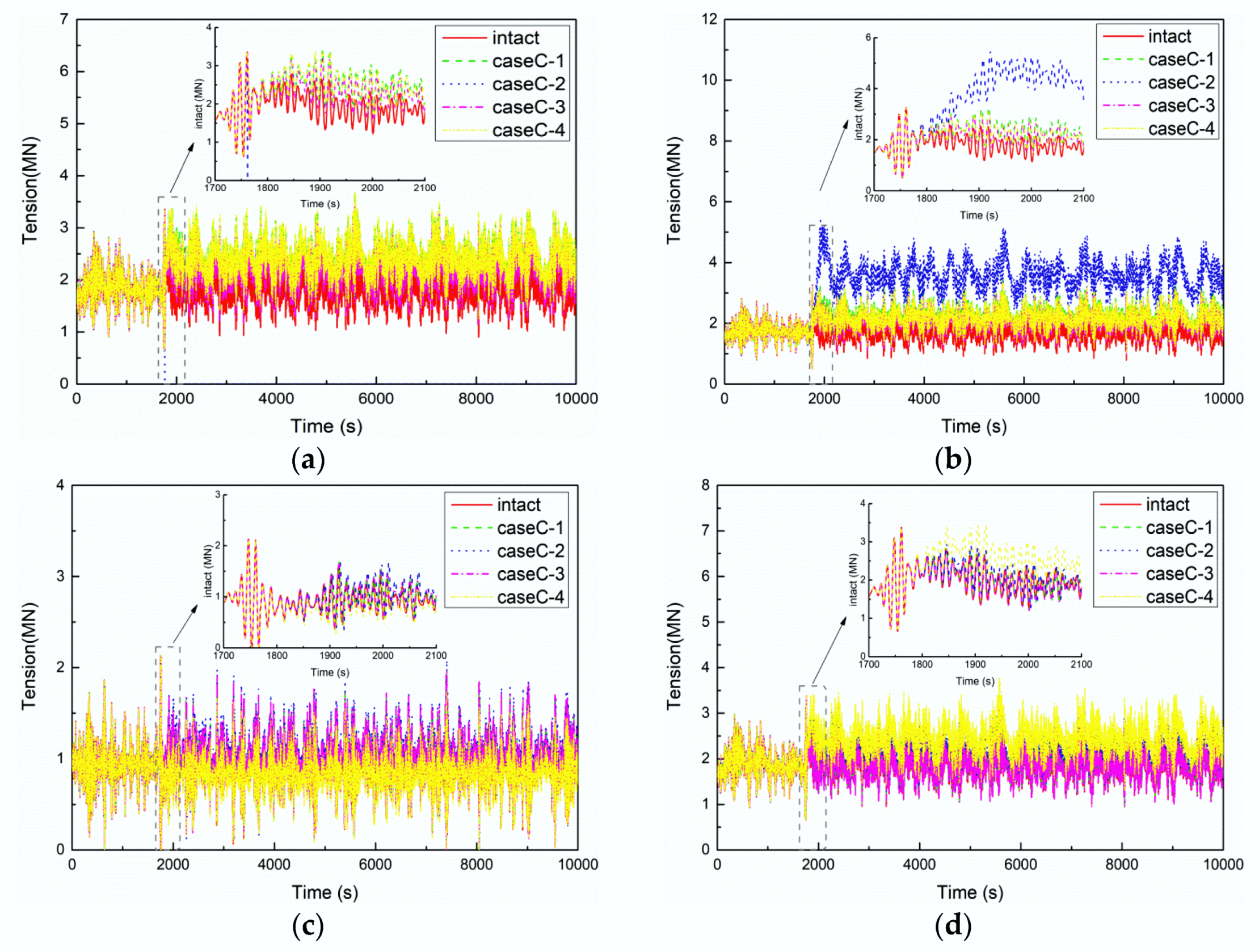
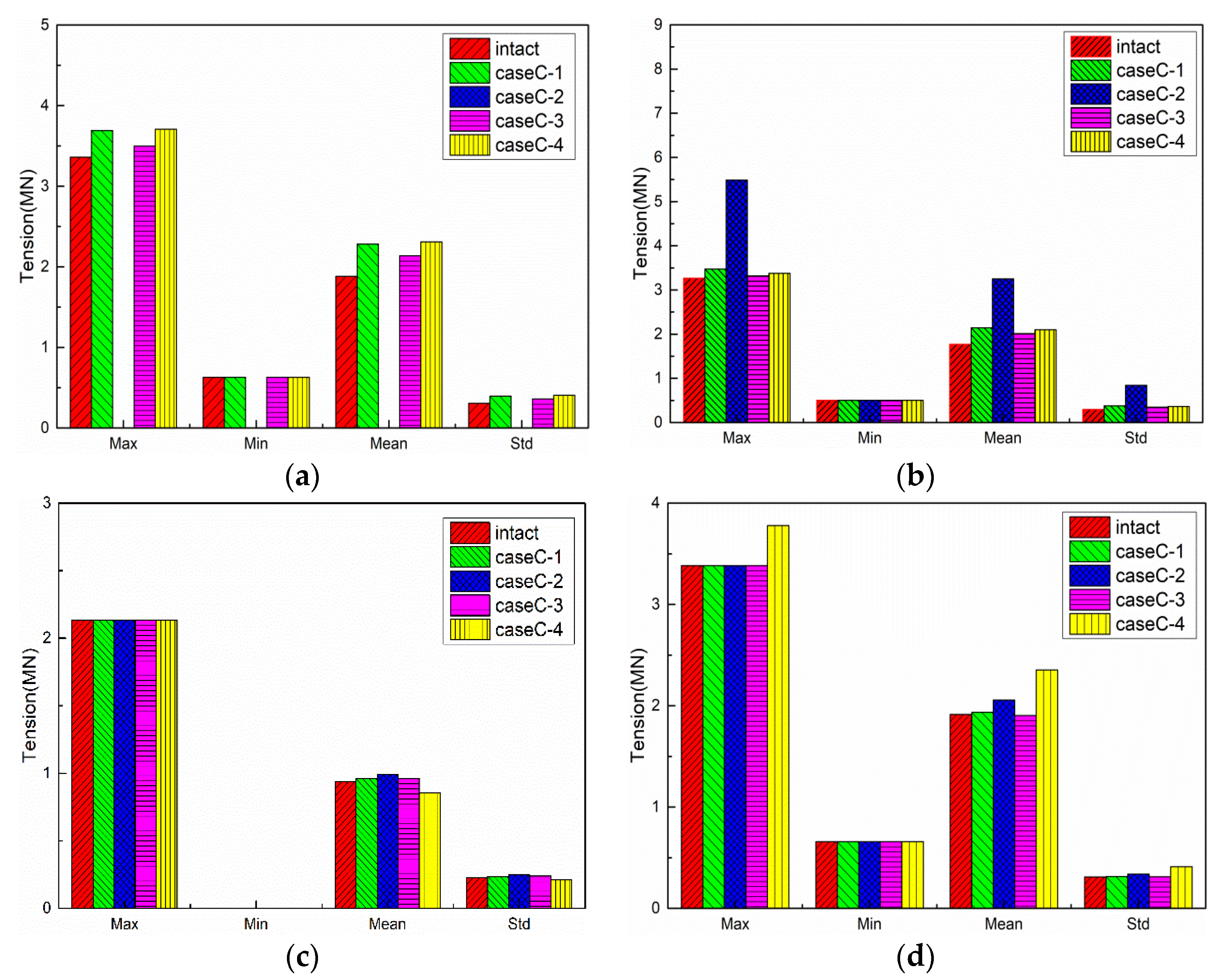
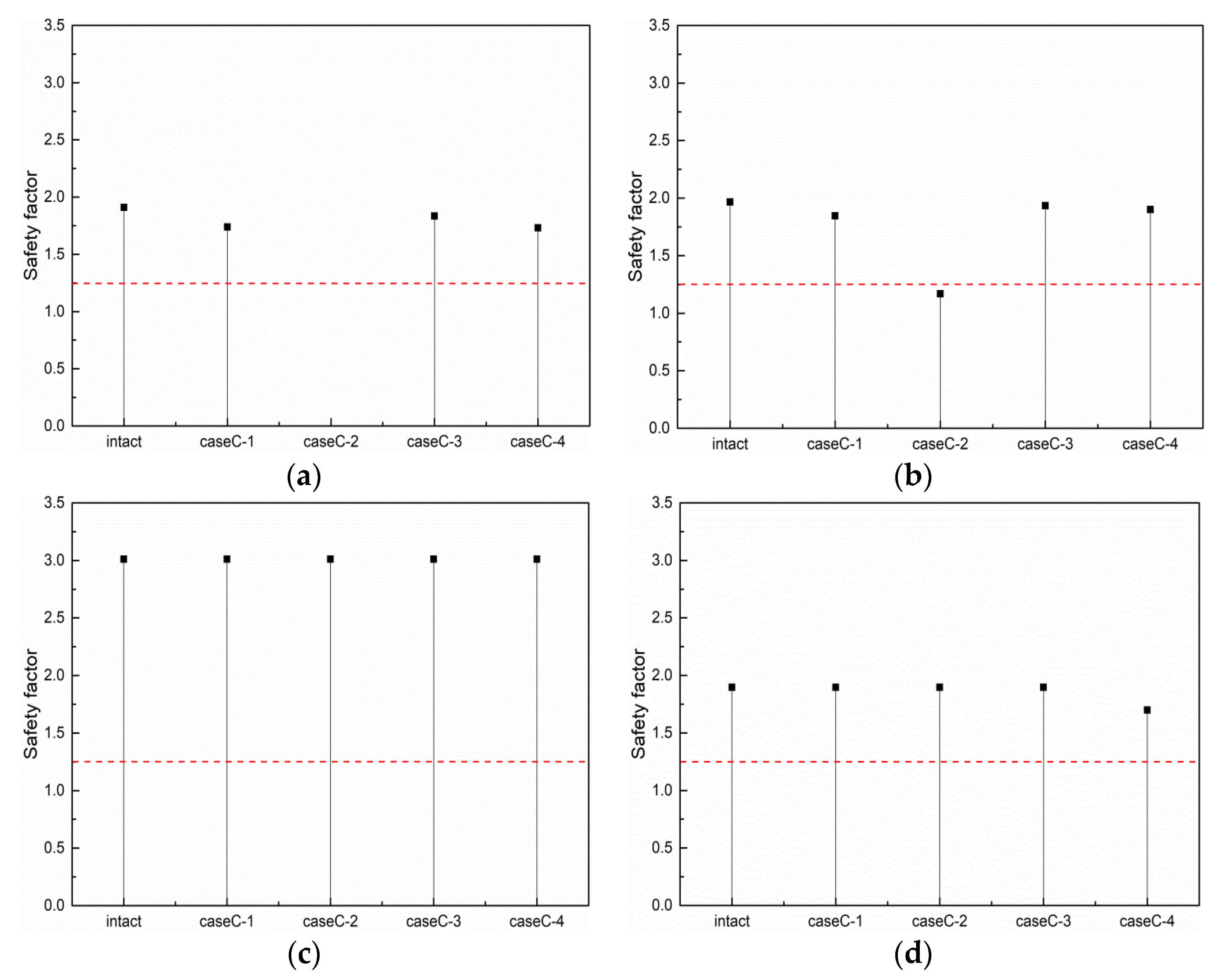
5.4. Results of CaseC
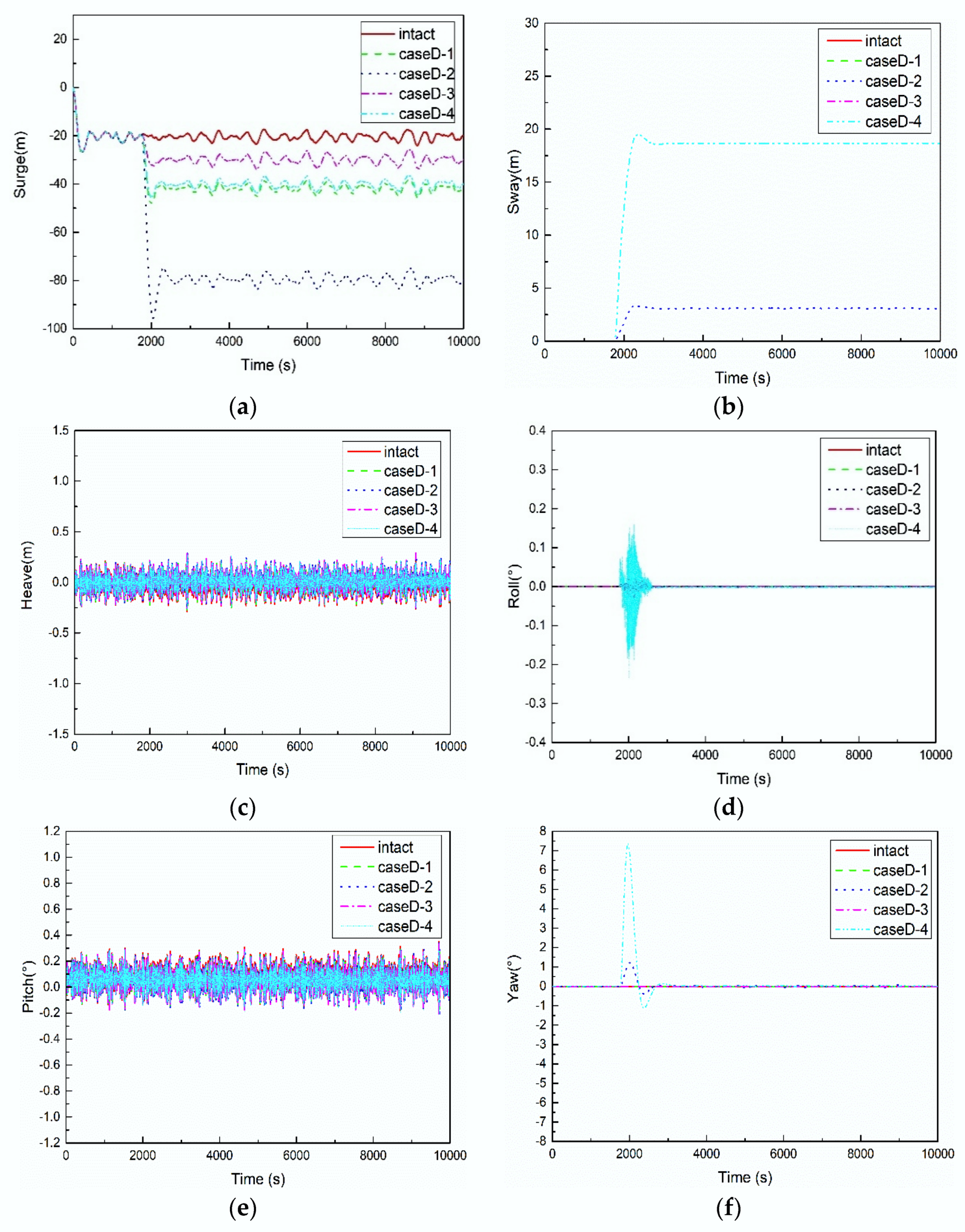
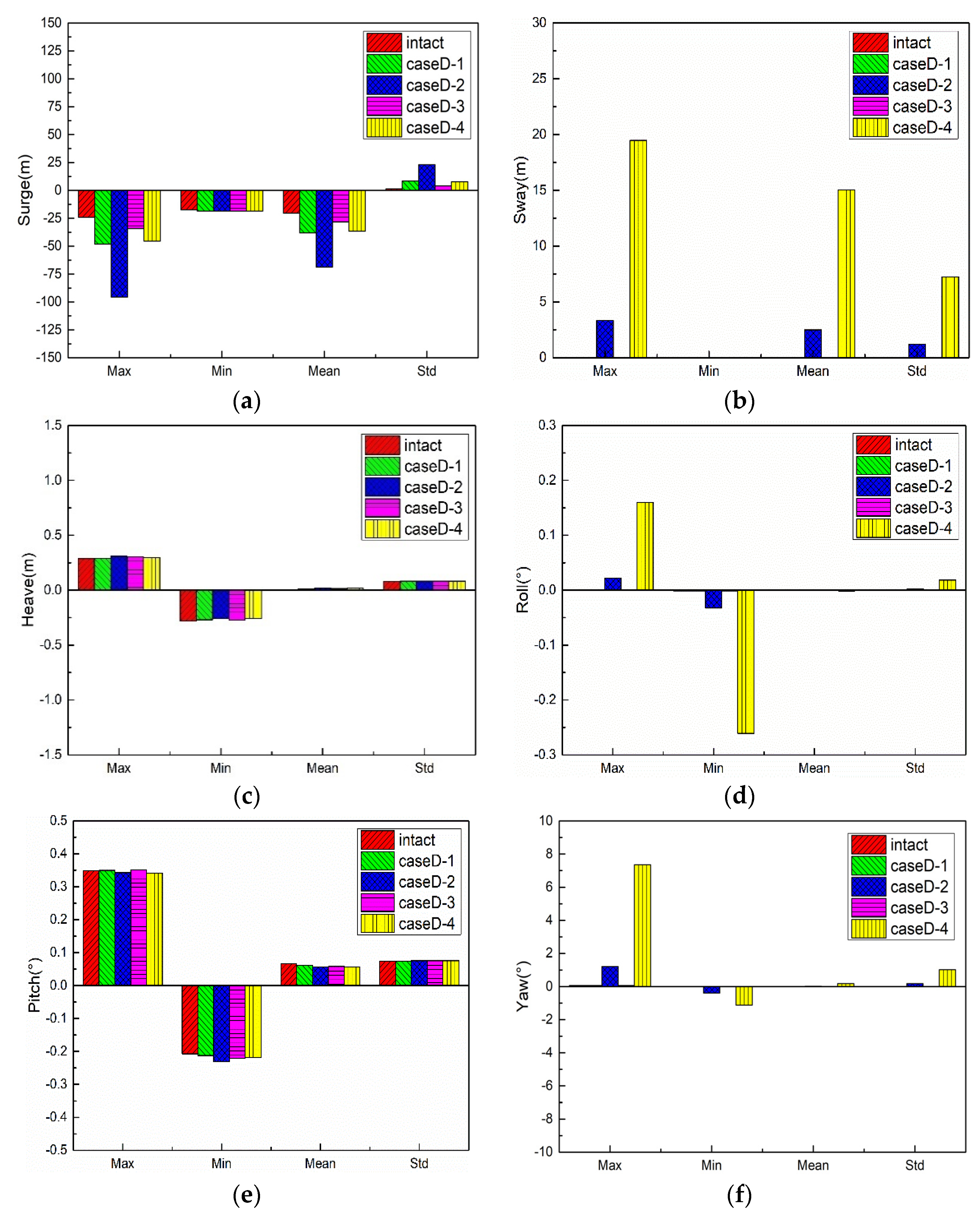
5.4.1. Motion Responses of FPSO
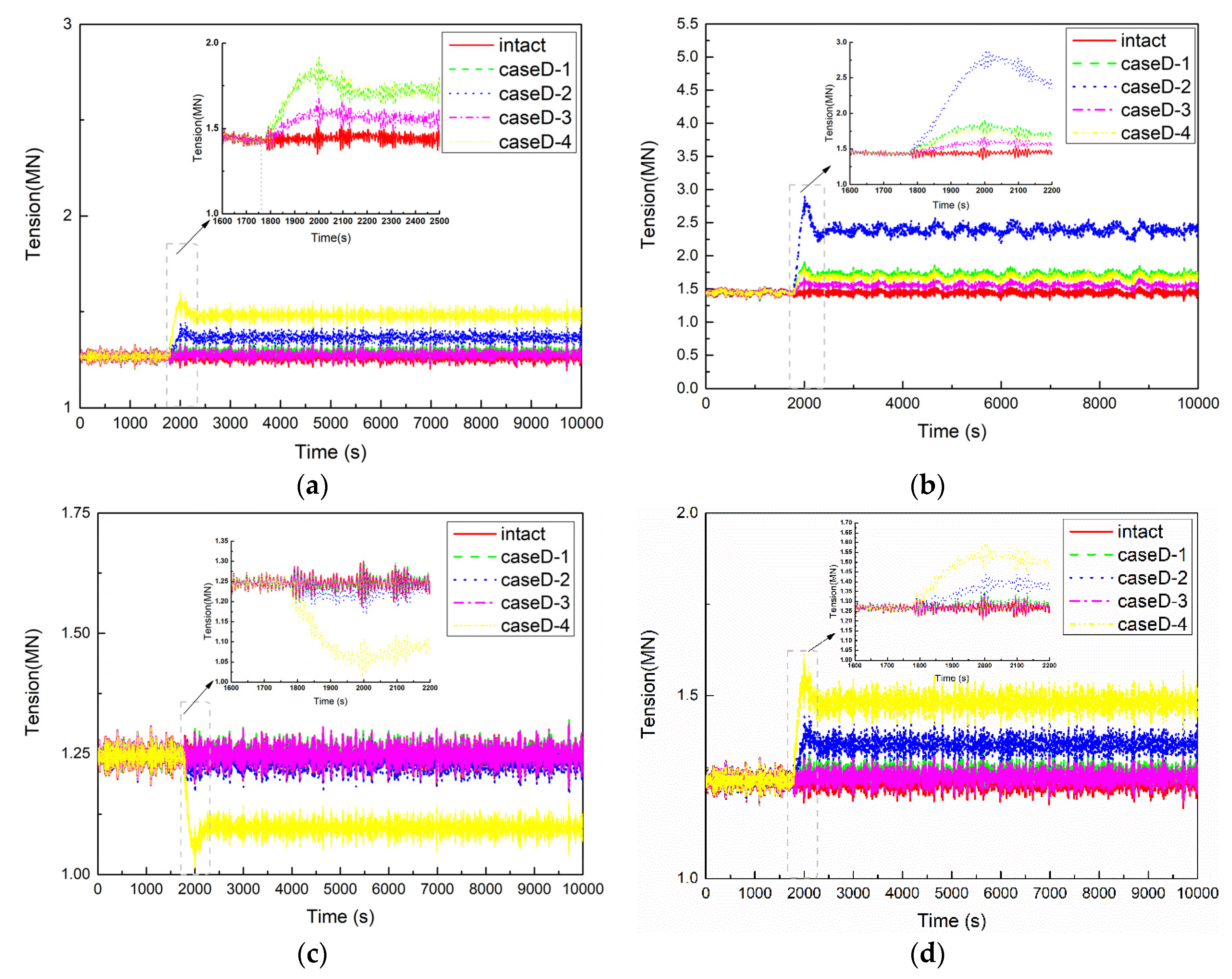
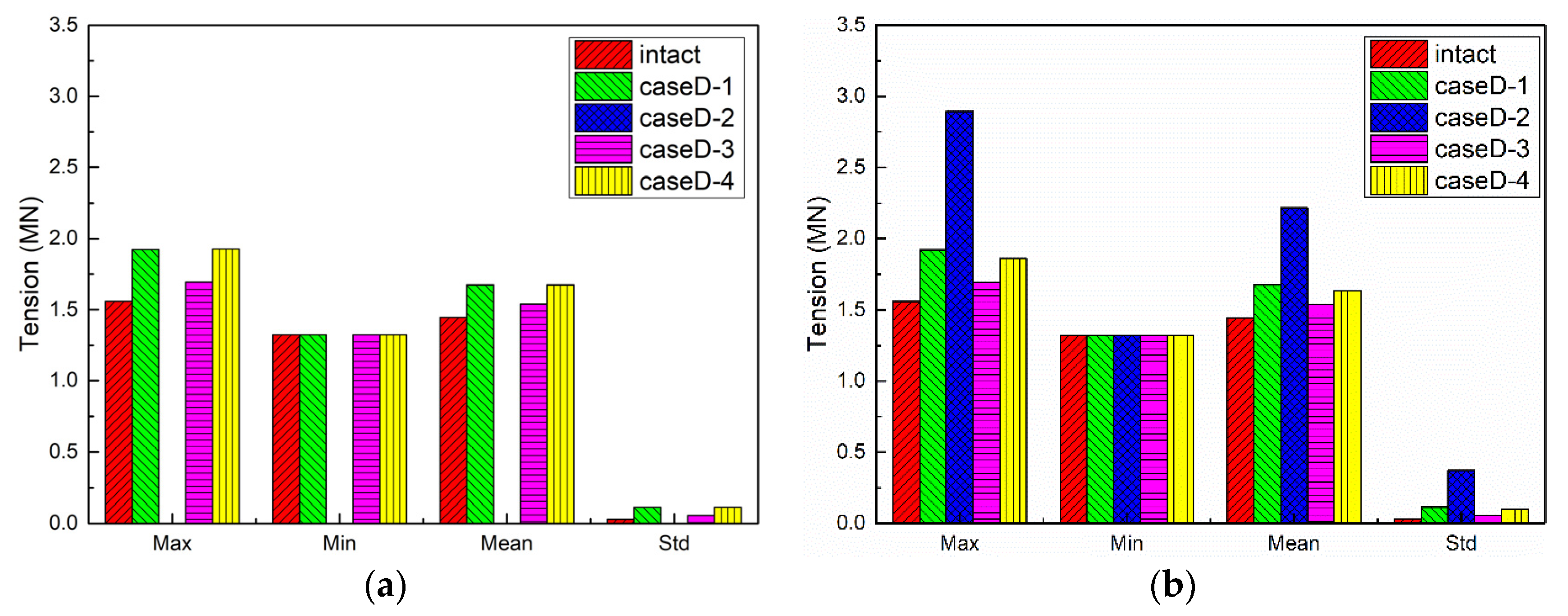
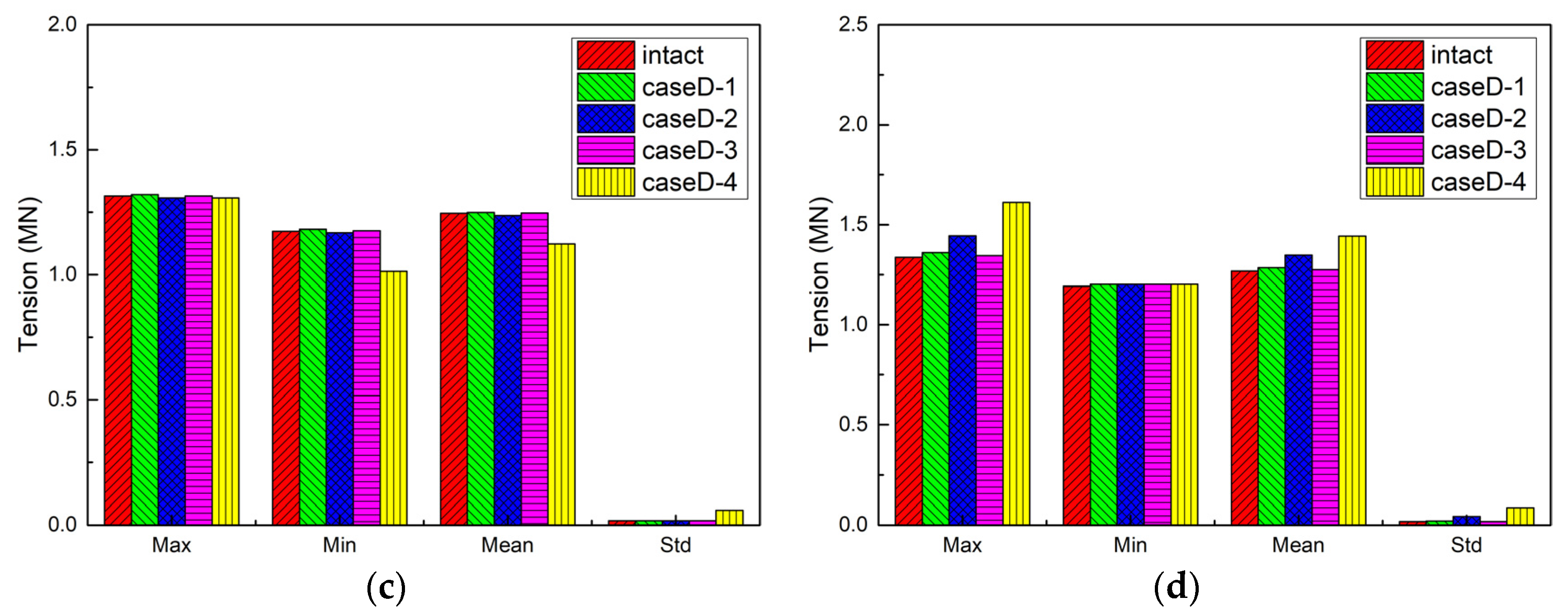
5.4.2. Mooring Line Tension
5.5. Comparison of Different Sea States
5.5.1. Motion Responses of FPSO
5.5.2. Mooring Line Tension
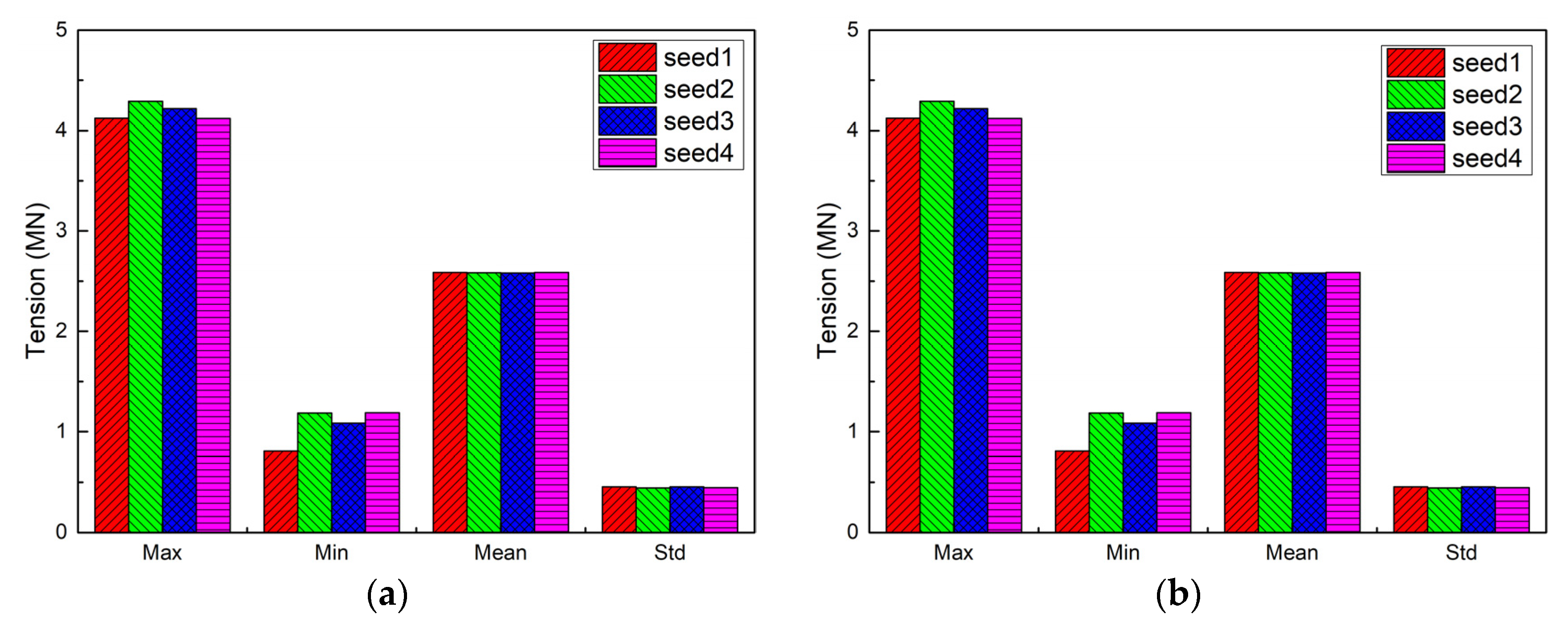
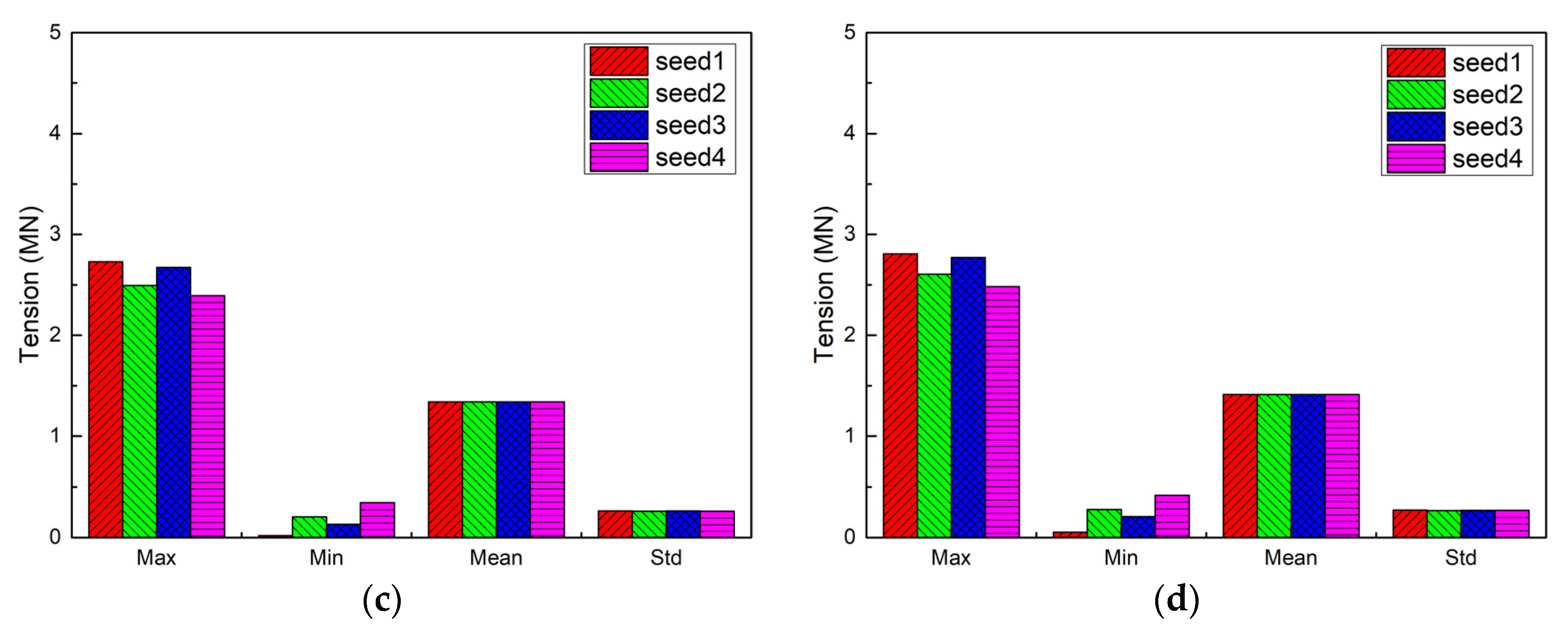
5.6. Comparisons of Different Random Seeds of Wave
6. Conclusions
- (1)
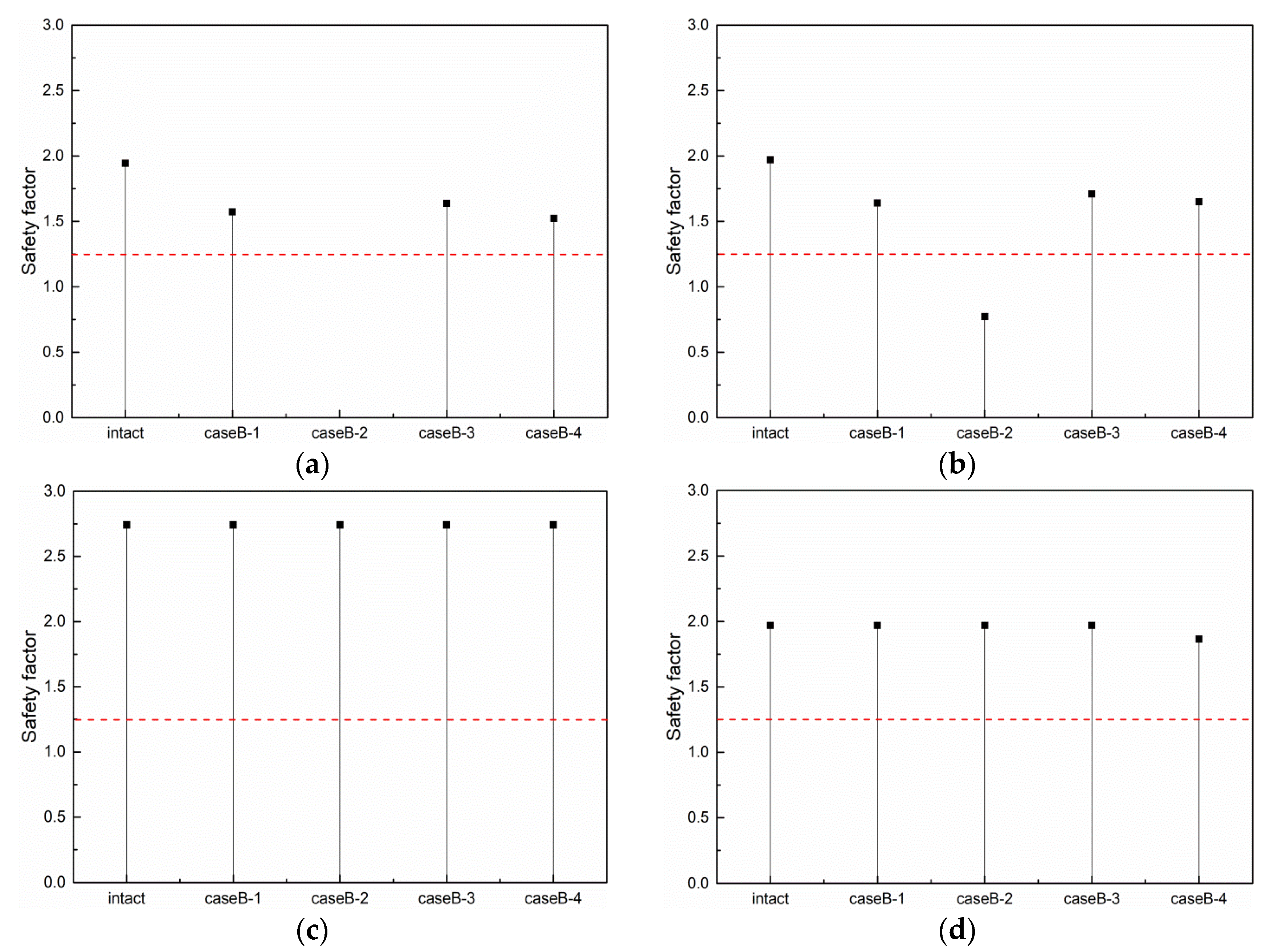
- The global assessment of motion responses of the floating platform and mooring line tensions should consider the different numbers and locations of mooring line failure, especially when the two ipsilateral mooring lines fail together, which may result in the mooring line tensions cannot meet the recommended safety factor and indicate a potential risk to the long-term reliability of the system. For instance, the results shown in Figure 15b indicate that the safety factor of CaseB-2 drops below the recommended factor of 1.25 for mooring line #3.
- (2)
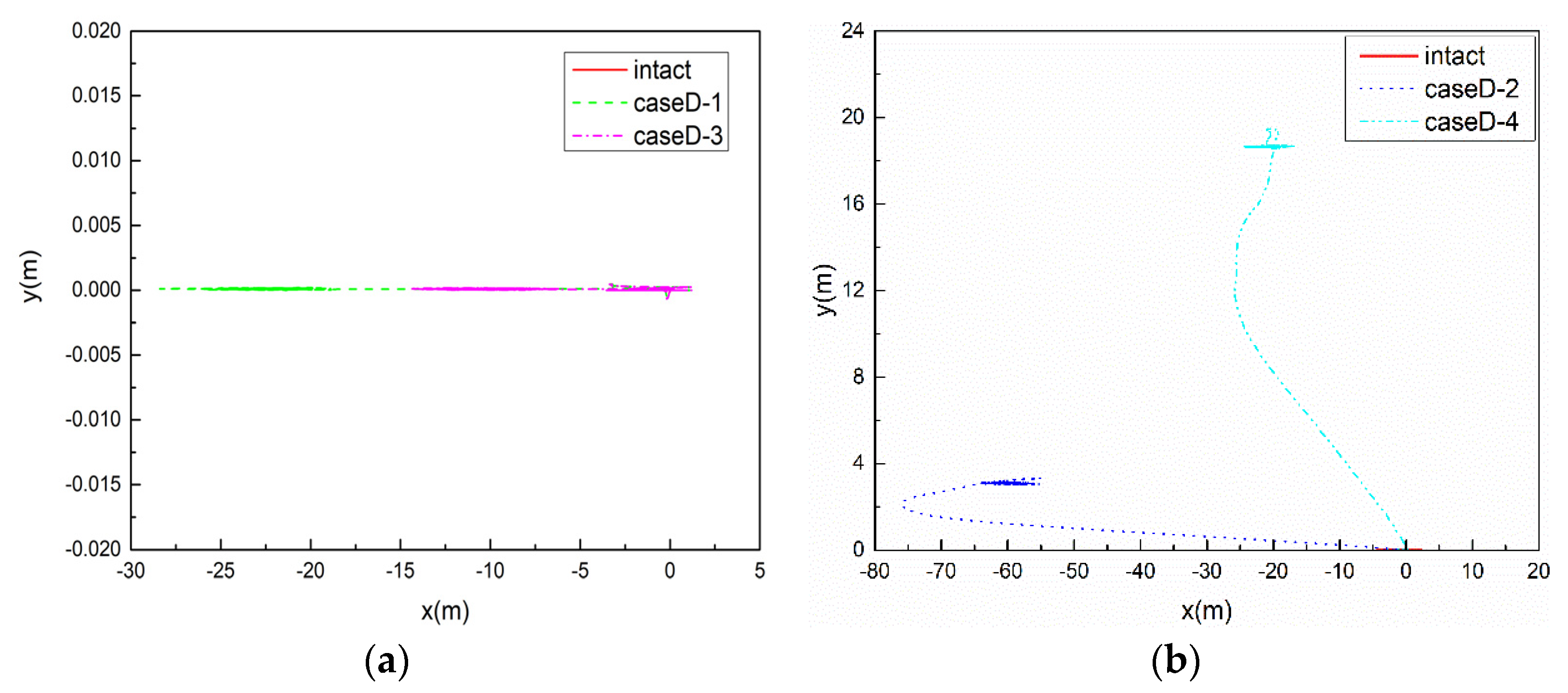
- The mooring lines failure mainly affect the motion responses of the FPSO in the horizontal plane, and the yaw motion has the largest changes due to the loss of symmetry of mooring tensions caused by failed lines. When a certain mooring line failure occurs, the FPSO re-moves to a new equilibrium position under the effect of the remaining mooring lines, and then it reaches the steady motion responses under the environmental loads.
- (3)
- The transient responses evaluation of FPSO with different failure scenarios of mooring lines should also consider the selection of design sea states. Under different sea states, the manner changes in motion responses and mooring line tensions are also different considering the same mooring line failure mode and environmental incident directions.
- (4)
- The average peak tension of the mooring line should consider about conservative 10% variable uncertainty if applying only one certain irregular wave condition in the random sea state analysis, based on the simulation results in this paper.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Xiao, L.F.; Yang, J.M. Review of the research on FPSO hydrodynamics. Ocean Eng. 2006, 24, 116–123. [Google Scholar]
- Shan, L.Z.; Dong, B.J.; Liu, M.; Wang, Q.; Li, Y.; Qi, D.S. Study of technical state and development tendency for FPSO. Oil Field Equip. 2008, 37, 26–30. [Google Scholar]
- Allahyarzadeh-Bidgoli, A.; Salviano, L.O.; Dezan, D.J. Energy optimization of an FPSO operating in the Brazilian Pre-salt region. Energy 2018, 164, 390–399. [Google Scholar] [CrossRef]
- Mastrangelo, C.F.; Lan, C.M.; Smith, C.E. From tanker-ships to the first FPSO in the US GoM. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2019. [Google Scholar]
- Vijayaraghavan, V. Operational Readiness and Operational Safety on FPSO Project. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 23–25 October 2018; Society of Petroleum Engineers: Richardson, TX, USA, 2018. [Google Scholar]
- Fontaine, E.; Kilner, A.; Carra, C.; Washington, D.; Ma, K.T.; Phadke, A.; Kusinski, G. Industry survey of past failures, pre-emptive replacements and reported degradations for mooring systems of floating production units. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2014. [Google Scholar]
- Yu, J.; Hao, S.; Yu, Y.; Chen, B.; Cheng, S.; Wu, J. Mooring analysis for a whole TLP with TTRs under tendon one-time failure and progressive failure. Ocean Eng. 2019, 182, 360–385. [Google Scholar] [CrossRef]
- Qi, Y.; Tian, X.; Guo, X. The hydrodynamic performance of a tension leg platform with one-tendon failure. Ships Offshore Struct. 2019, 14, 523–533. [Google Scholar] [CrossRef]
- Yang, C.K.; Padmanabhan, B.; Murray, J.; Kim, M.H. The transient effect of tendon disconnection on the global motion of ETLP. In Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008. [Google Scholar]
- Kim, Y.; Sclavounos, P.D. A finite-depth unified theory for the linear and second-order problems of slender ships. J. Ship Res. 1998, 42, 297–309. [Google Scholar] [CrossRef]
- Kim, M.H.; Zhang, Z. Transient effects of tendon disconnection on the survivability of a TLP in moderate-strength hurricane condition. Int. J. Nav. Archit. Ocean Eng. 2009, 1, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Tabeshpour, M.R.; Ahmadi, A.; Malayjerdi, E. Investigation of TLP behavior under tendon damage. Ocean Eng. 2018, 156, 580–595. [Google Scholar] [CrossRef]
- Gu, J.Y.; Chen, Y.; Geng, P.T.; Liu, W.M. Study on the dynamic response and tension characteristics of a TLP with one tendon broken. J. Ship Mech. 2015, 19, 1488–1497. [Google Scholar]
- Yang, C.K.; Kim, M.H. Transient effects of tendon disconnection of a TLP by hull–tendon–riser coupled dynamic analysis. Ocean Eng. 2010, 37, 667–677. [Google Scholar] [CrossRef]
- Oyejobi, D.O.; Jameel, M.; Sulong, N.H.R. Stochastic response of intact and a removed tendon tension leg platform to random wave and current forces. Arab. J. Sci. Eng. 2017, 42, 1065–1076. [Google Scholar] [CrossRef]
- Yang, C.K.; Kim, M.H. The structural safety assessment of a tie-down system on a tension leg platform during hurricane events. Ocean Syst. Eng. 2011, 1, 263–283. [Google Scholar] [CrossRef]
- Montasir, O.A.; Yenduri, A.; Kurian, V.J. Mooring system optimisation and effect of different line design variables on motions of truss spar platforms in intact and damaged conditions. China Ocean Eng. 2019, 33, 385–397. [Google Scholar] [CrossRef]
- Feng, J.; Yu, Y.; Qu, Y.; Xie, W.; Wu, M.; Zhao, J. A conjoint analysis of the stability and time-domain analysis on floating platform during mooring line breaking. In Proceedings of the ASME 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, Scotland, UK, 9–14 June 2019. [Google Scholar]
- Murai, M.; Suyama, N. Coupled motion response of a moored floating body in breaking a mooring line in waves. In Proceedings of the Twenty-Fifth International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015. [Google Scholar]
- Zhang, Z.; Kim, M.H.; Ward, E.G. Progressive mooring-line failure of a deepwater MODU in hurricane conditions. In Proceedings of the ASME 28th International Conference on Ocean, Offshore and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009. [Google Scholar]
- Kim, B.W.; Sung, H.G.; Hong, S.Y.; Hong, S.W. Dynamic coupled analysis of FSRU with broken mooring line. In Proceedings of the Twenty-Fourth International Ocean and Polar Engineering Conference, Busan, Korea, 15–20 June 2014. [Google Scholar]
- Han, J.S.; Son, Y.J.; Choi, H.S.; Rho, J.B. The transient behavior of mooring systems in line-broken condition. In Proceedings of the Twenty-First International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Girón, A.R.C.; Kim, B.W.; Farfán, J.A.M.; Hernández, A.O.V. Transient effects of an FPSO with a broken mooring line. In Proceedings of the Twenty-Fifth International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015. [Google Scholar]
- Ma, G.; Sun, L. The design and implementation of FPSO mooring management system. In Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008. [Google Scholar]
- Li, W.; Liu, H.; Lian, Y. Impacts of damaged ropes on the dynamic response of the taut-wire mooring system. Ocean Eng. 2017, 35, 11–20. [Google Scholar]
- Lian, Y.; Yim, S.C.; Zheng, J. Effects of damaged fiber ropes on the performance of a hybrid taut-wire mooring system. J. Offshore Mech. Arct. Eng. 2020, 142, 011607. [Google Scholar] [CrossRef]
- Kurian, V.J.; Yassir, M.A.; Harahap, I.S.H. Dynamic response of semisubmersibles with damaged mooring lines. In Proceedings of the Twenty-Second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012. [Google Scholar]
- Hong, J.P.; Cho, S.K.; Seo, J.H.; Sung, H.G.; Lee, D.Y.; Park, I.B.; Kim, D.W. Experimental study of effect of mooring line failure on behavior of turret-moored FPSO ship. J. Ocean Eng. Technol. 2015, 29, 231–240. [Google Scholar] [CrossRef]
- Bae, Y.H.; Kim, M.H.; Kim, H.C. Performance changes of a floating offshore wind turbine with broken mooring line. Renew. Energy 2017, 101, 364–375. [Google Scholar] [CrossRef]
- Bae, Y.H.; Kim, M.H.; Yu, Q. Coupled dynamic analysis of FOWT (Floating Offshore Wind Turbine) with partially broken blade. In Proceedings of the Twenty-Third International Offshore and Polar Engineering Conference, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
- Li, Y.; Zhu, Q.; Liu, L.; Tang, Y. Transient response of a SPAR-type floating offshore wind turbine with fractured mooring lines. Renew. Energy 2018, 122, 576–588. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, Y.; He, Y. Transient response of a TLP-type floating offshore wind turbine under tendon failure conditions. Ocean Eng. 2021, 220, 108486. [Google Scholar] [CrossRef]
- American Petroleum Institute. Design and Analysis of Station Keeping Systems for Floating Structures—API Recommended Practice 2SK, 3rd ed.; American Petroleum Institute: Washington, DC, USA, 2005. [Google Scholar]
- Berteaux, H.O. Buoy Engineering; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Hall, M.; Goupee, A. Validation of a lumped-mass mooring line model with DeepCwind semisubmersible model test data. Ocean Eng. 2015, 104, 590–603. [Google Scholar] [CrossRef] [Green Version]
- Wihers, J.E.W.; Devlin, P.V. Effect of Coupling of Mooring Lines and Risers on the Design Values for a Turret Moored FPSO in Deep Water of the Gulf of Mexico. In Proceedings of the Eleventh International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001. [Google Scholar]









| Designation | Symbol | Unit | Value |
|---|---|---|---|
| Length | Lpp | m | 310 |
| Breadth | B | m | 47.17 |
| Depth | H | m | 28.04 |
| Draft | T | m | 18.90 |
| Displacement | D | kg | 2.40 × 108 |
| Center of gravity above baseline | KG | m | 13.32 |
| Distance between turret and bow | - | m | 63.55 |
| Transverse radius of gyration | KXX | m | 14.77 |
| Longitudinal radius of gyration | KYY | m | 77.47 |
| Yaw radius of gyration | KZZ | m | 79.30 |
| Designation | Unit | Value | |
|---|---|---|---|
| Upper/Bottom Chain | Length (L1/L3) | m | 45.7/914.4 |
| Diameter | mm | 88.90 | |
| Dry weight | N/m | 1617.10 | |
| Wet weight | N/m | 1406.90 | |
| Stiffness | KN | 794,484 | |
| Minimum breaking load | KN | 6512 | |
| Normal/tangential drag coefficient | - | 2.00/0.65 | |
| Normal/tangential inertia coefficient | - | 1.00/0.50 | |
| Middle Wire | Length (L2) | m | 1127.80 |
| Diameter | mm | 88.90 | |
| Dry weight | N/m | 412.23 | |
| Wet weight | N/m | 349.75 | |
| Stiffness | KN | 689,858 | |
| Minimum breaking load | KN | 6418 | |
| Normal/tangential drag coefficient | - | 1.00/0.30 | |
| Normal/tangential inertia coefficient | - | 0.50/0.25 | |
| Data Sources | Surge (m) | Sway (m) | Roll (deg) | Yaw (deg) | Line #2 (MN) | Line #8 (MN) | |
|---|---|---|---|---|---|---|---|
| Max | Numerical analysis | −34.12 | 26.49 | 4.23 | 15.23 | 3.13 | 1.60 |
| MARIN tests | −34.60 | 28.59 | 4.54 | 16.68 | 2.97 | 1.55 | |
| Min | Numerical analysis | −84.84 | 5.79 | −3.87 | 1.75 | 0.67 | 0.32 |
| MARIN tests | −85.10 | 5.27 | −4.24 | 1.94 | 0.61 | 0.30 | |
| Mean | Numerical analysis | −54.11 | 16.43 | 0.34 | 7.53 | 2.01 | 0.77 |
| MARIN tests | −52.50 | 16.60 | 0.37 | 8.12 | 1.82 | 0.75 | |
| SD | Numerical analysis | 7.53 | 4.15 | 0.99 | 2.92 | 0.26 | 0.13 |
| MARIN tests | 6.90 | 4.50 | 1.10 | 2.70 | 0.24 | 0.12 |
| Description | Unit | Environment A | Environment B | Environment C | Environment D | |
|---|---|---|---|---|---|---|
| Wave | Hs | m | 12.19 | 12.19 | 12.19 | 3.96 |
| Tp | s | 14 | 14 | 14 | 9.0 | |
| Wave spectrum | - | JONSWAP | JONSWAP | JONSWAP | JONSWAP | |
| Wave direction | deg | 180 | 180 | 135 | 180 | |
| Wind | 1 h mean speed | m/s | 41.12 | 41.12 | 41.12 | 21.61 |
| Wind spectrum | - | API | API | API | API | |
| Direction | deg | 180 | 210 | 135 | 180 | |
| Current | Speed | m/s | 1.07 | 1.07 | 1.07 | 0.9 |
| Direction | deg | 180 | 150 | 135 | 180 |
| Cases | Mooring Line Failure Modes | |||
|---|---|---|---|---|
| CaseA | CaseA-1 (single) | CaseA-2 (ipsilateral) | CaseA-3 (opposite) | CaseA-4 (adjacent) |
| Mooring line #2 broken | Mooring line #2 and #1 broken | Mooring line #2 and #8 broken | Mooring line #2 and #11 broken | |
| CaseB | CaseB-1 | CaseB-2 | CaseB-3 | CaseB-4 |
| Mooring line #2 broken | Mooring line #2 and #1 broken | Mooring line #2 and #8 broken | Mooring line #2 and #11 broken | |
| CaseC | CaseC-1 | CaseC-2 | CaseC-3 | CaseC-4 |
| Mooring line #2 broken | Mooring line #2 and #1 broken | Mooring line #2 and #8 broken | Mooring line #2 and #11 broken | |
| CaseD | CaseD-1 | CaseD-2 | CaseD-3 | CaseD-4 |
| Mooring line #2 broken | Mooring line #2 and #1 broken | Mooring line #2 and #8 broken | Mooring line #2 and #11 broken | |
| Intact | CaseA/B/C/D-1 | CaseA/B/C/D-2 | CaseA/B/C/D-3 | CaseA/B/C/D-4 | |
|---|---|---|---|---|---|
| Surge direction (kN/m) | 54.59 | 45 | 32.55 | 37.23 | 44.57 |
| Reduction (%) | / | 17.57 | 40.37 | 31.80 | 18.36 |
| Sway direction (kN/m) | 54.59 | 54.17 | 53.60 | 54.09 | 44.57 |
| Reduction (%) | / | 0.77 | 1.80 | 0.92 | 18.36 |
| Intact | CaseA/B/C/D-1 | CaseA/B/C/D-2 | CaseA/B/C/D-3 | CaseA/B/C/D-4 | |
|---|---|---|---|---|---|
| Surge (m) | 0 | −16.99 | −44.94 | 0 | −17.19 |
| Sway (m) | 0 | 0 | 2.01 | 0 | 17.18 |
| Heave (m) | 0 | 0 | 0.01 | 0.01 | 0.01 |
| Roll (deg) | 0 | 0 | 0 | 0 | 0 |
| Pitch (deg) | 0 | 0 | 0 | 0 | 0 |
| Yaw (deg) | 0 | 0 | 0.34 | 0 | 0 |
| Analysis Method | Limitation of Maximum Mooring Line Tension (Percentage of Minimum Breaking Load) | Safety Factor | |
|---|---|---|---|
| Intact | Quasi-static | 50 | 2.0 |
| Intact | Dynamic | 60 | 1.67 |
| Mooring lines broken | Quasi-static | 70 | 1.43 |
| Mooring lines broken | Dynamic | 80 | 1.25 |
| Peak Tension (MN) | ||||
|---|---|---|---|---|
| Seed-1 | Seed-2 | Seed-3 | Seed-4 | |
| Mooring Line #1 | 4.29 | 4.123 | 4.212 | 4.12 |
| Mooring Line #3 | 4.29 | 4.123 | 4.217 | 4.12 |
| Mooring Line #5 | 2.496 | 2.729 | 2.674 | 2.394 |
| Mooring Line #12 | 2.607 | 2.808 | 2.772 | 2.484 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, D.; Li, B.; Yan, J.; Qin, Y.; Liang, H.; Ning, D. Transient Responses Evaluation of FPSO with Different Failure Scenarios of Mooring Lines. J. Mar. Sci. Eng. 2021, 9, 103. https://doi.org/10.3390/jmse9020103
Qiao D, Li B, Yan J, Qin Y, Liang H, Ning D. Transient Responses Evaluation of FPSO with Different Failure Scenarios of Mooring Lines. Journal of Marine Science and Engineering. 2021; 9(2):103. https://doi.org/10.3390/jmse9020103
Chicago/Turabian StyleQiao, Dongsheng, Binbin Li, Jun Yan, Yu Qin, Haizhi Liang, and Dezhi Ning. 2021. "Transient Responses Evaluation of FPSO with Different Failure Scenarios of Mooring Lines" Journal of Marine Science and Engineering 9, no. 2: 103. https://doi.org/10.3390/jmse9020103
APA StyleQiao, D., Li, B., Yan, J., Qin, Y., Liang, H., & Ning, D. (2021). Transient Responses Evaluation of FPSO with Different Failure Scenarios of Mooring Lines. Journal of Marine Science and Engineering, 9(2), 103. https://doi.org/10.3390/jmse9020103








