Rethinking the Proportional Design Principles of Timber-Framed Buddhist Buildings in the Goryeo Era

Abstract

This study examines how the wooden architecture of the Goryeo Dynasty in Korea evolved in an original way while incorporating Chinese architectural principles. For the Goryeo Era’s timber-framed buildings, eave purlin height was determined according to √2H times the eave column height (H), while the eave column height influenced the proportional location of each purlin, determined by the √2H times decrease rate in the cross-section. Thus, eave column height was proportionately connected to a geometric sequence with a common ratio of √2H. This technical approach, achieved using an L-square ruler and a drawing compass, contributed to determining eave purlin and ridge post placement, bracket system height, and outermost bay width. This study notes that the practical works were consistently preserved in East Asian Buddhist architecture, in that a universal rule of proportion was applied to buildings constructed during the Tang–Song and the Goryeo Dynasties, surmounting differences in local construction methods. These design principles were a vestige of socio-cultural exchange on the East Asian continent and a minimal step toward the establishment of structurally safe framed buildings.

1. Introduction

This study shows that a universal construction method exists and confirms that it has been used in regions of East Asia, such as Korea and China, for a long time. The universal design principle was combined with and adapted to vernacular exiting methods over time. This study notes that the wooden-framed buildings in the Goryeo Era in Korea were transformed according to the local architectural environment based on the universal framework of obtaining the proportional principle and yeongjocheok (construction measurement unit) by making circles and squares using an L-square ruler and a drawing compass. Accordingly, in comparison with ancient Chinese buildings in the same period, this study confirms that Goryeo architecture demonstrates certain commonalities and differences, sharing common universality and adjusting differences in regional construction methods.

In both the East and the West, ancient people applied certain architectural objects and real numbers in building design. Concerns regarding the fundamentals of beauty and proportionality provide parallels between Western classical orders following the Vitruvian module (Vitruvius Pollio and Morgan 1960; Stevens 1990; Kim 2016) and East Asian classical works on mathematics, such as the Zhoubi Suanjing 周髀算經 (The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven) (Anonymous n.d.c; Cullen 2007) and the Jiuzhang Suanshu 九章算術 (The Nine Chapters on the Mathematical Art) (Anonymous n.d.a; Guo 2009). The Jiuzhang Suanshu was composed through the interpretive efforts of several generations of scholars from the tenth through the second century BCE, followed by Liu Hui (225–295 CE), who edited and published the work in 263 CE, during the Wei Era1 (Cha and Kim 2019). This book greatly influenced mathematical logic in Korea and Japan2 and contributed to philosophical contemplation and cultural formation in ancient East Asia. As in the traditions of Western classical architecture, certain proportional systems were used to create line drawings of wooden buildings utilizing L-square rulers and compasses.

To prevent collapse, ancient wooden buildings in East Asia were constructed following a ground plan with a rectangular contour. In buildings composed of columns, bracket sets, and a roof, the columns were the most essential, and they served as a standard reference to adjust each component’s location.3 The use of a regular cubit system matched the arrangement and setting of the internal frame structure. Wooden architecture requires large trees to be cut and polished into components with regular dimensions that can be used to erect large timber-framed buildings by assembling columns, beams, and purlins using mortise and tenon joints.4 To make the desired timber sections, craftspeople cut massive trees according to a specific ratio. Using the standard cubit system to produce regular components and maintain structural stability is vital for this process. However, the “standard” cubit system would often differ, even within the same period and region (Yun 1975). This shows that while there was a universal way to build a stable structure, there was also a different cubit system employed depending on the region and period (Kim 2011).

Hence, to delve into the universal and vernacular ways practiced in the Korean Peninsula, this study examined nine buildings in South and North Korea from the mid-to-late Goryeo Era: Bongjeongsa Monastery’s Geungnakjeon Hall (鳳停寺 極樂殿, twelfth or thirteenth century) in Andong; Buseoksa Monastery’s Muryangsujeon (浮石寺 無量壽殿, eleventh or thirteenth century) and Josadang Halls (祖師堂, 1377) in Yeongju, Seongbulsa Monastery’s Eungjinjeon Hall (成佛寺 極樂殿, 1327); Bogwangjeon Hall at Simwonsa Monastery (心源寺 普光殿, fourteenth century) in Yeontan; Sudeoksa Monastery’s Daeungjeon Hall (修德寺 大雄殿, 1308) in Yesan; Seongbulsa Monastery’s Geungnakjeon Hall (成佛寺 極樂殿, 1374), Eunhaesa Geojoam Hermitage’s Yeongsanjeon Hall (銀海寺 居祖庵 靈山殿, 1375) in Yeongcheon; and Imyeonggwan Guesthouse’s Sammun Gate (臨瀛館 三門, fourteenth century) in Gangneung (Figure 1).

Seven of the buildings followed the jusimpo style (柱心包, bracket complexes placed directly on column heads), and two followed the dapo style (多包, intercolumnar bracket complexes) (Figure 2). Bongjeongsa Monastery’s Geungnakjeon Hall preserved the mid-Goryeo building’s appearance between the twelfth and thirteenth centuries (Cultural Heritage of Administration (hereafter CHA) 2003, p. 102), while Buseoksa Monastery’s Muryangsujeon Hall retained its distinctive architectural style and techniques between the eleventh and thirteenth centuries (CHA 2002, p. 64; Cha and Kim 2019) (

Table 1. Goryeo-era’s buildings in the Korean Peninsula.

Building Name	Construction Period	Bracket Set’s Style	References
Geungnakjeon Hall at Bongjeongsa Monastery	Replacing roof tiles in 1363Built between the twelfth and thirteenth centuries in that roof tile repairs are usually replaced at intervals of 120–150 years	Jusimpo	(CHA 2003, p. 102)
Muryangsujeon Hall at Buseoksa Monastery	Repairing in 1376Built between the eleventh and thirteenth centuries due to many structural techniques related to the eleventh-century construction	Jusimpo	(CHA 2002, p. 64)
Daeungjeon Hall at Sudeoksa Monastery	1308, first construction	Jusimpo	(CHA 2005a, p. 78)
Eungjinjeon Hall at Seongbulsa Monastery	1327, first construction	Dapo	(NRICH 1998, p. 39)
Geungnakjeon Hall at Seongbulsa Monastery	1374, first constructionExtended outermost bays at front façade in the sixteenth century	Jusimpo	(NRICH 1998, p. 39)
Yeongsanjeon Hall at Geojoam Hermitage, Eunhaesa Monastery	1375, first construction	Jusimpo	(CHA 2004, p. 59)
Josadang Hall at Buseoksa Monastery	1377, first construction	Jusimpo	(CHA 2005b, p. 63)
Bogwangjeon Hall at Simwonsa Monastery	Rebuilding in 1374The fourteenth century	Dapo	(NRICH 1998, p. 36)
Sammun Gate at Imyeonggwan Guesthouse in Gangneung City	The fourteenth century	Jusimpo	(CHA 2004, p. 140)

Dapo: inter-columnar bracket set; jusimpo: column top bracket set.

).

This study aimed to elucidate the proportional design principles of $\sqrt{2}$times the eave purlin height by examining wood-frame buildings in ancient Korea and China. Ancient wood-frame architecture in East Asia relied on columns, beams, and purlins to form a basic structure and determine a plan for the buildings’ construction. Critical factors regulating a building’s scale were the column height and purlin location. This study methodically and accurately analyzed the geometry used in nine examples of Goryeo architecture in Korea.

Essentially, this study examined how ancient Chinese architectural culture influenced the evolution of building principles in ancient Korea. Accordingly, architectural design principles in Goryeo Era buildings were analyzed, following which Chinese buildings were examined to focus on aspects relevant to these principles. This study identified similarities and differences through comparisons with Korean and Chinese buildings that shared the same design principles since the eighth century. As a common point, the positions of the purlins were determined by applying a proportionality of √2 times the eave pillar height. Such a universal point recognized that Goryeo architecture inherited the rules of ancient Chinese architecture. Differences can be found in the methods used to determine purlin location, purlin size, and the presence of column purlins. Thus, this study indicates the process of adapting as a universal method accepts the construction method of local architecture on the Korean Peninsula and is assimilated into vernacular buildings, sharing existing construction techniques thereon.

2. Preliminary Study of the Proportional System of Traditional Wood-Frame Architecture in East Asia

A few previous studies have been conducted on the proportional systems of traditional wood-frame buildings in Korea. Sim and Kim (1983) analyzed the proportional systems of the bracket elements in dapo intercolumnar bracket complexes, identifying formal similarities among the bracket systems of wooden buildings in Korea, China, and Japan, despite disparities caused by the lack of agreement on the width of the cai (材, a length unit in the cai-fen 材分 carpentry system). Kim (2003) addressed the proportional system of the front and side façades of buildings with intercolumnar bracket systems, including purlin location, roof type, and floor area. Kim (2008) examined the adoption of a cubit system based on an average of 31.29 cm and wooden components with proportions of 5:3, 9:5, and 3:5 used to construct the Daeungjeon Hall at the Sudeoksa Monastery.5 In a study on the Muryangsujeon Hall at the Buseoksa Monastery, Kim (2014) posited that an eleventh-century building method was used, based on the composition principle of the plan and cross-section and repetition of wooden components identical to a cubit system (30.3 cm), deduced from the actual measurements. Cha and Kim (2019) discussed mathematical proportional systems for the overall structural design of wooden architecture, identifying the √2 ratio system for arranging wooden components in an internal framed structure and the relationship between outer bay width and eave column height. Comparing construction methods in the Song Era with Korean wooden structures, Bak and Mun (1992) noted other details that indicated local differences, such as the width of wooden components, proportions of the front and side façades, and roof types.

Among the research from China and Japan on the proportional system of √2H times the eave column height for the proportion of interior timber-framed buildings, Chen (1981) found that eave column height determined the dimensions of the middle roof purlins and the queen posts from the ground level. Meanwhile, Fu’s (2001) research was more advanced, revealing that the height of the eave columns along the cross-section had a noticeable proportional link to the overall length of the frontal view on a ground plan along the longitudinal direction, corresponding to standard proportions in the application of mid-rise buildings with two or more above-ground stories (Figure 3). Wang (2011a) and Chen (1981) conducted significant studies on the height of eave columns and purlins, showing the feasibility of the √2 times proportional system6 (Figure 4).

Yoneda conducted significant research on the proportional system of framed stone elements during the Japanese colonial period at the Seokguram Buddhist Grotto7 (Yoneda 1944; Yoneda and Sin 1976). Although Chinese and Japanese scholars have provided important information regarding the proportional system of ancient wooden buildings, there are still no definitive answers to the questions that concern the purlin locations relying on the proportional link of $\sqrt{2}$H times the height of the eave columns in the cross-section. The $\sqrt{2}$H ratio is key to restoration studies. The current study provides a better understanding of Korean monuments by comparing them with ancient wooden structures in East Asia.

Most studies after the 2000s have examined the proportionality of aesthetic perfection in East Asia, but there are some records of the design of wood-frame buildings using proportional systems or accurate information regarding the manuals for line drawings and measurements (Fu 2001; Wang 2011a, 2011b; Wang 2017a, 2017b, 2017c, 2018a, 2018b, 2019; Wang et al. 2021a). In particular, the study of Guixiang Wang (2011a) is noteworthy in that the arithmetic of the square root of two from the ancient Chinese mathematical texts contributed to determining the 1:$\sqrt{2}$ ratio of the heights of the eave columns (exterior columns or perimeter columns, named yanzhu [檐柱] or weizhu [外柱]) and eave purlins (Wang 2011a, 2011b; Cha and Kim 2019).

Wang Nan’s research confirms that the “circle–square map” (yuanfangtu) and “square–circle map” (fangyuantu) were commonly applied during the design of ancient capital cities and timber-framed buildings for the utilization of geometric rules; similar techniques for structural composition appeared in the Buddhist halls, pavilions, and pagodas of the Tang, Liao, and Qing dynasties (Wang 2017a, 2017b, 2017c, 2018a, 2018b, 2019). Based on these achievements, Wang et al. (2021a)’s recent study concerning the wooden frame pagoda in Ying County, Shanxi Province, notes that during the design of Buddhist buildings in dynastic China, statues and their surrounding spaces were designed in a uniform style, allowing a harmonious proportion between the statues and the neighboring inner spaces on every floor. He indicates that the most frequently used proportions for the organization of interior spaces and placement of statues inside the pagoda are √2:1, 3:2, or 5:3 (or 8:5), and 9:5, which are compatible with the 1.5:1 ratio, approximately. The results show that a uniform measurement system was employed to determine the building scale between the spaces and sculptures in the Buddhist Wooden Pagoda (Wang et al. 2021a).

The application of the $\sqrt{2}$H ratio in deciding the placement and the length of individual members as a manual for building design spread to the Korean Peninsula around the seventh century and had an important influence as a building design principle on the Korean Peninsula until modern times (Cha and Kim 2019). Likewise, a morphological approach on multi-storied brick pagodas of the Tang Dynasty implies the use of proportion and modules that took other wooden structures as a reference (Wang et al. 2021b). This designates that a universal construction method existed and that it has been preserved in East Asia, for example, in countries such as Korea and China, for a long time (Kim 2011; Kim and Park 2017).

3. Research Method

To build a traditional wood-frame structure, builders placed plinth stones on a platform and then situated the columns on the platform. They positioned transverse beams beneath purlins to establish the building framework. They completed the basic wooden framework using timber-framed interior structures with rafters above. Roofs were shaped by two diagonally slanted struts whose heads were joined together and topped by a bearing block in the synthesis of a top beam with an upper roof purlin. The wooden structures relied on columns, beams, and purlins as their basic components, the location and size of which, and the method used to connect each part, determined the building scale.

The following settings were used to describe the concepts of squares, circles, and geometric models.

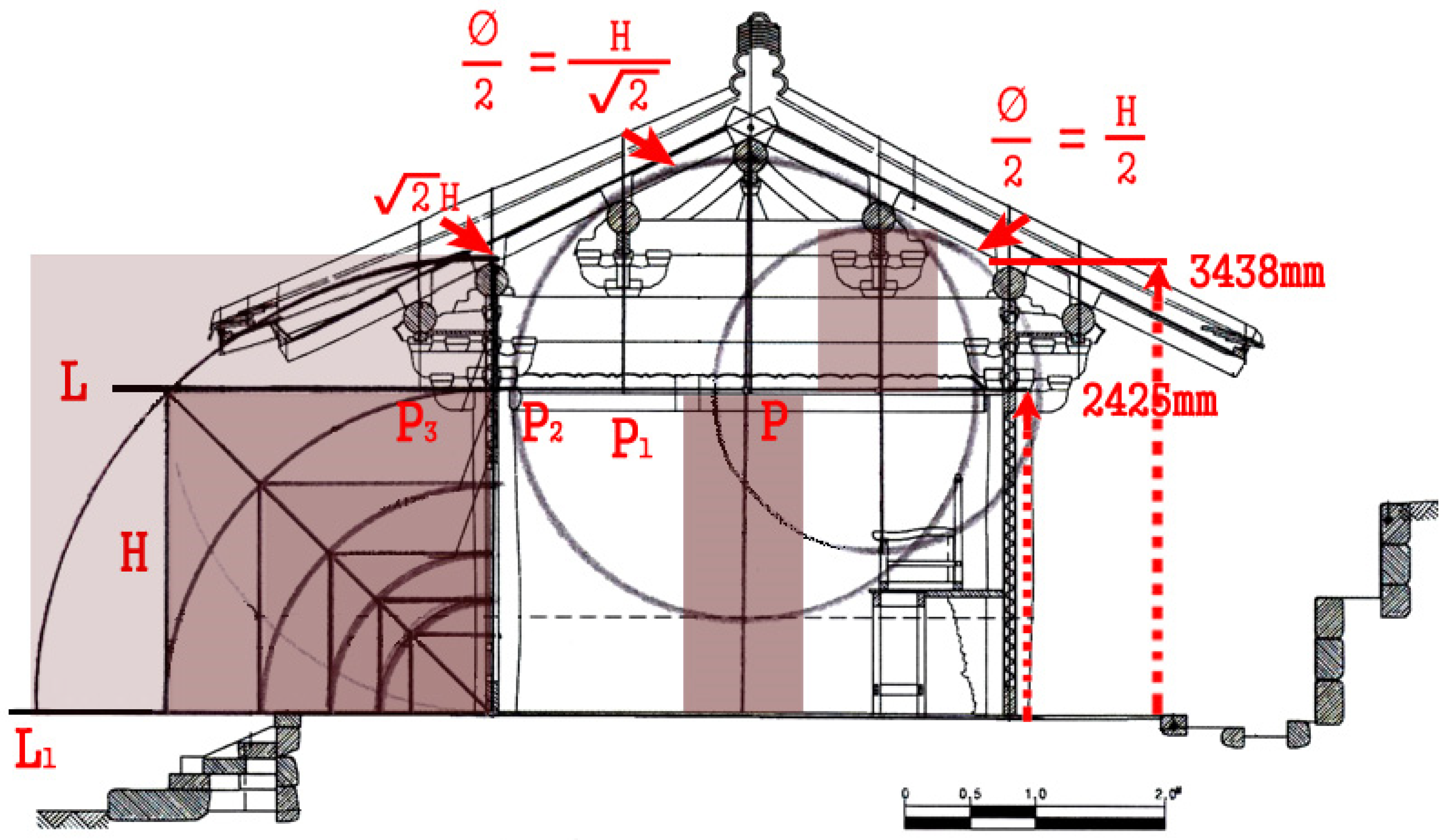
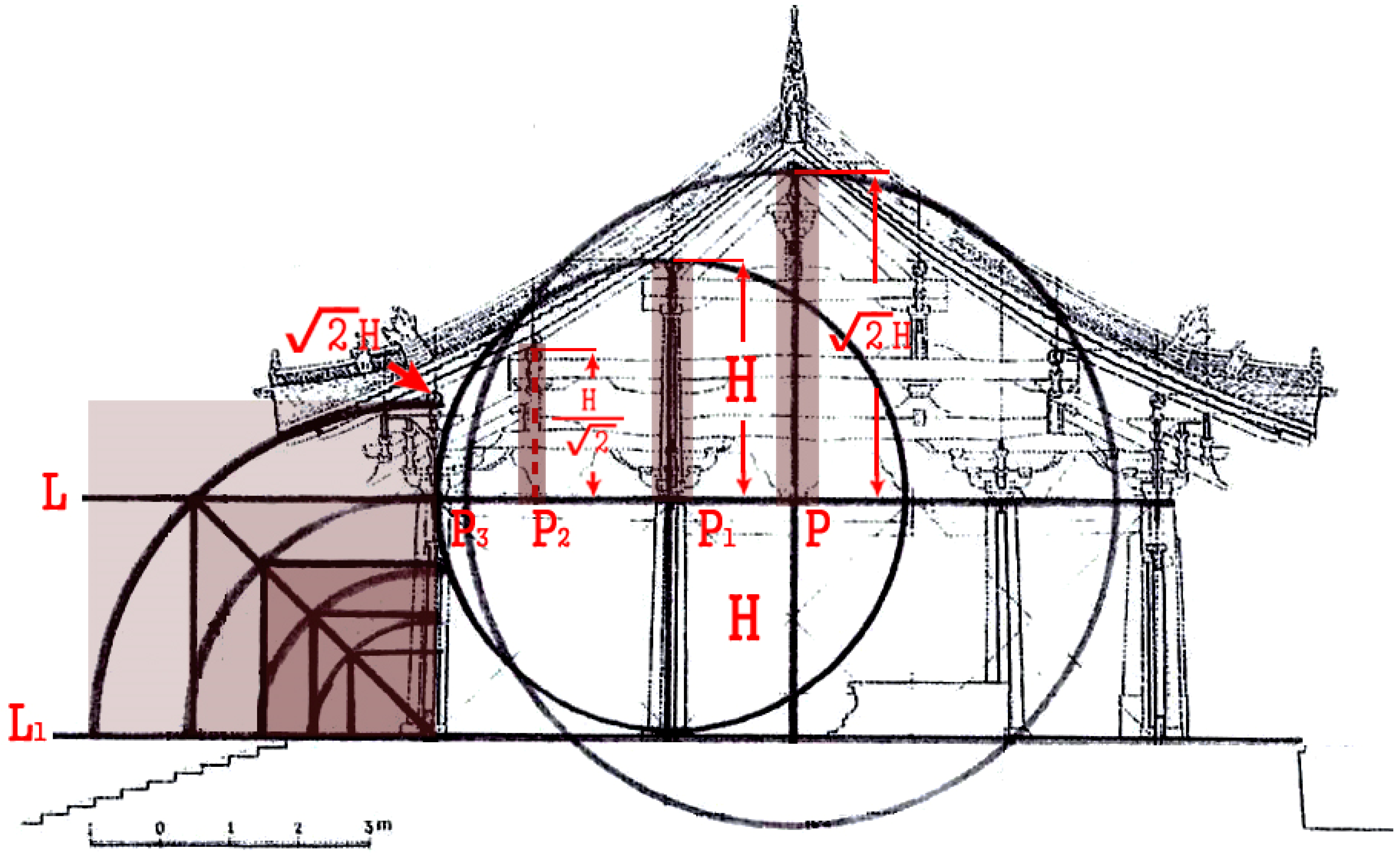
First, in this study, “(H)” means the eave column height of a wooden building and serves as a standard reference for the overall composition and scale of the timber-framed structure.

Second, the circle–square (圓方圖) and the square–circle (方圓圖) diagrams include the principle for making a circular form using a square (Figure 5), according to the Zhoubi Suanjing and Jiuzhang Suanshu. The unremitting and repetitive overlap of squares within circles and circles within squares shows that there were regular rules to calculate the length comparable to geometric sequences in modern mathematics. The proportional principle determines each diagonal line length made through the superimposition of squares and circles outwards or inwards, resting on the length ratio of verticality and horizontality (Figure 6). According to the “Cuifen” (衰分, Distribution by Proportion) of the Jiuzhang Suanshu, this book introduced the problem regarding “nuzhi” (women who weave textiles) to explain the principle as a geometric progression.8 The nuzhi show a ratio based on 2 in the sequence 1, 2, 4, 8, 16, etc.9 (Figure 7). The ancient Chinese knew the geometric law that was created through the repetitive combination of circles and squares for such a consistent system of proportions. Through this principle, a method of weaving was developed. The same calculation method was also used in the juzhe ((first) raise (the total height) and (then) break (for individual heights of purlins)) method of the Yingzao Fashi (State Building Standards) of the Song Dynasty (Li 1100).

Third, assuming that the roof curve from the eave purlins to the ridge purlin becomes steeper in the wooden framework, the purlins would be situated in a gradually higher position, with decreasing height ratios of 1/10, 1/20, 1/40, and 1/80, respectively, according to the juzhe method for roof curvature in the Yingzao Fashi, juan 5, “Major Carpentry System.” The ridge purlin height must be determined first by basically considering the main crossbeam length, and then other purlins’ heights can be determined to make the roof curvature by placing rafters on the roof purlins (Li 1100). Consequently, this shows that the geometric rule had been persistently used to shape a curved roof in ancient timber-framed buildings, conforming to the location and arrangement of all purlins (Figure 8).

Fourth, regarding the second and third assumptions, $\sqrt{2}$H times the eave column height is served in the cross-section of the wooden structure as a reference standard for the geometric concept. Therefore, in successive order, the numerical values are as follows: 2H, $\sqrt{2}$H, H, $\frac{\mathrm{H}}{\sqrt{2} }$, $\frac{\mathrm{H}}{2}$, $\frac{\sqrt{2} \mathrm{H}}{4}$, and $\frac{\mathrm{H}}{4}$ in regular sequence, implying a geometric sequence in which each term after the first is $\frac{\mathrm{H}}{\sqrt{2} }$ times the previous term. The geometric series with a ratio of $\frac{H}{\sqrt{2} }$ makes it possible to organize interior timber-framed structures by applying a proportional principle.10 The geometric concept is applied as the reference standard for eave column height, depending on the drawing of squares and circles that used a drawing compass and carpenter’s square, and is manipulated according to the proportion of $\sqrt{2}$H times the eave column height (Figure 9 and Figure 10).

Further, this study established a standard line for a detailed comparison of the purlin location and arrangement between each building using the following abbreviations: (H) is the eave column height, (L) is the horizontal standard line that touches the upper side of the front and rear eave columns, (L₁) is the horizontal line meeting the upper side of the front and rear plinth stones, and (P) is the intersection between (L) and the vertical downward line from the centerline of the ridge purlin. Where (L) connects to the upper side of the front and rear eave columns, the vertical downward lines from the upper-middle roof purlins, middle roof purlins, lower-middle roof purlins, and column purlins are identified as P₁, P₂, P₃, and P₄, respectively. As noted above, we analyzed the proportional rapport between the location and distance of the wooden components in timber-framed structures (Figure 9).

4. Interpretation of the Proportional System in Nine Goryeo Era Timber-Framed Buildings

4.1. Associations between the Eave Column Height (H) and $\sqrt{2}$H

The line drawing of the Bongjeongsa Monastery’s Geungnakjeon Hall reveals a notable point. Achieved using a square with a circle created with compasses and L-square rulers, the $\sqrt{2}$H times the eave column height from the top plinth stones to the top eave columns is equal to the height of the column purlins. In the Muryangsujeon Hall at the Buseoksa Temple, the ratio is entirely different. Although the builders used a method similar to that used for Bongjeongsa’s Geungnakjeon Hall, the eave column height of the Muryangsujeon Hall is $\sqrt{2}$H times the height from the top of the plinth stones to the top of the eave purlins, not the column purlins. Thus, the column purlin height was $\sqrt{2}$H times the eave column height (Figure 10 and Figure 11). The same method was used for other Buddhist monastery buildings, such as the Daeungjeon Hall at Sudeoksa, Josadang Hall at Buseoksa, Geojoam Hermitage’s Yeongsanjeon Hall at Eunhaesa, and Sammun Gate at Imyeonggwan Guesthouse (Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18). For these buildings, the height from the top of the plinth stones to the top of the column purlins was employed as $\sqrt{2}$H× the eave column height.

The Bogwangjeon Hall at Simwonsa Temple and Eungjinjeon Hall at Seongbulsa Temple differed somewhat from the above-mentioned buildings. The Eungjinjeon Hall did not have any column purlins except for its internal and external eave purlins. The distance from the top of the eave purlins to the top of the building platform was $\sqrt{2}$H times the eave column height. The Bogwangjeon Hall at the Simwonsa Temple had no column purlins but had external eave purlins (Figure 13 and Figure 19). Assuming that the height from the top of the stone plinths to the top of the architraves, including the eave columns, measured 1 unit, a length of $\sqrt{2}$H times the height of the eave columns would not reach the bottom of the eave purlins. Further, the eave column height was consistent with the top of the main crossbeams, which were made thicker to adjust for the height. Planks were also added below the eave purlins to control the height between the eave purlins and main crossbeams. There are several cases with similar proportions among the Tang, Song, and Liao buildings in ancient Chinese dynasties. They embrace the East Hall of the Foguangsi Temple and the Main Halls of the Zhenguosi, Hualinsi, and Kaiyuansi Temples. The height of $\sqrt{2}$times the eave columns is slightly larger than the top side of the eave purlins’ height, by a ratio of approximately 1.5 times. The majority of buildings in China that have descending cantilevers differ from those in Korea that do not have any descending cantilevers (Wang 2011a, pp. 41–42).

For the Geungnakjeon Hall at the Seongbulsa Monastery, there was a difference between (H) and $\sqrt{2}$H times the height from the top of the plinth stones to the top of the column purlins (Figure 15). The Geungnakjeon Hall’s proportional principle complied with a ratio of 1.55H times the eave column height, somewhat higher than $\sqrt{2}$H times, similar to the proportional rule used for the main halls of the Zhenguosi Monastery (鎮國寺 大殿, 963) and the Hualinsi Monastery (華林寺 大殿, 964) from the Five Dynasties and Ten Kingdoms Period (907–979) (Wang 2011a). However, the two Chinese buildings had relatively larger crossbeams and represented three downward-slanting cantilevers, unlike the structural systems of the Seongbulsa Monastery’s Geungnakjeon Hall, which did not use $\sqrt{2}$H times (H)11 (

Table 2. The proportional relationship between eave columns’ height (H) and √2 times.

Building Name	Component Location That Meets √2 Times the Eave Column Height (H)	Remarks
Geungnakjeon Hall at Bongjeongsa Monastery	The bottoms of column purlins	Other purlins are positioned at the bottoms
Muryangsujeon Hall at Buseoksa Monastery	The tops of eave purlins	Some purlins are positioned at the bottoms
Daeungjeon Hall at Sudeoksa Monastery	The bottoms of column purlins	Other purlins are positioned at the bottoms
Eungjinjeon Hall at Seongbulsa Monastery	The tops of eave purlins	Other purlins are positioned at the bottoms
Geungnakjeon Hall at Seongbulsa Monastery	A little higher than the tops of column purlins	Other purlins are positioned at the bottoms
Yeongsanjeon Hall at Geojoam Hermitage, Eunhaesa Monastery	The tops of column purlins	Some purlins are positioned at the bottoms
Josadang Hall at Buseoksa Monastery	The tops of column purlins	Some purlins are positioned at the bottoms
Bogwangjeon Hall at Simwonsa Monastery	The bottoms of eave purlins	Other purlins are positioned at the bottom sides
Sammun Gate at Imyeonggwan Guesthouse in Gangneung City	The tops of column purlins	Other purlins are positioned at the tops
The Main Hall at Nanchansi Monastery (Tang, early eighth century)	The tops of eave purlins
The East Hall at Foguangsi Monastery (Tang, 857)	The tops of eave purlins
The Main Hall at Hualinsi Monastery (Song, 964)	The tops of eave purlins
The Main Hall at Geyuansi Monastery (Liao, 966)	The tops of column purlins
The Shanmen Front Gate at Dulesi Monastery (Liao, 984),	The tops of column purlins	Including plinths height
The Main Hall at Baoguosi Monastery (Song, 1013)	The tops of column purlins	Including plinths height
The Main Hall at Fengguosi Monastery (Liao, 1020)	The tops of column purlins	Including plinths height
The Main Hall at the Chuzu’an Hermitage (Song, 1125)	The tops of column purlins

).

Of the nine buildings, seven followed the proportional principle that $\sqrt{2}$H times the eave column height should meet the top or bottom of the column purlins and the bottom of the eave purlins. The other two buildings (Eungjinjeon at Seongbulsa and Bogwangjeon at Simwonsa Monasteries) did not have column purlins; however, the overall proportional system was the same as for the other seven buildings.

4.2. Connections between (H), the Columns’ Vertical Positioning, and the Proportional Relationship to $\sqrt{2}$ Times

Pre-Joseon Dynasty documents regarding the Korean Peninsula do not describe a method for determining purlin arrangement to create a roof framework. Further, the Yeongjo Uigwe (Royal Protocols in the Joseon Dynasty) does not include decisions on building proportions or purlin height. Chinese literature mentions how to arrange purlins, with instructions in the Kaogongji (The Artificers’ Record) (Anonymous n.d.b) and the Yingzao Fashi (State Building Standards) of the Song Dynasty, and the Gongcheng Zuofa of the Qing Dynasty (Anonymous 1734). Two of these books indicated that in the Ming–Qing Era buildings, the height of each purlin’s position had slightly increased, a feature that distinguishes Song-Era buildings from those built during the Ming and Qing Dynasties (Li 1982).

First, in the Jiangren “architect–artisans” section of the Kaogongji, in setting out the method for determining roof height, the text of the Jiangren wei gouxu section reads as follows: (For a thatched roof, (the height of the roof from the eaves is) one-third (of the width of the building); for a tiled roof, one-fourth). This not only indicates that the roof height is usually germane to the width of a building, but it also clearly states that the height depends upon which type of roof is under construction, and the ratio between them leads to a progressive increase or decrease in the height of the ridge. Buildings have three modular units ((original annotation) as a falling cone): The (main) crossbeam and what is above it belong to the upper unit; what is above ground (except for the beam structure) belongs to the middle unit; the stairs belong to the lower unit (Wen 2008, p. 126).

Second, the Damiuzuo zhidu 大木作制度 (major carpentry system) in the section of the Yingzao Fashi notices that the construction system of the roof-height curve (juzhe), raising the roof (juwu), and inward-curving roofs (zhewu) correlate with the horizontal length from eave purlins (laoyanfang) to a ridge purlin (jishuan) and the vertical length between them, and the horizontal and vertical lengths have different dimensions depending on round roof tiles (banwa), semi-cylindrical roof tiles (tongwa), multi-story buildings (louge), and hall-type buildings (tingtang), and the construction system of inward-curving roofs, such that the irregular arrangement of the purlins brings about moderate increases or decreases. In all circumstances, the length of the (main) crossbeam governs the height of the ridge purlin, and the ratio between them leads to a progressive increase or decrease in the height of the ridge. Li Jie says that the recent code of the design of the roof-height curve is essentially developed from the code that takes a quarter of the houses to make the height of their roofs. It is in line with the classic text of the Kaogongji of the Zhouli (Liang and Li 1983).

In contrast, in Korea, anonymous buildings in the pre-Goryeo Era show odd bays at the side façade. In the case of Joseon-Era’s buildings constructed since the seventeenth century, most cases subsume an odd row of columns such as one, three, and five bays, and so on. Among them, wooden constructions with three bays at the side façade occupy the majority of cases, and generally, the central bay at the side façade is wider than the outermost bays’ widths at the front and back façades.

The roof height from eaves is one-third or one-fourth of the building width mentioned from the Zhouli and the Yingzao Fashi has the same length as each bay width at the side façade, whereas in ancient buildings in Korea, the bay widths are not equally distributed. These factors show that the ancient Korean buildings are structurally different from the Chinese. Nevertheless, it should be noted that Korean and Chinese buildings shared and preserved universal and standardized design principles for setting purlin locations and bracket-set heights.

The baseline (L) marks the connection between the top of the eave columns in the cross-section from front to back, creating a cross-point intersecting with the baseline (L) and descending from a ridge post to the eave purlins. The eave purlins were generally placed at the lowest point, while the ridge post was at the highest.

The Geungnakjeon Hall at the Bongjeongsa Temple had upper- and lower-middle roof purlins but no middle roof purlins. The lower-middle roof purlins aligned with a row of interior columns in the cross-section. Assuming that the eave column height was H above the baseline (L), a geometric progression with the ratio of $\frac{1}{\sqrt{2} }$ was established as 2H, $\sqrt{2}$H (=1.414), H, $\frac{\mathrm{H}}{\sqrt{2} }$, (=0.7), $\frac{\mathrm{H}}{2}$, $\frac{\sqrt{2} \mathrm{H}}{4}$, (=0.35), and $\frac{\mathrm{H}}{4}$, adjusting the numerical variations (Figure 10). The Bongjeongsa Monastery’s Geungnakjeon Hall shows that purlin height dictated the location of the eave purlins, column purlins, lower-middle roof purlins, and ridge purlin as $\frac{\sqrt{2} \mathrm{H}}{4}$, $\frac{\mathrm{H}}{2}$, $\frac{\mathrm{H}}{\sqrt{2} }$, and H times the eave column height, which is a geometric progression. The height of the upper-middle roof purlins was decided as the sum of $\frac{\sqrt{2} \mathrm{H}}{4}$ plus $\frac{\mathrm{H}}{2}$ times ratio, based on the height of the eave columns and the eave purlins. Determining each purlin height that supported the roof frame of the Geungnakjeon Hall relied on the column height (H).

The purlins of the Buseoksa Monastery’s Muryangsujeon Hall were not uniformly distributed but densely placed from the middle roof purlins to the upper-middle roof and ridge purlins. The height proportion of the top of the eave purlins and the bottom of the column purlins above the baseline (L) used the $\frac{\mathrm{H}}{2}$ times formula. The height from the column purlins to the upper-middle roof purlins was calculated according to the geometric sequence. That is, if the eave column height was H, the eave purlin height would be $\sqrt{2}$H, and the middle roof purlin height would be 2H, following a geometric sequence with the $\sqrt{2}$ratio. The height of the top of the upper-middle roof purlins above the baseline (L) corresponded to the $\sqrt{2}$H times formula, which had no distinction compared to the ridge purlin height, H plus $\frac{\mathrm{H}}{\sqrt{2} }$. The ridge purlin height deviated somewhat from the geometric sequence, as it did not maintain a common difference.

Similarly, the Sudeoksa Monastery’s Daeungjeon Hall used a geometric concept with a common ratio of $\sqrt{2}$from the eave purlins to the ridge post. The heights of the column purlins and the ridge post were decided by their tops, and the other purlins were situated according to their bottoms, revealing a relatively consistent proportional system. The Seongbulsa Monastery’s Eungjinjeon Hall had no eave columns, and both the external and internal eave purlins used the height ratio of $\frac{\sqrt{2} \mathrm{H}}{4}$ and $\frac{\mathrm{H}}{2}$ times separately, depending on the column purlin height and geometric progressions. Seongbulsa Monastery’s Geungnakjeon Hall added outer bays to the front façade in 1650 (the first year of King Hyojong’s reign). Thus, the outer bays were excluded in the present study. The location of the external eave purlins used a somewhat larger value than $\sqrt{2}$H, while the locations of the other eave purlins used a geometric progression (

Table 3. Each purlin height in the application of √2 times the height of eave columns above the baseline (L).

Building Name		Each Purlin Height Ratio above the Baseline (L) That Meets the Tops of the Front and the Rear Eave Columns
		Eave (External) Purlins’ Height	Column Purlins’ Height	Lower-Middle Roof Purlins Height	Middle Roof Purlins’ Height	Upper-Middle Roof Purlins’ Height	Ridge Purlin Height
Geungnakjeon Hall at Bongjeongsa Monastery	Eave Columns’ Height (H)	${\mathrm{P}}_4,\frac{\sqrt{2} \mathrm{H}}{4}$	${\mathrm{P}}_3,\frac{\mathrm{H}}{2}$	${\mathrm{P}}_2,\frac{\mathrm{H}}{\sqrt{2} }$	None	${\mathrm{P}}_1,\frac{\sqrt{2}\mathrm{H}}{4}$$+\frac{\mathrm{H}}{2}$	P, H
Muryangsujeon Hall at Buseoksa Monastery		${\mathrm{P}}_5,\frac{\sqrt{2} \mathrm{H}}{4}$	${\mathrm{P}}_4,\frac{\mathrm{H}}{2}$	${\mathrm{P}}_3,\frac{\mathrm{H}}{\sqrt{2} }$	P2, H	${\mathrm{P}}_1,\sqrt{2}$H	$\mathrm{P},\mathrm{H}+\frac{\mathrm{H}}{\sqrt{2}}$
Daeungjeon Hall at Sudeoksa Monastery		${\mathrm{P}}_5,\frac{\mathrm{H}}{4}$	${\mathrm{P}}_4,\frac{\sqrt{2} \mathrm{H}}{4}$	${\mathrm{P}}_3,\frac{\mathrm{H}}{2}$	${\mathrm{P}}_2,\frac{\mathrm{H}}{\sqrt{2} }$	P1, H	$\mathrm{P},\sqrt{2}$H
Eungjinjeon Hall at Seongbulsa Monastery		${\mathrm{P}}_3,\frac{\sqrt{2}\mathrm{H}}{4}$	${\mathrm{P}}_2,\frac{\mathrm{H}}{2}$ (inner eave purlins)	None	${\mathrm{P}}_1,\frac{\mathrm{H}}{\sqrt{2} }$	None	P, H
Geungnakjeon Hall at Seongbulsa Monastery		${\mathrm{P}}_3,\frac{\mathrm{H}}{4}$	${\mathrm{P}}_2,\frac{\sqrt{2}\mathrm{H}}{4}$	None	${\mathrm{P}}_1,\frac{\mathrm{H}}{\surd 2}$	None	P, H
Yeongsanjeon Hall at Geojoam Hermitage, Eunhaesa Monastery		${\mathrm{P}}_3,\frac{\mathrm{H}}{4}$	${\mathrm{P}}_2,\frac{\sqrt{2}\mathrm{H}}{4}$	None	${\mathrm{P}}_1,\frac{\mathrm{H}}{\sqrt{2}}$	None	$\mathrm{P},\frac{\mathrm{H}}{\sqrt{2}}$$+\frac{\mathrm{H}}{2}$
Josadang Hall at Buseoksa Monastery		${\mathrm{P}}_3,\frac{\mathrm{H}}{4}$	${\mathrm{P}}_2,\frac{\sqrt{2}\mathrm{H}}{4}$	None	${\mathrm{P}}_1,\frac{\mathrm{H}}{2}$	None	$\mathrm{P},\frac{\mathrm{H}}{\sqrt{2}}$
Bogwangjeon Hall at Simwonsa Monastery		${\mathrm{P}}_4,\frac{\mathrm{H}}{2}$	None	${\mathrm{P}}_2,\frac{\mathrm{H}}{\sqrt{2}}$	None	P1, H	$\mathrm{P},\sqrt{2}$H
Sammun Gate at Imyeonggwan Guesthouse in Gangneung City		${\mathrm{P}}_3,\frac{\mathrm{H}}{4}$	${\mathrm{P}}_2,\frac{\sqrt{2}\mathrm{H}}{4}$	None	${\mathrm{P}}_1,\frac{\mathrm{H}}{2}$	None	$\mathrm{P},\frac{\mathrm{H}}{\sqrt{2}}$
The Main Hall at Nanchansi Monastery (early eighth century)	Eave Columns’ Height (H)	${\mathrm{P}}_3,\frac{\sqrt{2}\mathrm{H}}{4}$	${\mathrm{P}}_2,\frac{\mathrm{H}}{2}$	None	${\mathrm{P}}_1,\frac{\mathrm{H}}{\surd 2}$	None	P, H
The East Hall at Foguangsi Monastery (857)		${\mathrm{P}}_3,\frac{\sqrt{2}\mathrm{H}}{4}$	${\mathrm{P}}_2,\frac{\mathrm{H}}{\sqrt{2}}$	None	P1, H	None	$\mathrm{P},\sqrt{2}$H
The Main Hall at Hualinsi Monastery (964)		${\mathrm{P}}_3,\frac{\sqrt{2}\mathrm{H}}{4}$	${\mathrm{P}}_2,\frac{\mathrm{H}}{\sqrt{2}}$	None	P1, H	None	$\mathrm{P},\sqrt{2}$H
The Main Hall at the Chuzu’an Hermitage (1125)		${\mathrm{P}}_3,\frac{\sqrt{2}\mathrm{H}}{4}$	${\mathrm{P}}_2,\frac{\mathrm{H}}{\sqrt{2}}$	None	P1, H	None	$\mathrm{P},\sqrt{2}$H

).

Vertically downward lines from upper-middle roof purlins, middle roof purlins, and lower-middle roof purlins are considered as P1, P2, P3, P4, and P5, respectively.

The Geojoam Hermitage’s Yeongsanjeon Hall at the Eunhaesa Temple employed a geometric progression with the $\sqrt{2}$ ratio from the eave purlins to the middle roof purlins. The ridge purlin height was established based on the sum of $\frac{\mathrm{H}}{\sqrt{2}}$ plus $\frac{\mathrm{H}}{2}$ times. Its height was higher than (H). The location of the ridge post was relatively high, indicating a proportional system similar to that of the Muryangsujeon Hall at the Buseoksa Monastery (Figure 11 and Figure 20).

The Josadang Hall at the Buseoksa Monastery and the Sammun Gate at the Imyeonggwan Guesthouse had three columns in their front façades. They complied with the ratio of $\frac{\mathrm{H}}{4}$, $\frac{\sqrt{2}\mathrm{H}}{4}$, $\frac{\mathrm{H}}{2}$, and $\frac{\mathrm{H}}{\sqrt{2}}$times the eave column height, from the middle roof purlins to the ridge purlin. Whereas the Sammun Gate had the location of each purlin based on the top side of all roof purlins, the Josadang Hall had the placement of each purlin based on the tops of the eave purlins and column purlins, and the bottoms of the middle roof purlins and ridge purlin (Figure 14). The Sammun Gate used the standard height from a stone platform to the top of all roof purlins, and the Josadang Hall used the standard height from a stone platform to the top of the eave and column purlins. The heights of the middle roof purlins and ridge purlin were based on the bottoms of the middle roof purlins and ridge purlin. The Bogwangjeon Hall at the Simwonsa Monastery and the Eungjinjeon Hall at the Seongbulsa Monastery had multilayer bracket systems and showed unique proportional features. Their design principle depended on the eave column height. The Bogwangjeon Hall had a few differences from the Eungjinjeon Hall; for example, the eave purlin height did not correspond to the $\sqrt{2}$ times ratio, although the rest were matched by the ratio of $\sqrt{2}$H times the eave column height, a standard for composing a complete proportional framework. Based on the eave column height, the location of each purlin, from the eave purlins to the ridge purlin, showed a geometric progression of $\frac{\mathrm{H}}{2}$, $\frac{\mathrm{H}}{\sqrt{2}}$, H, and $\sqrt{2}$H times as a proportional system, although there were no column purlins.

Thus, the design characteristics of these nine buildings provide evidence that the builders used (H) as a reference point connected with a geometric series ratio of $\sqrt{2}$H times to set the height of each purlin.

4.3. The Proportional Relationship between the Outer Bay width and the Eave Column Height (H)

Most buildings in the Goryeo Era had rows of columns at the side façade arranged on the same vertical location as the lower-middle and middle roof purlins. These buildings were evidently distinct from the wood-frame buildings with side columns and roof purlins that have been organized differently since the seventeenth century. Few Goryeo buildings had an even row of columns at the side façade. The Bongjeongsa Monastery’s Geungnakjeon Hall and the Sudeoksa Monastery’s Daeungjeon Hall had four bays at their side façades. The Seongbulsa Monastery’s Eungjinjeon Hall had two bays at the side façade, exclusive of the front outer bays. In comparison to the nine buildings in this study, the Geungnakjeon Hall at the Bongjeongsa Temple had the smallest width in the outer bays at the side façade. The Sudeoksa Temple’s Daeungjeon Hall had an almost equivalent lateral width in each bay at the side façade. The Seongbulsa Monastery’s Geungnakjeon Hall had high columns that did not meet a ridge post, similar to Sudeoksa Monastery’s Daeungjeon Hall, where the columns were sheltered into the bottom of the ridge post. In Bongjeongsa’s Geukrakjeon Hall, Seongbulsa’s Eungjinjeon Hall, and Simwonsa’s Bogwangjeon Hall, the width of the outer bays at the side façade showed a ratio of $\frac{\mathrm{H}}{2}$ plus $\frac{\sqrt{2}\mathrm{H}}{4}$ times, which was shorter than (H)—0.6H times larger than half the eave column height.

For the Muryangsujeon and Josadang Halls at the Buseoksa Monastery and the Yeongsanjeon Hall at the Geojoam Hermitage in the Eunhaesa Monastery, the outer bay width at the side façade was approximately $\frac{\mathrm{H}}{2}$ plus $\frac{\sqrt{2}\mathrm{H}}{4}$ (0.85H) times the eave column height. For the Sammun Gate at the Imyeonggwan Guesthouse and the Daeungjeon Hall at the Sudeoksa Monastery, the outer bay width at the side façades was $\frac{\mathrm{H}}{\sqrt{2}}$ times (0.7H) the eave column height. Likewise, the Seongbulsa Monastery’s Geungnakjeon Hall had high columns at the center of the side façades, divided into two bays from front to back. The outer bay width on the side façades was equal to the eave purlin height (

Table 4. Proportional relationship between outermost bay width and eave column height.

Building Name		The Ratio of Eave Columns’ Height (H) to Outermost Bays Width at the Side Façade	Remarks
Geungnakjeon Hall at Bongjeongsa Monastery	Eave Columns’ Height (H)	$\frac{\mathrm{H}}{4}$ + $\frac{\sqrt{2}\mathrm{H}}{4}$
Muryangsujeon Hall at Buseoksa Monastery		$\frac{\mathrm{H}}{2}$ + $\frac{\sqrt{2}\mathrm{H}}{4}$
Daeungjeon Hall at Sudeoksa Monastery		$\frac{\mathrm{H}}{\sqrt{2}}$
Eungjinjeon Hall at Seongbulsa Monastery		$\frac{\mathrm{H}}{4}$ + $\frac{\sqrt{2}\mathrm{H}}{4}$
Geungnakjeon Hall at Seongbulsa Monastery		H
Yeongsanjeon Hall at Geojoam Hermitage, Eunhaesa Monastery		$\frac{\mathrm{H}}{2}$ + $\frac{\sqrt{2}\mathrm{H}}{4}$
Josadang Hall at Buseoksa Monastery		$\frac{\mathrm{H}}{2}$ + $\frac{\sqrt{2}\mathrm{H}}{4}$
Bogwangjeon Hall at Simwonsa Monastery		$\frac{\mathrm{H}}{4}$ + $\frac{\sqrt{2}\mathrm{H}}{4}$
Sammun Gate at Imyeonggwan Guesthouse in Gangneung City		$\frac{\mathrm{H}}{\sqrt{2}}$
The Main Hall at Nanchansi Monastery (early eighth century)		$\frac{\mathrm{H}}{\sqrt{2}}$
The East Hall at Foguangsi Monastery (857)		$\frac{\mathrm{H}}{2}$ + $\frac{\sqrt{2}\mathrm{H}}{4}$
Yuhuagong Hall at Yongshou Monastery (1008)		H
The Main Hall at the Chuzu’an Hermitage (1125)		H

). This is similar to the proportional rule used in Chuzu’an Hermitage’s Main Hall (1125) of the Shaolinsi Monastery (Mount Song, Dengfeng, Henan) and Yuhuagong (1008) of the Yongshou Monastery (Yuci, Shanxi). Nanchansi Monastery’s Main Hall (early eighth century) in Wutaixian, Shaanxi, was the earliest wooden building built with three square bays and no inner columns. The outer bay width at the side façade was 0.7H times (H).

As was established in earlier sections, the nine buildings used a common proportional rule between (H) and the side façade width as a significant design principle, which was also likely used for other wooden buildings in ancient Korea and China (Figure 17, Figure 18, Figure 21 and Figure 22). The outer bay width at the side façade varied by 0.6H, 0.7H, and 0.85H times the eave column height, depending on (H), supporting the proposition that the builders used the $\sqrt{2}$H ratio to increase or decrease (H). For example, at Sudeoksa Monastery’s Daeungjeon Hall and Imgyeonggwan’s Sammun Gate, the (H) width matched the increase or decrease in the ratio of the side bays based on an arithmetic concept. The other buildings had a wood-frame structure incorporating $\sqrt{2}$H times the height ratio, increasing or decreasing according to arithmetic and geometric concepts.

4.4. Relationship between the Outer Bay Width and the Vertical Height of the Bracket Sets

Above the eave columns, ancient wooden buildings had bracket set systems to support the column purlins from the tops of eave columns. The height of the bracket sets was calculated by adjusting their alignment using $\sqrt{2}$H× eave columns’ height (H).

The height ratio of the bracket sets in the nine buildings can be classified into two types. For five buildings (i.e., Bongjeongsa Monastery’s Geungnakjeon Hall, Buseoksa Monastery’s Muryangsujeon and Josadang Halls, Seongbulsa Monastery’s Eungjinjeon Hall, and Bogwangjeon Hall at Simwonsa Monastery), the bracket set height was determined using a ratio of $\frac{\mathrm{H}}{2}$ (=0.5H) times complying with half of the eave columns’ height (H). However, the other four buildings (i.e., Sudeoksa Monastery’s Daeungjeon Hall, Seongbulsa Monastery’s Geungnakjeon Hall, Eunhaesa Geojoam Hermitage’s Yeongsanjeon Hall, and Imyeonggwan Guesthouse’s Sammun Gate) used a ratio of $\frac{\sqrt{2}\mathrm{H}}{4}$ (=0.35H) × eave columns’ height (H). The bracket sets in these four buildings were smaller than those in the other five, with a ratio of $\frac{\mathrm{H}}{2}$ times the eave columns’ height.

Buildings using both classifications were evenly distributed across the Korean Peninsula. This suggests that regional context did not dictate the differences in the height ratio of the bracket-set systems. The universal principle consistently advocated in this study has also been applied to the height ratio of the bracket set systems. This shows that there was a common proportion for constructing buildings across Chinese and Korean territories (Kim 2011). In particular, in the Goryeo buildings, a regular proportion was applied regardless of the type of two bracket-set classifications: dapo and jusimpo. A major implication is provided on account of the geographical conditions of the isolated peninsula, the existence of the Unified Silla, and of the Goryeo having maintained their power for a long time, as a combined result of which ancient Korean buildings already employed an established and indigenous architectural structure method. The Seongbulsa Monastery’s Eungjinjeon Hall and the Bogwangjeon Hall at the Simwonsa Monastery had intercolumnar bracket systems using the formula $\frac{\sqrt{2}\mathrm{H}}{4}$ (=0.35) times eave columns’ height (H), which differed from the other buildings with column-top bracket systems. However, this was limited to two cases. As the $\frac{\mathrm{H}}{2}$ (=0.5H) and $\frac{\sqrt{2}\mathrm{H}}{4}$ (=0.35H) ratios were used in buildings with column-top bracket systems.

In contrast, regarding the proportional association between the bracket set height (H₁) and the outer bay width, most buildings showed a geometric sequence, such as √2H₁, H₁, and 2H₁ times, depending on (H). Each successive term could be obtained by multiplying the previous term by $\sqrt{2}$H times. Bongjeongsa Monastery’s Geungnakjeon Hall and Seongbulsa Monastery’s Eungjinjeon Hall were exceptions because they did not maintain the $\sqrt{2}$H ratio formula (

Table 5. The proportional relationship between bracket set height and outermost bay width.

Building Names		Bracket Sets Height (H1)	Ratio of Bracket-Set Height (H1) to Outermost Bays Width at Side Façades	Remarks
Geungnakjeon Hall at Bongjeongsa Monastery	Eave Columns’ Height (H)	$\frac{\mathrm{H}}{2}$ = H₁		The bracket set height depends on the column purlin height
Muryangsujeon Hall at Buseoksa Monastery		$\frac{\mathrm{H}}{2}$ = H₁	$\sqrt{2}$H1	The bracket set height depends on the column purlin height
Daeungjeon Hall at Sudeoksa Monastery		$\frac{\sqrt{2}\mathrm{H}}{4}$ = H₁	2H1	The bracket set height depends on the column purlin height
Eungjinjeon Hall at Seongbulsa Monastery		$\frac{\mathrm{H}}{2}$ = H1		Due to no column purlins, the bracket set height depends on the eave purlin height
Geungnakjeon Hall at Seongbulsa Monastery		$\frac{\sqrt{2}\mathrm{H}}{4}$ = H₁	$\sqrt{2}$H1	The bracket set height depends on the column purlin height
Yeongsanjeon Hall at Geojoam Hermitage, Eunhaesa Monastery		$\frac{\sqrt{2}\mathrm{H}}{4}$ = H₁	$2\sqrt{2}$H1	The bracket set height depends on the column purlin height
Josadang Hall at Buseoksa Monastery		$\frac{\mathrm{H}}{2}$ = H₁	$\sqrt{2}$H1	The bracket set height depends on the column purlin height
Bogwangjeon Hall at Simwonsa Monastery		$\frac{\mathrm{H}}{2}$ = H₁	H1	Due to no column purlins, the bracket set height depends on the eave purlin height
Sammun Gate at Imyeonggwan Guesthouse in Gangneung City		$\frac{\sqrt{2}\mathrm{H}}{4}$ = H₁	$2\sqrt{2}$H1	The bracket set height depends on the column purlin height
The Main Hall at Nanchansi Monastery (early eighth century)		$\frac{\mathrm{H}}{2}$ = H₁	$\sqrt{2}$H1	The bracket set height depends on the eave purlin height
The East Hall at Foguangsi Monastery (857)		$\frac{\sqrt{2}\mathrm{H}}{4}$ = H₁	$\sqrt{2}$H1	The bracket set height depends on the eave purlin height
The Main Hall at Hualinsi Monastery (964)		$\frac{\sqrt{2}\mathrm{H}}{4}$ = H₁	$\sqrt{2}$H1	The bracket set height depends on the eave purlin height
The Main Hall at the Chuzu’an Hermitage (1125)		$\frac{\sqrt{2}\mathrm{H}}{4}$ = H₁	$\sqrt{2}$H1	The bracket set height depends on the column purlin height

).

5. Composition of the Internal Wood-Frame Structures between the $\sqrt{2}$ Times Proportional System and the Eave Column Height (H) in the Buildings of Korea and China

5.1. Common Characteristics in the Proportional Principle of Internal Framed Structures

The East Hall of the Foguangsi Monastery (857 CE) maintained √2H times the eave column height to determine eave purlin height (Figure 21). A baseline (L) marked along the top of the eave columns from the front to the rear façades created a vertical line intersecting with (L) and descending from a ridge post to the eave purlins. A contact point (P) was established where they joined. The distance from the ridge purlin to (P) was $\sqrt{2}$H times the eave column height. The distance of the intersection (P₁), which was perpendicular to the middle roof purlin, was H. With the vertical line below the column purlins marked, the distance from the intersection (P₁) was defined as $\frac{\mathrm{H}}{\sqrt{2}}$. Thus, the height of each purlin followed the geometric concept. The eave column height (H) multiplied by $\sqrt{2}$ times created a geometric sequence, such as $\sqrt{2}$H, H, $\frac{\mathrm{H}}{\sqrt{2}}$, $\frac{\mathrm{H}}{2}$, and $\frac{\sqrt{2}\mathrm{H}}{4}$. The outer bay width at the side façade was calculated as $\frac{\mathrm{H}}{2}$ plus $\frac{\sqrt{2}\mathrm{H}}{4}$. This proportional composition describes the Muryangsujeon and Josadang Halls at the Buseoksa Monastery and the Yeongsanjeon Hall at the Geojoam Hermitage at the Eunhaesa Monastery. The value of √2H times the height of the bracket sets below the eave purlins was equivalent to the outer bay width at the side façade (Figure 11, Figure 14 and Figure 20).

When the eave columns’ height (H) and the above-mentioned method were applied to Chuzu’an Hermitage’s Main Hall at the Shaolinsi Temple, the location of the eave purlins, column purlins, middle roof purlins, and ridge post were found to be in accordance with a proportional composition, and vertical height was maintained with ratios of $\frac{\sqrt{2}\mathrm{H}}{4}$, $\frac{\mathrm{H}}{2}$, H, and $\sqrt{2}$H, respectively. The ratio of (H₁) to the side bay width was H₁:2H₁ (Figure 18). This shows that (H) maintained a proportional system with a $\sqrt{2}$H ratio. This design principle is similar to that used for Sudeoksa’s Daeungjeon Hall, revealing a geometric concept with a common $\sqrt{2}$ ratio. The same method was used for Hualinsi Monastery’s Main Hall (964) (Fu 2017, p. 277). In the ancient buildings of South and North China, basing increased or decreased adjustments to (H) on the $\sqrt{2}$H ratio for internal timber-framed setting displays was a typical proportional composition (Figure 22). Hence, the geometric concept of the $\sqrt{2}$H ratio has been used with reference to (H) for internal frame structures and purlin placement in ancient wooden buildings in many parts of East Asia.

5.2. Differences between Proportional Principles for Internal Framed Structures in Korea and China

The eave columns’ height and setting of internal framed structures in ancient Chinese wooden architecture differed slightly from ancient Korean wooden buildings. First, the main halls at the Nanchansi and Foguangsi Monasteries in the Tang Era, the Guanyinge Pavilion and Shanmen Front Gate at the Dulesi Monastery in the Liao Era, the Hermitage Chuzu’an’s Main Hall at the Shaolinsi Monastery, and the Monidian Hall at the Longxingsi Monastery in the Song Era were Buddhist monuments that used the heights of the eave columns and eave purlins as reference points. Similarly, regarding the proportional correlation between eave purlins and eave columns, $\sqrt{2}$ times the height of the eave columns was equal to the height of the eave purlins. For wooden buildings in the Goryeo Era, $\sqrt{2}$ × (H) did not correspond to the eave purlin height but rather to the heights of the eave columns and column purlins. The Song Dynasty’s Yingzao Fashi did not mention column purlins for most wooden buildings, owing to the existence of descending cantilevers joined with eave purlins. Even if column purlins existed, their cross-sectional size was smaller than the other purlins. Unlike Chinese buildings, wooden-framed buildings in Korea during the Goryeo Era did not have descending cantilevers, and the cross-sectional sizes of the eave purlins and column purlins were identical. The Eungjinjeon Hall at the Seongbulsa Monastery and the Bogwangjeon Hall at the Simwonsa Monastery did not have column purlins, although the opposite was true for most Goryeo-Era buildings; the two buildings are rare examples. Therefore, how purlin placement was determined using the $\sqrt{2}$H ratio highlights a remarkable difference between ancient wood-frame buildings in China and Korea. Specifically, the Chinese buildings referenced the eave purlins, while the Korean buildings referenced the column purlins.

Second, for Chinese wooden buildings, the measurement differences among the wooden components were determined according to the choice of baseline, such as the bottom of the eave columns or the ground floor (Wang 2011a). Eave column height varied according to whether the lower limit line was defined as the bottom of the foundation stones or the columns. The following buildings applied $\sqrt{2}$H × (H) with the column purlin height, including the plinth height: Dulesi Monastery’s Shanmen Front Gate (Liao, 984), Baoguosi Monastery’s Main Hall (Song, 1013), and Fengguosi Monastery’s Main Hall (Liao, 1020). In contrast, the following buildings applied $\sqrt{2}$H × (H) with the eave purlin height: Nanchansi Monastery’s Main Hall (Tang, 782), Hualinsi Monastery’s Main Hall (Wu, 964), and Geyuansi Monastery’s Main Hall (Liao, 966). Similar to buildings in the Goryeo Era, eave purlin height was decided according to $\sqrt{2}$H times the eave column height. This demonstrates the utilization of geometric concepts for internal timber-framed structures in the architectural culture of East Asia (Table 2).

Third, applying $\sqrt{2}$H × (H), whether as a fractional or integer ratio, positioned each purlin according to the proportional principle. For the Chinese wooden buildings, each purlin height was determined by using the top and bottom of all purlins interchangeably. In contrast, wooden constructions built during the Goryeo Era had a different appearance. For Bongjeongsa Monastery’s Geungnakjeon Hall, Sudeoksa Monastery’s Daeungjeon Hall, Seongbulsa Monastery’s Geungnakjeon Hall, Buseoksa Monastery’s Muryangsujeon Hall, and Simwonsa Monastery’s Bogwangjeon Hall, the bottoms of all purlins (which backed up the eaves, columns, and roof framework) were used as standard points. For Imyeonggwan Guesthouse’s Sammun Gate and Seongbulsa Monastery’s Eungjinjeon, $\sqrt{2}$H × (H) referenced the tops of all purlins. Further, Buseoksa Monastery’s Josadang Hall and Hermitage Geojoam’s Yeongsanjeon Hall of the Eunhaesa Monastery used the tops of eave and column purlins and the bottoms of the middle roof and ridge purlins as standard points. This shows that purlin height was increased or decreased based on each purlin’s diameter, which might have reflected the carpenters’ personal preferences.

6. Conclusions

This study examined nine existing buildings constructed at the height of the Goryeo Dynasty regarding their use of common mathematical rules as design doctrines related to the column purlin height above the bracket sets. The authors compared these buildings to timber-framed buildings from ancient China and found that they commonly used the ratio of $\sqrt{2}$H× eave column height (H) to construct a wooden-frame work. During the Goryeo Era, some timber-framed monuments on the Korean Peninsula were built while a stable imperial power ruled. Local builders embraced mathematical design principles and determined the positioning of roof purlins by applying the $\sqrt{2}$H × (H) ratio to calculate outer bay widths and bracket set heights, consciously deciding which ratio to employ on a given project. The stipulations were not always imposed on the provinces; rather, they were combined with the universalized principles based on localized ideals.

The Goryeo-Era buildings embraced the principles of designing ancient Chinese architecture and created new timber-framed structures while adapting to the rules already existing in local buildings (Kim 2011). Then, through the buildings examined in this study, the attitude of building construction in the Goryeo Dynasty proves that East Asian universal and regional design principles were consistently shared in the Korean Peninsula.

The preface of the Yingzao Fashi describes the basic principles of ancient mathematics, including the geometric axioms of all things and the numerical values of diagonal length and circumference with reference to rectangles, circles, hexagons, octagons, and other shapes mentioned in the Jiuzhang Suanshu and Kaogongji. The principles can be inferred from the timber-framed buildings constructed in the Goryeo Era. The present study established that the nine examined buildings used the $\sqrt{2}$H × (H) ratio to determine the positions of all purlins, outer bay widths, and bracket set heights to create an internal timber-framed structure. The following conclusions can be drawn from this study.

First, this research makes it possible to identify the components that rely heavily on $\sqrt{2}$H × (H) in internal timber-framed structures by implementing the notion of geometric sequences, such as $\frac{\mathrm{H}}{4}$, $\frac{\sqrt{2}}{4}$, $\frac{\mathrm{H}}{2}$, $\frac{\mathrm{H}}{\sqrt{2}}$, H, and $\sqrt{2}$H, depending on advanced mathematical formulas that use L-square rulers and compasses to draw rectangles and circles. Embodied by buildings constructed during the Song and Liao Eras, such design principles have long been used in the wooden structures of East Asia.

Second, for five of the nine studied buildings, the $\sqrt{2}$H × (H) ratio was equivalent to the column purlin height. Most buildings in the Tang, Song, and Liao Eras referenced the eave purlins height. However, there were exceptions among the nine: Buseoksa Monastery’s Muryangsujeon Hall, Seongbulsa Monastery’s Eungjinjeon Hall, and Simwonsa Monastery’s Bogwangjeon Hall. For these three buildings, $\sqrt{2}$H × (H) was equivalent to the eave purlin height. The Eungjinjeon and Bogwangjeon Halls did not have column purlins, but the opposite was true for Muryangsujeon Hall. A notable finding is that Muryangsujeon Hall embraced the Chinese principle that $\sqrt{2}$H × (H) should be equivalent to the eave purlin height. All nine buildings applied the design principles of the Chinese examples to some degree.

Third, baseline (L) is defined as a horizontal line from the top side of the front and rear eave columns. The point at which each purlin met the baseline (L) was defined as P₁, P₂, P₃, and P₄, drawing a vertical line perpendicular to each purlin. Each purlin height (i.e., $\frac{\mathrm{H}}{4}$, $\frac{\sqrt{2}\mathrm{H}}{4}$, $\frac{\mathrm{H}}{2}$, $\frac{\mathrm{H}}{\sqrt{2}}$, H, and $\sqrt{2}$H, from the eave purlins to the ridge post) was determined with a ratio of $\sqrt{2}$H times the baseline (L) to each purlin. This represented an increased or decreased value using $\sqrt{2}$H × (H). The locations of the eave purlins, column purlins, and roof purlins were determined using $\sqrt{2}$H × (H). Notably, for Bongjeongsa’s Geungnakjeon Hall (P, H), Sudeoksa’s Daeungjeon Hall (P, $\sqrt{2}$H), and Seongbulsa’s Eungjinjeon (P, H) and Daeungjeon (P, H) Halls, the ridge purlin location was determined by H or $\sqrt{2}$H times the height of the front and rear eave columns. This is similar to Nanchansi’s Main Hall (P, H), Foguangsi Monastery’s East Hall (P, $\sqrt{2}$H), Hualinsi’s Main Hall (P, $\sqrt{2}$H), and Chuzu’an Hermitage’s Main Hall (P, $\sqrt{2}$H). Buseoksa Monastery’s Muryangsujeon Hall was an exception in that the height of the eave columns reached that of the upper-middle roof purlins (P₁, $\sqrt{2}$H). In addition, for Buseoksa Monastery’s Muryangsujeon (P, H + $\frac{\mathrm{H}}{\sqrt{2}}$) and Josadang Halls (P, $\frac{\mathrm{H}}{\sqrt{2}}$) and Geojoam Hermitage’s Yeongsanjeon Hall (P, $\frac{\mathrm{H}}{\sqrt{2}}$+$\frac{\mathrm{H}}{2}$), the concept of an arithmetic sequence was applied to determine the ridge purlin location, showing distinctly Korean characteristics in designing wooden-framed buildings (Table 3).

Fourth, considering the $\sqrt{2}$H times’ proportional relationship between the eave column height (H) and the outermost bay widths at the side façade, the Daeungjeon Hall of the Sudeoksa Monastery, and the Sammun Front Gate of the Imyeonggwan Guesthouse brought the $\frac{\mathrm{H}}{\sqrt{2}}$ times the eave column height into contact with the notion of geometric series. Seongbulsa Monastery’s Geungnakjeon Hall indicated H times, as well as Yongshou Monastery’s Yuhuagong Hall and Chuzu’an Hermitage’s Main Hall. The other buildings had a proportional system of $\frac{\mathrm{H}}{4}$ + $\frac{\sqrt{2}\mathrm{H}}{4}$ (Seongbulsa’s Eungjinjon Hall and Simwonsa’s Bogwangjeon Hall) or $\frac{\mathrm{H}}{2}$ + $\frac{\sqrt{2}\mathrm{H}}{4}$ (Buseoksa’s Muryangsujeon and Josadang Halls and Geojoam Hermitage’s Yeongsanjeon Hall, similar to Foguangsi Monastery’s East Hall). This shows that the concept of arithmetic series was used together with the geometric concept in the East Asian sphere (Table 4).

Fifth, regarding the correlation between the eave column height (H) and bracket set height, the bracket set height in all the buildings was proportional to $\frac{\mathrm{H}}{2}$ or $\frac{\sqrt{2}\mathrm{H}}{4}$times the eave column height (H) through a geometric progression with a common ratio ($\frac{\mathrm{H}}{2}$ = H₁) is affiliated with Buseoksa’s Muryangsujeon, Seongbulsa’s Eungjinjeon, and Simwonsa’s Bogwangjeon Halls, which are comparable to the Main Hall of Nanchansi. ($\frac{\sqrt{2}\mathrm{H}}{4}$ = H₁) is affiliated with Imyeonggwan’s Sammun Gate, Bongjeongsa’s Geungnakjeon, Sudeoksa’s Daeungjeon, Seongbulsa’s Geungnakjeon, Geojosam’s Yeongsanjeon, and Buseoksa’s Josadang Halls, which followed the same ratio rule ($\frac{\sqrt{2}\mathrm{H}}{4}$ = H₁) as the Main Halls of Foguangsi, Hualinsi, and Chuzu’an Monasteries in the Tang, Song, and Liao Dynasties (Table 5). The characteristic features of fourteenth-century architecture in the Goryeo Era were the gradual increase of multi-layered bracket-sets and progressive change to inter-columnar bracket-sets systems (dapo). However, despite these changes, the purlin placement height and bracket-set height were determined by applying the universal design principle (with a ratio of $\sqrt{2}$H times the eave column height) using the same proportional system, regardless of the format of the inter-columnar bracket set and column top bracket set (jusimpo).

Finally, the ratio of the bracket set height (H₁) to the outer bay width at the side façades indicated three types, 2H₁: H, H₁: H, and $\sqrt{2}$H₁: H, which permitted $\sqrt{2}$H or 2H times with a common ratio. The first type (2H₁: H) applied to Sudeoksa’s Daeungjeon Hall; the second type (H₁: H) applied to Simwonsa’s Bogwangjeon Hall; and the third type ($\sqrt{2}$H₁: H) applied to Seongbulsa’s Geungnakjeon, and Buseoksa’s Muryangsujeon and Josadang Halls, which are the same as the Main Halls of Nanchansi, Hualinsi, Foguangsi, and Chuzu’an Monasteries. The first and second types represent original building characteristics that used appropriate integer proportions (2H₁: H and H₁: H) on the Korean Peninsula, while the third type ($\sqrt{2}$H₁: H) maintained a universal pattern with common languages in East Asia. The comparison in the present study of bracket set and eave column heights reliant on outer bay widths suggests that the closest analogy to the proportionate attributes of existing wood-frame buildings from the Tang–Song Era is the Yeongsanjeon Hall at the Geojoam Hermitage, Eunhaesa Monastery (Table 5). The use of the ratio rule regulated the proportional value of the side façade width, particularly the outer bay width, which controlled the eave column and bracket set heights, as grounded in the proportional rules.

This study shows that the internal arrangement of timber-framed structures was constructed using the geometric series concept based on the increase or decrease in $\sqrt{2}$H × eave column height (H). These design rules were applied to all nine of the studied buildings from the Goryeo Era and to buildings from China’s Tang, Song, and Liao Dynasties. This study provides evidence that the wooden architecture of the Goryeo Era evolved in an original way while also accepting architectural principles from ancient China. It further demonstrated that the architecture of the Goryeo Era inherited design principles of ancient China by comparing them with similar buildings designed contemporaneously in Ancient China. The similarities and differences seen in these buildings show that the universal architectural attitude is being integrated with the previous technology of local architecture and adapting to a new architectural form. This research can contribute to new knowledge on East Asian architecture and provide useful information for future building restorations.

Further, the universality of an architectural culture cannot be understood in isolation from its diversity or particularity because the universality of culture is derived primarily from the assembly and harmonization of diversities. On the other hand, the particularity of a culture does not mean an independent culture of some indigenous form. This study indicates that the universality and particularity of culture remain in a state of co-existence.

This study followed a basic review approach to confirm the similarities and differences in the design principles of ancient architecture in Korea and China. In the future, through comparative analysis with the ancient wooden architectures of China and Japan, which were not reviewed in this study, the characteristics of ancient Korean architecture will be understood more clearly. A more fundamental characteristic of the timber-framed proportion system of East Asian ancient wooden architecture will be grasped, and more elaborated findings on universal and regional design principles will be progressed in future studies.