A High-Resolution Joint Angle-Doppler Estimation Sub-Nyquist Radar Approach Based on Matrix Completion
Abstract
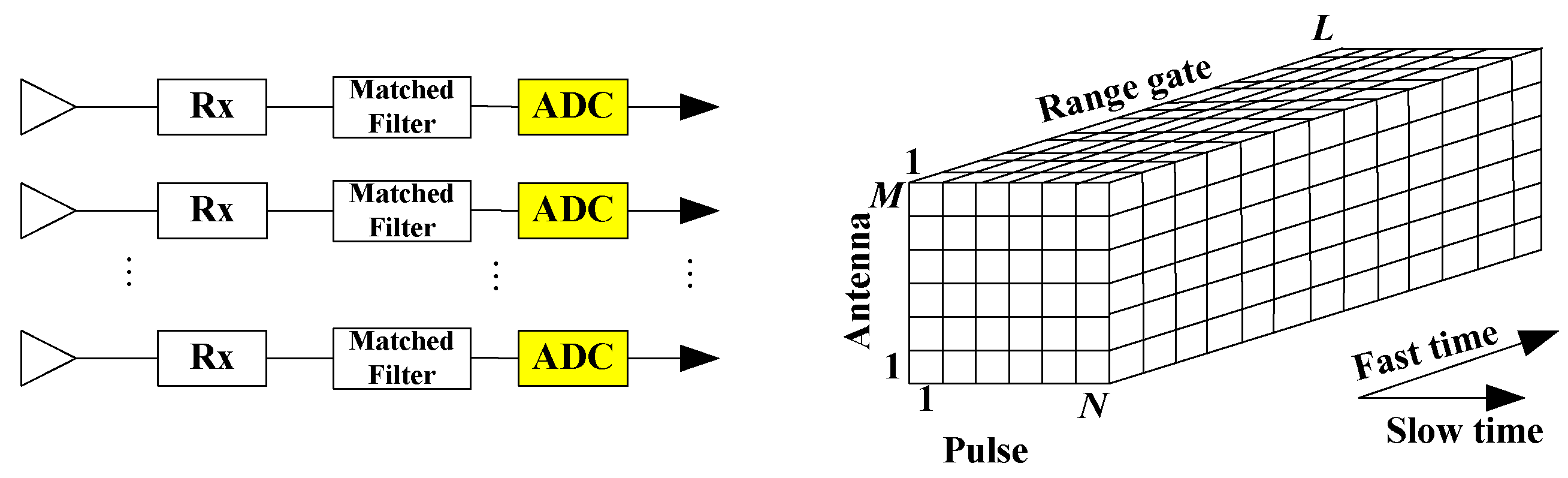
:1. Introduction
2. Methods
3. The Proposed Single-Channel Sub-Nyquist-MC Radar Approach
3.1. ULA Case
3.2. Arbitrary 2-D Array Case
4. Joint Angle-Doppler Estimation with Recovered Matrix
5. Numerical Results
5.1. Matrix Recovery Error under Noisy Observations
5.2. Angle-Doppler Frequency Estimation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Matrix Completion
Appendix B. Maximum Coherence of the Spaces
References
- Ward, J. Space-time adaptive processing for airborne radar. In Proceedings of the IEE Colloquium on Space-Time Adaptive Processing, London, UK, 6 April 1998; Volume 1998, p. 2. [Google Scholar]
- Li, X.; Ma, X.; Yan, S.; Hou, C. Single snapshot DOA estimation by compressive sampling. Appl. Acoust. 2013, 74, 926–930. [Google Scholar] [CrossRef]
- Herman, M.; Strohmer, T. Compressed sensing radar. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Rome, Italy, 26–30 May 2008; pp. 1509–1512. [Google Scholar]
- Baraniuk, R.; Steeghs, P. Compressive Radar Imaging. In Proceedings of the 2007 IEEE Radar Conference, Boston, MA, USA, 17–20 April 2007; pp. 128–133. [Google Scholar]
- Herman, M.A.; Strohmer, T. High-Resolution Radar via Compressed Sensing. IEEE Trans. Signal Process. 2009, 57, 2275–2284. [Google Scholar] [CrossRef]
- Ender, J.H.G. On compressive sensing applied to radar. Signal Process. 2010, 90, 1402–1414. [Google Scholar] [CrossRef]
- Xi, F.; Chen, S.; Liu, Z. Quadrature Compressive Sampling for Radar Signals. IEEE Trans. Signal Process. 2014, 62, 2787–2802. [Google Scholar]
- Vaughan, R.G.; Scott, N.L.; White, D.R. The theory of bandpass sampling. IEEE Trans. Signal Process. 1991, 39, 1973–1984. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Near-Optimal Signal Recovery from Random Projections: Universal Encoding Strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Tropp, J. Random Filters for Compressive Sampling. In Proceedings of the 2006 40th Annual Conference on Information Sciences and Systems, Princeton, NJ, USA, 22–24 March 2006; pp. 216–217. [Google Scholar]
- Kirolos, S.; Laska, J.; Wakin, M.; Duarte, M.; Baron, D.; Ragheb, T.; Massoud, Y.; Baraniuk, R. Analog-to-Information Conversion via Random Demodulation. In Proceedings of the 2006 IEEE Dallas/CAS Workshop on Design, Applications, Integration and Software, Richardson, TX, USA, 29–30 October 2006; pp. 71–74. [Google Scholar]
- Baransky, E.; Itzhak, G.; Shmuel, I.; Wagner, N.; Shoshan, E.; Eldar, Y.C. A Sub-Nyquist Radar Prototype: Hardware and Algorithms. 2012; arXiv, arXiv:1208.2515. [Google Scholar]
- Bar-Ilan, O.; Eldar, Y.C. Sub-Nyquist Radar via Doppler Focusing. IEEE Trans. Signal Process. 2014, 62, 1796–1811. [Google Scholar] [CrossRef]
- Gedalyahu, K.; Tur, R.; Eldar, Y.C. Multichannel Sampling of Pulse Streams at the Rate of Innovation. IEEE Trans. Signal Process. 2011, 59, 1491–1504. [Google Scholar] [CrossRef]
- Mishali, M.; Eldar, Y.C.; Tropp, J.A. Efficient sampling of sparse wideband analog signals. In Proceedings of the 2008 IEEE 25th Convention of Electrical and Electronics Engineers in Israel, Eilat, Israel, 3–5 December 2008; pp. 290–294. [Google Scholar]
- Candès, E.J.; Recht, B. Exact Matrix Completion via Convex Optimization. Found. Comput. Math. 2009, 9, 717–772. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. The Power of Convex Relaxation: Near-Optimal Matrix Completion. IEEE Trans. Inf. Theory 2010, 56, 2053–2080. [Google Scholar] [CrossRef]
- Candes, E.J.; Plan, Y. Matrix Completion with Noise. Proc. IEEE 2010, 98, 925–936. [Google Scholar] [CrossRef]
- Candès, E.J.; Plan, Y. Tight Oracle Inequalities for Low-Rank Matrix Recovery from a Minimal Number of Noisy Random Measurements. IEEE Trans. Inf. Theory 2011, 57, 2342–2359. [Google Scholar] [CrossRef]
- Keshavan, R.H.; Montanari, A.; Oh, S. Matrix Completion from a Few Entries. IEEE Trans. Inf. Theory 2010, 56, 2980–2998. [Google Scholar] [CrossRef]
- Dai, W.; Kerman, E.; Milenkovic, O. A Geometric Approach to Low-Rank Matrix Completion. IEEE Trans. Inf. Theory 2012, 58, 237–247. [Google Scholar] [CrossRef]
- Vandereycken, B. Low-Rank Matrix Completion by Riemannian Optimization. SIAM J. Optim. 2013, 23, 1214–1236. [Google Scholar] [CrossRef]
- Cai, J.-F.; Candès, E.J.; Shen, Z. A Singular Value Thresholding Algorithm for Matrix Completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Sun, S.; Petropulu, A.P.; Bajwa, W.U. Target estimation in colocated MIMO radar via matrix completion. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 4144–4148. [Google Scholar]
- Sun, S.; Bajwa, W.U.; Petropulu, A.P. MIMO-MC radar: A MIMO radar approach based on matrix completion. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1839–1852. [Google Scholar] [CrossRef]
- Sun, S.; Petropulu, A.P. On the applicability of matrix completion on MIMO radars. In Proceedings of the 2014 48th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 2014; pp. 306–310. [Google Scholar]
- Kalogerias, D.S.; Petropulu, A.P. Matrix Completion in Colocated MIMO Radar: Recoverability, Bounds & Theoretical Guarantees. IEEE Trans. Signal Process. 2014, 62, 309–321. [Google Scholar]
- Chen, C.Y.; Vaidyanathan, P.P. Compressed sensing in MIMO radar. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 41–44. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Podilchuk, C. Signal Recovery from Partial Information. In Digital Signal Processing Fundamentals; CRC Press: Boca Raton, FL, USA, 2009; pp. 1–22. ISBN 978-1-4200-4606-9. [Google Scholar]
- Blumensath, T.; Davies, M.E. Iterative Hard Thresholding for Compressed Sensing. arXiv, 2008; arXiv:0805.0510. [Google Scholar]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Sun, Y. A High-Resolution Joint Angle-Doppler Estimation Sub-Nyquist Radar Approach Based on Matrix Completion. Information 2019, 10, 124. https://doi.org/10.3390/info10040124
Wang Q, Sun Y. A High-Resolution Joint Angle-Doppler Estimation Sub-Nyquist Radar Approach Based on Matrix Completion. Information. 2019; 10(4):124. https://doi.org/10.3390/info10040124
Chicago/Turabian StyleWang, Quanhui, and Ying Sun. 2019. "A High-Resolution Joint Angle-Doppler Estimation Sub-Nyquist Radar Approach Based on Matrix Completion" Information 10, no. 4: 124. https://doi.org/10.3390/info10040124



