Project Procurement Method Selection Using a Multi-Criteria Decision-Making Method with Interval Neutrosophic Sets

Abstract

Project procurement method (PPM) selection influences the efficiency of project implementation. Owners are presented with different options for project delivery. However, selecting the appropriate PPM poses great challenges to owners, given the existence of ambiguous information. The interval neutrosophic set (INS) shows power to handle imprecise and ambiguous information. This paper aims to develop a PPM selection model under an interval neutrosophic environment for owners. The main contributions of this paper are as follows: (1) The similarity measure is innovatively introduced with interval neutrosophic information to handle the PPM selection problem. (2) The similarity measure based on minimum and maximum operators is applied to construct a decision-making model for PPM selection, through considering the truth, falsity, and indeterminacy memberships simultaneously. (3) This study establishes a PPM selection method with INS by applying similarity measures, that takes account into the determinacy, indeterminacy, and hesitation from the decision experts when giving an evaluation value. A case study on selecting PPM is made to show the applicability of the proposed approach. Finally, the results of the proposed method are compared with those of existing methods, which exhibit the superiority of the proposed PPM selection method.

1. Introduction

Intensifying competition among construction companies and increasing project complexity pose project management challenges to owners in the construction industry. The selection of an appropriate project procurement method (PPM) plays a key role in project management [1,2]. The appropriate PPM could reduce project costs by an average of 5% [3]. The most common PPMs in the construction industry include Design Bid Build (DBB), Design Build (DB), Construction Management (CM), Engineering Procurement Construction (EPC), construction management as program management (CM) [4,5], and Public Private Partnership (PPP) [6,7]. Each form of PPM is unique and cannot be effectively applied to all projects because of their different characteristics [4,8]. To determine the sustainability of a construction project, selecting an appropriate PPM is a key task for owners [1,2].

The PPM selection problem is also called project delivery system (PDS) selection in the engineering field. Researchers have conducted numerous works on PDS selection [5,8,9,10]. Gordon suggested that an organization and contract strategy should be considered in PDS selection [10]. Alhazmi and McCaffer divided PDSs into three types and proposed a four-step model selection process [8]. Li et al. proposed a PDS selection model wherein information entropy is used to calculate attribute weights and unascertained set theory is applied to select the suitable PDS [11]. Mahdi and Alreshaid proposed a multi-criteria decision-making methodology that utilizes the AHP method for PDS selection [12]. Ng et al. [13] proposed the membership functions of fuzzy criteria in an empirical study. A fuzzy PDS selection model was constructed by incorporating fuzzy relation rules and selection criterion weights [14]. An et al. established a group decision-making model for PDS selection under the interval intuitionistic fuzzy setting, wherein a new weight determination for a decision maker is introduced by using the information utility level [4]. Li et al. developed new similarity measures with interval Pythagorean fuzzy sets and applied them to choose a suitable PDS for a project [15]. Mafakheri et al. utilized the interval AHP to determine the interval priorities for alternative PDSs, which were then ranked using rough set theory [16].

From the existing research, the evaluation information for all criteria affecting PDS selection was characterized by fuzzy sets, such as intuitionistic fuzzy [17,18] and Pythagorean fuzzy [19], which require the sum or square sum of membership and non-membership degrees smaller than one. In other words, there is a constraint to decision experts when giving evaluation values. Actually, too many restraints imposed on decision experts can give a low effectiveness evaluation result, and then lead to the selection of a suboptimal PDS. Neutrosophic sets, introduced by Smarandache [20], need a very loose constraint, in which each component (truth membership, falsity membership, or indeterminacy) is smaller than 1 and larger than 0. Later, the neutrosophic set theory was generalized. Wang et al. [21,22] presented the concepts of single valued neutrosophic sets and interval neutrosophic sets (INS). Peng developed a new multi-parametric similarity measure and distance measure for interval neutrosophic sets, and applied them to evaluate the Internet of Things (IOT) industry decision-making issue [23]. Sahin developed two multi-criteria methods using the interval neutrosophic cross-entropy, and used them to select a company as an object investment [24]. Based on a single valued neutrosophic number, a model for evaluating and selecting a transport service provider was presented by Liu et al. [25].

Though the available research gave abundant theoretical foundation, two major aspects should be approached by further research: (1) The process of calculation in the existing similarity measures is too complex to apply to more practical fields, it is necessary to introduce a general theory measuring the closeness degree between two objects. (2) The existing similarity measures applying to PDS selection under INSs ignore the “true psychological” behavior and degree of confidence from decision experts. Mondal et al. proposed a tangent similarity measure under interval neutrosophic sets, which considered the weighted mean value of the degrees of truth membership, indeterminacy, and falsity membership [26]. Ye presented a cosine similarity measure under a neutrosophic environment, through calculating the relative proportion between truth membership and the Euclid distance of the degrees of truth membership, indeterminacy, and falsity membership [27]. Actually, to ensure the effective evaluation information, the degree of confidence for decision experts plays an important role in the process of PPM selection. To bridge these gaps, this work aims to develop a decision-making model for PPM selection under an interval neutrosophic environment. First, the main difficulty in INSs lies in the comparison of two interval numbers. To overcome this, the interval number is transformed into its alternative representation. Second, a PPM selection method under the interval neutrosophic setting is constructed using the similarity measures presented in [28]. The similarity measures used in this study are superior to other similarity measures because they consider the indeterminacy degrees of judgment from evaluators. Finally, the proposed PPM selection method is applied to solve a PPM selection problem.

The rest of this paper is organized as follows. The decision-making framework for PPM selection is provided in Section 2, including the criteria and the selection process of PPMs. Preliminaries regarding the interval number, neutrosophic sets, INSs, and similarity measures are introduced in Section 3. The establishment of the decision-making model for PPM selection based on similarity measures is discussed in Section 4. An example using the proposed PPM selection model is given in Section 5. The comparative analysis and conclusions are presented in Section 6 and Section 7, respectively.

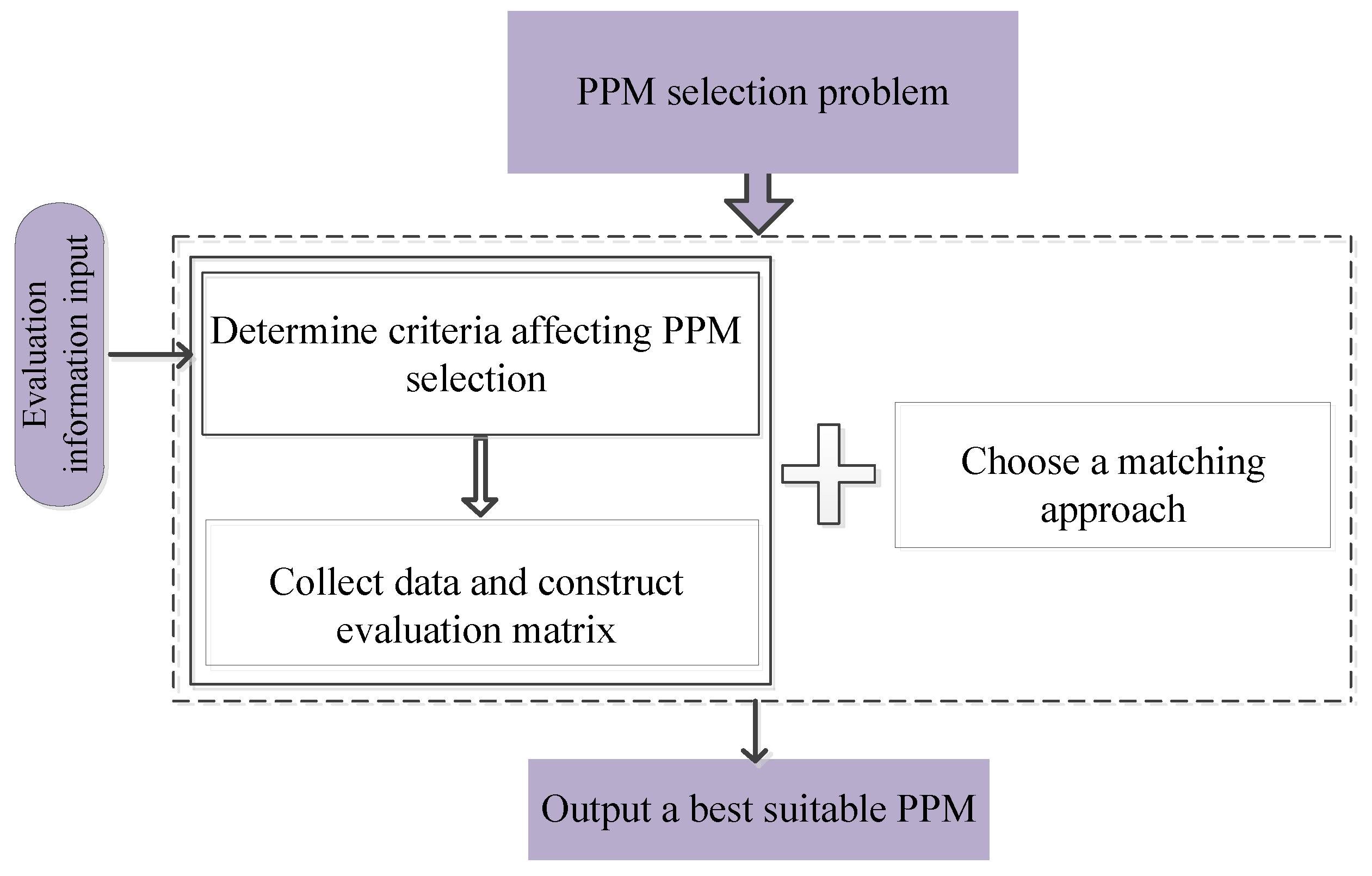
2. Decision-Making Framework for PPM Selection

The PPM for a proposed construction project can be selected from Design Bid Build (DBB), Design Build (DB), Construction Management (CM), and Engineering Procurement Construction (EPC). The DBB is a traditional contract approach in which design, build, and management are distributed to different units by the owner. The DB is a model in which the owner signs a contract with the contractor, and then the contract takes the design and build of the project. The CM is a model including construction and management, which adopts “design and construction” to accelerate the progress of construction. Finally, the EPC is a kind of general contracting, that is, the general contractor not only charges the project design, procurement, construction, and commissioning services, but also takes responsibility for the quality, safety, time, and cost overall responsibility, in accordance with the contract. Li et al. showed that numerous factors should be considered in PPM selection [16], in which all criteria for selecting PPMs are interpreted as shown in Figure 1.

Actually, PPM selection is a typical decision-making problem. Based on the line of decision-making, to obtain the best suitable PPM, the criteria for PPM selection are firstly determined, and the evaluation data about all criteria affecting PPM selection is collected. Then, a matching decision-making approach is chosen. Finally, combining data given by evaluation experts and a decision-making approach, the suitable PPM is obtained. The selection process of PPMs is shown in Figure 2.

3. Methodology for the PPM Selection

This section presents the methodology for PPM selection, which mainly includes two parts—preliminaries about interval numbers and INSs, and similarity measures between INSs based on minimum and maximum operators. These are the basic theories for establishing the selection of PPM.

3.1. Preliminaries

In this subsection, we provide some basic concepts and definitions of interval numbers and INSs, including their operational laws. They are utilized in the analysis.

Interval numbers and their operations are of utmost significance for developing the operations of INSs. Some definitions and operational laws of interval numbers are introduced below.

Definition 1.

[29]Let$\tilde{a}=\left[a^L,a^R\right]=\left\{a|a^L\le a\le a^R\right\}$,then$\tilde{a}$is called an interval number. In particular, if$a^L=a^R$, then$\tilde{a}=\left[a^L,a^R\right]$is a real number.

Interval number $\tilde{x}$ is alternatively represented as $\tilde{a}=\langle m\left(\tilde{a}\right),w\left(\tilde{a}\right)\rangle$ [29], where $m\left(\tilde{a}\right)=\frac{1}{2}\left(a^L+a^R\right)$ and $w\left(\tilde{a}\right)=\frac{1}{2}\left(a^L-a^R\right)$.

Accordingly, we provide a representation of an interval number and compare two interval numbers.

Definition 2.

[30]Let$\tilde{a}=\left[a^L,a^R\right]$and$\tilde{b}=\left[b^L,b^R\right]$be two interval numbers, then

$$\tilde{a}+\tilde{b}=\left[\min \left(a^L+b^R,a^R+b^L\right),\max \left(a^L+b^R,a^R+b^L\right)\right]; \tilde{a}=\left[a^L,a^R\right];$$

$$\tilde{a}\times \tilde{b}=\left[\min \left(a^L\cdot b^R,a^R\cdot b^L\right),\max \left(a^L\cdot b^R,a^R\cdot b^L\right)\right]; 1/\tilde{a}=\left[1/a^R,1/a^L\right].$$

Definition 3.

[28]Let$\tilde{a}=\left[a^L,a^R\right]$be an interval number, and then

$$\tilde{a}=m\left(\tilde{a}\right)+w\left(\tilde{a}\right)\mathrm{i},$$

(1)

where$\mathrm{i}\in \left[-1,1\right]$, $m\left(\tilde{a}\right)=\frac{1}{2}\left(a^L+a^R\right)$, and$w\left(\tilde{a}\right)=\frac{1}{2}\left(a^L-a^R\right)$.

Considering two non-negative interval numbers $\tilde{a}=\left[a^L,a^R\right]$ and $\tilde{b}=\left[b^L,b^R\right]$, where $0\le a^L\le \tilde{a}\le a^R$ and $0\le b^L\le \tilde{b}\le b^R$, we define the following:

(a)

If $m(\tilde{a})\ge m(\tilde{b})$ and $w(\tilde{a})\ge w(\tilde{b})$, then $\tilde{a}$ is greater than $\tilde{b}$, that is, $\tilde{a}\ge \tilde{b}$;

(b)

If $m(\tilde{a})\ge m(\tilde{b})$, then $\tilde{a}$ is quasi-greater than $\tilde{b}$, that is, $\tilde{a}\succ \tilde{b}$.

Definition 4.

[20]Let$X$be a space of points (objects). Then, a neutrosophic set$A$is defined as$A=\left\{\langle x:T_A\left(x\right),I_A\left(x\right),F_A\left(x\right)\rangle ,x\in X\right\}$, where functions$I_A\left(x\right)$, $T_A\left(x\right)$, $F_A\left(x\right)$: $X\to \left[{}^{-}0,1^{+}\right]$are the truth, indeterminacy, and falsity memberships, respectively, and satisfy the condition${}^{-}0\le \sup T_A\left(x\right)+\sup I_A\left(x\right)+\sup F_A\left(x\right)\le 3^{+}$.

In contrast to a neutrosophic set, an INS has a wide range of applications. An INS is defined as follows.

Definition 5.

[31]Let$X$be a space of points (objects) with a generic element$x\in X$. An INS$A$is defined as$A=\left\{\langle x:T_A\left(x\right),I_A\left(x\right),F_A\left(x\right)\rangle ,x\in X\right\}$, where functions$T_A\left(x\right)=\left[T_A^L\left(x\right),T_A^R\left(x\right)\right]\subseteq \left[0,1\right]$,$I_A\left(x\right)=\left[I_A^L\left(x\right),I_A^R\left(x\right)\right]\subseteq \left[0,1\right]$, and$F_A\left(x\right)=\left[F_A^L\left(x\right),F_A^R\left(x\right)\right]\subseteq \left[0,1\right]$are the degrees of truth membership, indeterminacy, and falsity membership, respectively, and satisfy the condition$0\le T_A^R\left(x\right)+I_A^R\left(x\right)+F_A^R\left(x\right)\le 3$.

Two INSs have the following relationships:

Definition 6.

[20]An INS$A$is contained in another INS$B$, i.e.,$A\subseteq B$, if and only if

$$\begin{gathered} T_A^L\left(x\right)\le T_B^L\left(x\right), T_A^R\left(x\right)\le T_B^R\left(x\right), \\ {I}_A^L\left(x\right)\ge I_B^L\left(x\right), I_A^R\left(x\right)\ge I_B^R\left(x\right), \\ {F}_A^L\left(x\right)\ge F_B^L\left(x\right), F_A^R\left(x\right)\ge F_B^R\left(x\right). \end{gathered}$$

Definition 7.

[31]Two INSs$A$and$B$are equal, i.e.,$A=B$, if and only if$A\subseteq B$and$A\supseteq B$.

3.2. Similarity Measures Between INSs Based on Minimum and Maximum Operators

This subsection introduces three similarity measures between two INSs, $A$ and $B$, and their properties, based on the minimum and maximum operators.

Proposition 1.

[28]Let$A$and$B$be two INSs in a universe of discourse,$X=\left\{x_1,x_2,\dots ,x_n\right\}$. Then, the 1-type INS similarity measure:

$$Y_1\left(A,B\right)=\frac{1}{3n}{\displaystyle \sum _{i=1}^n\left(\frac{\min \left(T_A\left(x_i\right),T_B\left(x_i\right)\right)}{\max \left(T_A\left(x_i\right),T_B\left(x_i\right)\right)}+\frac{\min \left(I_A\left(x_i\right),I_B\left(x_i\right)\right)}{\max \left(I_A\left(x_i\right),I_B\left(x_i\right)\right)}+\frac{\min \left(F_A\left(x_i\right),F_B\left(x_i\right)\right)}{\max \left(F_A\left(x_i\right),F_B\left(x_i\right)\right)}\right)},$$

(2)

which should satisfy the following properties:

(1)

$0\le Y_1\left(A,B\right)\le 1$;

(2)

$Y_1\left(A,B\right)=1$if$A=B$;

(3)

$Y_1\left(A,B\right)=Y_1\left(B,A\right)$;

(4)

$Y_1\left(A,C\right)\le Y_1\left(A,B\right)$and$Y_1\left(A,C\right)\le Y_1\left(B,C\right)$if$A\subseteq B\subseteq C$for INS$C$.

Proposition 2.

[28]Let$A$and$B$be two INSs in a universe of discourse,$X=\left\{x_1,x_2,\dots ,x_n\right\}$. Then, the 2-type INS similarity measure:

$$Y_2\left(A,B\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left(\alpha \frac{\min \left(T_A\left(x_i\right),T_B\left(x_i\right)\right)}{\max \left(T_A\left(x_i\right),T_B\left(x_i\right)\right)}+\beta \frac{\min \left(I_A\left(x_i\right),I_B\left(x_i\right)\right)}{\max \left(I_A\left(x_i\right),I_B\left(x_i\right)\right)}+\gamma \frac{\min \left(F_A\left(x_i\right),F_B\left(x_i\right)\right)}{\max \left(F_A\left(x_i\right),F_B\left(x_i\right)\right)}\right)},$$

(3)

which should satisfy the following properties:

(1)

$0\le Y_2\left(A,B\right)\le 1$;

(2)

$Y_2\left(A,B\right)=1$if$A=B$;

(3)

$Y_2\left(A,B\right)=Y_2\left(B,A\right)$;

(4)

$Y_2\left(A,C\right)\le Y_2\left(A,B\right)$and$Y_2\left(A,C\right)\le Y_2\left(B,C\right)$if$A\subseteq B\subseteq C$for INS$C$, where$\alpha$, $\beta$, and$\gamma$are the weights of the three independent elements (i.e., the truth, indeterminacy, and falsity memberships) in an INS and$\alpha +\beta +\gamma =1$.

Proposition 3.

[28]Let A and B be two INSs in a universe of discourse,$X=\left\{x_1,x_2,\dots ,x_n\right\}$, then the 3-type INS similarity measure:

$$Y_3\left(A,B\right)={\displaystyle \sum _{i=1}^n{w}_i\left(\alpha \frac{\min \left(T_A\left(x_i\right),T_B\left(x_i\right)\right)}{\max \left(T_A\left(x_i\right),T_B\left(x_i\right)\right)}+\beta \frac{\min \left(I_A\left(x_i\right),I_B\left(x_i\right)\right)}{\max \left(I_A\left(x_i\right),I_B\left(x_i\right)\right)}+\gamma \frac{\min \left(F_A\left(x_i\right),F_B\left(x_i\right)\right)}{\max \left(F_A\left(x_i\right),F_B\left(x_i\right)\right)}\right)},$$

(4)

which should satisfy the following properties:

(1)

$0\le Y_3\left(A,B\right)\le 1$;

(2)

$Y_3\left(A,B\right)=1$if$A=B$;

(3)

$Y_3\left(A,B\right)=Y_3\left(B,A\right)$;

(4)

$Y_3\left(A,C\right)=Y_3\left(A,B\right)$and$Y_3\left(A,C\right)\le Y_3\left(B,C\right)$if$A\subseteq B\subseteq C$for INS$C$.

If the importance of the three independent elements—the truth, indeterminacy, and falsity memberships—in an INS are considered in Equation (2), then Equation (2) is equivalent to Equation (3). That is, when $\alpha =\beta =\gamma =1/3$, Equation (3) is reduced to Equation (2). Furthermore, if important differences among all the elements in a universe of discourse are considered, $X=\left\{x_1,x_2,\dots ,x_n\right\}$, the weight of each element $x_i$$\left(i=1,2,\dots ,n\right)$ must be considered in Equation (3). Then, Equation (3) is equivalent to Equation (4). That is, when weight $w_1=w_2=\cdots =w_n=1/n$, Equation (4) is reduced to Equation (3). Finally, when $\alpha =\beta =\gamma =1/3$ and $w_1=w_2=\cdots =w_n=1/n$, Equation (4) is reduced to Equation (2).

4. Decision-Making Model for PPM Selection Based on Similarity Measures

4.1. Description of Decision-Making for PPM Selection

Let $A=\left\{A_1,A_2,\dots ,A_m\right\}$ be a set of alternative PPMs, and $C=\left\{C_1,C_2,\dots ,C_n\right\}$ be a set of evaluation criteria for each PPM. We assumed that the weights of the evaluation criteria $C_i$$\left(i=1,2,\dots ,n\right)$ were $w_i$, $w_i\in \left[0,1\right]$, ${\displaystyle \sum _{i=1}^n{w}_i}=1$, and the weights of the three elements were $\alpha ,\beta$, and $\gamma$, determined by the decision maker. The characteristic of the alternative PPM $A_j$$\left(j=1,2,\dots ,m\right)$ is expressed as follows:

$$\begin{array}{c}{A}_j=\left\{\langle C_i,T_{A_j}\left(C_i\right),I_{A_j}\left(C_i\right),F_{A_j}\left(C_i\right)\rangle |C_i\in C\right\}\\ =\left\{\langle C_i,\left[T_A^L\left(C_i\right),T_A^R\left(C_i\right)\right],\left[I_A^L\left(C_i\right),I_A^R\left(C_i\right)\right],\left[F_A^L\left(C_i\right),F_A^R\left(C_i\right)\right]\rangle |C_i\in C\right\},\end{array}$$

(5)

where $W_{A_i}=\left[W_{A_i}^L\left(C_i\right),W_{A_i}^R\left(C_i\right)\right]\subseteq \left[0,1\right]$, $W=T,I$, and $F$, respectively, and $0\le T_{A_j}^R\left(C_i\right)+I_{A_j}^R\left(C_i\right)+F_{A_j}^R\left(C_i\right)\le 3$ for $C_i\in C$, $i=1,2,\dots ,n$ and $j=1,2,\dots ,m$.

If the evaluation value, which is usually obtained from the evaluation of an alternative PPM $A_j$ under an evaluation criterion $C_i$ is abbreviated as $d_{ji}=\langle \left[x_{ji}^L,x_{ji}^R\right],\left[y_{ji}^L,y_{ji}^R\right],\left[z_{ji}^L,z_{ji}^R\right]\rangle$, then the established interval neutrosophic decision matrix is $D={\left(d_{ji}\right)}_{m\times n}$.

For a PPM selection problem, the concept of an ideal point is used to identify the best PPM in the alternative PPM set. Although the ideal selection usually does not exist in the real world, it can provide useful theoretical support for the selection of an alternative PPM. Generally, two types of evaluation criteria are used: benefit and cost criteria. In the proposed PPM selection model, an ideal alternative PPM can be expressed by using the maximum evaluation value for the benefit criteria and a minimum evaluation value for the cost criteria. If we assume that $H$ is a collection of benefit criteria and $K$ is a collection of cost criteria, then a benefit criterion with interval neutrosophic information in the ideal alternative $A^{\ast }$ is represented as:

$$\begin{array}{c}{d}_i^{\ast }=\langle \left[x_i^{L\ast },x_i^{R\ast }\right],\left[y_i^{L\ast },y_i^{R\ast }\right],\left[z_i^{L\ast },z_i^{R\ast }\right]\rangle \\ =\langle \left[\max \left(x_{ji}^L\right),\max \left(x_{ji}^R\right)\right],\left[\min \left(y_{ji}^L\right),\min \left(y_{ji}^R\right)\right],\left[\min \left(z_{ji}^L\right),\min \left(z_{ji}^R\right)\right]\rangle ,\end{array}$$

(6)

for $i\in H$; for a cost criterion,

$$\begin{array}{c}{d}_i^{\ast }=\langle \left[x_i^{L\ast },x_i^{R\ast }\right],\left[y_i^{L\ast },y_i^{R\ast }\right],\left[z_i^{L\ast },z_i^{R\ast }\right]\rangle \\ =\langle \left[\min \left(x_{ji}^L\right),\min \left(x_{ji}^R\right)\right],\left[\max \left(y_{ji}^L\right),\max \left(y_{ji}^R\right)\right],\left[\max \left(z_{ji}^L\right),\max \left(z_{ji}^R\right)\right]\rangle ,\end{array}$$

(7)

for $j\in K$.

Another representation of ideal alternative $A^{\ast }$ and the value of criteria $d_{ji}$ should be obtained by using Equation (1) in Definition 3. This representation is as follows:

$$\begin{array}{l}{d}_i^{\ast \ast }=\langle x_i^{\ast \ast },y_i^{\ast \ast },z_i^{\ast \ast }\rangle =\langle \left(\max \left(x_{ji}^L\right)+\max \left(x_{ji}^R\right)\right)/2+\left(\max \left(x_{ji}^L\right)-\max \left(x_{ji}^R\right)\right)\mathrm{i}/2,\\ \begin{array}{cc}& \left(\min \left(y_{ji}^L\right)+\min \left(y_{ji}^R\right)\right)/2+\left(\min \left(y_{ji}^L\right)-\min \left(y_{ji}^R\right)\right)\mathrm{i}/2,\end{array}\\ \begin{array}{cc}& \left(\min \left(z_{ji}^L\right)+\min \left(z_{ji}^R\right)\right)/2+\left(\min \left(z_{ji}^L\right)-\min \left(z_{ji}^R\right)\right)\mathrm{i}/2\rangle \end{array}\end{array},$$

(8)

for $i\in H$;

$$\begin{array}{l}{d}_i^{\ast \ast }=\langle x_i^{\ast \ast },y_i^{\ast \ast },z_i^{\ast \ast }\rangle =\langle \left(\min \left(x_{ji}^L\right)+\min \left(x_{ji}^R\right)\right)/2+\left(\min \left(x_{ji}^L\right)-\min \left(x_{ji}^R\right)\right)\mathrm{i}/2,\\ \begin{array}{cc}& \left(\max \left(y_{ji}^L\right)+\max \left(y_{ji}^R\right)\right)/2+\left(\max \left(y_{ji}^L\right)-\max \left(y_{ji}^R\right)\right)\mathrm{i}/2,\end{array}\\ \begin{array}{cc}& \left(\max \left(z_{ji}^L\right)+\max \left(z_{ji}^R\right)\right)/2+\left(\max \left(z_{ji}^L\right)-\max \left(z_{ji}^R\right)\right)\mathrm{i}/2\rangle \end{array}\end{array},$$

(9)

for $j\in K$; and the evaluation value of the alternative PPM $A_j$ is transformed into the following expression:

$$\begin{array}{c}{d}_{ji}=\langle x_{ji},y_{ji},z_{ji}\rangle =\langle \left(x_{ji}^L+x_{ji}^R\right)/2+\left(x_{ji}^L-x_{ji}^R\right)\mathrm{i}/2,\left(y_{ji}^L+y_{ji}^R\right)/2+\left(y_{ji}^L-y_{ji}^R\right)\mathrm{i}/2,\\ \left(z_{ji}^L+z_{ji}^R\right)/2+\left(z_{ji}^L-z_{ji}^R\right)\mathrm{i}/2\rangle ,\end{array}$$

(10)

$i=1,2,\dots ,n$ and $j=1,2,\dots ,m$.

Using the similarity measure defined in Equation (2), we have:

$$\begin{array}{c}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{Y}_1\left(A^{\ast },A_j\right)=\frac{1}{3n}{\displaystyle \sum _{i=1}^n\{\frac{\min \left(\left[x_i^{L\ast },x_i^{R\ast }\right],\left[x_{ji}^L,x_{ji}^R\right]\right)}{\max \left(\left[x_i^{L\ast },x_i^{R\ast }\right],\left[x_{ji}^L,x_{ji}^R\right]\right)}}\\ +\frac{\min \left(\left[x_i^{L\ast },x_i^{R\ast }\right],\left[x_{ji}^L,x_{ji}^R\right]\right)}{\max \left(\left[x_i^{L\ast },x_i^{R\ast }\right],\left[x_{ji}^L,x_{ji}^R\right]\right)}+\frac{\min \left(\left[z_i^{L\ast },z_i^{R\ast }\right],\left[z_{ji}^L,z_{ji}^R\right]\right)}{\max \left(\left[z_i^{L\ast },z_i^{R\ast }\right],\left[z_{ji}^L,z_{ji}^R\right]\right)}\}.\end{array}$$

Comparing the three terms in (7) and (9), namely, comparing $x_i^{\ast \ast }$ and $x_{ji}$, $z_i^{\ast \ast }$ and $y_{ji}$, $z_i^{\ast \ast }$ and $z_{ji}$, respectively, the minimum and maximum interval numbers in the numerator or denominator can be derived, and the terms in the braces can be calculated in accordance with the rules of interval number division and addition in Definition 2.

Similarly, two other measures, $Y_2\left(A^{\ast },A_j\right)$ and $Y_3\left(A^{\ast },A_j\right)$, can be obtained by applying Equations (3) and (4).

All alternatives can be ranked on the basis of the measures of similarity $Y_1\left(A^{\ast },A_j\right)$, $Y_2\left(A^{\ast },A_j\right)$ or $Y_3\left(A^{\ast },A_j\right)$ $\left(j=1,2,\dots ,m\right)$ between each alternative and the ideal alternative. Then, the best alternative can be easily identified.

4.2. Steps for Selection of PPM Using the Proposed Method

Due to the complexity of construction projects, the problem of PPM selection is a decision-making issue under an uncertainty environment, and the experts usually can’t give an accurate judgement. Therefore, the degree of confidence from experts when giving the evaluation information needed to be considered in the process of PPM selection. Based on this, the proposed method considers the degrees of confidence of experts on truth indeterminacy, and falsity memberships of the evaluation information, and will show power in a wide application field.

The decision steps for PPM selection are shown in Figure 3 in reference to the above illustration. The decision-making procedure of the proposed method is as follows:

Step 1:

Decision matrices determined.

The decision information of all alternative PPMs with respect to all criteria were characterized by the INSs. In the first step, the evaluation values of each alternative PPM under the different criteria were obtained from questionnaires to form decision matrices.

$$D=\left(\begin{array}{cccc}{d}_{11}& d_{12}& \cdots & d_{1n}\\ d_{21}& d_{22}& \cdots & d_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ d_{m1}& d_{m2}& \cdots & d_{mn}\end{array}\right),$$

where $d_{ji}=\langle \left[x_{ji}^L,x_{ji}^R\right],\left[y_{ji}^L,y_{ji}^R\right],\left[z_{ji}^L,z_{ji}^R\right]\rangle$ is the evaluation value for the alternative PPM $A_j$ given by the $k\mathrm{th}$ expert in accordance with criteria $C_i$, $k=1,2,\dots ,l$, $j=1,2,\dots ,n$, $i=1,2,\dots ,m$.

Step 2:

Ideal alternative PPM identified, using Equations (5) and (6).

Step 3:

Evaluation matrix $D$ and ideal alternative PPM were transformed into other representations, using Equation (1).

Step 4:

The weights of the criteria were calculated.

Many approaches can be used to determine the weights of criteria, including the analytic hierarchy process (AHP) [32], best worst method (BWM) [33], entropy method [34], and the full consistency method (FUCOM) [35]. The averaging weighing method was used for convenience in this study.

Step 5:

The measures of similarity between the ideal alternative PPM and each alternative PPM were calculated, using the proposed similarity measures.

Step 6:

The alternative PPMs were ranked in accordance with the results obtained in Step 5.

5. Practical Example

As discussed in this section, the proposed PPM selection model was applied to a real-world infrastructure project. Four alternative PPMs—DB, EPC, the CM method, and DBB—were considered. Their evaluation criteria were cost (C), schedule (S), quality (Q), complexity (Com), scope change (SC), experience (E), financial guarantee (FG), risk management (RM), uniqueness (U), and project size (Size). These criteria are shown as in Figure 1. To ensure the reliability and availability of the data, the experienced experts from different fields (including engineer, economics, law) should be invited to evaluate the project before carrying out the decision-making issue. Firstly, experts were introduced to the capacity and the goal of project by the owners. Secondly, further investigation to the construction site was conducted, and the related principals described the whole project in detail. Finally, according to the score chart and score criterion, the evaluation results of the project from the experts were obtained, and the final evaluation result was given through aggregating the evaluation information of the experts. Using the proposed method in Section 4, the suitable PPM could be selected. The final rank result was delivered to the owner by the experts, and the owner would choose the best suitable PPM according to the characteristics of project and their own management ability. The steps were as follows:

Step 1:

The evaluation matrix $A={\left(A_1,A_2,A_3,A_4\right)}^T$, was constructed, where $A_1$, $A_2$, $A_3$, and $A_4$ were the evaluation information for the four PPMs, and

$$\begin{array}{l}{A}_1=\{\langle \left[0.58,0.69\right],\left[0.31,0.48\right],\left[0.28,0.37\right]\rangle ,\langle \left[0.64,0.70\right],\left[0.44,0.53\right],\left[0.21,0.30\right]\rangle ,\\ \begin{array}{cc}& \begin{array}{cc}& \hspace{1em} \langle \left[0.56,0.68\right],\left[0.46,0.51\right],\left[0.13,0.36\right]\rangle ,\langle \left[0.57,0.66\right],\left[0.33,0.39\right],\left[0.12,0.33\right]\rangle ,\end{array}\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.42,0.51\right],\left[0.13,0.21\right],\left[0.12,0.21\right]\rangle ,\langle \left[0.40,0.53\right],\left[0.34,0.44\right],\left[0.10,0.13\right]\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.55,0.69\right],\left[0.30,0.41\right],\left[0.31,0.35\right]\rangle ,\langle \left[0.57,0.62\right],\left[0.29,0.39\right],\left[0.33,0.35\right]\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.61,0.71\right],\left[0.11,0.20\right],\left[0.16,0.21\right]\rangle ,\langle \left[0.50,0.58\right],\left[0.34,0.49\right],\left[0.14,0.19\right]\rangle \}\end{array};\end{array}$$

$$\begin{array}{l}{A}_2=\{\langle \left[0.66,0.71\right],\left[0.28,0.34\right],\left[0.17,0.22\right]\rangle ,\langle \left[0.58,0.64\right],\left[0.32,0.41\right],\left[0.20,0.31\right]\rangle ,\\ \begin{array}{cc}& \begin{array}{cc}& \hspace{1em} \langle \left[0.55,0.58\right],\left[0.10,0.21\right],\left[0.12,0.21\right]\rangle ,\langle \left[0.69,0.71\right],\left[0.11,0.16\right],\left[0.16,0.22\right]\rangle ,\end{array}\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.56,0.63\right],\left[0.20,0.30\right],\left[0.11,0.24\right]\rangle ,\langle \left[0.63,0.71\right],\left[0.28,0.36\right],\left[0.20,0.30\right]\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.58,0.69\right],\left[0.32,0.41\right],\left[0.11,0.18\right]\rangle ,\langle \left[0.56,0.68\right],\left[0.15,0.23\right],\left[0.15,0.21\right]\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.30,0.41\right],\left[0.22,0.31\right],\left[0.17,0.28\right]\rangle ,\langle \left[0.70,0.76\right],\left[0.38,0.41\right],\left[0.19,0.28\right]\rangle \}\end{array};\end{array}$$

$$\begin{array}{l}{A}_3=\{\langle \left[0.35,0.41\right],\left[0.17,0.31\right],\left[0.15,0.20\right]\rangle ,\langle \left[0.31,0.48\right],\left[0.22,0.28\right],\left[0.20,0.28\right]\rangle ,\\ \begin{array}{cc}& \begin{array}{cc}& \hspace{1em} \langle \left[0.46,0.56\right],\left[0.14,0.21\right],\left[0.16,0.24\right]\rangle ,\langle \left[0.38,0.47\right],\left[0.22,0.31\right],\left[0.15,0.27\right]\rangle ,\end{array}\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.30,0.41\right],\left[0.39,0.59\right],\left[0.15,0.22\right]\rangle ,\langle \left[0.44,0.58\right],\left[0.40,0.50\right],\left[0.20,0.30\right]\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.39,0.48\right],\left[0.30,0.41\right],\left[0.18,0.26\right]\rangle ,\langle \left[0.55,0.63\right],\left[0.12,0.22\right],\left[0.21,0.28\right]\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.44,0.54\right],\left[0.27,0.36\right],\left[0.13,0.19\right]\rangle ,\langle \left[0.37,0.47\right],\left[0.11,0.20\right],\left[0.18,0.26\right]\rangle \}\end{array};\end{array}$$

$$\begin{array}{l}{A}_4=\{\langle \left[0.66,0.74\right],\left[0.10,0.15\right],\left[0.10,0.20\right]\rangle ,\langle \left[0.78,0.89\right],\left[0.20,0.30\right],\left[0.20,0.31\right]\rangle ,\\ \begin{array}{cc}& \begin{array}{cc}& \hspace{1em} \langle \left[0.65,0.76\right],\left[0.10,0.20\right],\left[0.17,0.24\right]\rangle ,\langle \left[0.74,0.88\right],\left[0.15,0.26\right],\left[0.14,0.23\right]\rangle ,\end{array}\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.63,0.72\right],\left[0.14,0.24\right],\left[0.18,0.24\right]\rangle ,\langle \left[0.70,0.80\right],\left[0.20,0.27\right],\left[0.16,0.23\right]\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.69,0.81\right],\left[0.10,0.19\right],\left[0.10,0.20\right]\rangle ,\langle \left[0.56,0.65\right],\left[0.13,0.24\right],\left[0.15,0.26\right]\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.60,0.70\right],\left[0.10,0.17\right],\left[0.11,0.20\right]\rangle ,\langle \left[0.64,0.73\right],\left[0.20,0.30\right],\left[0.18,0.25\right]\rangle \}\end{array}.\end{array}$$

Step 2:

The ideal alternative PPM was determined, using Equations (8) and (9):

$$\begin{array}{l}{A}^{\ast }=\{\langle \left[0.35,0.41\right],\left[0.31,0.48\right],\left[0.28,0.37\right]\rangle ,\langle \left[0.35,0.41\right],\left[0.31,0.48\right],\left[0.28,0.37\right]\rangle ,\\ \begin{array}{cc}& \begin{array}{cc}& \hspace{1em} \langle \left[0.78,0.89\right],\left[0.20,0.28\right],\left[0.20,0.28\right]\rangle ,\langle \left[0.38,0.47\right],\left[0.33,0.39\right],\left[0.16,0.33\right]\rangle ,\end{array}\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.63,0.72\right],\left[0.13,0.21\right],\left[0.11,0.21\right]\rangle ,\langle \left[0.70,0.80\right],\left[0.20,0.27\right],\left[0.10,0.13\right]\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.69,0.81\right],\left[0.10,0.19\right],\left[0.10,0.18\right]\rangle ,\langle \left[0.57,0.68\right],\left[0.12,0.22\right],\left[0.15,0.21\right]\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle \left[0.30,0.41\right],\left[0.27,0.36\right],\left[0.17,0.28\right]\rangle ,\langle \left[0.70,0.76\right],\left[0.11,0.20\right],\left[0.14,0.19\right]\rangle \}\end{array}.\end{array}$$

Step 3:

The raw evaluation data matrix and the ideal alternative PPM were transformed, using Equation (1).

$$\begin{array}{l}{A}_1^{\prime }=\{\langle 0.64+0.06\mathrm{i},0.40+0.09\mathrm{i},0.33+0.05\mathrm{i}\rangle ,\langle 0.67+0.03\mathrm{i},0.49+0.05\mathrm{i},0.26+0.05\mathrm{i}\rangle ,\\ \begin{array}{cc}& \begin{array}{cc}& \hspace{1em} \langle 0.62+0.06\mathrm{i},0.49+0.03\mathrm{i},0.25+0.12\mathrm{i}\rangle ,\langle 0.62+0.05\mathrm{i},0.35+0.03\mathrm{i},0.23+0.11\mathrm{i}\rangle ,\end{array}\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.47+0.05\mathrm{i},0.36+0.03\mathrm{i},0.17+0.05\mathrm{i}\rangle ,\langle 0.47+0.07\mathrm{i},0.39+0.05\mathrm{i},0.12+0.02\mathrm{i}\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.62+0.07\mathrm{i},0.36+0.06\mathrm{i},0.33+0.02\mathrm{i}\rangle ,\langle 0.60+0.03\mathrm{i},0.34+0.05\mathrm{i},0.34+0.01\mathrm{i}\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.66+0.05\mathrm{i},0.16+0.05\mathrm{i},0.19+0.03\mathrm{i}\rangle ,\langle 0.54+0.04\mathrm{i},0.42+0.08\mathrm{i},0.17+0.03\mathrm{i}\rangle \}\end{array};\end{array}$$

$$\begin{array}{l}{A}_2^{\prime }=\{\langle 0.69+0.03\mathrm{i},0.31+0.03\mathrm{i},0.20+0.03\mathrm{i}\rangle ,\langle 0.61+0.03\mathrm{i},0.37+0.05\mathrm{i},0.26+0.05\mathrm{i}\rangle ,\\ \begin{array}{cc}& \begin{array}{cc}& \hspace{1em} \langle 0.57+0.02\mathrm{i},0.16+0.06\mathrm{i},0.17+0.05\mathrm{i}\rangle ,\langle 0.70+0.01\mathrm{i},0.14+0.03\mathrm{i},0.19+0.03\mathrm{i}\rangle ,\end{array}\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.60+0.04\mathrm{i},0.25+0.05\mathrm{i},0.18+0.07\mathrm{i}\rangle ,\langle 0.67+0.04\mathrm{i},0.32+0.04\mathrm{i},0.25+0.05\mathrm{i}\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.64+0.06\mathrm{i},0.37+0.05\mathrm{i},0.15+0.04\mathrm{i}\rangle ,\langle 0.62+0.06\mathrm{i},0.19+0.04\mathrm{i},0.18+0.03\mathrm{i}\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.36+0.06\mathrm{i},0.27+0.05\mathrm{i},0.23+0.06\mathrm{i}\rangle ,\langle 0.73+0.03\mathrm{i},0.40+0.02\mathrm{i},0.24+0.05\mathrm{i}\rangle \}\end{array};\end{array}$$

$$\begin{array}{l}{A}_3^{\prime }=\{\langle 0.38+0.03\mathrm{i},0.24+0.07\mathrm{i},0.18+0.03\mathrm{i}\rangle ,\langle 0.40+0.09\mathrm{i},0.25+0.03\mathrm{i},0.24+0.04\mathrm{i}\rangle ,\\ \begin{array}{cc}& \begin{array}{cc}& \hspace{1em} \langle 0.51+0.05\mathrm{i},0.18+0.04\mathrm{i},0.20+0.04\mathrm{i}\rangle ,\langle 0.43+0.05\mathrm{i},0.27+0.05\mathrm{i},0.21+0.06\mathrm{i}\rangle ,\end{array}\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.36+0.06\mathrm{i},0.49+0.10\mathrm{i},0.19+0.04\mathrm{i}\rangle ,\langle 0.51+0.07\mathrm{i},0.45+0.05\mathrm{i},0.25+0.05\mathrm{i}\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.44+0.05\mathrm{i},0.36+0.06\mathrm{i},0.22+0.04\mathrm{i}\rangle ,\langle 0.59+0.04\mathrm{i},0.17+0.05\mathrm{i},0.25+0.04\mathrm{i}\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.49+0.05\mathrm{i},0.32+0.05\mathrm{i},0.16+0.03\mathrm{i}\rangle ,\langle 0.42+0.05\mathrm{i},0.16+0.05\mathrm{i},0.22+0.04\mathrm{i}\rangle \}\end{array};\end{array}$$

$$\begin{array}{l}{A}_4^{\prime }=\{\langle 0.70+0.04\mathrm{i},0.13+0.03\mathrm{i},0.15+0.05\mathrm{i}\rangle ,\langle 0.84+0.06\mathrm{i},0.25+0.05\mathrm{i},0.26+0.06\mathrm{i}\rangle ,\\ \begin{array}{cc}& \begin{array}{cc}& \hspace{1em} \langle 0.71+0.06\mathrm{i},0.15+0.05\mathrm{i},0.26+0.06\mathrm{i}\rangle ,\langle 0.81+0.07\mathrm{i},0.21+0.06\mathrm{i},0.19+0.05\mathrm{i}\rangle ,\end{array}\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.68+0.05\mathrm{i},0.19+0.05\mathrm{i},0.21+0.03\mathrm{i}\rangle ,\langle 0.75+0.05\mathrm{i},0.24+0.04\mathrm{i},0.20+0.04\mathrm{i}\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.75+0.06\mathrm{i},0.15+0.05\mathrm{i},0.15+0.05\mathrm{i}\rangle ,\langle 0.61+0.05\mathrm{i},0.19+0.06\mathrm{i},0.21+0.06\mathrm{i}\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.65+0.05\mathrm{i},0.14+0.04\mathrm{i},0.16+0.05\mathrm{i}\rangle ,\langle 0.69+0.05\mathrm{i},0.25+0.05\mathrm{i},0.22+0.04\mathrm{i}\rangle \}\end{array};\end{array}$$

$$\begin{array}{l}{A}^{\ast \ast }=\{\langle 0.38+0.03\mathrm{i},0.40+0.09\mathrm{i},0.33+0.05\mathrm{i}\rangle ,\langle 0.84+0.06\mathrm{i},0.24+0.04\mathrm{i},0.24+0.04\mathrm{i}\rangle ,\\ \begin{array}{cc}& \begin{array}{cc}& \hspace{1em} \langle 0.51+0.05\mathrm{i},0.49+0.04\mathrm{i},0.24+0.04\mathrm{i}\rangle ,\langle 0.43+0.05\mathrm{i},0.36+0.03\mathrm{i},0.25+0.09\mathrm{i}\rangle ,\end{array}\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.43+0.05\mathrm{i},0.36+0.03\mathrm{i},0.25+0.09\mathrm{i}\rangle ,\langle 0.75+0.05\mathrm{i},0.24+0.04\mathrm{i},0.12+0.02\mathrm{i}\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.75+0.06\mathrm{i},0.15+0.05\mathrm{i},0.14+0.04\mathrm{i}\rangle ,\langle 0.63+0.06\mathrm{i},0.17+0.05\mathrm{i},0.18+0.03\mathrm{i}\rangle ,\end{array}\\ \begin{array}{ccc}& & \hspace{1em} \langle 0.36+0.06\mathrm{i},0.32+0.05\mathrm{i},0.23+0.06\mathrm{i}\rangle ,\langle 0.73+0.03\mathrm{i},0.16+0.05\mathrm{i},0.17+0.03\mathrm{i}\rangle \}\end{array}.\end{array}$$

Step 4:

The similarity measures between the ideal PPM and each alternative PPM were calculated, using Equation (4) with $w_1=w_2=\cdots =w_{10}=0.1$ and $\alpha =\beta =\gamma =1/3$.

$$Y_1^{\ast }=0.8038+0.2521\mathrm{i}; Y_2^{\ast }=0.8006+0.2504\mathrm{i}; Y_3^{\ast }=0.7764+0.2590\mathrm{i}; Y_4^{\ast }=0.8476+0.3067\mathrm{i}.$$

Thus, the four options were ranked as ${\mathrm{o}}_4\succ {\mathrm{o}}_1\succ {\mathrm{o}}_2\succ {\mathrm{o}}_3$, that is, $\mathrm{EPC}\succ \mathrm{DB}\succ \mathrm{DBB}\succ \mathrm{CM}$. Therefore, EPC was the best choice among the four options. These results indicate that the ranking order is acceptable for practical application. According to the ranking result, the EPC was in first place, and the DB was second. However, practically, the owner did not have to choose the EPC, due to limited management ability. The final selection needed to consider both the characteristics of project and the owner’s management ability, which integrated design, construction, and procurement of the project into a contract to relieve management pressure for the owner.

6. Comparative Analysis

Depending on the line of sensitive analysis in [36], the advantage of the proposed model is determined through comparison with the existing method in this section.

We employed the technique of order of preference by similarity to the ideal solution (TOPSIS) as the comparative method [37]. The line of the classical TOPSIS method was applied to the case study presented in Section 5.

To enable comparison with the classical TOPSIS method, we first introduced the concepts of distance similarity between two INSs and the complement of an INS.

Let $x=\left(\left[T_1^L\left(x_j\right),T_1^R\left(x_j\right)\right],\left[I_1^L\left(x_j\right),I_1^R\left(x_j\right)\right],\left[F_1^L\left(x_j\right),F_1^R\left(x_j\right)\right]\right)$ and $y=\left(\left[T_2^L\left(x_j\right),T_2^R\left(x_j\right)\right],\left[I_2^L\left(x_j\right),I_2^R\left(x_j\right)\right],\left[F_2^L\left(x_j\right),F_2^R\left(x_j\right)\right]\right)$ be the two INSs [38], then, the normalized Hamming distance is [39,40]

$$\begin{gathered} D_H\left(x,y\right)=\frac{1}{6n}{\displaystyle \sum _{j=1}^n(\left|T_1^L\left(x_j\right)-T_2^L\left(x_j\right)\right|+\left|T_1^R\left(x_j\right)-T_2^R\left(x_j\right)\right|+\left|I_1^L\left(x_j\right)-I_2^L\left(x_j\right)\right|} \\ +\left|I_1^R\left(x_j\right)-I_2^R\left(x_j\right)\right|+\left|F_1^L\left(x_j\right)-F_2^L\left(x_j\right)\right|+\left|F_1^R\left(x_j\right)-F_2^R\left(x_j\right)\right|), \end{gathered}$$

(11)

and the complement of x is $x^c=\left(\left[F_1^L\left(x_j\right),F_1^R\left(x_j\right)\right],\left[1-I_1^R\left(x_j\right),1-I_1^L\left(x_j\right)\right],\left[T_1^L\left(x_j\right),T_1^R\left(x_j\right)\right]\right)$.

We assumed that the weights of ten criteria were $w_1=w_2=\cdots =w_n$. The TOPSIS method ranked the four PPMs as $\mathrm{EPC}\succ \mathrm{DBB}\succ \mathrm{DB}\succ \mathrm{CM}$. Thus, EPC was the best option for this project, followed by DBB. The order of the four PPMs obtained by the proposed method was $\mathrm{EPC}\succ \mathrm{DB}\succ \mathrm{DBB}\succ \mathrm{CM}$, as shown in

Table 1. Comparison of the proposed method with the classical TOPSIS method.

PPMs	Classical TOPSIS		Proposed Method
	Results	Rank	Results	Rank
DB	0.4770	3	$0.8038+0.2521\mathrm{i}$	2
DBB	0.5340	2	$0.8006+0.2504\mathrm{i}$	3
CM	0.3729	4	$0.7764+0.2590\mathrm{i}$	4
EPC	0.6112	1	$0.8476+0.3067\mathrm{i}$	1

. The best appropriate PPM obtained by the proposed method was same as that obtained by classical TOPSIS method, that is, the EPC was the best suitable option, according to both methods. The CM was in the last rank using both methods. The DBB was in the second position from the classical TOPSIS and in the third rank for the proposed method.

The rankings of the results exhibited slight differences. The proposed method considered not only the weights of the ten criteria, but also the weights of the truth membership and falsity membership degrees. In other words, the strongest advantage of the proposed method over the existing decision-making methods is the degree of confidence from evaluators, which can be acquired by considering the weights of truth membership and falsity membership degrees. Thus, a more reasonable final result was generated. In practice, the construction project was implemented under a high level of complexity and uncertainty. The owner had few staff members and limited experience in managing the proposed project, and coordination between design and construction was difficult for the owner. Thus, the owner needed a single-responsibility delivery method for design and construction. A highly efficient and easy operating method was preferred. The development and application of the proposed method could enrich theoretical knowledge and practice.

7. Conclusions

PPM selection plays an important role in influencing the efficiency of project implementation. Selecting the appropriate PPM poses considerable challenges to owners, given the complexity of the objective world and the ambiguity of human thinking in real-life decision-making. INSs show power in dealing with imprecise and ambiguous information and manage complex uncertainties in applications, in which a main obstacle is to compare two interval numbers. To overcome this, the interval number was transformed into another parallel representation. Then, a PPM selection method with interval neutrosophic information was built. An example of the selection of a PPM was given to demonstrate the applications and effectiveness of the proposed selection approach. Finally, to show the advantage of the proposed method, a comparison analysis of results between the proposed and existing methods was given.

The main motivation of this work was to develop a PPM selection model to guide decision-making for owners. INSs can handle imprecise and ambiguous information and manage complex uncertainties in applications. Similarity measures are also important tools for judging the closeness between the ideal alternative PPM and the proposed PPM in decision-making. The contributions of this paper are as follows: (1) This study innovatively introduced the similarity measure under an interval neutrosophic environment to deal with PPM selection problems. (2) Considering the truth, falsity, and indeterminacy memberships simultaneously, the similarity measure based on minimum and maximum operators was applied to construct a decision-making model for PPM selection. (3) This study established a PPM selection method with an interval neutrosophic set by applying similarity measures, which takes account into the determinacy, indeterminacy, and hesitation from the decision experts in the evaluation process. In a practical PPM selection, to make the selected PPM more reasonable and reliable under uncertainty, the “true psychological” behavior and degree of confidence from experts are necessary in the process of PPM selection.

Comparing the results of our proposed method with those of existing methods, the proposed method considers the degree of confidence from the evaluators, which will enhance and expand decision-making knowledge theory. Numerous problems can be solved with the help of the presented method and theory. The proposed PPM selection method has the characteristics of simple design concept and easy implementation. Moreover, in contrast to existing methods, it considers the degree of confidence from evaluators. From the operation process, it realizes that the development of an interval number theory is important for obtaining precise results through the whole process of research and practice. Thus, the applications of similarity measures between INSs would be investigated in other areas, such as pattern recognition, clustering analysis, and image processing. Work on the comparison of intervals should also be conducted.