Abstract
This paper introduces a new method for determining the shape similarity of complex three-dimensional (3D) mesh structures based on extracting a vector of important vertices, ordered according to a matrix of their most important geometrical and topological features. The correlation of ordered matrix vectors is combined with perceptual definition of salient regions in order to aid detection, distinguishing, measurement and restoration of real degradation and digitization errors. The case study is the digital 3D structure of the Camino Degli Angeli, in the Urbino’s Ducal Palace, acquired by the structure from motion (SfM) technique. In order to obtain an accurate, featured representation of the matching shape, the strong mesh processing computations are performed over the mesh surface while preserving real shape and geometric structure. In addition to perceptually based feature ranking, the new theoretical approach for ranking the evaluation criteria by employing neural networks (NNs) has been proposed to reduce the probability of deleting shape points, subject to optimization. Numerical analysis and simulations in combination with the developed virtual reality (VR) application serve as an assurance to restoration specialists providing visual and feature-based comparison of damaged parts with correct similar examples. The procedure also distinguishes mesh irregularities resulting from the photogrammetry process.
Keywords:
3D geometry; AR; cultural heritage; digitization errors; preservation; restoration; shape analysis; neural networks; VR 1. Introduction
Many cultural heritage (CH) archives are currently undergoing extensive 3D digitization to preserve artifacts from inevitable decay and provide visitors remote access to rich cultural collections. In recent years, numerous digitization techniques have arisen, varying in accordance with the various nature of 3D objects. However, the possibility of digitization error occurring is high due to the complexity of the 3D digitization process that includes preparation, digital recordings and data processing [1].
The superiority of computational algorithms for digital shape analysis and comparisons in combination with advanced concepts of artificial intelligence (AI) ensures qualitative representation of 3D models in virtual reality (VR) and augmented reality (AR) environments [2]. Increasing the efficiency of the CH model dissemination relies mostly on the quality of equipment for the acquisition and the hardware elements that deal with collected data, providing both semantic and visual information. For example, laser scanning and digital photogrammetry techniques accompanied with developed image processing software can provide very exact information regarding artifacts, ranging from miniature sculptures to large-scale monuments. However, even the state-of-the-art hardware generates digitization errors due to the technological limitations, variation of environmental light, small resolution of captured images or insufficient number of scanning steps. On the other hand, imperfections of digitized 3D models can also be related to the nature of artifact, i.e., the physicochemical characteristics of its material, the complexity of its shape and structure, as well as its size and the environmental influence amongst others. These problems are addressed by improvements in the resolution and quality of digital sensors followed by the integration of geo-positioning sensors, with a permanent increase in the computation power [3]. The other direction implies the development of new efficient algorithms that estimate camera parameters using the large number of captured images, such as structure from motion (SfM) [4] and visual simultaneous localization and mapping (VSLAM) [5]. Although the processed 3D objects satisfy the demands of a wider audience, they are still inadequate for restoration requirements due to their vulnerability to even non-malicious geometrical and topological deformations and transformations. In this paper, we propose an advanced shape analysis method that meets restoration requirements by considering all geometric deviations including holes and missing geometry structures of the particular 3D structure. The shape analysis and similarity algorithms combined with VR applications may help restoration specialists to compare damaged parts of both the physical artifact and its 3D representation with the correct similar sample.
The importance of shape similarity was first underlined in the fields of computer vision, mechanical engineering and molecular biology applications [6]. As a response to new requirements, the automatic comparison of 3D models has been introduced in the form of tools that use algorithms for shape matching such as the well-known iterative closest point (ICP) [7]. As a result of complex restoration requirements, a lot of literature also offers significant content-based similarity matching solutions and algorithms for filling holes [8,9]. A myriad of visualization techniques has also been proposed for the manual reconstruction in order to reach the qualitative visualization. However, such methods mainly rely on computer-aided design (CAD) or geographic information system (GIS) software use [10,11]. This kind of approach provides high-quality representations of restored models that actually do not correspond to their original geometric form.
This paper introduces a new method for determining the shape similarity of complex 3D mesh structures based on extracting a vector of important vertices, ordered according to matrix of their most important geometrical and topological features. The case study is the digital 3D structure of the Camino Degli Angeli, in the Urbino’s Ducal Palace, acquired by the SfM technique [12,13], the practical result of which is illustrated in detail in Appendix A (Figure A1) with a given technical performance and adjustments of the camera used (Table A1). In order to obtain accurate featured representation of the matching shape, the strong mesh processing computations were performed over the mesh surface with the preservation of the real shape and geometric structure.
In addition to perceptually based feature ranking, the new theoretical approach for ranking the evaluation criteria by employing the neural networks (NNs) has been proposed to reduce the probability of deleting shape points, subject to optimization. Construction of NNs with the input neuron values obtained from 3D mesh features technically contributes to the direct computation of the salient parts of the geometry, avoiding the additional usage of other systems, which supports queries based on 3D sketches, 2D sketches, 3D models, text and image and their association to particular 3D structures [14,15].
Numerical analysis and simulations in combination with the developed VR application serve as an assurance to restoration specialists providing visual and feature-based comparison of damaged parts with correct similar examples. The procedure also distinguishes mesh irregularities resulting from the photogrammetry process.
This paper is organized as follows: Section 2 describes prior work that addressed the shape similarity problem in analyzing complex geometrical structures. In this section, we also briefly describe methods and achievements that are exploited in our approach. Notation and concepts used throughout the paper are described in detail within Section 3. Section 4 contains a detailed description of our algorithm and a theoretical background of the techniques used with mathematical and geometrical notations. Numerical results with the corresponding visual illustrations are shown in Section 5. A brief discussion, conclusions and future work directions are given in Section 6.
2. Prior Work
The principal of geometric similarity and symmetry has been established in theory as a crucial shape description problem [16,17,18]. Recent studies [19,20] have been linked to measuring the distances between descriptors using the dissimilarity measurements to reduce the set of measured values and achieve accurate results. Mathematical generalization that satisfactorily represents the salient regions and shapes of any 3D structure is an imperative and also a starting point of research. One direction of research is focused on defining the most suitable formula to perform the representation invariant to the pose of 3D object and to the method or the way it is created. The comparison of 3D shapes using covariance matrices of features instead of the computation of features separately is an example [21]. At the same time, combining different shape matching methods becomes more challenging and promising [22].
An interesting idea in employing the surface analysis and filling holes with the patches from valid regions of the given surface is presented in [23] within the recent context-based method of restoration of 3D structures. Another concept of the model repairing and simplification [24] converts polygonal models into voxels, employing either the parity-count method or the ray-stabbing method according to the type of deformations. In the final procedure, they convert back a volumetric-based model into polygons using an iso-surface extraction for the final output. Unlike the approaches that use similarity for repairing architectural models [25], Chen et al. [26] propose a visual-similarity-based approach for 3D model retrieval, using features of encoded orthogonal projection by Zernike moments and Fourier descriptors. Although it achieves good results in decreasing errors in the 3D model generation by selection and elimination of planar polygons, coincident coplanar polygons, improper polygon intersections and face orientation, it is not efficient enough for error correction in the general case.
The philosophy of our approach is different. We employ strong signal processing during the vertex feature detection to ensure proper synchronization prior to similarity detection, while the quantization is adaptive and operates only on a matching example and not on the whole complex mesh. The reasoning for such an approach is the following. Our content-aware extraction selects the mesh vertices that stay invariant during the mesh transformations, thus reducing the probability of descriptor deletion. The heart of this method for selecting “important” vertices is the ordered statistics vertex extraction and tracing algorithm (OSVETA) [27]. This is a sophisticated and powerful algorithm that combines several mesh topologies with human visual system (HVS) metrics to calculate vertex stabilities and trace vertices most susceptible for extraction. Such vertex preprocessing allows the use of low-complexity algorithms tailored to the matching computation.
3. Preliminaries
In this section, we introduce the notation and the concepts used through the paper. We start with a brief discussion of the most important features and introduce geometrical and topological features that will be used in calculations. Then, we will introduce the quantization of important vertices and the concept of calculation of the Hausdorff distance between points. We also introduce basic terminology of the constructed NN that will be used in the theoretical concept of ranking criteria and vertices.
3.1. Gaussian and Mean Curvature Descriptors
From the differential geometry [28], we can locally approximate the manifold surface in by its tangent plane that is orthogonal to the normal vector n. We define e as a unit direction in the tangent plane and the normal curvature as a curvature of the curve that belongs to both the surface and the tangent plane that contains both n and e. The average value and product of both principal curvatures and of the surface defines the mean curvature and Gaussian curvature . The mean curvature and unit normal at the vertex are given by mean curvature normal (Laplace–Beltrami operator) . Using the derived expression for the discrete mean curvature normal operator [29],
and if we define at the point —a number of adjacent triangular faces, and —an angle of th adjacent triangle, and —area of the first ring of triangles around the point , we can find the Gaussian curvature and the mean curvature of the discrete surface, which depend only on a vertex position and adjacent triangles angles:
The index “B” is a notation of using the barycenter region in the computation of the area .
3.2. Fitting Quadric Curvature Estimation
The idea of the fitting quadric curvature estimation method is that a smooth surface geometry can be locally approximated with a quadratic polynomial surface by fitting a quadric to point in a local neighborhood of each chosen point in a local coordinate frame. The quadric’s curvature at the chosen point is taken to be the estimation of the curvature for the discrete surface.
For a simple quadric form , we estimate a surface normal n at the point v either by simple or weighted averaging or by finding the least-squares fitted plane to the point and its neighbors. Then, we position a local coordinate system at the point v and align axis along the estimated normal. We use the McIvor and Valkenburg suggestion [30] for aligning of the coordinate axis with a projection of the global axis onto the tangent plane defined by n. If we use the suggested improvements and fit the mapped data to extended quadric: , and solve the resulting system of linear equations, we finally obtain the estimation for the Gaussian and mean curvature:
where are the parameters of the last quadric fitted.
3.3. Mesh Quantization
For a given triangular mesh with vertices, each vertex is conventionally represented using absolute Cartesian coordinates, denoted by . The nominal uniform quantizer in the classification stage maps the input value to a quantization index , i.e., it distributes vertices into quantization levels with a step according to the value of their coordinates [31].
where, with a slight abuse of notation, denotes the rounding operation, i.e., for a real , is the integer closest to .
Irregular meshes and complex geometrical structures require non-uniform or adaptive quantizers that provide a quantization space partitioned according to input data. For any mesh with a non-proportional dimensional sizes, the quantizer , adaptive to particular dimension, will be constructed as a triplet of quantizers with the same number of quantization levels, , but with a particular step size for each dimension , where
3.4. Ordered Statistics Vertex Extraction
Let be defined as the set of functions over the vector of mesh vertices and their corresponding indices in a triangular face construction . If the function has both positive and negative values, its argument vector can be ordered by at least two criteria , where denotes ordering the argument vector in descending or ascending order in accordance to the criteria and respectively (the values , of all features, except and , correspond to vertices belonging to surface regions irelevant for our consideration). For the given set of functions one can define the new set of criteria weighted by the importance coefficients , and extract a new vector of vertices
which is ordered according to the sum of all elements from [27].
4. Our Algorithm
The core of our method is fundamental shape analysis of 3D structure and the extraction of geometric primitives depending on their involvement in the shape creation. Each primitive is determined by its importance using the ordered statistics ranking of crucial geometrical and topological features. In order to decrease the computational time taken to describe their connectivity, all vertices are quantized by their Euclidian coordinates, assigning only the indexes of vertices with the highest importance to quantization levels. This quantized mesh ensures fast preliminary descriptor computation and, thus, good similarity results even using very small quantization levels. The refinement of matching results is achieved by additionally increasing the quantization levels with the tightening of the descriptor criteria.
The algorithm operates within four basic steps: (i) computation of geometrical and topological features over the whole 3D mesh structure; (ii) extraction of the vector of vertices ordered according to their features’ ranking ; (iii) adaptive mesh quantization depending on the selected sample mesh region, and (iv) similarity description computation.
Figure 1 illustrates the flow of the whole process of our algorithm including the task of the topological error determination.
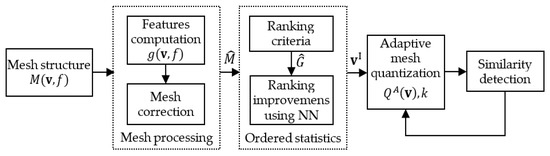
Figure 1.
The flowchart of the operations within our algorithm.
The contribution of our algorithm is threefold: (i) proposed novel method for extracting a set of crucial geometrical and topological features from using strong signal processing, (ii) introducing the fast and accurate ordered statistic ranking criteria algorithm for important vertex extraction, and(iii) new adaptive 3D quantization technique that operates with iteratively determined quantization steps. Correlation and cooperation between all the above methods ensure reliable set of vertices for the final computation of similarity matching descriptors. The value of the calculated Hausdorff distance between the matching shape descriptors and the sample shape descriptors triggers an increase or decrease of the quantization level, , striving to reduce the quantization error.
4.1. Mesh Processing
Prior to consider the similarity problems, we perform strong 3D mesh processing that includes calculation of most of geometrical and topological features of the given mesh geometry. All computed values of crucial shape description features are collected in the matrix form that is suitable for all further fast computations and statistical analyses. The mesh correction step also includes the extraction of boundary vertices and topological errors, thus decreasing the possibility of faults in all further steps. On the other hand, some topological errors can represent the appearance of digitization errors, the detection of which is also important in distinguishing them from geometric decay deformations of the considered artifact.
4.2. Ordered Statistics Algorithm
The core of our approach toward the extraction of important vertices is an ordered statistic ranking criteria algorithm [27], which has already been proven in the field of 3D mesh watermarking [32] and adapted to the shape recognition and similarity detection. Our idea is to assign weights to all criteria according to the statistical information of their participation in determining the shape importance (Section 3.4), instead of separately sorting important vertices according to each geometric and topological criteria, which further participate in the quantization and similarity determining process. In this way, we not only reduce the computation time due to a significant reduction of the number of loops in the execution of software procedures but also enable an additional use of neural networks in the criteria ranking.
All weight values in previous table were used from our experimental computation and improved by results from our recent research using the NN ranking [33]. The result of this step is the vector of vertex indices ordered according to their computed importance.
4.3. Adaptive Mesh Quantization
The second significant achievement of this paper is introducing the adaptive quantization of important vertices in simplifying the complex mesh structure for the next computation use. The first step of the algorithm is the sample mesh quantization that sorts only the important vertices of the chosen sample structure into cells for each dimension in . From the set of vertices whose Euclidean coordinates belong to the particular quantization level, the algorithm selects only one with the highest position in the previously ordered vector (Section 4.2). The starting minimal number of quantization levels facilitates the very fast extraction of vertices.
Considering a pair or triplet matching vertices, using a low number of quantization levels is usually not enough for the shape description, but this step ensures a valid starting point and very fast computations of the selected distances. Increasing the quantization levels in the loop within the next steps, the algorithm will provide higher precision of the important vertices and, thus, a more accurate 3D shape description.
4.4. Similarity Matching Procedure
The simplified mesh structure obtained using both previous steps of the algorithm ensures low computational time for the vertex distance computation and determination of a correlation between the obtained measures. In other words, this step of the algorithm operates on a number of descriptors that is more than two orders smaller than that of an ordinary complex mesh. The result of our quantization algorithm is the matrix with the information of selected set of important vertices, the density of their distribution and also their position level in the vector of ordered vertices . Thus, contrary to standard methods, our algorithm provides additional information prior to the rigid similarity calculations based on distances between selected points.
Assuming that most of the geometric information is concentrated into dense quants, we first determine the quants of the whole mesh that meet that condition. The second similarity criterion is the connection of selected important vertices to the adjacent quants according to the low-level quantized sample and their “importance” position. Finally, the mutual distance between the selected vertices in the sample mesh and all resulting matching vertices is calculated as the Hausdorff distance:
The vertices with a minimal value of the calculated are considered as matching points in the first iteration step. The fine tuning of the selected matching points includes increasing the quantization level , repeating the calculation procedure and considering the more-important vertices. Minimizing the number of matching mesh surface regions interrupts the iterative procedure.
It is quite clear that a better choice of important points leads to a reduction in the number of iterations and a faster and accurate matching region detection. In this paper, we propose improvements by introducing NNs for the vertex extraction criteria ranking.
4.5. Neural Networks for 3D Feature Ranking
An additional contribution of our method is a theoretical approach in employing neural networks to the already described vertex extraction algorithm. It enables more-precise feature ranking within the mesh geometry and topology estimation. Following the principles of feature-based neural networks and including all relevant 3D mesh features , we designed a feature learning framework that directly uses a vector of all vertex features and their derived criteria as the NN inputs [33]. In order to avoid an irregularity problem of the 3D mesh geometry and topology, we set each of our hidden neurons to be activated by the same input weight value and also have the same bias for all input neurons. The NN learns by adjusting all weights and biases through backpropagation to obtain the ordered vector of vertex indices that provides information on vertex importance.
In the backpropagation process, hidden neurons receive inputs from the input neurons . The activations of these neurons are the components of the input vector respectively. The weight between the input and our hidden layer is . In this context, the NN input to th neuron is the sum of weighted signals from neurons , where the sigmoid function is and the bias is included by adding it to the input vector. Updating the hidden layer weights is the standard procedure for minimizing an error using a training set. Since each of our hidden layer neurons are weighted by the same weights and biases from all input neurons, the gradient weight of the hidden layer is given as , where is the learning rate.
This theoretical approach relies on 3D feature-based NN application that is considered only within the step of stabile vertice extraction. Additional overall improvements can be achieved using some of the already developed machine learning algorithms in the final similarity matching phase, particularly in the predictive selection of neighboring vertices after our quantization step.
5. Numerical Results
In order to obtain valuable and perceptually measurable results, we deliberately chose the digital 3D model of the Camino Degli Angeli, in the Urbino’s Ducal Palace as the case study. This 3D model is, at a glance, perceptually appropriate for the experimental purpose for at least three reasons: (i) There is obvious central symmetry and, thus, similarity between the left and right sides of an object. (ii) The model contains figures whose recognizable similar shapes represent a strict functionality test and measurable evaluation of the algorithm accuracy. (iii) Digitization errors on the right are also clearly visible and help an assessment of the algorithm’s efficiency in classifying this type of shortcoming.
5.1. Mesh Processing Performance
We started the simulation with separately performed computations for five parts of the model:
- angelo-1L.obj—the sculpture of an angel on the top-left,
- angelo-1R.obj—the symmetrical pair at the right,
- angelo-2L.obj—the left angel ornament,
- angelo-2R.obj—the symmetrical pair at the right, and
- camino degli angeli.obj—the whole fireplace 3D model.
The artifacts inside these parts were assumed to be the best example of the restoration process’ requirement and the right guidance in performing a simulation. In addition, previous assumptions also included that a type of decay at the right is not a priori defined. All input models were without textures, which would actually interfere with perceptual tests. The renders are shown on the next (Figure 2).

Figure 2.
Render of the input 3D models: (a) angelo-1L.obj, (b) angelo-2L.obj, (c) camino degli angeli.obj, (d) angelo-2R.obj, (e) angelo-1R.obj.
Our algorithm estimates the curvature and shape of the model by computing 24 geometrical and topological features at each vertex over the mesh surface. According to specificity of the similarity problem, in all the next steps, we used the resulting vectors of eight features (Table 1). Figure 3 and additional figures in Figure A2 illustrate a level of success of the computed features in the process of determining the salient regions of the mesh surface and, thus, in the shape recognition.

Table 1.
Ordered statistic criteria ranking (Section 3.4 [27]).

Figure 3.
The same input models as in Figure 2 rendered and texturized by the color map in accordance with the computed features, respectively: (a) Gaussian curvature, (b) mean curvature, (c) gradient of the Gaussian curvature, (d) maximal dihedral angle, and (e) theta angle. In the used color map, blue corresponds to low values and red to high values of the computed feature.
5.2. Ordered Statistics Vertex Extraction Performance
The first stage of this algorithm is selecting all the vertices and ordering their vector indices according to the value in the matrix of all defined criteria described in Table 1 and Section 4.2. Each resulting extracted matrix column now contains ordered vertex indices obtained by using all the criteria from the same table. Roughly speaking, we can visually illustrate the result of this step by observing all the images from Figure A2, in which each vertex color (from blue to red) represents the value of the corresponding feature.
The next stage statistically or empirically defines the “importance” value of each criterion or, more precisely, the importance of each derived criteria in the shape definition process. In other words, the purpose of using criteria is to determine the grades of the vertices in the ranking criteria phase. For example, ranking criteria and with the highest-grades algorithm will extract only convex regions. However, in the shape creation, all criteria have an influence and particular contribution. The result and output of this phase is an extracted vector of vertex indices in accordance with the sum vector of all 14 criteria (Section 3.4). Figure 4 presents visual effects of the ranking technique’s result, applied to renderings of individual criteria, as well as the illustration of our algorithm’s accuracy, showing the spatial position of the extracted important vertices.
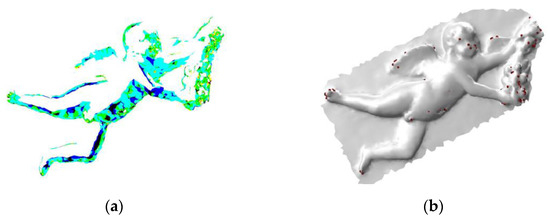
Figure 4.
Illustration of our algorithm’s accuracy: (a) visual example of the angelo-2L.obj renderings multiplied by ranked criteria, (b) spatial position of the top-60 ordered vertices out of 4056.
Another proof of our approach is the noticeable invariance of the top selected vertices after the simplification and optimization processes, even after strong optimization with only 5% of the surviving vertices (Figure 5).
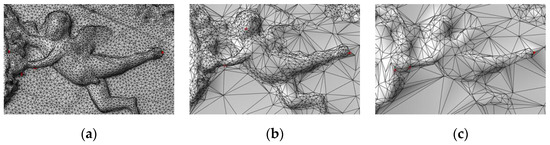
Figure 5.
Red dots illustrate the invariance of vector to different strengths of optimization: (a) original 3D mesh without deletions, (b) 80% deleted vertices and (c) 95% deleted vertices.
5.3. Results of the Quantization
Our previously extracted set of important vertices, ensures valid data for the next quantization procedure. As expected, our quantizer provides better results for the higher level of quantization, , but unexpectedly good result for the small number of levels, which is actually very useful in the proposed iterative computation (Section 4.3).
Our algorithm allows a user to interactively enter a desired level of quantization, , but we can clearly notice, from Figure 6, the satisfactory results of our quantizer’s efficiency using . The table below provides more extensive data for each level of quantization.
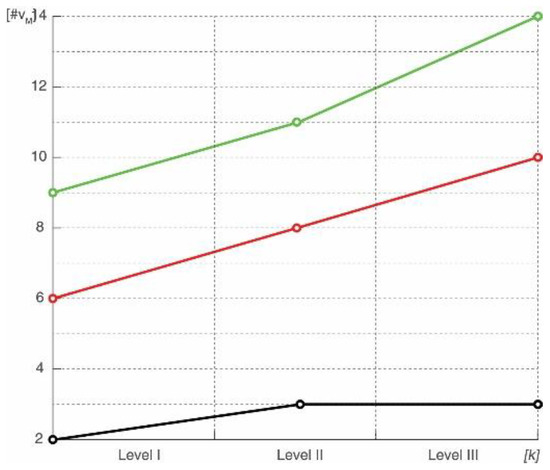
Figure 6.
The number of matched vertices using quantization levels . The shown values vary depending on the selected tolerance and the total number of selected vertices (Table 2).
Supplementing the tabular data, Figure 7 illustrates the spatial distribution of the matched vertices by quantization. Regardless of the presented results in the above table, we can notice, even perceptually, the similarity of the black points’ distribution in the sample area of the left angel ornament and the red points’ distribution on the right. This is promising information for the final matching step.
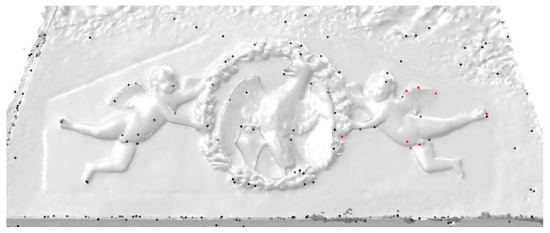
Figure 7.
The cropped view of the 3D mesh with extracted matching vertices using the quantization level of 14 × 42 × 20 and tolerance 1/6: all extracted quantized vertices in this area (black markers), and matched vertices (red markers).
For better visual comparison of the results of each considered quantization level, an additional set of illustrations is provided in Appendix B (Figure A3).
5.4. Matching Shapes Performance
The adaptive 3D quantizer operates with iterative determined quantization steps and correlates with ordered-statistics vertex extraction algorithm ensuring a reliable set of vertices for the final computation of similarity matching descriptors. The value of the calculated Hausdorff distance between the matching shape descriptors and the sample shape descriptors triggers an increase or decrease in the quantization level striving to reduce the quantization error.
Figure 8 illustrates the successfully detected similarity of the shape in the selected mesh area and the corresponding shape inside the considered whole mesh.

Figure 8.
Illustration of a matching distance descriptor calculated using quantization level for the sample area quantization and corresponding number of the whole mesh quantization. (a) Set of vertices selected in the sample area, (b) matched area with calculated distance descriptors.
The shape matching algorithm is calibrated to exclude all sample vertices from the whole mesh distance computing, thus decreasing the number of required combination.
All computations in the paper are performed using our developed software, and obtained results are verifiable by the open software code available online [34]. The supplemented materials, include all used 3D models are also available at the link [34].
6. Discussion, Conclusions and Future Work
In this paper, we aimed to reach a satisfactory level in the non-trivial field of 3D geometry estimation and especially in determining the geometrical similarities of shapes. Our novel theoretical approach is described in detail with a clear explanation of the algorithm structure including each of its steps and procedures. The method’s efficiency is experimentally proven with the presented numerical results and appropriate illustrations. The complete computational software engine is developed with provided interactivity for the research use. All developed source code is available online and free for use, review and improvements.
The contribution of this paper is threefold: (i) proposed novel method for extracting a set of crucial geometrical and topological features, using strong signal processing; (ii) introducing the fast and accurate ordered-statistic ranking criteria algorithm for important-vertex extraction and (iii) new adaptive 3D quantization technique that operates with iteratively determined quantization steps. Correlation and cooperation between all the above methods ensure a reliable set of vertices for the final computation of similarity matching descriptors. The value of the calculated Hausdorff distance between the matching shape descriptors and the sample shape descriptors triggers the increase or decrease of the quantization level striving to reduce the quantization error.
The presented experimental results demonstrate that the similarity of two shapes (ornamental angels in our case study) can be fairly estimated using eight features from the Table 1. We show that our quantizer using , quantization levels 14 × 42 × 20 for the whole mesh and the tolerance 1/6 ensures an accurate-featured representation of the matching shape. Moreover, our novel adaptive quantization technique overcomes a mesh complexity shortcoming by improving the computation speed. The experimental data presented in this paper satisfactorily suit the requirements of experts in the restoration of CH artifacts, providing numerical and perceptual support for their needs.
In addition to all achievements, we introduced the new theoretical approach in employing AI that enables more-precise feature ranking within the mesh geometry and topology estimation. The limitation of this approach is the small available training set and usually large and complex mesh structures that result in long computational time. However, the further improvements of the proposed novel method and its combination with other image-based NN applications are promising.
Our future work envisages the application and testing the method on the broader set of CH artifacts. The expected result will automatize the feature ranking process and improve quantization technique and their positive impact on matching similarity and also on the mesh and point cloud simplification. We also aim to expand our research with the introduction of different types of 3D models such as point cloud data as a common CH digitization format.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/info13030145/s1. These materials include all images, 3D models, and software code.
Author Contributions
Conceptualization, I.V. and R.Q.; Formal analysis, E.F.; Funding acquisition, R.Q.; Investigation, I.V.; Methodology, I.V.; Project administration, R.P.; Resources, R.Q.; Software, B.V.; Supervision, E.F. and B.V.; Validation, I.V., R.Q. and B.V.; Visualization, R.P.; Writing—original draft, I.V. and B.V.; Writing—review & editing, R.Q., R.P. and B.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding, and it is a part of the strategic project of Università Politecnica delle Marche “CIVITAS—Chain for excellence of reflective societies to exploit digital cultural heritage and museums”. The APC was offered by the editor considering the paper as an extended version of the awarded conference paper published in the proceedings of the SALENTO AVR 2021.
Data Availability Statement
The data presented in this study are available in [http://iva.silicon-studio.com/AngeliSImilarityResearch.zip, accessed on 8 January 2022].
Acknowledgments
The survey activities were authorized by the concession of the MIC, Ministry of Culture—General Directorate for Museums—National Gallery of Marche. The elaborations produced are property of the MIC—National Gallery of Marche. Thanks to the Director of the National Gallery of Marche, Luigi Gallo, for his hospitality and for enabling access to the museum. The authors also want to thank Paolo Clini (DICEA, Department of Civil, Building Engineering and Architecture of Polytechnic University of Marche) as Principal Investigator of the CIVITAS project. The SfM data processing of the Camino degli Angeli is part of the master’s degree thesis in Building Engineering—Architecture by Giorgia De Angelis and Umberto Ferretti, supervisor R.Q., co-supervisor R.P. Moreover, the authors acknowledge that the present research is framed in the DC-Box project, Erasmus + project no. 2021-1-IT02-KA220-HED-000032253.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Case Study: Description and Data Survey
The case study, on which the present methodology was implemented and tested for the first time on a cultural artifact, was the “Camino degli Angeli” (the “Chimney of Angels”), from which the name of the Sala degli Angeli (Hall of Angels) derives, one of the most famous rooms of the Apartment of Duke Federico, located on the Piano Nobile of the Ducal Palace of Urbino. The rich and imaginative decoration of the room is due to the sculptural skill of Domenico Rosselli (1439–1498): in the large receiving room, he created a wide and refined repertoire of stone and stucco carvings, with which he celebrated the Montefeltro family. In particular, he produced the most richly decorated fireplace in the entire palace. The fireplace owes its name to the procession of “putti” with gilded hair and wings that unfolds on a blue background; above the fireplace is placed, within a circular garland, an eagle holding the Montefeltro coat of arms with its claw.
The photos were taken both with parallel axes (nadiral) and converging axes (oblique). Considering the characteristics of the camera, the dimensions of the object and the maximum distance at which to position oneself, the grip design is summarized in the following table (Table A1).

Table A1.
Technical performance of the camera model SONY Alpha9.
Table A1.
Technical performance of the camera model SONY Alpha9.
| Feature | Sensor Dimension | Value | Unit | Bounding Box | Value | Unit |
|---|---|---|---|---|---|---|
| w | Length | 35.6 | mm | Length | 423 | mm |
| h | Height | 23.8 | mm | Height | 420 | mm |
| D | Target distance | 1000 | mm | Sidelap | 60 | % |
| f | Focal length | 24 | mm | Overlap | 60 | % |
| w | Horizontal image size | 6000 | pix | Sidelap | 89 | cm |
| h | Vertical image size | 3376 | pix | Overlap | 60 | cm |
| Camera resolution | (Mpix) | Displacement x | 59 | cm | ||
| pix h | Sensor pixel size (horiz.) | 0.006 | mm | Displacement y | 40 | cm |
| pix v | Sensor pixel size (vert.) | 0.007 | mm | Shooting Stations | - | |
| s | Magnification | 41.667 | no. of stations along the x axis | 7 | - | |
| Artifact Dimension | no. of stations along the y axis | 11 | - | |||
| w | Length | 148 | cm | Total of nadiral photos | 75 | - |
| h | Height | 99.17 | cm | no. of oblique x axis stations | 4 | - |
| Pixel dimension | no. of oblique y axis stations | 5 | - | |||
| w | Length | 0.247 | mm | Total of side photos | 62 | - |
| h | Height | 0.294 | mm | Total photos | 137 | - |
Photos were taken in RAW format, taking care to also acquire an additional picture with the “Color Checker”, intended to reproduce the color faithfully. The photos were then processed in Adobe Photoshop Camera RAW and exported to JPEG format. These images were then processed in Agisoft Metashape software according to the established procedures to obtain the cloud of the chimney. The 3D model of the fireplace of the Sala degli Angeli, also obtained with Metashape, contained a total of 499,984 faces. The steps of this part of procedure are shown in Figure A1 below.

Figure A1.
The illustration of all digitization and mesh constructing steps.
Appendix B
Figure A2 represents additional visualizations of the computed criteria specified in Table 1 and Section 4.2 and their perceptual results. A brief explanation for the rendering color scheme used is given in the figure caption below.


Figure A2.
The input models ((a) angelo-1L.obj, (b) angelo-2L.obj, (c) camino degli angeli.obj, (d) angelo-2R.obj, (e) angelo-1R.obj) rendered and texturized by the color map in accordance with all computed criteria from Table 1 and Section 4.2. Blue corresponds to low values and red to high values of the computed criteria.
Within the mesh quantization step, we performed computations using various tolerance factors and quantization levels. The illustrated comparison of the best obtained results is presented in Figure A3.

Figure A3.
Illustration of quantization results using specified quantization levels and corresponding adaptive levels: (a) k = 2: (9 , (b) : , (c) : . The red, black and magenta markers in all illustrations denote the tolerance levels 1/2, 1/6, and 1/12, respectively.
References
- Pavlidis, G.; Koutsoudis, A.; Arnaoutoglou, F.; Tsioukas, V.; Chamzas, C. Methods for 3D digitization of Cultural Heritage. J. Cult. Herit. 2007, 8, 93–98. [Google Scholar] [CrossRef] [Green Version]
- Vasic, I.; Pierdicca, R.; Frontoni, E.; Vasic, B. A New Technique of the Virtual Reality Visualization of Complex Volume Images from the Computer Tomography and Magnetic Resonance Imaging. In Augmented Reality, Virtual Reality, and Computer Graphics, 1st ed.; De Paolis, L.T., Arpaia, P., Bourdot, P., Eds.; Springer International Publishing: Cham, The Netherlands, 2021; pp. 376–391. [Google Scholar] [CrossRef]
- Furukawa, Y.; Hernández, C. Multi-View Stereo: A Tutorial. Found. Trends Comput. Graph. Vis. 2015, 9, 1–48. [Google Scholar] [CrossRef] [Green Version]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar] [CrossRef] [Green Version]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-Time Single Camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Osada, R.; Funkhouser, T.; Chazelle, B.; Dobkin, D. Matching 3D models with shape distributions. In Proceedings of the International Conference on Shape Modeling and ApplicationsMay, Genova, Italy, 7–11 May 2001; IEEE: Manhattan, NY, USA, 2001; pp. 154–166. [Google Scholar] [CrossRef] [Green Version]
- Besl, P.J.; McKay, N.D. A Method for Registration of 3-D Shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Itskovich, A.; Tal, A. Surface Partial Matching & Application to Archaeology. Comput. Graph. 2011, 35, 334–341. [Google Scholar] [CrossRef]
- Harary, G.; Tal, A.; Grinspun, E. Context-based Coherent Surface Completion. ACM Trans. Graph. (TOG) 2014, 33, 1–12. [Google Scholar] [CrossRef]
- McKinney, K.; Fischer, M. Generating, evaluating and visualizing construction schedules with CAD tools. Autom. Constr. 1998, 7, 433–447. [Google Scholar] [CrossRef]
- Kersting, O.; Döllner, J. Interactive 3D visualization of vector data in GIS. In Proceedings of the 10th ACM International Symposium on Advances in Geographic Information, McLean, VA, USA, 8–9 November 2002; Association for Computing Machinery: New York, NY, USA, 2002; pp. 107–112. [Google Scholar] [CrossRef] [Green Version]
- Deleart, F.; Seitz, S.M.; Thrope, C.E.; Thrun, S. Structure from motion without correspondence. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2000 (Cat. No.PR00662), Hilton Head, SC, USA, 13–15 June 2000; IEEE: Manhattan, NY, USA, 2000; Volume 2, pp. 557–564. [Google Scholar] [CrossRef]
- Van den Hengel, A.; Dick, A.R.; Thormählen, T.; Ward, B.; Torr, P.H.S. Videotrace: Rapid Interactive Scene Modelling from Video. In ACM SIGGRAPH 2007 Papers; Association for Computing Machinery: New York, NY, USA, 2007; p. 86-es. [Google Scholar] [CrossRef]
- Funkhouser, T.; Min, P.; Kazhdan, M.; Chen, J.; Halderman, A.; Dobkin, D.; Jacobs, D. A search engine for 3D models. ACM Trans. Graph. 2003, 22, 83–105. [Google Scholar] [CrossRef]
- Qin, S.; Li, Z.; Chen, Z. Similarity Analysis of 3D Models Based on Convolutional Neural Networks with Threshold. In Proceedings of the 2018 the 2nd International Conference on Video and Image Processing, Tokyo, Japan, 29–31 December 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 95–102. [Google Scholar] [CrossRef]
- Rossignac, J. Corner-operated Tran-similar (COTS) Maps, Patterns, and Lattices. ACM Trans. Graph. 2020, 39, 1–14. [Google Scholar] [CrossRef]
- Ju, T.; Schaefer, S.; Warren, J. Mean value coordinates for closed triangular meshes. ACM Trans. Graph. 2005, 24, 561–566. [Google Scholar] [CrossRef]
- Mitra, N.J.; Pauly, M.; Wand, M.; Ceylan, D. Symmetry in 3D geometry: Extraction and applications. Comput. Graph. Forum 2013, 32, 1–23. [Google Scholar] [CrossRef]
- Chang, M.C.; Kimia, B.B. Measuring 3D Shape Similarity by Matching the Medial Scaffolds. In Proceedings of the IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; IEEE: Manhattan, NY, USA, 2009; pp. 1473–1480. [Google Scholar] [CrossRef]
- Bustos, B.; Keim, D.A.; Saupe, D.; Schreck, T.; Vranic, D.V. Feature-based similarity search in 3D object databases. ACM Comput. Surv. 2005, 37, 345–387. [Google Scholar] [CrossRef] [Green Version]
- Tabia, H.; Laga, H. Covariance-Based Descriptors for Efficient 3D Shape Matching, Retrieval, and Classification. IEEE Trans. Multimed. 2015, 17, 1591–1603. [Google Scholar] [CrossRef]
- Tangelder, J.W.H.; Veltkamp, R.C. A survey of content based 3D shape retrieval methods. Multimed. Tools Appl. 2007, 39, 441–471. [Google Scholar] [CrossRef]
- Sharf, A.; Alexa, M.; Cohen-Or, D. Context-Based Surface Completion. ACM Trans. Graph. 2004, 23, 878–887. [Google Scholar] [CrossRef] [Green Version]
- Nooruddin, F.S.; Turk, G. Simplification and Repair of Polygonal Models Using Volumetric Techniques. IEEE Educ. Act. Dep. 2003, 9, 191–205. [Google Scholar] [CrossRef] [Green Version]
- Khorramabadi, D. A Walk through the Planned CS Building, 1st ed.; University of California at Berkeley: Berkeley, CA, USA, 1991. [Google Scholar]
- Chen, D.Y.; Tian, X.P.; Shen, Y.T.; Ouhyoung, M. On Visual Similarity Based 3D Model Retrieval. Comput. Graph. Forum 2003, 22, 223–232. [Google Scholar] [CrossRef]
- Vasic, B. Ordered Statistics Vertex Extraction and Tracing Algorithm (OSVETA). Adv. Electr. Comput. Eng. 2012, 12, 25–32. [Google Scholar] [CrossRef]
- Spivak, M. A Comprehensive Introduction to Differential Geometry, 3rd ed.; Publish or Perish: Los Angeles, WA, USA, 1999. [Google Scholar]
- Meyer, M.; Desbrun, M.; Schröder, P.; Barr, A.H. Discrete Differential-Geometry Operators for Triangulated 2-Manifolds. In Visualization and Mathematics III; Hege, H.C., Ed.; Springer Berlin/Heidelberg: Berlin/Heidelberg, Germany, 2003; pp. 35–57. [Google Scholar] [CrossRef] [Green Version]
- McIvor, A.M.; Valkenburg, R.J. A comparison of local surface geometry estimation methods. Mach. Vis. Appl. 1997, 10, 17–26. [Google Scholar] [CrossRef]
- Gray, R.M.; Neuhoff, D.L. Quantization. IEEE Trans. Inf. Theory 1998, 44, 2325–2383. [Google Scholar] [CrossRef]
- Vasic, B.; Vasic, B. Simplification Resilient LDPC-Coded Sparse-QIM Watermarking for 3D-Meshes. IEEE Trans. Multimed. 2013, 15, 1532–1542. [Google Scholar] [CrossRef]
- Vasic, B.; Raveendran, N.; Vasic, B. Neuro-OSVETA: A Robust Watermarking of 3D Meshes. In Proceedings of the International Telemetering Conference, Las Vegas, NV, USA, 21–24 October 2019; International Foundation for Telemetering: Las Vegas, NV, USA, 2019; Volume 55, pp. 387–396. [Google Scholar]
- Vasic, B.; Vasic, I. Angeli Similarity Research. 2021. Available online: http://iva.silicon-studio.com/AngeliSImilarityResearch.zip (accessed on 8 January 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).