Cost-Sensitive Models to Predict Risk of Cardiovascular Events in Patients with Chronic Heart Failure
Abstract
:1. Introduction
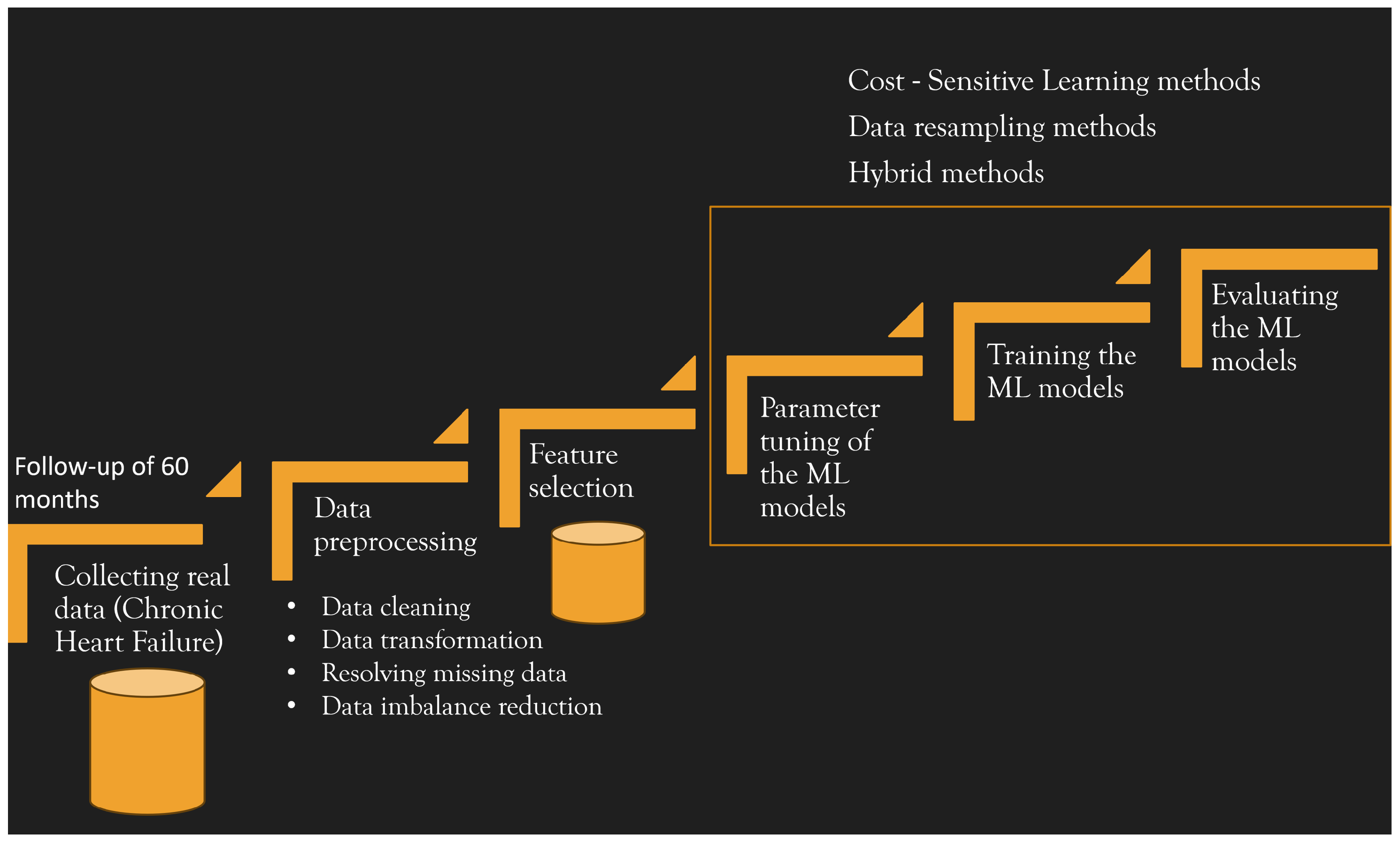
2. Real Data Collection and Dataset Construction
Study Population
Patient Characteristics
Events during Follow-Up
2.1. Data Preprocessing
2.2. Feature Selection
3. Machine Learning Process
3.1. Dealing with Imbalance Data: Cost-Sensitive Learning and Methods for Model Assessment
3.2. Hybrid Method for Imbalanced Dataset and Hyper-Parameter Optimisation Approach
3.3. Performance Metrics for Imbalanced Dataset
- AUC measures the classifier’s ability to avoid false classification [52]. It is the area under the curve of the true positive ratio vs. the false positive ratio that indicates the probability that the model will rank a positive case more highly than a negative case. A model whose predictions are 100% correct has an AUC of 1.0.
- Sensitivity, also referred to as true positive rate or recall, measures the proportion of positive instances that are correctly identified, i.e., it is the ability to predict a CV event:
- Specificity (also known as true negative rate) is used to determine the ability to correctly classify. It measures the proportion of negatives that are correctly identified, and is defined as
- The accuracy metric can be misleading for our imbalanced dataset. As it is equally important to accurately predict the events of the positive and negative classes for the addressed problem, we used the balanced accuracy metric [53,54], which is defined as the arithmetic mean of sensitivity and specificity:
- Another useful metric is the so-called geometric mean or G-Mean that balances both sensitivity and specificity by combining them. It is defined as
4. Results and Discussions
- Method1: cost-sensitive learning methods;
- Method2: data resampling methods;
- Method3: cost-sensitive learning methods combined with data resampling methods.
- SVM:
- We tested SVM with three kernel functions, i.e., the linear kernel, polynomial kernel, and RBF kernel. The hyper-parameter C and those related to the polynomial kernel and RBF kernel were optimised by searching for the best values within the specified range, as reported in Table 3. The incremental value used for optimisation is denoted in the fourth column as “Step.”
- MLP:
- The model parameter optimisation involves choosing the number of hidden layers, the number of neurons in each layer, the number of epochs, the learning rate, and the momentum. We tested different MLP models consisting of one input layer, one output layer, and one hidden layer. The number of neurons in the hidden layer was set according to the formulaWe optimised the learning rate, the momentum, and the number of epochs in a defined range of values, as reported in Table 3. The incremented value is denoted in the fourth column as “Step”.
Predictive Models Performance Metrics
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Disease and Injury Incidence and Prevalence Collaborators. Global, regional, and national incidence, prevalence, and years lived with disability for 354 diseases and injuries for 195 countries and territories, 1990–2017: A systematic analysis for the Global Burden of Disease Study 2017. Lancet 2018, 392, 1789–1858. [Google Scholar] [CrossRef] [PubMed]
- McMurray, J.J. Improving outcomes in heart failure: A personal perspective. Eur. Heart J. 2015, 36, 3467–3470. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Evans, J.C.; Benjamin, E.; Lévy, D.; Leroy, E.; Vasan, R. Natural History of Asymptomatic Left Ventricular Systolic Dysfunction in the Community. Circ. J. Am. Heart Assoc. 2003, 108, 977–982. [Google Scholar] [CrossRef] [PubMed]
- Dunlay, S.M.; Redfield, M.M.; Weston, S.A.; Therneau, T.M.; Long, K.H.; Shah, N.D.; Roger, V.L. Hospitalizations after Heart Failure Diagnosis. J. Am. Coll. Cardiol. 2009, 54, 1695–1702. [Google Scholar] [CrossRef]
- Ponikowski, P.; Voors, A.A.; Anker, S.D.; Bueno, H.; Cleland, J.G.F.; Coats, A.J.S.; Falk, V.; González-Juanatey, J.R.; Harjola, V.P.; Jankowska, E.A.; et al. 2016 ESC Guidelines for the diagnosis and treatment of acute and chronic heart failure: The Task Force for the diagnosis and treatment of acute and chronic heart failure of the European Society of Cardiology (ESC)Developed with the special contribution of the Heart Failure Association (HFA) of the ESC. Eur. Heart J. 2016, 37, 2129–2200. [Google Scholar] [CrossRef]
- McDonagh, T.A.; Metra, M.; Adamo, M.; Gardner, R.S.; Baumbach, A.; Bohm, M.; Burri, H.; Butler, J.; Celutkien, J.; Chioncel, O.; et al. 2021 ESC Guidelines for the diagnosis and treatment of acute and chronic heart failure: Developed by the Task Force for the diagnosis and treatment of acute and chronic heart failure of the European Society of Cardiology (ESC) With the special contribution of the Heart Failure Association (HFA) of the ESC. Eur. Heart J. 2021, 42, 3599–3726. [Google Scholar]
- Stevenson, L.W.; Pagani, F.D.; Young, J.B.; Jessup, M.; Miller, L.; Kormos, R.L.; Naftel, D.C.; Ulisney, K.; Desvigne-Nickens, P.; Kirklin, J.K. INTERMACS profiles of advanced heart failure: The current picture. J. Heart Lung Transplant. Off. Publ. Int. Soc. Heart Transplant. 2009, 28, 535–541. [Google Scholar] [CrossRef]
- Ziaeian, B.; Fonarow, G. Epidemiology and aetiology of heart failure. Nat. Rev. Cardiol. 2016, 13, 368–378. [Google Scholar] [CrossRef]
- Mehta, P.A.; Dubrey, S.W.; McIntyre, H.F.; Walker, D.M.; Hardman, S.M.C.; Sutton, G.C.; McDonagh, T.A.; Cowie, M.R. Improving survival in the 6 months after diagnosis of heart failure in the past decade: Population-based data from the UK. Heart 2009, 95, 1851–1856. [Google Scholar] [CrossRef]
- Tavazzi, L.; Senni, M.; Metra, M.; Gorini, M.; Cacciatore, G.; Chinaglia, A.; Lenarda, A.D.; Mortara, A.; Oliva, F.; Maggioni, A.P. Multicenter Prospective Observational Study on Acute and Chronic Heart Failure. Circ. Heart Fail. 2013, 6, 473–481. [Google Scholar] [CrossRef]
- Liao, L.; Allen, L.A.; Whellan, D.J. Economic burden of heart failure in the elderly. PharmacoEconomics 2008, 26, 447–462. [Google Scholar] [CrossRef]
- Stewart, S.; Jenkins, A.; Buchan, S.; McGuire, A.; Capewell, S.; McMurray, J. The current cost of heart failure to the National Health Service in the UK. Eur. J. Heart Fail. 2002, 4, 361–371. [Google Scholar] [CrossRef] [PubMed]
- Marangoni, E.; Lissoni, F.; Raimondi Cominesi, I.; Tinelli, S. Heart failure: Epidemiology, costs and healthcare programs in Italy. G. Ital. Cardiol. 2012, 13, 139S–144S. [Google Scholar] [CrossRef]
- Krumholz, H.M.; Chen, Y.T.; Vaccarino, V.; Wang, Y.; Radford, M.J.; Bradford, W.; Horwitz, R.I. Correlates and impact on outcomes of worsening renal function in patients ≥ years of age with heart failure. Am. J. Cardiol. 2000, 85, 1110–1113. [Google Scholar] [CrossRef] [PubMed]
- Brons, M.; Koudstaal, S.; Asselbergs, F.W. Algorithms used in telemonitoring programmes for patients with chronic heart failure: A systematic review. Eur. J. Cardiovasc. Nurs. 2018, 17, 580–588. [Google Scholar] [CrossRef]
- Kurtz, B.; Lemercier, M.; Pouchin, S.C.; Benmokhtar, E.; Vallet, C.; Cribier, A.; Bauer, F. Automated home telephone self-monitoring reduces hospitalization in patients with advanced heart failure. J. Telemed. Telecare 2011, 17, 298–302. [Google Scholar] [CrossRef]
- Olsen, C.R.; Mentz, R.J.; Anstrom, K.J.; Page, D.; Patel, P.A. Clinical applications of machine learning in the diagnosis, classification, and prediction of heart failure. Am. Heart J. 2020, 229, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Averbuch, T.; Sullivan, K.; Sauer, A.; Mamas, M.A.; Voors, A.A.; Gale, C.P.; Metra, M.; Ravindra, N.; Van Spall, H.G.C. Applications of artificial intelligence and machine learning in heart failure. Eur. Heart J.-Digit. Health 2022, 3, 311–322. [Google Scholar] [CrossRef] [PubMed]
- Lofaro, D.; Groccia, M.C.; Guido, R.; Conforti, D.; Caroleo, S.; Fragomeni, G. Machine learning approaches for supporting patient-specific cardiac rehabilitation programs. In Proceedings of the 2016 Computing in Cardiology Conference (CinC), Vancouver, BC, Canada, 11–14 September 2016; pp. 149–152. [Google Scholar]
- Groccia, M.C.; Lofaro, D.; Guido, R.; Conforti, D.; Sciacqua, A. Predictive Models for Risk Assessment of Worsening Events in Chronic Heart Failure Patients. In Proceedings of the 2018 Computing in Cardiology Conference (CinC), Maastricht, The Netherlands, 23–26 September 2018; Volume 45, pp. 1–4. [Google Scholar] [CrossRef]
- Tripoliti, E.E.; Papadopoulos, T.G.; Karanasiou, G.S.; Naka, K.K.; Fotiadis, D.I. Heart failure: Diagnosis, severity estimation and prediction of adverse events through machine learning techniques. Comput. Struct. Biotechnol. J. 2017, 15, 26–47. [Google Scholar] [CrossRef]
- Lorenzoni, G.; Sabato, S.S.; Lanera, C.; Bottigliengo, D.; Minto, C.; Ocagli, H.; De Paolis, P.; Gregori, D.; Iliceto, S.; Pisanò, F. Comparison of machine learning techniques for prediction of hospitalization in heart failure patients. J. Clin. Med. 2019, 8, 1298. [Google Scholar] [CrossRef]
- Lemaître, G.; Nogueira, F.; Aridas, C.K. Imbalanced-learn: A python toolbox to tackle the curse of imbalanced datasets in machine learning. J. Mach. Learn. Res. 2017, 18, 559–563. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Beckmann, M.; Ebecken, N.F.; de Lima, B.S.P. A KNN undersampling approach for data balancing. J. Intell. Learn. Syst. Appl. 2015, 7, 104. [Google Scholar] [CrossRef]
- Akbani, R.; Kwek, S.; Japkowicz, N. Applying support vector machines to imbalanced datasets. In Proceedings of the European Conference on Machine Learning, Pisa, Italy, 20–24 September 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 39–50. [Google Scholar]
- Cheng, F.; Zhang, J.; Wen, C. Cost-sensitive large margin distribution machine for classification of imbalanced data. Pattern Recognit. Lett. 2016, 80, 107–112. [Google Scholar] [CrossRef]
- Veropoulos, K.; Campbell, C.; Cristianini, N. Controlling the sensitivity of support vector machines. In Proceedings of the International Joint Conference on AI, Stockholm, Sweden, 31 July–6 August 1999; Volume 55, p. 60. [Google Scholar]
- Qi, Z.; Tian, Y.; Shi, Y.; Yu, X. Cost-sensitive support vector machine for semi-supervised learning. Procedia Comput. Sci. 2013, 18, 1684–1689. [Google Scholar] [CrossRef]
- Tao, X.; Li, Q.; Guo, W.; Ren, C.; Li, C.; Liu, R.; Zou, J. Self-adaptive cost weights-based support vector machine cost-sensitive ensemble for imbalanced data classification. Inf. Sci. 2019, 487, 31–56. [Google Scholar] [CrossRef]
- Thai-Nghe, N.; Gantner, Z.; Schmidt-Thieme, L. Cost-sensitive learning methods for imbalanced data. In Proceedings of the The 2010 International Joint Conference on Neural Networks (IJCNN), Barcelona, Spain, 18–23 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–8. [Google Scholar]
- Kohavi, R.; Provost, F. Glossary of terms. Mach. Learn. 1998, 30, 271–274. [Google Scholar]
- R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017.
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Burges, C. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Hofmann, T.; Scholkopf, B.; Smola, A.J. Kernel Methods in Machine Learning. Ann. Statist. 2008, 36, 1171–1220. [Google Scholar] [CrossRef]
- Krenker, A.; Bešter, J.; Kos, A. Introduction to the artificial neural networks. In Artificial Neural Networks: Methodological Advances and Biomedical Applications; InTech: Houston, TX, USA, 2011; pp. 1–18. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation; Technical Report; California Univ San Diego La Jolla Inst for Cognitive Science: La Jolla, CA, USA, 1985. [Google Scholar]
- Rish, I. An Empirical Study of the Naive Bayes Classifier. Technical Report. 2001. Available online: https://www.cc.gatech.edu/home/isbell/classes/reading/papers/Rish.pdf (accessed on 29 September 2023).
- Shalev-Shwartz, S.; Ben-David, S. Decision Trees. In Understanding Machine Learning; Cambridge University Press: Cambridge, UK, 2014; Chapter 18. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Alam, M.Z.; Rahman, M.S.; Rahman, M.S. A Random Forest based predictor for medical data classification using feature ranking. Inform. Med. Unlocked 2019, 15, 100180. [Google Scholar] [CrossRef]
- Yang, F.; Wang, H.; Mi, H.; Lin, C.; Cai, W. Using random forest for reliable classification and cost-sensitive learning for medical diagnosis. BMC Bioinform. 2009, 10, S22. [Google Scholar] [CrossRef] [PubMed]
- Elkan, C. The Foundations of Cost-Sensitive Learning. In Proceedings of the 17th International Joint Conference on Artificial Intelligence—Volume 2, Seattle, WA, USA, 4–10 August 2001; IJCAI’01. Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2001; pp. 973–978. [Google Scholar]
- Santos, M.S.; Soares, J.P.; Abreu, P.H.; Araujo, H.; Santos, J. Cross-Validation for Imbalanced Datasets: Avoiding Overoptimistic and Overfitting Approaches [Research Frontier]. IEEE Comput. Intell. Mag. 2018, 13, 59–76. [Google Scholar] [CrossRef]
- Kong, J.; Kowalczyk, W.; Menzel, S.; Bäck, T. Improving Imbalanced Classification by Anomaly Detection. In Proceedings of the 16th International Conference, PPSN 2020, Leiden, The Netherlands, 5–9 September 2020; pp. 512–523. [Google Scholar] [CrossRef]
- Mienye, I.D.; Sun, Y. Performance analysis of cost-sensitive learning methods with application to imbalanced medical data. Inform. Med. Unlocked 2021, 25, 100690. [Google Scholar] [CrossRef]
- Guido, R.; Groccia, M.C.; Conforti, D. A hyper-parameter tuning approach for cost-sensitive support vector machine classifiers. Soft Comput. 2023, 27, 12863–12881. [Google Scholar] [CrossRef]
- Guido, R.; Groccia, M.C.; Conforti, D. Hyper-Parameter Optimization in Support Vector Machine on Unbalanced Datasets Using Genetic Algorithms. In Optimization in Artificial Intelligence and Data Sciences; Amorosi, L., Dell’Olmo, P., Lari, I., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 37–47. [Google Scholar]
- Zhang, F.; Petersen, M.; Johnson, L.; Hall, J.; O’Bryant, S.E. Hyperparameter Tuning with High Performance Computing Machine Learning for Imbalanced Alzheimer Disease Data. Appl. Sci. 2022, 12, 6670. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Rumelhart, D.E.; McClelland, J.L.; PDP Research Group, C. (Eds.) Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1: Foundations; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Sun, Y.; Wong, A.K.C.; Kamel, M.S. Classification of Imbalanced Data: A Review. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 687–719. [Google Scholar] [CrossRef]
- Branco, P.; Torgo, L.; Ribeiro, R. A Survey of Predictive Modelling under Imbalanced Distributions. arXiv 2015, arXiv:cs.LG/1505.01658. [Google Scholar]
- Eibe, F.; Hall, M.A.; Witten, I.H. The WEKA Workbench. In Online Appendix for Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]


| Characteristic | ||
|---|---|---|
| Age | (years ± SD) | 72.5 ± 14.2 |
| Sex | Male | 36 (72%) |
| Female | 14 (28%) | |
| NYHA Class | I | 3 (6%) |
| II | 38 (76%) | |
| III | 9 (18%) | |
| CHF aetiology | Ischemic heart disease | 23 (46%) |
| Idiopathic dilatation | 9 (18%) | |
| Hypertension | 4 (8%) | |
| Valvular diseases | 8 (16%) | |
| Valvular diseases + hypertension | 4 (8%) | |
| Alcoholic habit | 2 (4%) | |
| Cardiovascular history | Instable angina | 1 (2%) |
| PTCA | 1 (2%) | |
| By-pass | 7 (14%) | |
| Atrial flutter | 13 (26%) | |
| Pacemaker | 3 (6%) | |
| Cardiac resynchronisation | 1 (2%) | |
| ICD | 2 (4%) | |
| Mitral insufficiency | 21 (42%) | |
| Aortic insufficiency | 4 (8%) | |
| Hypertension | 28 (56%) | |
| TIA | 2 (4%) | |
| Other diseases | Diabetes | 11 (22%) |
| Hypothyroidism | 1 (2%) | |
| Renal failure | 4 (8%) | |
| COPD | 5 (10%) | |
| Asthma | 1 (2%) | |
| Sleep apnea | 4 (8%) | |
| Pulmonary fibrosis | 1 (2%) | |
| Gastrointestinal diseases | 4 (8%) | |
| Hepatic diseases | 3 (6%) | |
| Pharmacological treatment | ACE-I/ARB | 47 (94%) |
| Diuretic therapy | 29 (58%) | |
| Beta-blockers | 44 (88%) | |
| Corticosteroids/NSAIDs | 0 (0%) |
| Actual Class | |||
|---|---|---|---|
| Positive | Negative | ||
| Predicted class | Positive | ||
| Negative | |||
| ML Model | Parameter | Search Space | Step | Selected Value |
|---|---|---|---|---|
| SVM | d | [1, 5] | 1 | 2 |
| (polynomial kernel) | C | [1, 10] | 0.5 | 5 |
| SVM | [0.01, 1.00] | 0.01 | 0.82 | |
| (RBF kernel) | C | [1, 10] | 0.5 | 3 |
| MLP | Learning rate | [0.1, 1.0] | 0.1 | 0.6 |
| Momentum | [0.1, 1.0] | 0.1 | 0.1 | |
| Number of epochs | [400, 600] | 100 | 500 |
| Model | Parameter | Value |
|---|---|---|
| SVM with linear kernel | C | 1 |
| SVM with polynomial kernel | d | 2 |
| C | 5 | |
| SVM with RBF kernel | 0.82 | |
| C | 3 | |
| MLP | Learning rate | 0.6 |
| Momentum | 0.1 | |
| Number of epochs | 500 | |
| Number of neurons in input layer | 4 | |
| Number of neurons in hidden layer | 3 | |
| Number of neurons in output layer | 2 | |
| Naive Bayes | useKernelEstimator | False |
| useSupervisedDiscretisation | False | |
| Decision tree | Confidence factor | 0.25 |
| Random forest | Bag size percent | 100 |
| Number of iterations | 100 |
| 3-Fold Cross-Validation | 5-Fold Cross-Validation | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | c12 | c21 | AUC | Sens | Spec | B-acc | G-mean | AUC | Sens | Spec | B-acc | G-mean |
| SVM with linear kernel | 1 | 10 | 0.535 | 0.130 | 0.940 | 0.536 | 0.278 | 0.611 | 0.257 | 0.964 | 0.611 | 0.498 |
| 1 | 20 | 0.597 | 0.394 | 0.801 | 0.598 | 0.542 | 0.703 | 0.586 | 0.820 | 0.703 | 0.693 | |
| 1 | 30 | 0.576 | 0.558 | 0.594 | 0.576 | 0.557 | 0.670 | 0.719 | 0.620 | 0.670 | 0.668 | |
| 1 | 35 | 0.499 | 0.621 | 0.376 | 0.499 | 0.429 | 0.601 | 0.752 | 0.449 | 0.601 | 0.581 | |
| 1 | 40 | 0.482 | 0.788 | 0.176 | 0.482 | 0.182 | 0.535 | 0.881 | 0.189 | 0.535 | 0.408 | |
| SVM with polynomial kernel | 1 | 10 | 0.542 | 0.13 | 0.954 | 0.542 | 0.278 | 0.583 | 0.195 | 0.972 | 0.584 | 0.435 |
| 1 | 20 | 0.609 | 0.33 | 0.889 | 0.610 | 0.515 | 0.635 | 0.357 | 0.913 | 0.635 | 0.571 | |
| 1 | 30 | 0.544 | 0.397 | 0.692 | 0.545 | 0.488 | 0.586 | 0.843 | 0.329 | 0.586 | 0.527 | |
| 1 | 35 | 0.544 | 0.745 | 0.341 | 0.544 | 0.485 | 0.565 | 0.719 | 0.412 | 0.566 | 0.544 | |
| 1 | 40 | 0.472 | 0.621 | 0.322 | 0.472 | 0.414 | 0.544 | 0.786 | 0.303 | 0.545 | 0.488 | |
| SVM with RBF kernel | 1 | 10 | 0.557 | 0.161 | 0.952 | 0.557 | 0.317 | 0.583 | 0.19 | 0.976 | 0.583 | 0.431 |
| 1 | 20 | 0.546 | 0.227 | 0.865 | 0.546 | 0.428 | 0.661 | 0.424 | 0.898 | 0.661 | 0.617 | |
| 1 | 30 | 0.578 | 0.558 | 0.599 | 0.579 | 0.559 | 0.677 | 0.719 | 0.635 | 0.677 | 0.676 | |
| 1 | 35 | 0.551 | 0.555 | 0.548 | 0.552 | 0.534 | 0.589 | 0.69 | 0.487 | 0.589 | 0.580 | |
| 1 | 40 | 0.505 | 0.558 | 0.452 | 0.505 | 0.470 | 0.548 | 0.724 | 0.371 | 0.548 | 0.518 | |
| MLP | 1 | 10 | 0.579 | 0.464 | 0.641 | 0.553 | 0.279 | 0.72 | 0.362 | 0.83 | 0.596 | 0.548 |
| 1 | 15 | 0.528 | 0.464 | 0.652 | 0.558 | 0.280 | 0.716 | 0.633 | 0.382 | 0.508 | 0.492 | |
| 1 | 20 | 0.609 | 1.000 | 0.000 | 0.500 | 0.000 | 0.559 | 1.000 | 0.000 | 0.500 | 0.000 | |
| Naive Bayes | 1 | 10 | 0.619 | 0.324 | 0.886 | 0.606 | 0.528 | 0.667 | 0.257 | 0.91 | 0.584 | 0.484 |
| 1 | 20 | 0.619 | 0.391 | 0.807 | 0.599 | 0.555 | 0.667 | 0.390 | 0.826 | 0.608 | 0.568 | |
| 1 | 30 | 0.619 | 0.455 | 0.724 | 0.590 | 0.565 | 0.667 | 0.490 | 0.746 | 0.618 | 0.605 | |
| 1 | 40 | 0.619 | 0.485 | 0.621 | 0.553 | 0.539 | 0.667 | 0.586 | 0.655 | 0.621 | 0.620 | |
| 1 | 50 | 0.619 | 0.518 | 0.510 | 0.515 | 0.509 | 0.667 | 0.619 | 0.562 | 0.591 | 0.590 | |
| 1 | 60 | 0.619 | 0.615 | 0.448 | 0.532 | 0.519 | - | - | - | - | - | |
| Decision tree | 1 | 10 | 0.553 | 0.197 | 0.916 | 0.557 | 0.412 | 0.526 | 0.133 | 0.921 | 0.527 | 0.35 |
| 1 | 20 | 0.56 | 0.197 | 0.924 | 0.561 | 0.415 | 0.527 | 0.133 | 0.919 | 0.526 | 0.350 | |
| 1 | 30 | 0.563 | 0.230 | 0.898 | 0.564 | 0.434 | 0.553 | 0.200 | 0.897 | 0.549 | 0.424 | |
| 1 | 40 | 0.533 | 0.197 | 0.870 | 0.534 | 0.402 | 0.568 | 0.233 | 0.892 | 0.563 | 0.456 | |
| 1 | 50 | 0.543 | 0.230 | 0.863 | 0.547 | 0.425 | 0.577 | 0.267 | 0.874 | 0.571 | 0.483 | |
| 1 | 100 | 0.572 | 0.364 | 0.773 | 0.568 | 0.477 | 0.578 | 0.324 | 0.805 | 0.565 | 0.511 | |
| 1 | 200 | 0.554 | 0.430 | 0.672 | 0.551 | 0.484 | 0.618 | 0.590 | 0.611 | 0.601 | 0.600 | |
| 1 | 300 | 0.538 | 0.524 | 0.515 | 0.520 | 0.496 | 0.642 | 0.652 | 0.473 | 0.563 | 0.555 | |
| 1 | 350 | 0.516 | 0.691 | 0.296 | 0.493 | 0.292 | - | - | - | - | - | |
| 1 | 400 | 0.516 | 0.691 | 0.296 | 0.493 | 0.292 | - | - | - | - | - | |
| Random forest | 1 | 10 | 0.593 | 0.164 | 0.961 | 0.563 | 0.380 | 0.639 | 0.100 | 0.972 | 0.536 | 0.312 |
| 1 | 20 | 0.579 | 0.164 | 0.961 | 0.563 | 0.380 | 0.617 | 0.100 | 0.964 | 0.532 | 0.310 | |
| 1 | 30 | 0.596 | 0.164 | 0.958 | 0.561 | 0.379 | 0.618 | 0.200 | 0.958 | 0.579 | 0.438 | |
| 1 | 40 | 0.585 | 0.197 | 0.954 | 0.576 | 0.405 | 0.626 | 0.167 | 0.957 | 0.562 | 0.400 | |
| 1 | 50 | 0.572 | 0.197 | 0.952 | 0.575 | 0.405 | 0.624 | 0.200 | 0.949 | 0.575 | 0.436 | |
| 1 | 100 | 0.587 | 0.164 | 0.929 | 0.547 | 0.374 | 0.629 | 0.262 | 0.930 | 0.596 | 0.494 | |
| 1 | 200 | 0.595 | 0.230 | 0.879 | 0.555 | 0.413 | 0.601 | 0.324 | 0.865 | 0.595 | 0.529 | |
| 1 | 300 | 0.568 | 0.364 | 0.787 | 0.576 | 0.496 | 0.597 | 0.390 | 0.759 | 0.575 | 0.544 | |
| 1 | 400 | 0.568 | 0.330 | 0.684 | 0.508 | 0.429 | 0.599 | 0.486 | 0.690 | 0.588 | 0.579 | |
| 1 | 500 | 0.562 | 0.397 | 0.610 | 0.508 | 0.429 | 0.588 | 0.552 | 0.602 | 0.577 | 0.576 | |
| 3-Fold Cross-Validation | 5-Fold Cross-Validation | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | c12 | c21 | AUC | Sens | Spec | B-acc | G-mean | AUC | Sens | Spec | B-acc | G-mean |
| SVM with linear kernel | 1 | 1 | 0.573 | 0.394 | 0.752 | 0.573 | 0.522 | 0.680 | 0.557 | 0.802 | 0.680 | 0.668 |
| 1 | 1.5 | 0.522 | 0.527 | 0.517 | 0.573 | 0.522 | 0.670 | 0.781 | 0.560 | 0.671 | 0.661 | |
| 1 | 2 | 0.459 | 0.685 | 0.232 | 0.459 | 0.279 | 0.545 | 0.876 | 0.214 | 0.545 | 0.433 | |
| 1 | 5 | 0.500 | 1.000 | 0.000 | 0.500 | 0.000 | 0.500 | 1.000 | 0.000 | 0.500 | 0.000 | |
| SVM with polynomial kernel | 1 | 1 | 0.536 | 0.355 | 0.717 | 0.536 | 0.498 | 0.578 | 0.324 | 0.832 | 0.578 | 0.519 |
| 1 | 1.5 | 0.569 | 0.812 | 0.325 | 0.536 | 0.498 | 0.577 | 0.843 | 0.310 | 0.577 | 0.511 | |
| 1 | 2 | 0.541 | 0.812 | 0.271 | 0.542 | 0.447 | 0.520 | 0.814 | 0.226 | 0.520 | 0.429 | |
| 1 | 5 | 0.515 | 0.842 | 0.187 | 0.515 | 0.374 | 0.471 | 0.843 | 0.099 | 0.471 | 0.289 | |
| 1 | 10 | 0.476 | 0.936 | 0.017 | 0.477 | 0.099 | 0.505 | 1.000 | 0.009 | 0.505 | 0.095 | |
| 1 | 20 | 0.500 | 1.000 | 0.000 | 0.500 | 0.000 | 0.500 | 1.000 | 0.000 | 0.500 | 0.000 | |
| 1 | 30 | 0.473 | 0.906 | 0.041 | 0.474 | 0.145 | 0.503 | 1.000 | 0.006 | 0.503 | 0.077 | |
| SVM with RBF kernel | 1 | 1 | 0.596 | 0.427 | 0.763 | 0.596 | 0.550 | 0.644 | 0.452 | 0.835 | 0.644 | 0.614 |
| 1 | 1.5 | 0.519 | 0.458 | 0.580 | 0.596 | 0.550 | 0.638 | 0.657 | 0.619 | 0.638 | 0.638 | |
| 1 | 2 | 0.521 | 0.558 | 0.484 | 0.521 | 0.480 | 0.586 | 0.748 | 0.425 | 0.587 | 0.564 | |
| 1 | 5 | 0.466 | 0.812 | 0.120 | 0.466 | 0.234 | 0.465 | 0.876 | 0.054 | 0.465 | 0.218 | |
| 1 | 10 | 0.500 | 1.000 | 0.000 | 0.500 | 0.000 | 0.500 | 1.000 | 0.000 | 0.500 | 0.000 | |
| MLP | 1 | 1 | 0.634 | 0.397 | 0.680 | 0.538 | 0.475 | 0.659 | 0.557 | 0.764 | 0.661 | 0.652 |
| 1 | 2 | 0.606 | 0.697 | 0.293 | 0.495 | 0.094 | 0.715 | 0.652 | 0.555 | 0.604 | 0.602 | |
| 1 | 5 | 0.598 | 0.652 | 0.574 | 0.613 | 0.591 | 0.695 | 0.781 | 0.396 | 0.589 | 0.556 | |
| 1 | 10 | 0.548 | 0.767 | 0.351 | 0.559 | 0.385 | 0.663 | 0.724 | 0.348 | 0.536 | 0.502 | |
| 1 | 20 | 0.498 | 0.652 | 0.385 | 0.519 | 0.446 | 0.629 | 0.790 | 0.136 | 0.463 | 0.328 | |
| 1 | 30 | 0.533 | 0.632 | 0.416 | 0.524 | 0.500 | 0.570 | 0.752 | 0.180 | 0.466 | 0.368 | |
| Naive Bayes | 1 | 1 | 0.619 | 0.391 | 0.789 | 0.590 | 0.548 | 0.680 | 0.424 | 0.797 | 0.611 | 0.581 |
| 1 | 1.5 | 0.619 | 0.488 | 0.681 | 0.590 | 0.548 | 0.680 | 0.552 | 0.716 | 0.634 | 0.629 | |
| 1 | 2 | 0.619 | 0.548 | 0.588 | 0.569 | 0.560 | 0.680 | 0.619 | 0.607 | 0.613 | 0.613 | |
| 1 | 5 | 0.619 | 0.879 | 0.201 | 0.540 | 0.388 | 0.680 | 0.843 | 0.202 | 0.523 | 0.413 | |
| 1 | 10 | 0.619 | 0.879 | 0.093 | 0.486 | 0.170 | 0.680 | 0.910 | 0.0434 | 0.477 | 0.199 | |
| 1 | 20 | 0.619 | 0.939 | 0.057 | 0.498 | 0.125 | 0.680 | 1.000 | 0.012 | 0.506 | 0.110 | |
| 1 | 30 | 0.619 | 0.939 | 0.039 | 0.489 | 0.103 | 0.680 | 1.000 | 0.006 | 0.503 | 0.078 | |
| Decision tree | 1 | 1 | 0.524 | 0.164 | 0.884 | 0.524 | 0.293 | 0.617 | 0.357 | 0.864 | 0.611 | 0.555 |
| 1 | 2 | 0.540 | 0.197 | 0.874 | 0.536 | 0.389 | 0.602 | 0.324 | 0.871 | 0.598 | 0.531 | |
| 1 | 5 | 0.515 | 0.297 | 0.754 | 0.526 | 0.445 | 0.615 | 0.457 | 0.741 | 0.599 | 0.582 | |
| 1 | 10 | 0.500 | 0.464 | 0.520 | 0.492 | 0.418 | 0.621 | 0.586 | 0.618 | 0.602 | 0.602 | |
| 1 | 20 | 0.509 | 0.555 | 0.430 | 0.493 | 0.460 | 0.613 | 0.648 | 0.448 | 0.548 | 0.539 | |
| 1 | 30 | 0.475 | 0.621 | 0.339 | 0.480 | 0.304 | 0.473 | 0.748 | 0.155 | 0.452 | 0.340 | |
| Random forest | 1 | 1 | 0.595 | 0.164 | 0.921 | 0.542 | 0.372 | 0.640 | 0.195 | 0.931 | 0.563 | 0.426 |
| 1 | 2 | 0.570 | 0.230 | 0.916 | 0.573 | 0.422 | 0.638 | 0.257 | 0.933 | 0.595 | 0.490 | |
| 1 | 5 | 0.599 | 0.230 | 0.879 | 0.555 | 0.431 | 0.638 | 0.257 | 0.895 | 0.576 | 0.480 | |
| 1 | 10 | 0.580 | 0.330 | 0.807 | 0.569 | 0.485 | 0.613 | 0.390 | 0.828 | 0.609 | 0.568 | |
| 1 | 20 | 0.568 | 0.430 | 0.630 | 0.531 | 0.473 | 0.634 | 0.552 | 0.675 | 0.614 | 0.610 | |
| 1 | 30 | 0.572 | 0.558 | 0.505 | 0.531 | 0.500 | 0.601 | 0.619 | 0.503 | 0.561 | 0.558 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Groccia, M.C.; Guido, R.; Conforti, D.; Pelaia, C.; Armentaro, G.; Toscani, A.F.; Miceli, S.; Succurro, E.; Hribal, M.L.; Sciacqua, A. Cost-Sensitive Models to Predict Risk of Cardiovascular Events in Patients with Chronic Heart Failure. Information 2023, 14, 542. https://doi.org/10.3390/info14100542
Groccia MC, Guido R, Conforti D, Pelaia C, Armentaro G, Toscani AF, Miceli S, Succurro E, Hribal ML, Sciacqua A. Cost-Sensitive Models to Predict Risk of Cardiovascular Events in Patients with Chronic Heart Failure. Information. 2023; 14(10):542. https://doi.org/10.3390/info14100542
Chicago/Turabian StyleGroccia, Maria Carmela, Rosita Guido, Domenico Conforti, Corrado Pelaia, Giuseppe Armentaro, Alfredo Francesco Toscani, Sofia Miceli, Elena Succurro, Marta Letizia Hribal, and Angela Sciacqua. 2023. "Cost-Sensitive Models to Predict Risk of Cardiovascular Events in Patients with Chronic Heart Failure" Information 14, no. 10: 542. https://doi.org/10.3390/info14100542
APA StyleGroccia, M. C., Guido, R., Conforti, D., Pelaia, C., Armentaro, G., Toscani, A. F., Miceli, S., Succurro, E., Hribal, M. L., & Sciacqua, A. (2023). Cost-Sensitive Models to Predict Risk of Cardiovascular Events in Patients with Chronic Heart Failure. Information, 14(10), 542. https://doi.org/10.3390/info14100542









