Certificateless Public Key Authenticated Encryption with Keyword Search Achieving Stronger Security

Abstract

Transforming data into ciphertexts and storing them in the cloud database is a secure way to simplify data management. Public key encryption with keyword search (PEKS) is an important cryptographic primitive as it provides the ability to search for the desired files among ciphertexts. As a variant of PEKS, certificateless public key authenticated encryption with keyword search (CLPAEKS) not only simplifies certificate management but also could resist keyword guessing attacks (KGA). In this paper, we analyze the security models of two recent CLPAEKS schemes and find that they ignore the threat that, upon capturing two trapdoors, the adversary could directly compare them and distinguish whether they are generated using the same keyword. To cope with this threat, we propose an improved security model and define the notion of strong trapdoor indistinguishability. We then propose a new CLPAEKS scheme and prove it to be secure under the improved security model based on the intractability of the DBDH problem and the DDH problem in the targeted bilinear group.

1. Introduction

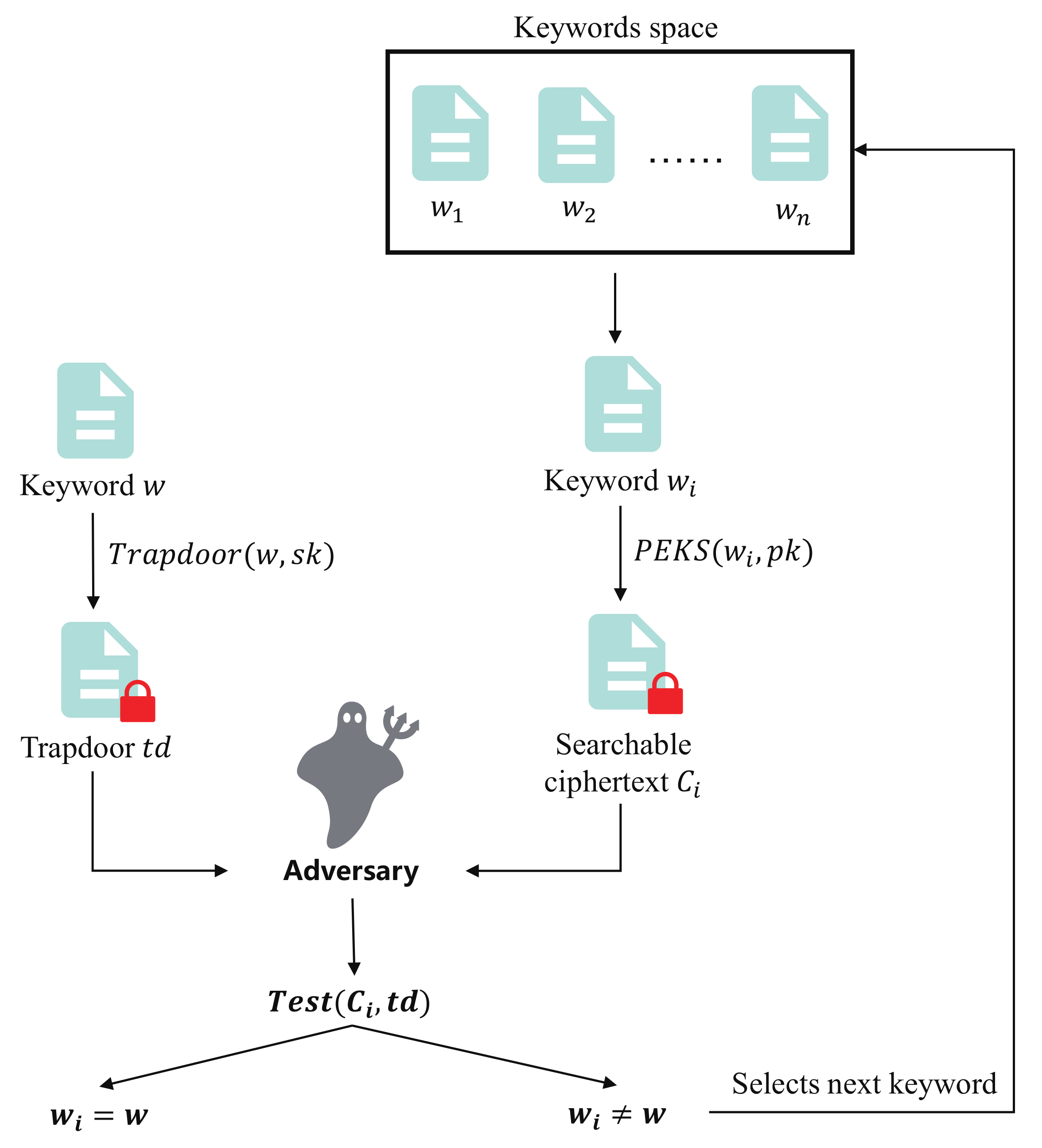
Boneh et al. [1] first proposed the notion of public key encryption with keyword search (PEKS). As shown in Figure 1, the workflow of PEKS includes:

1.

The data sender uses the file’s keyword to generate the searchable ciphertext C and uploads it along with the encrypted file to the cloud server.

2.

The data receiver uses its desired keyword to generate the trapdoor $td$ and sends it to the cloud server.

3.

The cloud server runs an algorithm called $\mathsf{Test}$ to check whether C and $td$ contain the same keyword and returns the corresponding file to the receiver if it does. During the search, the cloud server is unable to know the keyword as well as the content of the file.

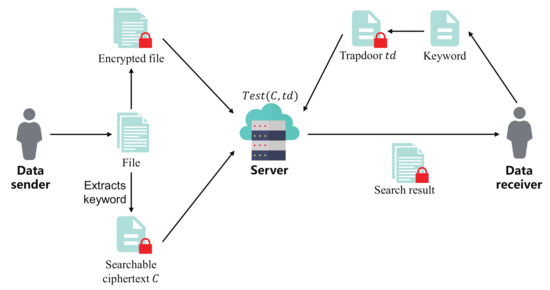
Figure 1. The general framework of PEKS.

Figure 1. The general framework of PEKS.

PEKS could be applied to encrypted instant messaging apps. The client-side archive of chat logs may suffer from mistaken deletion and limited storage space. Therefore, some instant messaging apps (e.g., Google Talk and Yahoo Messenger 11 Beta) support saving chat logs on a server for future retrieval. Encrypting chat logs before uploading is a proactive defense against cyber attacks and data breaches. However, encryption destroys the original features of data and thus invalidates the traditional searching methods. Downloading and decrypting all chat logs before searching seems like a solution, but this process incurs unnecessary transmission overhead. As mentioned earlier, PEKS provides an efficient way for users to search for their desired files among encrypted chat logs.

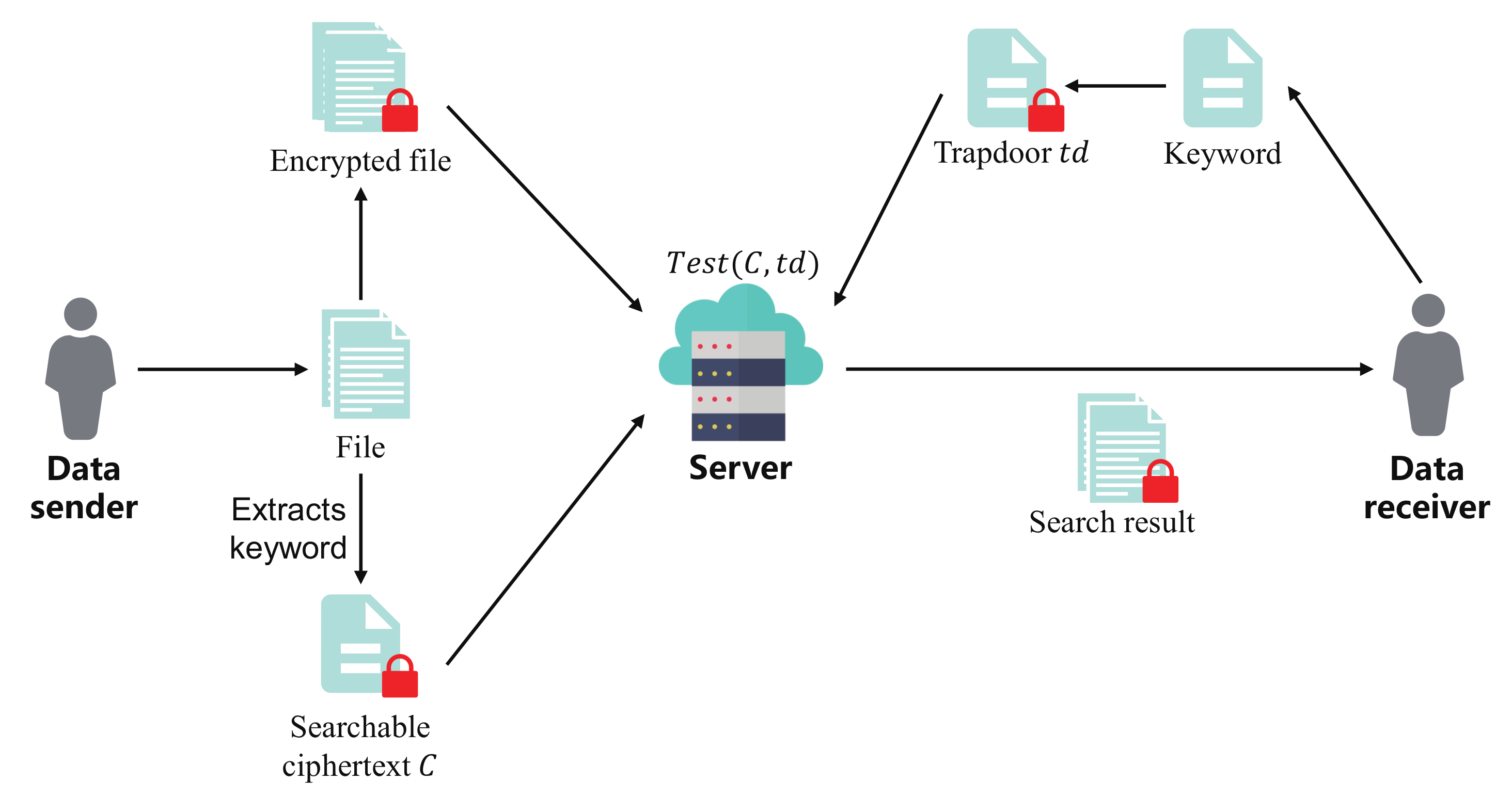
Ideally, the distribution of keywords is assumed to be uniform, and the size of keywords space is assumed to be super-polynomial. However, in practice, the distribution of keywords may be uneven, and keywords space may be much smaller. Therefore, it may be feasible for the adversary to guess the keyword of a file by launching keyword guessing attacks (KGA) [2,3]. As shown in Figure 2, upon capturing the trapdoor, the adversary guesses the keyword w concealed in the trapdoor $td$ by encrypting every possible keyword and running $\mathsf{Test}$ algorithm. There are two types of KGA: the first type is outside KGA, launched by anyone other than the cloud server; the second type is inside KGA, launched by the cloud server. A searchable encryption scheme that could resist KGA should simultaneously satisfy ciphertext indistinguishability and trapdoor indistinguishability [4].

Figure 2. Keyword guessing attacks.

1.1. Related Works

Song et al. [5] proposed a searchable symmetric encryption scheme. However, it suffers from problematic key distribution in symmetric key cryptography. To solve this problem, Boneh et al. [1] proposed public key encryption with keyword search (PEKS). However, the initial PEKS scheme [1] is vulnerable to KGA [2,3]. Rhee et al. [4] first formally defined trapdoor indistinguishability and proved that trapdoor indistinguishability is a necessary condition for a PEKS scheme to be secure against KGA. They also proposed a designated-tester PEKS (dPEKS) scheme that could resist outside KGA. Later, some improved dPEKS schemes [6,7] were proposed, but none of them could resist inside KGA.

To resist both outside and inside KGA, Wang and Tu [8] proposed a PEKS scheme based on a dual-server setting. However, their scheme is still vulnerable inside KGA if two servers collude. Huang and Li [9] proposed the first public key authenticated encryption with keyword search (PAEKS) scheme, which is similar to $signcrpytion$ [10]. In PAEKS, the sender’s secret key is involved in the ciphertext generation. As a result, the cloud server cannot launch inside KGA successfully unless it obtains either the sender’s secret key or the receiver’s secret key. Later, some PAEKS schemes with stronger ciphertext indistinguishability were proposed [11,12]. Pan and Li [13] proposed a PAEKS scheme with stronger trapdoor indistinguishability. However, their scheme cannot provide stronger ciphertext indistinguishability [14].

The aforementioned schemes are based on public key infrastructure and thus suffer from complicated certificate management. To solve this problem, Abdalla et al. [15] proposed the notion of identity-based encryption with keyword search (IBEKS), which integrates search function into identity-based encryption [16]. Li et al. [17] proposed the first IBEKS scheme that could resist both outside and inside KGA.

To solve the key escrow problem in IBEKS, Peng et al. [18] proposed the first searchable encryption scheme based on certificateless public key cryptography [19]. However, Peng et al.’s scheme are vulnerable to both outside and inside KGA. Therefore, some certificates PAEKS (CLPAEKS) schemes [20,21,22] were proposed. Pakniat et al. [23] analyzed the flaws of the security models defined in [20,21,22] and proposed an improved security model. They also presented a new CLPAEKS scheme with provable security in the proposed security model. Shiraly et al. [24] proposed an efficient CLPAEKS scheme that gets rid of the time-consuming Hash-To-Point [25] computation and bilinear pairing [16] computation.

1.2. Motivation and Contribution

We notice that in Pakniat et al.’s work [23] and Shiraly et al.’s work [24], in the games that formally define trapdoor indistinguishability, the adversary cannot query $(I{D}_s^{\diamond },I{D}_r^{\diamond },w_i)$ to trapdoor oracle, in which $I{D}_s^{\diamond }$ is the challenge sender, $I{D}_r^{\diamond }$ is the challenge receiver, and $w_i(i\in \{0,1\})$ is the challenge keyword.

However, in practice, the same keyword may be used for different searches. As a result, the trapdoor corresponding to $(I{D}_s^{\diamond },I{D}_r^{\diamond },w_i)$ may appear repeatedly. For privacy protection, it would be necessary to prevent the adversary from successfully determining whether two trapdoors are generated using the same keyword. Therefore, it is necessary to get rid of the aforementioned limitation when defining trapdoor indistinguishability.

Following are the contributions we make in this paper:

1.

We propose an improved security model, in which the notion of strong trapdoor indistinguishability is defined.

2.

We propose a new CLPAEKS scheme and prove it to be secure under the improved security model based on the intractability of the DBDH problem and the DDH problem in the targeted bilinear group.

2. Preliminaries

Suppose that $\mathcal{A}$ is a probabilistic-polynomial-time (PPT) adversary, ${\mathbb{G}}_1$ and ${\mathbb{G}}_T$ are cyclic groups with the same prime order p.

2.1. Bilinear Pairing

A bilinear pairing $\widehat{e}:{\mathbb{G}}_1\times {\mathbb{G}}_1\to {\mathbb{G}}_T$ has the following features:

• Bilinearity: For any $({\phi }_1,{\phi }_2)\in {\mathbb{G}}_1^2$ and any $({\eta }_1,{\eta }_2)\in {\mathbb{Z}}_p^2$, $\widehat{e}({\phi }_1^{{\eta }_1},{\phi }_2^{{\eta }_2})={\widehat{e}({\phi }_1,{\phi }_2)}^{{\eta }_1·{\eta }_2}$.
• Non-degeneracy: Suppose that $\phi$ is a generator of ${\mathbb{G}}_1$, $\widehat{e}(\phi ,\phi )\ne 1$.
• Computability: For any $({\phi }_1,{\phi }_2)\in {\mathbb{G}}_1^2$, $\widehat{e}({\phi }_1,{\phi }_2)$ can be computed in polynomial time.

2.2. Decisional Diffie–Hellman (DDH) Assumption in ${\mathbb{G}}_T$

Given $({\phi }_t,{\phi }_t^{{\eta }_1},{\phi }_t^{{\eta }_2},Z)\in {\mathbb{G}}_T^4$, in which ${\phi }_t$ is a generator of ${\mathbb{G}}_T$, $({\eta }_1,{\eta }_2)\in {\mathbb{Z}}_p^2$. $\mathcal{A}$’s aim is to determine whether $Z={\phi }_t^{{\eta }_1·{\eta }_2}$ or $Z={\phi }_t^r$, in which r is randomly selected from ${\mathbb{Z}}_p$. The DDH assumption in ${\mathbb{G}}_T$ holds if $\mathcal{A}$’s advantage

$${\mathrm{Adv}}_{\mathcal{A}}^{DDH}=|\mathrm{Pr}[\mathcal{A}({\phi }_t,{\phi }_t^{{\eta }_1},{\phi }_t^{{\eta }_2},{\phi }_t^{{\eta }_1·{\eta }_2})=1]-\mathrm{Pr}[\mathcal{A}({\phi }_t,{\phi }_t^{{\eta }_1},{\phi }_t^{{\eta }_2},{\phi }_t^r)=1]|$$

is negligible.

2.3. Decisional Bilinear Diffie–Hellman (DBDH) Assumption

Given $(\phi ,{\phi }^{{\eta }_1},{\phi }^{{\eta }_2},{\phi }^{{\eta }_3})\in {\mathbb{G}}_1^4$ and $Z\in {\mathbb{G}}_T$, in which $({\eta }_1,{\eta }_2,{\eta }_3)\in {\mathbb{Z}}_p^3$. $\mathcal{A}$’s aim is to determine whether $Z=\widehat{e}{(\phi ,\phi )}^{{\eta }_1·{\eta }_2·{\eta }_3}$ or $Z=\widehat{e}{(\phi ,\phi )}^r$, in which r is randomly selected from ${\mathbb{Z}}_p$. The DBDH assumption holds if $\mathcal{A}$’s advantage

$${\mathrm{Adv}}_{\mathcal{A}}^{DBDH}=|\mathrm{Pr}[\mathcal{A}(\phi ,{\phi }^{{\eta }_1},{\phi }^{{\eta }_2},{\phi }^{{\eta }_3},\widehat{e}{(\phi ,\phi )}^{{\eta }_1·{\eta }_2·{\eta }_3})=1]$$

$$-\mathrm{Pr}[\mathcal{A}(\phi ,{\phi }^{{\eta }_1},{\phi }^{{\eta }_2},{\phi }^{{\eta }_3},\widehat{e}{(\phi ,\phi )}^r)=1]|$$

is negligible.

3. Definition of CLPAEKS

3.1. System Model

The following three types of entities are involved in our CLPAEKS scheme.

• Key generation center (KGC): KGC generates the master secret key, the public parameters, and every user’s partial secret key.
• Users: Include the sender and the receiver, which have been introduced in Section 1. Every user randomly selects a secret value and then generates its secret key using its partial secret key and the secret value.
• Cloud Server: It is a semi-trusted party managing the encrypted cloud database and responding to search requests.

3.2. Algorithms

The frequently used symbols are defined in Table 1. Our CLPAEKS scheme consists of the following algorithms.

Table 1. Notations.

Symbols	Meaning
$\lambda$	Security parameter
$pp$	Public parameters
$msk$	Master secret key
$I{D}_i$	A user’s identity
$ps{k}_i,x_i,s{k}_i,p{k}_i$	$I{D}_i$’s partial secret key, secret value, secret key, and public key, respectively
$I{D}_s,p{k}_s,s{k}_s$	A sender’s identity, public key, and secret key, respectively
$I{D}_r,p{k}_r,s{k}_r$	A receiver’s identity, public key, and secret key, respectively
C	Searchable ciphertext
$td$	Trapdoor

1.

$\mathsf{Setup}\left(\lambda \right)$: Run by KGC.

• Input: $\lambda$.
• Output: $msk$ and $pp$.

2.

$\mathsf{Extract}\mathsf{Partial}\mathsf{Secret}\mathsf{Key}(pp,msk,I{D}_i)$: Run by KGC.

• Input: $pp$, $msk$, and $I{D}_i$.
• Output: $ps{k}_i$.

3.

$\mathsf{Extract}\mathsf{Secret}\mathsf{Value}(pp,I{D}_i)$: Run by the user $I{D}_i$.

• Input: $pp$, $I{D}_i$.
• Output: $x_i$.

4.

$\mathsf{Extract}\mathsf{Secret}\mathsf{Key}(pp,ps{k}_i,x_i)$: Run by the user $I{D}_i$.

• Input: $pp$, $ps{k}_i$, $x_i$.
• Output: $s{k}_i$.

5.

$\mathsf{Extract}\mathsf{Public}\mathsf{Key}(pp,x_i)$: Run by the user $I{D}_i$.

• Input: $pp$, $x_i$.
• Output: $p{k}_i$.

6.

$\mathsf{CLPAEKS}(pp,I{D}_s,s{k}_s,I{D}_r,p{k}_r,w)$: Run by the sender $I{D}_s$.

• Input: $pp$, $I{D}_s$, $s{k}_s$, $I{D}_r$, $p{k}_r$, and a keyword w.
• Output: C.

7.

$\mathsf{Trapdoor}(pp,I{D}_s,p{k}_s,I{D}_r,s{k}_r,w)$: Run by the receiver $I{D}_r$.

• Input: $pp$, $I{D}_s$, $p{k}_s$, $I{D}_r$, $s{k}_r$, w.
• Output: $td$.

8.

$\mathsf{Test}(C,td)$: Run by the cloud server.

• Input: $C=\mathsf{CLPAEKS}(pp,I{D}_s,s{k}_s,I{D}_r,p{k}_r,w)$ and $td=\mathsf{Trapdoor}(pp,I{D}_s,p{k}_s,I{D}_r,s{k}_r,w^{\prime })$.
• Output: 1 will be output if $w=w^{\prime }$, and 0 otherwise.

3.3. Security Model

The following two types of PPT adversaries are considered:

• Type-1 adversary: Denote this type of adversary with ${\mathcal{A}}_1$. ${\mathcal{A}}_1$ can replace any user’s public key but cannot get the master secret key.
• Type-2 adversary: Denote this type of adversary with ${\mathcal{A}}_2$. ${\mathcal{A}}_2$ can get the master secret key but cannot replace any user’s public key.

We consider two security properties, ciphertext indistinguishability and trapdoor indistinguishability. Since there are two types of adversaries in certificateless cryptosystems, we define the semantic security of CLPAEKS via four games. In Game ${\mathcal{G}}_1$ and Game ${\mathcal{G}}_2$, we formally define ciphertext indistinguishability in the same way as [23,24]. In Game ${\mathcal{G}}_3$ and Game ${\mathcal{G}}_4$, we formally define a stronger version of trapdoor indistinguishability. Different from [23,24], the adversary against trapdoor indistinguishability could freely access the trapdoor oracle in the games, which makes our definition of trapdoor indistinguishability stronger.

3.3.1. Game ${\mathcal{G}}_1$

1.

Setup: The challenger $\mathcal{C}$ sends $pp$ to ${\mathcal{A}}_1$.

2.

Phase 1: ${\mathcal{A}}_1$ is allowed to access the following oracles.

• ${\mathcal{O}}_{pk}\left(I{D}_i\right)$: Given $I{D}_i$, $\mathcal{C}$ returns $p{k}_i$.
• ${\mathcal{O}}_{psk}\left(I{D}_i\right)$: Given $I{D}_i$, $\mathcal{C}$ returns $ps{k}_i$.
• ${\mathcal{O}}_{sk}\left(I{D}_i\right)$: Given $I{D}_i$, $\mathcal{C}$ returns $s{k}_i$. $I{D}_i$ cannot occur in ${\mathcal{O}}_{sk}$ if $I{D}_i$’s public key has been replaced.
• ${\mathcal{O}}_{rpk}(I{D}_i,p{k}_i^{\prime })$: Given $I{D}_i$ and a new public key $p{k}_i^{\prime }$, $\mathcal{C}$ replaces $p{k}_i$ with $p{k}_i^{\prime }$.
• ${\mathcal{O}}_{CLPAEKS}(I{D}_s,I{D}_r,w)$: Given $I{D}_s$, $I{D}_r$ and w, $\mathcal{C}$ returns $C\leftarrow \mathsf{CLPAEKS}(pp,I{D}_s,s{k}_s,I{D}_r,p{k}_r,w)$.
• ${\mathcal{O}}_T(I{D}_s,I{D}_r,w)$: Given $I{D}_s$, $I{D}_r$ and w, $\mathcal{C}$ returns $td\leftarrow \mathsf{Trapdoor}(pp,I{D}_s,p{k}_s,I{D}_r,s{k}_r$, $w)$.

3.

Challenge: ${\mathcal{A}}_1$ selects $I{D}_{s^{*}}$, $I{D}_{r^{*}}$, and two keywords ($w_0^{*}$, $w_1^{*}$) for the challenge, with the following restrictions: (1) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{psk}$; (2) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{sk}$; (3) Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) has been submitted to ${\mathcal{O}}_T$. $\mathcal{C}$ randomly selects $b\in \left\{0,1\right\}$ and sends $C^{*}\leftarrow \mathsf{CLPAEKS}(pp,I{D}_{s^{*}},s{k}_{s^{*}},I{D}_{r^{*}},p{k}_{r^{*}},w_b^{*})$ to ${\mathcal{A}}_1$.

4.

Phase 2: ${\mathcal{A}}_1$ is allowed to access the oracles as in Phase 1, with the following restrictions:

• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{psk}$.
• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{sk}$.
• Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) can be submitted to ${\mathcal{O}}_T$.

5.

Guess: ${\mathcal{A}}_1$ submits $b^{\prime }\in \{0,1\}$. If $b=b^{\prime }$, ${\mathcal{A}}_1$ wins the game. ${\mathcal{A}}_1$’s advantage is defined as

$${\mathrm{Adv}}_{{\mathcal{A}}_1}^{CT-IND-CKA}=\left|Pr[b=b^{\prime }]-\frac{1}{2}\right|.$$

Definition 1.

Our scheme satisfies ciphertext indistinguishability under adaptive chosen-keyword attacks (CT-IND-CKA) against Type-1 adversary if ${\mathrm{Adv}}_{{\mathcal{A}}_1}^{CT-IND-CKA}$ is negligible.

3.3.2. Game ${\mathcal{G}}_2$

1.

Setup: The challenger $\mathcal{C}$ sends $pp$ and $msk$ to ${\mathcal{A}}_2$.

2.

Phase 1: ${\mathcal{A}}_2$ can is allowed to access the following oracles.

• ${\mathcal{O}}_{pk}\left(I{D}_i\right)$: Same as ${\mathcal{O}}_{pk}$ in Game ${\mathcal{G}}_1$.
• ${\mathcal{O}}_{psk}\left(I{D}_i\right)$: Same as ${\mathcal{O}}_{psk}$ in Game ${\mathcal{G}}_1$.
• ${\mathcal{O}}_{sk}\left(I{D}_i\right)$: Given $I{D}_i$, $\mathcal{C}$ returns $s{k}_i$.
• ${\mathcal{O}}_{CLPAEKS}(I{D}_s,I{D}_r,w)$: Same as ${\mathcal{O}}_{CLPAEKS}$ in Game ${\mathcal{G}}_1$.
• ${\mathcal{O}}_T(I{D}_s,I{D}_r,w)$: Same as ${\mathcal{O}}_T$ in Game ${\mathcal{G}}_1$.

3.

Challenge: ${\mathcal{A}}_2$ selects $I{D}_{s^{*}}$, $I{D}_{r^{*}}$, and two keywords ($w_0^{*}$, $w_1^{*}$) for challenge, with the following restrictions: (1) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{sk}$; (2) Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) has been submitted to ${\mathcal{O}}_T$. $\mathcal{C}$ randomly selects $b\in \left\{0,1\right\}$ and sends $C^{*}\leftarrow \mathsf{CLPAEKS}(pp,I{D}_{s^{*}},s{k}_{s^{*}},I{D}_{r^{*}},p{k}_{r^{*}},w_b^{*})$ to ${\mathcal{A}}_2$.

4.

Phase 2: ${\mathcal{A}}_2$ is allowed to access the oracles as in Phase 1, with the following restrictions:

• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{sk}$.
• Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) can be submitted to ${\mathcal{O}}_T$.

5.

Guess: ${\mathcal{A}}_2$ submits $b^{\prime }\in \{0,1\}$. If $b=b^{\prime }$, ${\mathcal{A}}_2$ wins the game. ${\mathcal{A}}_2$’s advantage is defined as

$${\mathrm{Adv}}_{{\mathcal{A}}_2}^{CT-IND-CKA}=\left|Pr[b=b^{\prime }]-\frac{1}{2}\right|.$$

Definition 2.

Our scheme satisfies CT-IND-CKA against Type-2 adversary if ${\mathrm{Adv}}_{{\mathcal{A}}_2}^{CT-IND-CKA}$ is negligible.

3.3.3. Game ${\mathcal{G}}_3$

1.

Setup: The challenger $\mathcal{C}$ sends $pp$ to ${\mathcal{A}}_1$.

2.

Phase 1: Same as Phase 1 in Game ${\mathcal{G}}_1$.

3.

Challenge: ${\mathcal{A}}_1$ selects $I{D}_{s^{*}}$, $I{D}_{r^{*}}$, and two keywords ($w_0^{*}$, $w_1^{*}$) for the challenge, with the following restrictions: (1) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{psk}$; (2) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{sk}$; (3) Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) has been submitted to ${\mathcal{O}}_{CLPAEKS}$. $\mathcal{C}$ randomly selects $b\in \left\{0,1\right\}$ and sends $t{d}^{*}\leftarrow \mathsf{Trapdoor}(pp,I{D}_{s^{*}},p{k}_{s^{*}},I{D}_{r^{*}},s{k}_{r^{*}},w_b^{*})$ to ${\mathcal{A}}_1$.

4.

Phase 2: ${\mathcal{A}}_1$ is allowed to access the oracles as in Phase 1, with the following restrictions:

• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{psk}$.
• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{sk}$.
• Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) can be submitted to ${\mathcal{O}}_{CLPAEKS}$.

5.

Guess: ${\mathcal{A}}_1$ submits $b^{\prime }\in \{0,1\}$. If $b=b^{\prime }$, ${\mathcal{A}}_1$ wins the game. ${\mathcal{A}}_1$’s advantage is defined as

$${\mathrm{Adv}}_{{\mathcal{A}}_1}^{S-TD-IND-CKA}=\left|Pr[b=b^{{}^{\prime }}]-\frac{1}{2}\right|.$$

Definition 3.

Our scheme satisfies strong trapdoor indistinguishability under adaptive chosen-keyword attacks (S-TD-IND-CKA) against Type-1 adversary if ${\mathrm{Adv}}_{{\mathcal{A}}_1}^{S-TD-IND-CKA}$ is negligible.

3.3.4. Game ${\mathcal{G}}_4$

1.

Setup: The challenger $\mathcal{C}$ sends $pp$ and $msk$ to ${\mathcal{A}}_2$.

2.

Phase 1: Same as Phase 1 in Game ${\mathcal{G}}_2$.

3.

Challenge: ${\mathcal{A}}_2$ selects $I{D}_{s^{*}}$, $I{D}_{r^{*}}$, and two keywords ($w_0^{*}$, $w_1^{*}$) for the challenge, with the following restrictions: (1) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{sk}$; (2) Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) has been submitted to ${\mathcal{O}}_{CLPAEKS}$. $\mathcal{C}$ randomly selects $b\in \left\{0,1\right\}$ and sends $t{d}^{*}\leftarrow \mathsf{Trapdoor}(pp,I{D}_{s^{*}},p{k}_{s^{*}},I{D}_{r^{*}},s{k}_{r^{*}},w_b^{*})$ to ${\mathcal{A}}_2$.

4.

Phase 2: ${\mathcal{A}}_2$ is allowed to access the oracles as in Phase 1, with the following restrictions:

• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{sk}$.
• Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) can be submitted to ${\mathcal{O}}_{CLPAEKS}$.

5.

Guess: ${\mathcal{A}}_2$ submits $b^{\prime }\in \{0,1\}$. If $b=b^{\prime }$, ${\mathcal{A}}_2$ wins the game. ${\mathcal{A}}_2$’s advantage is defined as

$${\mathrm{Adv}}_{{\mathcal{A}}_2}^{S-TD-IND-CKA}=\left|Pr[b=b^{\prime }]-\frac{1}{2}\right|.$$

Definition 4.

Our scheme satisfies S-TD-IND-CKA against Type-2 adversary if ${\mathrm{Adv}}_{{\mathcal{A}}_2}^{S-TD-IND-CKA}$ is negligible.

4. The Proposed CLPAEKS Scheme

The frequently used symbols have been defined in Table 1. Following are the details of our CLPAEKS scheme.

1.

$\mathsf{Setup}\left(\lambda \right)$: Run by KGC.

• Input: Security parameter $\lambda$.
• Select two cyclic groups ${\mathbb{G}}_1$ and ${\mathbb{G}}_T$ with the same prime order $p>2^{\lambda }$ and a bilinear pairing $\widehat{e}:{\mathbb{G}}_1\times {\mathbb{G}}_1\to {\mathbb{G}}_T$. Randomly select two generators $g\in {\mathbb{G}}_1$ and $g_t\in {\mathbb{G}}_T$.
• Define 3 collision-resistant hash functions:

  −

  $H_1:{\{0,1\}}^{*}\to {\mathbb{G}}_1$. It takes the user’s identity as input.

  −

  $H_2:{\{0,1\}}^{*}\to {\mathbb{G}}_1$. It takes the keyword as input.

  −

  $H_3:{\{0,1\}}^{*}\times {\{0,1\}}^{*}\times {\mathbb{G}}_T\to {\mathbb{Z}}_p$.

• Randomly select $y\in {\mathbb{Z}}_p$. Set master secret key $msk=y$ and master public key $mpk=g^y$.
• Output: $pp=\{p,{\mathbb{G}}_1,{\mathbb{G}}_T,\widehat{e},g,g_t,H_1,H_2,H_3,mpk\}$.

2.

$\mathsf{Extract}\mathsf{Partial}\mathsf{Secret}\mathsf{Key}(pp,msk,I{D}_i)$: Run by KGC.

• Input: $pp$, $msk$, and a user’s identity $I{D}_i$.
• Output: $I{D}_i$’s partial secret key $ps{k}_i=H_1{\left(I{D}_i\right)}^y$.

3.

$\mathsf{Extract}\mathsf{Secret}\mathsf{Value}(pp,I{D}_i)$: Run by the user $I{D}_i$.

• Input: $pp$, $I{D}_i$.
• Output: $I{D}_i$’s secret value $x_i$, which is randomly selected from ${\mathbb{Z}}_p$.

4.

$\mathsf{Extract}\mathsf{Secret}\mathsf{Key}(pp,ps{k}_i,x_i)$: Run by the user $I{D}_i$.

• Input: $pp$, $ps{k}_i$, $x_i$.
• Output: $I{D}_i$’s secret key $s{k}_i=(s{k}_{i,1},s{k}_{i,2})=(x_i,ps{k}_i)$.

5.

$\mathsf{Extract}\mathsf{Public}\mathsf{Key}(pp,x_i)$: Run by the user $I{D}_i$.

• Input: $pp$, $x_i$.
• Output: $I{D}_i$’s public key $p{k}_i=g_t^{x_i}$.

6.

$\mathsf{CLPAEKS}(pp,I{D}_s,s{k}_s,I{D}_r,p{k}_r,w)$: Run by the sender $I{D}_s$.

• Input: $pp$, $I{D}_s$, $s{k}_s=(s{k}_{s,1},s{k}_{s,2})=(x_s,H_1{\left(I{D}_s\right)}^y)$, $I{D}_r$, $p{k}_r=g_t^{x_r}$, and a keyword w.
• Randomly select $\alpha \in {\mathbb{Z}}_p$.
• Compute $C=(c_1,c_2,c_3)$:

  $$c_1=\widehat{e}{(g,H_2\left(w\right))}^{\alpha ·k},c_2=g^{\alpha },c_3=g^{\frac{\alpha }{k}},$$

  in which

  $$\begin{array}{cc}\hfill k& =H_3(I{D}_s\Vert I{D}_r\Vert p{k}_r^{s{k}_{s,1}}·\widehat{e}(s{k}_{s,2},H_1\left(I{D}_r\right)))\hfill \\ \hfill & =H_3(I{D}_s\Vert I{D}_r\Vert g_t^{x_s·x_r}·\widehat{e}{(H_1\left(I{D}_s\right),H_1\left(I{D}_r\right))}^y).\hfill \end{array}$$
• Output: $C=(c_1,c_2,c_3)$.

7.

$\mathsf{Trapdoor}(pp,I{D}_s,p{k}_s,I{D}_r,s{k}_r,w)$: Run by the receiver $I{D}_r$.

• Input: $pp$, $I{D}_s$, $p{k}_s=g_t^{x_s}$, $I{D}_r$, $s{k}_r=(s{k}_{r,1},s{k}_{r,2})=(x_r,H_1{\left(I{D}_r\right)}^y)$, and a keyword w.
• Randomly select $(\beta ,\gamma )\in {\mathbb{Z}}_p^2$.
• Compute $td=(t{d}_1,t{d}_2,t{d}_3)$:

  $$t{d}_1=H_2{\left(w\right)}^{\beta +\frac{\gamma }{k}},t{d}_2=H_2{\left(w\right)}^{\frac{k^3}{\beta }-\gamma },t{d}_3=\frac{\beta }{k}+\frac{k}{\beta },$$

  in which

  $$\begin{array}{cc}\hfill k& =H_3(I{D}_s\Vert I{D}_r\Vert p{k}_s^{s{k}_{r,1}}·\widehat{e}(s{k}_{r,2},H_1\left(I{D}_s\right)))\hfill \\ \hfill & =H_3(I{D}_s\Vert I{D}_r\Vert g_t^{x_s·x_r}·\widehat{e}{(H_1\left(I{D}_s\right),H_1\left(I{D}_r\right))}^y).\hfill \end{array}$$
• Output: $td=(t{d}_1,t{d}_2,t{d}_3)$.

8.

$\mathsf{Test}(C,td)$: Run by the cloud server.

• Input: $C=(c_1,c_2,c_3)$ and $td=(t{d}_1,t{d}_2,t{d}_3)$.
• Output: Check whether

  $$c_1^{t{d}_3}=\widehat{e}(c_2,t{d}_1)·\widehat{e}(c_3,t{d}_2)$$

  holds, if it holds then output 1, and 0 otherwise.

5. Security Analysis

5.1. CT-IND-CKA against Type-1 Adversary

Theorem 1.

Our scheme satisfies CT-IND-CKA against Type-1 adversary in the random oracle model if the DBDH assumption holds.

Proof. 

Suppose that ${\mathrm{Adv}}_{{\mathcal{A}}_1}^{CT-IND-CKA}=ϵ$. Given a DBDH instance $({\mathbb{G}}_1,{\mathbb{G}}_T,\widehat{e},g,g^{{\eta }_1},g^{{\eta }_2},g^{{\eta }_3},Z)$. Denoted by $\zeta =0$ that $Z={\widehat{e}(g,g)}^{{\eta }_1·{\eta }_2·{\eta }_3}$, and by $\zeta =1$ that Z is random. In the following, we construct a simulator $\mathcal{B}$ that runs ${\mathcal{A}}_1$ as a subroutine to correctly guess the value of $\zeta$.

1.

Setup: $\mathcal{B}$ sets $mpk=g^{{\eta }_1}$, implying that $msk={\eta }_1$, in which ${\eta }_1$ is unknown to $\mathcal{B}$. Then sends $pp$ to ${\mathcal{A}}_1$.

2.

Phase 1: ${\mathcal{A}}_1$ is allowed to access the following oracles.

• ${\mathcal{O}}_{H_1}\left(I{D}_i\right)$: Suppose that there are $q_{H_1}$ distinct queries to ${\mathcal{O}}_{H_1}$. $\mathcal{B}$ randomly selects $(i^{*},j^{*})\in \{1,···,q_{H_1}\}$ as its guess of the identities selected by ${\mathcal{A}}_1$ for challenge. For $I{D}_i$:

  −

  If $i=i^{*}$, $\mathcal{B}$ adds $\{I{D}_{i^{*}},-,g^{{\eta }_2}\}$ to list $L_{H_1}$ and returns $g^{{\eta }_2}$ to ${\mathcal{A}}_1$.

  −

  If $i=j^{*}$, $\mathcal{B}$ adds $\{I{D}_{j^{*}},-,g^{{\eta }_3}\}$ to list $L_{H_1}$ and returns $g^{{\eta }_3}$ to ${\mathcal{A}}_1$.

  −

  Otherwise, $\mathcal{B}$ randomly selects $h_{1,i}\in {\mathbb{Z}}_p$, adds $\left\{I{D}_i,h_{1,i},g^{h_{1,i}}\right\}$ to list $L_{H_1}$, and returns $g^{h_{1,i}}$ to ${\mathcal{A}}_1$.

  If the repeated queries are submitted, the answer that already exists in $L_{H_1}$ will be returned.
• ${\mathcal{O}}_{H_2}$: Given $w\in {\left\{0,1\right\}}^{*}$, $\mathcal{B}$ randomly selects $h_2\in {\mathbb{G}}_1$, adds $\left\{w,h_2\right\}$ to list $L_{H_2}$, and returns $h_2$. If the repeated queries are submitted, the answer that already exists in $L_{H_2}$ will be returned.
• ${\mathcal{O}}_{H_3}$: Given $(u_1,u_2,u_3)\in {\{0,1\}}^{*}\times {\{0,1\}}^{*}\times {\mathbb{G}}_T$. $\mathcal{B}$ randomly selects $h_3\in {\mathbb{Z}}_p$, adds $\left\{u_1,u_2,u_3,h_3\right\}$ to list $L_{H_3}$, and returns $h_3$. If the repeated queries are submitted, the answer that already exists in $L_{H_3}$ will be returned.
• ${\mathcal{O}}_{pk}\left(I{D}_i\right)$: $\mathcal{B}$ randomly selects $x_i\in {\mathbb{Z}}_p$, then:

  −

  If $i\ne i^{*}\wedge i\ne j^{*}$, $\mathcal{B}$ calls ${\mathcal{O}}_{H_1}\left(I{D}_i\right)$, retrieves $\left\{I{D}_i,h_{1,i},g^{h_{1,i}}\right\}$ from $L_{H_1}$, sets

  $$p{k}_i=g_t^{x_i},ps{k}_i=g^{{\eta }_1·h_{1,i}},$$

  adds $\{I{D}_i,p{k}_i,ps{k}_i,x_i\}$ to list $L_{key}$, and returns $p{k}_i$.

  −

  Otherwise, $\mathcal{B}$ calls ${\mathcal{O}}_{H_1\left(I{D}_i\right)}$ and sets

  $$p{k}_i=g_t^{x_i},$$

  adds $\{I{D}_i,p{k}_i,-,x_i\}$ to list $L_{key}$, and returns $p{k}_i$.

  If the repeated queries are submitted, the answer that already exists in $L_{key}$ will be returned.
• ${\mathcal{O}}_{psk}\left(I{D}_i\right)$:

  −

  If $i=i^{*}\vee i=j^{*}$, $\mathcal{B}$ aborts.

  −

  Otherwise, $\mathcal{B}$ calls ${\mathcal{O}}_{pk}\left(I{D}_i\right)$, retrieves $\{I{D}_i,p{k}_i,ps{k}_i,x_i\}$ from $L_{key}$, and returns $ps{k}_i$.

• ${\mathcal{O}}_{sk}\left(I{D}_i\right)$:

  −

  If $i=i^{*}\vee i=j^{*}$, $\mathcal{B}$ aborts.

  −

  Otherwise, $\mathcal{B}$ calls ${\mathcal{O}}_{pk}\left(I{D}_i\right)$, retrieves $\{I{D}_i,p{k}_i,ps{k}_i,x_i\}$ from $L_{key}$, and returns $s{k}_i=(ps{k}_i,x_i)$.

  $I{D}_i$ cannot occur in ${\mathcal{O}}_{sk}$ if $I{D}_i$’s public key has been replaced.
• ${\mathcal{O}}_{rpk}(I{D}_i,p{k}_i^{\prime })$: $\mathcal{B}$ calls ${\mathcal{O}}_{pk}\left(I{D}_i\right)$ and replaces $\{I{D}_i,p{k}_i,ps{k}_i,x_i\}$ with $\{I{D}_i,p{k}_i^{\prime },ps{k}_i,-\}$.
• ${\mathcal{O}}_{CLPAEKS}(I{D}_s,I{D}_r,w)$: $\mathcal{B}$ randomly selects $\alpha \in {\mathbb{Z}}_p$ and returns $C=(c_1,c_2,c_3):$

  $$c_1=\widehat{e}{(g,H_2\left(w\right))}^{\alpha ·k},c_2=g^{\alpha },c_3=g^{\frac{\alpha }{k}},$$

  in which k is different based on the following cases.

  −

  If $s=i^{*}\wedge r=j^{*}$, $k=H_3(I{D}_{i^{*}}\Vert I{D}_{j^{*}}\Vert g_t^{x_{i^{*}}·x_{j^{*}}}·Z)$.

  −

  If $s=j^{*}\wedge r=i^{*}$, $k=H_3(I{D}_{j^{*}}\Vert I{D}_{i^{*}}\Vert g_t^{x_{i^{*}}·x_{j^{*}}}·Z)$.

  −

  Otherwise, it means that $(s\ne i^{*}\wedge s\ne j^{*})\vee (r\ne i^{*}\wedge r\ne j^{*})$.

  ∗ 

  If $s\ne i^{*}\wedge s\ne j^{*}$, $\mathcal{B}$ retrieves $\left\{I{D}_s,h_{1,s},g^{h_{1,s}}\right\}$ from $L_{H_1}$ and computes $k=H_3(I{D}_s\Vert I{D}_r\Vert g_t^{x_s·x_r}·\widehat{e}{(g^{{\eta }_1},H_1\left(I{D}_r\right))}^{h_{1,s}})$.

  ∗ 

  Otherwise, $\mathcal{B}$ retrieves $\left\{I{D}_r,h_{1,r},g^{h_{1,r}}\right\}$ from $L_{H_1}$ and computes $k=H_3(I{D}_s\Vert I{D}_r\Vert g_t^{x_s·x_r}·\widehat{e}{(g^{{\eta }_1},H_1\left(I{D}_s\right))}^{h_{1,r}})$.

• ${\mathcal{O}}_T(I{D}_s,I{D}_r,w)$: $\mathcal{B}$ randomly selects $(\beta ,\gamma )\in {\mathbb{Z}}_p^2$ and returns $td=(t{d}_1,t{d}_2,t{d}_3):$

  $$t{d}_1=H_2{\left(w\right)}^{\beta +\frac{\gamma }{k}},t{d}_2=H_2{\left(w\right)}^{\frac{k^3}{\beta }-\gamma },t{d}_3=\frac{\beta }{k}+\frac{k}{\beta },$$

  in which k is different based on the following cases.

  −

  If $s=i^{*}\wedge r=j^{*}$, $k=H_3(I{D}_{i^{*}}\Vert I{D}_{j^{*}}\Vert g_t^{x_{i^{*}}·x_{j^{*}}}·Z)$.

  −

  If $s=j^{*}\wedge r=i^{*}$, $k=H_3(I{D}_{j^{*}}\Vert I{D}_{i^{*}}\Vert g_t^{x_{i^{*}}·x_{j^{*}}}·Z)$.

  −

  Otherwise, it means that $(s\ne i^{*}\wedge s\ne j^{*})\vee (r\ne i^{*}\wedge r\ne j^{*})$.

  ∗ 

  If $s\ne i^{*}\wedge s\ne j^{*}$, $\mathcal{B}$ retrieves $\left\{I{D}_s,h_{1,s},g^{h_{1,s}}\right\}$ from $L_{H_1}$ and computes $k=H_3(I{D}_s\Vert I{D}_r\Vert g_t^{x_s·x_r}·\widehat{e}{(g^{{\eta }_1},H_1\left(I{D}_r\right))}^{h_{1,s}})$.

  ∗ 

  Otherwise, $\mathcal{B}$ retrieves $\left\{I{D}_r,h_{1,r},g^{h_{1,r}}\right\}$ from $L_{H_1}$ and computes $k=H_3(I{D}_s\Vert I{D}_r\Vert g_t^{x_s·x_r}·\widehat{e}{(g^{{\eta }_1},H_1\left(I{D}_s\right))}^{h_{1,r}})$.

3.

Challenge: ${\mathcal{A}}_1$ selects $I{D}_{s^{*}}$, $I{D}_{r^{*}}$, and two keywords ($w_0^{*}$, $w_1^{*}$) for the challenge, with the following restrictions: (1) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{psk}$; (2) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{sk}$; (3) Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) has been submitted to ${\mathcal{O}}_T$. If $\neg (s^{*}=i^{*}\wedge r^{*}=j^{*})\wedge \neg (s^{*}=j^{*}\wedge r^{*}=i^{*})$, $\mathcal{B}$ aborts and randomly returns ${\zeta }^{\prime }\in \{0,1\}$. Otherwise, $\mathcal{B}$ randomly selects $b\in \left\{0,1\right\}$ and sends $C^{*}=(c_1^{*},c_2^{*},c_3^{*})$ to ${\mathcal{A}}_1$, in which

$${\alpha }^{*}\in {\mathbb{Z}}_p,k^{*}=H_3(I{D}_{s^{*}}\Vert I{D}_{r^{*}}\Vert g_t^{x_{s^{*}}·x_{r^{*}}}·Z),$$

$$c_1^{*}=\widehat{e}{(g,H_2\left(w_b^{*}\right))}^{{\alpha }^{*}·k^{*}},c_2=g^{{\alpha }^{*}},c_3=g^{\frac{{\alpha }^{*}}{k^{*}}}.$$

4.

Phase 2: ${\mathcal{A}}_1$ is allowed to access the oracles as in Phase 1, with the following restrictions:

• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{psk}$.
• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{sk}$.
• Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) can be submitted to ${\mathcal{O}}_T$.

5.

Guess: ${\mathcal{A}}_1$ submits $b^{\prime }$. If $b=b^{\prime }$, ${\mathcal{A}}_1$ wins, and $\mathcal{B}$ returns ${\zeta }^{\prime }=0$. Otherwise, ${\mathcal{A}}_1$ loses, and $\mathcal{B}$ returns ${\zeta }^{\prime }=1$.

If $\zeta =0$, $\mathcal{B}$ perfectly simulates Section 3.3.1, and ${\mathcal{A}}_1$’s probability of winning is $ϵ+1/2$. Otherwise, $C^{*}$ is independent of $w_b^{*}$, and ${\mathcal{A}}_1$’s probability of winning is $1/2$. $\mathcal{B}$ aborts and randomly returns ${\zeta }^{\prime }\in \{0,1\}$ if its guess of the identities selected by ${\mathcal{A}}_1$ for challenge is wrong. Denote $\mathcal{B}$’s abortion with $abt$, we have

$$\mathrm{Pr}[{\zeta }^{\prime }=\zeta |abt]=\frac{1}{2},$$

$$\mathrm{Pr}[{\zeta }^{\prime }=\zeta |\overline{abt}]=(ϵ+\frac{1}{2})·\frac{1}{2}+\frac{1}{2}·\frac{1}{2}=\frac{ϵ}{2}+\frac{1}{2},$$

$$\mathrm{Pr}\left[\overline{abt}\right]\ge \frac{1}{{\mathrm{C}}_{q_{H_1}}^2}=\frac{2}{q_{H_1}(q_{H_1}-1)}.$$

$\mathcal{B}$’s advantage in solving the DBDH problem is

$$\begin{array}{cc}\hfill & {\mathrm{Adv}}^{DBDH}\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta ]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta \wedge \overline{abt}]+\mathrm{Pr}[{\zeta }^{\prime }=\zeta \wedge abt]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta |\overline{abt}]·\mathrm{Pr}\left[\overline{abt}\right]+\mathrm{Pr}[{\zeta }^{\prime }=\zeta |abt]·\mathrm{Pr}\left[abt\right]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|(\frac{ϵ}{2}+\frac{1}{2})·\mathrm{Pr}\left[\overline{abt}\right]+\frac{1}{2}·(1-\mathrm{Pr}\left[\overline{abt}\right])-\frac{1}{2}\right|\hfill \\ \hfill & =\frac{ϵ}{2}·\mathrm{Pr}\left[\overline{abt}\right]\hfill \\ \hfill & \ge \frac{ϵ}{q_{H_1}(q_{H_1}-1)}.\hfill \end{array}$$

$ϵ$ is negligible due to the intractability of the DBDH problem. This completes the proof. □

5.2. CT-IND-CKA against Type-2 Adversary

Theorem 2.

Our scheme satisfies CT-IND-CKA against Type-2 adversary in the random oracle model if the DDH assumption in ${\mathbb{G}}_T$ holds.

Proof. 

Suppose that ${\mathrm{Adv}}_{{\mathcal{A}}_2}^{CT-IND-CKA}=ϵ$. Given a DDH instance $(g_t,g_t^{{\eta }_1},g_t^{{\eta }_2},Z)\in {\mathbb{G}}_T^4$. Denoted by $\zeta =0$ that $Z=g_t^{{\eta }_1·{\eta }_2}$, and by $\zeta =1$ that Z is random. In the following, we construct a simulator $\mathcal{B}$ that runs ${\mathcal{A}}_2$ as a subroutine to correctly guess the value of $\zeta$.

1.

Setup: $\mathcal{B}$ sends $pp$ and $msk=y$ to ${\mathcal{A}}_2$.

2.

Phase 1: ${\mathcal{A}}_2$ is allowed to access the following oracles:

• ${\mathcal{O}}_{H_1}\left(I{D}_i\right)$: $\mathcal{B}$ randomly selects $h_{1,i}\in {\mathbb{Z}}_p$, adds $\left\{I{D}_i,h_{1,i},g^{h_{1,i}}\right\}$ to list $L_{H_1}$, and returns $g^{h_{1,i}}$. If the repeated queries are submitted, the answer that already exists in $L_{H_1}$ will be returned. Suppose that there are $q_{H_1}$ distinct queries to ${\mathcal{O}}_{H_1}$. $\mathcal{B}$ randomly selects $(i^{*},j^{*})\in \{1,···,q_{H_1}\}$ as its guess of the identities selected by ${\mathcal{A}}_1$ for challenge.
• ${\mathcal{O}}_{H_2}$: Same as ${\mathcal{O}}_{H_2}$ in the proof of Theorem 1.
• ${\mathcal{O}}_{H_3}$: Same as ${\mathcal{O}}_{H_3}$ in the proof of Theorem 1.
• ${\mathcal{O}}_{pk}\left(I{D}_i\right)$: $\mathcal{B}$ calls ${\mathcal{O}}_{H_1}\left(I{D}_i\right)$ and retrieves $\left\{I{D}_i,h_{1,i},g^{h_{1,i}}\right\}$ from $L_{H_1}$, then:

  −

  If $i=i^{*}$, $\mathcal{B}$ sets

  $$p{k}_i=g_t^{{\eta }_1},ps{k}_i=g^{y·h_{1,i}},$$

  adds $\{I{D}_i,p{k}_i,ps{k}_i,-\}$ to list $L_{key}$, and returns $p{k}_i$ to ${\mathcal{A}}_2$.

  −

  If $i=j^{*}$, $\mathcal{B}$ sets

  $$p{k}_i=g_t^{{\eta }_2},ps{k}_i=g^{y·h_{1,i}},$$

  adds $\{I{D}_i,p{k}_i,ps{k}_i,-\}$ to list $L_{key}$, and returns $p{k}_i$ to ${\mathcal{A}}_2$.

  −

  Otherwise, $\mathcal{B}$ randomly selects $x_i\in {\mathbb{Z}}_p$, sets

  $$p{k}_i=g_t^{x_i},ps{k}_i=g^{y·h_{1,i}},$$

  adds $\{I{D}_i,p{k}_i,ps{k}_i,x_i\}$ to list $L_{key}$, and returns $p{k}_i$ to ${\mathcal{A}}_2$.

  If the repeated queries are submitted, the answer that already exists in $L_{key}$ will be returned.
• ${\mathcal{O}}_{psk}\left(I{D}_i\right)$: $\mathcal{B}$ calls ${\mathcal{O}}_{pk}\left(I{D}_i\right)$, retrieves $\{I{D}_i,p{k}_i,ps{k}_i,x_i\}$ from $L_{key}$, and returns $ps{k}_i$ to ${\mathcal{A}}_2$.
• ${\mathcal{O}}_{sk}\left(I{D}_i\right)$:

  −

  If $i=i^{*}\vee i=j^{*}$, $\mathcal{B}$ aborts.

  −

  Otherwise, $\mathcal{B}$ calls ${\mathcal{O}}_{pk}\left(I{D}_i\right)$, retrieves $\{I{D}_i,p{k}_i,ps{k}_i,x_i\}$ from $L_{key}$, and returns $s{k}_i=(ps{k}_i,x_i)$.

• ${\mathcal{O}}_{CLPAEKS}(I{D}_s,I{D}_r,w)$: $\mathcal{B}$ randomly selects $\alpha \in {\mathbb{Z}}_p$ and returns $C=(c_1,c_2,c_3):$

  $$c_1=\widehat{e}{(g,H_2\left(w\right))}^{\alpha ·k},c_2=g^{\alpha },c_3=g^{\frac{\alpha }{k}},$$

  in which k is different based on the following cases.

  −

  If $s=i^{*}\wedge r=j^{*}$, $k=H_3(I{D}_{i^{*}}\Vert I{D}_{j^{*}}\Vert Z·\widehat{e}{(H_1\left(I{D}_{i^{*}}\right),H_1\left(I{D}_{j^{*}}\right))}^y)$.

  −

  If $s=j^{*}\wedge r=i^{*}$, $k=H_3(I{D}_{j^{*}}\Vert I{D}_{i^{*}}\Vert Z·\widehat{e}{(H_1\left(I{D}_{i^{*}}\right),H_1\left(I{D}_{j^{*}}\right))}^y)$.

  −

  Otherwise, it means that $(s\ne i^{*}\wedge s\ne j^{*})\vee (r\ne i^{*}\wedge r\ne j^{*})$.

  ∗ 

  If $s\ne i^{*}\wedge s\ne j^{*}$, $\mathcal{B}$ retrieves $\{I{D}_s,p{k}_s,ps{k}_s,x_s\}$ from $L_{key}$ and computes $k=H_3(I{D}_s\Vert I{D}_r\Vert p{k}_r^{x_s}·\widehat{e}{(H_1\left(I{D}_s\right),H_1\left(I{D}_r\right))}^y)$.

  ∗ 

  Otherwise, $\mathcal{B}$ retrieves $\{I{D}_r,p{k}_r,ps{k}_r,x_r\}$ from $L_{key}$ and computes $k=H_3(I{D}_s\Vert I{D}_r\Vert p{k}_s^{x_r}·\widehat{e}{(H_1\left(I{D}_s\right),H_1\left(I{D}_r\right))}^y)$.

• ${\mathcal{O}}_T(I{D}_s,I{D}_r,w)$: $\mathcal{B}$ randomly selects $(\beta ,\gamma )\in {\mathbb{Z}}_p^2$ and returns $td=(t{d}_1,t{d}_2,t{d}_3):$

  $$t{d}_1=H_2{\left(w\right)}^{\beta +\frac{\gamma }{k}},t{d}_2=H_2{\left(w\right)}^{\frac{k^3}{\beta }-\gamma },t{d}_3=\frac{\beta }{k}+\frac{k}{\beta },$$

  in which k is different based on the following cases.

  −

  If $s=i^{*}\wedge r=j^{*}$, $k=H_3(I{D}_{i^{*}}\Vert I{D}_{j^{*}}\Vert Z·\widehat{e}{(H_1\left(I{D}_{i^{*}}\right),H_1\left(I{D}_{j^{*}}\right))}^y)$.

  −

  If $s=j^{*}\wedge r=i^{*}$, $k=H_3(I{D}_{j^{*}}\Vert I{D}_{i^{*}}\Vert Z·\widehat{e}{(H_1\left(I{D}_{i^{*}}\right),H_1\left(I{D}_{j^{*}}\right))}^y)$.

  −

  Otherwise, it means that $(s\ne i^{*}\wedge s\ne j^{*})\vee (r\ne i^{*}\wedge r\ne j^{*})$.

  ∗ 

  If $s\ne i^{*}\wedge s\ne j^{*}$, $\mathcal{B}$ retrieves $\{I{D}_s,p{k}_s,ps{k}_s,x_s\}$ from $L_{key}$ and computes $k=H_3(I{D}_s\Vert I{D}_r\Vert p{k}_r^{x_s}·\widehat{e}{(H_1\left(I{D}_s\right),H_1\left(I{D}_r\right))}^y)$.

  ∗ 

  Otherwise, $\mathcal{B}$ retrieves $\{I{D}_r,p{k}_r,ps{k}_r,x_r\}$ from $L_{key}$ and computes $k=H_3(I{D}_s\Vert I{D}_r\Vert p{k}_s^{x_r}·\widehat{e}{(H_1\left(I{D}_s\right),H_1\left(I{D}_r\right))}^y)$.

3.

Challenge: ${\mathcal{A}}_2$ selects $I{D}_{s^{*}}$, $I{D}_{r^{*}}$, and two keywords ($w_0^{*}$, $w_1^{*}$) for the challenge, with the following restrictions: (1) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{sk}$; (2) Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) has been submitted to ${\mathcal{O}}_T$. If $\neg (s^{*}=i^{*}\wedge r^{*}=j^{*})\wedge \neg (s^{*}=j^{*}\wedge r^{*}=i^{*})$, $\mathcal{B}$ aborts and randomly returns ${\zeta }^{\prime }\in \{0,1\}$. Otherwise, $\mathcal{B}$ randomly selects $b\in \left\{0,1\right\}$ and sends $C^{*}=(c_1^{*},c_2^{*},c_3^{*})$ to ${\mathcal{A}}_2$, in which

$${\alpha }^{*}\in {\mathbb{Z}}_p,k^{*}=H_3(I{D}_{s^{*}}\Vert I{D}_{r^{*}}\Vert Z·\widehat{e}{(H_1\left(I{D}_{s^{*}}\right),H_1\left(I{D}_{r^{*}}\right))}^y),$$

$$c_1^{*}=\widehat{e}{(g,H_2\left(w_b^{*}\right))}^{{\alpha }^{*}·k^{*}},c_2=g^{{\alpha }^{*}},c_3=g^{\frac{{\alpha }^{*}}{k^{*}}}.$$

4.

Phase 2: ${\mathcal{A}}_2$ is allowed to access the oracles as in Phase 1, with the following restrictions:

• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{sk}$.
• Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) can be submitted to ${\mathcal{O}}_T$.

5.

Guess: ${\mathcal{A}}_2$ submits $b^{\prime }$. If $b=b^{\prime }$, ${\mathcal{A}}_2$ wins, and $\mathcal{B}$ returns ${\zeta }^{\prime }=0$. If $b\ne b^{\prime }$, ${\mathcal{A}}_2$ loses, and $\mathcal{B}$ returns ${\zeta }^{\prime }=1$.

If $\zeta =0$, $\mathcal{B}$ perfectly simulates Section 3.3.2, and ${\mathcal{A}}_2$’s probability of winning is $ϵ+1/2$. Otherwise, $C^{*}$ is independent of $w_b^{*}$, and ${\mathcal{A}}_2$’s probability of winning is $1/2$. $\mathcal{B}$ aborts and randomly returns ${\zeta }^{\prime }\in \{0,1\}$ if its guess of the identities selected by ${\mathcal{A}}_2$ for challenge is wrong. Denote $\mathcal{B}$’s abortion with $abt$, we have

$$\mathrm{Pr}[{\zeta }^{\prime }=\zeta |abt]=\frac{1}{2},$$

$$\mathrm{Pr}[{\zeta }^{\prime }=\zeta |\overline{abt}]=(ϵ+\frac{1}{2})·\frac{1}{2}+\frac{1}{2}·\frac{1}{2}=\frac{ϵ}{2}+\frac{1}{2},$$

$$\mathrm{Pr}\left[\overline{abt}\right]\ge \frac{1}{{\mathrm{C}}_{q_{H_1}}^2}=\frac{2}{q_{H_1}(q_{H_1}-1)}.$$

$\mathcal{B}$’s advantage in solving the DDH problem in ${\mathbb{G}}_T$ is

$$\begin{array}{cc}\hfill & {\mathrm{Adv}}^{DDH}\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta ]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta \wedge \overline{abt}]+\mathrm{Pr}[{\zeta }^{\prime }=\zeta \wedge abt]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta |\overline{abt}]·\mathrm{Pr}\left[\overline{abt}\right]+\mathrm{Pr}[{\zeta }^{\prime }=\zeta |abt]·\mathrm{Pr}\left[abt\right]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|(\frac{ϵ}{2}+\frac{1}{2})·\mathrm{Pr}\left[\overline{abt}\right]+\frac{1}{2}·(1-\mathrm{Pr}\left[\overline{abt}\right])-\frac{1}{2}\right|\hfill \\ \hfill & =\frac{ϵ}{2}·\mathrm{Pr}\left[\overline{abt}\right]\hfill \\ \hfill & \ge \frac{ϵ}{q_{H_1}(q_{H_1}-1)}.\hfill \end{array}$$

$ϵ$ is negligible due to the intractability of the DDH problem in ${\mathbb{G}}_T$. This completes the proof. □

5.3. S-TD-IND-CKA against Type-1 Adversary

Theorem 3.

Our scheme satisfies S-TD-IND-CKA against Type-1 adversary in the random oracle model if the DBDH assumption holds.

Proof. 

Suppose that ${\mathrm{Adv}}_{{\mathcal{A}}_1}^{S-TD-IND-CKA}=ϵ$. Given a DBDH instance $({\mathbb{G}}_1,{\mathbb{G}}_T,\widehat{e},g,g^{{\eta }_1},g^{{\eta }_2},g^{{\eta }_3},Z)$. Denoted by $\zeta =0$ that $Z={\widehat{e}(g,g)}^{{\eta }_1·{\eta }_2·{\eta }_3}$, and by $\zeta =1$ that Z is random. In the following, we construct a simulator $\mathcal{B}$ that runs ${\mathcal{A}}_1$ as a subroutine to correctly guess the value of $\zeta$.

1.

Setup: $\mathcal{B}$ sets $mpk=g^{{\eta }_1}$, implying that $msk={\eta }_1$, in which ${\eta }_1$ is unknown to $\mathcal{B}$. Then sends $pp$ to ${\mathcal{A}}_1$.

2.

Phase 1: Same as Phase 1 in the proof of Theorem 1.

3.

Challenge: ${\mathcal{A}}_1$ selects $I{D}_{s^{*}}$, $I{D}_{r^{*}}$, and two keywords ($w_0^{*}$, $w_1^{*}$) for the challenge, with the following restrictions: (1) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{psk}$; (2) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{sk}$; (3) Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) has been submitted to ${\mathcal{O}}_{CLPAEKS}$. If $\neg (s^{*}=i^{*}\wedge r^{*}=j^{*})\wedge \neg (s^{*}=j^{*}\wedge r^{*}=i^{*})$, $\mathcal{B}$ aborts and randomly returns ${\zeta }^{\prime }\in \{0,1\}$. Otherwise, $\mathcal{B}$ randomly selects $b\in \left\{0,1\right\}$ and sends $t{d}^{*}=(t{d}_1^{*},t{d}_2^{*},t{d}_3^{*})$ to ${\mathcal{A}}_1$, in which

$$({\beta }^{*},{\gamma }^{*})\in {\mathbb{Z}}_p^2,k^{*}=H_3(I{D}_{s^{*}}\Vert I{D}_{r^{*}}\Vert g_t^{x_{s^{*}}·x_{r^{*}}}·Z),$$

$$t{d}_1^{*}=H_2{\left(w_b^{*}\right)}^{{\beta }^{*}+\frac{{\gamma }^{*}}{k^{*}}},t{d}_2^{*}=H_2{\left(w_b^{*}\right)}^{\frac{{\left(k^{*}\right)}^3}{{\beta }^{*}}-{\gamma }^{*}},t{d}_3^{*}=\frac{{\beta }^{*}}{k^{*}}+\frac{k^{*}}{{\beta }^{*}}.$$

4.

Phase 2: ${\mathcal{A}}_1$ is allowed to access the oracles as in Phase 1, with the following restrictions:

• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{psk}$.
• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{sk}$.
• Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) can be submitted to ${\mathcal{O}}_{CLPAEKS}$.

5.

Guess: ${\mathcal{A}}_1$ submits $b^{\prime }$. If $b=b^{\prime }$, ${\mathcal{A}}_1$ wins, and $\mathcal{B}$ returns ${\zeta }^{\prime }=0$. Otherwise, ${\mathcal{A}}_1$ loses, and $\mathcal{B}$ returns ${\zeta }^{\prime }=1$.

If $\zeta =0$, $\mathcal{B}$ perfectly simulates Section 3.3.3, and ${\mathcal{A}}_1$’s probability of winning is $ϵ+1/2$. Otherwise, $t{d}^{*}$ is independent of $w_b^{*}$, and ${\mathcal{A}}_1$’s probability of winning is $1/2$. $\mathcal{B}$ aborts and randomly returns ${\zeta }^{\prime }\in \{0,1\}$ if its guess of the identities selected by ${\mathcal{A}}_1$ for challenge is wrong. Denote $\mathcal{B}$’s abortion with $abt$, we have

$$\mathrm{Pr}[{\zeta }^{\prime }=\zeta |abt]=\frac{1}{2},$$

$$\mathrm{Pr}[{\zeta }^{\prime }=\zeta |\overline{abt}]=(ϵ+\frac{1}{2})·\frac{1}{2}+\frac{1}{2}·\frac{1}{2}=\frac{ϵ}{2}+\frac{1}{2},$$

$$\mathrm{Pr}\left[\overline{abt}\right]\ge \frac{1}{{\mathrm{C}}_{q_{H_1}}^2}=\frac{2}{q_{H_1}(q_{H_1}-1)}.$$

$\mathcal{B}$’s advantage in solving the DBDH problem is

$$\begin{array}{cc}\hfill & {\mathrm{Adv}}^{DBDH}\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta ]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta \wedge \overline{abt}]+\mathrm{Pr}[{\zeta }^{\prime }=\zeta \wedge abt]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta |\overline{abt}]·\mathrm{Pr}\left[\overline{abt}\right]+\mathrm{Pr}[{\zeta }^{\prime }=\zeta |abt]·\mathrm{Pr}\left[abt\right]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|(\frac{ϵ}{2}+\frac{1}{2})·\mathrm{Pr}\left[\overline{abt}\right]+\frac{1}{2}·(1-\mathrm{Pr}\left[\overline{abt}\right])-\frac{1}{2}\right|\hfill \\ \hfill & =\frac{ϵ}{2}·\mathrm{Pr}\left[\overline{abt}\right]\hfill \\ \hfill & \ge \frac{ϵ}{q_{H_1}(q_{H_1}-1)}.\hfill \end{array}$$

$ϵ$ is negligible due to the intractability of the DDH problem. This completes the proof. □

5.4. S-TD-IND-CKA against Type-2 Adversary

Theorem 4.

Our scheme satisfies S-TD-IND-CKA against Type-2 adversary in the random oracle model if the DDH assumption in ${\mathbb{G}}_T$ holds.

Proof. 

Suppose that ${\mathrm{Adv}}_{{\mathcal{A}}_2}^{S-TD-IND-CKA}=ϵ$. Given a DDH instance $(g_t,g_t^{{\eta }_1},g_t^{{\eta }_2},Z)\in {\mathbb{G}}_T^4$. Denoted by $\zeta =0$ that $Z=g_t^{{\eta }_1·{\eta }_2}$, and by $\zeta =1$ that Z is random. In the following, we construct a simulator $\mathcal{B}$ that runs ${\mathcal{A}}_2$ as a subroutine to correctly guess the value of $\zeta$.

1.

Setup: $\mathcal{B}$ sends $pp$ and $msk=y$ to ${\mathcal{A}}_2$.

2.

Phase 1: Same as Phase 1 in the proof of Theorem 2.

3.

Challenge: ${\mathcal{A}}_2$ selects $I{D}_{s^{*}}$, $I{D}_{r^{*}}$, and two keywords ($w_0^{*}$, $w_1^{*}$) for the challenge, with the following restrictions: (1) Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ has been submitted to ${\mathcal{O}}_{sk}$; (2) Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) has been submitted to ${\mathcal{O}}_{CLPAEKS}$. If $\neg (s^{*}=i^{*}\wedge r^{*}=j^{*})\wedge \neg (s^{*}=j^{*}\wedge r^{*}=i^{*})$, $\mathcal{B}$ aborts and randomly returns ${\zeta }^{\prime }\in \{0,1\}$. Otherwise, $\mathcal{B}$ randomly selects $b\in \left\{0,1\right\}$ and sends $t{d}^{*}=(t{d}_1^{*},t{d}_2^{*},t{d}_3^{*})$ to ${\mathcal{A}}_2$, in which

$$({\beta }^{*},{\gamma }^{*})\in {\mathbb{Z}}_p^2,k^{*}=H_3(I{D}_{s^{*}}\Vert I{D}_{r^{*}}\Vert Z·\widehat{e}{(H_1\left(I{D}_{s^{*}}\right),H_1\left(I{D}_{r^{*}}\right))}^y),$$

$$t{d}_1^{*}=H_2{\left(w_b^{*}\right)}^{{\beta }^{*}+\frac{{\gamma }^{*}}{k^{*}}},t{d}_2^{*}=H_2{\left(w_b^{*}\right)}^{\frac{{\left(k^{*}\right)}^3}{{\beta }^{*}}-{\gamma }^{*}},t{d}_3^{*}=\frac{{\beta }^{*}}{k^{*}}+\frac{k^{*}}{{\beta }^{*}}.$$

4.

Phase 2: ${\mathcal{A}}_2$ is allowed to access the oracles as in Phase 1, with the following restrictions:

• Neither $I{D}_{s^{*}}$ nor $I{D}_{r^{*}}$ can be submitted to ${\mathcal{O}}_{sk}$.
• Neither ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_0^{*}$) nor ($I{D}_{s^{*}}$, $I{D}_{r^{*}}$, $w_1^{*}$) can be submitted to ${\mathcal{O}}_{CLPAEKS}$.

5.

Guess: ${\mathcal{A}}_2$ submits $b^{\prime }$. If $b=b^{\prime }$, ${\mathcal{A}}_2$ wins, and $\mathcal{B}$ returns ${\zeta }^{\prime }=0$. If $b\ne b^{\prime }$, ${\mathcal{A}}_2$ loses, and $\mathcal{B}$ returns ${\zeta }^{\prime }=1$.

If $\zeta =0$, $\mathcal{B}$ perfectly simulates Section 3.3.4, and ${\mathcal{A}}_2$’s probability of winning is $ϵ+1/2$. Otherwise, $t{d}^{*}$ is independent of $w_b^{*}$, and ${\mathcal{A}}_2$’s probability of winning is $1/2$. $\mathcal{B}$ aborts and randomly returns ${\zeta }^{\prime }\in \{0,1\}$ if its guess of the identities selected by ${\mathcal{A}}_2$ for challenge is wrong. Denote $\mathcal{B}$’s abortion with $abt$, we have

$$\mathrm{Pr}[{\zeta }^{\prime }=\zeta |abt]=\frac{1}{2},$$

$$\mathrm{Pr}[{\zeta }^{\prime }=\zeta |\overline{abt}]=(ϵ+\frac{1}{2})·\frac{1}{2}+\frac{1}{2}·\frac{1}{2}=\frac{ϵ}{2}+\frac{1}{2},$$

$$\mathrm{Pr}\left[\overline{abt}\right]\ge \frac{1}{{\mathrm{C}}_{q_{H_1}}^2}=\frac{2}{q_{H_1}(q_{H_1}-1)}.$$

$\mathcal{B}$’s advantage in solving the DDH problem in ${\mathbb{G}}_T$ is

$$\begin{array}{cc}\hfill & {\mathrm{Adv}}^{DDH}\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta ]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta \wedge \overline{abt}]+\mathrm{Pr}[{\zeta }^{\prime }=\zeta \wedge abt]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|\mathrm{Pr}[{\zeta }^{\prime }=\zeta |\overline{abt}]·\mathrm{Pr}\left[\overline{abt}\right]+\mathrm{Pr}[{\zeta }^{\prime }=\zeta |abt]·\mathrm{Pr}\left[abt\right]-\frac{1}{2}\right|\hfill \\ \hfill & =\left|(\frac{ϵ}{2}+\frac{1}{2})·\mathrm{Pr}\left[\overline{abt}\right]+\frac{1}{2}·(1-\mathrm{Pr}\left[\overline{abt}\right])-\frac{1}{2}\right|\hfill \\ \hfill & =\frac{ϵ}{2}·\mathrm{Pr}\left[\overline{abt}\right]\hfill \\ \hfill & \ge \frac{ϵ}{q_{H_1}(q_{H_1}-1)}.\hfill \end{array}$$

$ϵ$ is negligible due to the intractability of the DDH problem in ${\mathbb{G}}_T$. This completes the proof. □

6. Performance Evaluation and Discussion

We compare our scheme with two related schemes [23,24]. The comparison includes storage overhead, computation overhead, and security. For simplicity, we only consider the following time-consuming operations:

• E: An exponentiation operation in $\mathbb{G}$.
• $E_1$: An exponentiation operation in ${\mathbb{G}}_1$.
• $E_T$: An exponentiation operation in ${\mathbb{G}}_T$.
• P: A bilinear pairing operation.
• H: A Hash-To-Point operation.

The comparison of storage overhead, computation overhead, and security is shown in Table 2, Table 3 and Table 4, respectively. Our scheme has higher storage and computation overhead. However, our scheme achieves stronger security. Besides, in practice, users may not need to encrypt all files but only a small part of files that contain sensitive information. Therefore, we consider that the storage and computation overhead paid for stronger security is affordable.

Table 2. Storage overhead comparison.

	Pakniat et al.’s [23]	Shiraly et al.’s [24]	Ours
$\left|C\right|$	$2|{\mathbb{G}}_1|$	$2\left|\mathbb{G}\right|$	$2|{\mathbb{G}}_1|+1|{\mathbb{G}}_T|$
$\left|td\right|$	$1|{\mathbb{Z}}_p|$	$1|{\mathbb{Z}}_p|$	$2|{\mathbb{G}}_1|+1{\mathbb{Z}}_p$

$\left|C\right|$, $\left|td\right|$: Size of the ciphertext and the trapdoor, respectively; $\left|\mathbb{G}\right|$, $|{\mathbb{G}}_1|$, $|$, $|{\mathbb{Z}}_p|$: Size of an element in $\mathbb{G}$, ${\mathbb{G}}_1$, ${\mathbb{G}}_T$, and ${\mathbb{Z}}_p$, respectively.

Table 3. Computation overhead comparison.

	Pakniat et al.’s [23]	Shiraly et al.’s [24]	Ours
Ciphertext generation	$3E_1+P+H$	$5E$	$2E_1+2E_T+2P+2H$
Trapdoor generation	$E_1+P+H$	$3E$	$2E_1+E_T+P+2H$
Test	$E_1$	E	$E_T+2P$

Table 4. Security comparison.

	Pakniat et al.’s [23]	Shiraly et al.’s [24]	Ours
CT-IND	yes	yes	yes
S-TD-IND	no	no	yes
Model	ROM	ROM	ROM
Assumption	GBDH & CDH	GDH	DBDH & DDH

CT-IND: Ciphertext indistinguishability; S-TD-IND: Strong trapdoor indistinguishability; ROM: Random oracle model.

7. Conclusions and Future Works

In this paper, we proposed an improved security model, in which a stronger version of trapdoor indistinguishability is defined. Then we proposed a new CLPAEKS scheme, which differs from the existing CLPAEKS schemes mainly in that the trapdoor is generated using two random elements in ${\mathbb{Z}}_p$. As far as we know, this is the first CLPAEKS scheme with provable security under the improved security model.

In the future, we will try to extend our scheme to make it support multi-receiver settings in order to cope with the scenario of group chat. Besides, considering that a file may contain multiple keywords, it would be valuable to extend our scheme to make it support multi-keyword settings. Furthermore, as quantum computing is emerging, traditional intractable problems, e.g., discrete logarithm problems, could be solved with a powerful quantum computer. Some quantum-safe cryptographic primitives were proposed (e.g., lattice-based cryptography, code-based cryptography, multivariate-based cryptography, and hash-based cryptography). Among the mentioned candidates, lattice-based cryptography is an attractive choice because it offers provable security and a good trade-off between efficiency and security [26,27,28]. Therefore, it is advisable to design a lattice-based CLPAEKS scheme to resist quantum computing attacks.