A Lattice-Based Certificateless Traceable Ring Signature Scheme
Abstract
:1. Introduction
1.1. Related Works
1.2. Our Contributions
- The security of most TRS schemes relies on difficult assumptions in number theory, and the security of these schemes may become insecure for quantum computers, so we designed a lattice-based CLTRS. In our scheme, we treat the member’s identity information as the member’s public key, thus effectively solving the CMP in [50]. Meanwhile, we divide the member’s private key into two parts, one produced by KGC and one chosen by member, and by doing so, our scheme also does not have the KEP like in [29,36,47].
- Based on SIS, DLWE hard assumptions, uniqueness of function F and multi-input correlation intractability of hash family, our scheme is proved to be security and it is satisfies the tag-linkability, type I anonymity, type II anonymity, type I exculpability and type II exculpability under the ROM. Furthermore, compared to [51,52], although the signature size of our scheme is larger, our member secret key is smaller and also achieves public traceability, which the identity will no longer be anonymous if the member maliciously signs twice under the same label.
- Our scheme combines the efficient zero-knowledge protocol proposed by [53], and to argue the relation that our scheme wants to prove, we make modifications based on [53] to construct the privacy-preserving primitives suitable for our scheme. The Stern protocol used in [50] has a soundness error of 2/3 for single run protocol, while the efficient zero-knowledge protocol used in our scheme has a soundness error of 1/poly for single run protocol. To obtain negligible soundness error, our scheme repeats the zero-knowledge protocol fewer times than [50]. Thus, compared to the scheme in the [50], the size of the zero-knowledge proof generated by our scheme will be smaller for the same parameters. When computing the root node of the Merkle tree, [50] retains only one auxiliary node at each level, therefore, for the verification of the path from leaf node to root node, the parent node of leaf node needs to be calculated by the leaf node and its sibling nodes first, and then the parent node of the upper layer can be calculated by the sibling nodes of the layer where the parent node and the parent node reside, and so on, and finally the root node can be obtained. This verification process is a serial calculation process. In this paper, two auxiliary nodes are reserved in each layer of the tree. Therefore, when calculating the root node, the process of calculating the left and right child nodes of each layer to obtain the parent node can be calculated in parallel, and there is no need to calculate step by step from the lowest leaf node. Therefore, the verification process of our scheme is more efficient.
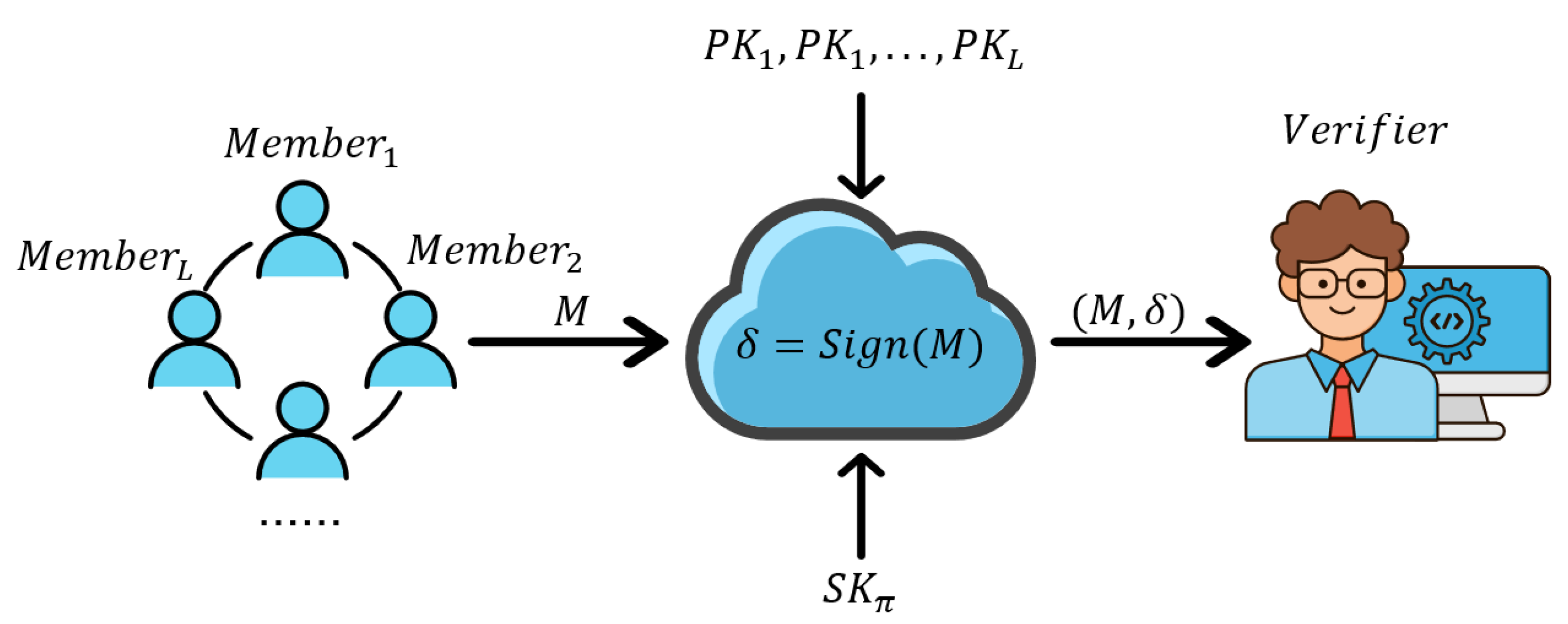
2. Certificate-Less Traceable Ring Signature
2.1. Definition
- : Input the security parameter , and outputs a public system parameter pp and a master secret key msk.
- ExtractPartialPrivateKey: Input pp, an identity of user for , and msk, then generate a partial private key with respect to .
- SetSecretValue: Input pp, of user for , then returns a secret value to the user .
- SetPrivateKey: Input pp, and , then returns a secret key corresponding to the user .
- SetPublicKey: Input pp and , then returns a public key corresponding to the user .
- : Input pp, an issue I, a ring R, a message M, an identity id and , outputs a ring signature .
- : Input pp, an issue I, a ring R, a message M and a ring signature , return if accepting the signature or for rejecting it.
- : Input , an issue I, a ring R, and two valid tuples and , outputs .
2.2. Security Models
- 1.
- Setup. Execute algorithm, the challenger obtains and , and then sends to but is saved itself.
- 2.
- . conducts the following queries:
- . When the adversary submits a user , checks it in , if is exists, then returns ; otherwise, runs algorithms , to generate , , and , then returns to adversary and adds tuple to .
- . When the adversary submits a user , checks in the and returns to .
- . When the adversary submits the user and , substitutes for .
- . When the adversary submits the user , issue I, ring R and message M, return to .
- 3.
- . forgeries tuples with . wins if
- (a)
- for ;
- (b)
- for all with .
- (c)
- has at most L ring member , and the pk of these ring members are all in tag Γ.
- 1.
- . Execute algorithm, the challenger obtains and , and saves secretly, obtains pp from .
- 2.
- . conducts the following four kinds of queries:
- . When the adversary submits a user , checks it in , if is exists, then returns ; otherwise, runs algorithms , to generate , , and , then returns to adversary and adds tuple to .
- . When the adversary submits a user , checks in the and returns to .
- . When the adversary submits the user and , substitutes for .
- . When the adversary submits the user , issue I, ring R and message M, return , to .
- 3.
- . refers two tuples and to , where such that , and have not been referred to . chooses randomly , returns to .
- 4.
- . Similarly to , in addition to does not have access to and .
- 5.
- . outputs a guess b’ for b. wins if b’ = b.
- 1.
- . Execute algorithm, the challenger obtains and , and then sends them to .
- 2.
- . conducts the following four kinds of queries:
- . The same as of type I Anonymity.
- . The same as of type I Anonymity.
- . The same as of type I Anonymity.
- . When the adversary submits the user , issue I, ring R and message M, return , to .
- 3.
- . refers two tuples and to , where such that , andhave not been referred to . chooses randomly , returns to .
- 4.
- . Similarly to , in addition to does not have access to and .
- 5.
- . outputs a guess b’ for b. wins if b’ = b.
- 1.
- . Execute algorithm, the challenger obtains and , and saves secretly, obtains pp from .
- 2.
- . conducts the following four kinds of queries:
- . When the adversary submits a user , generates , , and , returns to adversary , and then adds tuple to .
- . When the adversary submits a user , checks in the and returns to .
- . When the adversary submits the user and the public key , substitutes for .
- . When the adversary submits the user , issue I, ring R and message M, return , to .
- 3.
- . forgeries two tuples and . It wins if
- (a)
- ;
- (b)
- ;
- (c)
- has not been queried about and where ;
- (d)
- has made at most one of and , ;
- (e)
- .
- 1.
- . Execute algorithm, the challenger obtains and , and sends them to .
- 2.
- . conducts the following four kinds of queries:
- . The same as of type I exculpability.
- . The same as of type I exculpability.
- . The same as of type I exculpability.
- . The same as of type I exculpability.
- 3.
- . forgeries two tuples and . It wins if
- (a)
- ;
- (b)
- ;
- (c)
- has not been queried about and where ;
- (d)
- has made at most one of and , ;
- (e)
- .
3. Preliminaries
3.1. Hardness Assumptions
3.2. Trapdoor Mechanism
- (GenTrap Algorithm [56]): Given a uniformly random matrix and an invertible matrix , the PPT algorithm outputs a random matrix and a G-trapdoor (the ∼ indicates that the distribution of G-trapdoor obeys the Gaussian distribution ). Also, .
- (SampleD Algorithm [56]): Given a G-trapdoor for , an invertible matrix , a uniform vector and Gaussian parameter , the PPT algorithm outputs a vector sampled from a distribution that is statistically close to .
3.3. Pseudorandom Function Family
- KeyGen. The key generation algorithm randomly chooses a vector and outputs the vector .
- Eval. Given a string of any length, the evaluation algorithm returns .
- For a string of arbitrary length , the following probabilities conditions are satisfied:
- For any two distinct vectors and any polynomial , the following probabilities conditions are satisfied:where Y is composed of vectors with rational numbers as elements.
3.4. Lattice-Based Accumulator
- . Sample a random matrix and returns the value of the public parameter .
- . The algorithm sets when given . Next for and , it defines . Lastly, the accumulated value is returned.
- . The algorithm generates just like the accumulate algorithm when given and an element . Finally, is returned, where and .
- . Given an accumulated value , an element and a witness , , the algorithm returns 1 if
4. Our Certificate-Less Traceable Ring Signature Scheme
4.1. Construction
- ()
- Choose lattice parameter , Gaussian parameter , a U-bound distribution , integer and prime p satisfies , , , , , , , , .
- Set , choose hash functions , and .
- Choose random matrices , , .
- Randomly select a matrix , then running to obtain , and set and .Output .
- ()For an arbitrary identity , define the associated vector asrun to get , where , , and is statistically close to . Output .
- ()The signer selects a random vector , satisfying and set his secret value .
- ()On input the public parameters , signer’s partial ptivate key and secret value , this algorithm sets full priavte key .
- ()On input the public parameters and user’s full priavte key , the user computes and returns his public key .
- ()Prase , .
- Compute .
- Compute , and .
- Compute , and for all .
- Compute for , and define .
- Compute and where .
- Define as the statement, and define as the witness. Run of NIZKAoK to obtain a proof:
- Output the signature .
- ()Prase , , .
- Let and .
- For all , we caculate .
- Caculate for , let .
- Caculate .
- Define as statement, and run of NIZKAoK.
- Output 1 if . Otherwise, output 0.
- ()Prase , , , .
- Let , then calculate for all .
- Let , then calculate for all .
- If for all there is , return linked.
- If only one index satisfies , return .
- otherwise, return accept.
4.2. Correctness
- . In our scheme, is generated by subtracting two integer vectors and then dividing by , where is an integer since p is a large prime number and is much larger than L, so is relatively prime to the prime p, then is always an integer vector. The verifier can always restore the sequence based on , label , and message M. Because of the of the NIZKAoK protocol, for honestly generated signatures, the verifier always outputs .
- . According to the definition of public traceability, there are three cases.
- When and , it means that the signer signs the same message twice, so we can get and , then can be easily computed. According to the equation , we know that for all . Thereby, algorithm will output .
- When and , it means that the signer signs different messages. In this case we can get but . According to the equation , we observe that when i is the position of the signer in the ring. So algorithm will output .
- When , it means that different signers sign messages. As shown in [50], the algorithm will output accept with overwhelming probability.
5. The Underlying Zero-Knowledge Argument System
5.1. ZKAoK of Linear Equation with Short Solution
5.2. ZKAoK of PRF Preimage
6. Security Analysis
- SIS instance. The challenger receives an SIS instance , needs to look for a non-zero vector satisfying , which and .
- : Given the system parameter , instead of running the real zero-knowledge, invokes simulator to generate the public parameters, the remaining parameters are generated unchanged except that is replaced with , then sends to and is kept itself.
- . initializes initially empty lists , , , , and keeps the consistency of answers to adversaries by maintaining these tables,
- (a)
- HQuery. When submits a label to this oracle, first checks if in the , if it exists, returns the corresponding . Otherwise, picks a random matrix , and returns it to .
- (b)
- HQuery. When submits a tuple , first checks if the tuple in the , if it exists, returns the corresponding . Otherwise, picks a random vector , and returns it to .
- (c)
- HQuery. When submits an to this oracle, first checks if in the , if it exists, returns the corresponding . Otherwise, randomly selects a where is statistically close to , computes , and returns it to .
- (d)
- . When submits an , first checks if in the , if it exists, returns the corresponding key pairs . Otherwise, calls the with to obtain , and then runs , , algorithm to generate , and , returns to adversary , then adds tuple to .
- (e)
- . When submits an , first checks if in the , if it exists, returns the corresponding partial private key . Otherwise, runs to generate and returns it to .
- (f)
- . When submits an and a to this oracle, substitutes for .
- (g)
- . When the adversary submits the user , issue I, ring R and message M, return to .
- . We assume that the signature contains the sequence , . This assumption is well-founded because we can simply recover the sequence from the tuple . The probability that forges valid signatures on tuples while the trace algorithm takes any two signatures as input and obtains an output that is both accept is non-negligible, where That means
- (a)
- ,
- (b)
- .
- . During the initialization phase, although we do not run the real ZKAoK protocol but invoke a simulator for the ZKAoK protocol, the adversary cannot detect our substitution due to the zero-knowledge property. According to the proof of knowledge property, the extractor capable of extracting the witness from each , where witness , since condition (ii) holds and the unique of the function F, so there is no where . For each secret key we have the following relationship holding:There are only L public keys in R. Then it means that there exists one pk matching two different sk. For the equation , if there exists another satisfying , then it can get , and is a resolution to the SIS problem, therefore, the probability of this happening is negligible. For the equation , if there exists another satisfying , then it breaks Uniqueness of F, the probability of this happening is also negligible. In summary, the probability of the adversary being able to forge a successful forgery is negligible. Therefore, our scheme is satisfies tag-linkability.
- Game 0: It is type I anonymous game which . operates algorithm in the Setup phase, saves secretly, obtains from .
- Game 1: The game and Game 0 are identical, besides when submits a to , the challenger chooses randomly and set , then keeps a to respond consistently. In ROM, is unable to discern the difference between Game 1 and Game 0. Therefore, we obtain
- Game 2: The game and Game 1 are identical, besides uses simulator replace the real NIZK proof system. uses to obtain instead of using the real NIZK. By doing so, the challenger is able to generate valid proofs properly without the use of . When submits the challenge message during the challenge phase, invokes to generate the valid simulation proof instead of running the real NIZK to generate . Based on the zero-knowledge property, we have
- Game 3: The game and Game 2 are identical, besides when it is necessary to run the , first finds whether a corresponding tuple exists for the and, if so, returns the corresponding . Otherwise, takes a stochastic vector , sends it to , and adds the vector to the . So can simulate by keeping . For any vector , We can convert it to where , if adversary can distinguish between and without knowing secret key and error , may utilize the adversary to crack DLWE problem. Due to the difficulty of the DLWE problem, the probability of to distinguish between and is negligible. Thus, we haveAnd thusObviously, in Game 3, the generation of signatures is essentially replaced by random numbers, meaning that the generation of is already independent of . By the same token, when Game 0 is selected with b of 1, the change between each two games is the same as the change from Game 0 to Game 3 above, so when , Game 0 is also indistinguishable from Game 3, and since whether or , the final Game 3 obtained is identical, it can be easily obtained that when is selected and when is selected, it is indistinguishable for the adversary is indistinguishable for the adversary . Thus we haveSo our scheme satisfies type I anonymity.
- Game 0: It is type II anonymous game which . operates algorithm in the Setup phase, then sends and to .
- Game 1: The game and Game 0 are identical, besides use simulator replace the real NIZK proof system. calls simulator to produce the public parameters instead of using the real NIZK. By doing so, the challenger is able to generate valid proofs properly without the use of . When submits the challenge message during the challenge phase, invokes simulator to generate a valid simulation proof instead of running the real NIZK to generate . Based on the zero-knowledge property, we have
- Game 2: The game and Game 1 are identical, besides when it is necessary to run the , first finds whether a corresponding tuple exists for the and, if so, returns the corresponding . Otherwise, takes a stochastic vector , sends it to , and adds the vector to the . So can simulate by keeping . For any vector , We can convert it to where , if adversary can distinguish between and without knowing secret key and error , may utilize the adversary to crack DLWE problem. Due to the difficulty of the DLWE problem, the probability of an adversary being able to distinguish between and is negligible. Thus, we haveAnd thusThe same principle as the type I anonymity, we change of Game 0 to and then to Game 2, the adversary still cannot identify the distinction between Game 0 and Game 2 at , so we can get a real anonymous game where the adversary cannot distinguish whether the value of b is selected as 0 or 1. Thus, we haveSo our scheme satisfies type II anonymity.
- Adversary. Given a challenge matrix which is random, it is an instance of function uniqueness. The adversary need to look for a non-zero vector and a vector satisfying , adversary constructs the following game to attack the uniqueness of the function.
- 1.1
- . Given the system parameter , instead of running the real zero-knowledge protocol, calls simulator to produce the public parameters, and remaining parameters are generated unchanged, then sends to and is kept itself.
- 1.2
- . initializes initially empty lists , , , , and keeps the consistency of answers to adversaries by maintaining these tables. We assume that adversary must have done the following queries before forging: will submit a query with label to for the -th time where and submit a query with tuple to for the -th time where and .
- (a)
- HQuery. For the times of asking, if , will submit the label , picks a random matrix , and then sets , at last returns it to ; otherwise if , will submit the label , picks a random matrix and outputs it to .
- (b)
- HQuery. When submits a tuple , first checks if the tuple in the , if it exists, returns the corresponding . Otherwise, picks a random vector , and returns it to .
- (c)
- HQuery. When submits an , first checks if in the , if it exists, returns the corresponding . Otherwise, randomly selects a vector where satisfying , computes , and returns it to .
- (d)
- . When submits an , first checks if in the , if it exists, returns the corresponding key pairs . Otherwise, calls the with to obtain , and then runs , , algorithm to generate , and , returns to adversary , then adds tuple to .
- (e)
- . When submits an , first checks if in the , if it exists, returns the corresponding . Otherwise, runs to generate and outputs it to .
- (f)
- . When submits an and a , substitutes for .
- (g)
- . For the times of asking, if , will submit a tuple , instead of running , computes , and invokes simulator to generate the proof, the remaining steps remain unchanged, returns the generated signature to . Otherwise if , will submit a tuple , runs to compute , the remaining steps remain unchanged, returns the generated signature to .
- 1.3
- . Assume outputs two tuples and s.t.
- (a)
- ;
- (b)
- ;
- (c)
- has not been queried about and where ;
- (d)
- has made at most one of and , ;
- (e)
- .
Suppose is the location of in . - 1.4
- . Here, we assume that one of the two signatures output by the adversary is the challenge signature of the previous query, which indicates a situation where the user honestly generates a signature and the adversary forges another valid signature to trap the honest user. We supposes that is the challenge signature . According to proof of knowledge, the extractor capable of extracting witnesses of , since condition (iii) holds, according to the algorithm, there is one and only one vector at the identical position in the sequence of and is equal, which means , then we can obtain . This means that for a random matrix , we find the nonzero vector and the vector satisfying . So we have broken through the unique of function F with non-negligible probability . Therefore, it is infeasible that the adversary will succeed in attacking in this case.
- Adversary. Adversary will construct the following game. If is capable of winning type I exculpability game by a probability of , then uses adversary to break multi-input correlation intractability of H with probability .
- 2.1
- . Same as 1.1 Setup.
- 2.2
- . initializes initially empty lists , , , , and keeps consistency of answers to adversaries by maintaining these tables.
- (a)
- HQuery. When submits a label to this oracle, first checks if in the , if it exists, returns the corresponding . Otherwise, picks a random matrix , and returns it to .
- (b)
- HQuery. Same as 1.2 HQuery.
- (c)
- HQuery. Same as 1.2 HQuery.
- (d)
- . Same as 1.2 CreateUserQuery.
- (e)
- . Same as 1.2 PartialPrivateKeyQuery.
- (f)
- . Same as 1.2 ReplacePublicKeyQuery.
- (g)
- . When submits a tuple to this oracle, first checks if tuple in the , if it exists, returns the corresponding signature . Otherwise, runs to generate signature and returns it to , then adds the tuple to .
- 2.3
- . Same as 1.3 Forgery.
- 2.4
- . In this case, neither tuple nor tuple has been made . That is, the user did not perform a signature, but the adversary forged two valid signatures to trap the user. Since condition (v) holds, according to the definition of algorithm, the sequence and value of index in the sequence are equal which meansSame as case 1, according to proof of knowledge, there exists an extractor capable of extracting witnesses and from and respectively,Then, it holds thatHere we also consider two situations, the first situation is when , but in this case, means that there is a dishonest user who signs two different messages, so the output is targeted to that dishonest user. Another situation is when , we can getit means that , . As shown in [50], is a sparse relation. Thus, if wins the type I exculpability game with non-negligible probability , then can break the multi-input correlation intractability of with non-negligible probability . It contradicts the multi-input correlation intractability of .
- Adversary. Given a challenge matrix which is random, it is an instance of function uniqueness. The adversary need to look for a non-zero vector and a vector satisfying , adversary constructs the following game to attack the uniqueness of the function.
- 3.1
- Setup. Similar to 1.1 Setup, except that does not require confidentiality but is sent to the adversary along with the public parameter .
- 3.2
- . initializes initially empty lists , , , , , and keeps consistency of answers to adversaries by maintaining these tables. We assume that adversary must have done the following queries before forging: will submit a query with label to for the -th time where and submit a query with tuple to for the -th time where and .
- (a)
- Query. For the times of asking, if , will submit the label , picks a random matrix and sets , at last returns it to ; otherwise if , will submit the label , picks a random matrix and returns it to .
- (b)
- Query. Same as 1.2 Query.
- (c)
- Query. When submits an , randomly selects a vector and sets , then returns to .
- (d)
- CreateUserQuery. When submits an , first checks if in the , if it exists, returns the corresponding key pairs . Otherwise, calls to obtain when exists in , if exists in , calls algorithm to obtain , and then runs , , algorithm to generate , and , sends to adversary , then adds tuple to .
- (e)
- ParticalPrivateKeyQuery. When submits an , first checks if the exists in , if it exists, returns the corresponding ; otherwise checks if the exists in , if it exists, returns the corresponding ; otherwise checks if the exists in , if it exists, runs to get and returns it to ; otherwise, runs to get , and returns to .
- (f)
- ReplacePublicKeyQuery. When submits an and a , replaces the user’s public key with .
- (g)
- SignQuery. For the times of asking, if , will submit a tuple , instead of running , computes , and invokes simulator to generate the proof, the remaining steps remain unchanged, returns the generated signature to . Otherwise if , will submit a tuple , runs to compute , the remaining steps remain unchanged, returns the generated signature to .
- 3.3
- . Assume outputs two tuples and s.t.
- (a)
- ;
- (b)
- ;
- (c)
- has not been queried about and where ;
- (d)
- has made at most one of and ;
- (e)
- .
Suppose is the location of in . - 3.4
- . Here, we assume that one of the two signatures output by the adversary is the challenge signature of the previous query, which indicates a situation where the user honestly generates a signature and the adversary forges another valid signature to trap the honest user. We supposes that is the challenge signature . According to proof of knowledge, the extractor capable of extracting witnesses of , since condition (iii) holds, according to the algorithm, there is one and only one vector at the identical position in the sequence of and is equal, which means , then we can obtain . This means that for a random matrix , we find the nonzero vector and the vector satisfying . So we have broken through the unique of function F with non-negligible probability . Therefore, it is infeasible that the adversary will succeed in attacking in this case.
- Adversary. Adversary will construct the following game. If adversary can break the type II exculpability game with probability , then uses adversary to break the multi-input correlation intractability of the hash function H with probability .
- 4.1
- . Same as 3.1 Setup.
- 4.2
- . initializes initially empty lists , , , , and keeps consistency of answers to adversaries by maintaining these tables.
- (a)
- HQuery. Same as 2.2 HQuery.
- (b)
- HQuery. Same as 1.2 HQuery.
- (c)
- HQuery. Same as 3.2 HQuery.
- (d)
- . Same as 3.2 CreateUserQuery.
- (e)
- . Same as 3.2 PartialPrivateKeyQuery.
- (f)
- . Same as 3.2 ReplacePublicKeyQuery.
- (g)
- . Same as 2.2 SignQuery.
- 4.3
- . Same as 3.3 Forgery.
- 4.4
- . In this case, neither tuple nor tuple has been made . Similar to the Analysis in 4.4, we can obtain the following equation as wellit means that , . As shown in [50], is a sparse relation. Thus, if break the type II exculpability game with non-negligible probability , then may break the multi-input correlation intractability of with non-negligible probability . It contradicts the multi-input correlation intractability of .
7. Efficiency
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full Name |
| RS | Ring Signature |
| LRS | Linkable Ring Signature |
| TRS | Traceable Ring Signature |
| SIS | Short Integer Solution |
| DLWE | Decisional Learning With Error |
| ROM | Random Oracle Model |
| QROM | Quantum Random Oracle Model |
| ZK | Zero-Knowledge |
| ZKAoK | Zero-Knowledge Argument of Knowledge |
| NIZKAoK | Non-interactive Zero-Knowledge Argument of Knowledge |
| PRF | Pseudorandomness Function |
| VANET | Vehicular Ad-Hoc Network |
| PKI | Public Key Infrastructure |
| CA | Certificate Authority |
| CMP | Certificate Management Problem |
| KGC | Key Generation Center |
| KEP | Key Escrow Problem |
| SPK | Signature Proof Knowledge |
| CLPKC | Certificate-less Public Key Encryption |
| CLTRS | Certificate-less Traceable Ring Signature |
| CUQ | Create User Query |
| PPKQ | Partial Private Key Query |
| RPKQ | Replace Public Key Query |
| SQ | Sign Query |
References
- Chow, S.S.M.; Liu, J.K.; Wong, D.S. Robust Receipt-Free Election System with Ballot Secrecy and Verifiability. In Proceedings of the Network and Distributed System Security Symposium, NDSS 2008, The Internet Society, San Diego, CA, USA, 10–13 February 2008. [Google Scholar]
- Zhou, Y.; Dong, S.; Yang, Y. Ring signature scheme based on lattice and its application on anonymous electronic voting. Ksii Trans. Internet Inf. Syst. (Tiis) 2022, 16, 287–304. [Google Scholar]
- Tsang, P.P.; Wei, V.K. Short Linkable Ring Signatures for E-Voting, E-Cash and Attestation. In Proceedings of the Information Security Practice and Experience, First International Conference, ISPEC 2005, Singapore, 11–14 April 2005; Volume 3439, pp. 48–60. [Google Scholar] [CrossRef]
- Tang, F.; Pang, J.; Cheng, K.; Gong, Q. Multiauthority Traceable Ring Signature Scheme for Smart Grid Based on Blockchain. Wirel. Commun. Mob. Comput. 2021, 2021, 5566430:1–5566430:9. [Google Scholar] [CrossRef]
- Han, L.; Cao, S.; Yang, X.; Zhang, Z. Privacy Protection of VANET Based on Traceable Ring Signature on Ideal Lattice. IEEE Access 2020, 8, 206581–206591. [Google Scholar] [CrossRef]
- Gu, K.; Wang, L.; Wu, N.; Liao, N. Traceable Certificateless Ring Signature Scheme for no Full Anonymous Applications. Int. J. Netw. Secur. 2018, 20, 762–773. [Google Scholar]
- Diffie, W.; Hellman, M.E. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef] [Green Version]
- Shamir, A. Identity-Based Cryptosystems and Signature Schemes. In Proceedings of the Advances in Cryptology, Proceedings of CRYPTO ’84, Santa Barbara, CA, USA, 19–22 August 1984; Volume 196, pp. 47–53. [Google Scholar] [CrossRef] [Green Version]
- Al-Riyami, S.S.; Paterson, K.G. Certificateless Public Key Cryptography. In Proceedings of the Advances in Cryptology—ASIACRYPT 2003, 9th International Conference on the Theory and Application of Cryptology and Information Security, Taipei, Taiwan, 30 November–4 December 2003; Volume 2894, pp. 452–473. [Google Scholar] [CrossRef] [Green Version]
- Bisheh-Niasar, M.; Azarderakhsh, R.; Kermani, M.M. Cryptographic Accelerators for Digital Signature Based on Ed25519. IEEE Trans. Very Large Scale Integr. Syst. 2021, 29, 1297–1305. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for Quantum Computation: Discrete Logarithms and Factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, IEEE Computer Society, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar] [CrossRef]
- Ni, Z.; Kundi, D.; O’Neill, M.; Liu, W. A High-Performance SIKE Hardware Accelerator. IEEE Trans. Very Large Scale Integr. Syst. 2022, 30, 803–815. [Google Scholar] [CrossRef]
- Tian, J.; Wu, B.; Wang, Z. High-Speed FPGA Implementation of SIKE Based on an Ultra-Low-Latency Modular Multiplier. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3719–3731. [Google Scholar] [CrossRef]
- Sarker, A.; Kermani, M.M.; Azarderakhsh, R. Efficient Error Detection Architectures for Postquantum Signature Falcon’s Sampler and KEM SABER. IEEE Trans. Very Large Scale Integr. Syst. 2022, 30, 794–802. [Google Scholar] [CrossRef]
- Berzati, A.; Viera, A.C.; Chartouni, M.; Madec, S.; Vergnaud, D.; Vigilant, D. A Practical Template Attack on CRYSTALS-Dilithium. Cryptology ePrint Archive, Paper 2023/050. Available online: https://eprint.iacr.org/2023/050 (accessed on 20 February 2023).
- Ajtai, M. Generating Hard Instances of Lattice Problems (Extended Abstract). In Proceedings of the Twenty-Eighth Annual ACM Symposium on the Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 99–108. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Tauman, Y. How to Leak a Secret. In Proceedings of the Advances in Cryptology—ASIACRYPT 2001, 7th International Conference on the Theory and Application of Cryptology and Information Security, Gold Coast, Australia, 9–13 December 2001; Volume 2248, pp. 552–565. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Kim, K. ID-Based Blind Signature and Ring Signature from Pairings. In Proceedings of the Advances in Cryptology—ASIACRYPT 2002, 8th International Conference on the Theory and Application of Cryptology and Information Security, Queenstown, New Zealand, 1–5 December 2002; Volume 2501, pp. 533–547. [Google Scholar] [CrossRef] [Green Version]
- Dodis, Y.; Kiayias, A.; Nicolosi, A.; Shoup, V. Anonymous Identification in Ad Hoc Groups. In Proceedings of the Advances in Cryptology—EUROCRYPT 2004, International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; Volume 3027, pp. 609–626. [Google Scholar] [CrossRef] [Green Version]
- Herranz, J.; Sáez, G. New Identity-Based Ring Signature Schemes. In Proceedings of the Information and Communications Security, 6th International Conference, ICICS 2004, Malaga, Spain, 27–29 October 2004; Volume 3269, pp. 27–39. [Google Scholar] [CrossRef]
- Chan, T.K.; Fung, K.; Liu, J.K.; Wei, V.K. Blind Spontaneous Anonymous Group Signatures for Ad Hoc Groups. In Proceedings of the Security in Ad-Hoc and Sensor Networks, First European Workshop, ESAS 2004, Berlin/Heidelberg, Germany, 6 August 2004; Volume 3313, pp. 82–94. [Google Scholar] [CrossRef]
- Chow, S.S.M.; Yiu, S.; Hui, L.C.K. Efficient Identity Based Ring Signature. In Proceedings of the Applied Cryptography and Network Security, Third International Conference, ACNS 2005, New York, NY, USA, 7–10 June 2005; Volume 3531, pp. 499–512. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Susilo, W.; Mu, Y. Convertible identity-based anonymous designated ring signatures. Int. J. Secur. Netw. 2006, 1, 218–225. [Google Scholar] [CrossRef]
- Liu, J.K.; Wei, V.K.; Wong, D.S. Linkable Spontaneous Anonymous Group Signature for Ad Hoc Groups (Extended Abstract). In Proceedings of the Information Security and Privacy: 9th Australasian Conference, ACISP 2004, Sydney, Australia, 13–15 July 2004; Volume 3108, pp. 325–335. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.K.; Wong, D.S. Enhanced Security Models and a Generic Construction Approach for Linkable Ring Signature. Int. J. Found. Comput. Sci. 2006, 17, 1403–1422. [Google Scholar] [CrossRef]
- Bender, A.; Katz, J.; Morselli, R. Ring Signatures: Stronger Definitions, and Constructions without Random Oracles. J. Cryptol. 2009, 22, 114–138. [Google Scholar] [CrossRef]
- Au, M.H.; Liu, J.K.; Susilo, W.; Yuen, T.H. Certificate Based (Linkable) Ring Signature. In Proceedings of the Information Security Practice and Experience, Third International Conference, ISPEC 2007, Hong Kong, China, 7–9 May 2007; Volume 4464, pp. 79–92. [Google Scholar] [CrossRef]
- Yuen, T.H.; Liu, J.K.; Au, M.H.; Susilo, W.; Zhou, J. Efficient Linkable and/or Threshold Ring Signature Without Random Oracles. Comput. J. 2013, 56, 407–421. [Google Scholar] [CrossRef] [Green Version]
- Deng, L.; Jiang, Y.; Ning, B. Identity-Based Linkable Ring Signature Scheme. IEEE Access 2019, 7, 153969–153976. [Google Scholar] [CrossRef]
- Deng, L.; Shi, H.; Gao, Y. Certificateless Linkable Ring Signature Scheme. IEEE Access 2020, 8, 54641–54651. [Google Scholar] [CrossRef]
- Fujisaki, E.; Suzuki, K. Traceable Ring Signature. In Proceedings of the Public Key Cryptography—PKC 2007, 10th International Conference on Practice and Theory in Public-Key Cryptography, Beijing, China, 16–20 April 2007; Volume 4450, pp. 181–200. [Google Scholar] [CrossRef] [Green Version]
- Fujisaki, E. Sub-Linear Size Traceable Ring Signatures without Random Oracles. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2012, 95-A, 151–166. [Google Scholar] [CrossRef]
- Au, M.H.; Liu, J.K.; Susilo, W.; Yuen, T.H. Secure ID-based linkable and revocable-iff-linked ring signature with constant-size construction. Theor. Comput. Sci. 2013, 469, 1–14. [Google Scholar] [CrossRef]
- Bultel, X.; Lafourcade, P. k-Times Full Traceable Ring Signature. In Proceedings of the 11th International Conference on Availability, Reliability and Security, ARES 2016 IEEE Computer Society, Salzburg, Austria, 31 August–2 September 2016; pp. 39–48. [Google Scholar] [CrossRef] [Green Version]
- Gu, K.; Dong, X.; Wang, L. Efficient traceable ring signature scheme without pairings. Adv. Math. Commun. 2020, 14, 207–232. [Google Scholar] [CrossRef] [Green Version]
- Peng, X.; Gu, K.; Liu, Z.; Zhang, W. Traceable Identity-Based Ring Signature for Protecting Mobile IoT Devices. In Proceedings of the Data Mining and Big Data—6th International Conference, DMBD 2021, Guangzhou, China, 20–22 October 2021; 2021; Volume 1454, pp. 158–166. [Google Scholar] [CrossRef]
- Brakerski, Z.; Kalai, Y.T. A Framework for Efficient Signatures, Ring Signatures and Identity Based Encryption in the Standard Model. IACR Cryptol. ePrint Arch. 2010, 2010, 86. [Google Scholar]
- Tian, M.M.; Huang, L.S.; Yang, W. Efficient lattice-based ring signature scheme. Jisuanji Xuebao (Chin. J. Comput.) 2012, 35, 712–718. [Google Scholar] [CrossRef]
- Lyubashevsky, V. Lattice Signatures without Trapdoors. In Proceedings of the Advances in Cryptology—EUROCRYPT 2012—31st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Volume 7237, pp. 738–755. [Google Scholar] [CrossRef] [Green Version]
- Libert, B.; Ling, S.; Nguyen, K.; Wang, H. Zero-Knowledge Arguments for Lattice-Based Accumulators: Logarithmic-Size Ring Signatures and Group Signatures Without Trapdoors. In Proceedings of the Advances in Cryptology—EUROCRYPT 2016—35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, 8–12 May 2016; Volume 9666, pp. 1–31. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Zhao, R.; Zhang, Y. Lattice-based ring signature scheme under the random oracle model. Int. J. High Perform. Comput. Netw. 2018, 11, 332–341. [Google Scholar] [CrossRef]
- Lu, X.; Au, M.H.; Zhang, Z. Raptor: A Practical Lattice-Based (Linkable) Ring Signature. In Proceedings of the Applied Cryptography and Network Security—17th International Conference, ACNS 2019, Bogota, Colombia, 5–7 June 2019; Volume 11464, pp. 110–130. [Google Scholar] [CrossRef]
- Melchor, C.A.; Bettaieb, S.; Boyen, X.; Fousse, L.; Gaborit, P. Adapting Lyubashevsky’s Signature Schemes to the Ring Signature Setting. In Proceedings of the Progress in Cryptology—AFRICACRYPT 2013, 6th International Conference on Cryptology in Africa, Cairo, Egypt, 22–24 June 2013; Volume 7918, pp. 1–25. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.; Au, M.H.; Lai, J.; Xu, Q.; Yu, Z. Lattice-Based Techniques for Accountable Anonymity: Composition of Abstract Stern’s Protocols and Weak PRF with Efficient Protocols from LWR. IACR Cryptol. ePrint Arch. 2017, 2017, 781. [Google Scholar]
- Torres, W.A.A.; Steinfeld, R.; Sakzad, A.; Liu, J.K.; Kuchta, V.; Bhattacharjee, N.; Au, M.H.; Cheng, J. Post-Quantum One-Time Linkable Ring Signature and Application to Ring Confidential Transactions in Blockchain (Lattice RingCT v1.0). In Proceedings of the Information Security and Privacy—23rd Australasian Conference, ACISP 2018, Wollongong, NSW, Australia, 11–13 July 2018; Volume 10946, pp. 558–576. [Google Scholar] [CrossRef]
- Baum, C.; Lin, H.; Oechsner, S. Towards Practical Lattice-Based One-Time Linkable Ring Signatures. In Proceedings of the Information and Communications Security—20th International Conference, ICICS 2018, Lille, France, 29–31 October 2018; Volume 11149, pp. 303–322. [Google Scholar] [CrossRef] [Green Version]
- Le, H.Q.; Vo, B.; Duong, D.H.; Susilo, W.; Le, N.T.; Fukushima, K.; Kiyomoto, S. Identity-Based Linkable Ring Signatures From Lattices. IEEE Access 2021, 9, 84739–84755. [Google Scholar] [CrossRef]
- Hu, M.; Liu, Z. Lattice-Based Linkable Ring Signature in the Standard Model. IACR Cryptol. ePrint Arch. 2022, 9, 101. [Google Scholar]
- Ye, Q.; Wang, M.; Meng, H.; Xia, F.; Yan, X. Efficient Linkable Ring Signature Scheme over NTRU Lattice with Unconditional Anonymity. Comput. Intell. Neurosci. 2022, 2022, 8431874. [Google Scholar] [CrossRef]
- Feng, H.; Liu, J.; Li, D.; Li, Y.; Wu, Q. Traceable ring signatures: General framework and post-quantum security. Des. Codes Cryptogr. 2021, 89, 1111–1145. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, X. A Post-quantum Certificateless Ring Signature Scheme for Privacy-Preserving of Blockchain Sharing Economy. In Proceedings of the Artificial Intelligence and Security—7th International Conference, ICAIS 2021, Dublin, Ireland, 19–23 July 2021; Volume 12737, pp. 265–278. [Google Scholar] [CrossRef]
- Dong, S.; Zhou, Y.; Yang, Y.; Yao, Y. A certificateless ring signature scheme based on lattice. Concurr. Comput. Pract. Exp. 2022, 34, e7385. [Google Scholar] [CrossRef]
- Yang, R.; Au, M.H.; Zhang, Z.; Xu, Q.; Yu, Z.; Whyte, W. Efficient Lattice-Based Zero-Knowledge Arguments with Standard Soundness: Construction and Applications. In Proceedings of the Advances in Cryptology—CRYPTO 2019—39th Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2019; Volume 11692, pp. 147–175. [Google Scholar] [CrossRef]
- Regev, O. On lattices, learning with errors, random linear codes, and cryptography. In Proceedings of the 37th Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 22–24 May 2005; pp. 84–93. [Google Scholar] [CrossRef]
- Banerjee, A.; Peikert, C.; Rosen, A. Pseudorandom Functions and Lattices. In Proceedings of the Advances in Cryptology—EUROCRYPT 2012—31st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Volume 7237, pp. 719–737. [Google Scholar] [CrossRef] [Green Version]
- Micciancio, D.; Peikert, C. Trapdoors for Lattices: Simpler, Tighter, Faster, Smaller. In Proceedings of the Advances in Cryptology—EUROCRYPT 2012—31st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Volume 7237, pp. 700–718. [Google Scholar] [CrossRef] [Green Version]
- Holmgren, J.; Lombardi, A. Cryptographic Hashing from Strong One-Way Functions (Or: One-Way Product Functions and Their Applications). In Proceedings of the 59th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2018, Paris, France, 7–9 October 2018; pp. 850–858. [Google Scholar] [CrossRef]
- Libert, B.; Ling, S.; Nguyen, K.; Wang, H. Zero-Knowledge Arguments for Lattice-Based PRFs and Applications to E-Cash. In Proceedings of the Advances in Cryptology—ASIACRYPT 2017—23rd International Conference on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, 3–7 December 2017; Volume 10626, pp. 304–335. [Google Scholar] [CrossRef] [Green Version]
- Ling, S.; Nguyen, K.; Stehlé, D.; Wang, H. Improved Zero-Knowledge Proofs of Knowledge for the ISIS Problem, and Applications. In Proceedings of the Public-Key Cryptography—PKC 2013—16th International Conference on Practice and Theory in Public-Key Cryptography, Nara, Japan, 26 February–1 March 2013; Volume 7778, pp. 107–124. [Google Scholar] [CrossRef] [Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Huang, J.; Huang, Q.; Lan, L.; Au, M.H.A. A Lattice-Based Certificateless Traceable Ring Signature Scheme. Information 2023, 14, 160. https://doi.org/10.3390/info14030160
Liang J, Huang J, Huang Q, Lan L, Au MHA. A Lattice-Based Certificateless Traceable Ring Signature Scheme. Information. 2023; 14(3):160. https://doi.org/10.3390/info14030160
Chicago/Turabian StyleLiang, Junbin, Jianye Huang, Qiong Huang, Liantao Lan, and Man Ho Allen Au. 2023. "A Lattice-Based Certificateless Traceable Ring Signature Scheme" Information 14, no. 3: 160. https://doi.org/10.3390/info14030160





