Abstract
The use of decision trees for obtaining and representing clustering solutions is advantageous, due to their interpretability property. We propose a method called Decision Trees for Axis Unimodal Clustering (DTAUC), which constructs unsupervised binary decision trees for clustering by exploiting the concept of unimodality. Unimodality is a key property indicating the grouping behavior of data around a single density mode. Our approach is based on the notion of an axis unimodal cluster: a cluster where all features are unimodal, i.e., the set of values of each feature is unimodal as decided by a unimodality test. The proposed method follows the typical top-down splitting paradigm for building axis-aligned decision trees and aims to partition the initial dataset into axis unimodal clusters by applying thresholding on multimodal features. To determine the decision rule at each node, we propose a criterion that combines unimodality and separation. The method automatically terminates when all clusters are axis unimodal. Unlike typical decision tree methods, DTAUC does not require user-defined hyperparameters, such as maximum tree depth or the minimum number of points per leaf, except for the significance level of the unimodality test. Comparative experimental results on various synthetic and real datasets indicate the effectiveness of our method.
1. Introduction
Decision trees are popular machine learning models mainly due to their interpretability since their decision-making process can be directly represented as a set of rules. Each internal node in a decision tree contains a decision rule that determines the child node to be visited, while leaf nodes provide the final decision. In a typical decision tree, the decision rule of an internal node involves simple thresholding on a feature value, thus it is straightforward to interpret. From a geometrical point of view, typical decision trees (often called axis-aligned trees) partition the data space into hyperrectangular regions.
Decision trees have been widely employed for supervised learning tasks. The general approach for building decision trees follows a greedy top-down iterative splitting strategy of the original dataset into subsets. At each step, a decision rule is determined that splits the dataset under consideration so that a certain criterion is improved. For example, in the case of classification problems the criterion is related to the homogeneity of the resulting partition with respect to class labels. In this way partitions into subsets that contain data of the same class are preferred. Well-known supervised decision tree algorithms include Classification and Regression Trees (CART) [1], Iterative Dichotomiser 3 (ID3) [2], C4.5 [3] and Chi-squared Automatic Interaction Detector (CHAID) [4]. In CART the partition tree is built using a few binary conditions obtained from the original data features and uses the Gini index as a splitting criterion. ID3 and C4.5 (an improvement upon ID3), employ the class entropy measure as the splitting criterion, while CHAID uses the statistical test to determine the best split during the tree-growing process. It should be stressed that in the supervised case, the use of cross-validation techniques enables the determination of appropriate values for the various hyperparameters of the methods (e.g., maximum tree depth, minimum number of leaves, etc.).
1.1. Decision Trees for Interpretable Clustering
Clustering methods aim at partitioning a set of points into groups, the clusters, such that data within the same group share common characteristics and differ from data in other groups. Most of the popular clustering algorithms, such as k-means, do not directly provide any explanation of the clustering result. To overcome this limitation, some research works propose the use of decision tree models for clustering in order to achieve explainability. Tree-based clustering methods return unsupervised binary trees that provide an interpretation of the data partitioning.
While in the supervised case, the construction of decision trees is relatively straightforward due to the presence of target information, this task becomes more challenging in the unsupervised case (e.g., clustering) where only data points are available. The difficulty arises for two reasons:
- Definition of splitting criterion. Metrics like information gain or Gini index, which are commonly used to guide the splitting process in supervised learning, cannot be applied in unsupervised learning, since no data labels are available.
- Specification of hyperparameters (e.g., number of clusters), since cross-validation cannot be applied.
Despite the apparent difficulties, several methods have been proposed to build decision trees for clustering. The category of indirect methods typically follows a two-step procedure: first, they obtain cluster labels using a clustering algorithm, such as k-means, and then they apply a supervised decision tree algorithm to build a decision tree that interprets the resulting clusters. For example, in [5], labels obtained from k-means are used as a preliminary step in tree construction. Similarly, in [6], the centroids derived from k-means are also involved in splitting procedures. Indirect methods heavily rely on the clustering result of their first stage. Moreover, fitting the cluster labels with an axis-aligned decision tree may be problematic since the clusters are typically of spherical or ellipsoidal shape. It is also assumed that the number of clusters is given by the user.
Direct methods integrate decision tree construction and partitioning into clusters. Many of them follow the typical top-down splitting procedure used in the supervised case but exploit unsupervised splitting criteria, e.g., compactness of the resulting subsets. Some direct unsupervised methods are described below.
In [7] a top-down tree induction framework with applicability to clustering (Predictive Clustering Trees) as well as to supervised learning tasks is proposed. It works similarly to a standard decision tree with the main difference being that the variance function and the prototype function, used to compute a label for each leaf, are treated as parameters that must be instantiated according to the specific learning task. The splitting criterion is based on the maximum separation (inter-cluster distances) between two clusters, while after the construction of the tree, a pruning step is applied using a validation set.
In [8] four measures for selecting the most appropriate split feature and two algorithms for partitioning the data at each decision node are proposed. The split thresholds are computed either by detecting the top valley points of the histogram along a specific feature or by considering the inhomogeneity (information content) of the data with respect to some feature. Distance-related measures and histogram-based measures are proposed for selecting an appropriate split feature. For example, the deviation of a feature histogram from the uniform distribution is considered (although it depends on the bin size).
In [9] an unsupervised method is proposed, called Clustering using Unsupervised Binary Trees (CUBT), which achieves clustering through binary trees. This method involves a three-stage procedure: maximal tree construction, pruning, and joining. First, a maximal tree is grown by applying recursive binary splits to reduce the heterogeneity of the data (based on the input’s covariance matrices) within the new subsamples. Next, tree pruning is applied using a criterion of minimal dissimilarity. Finally, similar clusters (leaves of the tree) are joined, even if they do not necessarily share the same direct ascendant. Although CUBT constructs clusters directly using trees, it relies on several parameters throughout the three-stage process, while post hoc methods are required to combine leaves into unified clusters, which adds to the complexity and parameter dependency of the approach.
An alternative method for constructing decision trees for clustering is proposed in [10]. At first, noisy data points (uniformly distributed) are added to the original data space. Then, a standard (supervised) decision tree is constructed by classifying both the original data points and the noisy data points under the assumption that the original data points and the noisy data points belong to two different classes. A modified purity criterion is used to evaluate each split, in a way that dense regions (original data) as well as sparse regions (noisy data) are identified. However, this method requires additional preprocessing through the introduction of synthetic data in order to create the binary classification setting.
In contrast to axis-aligned trees, oblique trees allow test conditions that involve multiple features simultaneously, enabling oblique splits across the feature space. In [11] oblique trees for clustering are proposed, where each split is a hyperplane defined by a small number of features. Although oblique trees can produce more compact trees, finding the optimal test condition for a given node can be computationally expensive, while they may not always be interpretable [12].
An interesting direct approach [13] exploits the method of Optimal Classification Trees (OCT) [14], which are built in a single step by solving a mixed-integer optimization problem. Specifically, in [13] the Interpretable Clustering via Optimal Trees (ICOT) algorithm is presented, where two cluster validation criteria, the Silhouette Metric [15] and the Dunn Index [16] are chosen as objective functions. The ICOT algorithm begins with the initialization of a tree, which serves as the starting point. Two options are provided for a tree initialization: either a greedy tree is constructed or the k-means is used as a warm-start algorithm to partition the data into clusters and then OCT is used to generate a tree that separates these clusters. Next, ICOT runs a local search procedure until the objective value (Silhouette Metric or Dunn Index) reaches an optimum value. This process is repeated from many different starting trees, generating many candidate clustering trees. The final tree is chosen as the one with the highest cluster quality score across all candidate trees and is returned as the output of the algorithm. ICOT is able to handle both numerical and categorical features as well as mixed-type features efficiently, by introducing an appropriate distance metric. Although it performs well on very small datasets and trees, it is slower compared to other methods. In addition, there exist hyperparameters that have to be tuned by the user, such as the maximum depth of the tree and the minimum number of observations in each cluster.
1.2. Unimodality-Based Clustering
Data unimodality is closely related to clustering since unimodality indicates grouping behavior around a single mode (peak). A distribution that is not unimodal is called multimodal with two or more modes. Assessing data unimodality means estimating whether the data have been generated by an arbitrary unimodal distribution. Recognizing unimodality is fundamental for understanding data structure; for instance, clustering methods are irrelevant for unimodal data as they form a single coherent cluster [17].
A few methods exist for assessing the unimodality of univariate datasets such as the well-known dip-test for unimodality [18] and the more recent UU-test [19]. It should be noted that those tests are applied to univariate data only. To decide on the unimodality of a multidimensional dataset, some techniques have been proposed that apply the dip-test on univariate datasets containing for example 1-d projections of the data or distances between data points. Several have been also used in the case of multidimensional datasets. Unimodality assessment has been used either in a top-down fashion, by splitting clusters that are decided as multimodal [20,21], or in a bottom-up fashion by merging clusters whose union is decided as unimodal [22]. In addition to intuitive justification, the use of unimodality provides a natural way to terminate the splitting or merging procedure, thus allowing for the automated estimation of the number of clusters. Since those methods provide ellipsoidal or arbitrarily shaped clusters the results are not interpretable. We aim to tackle this issue by proposing a unimodality-based method for the construction of decision trees for clustering.
1.3. Contribution
Our approach is based on the notion of an axis unimodal cluster: a cluster where all features are unimodal, i.e., the set of values of each feature is unimodal as decided by a unimodality test. The proposed method, called Decision Trees for Axis Unimodal Clustering (DTAUC), follows the typical top-down splitting paradigm for building axis-aligned decision trees and aims to partition the initial dataset into axis unimodal clusters. The decision rule at each node involves an appropriately selected feature and the corresponding threshold value. More specifically, given the dataset at each node, the multimodal features are first detected. For each multimodal feature, we follow a greedy strategy to detect the best threshold value (denoted as split threshold) that splits the set of feature values into subsets so that the unimodality of the partition is increased. We propose a criterion to assess the unimodality of the partition based on the p-values provided by the unimodality test. To improve performance, we combine this criterion with another one that measures the separation of data points before and after the split point, thus obtaining the final criterion used to assess the quality of splitting. Based on this criterion, the best-split threshold for a multimodal feature is determined. The procedure is repeated for every multimodal feature and the feature-threshold pair of highest quality is used to define the decision rule of the node. When the data subset in a node does not contain any multimodal features, i.e., it is axis unimodal, no further splitting occurs, the node is characterized as leaf and a cluster label is assigned to this node. In this way at the end of the method, a partitioning of the original dataset into axis unimodal clusters has been achieved that is interpretable since it is represented by an axis-aligned decision tree.
The proposed DTAUC algorithm is direct (e.g., does not employ k-means as a preprocessing step), end-to-end and relies on the intuitively justified notion of unimodality. It is simple to implement and does not employ computationally expensive optimization methods. It contains no hyperparameters except for the statistical significance level of the unimodality test. The latter remark is important since most unsupervised decision tree methods include hyperparameters such as number of clusters, maximum tree depth, etc., which are difficult to tune in an unsupervised setting.
The outline of the paper is as follows: in Section 2 we provide the necessary definitions and notations. The notion of unimodality is explained, the dip-test for unimodality is briefly presented and the definition of axis unimodal cluster is provided. In Section 3 we describe the proposed method (DTAUC) for constructing unsupervised decision trees for clustering that mainly relies on the computation of appropriate split thresholds for partitioning multimodal features. Comparative experimental results are provided in Section 4, while in Section 5 we provide conclusions and directions for future work.
2. Notations—Definitions
In this section, we provide some definitions needed to present and clarify our method. At first, we define the unimodality for univariate datasets and refer to a widely used statistical test, namely the dip-test [18], for deciding on the unimodality of a univariate dataset. Next, we present the definition for an axis unimodal dataset and provide notations related to the binary decision tree which is built by our method.
2.1. Unimodality of Univariate Data
Let , and an ordered univariate dataset containing distinct real numbers. For an interval [a,b], we define the subset of X whose elements belong to that interval. Moreover, we denote as the empirical cumulative distribution function (ecdf) of X, defined as follows:
where is the indicator function: . It also holds that if , if .
In what concerns the unimodality of a distribution there are two definition options. The first relies on the probability density function (pdf): a pdf is unimodal if it has a single mode; a region where the density becomes maximum, while non-increasing density is observed when moving away from the mode. In other words, a pdf is a unimodal function if for some value m, it is monotonically increasing for and monotonically decreasing for . In that case, the maximum value of is and there are no other local maxima. The second definition option relies on the cumulative distribution function (cdf): a cdf is unimodal if there exist two points and such that can be divided into three parts: (a) a convex part , (b) a constant part and (c) a concave part . It is worth mentioning that it is possible for either the first two parts or the last two parts to be missing. It should be stressed that the uniform distribution is unimodal and its cdf is linear. A distribution that is not unimodal is called multimodal with two or more modes. Those modes typically appear as distinct peaks (local maxima) in the pdf plot. A distribution with exactly two modes is called bimodal.
2.2. The Dip-Test for Unimodality
In order to decide on the unimodality of a univariate dataset, we use Hartigans’ dip-test [18] which constitutes the most popular unimodality test. Given a 1-d dataset , , it computes the dip statistic as the maximum difference between the ecdf of the data and the unimodal distribution function that minimizes that maximum difference. The uniform distribution is the asymptotically least favorable unimodal distribution, thus the distribution of the test statistic (dip statistic) is determined asymptotically and empirically through sampling from the uniform distribution. Specifically, the dip-test computes the value, which is the departure from the unimodality of the ecdf. In other words, the dip statistic computes the minimum among the maximum deviations observed between the ecdf F and the cdfs from the family of unimodal distributions. The dip-test returns not only the dip value but also the statistical significance of the computed dip value, i.e., a p-value. To compute the p-value, the class of uniform distributions U is used as the null hypothesis, since its dip values are stochastically larger compared to other unimodal distributions, such as those having exponentially decreasing tails. The computation of the p-value uses b bootstrap sets () of n observations each sampled from the uniform distribution. p-value is computed as the probability of being less than the :
The null hypothesis that F is unimodal, is accepted at significance level a if p-value , otherwise is rejected in favor of the alternative hypothesis which suggests multimodality. The dip-test has a runtime of [18], but since its input must be sorted to create the ecdf, the effective runtime for this part of the technique is .
Figure 1 illustrates examples of unimodal and multimodal datasets in terms of pdf plots (histograms) and ecdf plots. The p-values provided by the dip-test are also presented above each subfigure. In Figure 1a a unimodal dataset generated by a Gaussian distribution is illustrated along with the corresponding p-value . p-values close to 1 indicate unimodality and this is also evident in that case. In contrast, Figure 1b presents a dataset generated by two close Gaussian distributions which does not clearly constitute a unimodal or multimodal dataset. This uncertainty is indicated by the computed p-value of 0.08, which is closer to 0. In this case, the significance level defined by the user plays a crucial role in determining unimodality. For example, if the significance level is set to , then a p-value less than leads to the dataset being determined multimodal. However, with significance levels of or , the dataset would be considered unimodal. In Figure 1c,d two strongly multimodal datasets are shown, with two and three peaks, respectively. The p-value is 0 in both datasets, and the test decides multimodality regardless of the significance level chosen by the user.
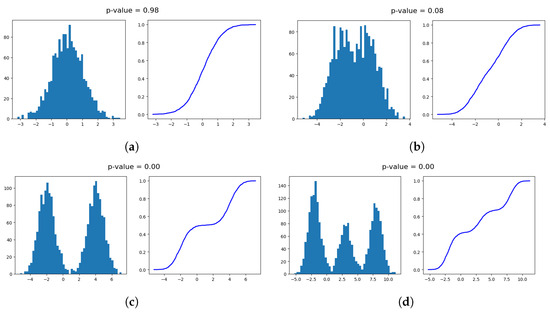
Figure 1.
Histogram and ecdf plots of unimodal and multimodal univariate datasets. The p-values provided by the dip-test are also presented. (a) Unimodal dataset. (b) Borderline case of unimodal dataset (with two close peaks). (c) Multimodal dataset (with two peaks). (d) Multimodal dataset (with three peaks).
2.3. Axis Unimodal Dataset
Let be a dataset consisting of data vectors in a d-dimensional space. Each point can be represented as a vector , where denotes the j-th feature of x for . We also denote as the j-th feature vector of the dataset X, which consists of the j-th feature values of all points in X. Given a dataset X, a feature j is characterized as unimodal or multimodal based on the unimodality or multimodality of .
Definition 1.
A d-dimensional dataset X is axis unimodal if every feature j is unimodal, i.e., each univariate subset () (consisting of the j-th feature values) is unimodal.
Obviously, in order for a dataset X to be decided as axis unimodal, a unimodality test (e.g., dip-test) should decide unimodality for each subset . A dataset that is not axis unimodal will be called axis multimodal.
2.4. Node Splitting
Let u be a node during decision tree construction and X the corresponding set of data vectors to be split by applying a thresholding rule on a feature value. A split rule for u is defined as the pair , where j is the feature on which the rule is applied and is the corresponding threshold level. A splitting rule of the form is then applied to the node. We denote the subset of X that satisfies this condition as , while the set of points that do not satisfy this condition is denoted as . Two child nodes and are then created corresponding to the subsets and , respectively. In our method, we aim to determine the feature-threshold pair that results in a decrease in the multimodality of the partition as computed by an appropriately defined criterion. We denote the best-split pair as (), where and denote the best feature and the best split threshold, respectively. If for the dataset X, no features are detected for splitting, then node u is considered a leaf. This occurs when the dataset X is axis unimodal.
3. Axis Unimodal Clustering with a Decision Tree Model
The proposed method can be considered as a divisive (i.e., incremental) clustering approach that is based on binary cluster splitting and produces rectangular axis unimodal clusters. It starts with the whole dataset as a single cluster and, at each iteration, it selects an axis multimodal cluster and splits this cluster into two subclusters. The method terminates when all produced clusters are axis unimodal. Binary cluster splitting is implemented by applying a decision threshold on the values of a multimodal feature. In this way the cluster assignment procedure can be represented with a typical (axis-aligned) decision tree, ensuring the interpretability of the clustering decision. Obviously, the leaves of the decision tree correspond to axis unimodal clusters.
Since our objective is to produce axis unimodal clusters, we consider multimodal features for cluster splitting. Let X be the multimodal cluster to be split and be the set of values of a multimodal feature j. Since is multimodal, our objective is to determine a splitting threshold such that the splitting of will result in two subsets and that are less multimodal than (ideally they should be both unimodal). We define a criterion to evaluate the partition (, ) in terms of unimodality and separation. As in a typical case for decision tree construction, we evaluate several partitions obtained by considering all multimodal features and several candidate threshold values for each feature. The best partition is determined according to the criterion and the corresponding feature-threshold pair, which defines the decision rule for splitting cluster X. The criterion used to evaluate a partition is presented next.
3.1. Splitting Multimodal Features
Let denote the set of values corresponding to a multimodal feature. Initially, we sort the values , in ascending order. For each we consider the average between and its successor as candidate split threshold . Given a threshold value , S is partitioned into two subsets: a left subset (values on the left of ) and a right subset (values on the right of ). Let also and be the sizes of and , respectively. The dip-test is then applied to both subsets to assess their unimodality, yielding two p-values: for and for . To evaluate the effectiveness of threshold , we define a weighted p-value of the partition: .
An intuitive justification of the formula is the following:
- If both subsets and are multimodal, then the -value and -value are low resulting in a low value.
- If both subsets and are unimodal, then the -value and -value are high resulting in a high value.
- In case one subset (let ) is unimodal and the other (let ) is multimodal, we need to consider the size of each subset: if and since (unimodal , multimodal ) then the resulting value is high. In the opposite case, the set becomes the dominant set and thus demonstrates a lower value.
Case 2 describes a scenario where the data splits into two unimodal sets resulting in high values. In case 3 a dominant unimodal subset is compared against a relatively small multimodal subset, also yielding high values. These findings indicate that high values occur when the split highlights one or two unimodal subsets. By selecting the candidate threshold value providing the highest value we obtain a partition of S into subsets of increased average unimodality.
Following the above procedure, we have experimentally noticed that although sensible splittings were generally obtained, the selected threshold was not always very accurate. For example, Figure 2a illustrates the histogram of a bimodal dataset along with the computed marked with a star. Splitting can be considered successful since the dataset is split into two unimodal subsets; however, the presented in Figure 2b is a more accurate split point than the one in Figure 2a. Thus, there is some room for improvement in threshold determination. To tackle this issue we consider not only the unimodality partition, but also the separation of points before and after the threshold . More specifically, we consider a subset of w successive points right before and a second subset of w successive points right after . We define the separation () of a threshold value as the average distance among all pairs of points belonging to different subsets. A large distance value indicates a high separation between the points before and after , thus lies in a density valley. Therefore, the split corresponding to is efficient, if the separation is high. We denote as the separation of the points defined by a split point . We choose a small value of w (e.g., ), with the choice of value w not affecting the final result. Since computation requires at least w points before and after , we do not consider candidate threshold values defined by the first w and last w points of S.
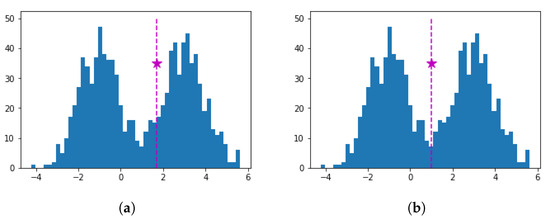
Figure 2.
Histogram of a bimodal dataset along with its split threshold (star). (a) The split threshold was computed without utilizing the separation criterion. (b) The split threshold was computed taking into account the separation criterion.
Therefore, since our objective is to determine a threshold with both a high value and high value, we define a new criterion to measure the quality of a split. A high q value provides a split into two highly separated (high value) and unimodal (high value) subsets. Thus, we choose the candidate threshold resulting in a maximum q value as the best split threshold and denote it as . Algorithm 1 presents the steps of computing the best-split point of a univariate dataset S. It first takes as input the univariate dataset S and the significance level and returns the best-split point of S along with the corresponding value. In case S is unimodal as decided by the dip-test, then Algorithm 1 returns the empty set. Figure 3 illustrates the histogram plots and the best split points (marked as stars) of several datasets which are generated by sampling from mixtures of Gaussian, uniform and triangular distributions.
| Algorithm 1 best_split_point |
|

Figure 3.
Histogram plots of synthetic datasets along with the best split thresholds found (stars).
3.2. Decision Tree Construction
Next, we describe our method, called Decision Trees for Axis Unimodal Clustering (DTAUC), for obtaining interpretable axis unimodal partitions of a multidimensional dataset. Our method employs a divisive (top-down) procedure, thus we first assign the whole initial dataset to the root node. Assuming that at some iteration a node u contains a dataset X, our goal is to determine the splitting rule for node u. This involves determining the best pair consisting of a multimodal feature and the corresponding split threshold.
To identify the best split for u we work as follows: first, we apply the dip-test to detect the multimodal features of X. If all features are unimodal, node u is considered a leaf and no split occurs. If multimodal features exist, then for each multimodal feature j, Algorithm 1 is used to compute its best split threshold and the corresponding evaluation of the resulting partition. Among the multimodal features, we select as best the one with maximum value. Algorithm 2 describes the steps for determining the splitting rule of a dataset X. It takes the set X and a significance level as input and returns the best pair where is the selected multimodal feature and the corresponding threshold.
| Algorithm 2 = best_split() |
|
In case the best split for u exists (i.e., u is not considered as a leaf), the data vectors of X are partitioned into two subsets, and , based on the feature values: and . Therefore two child nodes of u, denoted as and , are added to the tree, corresponding to sets and , respectively. Finally, the method is applied recursively on each resulting node, until all nodes are identified as leaves, i.e., the subsets in all nodes are axis unimodal. We assign each leaf a cluster label meaning that each leaf represents a single cluster. Therefore, an axis unimodal partition of the initial dataset X into hyperrectangles is obtained. Algorithm 3 describes the proposed DTAUC method. It takes a multidimensional dataset X and a significance level as input and returns the constructed tree. It should be emphasized that the algorithm does not require as input the number of clusters which is automatically determined by the method.
| Algorithm 3 DTAUC() |
|
3.3. An Illustrative Example
Table 1 presents the intermediate steps from the application of DTAUC on the two-dimensional dataset (called X) illustrated in the first plot of Figure 4a. For each subset of X (listed in first column), we provide the feature along with its unimodal (U)/multimodal (M) property (second column) as determined by the dip-test. The best split thresholds and the corresponding q values for each feature are given in the third and fourth columns, respectively. The fifth column indicates whether to split or save the set mentioned in the first column. If a split decision is made, the best split feature is mentioned in parentheses. Either two subsets are created (in case of a split decision) or the set specified in the first column is axis unimodal, thus it is saved in set C which contains the axis unimodal subsets.

Table 1.
Stepwise partitioning of the two-dimensional dataset of Figure 4a.
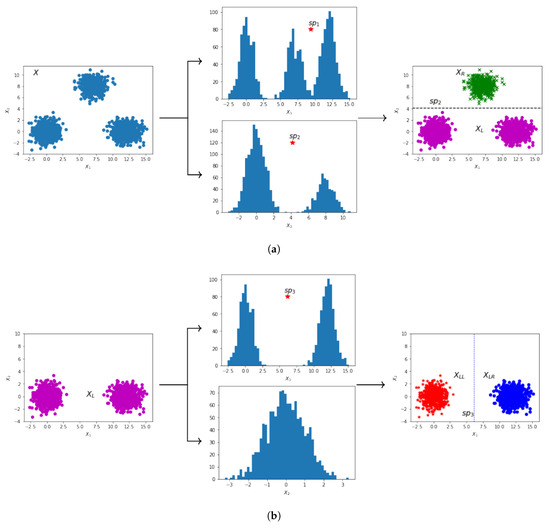
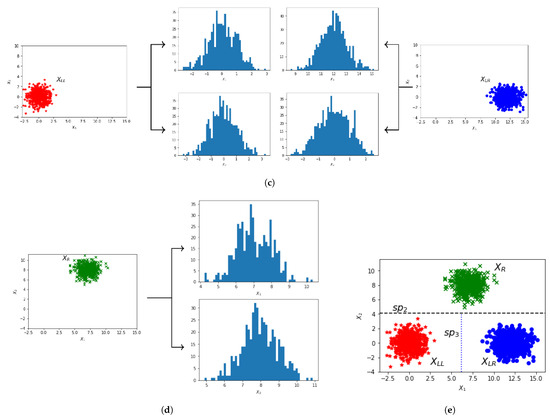
Figure 4.
Stepwise partitioning of a 2-D dataset (X) into axis unimodal rectangular regions. (a) 2-D plot of the original dataset X, with histogram plots of each feature, the obtained split points, and the resulting 2-D plot illustrating X split (by ) into two clusters (, ). (b) 2-D plot of , with histogram plots of each feature, the obtained split point, and the resulting 2-D plot illustrating split (by ) into two clusters (, ). (c) 2-D plots of and , along with the unimodal histogram plots of each feature. (d) 2-D plot of , along with the unimodal histogram plots of each feature. (e) Final 2-D plot of X, illustrating the final split points () that partition X into three axis unimodal clusters ().
In Figure 4 we provide illustrative plots corresponding to the step-by-step partition of the 2-D set X. Figure 4a displays the 2-D plot of the initial dataset X, along with the histogram plots of feature vectors and . A higher q value is computed for feature () as shown in Table 1, thus we apply the split on feature with the threshold value . The partitioning of X into two subsets and is given in the right plot of Figure 4a. The dotted line illustrates the split threshold . The plot of is presented in Figure 4b. The first feature is bimodal, while the second is unimodal, as indicated by the histogram plots and the q values for and in Table 1. Therefore, the split is applied considering the first feature using the threshold value (dotted line in the right plot of Figure 4b). This split results in two subsets, denoted as and . Figure 4c illustrates the 2-D plots of and along with the corresponding histograms for each feature. It is clear that and are axis unimodal, thus we save them in C. The 2-D plot of is presented in Figure 4d, where it is clear that each feature is unimodal (the histogram plots and q values for in Table 1 indicate unimodality), thus we save it in set C. The final 2-D plot of X is given in Figure 4e, where the two resulting split thresholds (horizontal split and vertical split ) and the final partition of X are illustrated. The corresponding binary decision tree for dataset X is presented in Figure 5.
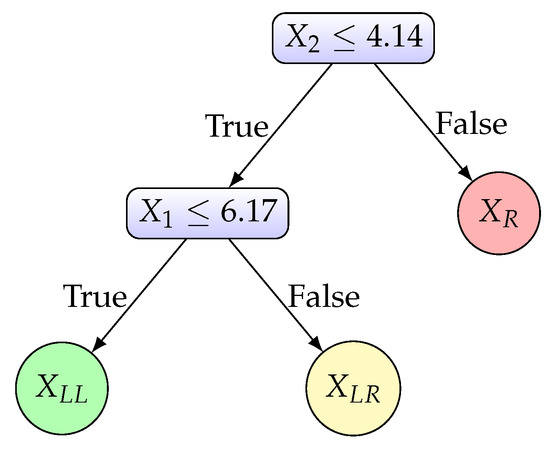
Figure 5.
Binary decision tree constructed for the two-dimensional dataset of Figure 4a.
4. Experimental Results
In this section we assess the performance of DTAUC on clustering synthetic and real data, focusing on the accurate estimation of the number of clusters and the quality of data partitioning. We compare the DTAUC method with the ICOT method [13] and the ExShallow method [5]. To the best of our knowledge, ICOT is the only method that provides a partition of the data into axis-aligned regions without using the ground-truth number of clusters during training. We also include an indirect method (ExShallow) in our experimental evaluation, in order to compare DTAUC and ICOT with a method that uses the ground-truth number of clusters.
The three methods were applied to both synthetic (from the Fundamental Clustering Problems Suite (FCPS) [23]) and real datasets (from UCI [24]). Since ground truth clustering information is available for each dataset, we evaluated the two methods in terms of splitting (clustering) performance using the widely used Normalized Mutual Information (NMI) score defined as follows:
where Y denotes the ground-truth labels, C denotes the cluster labels, is the mutual information measure and the entropy. This score ranges between 0 and 1, with a value close to 1 indicating that the ground truth partition has been found. All three methods build binary decision trees; therefore, we selected datasets suitable for partitioning into axis-aligned clusters for our experimental evaluation. Table 2 presents the parameters of each dataset (n: number of samples, d: number of features, : ground-truth number of clusters). We used min-max scaling for all datasets to ensure comparability with the ICOT method, which assumes features in the range.

Table 2.
Parameters of synthetic and real datasets used in the experiments.
The DTAUC method uses a single parameter, the significance level , which is necessary for the dip-test to determine data unimodality during the splitting procedure. To determine an appropriate for each dataset, we used the silhouette score [15] that is commonly used to assess the quality of a clustering solution. Specifically, for each dataset, we run the method for each value of , compute the silhouette score for each obtained partition and keep the partition of maximum score as the final partition. In the ICOT method, we utilized a k-means warm start and retained the remaining parameters as specified in [13]. We encountered challenges running ICOT on datasets with a large number of features or clusters. This aligns with observations made by the authors in [13], who reported excessive runtimes for some datasets. For the ExShallow method, we provided the ground-truth number of clusters to run k-means and obtain the cluster labels. Then, a supervised binary decision tree is built by minimizing appropriate metrics as proposed in [5].
Table 3 and Table 4 present for each dataset the NMI values and the number of clusters (k) as provided by the methods (it should be noted that in ExShallow the number of clusters is given). The ground-truth number of clusters () is also provided in the second column of each table. The performance of DTAUC is superior compared to ICOT in most cases, achieving higher NMI values and closer estimations (k) of the ground-truth number of clusters (). However, DTAUC encounters challenges with some datasets, such as the Tetra dataset, where there is significant overlap among clusters. Another dataset where DTAUC demonstrates inferior performance is the Ruspini dataset. This dataset is relatively small () and one of the four clusters is not compact. Consequently, DTAUC splits the noncompact cluster into two subclusters, detecting five clusters instead of four.

Table 3.
Partition results on synthetic data reported: (i) The estimated number of clusters (k) and (ii) NMI values with respect to the ground truth labels. The ground truth number of clusters () is also reported.

Table 4.
Partition results on real data reported: (i) The estimated number of clusters (k) and (ii) NMI values with respect to the ground truth labels. The ground truth number of clusters () is also reported.
Another dataset to be discussed is Synthetic I, a three-dimensional dataset where feature vectors and were generated using two Gaussian distributions and two uniform rectangles, and was generated using a uniform distribution. A 2-D plot of Synthetic I, with axes representing features and , is provided in the left plot of Figure 6a. It should be noted that since feature is uniformly distributed it does not contribute to the splitting process. This dataset is separated by axis-aligned splits; however, the ICOT and ExShallow methods fail in this task. As shown in Figure 6a, ICOT fails to estimate the correct number of clusters ( instead of the actual ) (right plot), while the partition obtained by DTAUC (middle plot) is successful. The 2-D plot of the ExShallow solution is almost identical to the ICOT plot (right plot in Figure 6a).
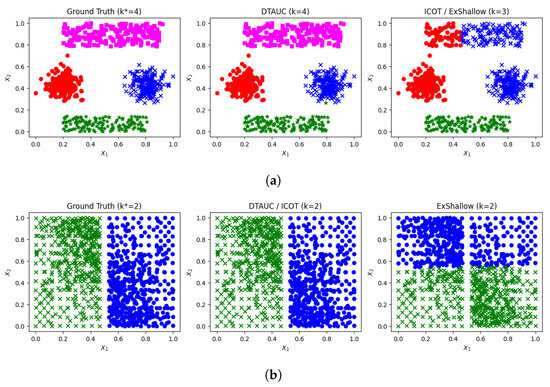
Figure 6.
2-D plots of (a) Synthetic I and (b) WingNut. The ground truth partition and the partitions
obtained by DTAUC, ICOT and ExShallow are provided.
DTAUC provides successful data partitions and accurately (or very closely) estimates the number of clusters for most synthetic and real datasets. In datasets (e.g., Ruspini) where sparse clusters exist, DTAUC demonstrates inferior performance compared to ICOT, since, based on the criterion of unimodality, it decides to split those clusters. However, ICOT is inferior in simple datasets, such as Synthetic I and Lsun, particularly when the clusters are close to each other and have a rectangular shape. In what concerns the indirect method (ExShallow), the information provided about the ground truth number of clusters seems to be helpful, in general. However, there are simple datasets where it provides inferior results, such as Synthetic I, Lsun and WingNut. For example, in the case of the WingNut dataset (as illustrated in Figure 6b), a single vertical line is required to split the data into two clusters (left plot); however, ExShallow fails to correctly determine this split (right plot). This mainly occurs due to an incorrect initial partition provided by the k-means algorithm, that is employed in the initial processing step. In this dataset, both DTAUC and ICOT provide a successful solution (middle plot).
5. Conclusions and Future Work
We have proposed a method (DTAUC) for constructing binary trees for clustering based on axis unimodal partitions. This method follows the typical top-down paradigm for decision tree construction. It implements dataset splitting at each node by applying thresholding on the values of an appropriately selected multimodal feature. In order to select features and thresholds, a criterion has been proposed for the quality of the resulting partition that takes into account unimodality and separation. The method automatically terminates when the subsets in all nodes are axis unimodal.
The DTAUC method relies on the idea of unimodality, which is closely related to clustering. It is simple to implement and provides axis-aligned partitions of the data, thus it offers interpretable clustering solutions. In addition, it does not involve any computationally expensive optimization technique, while it demonstrates the significant advantage that (apart from the typical statistical significance level) it does not include user-specified hyperparameters, for example, the number of clusters, the maximum depth of the tree or post-processing techniques, such as a pruning step.
Future work could focus on using a set of features/splitting rules (instead of a single feature/splitting rule) at each node, as oblique trees do. While this would make the resulting trees less interpretable, it would offer more accurate clustering solutions. It is also interesting to implement post-processing steps to improve the performance of DTAUC. In DTAUC each tree leaf represents a single cluster. Several methods merge adjacent leaves into larger clusters, thereby capturing more complex structures in the data. After obtaining the final tree, we could consider the possibility of merging leaves if the unimodality assumption is retained.
Author Contributions
Conceptualization, P.C. and A.L.; methodology, P.C. and A.L.; software, P.C.; validation, P.C.; supervision, A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CART | Classification and regression trees |
| CDF | Cumulative distribution function |
| CHAID | Chi-squared automatic interaction detector |
| CUBT | Clustering using unsupervised binary trees |
| DTAUC | Decision trees for axis unimodal clustering |
| ECDF | Empirical cumulative distribution function |
| ICOT | Interpretable clustering via optimal trees |
| ID3 | Iterative dichotomiser 3 |
| NMI | Normalized mutual information |
| OCT | Optimal classification trees |
| Probability density function | |
| SEP | Separation |
| SP | Split threshold |
References
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Quinlan, J.R. Discovering rules by induction from large collections of examples. In Expert Systems in the Micro Electronics Age; Edinburgh University Press: Edinburgh, UK, 1979. [Google Scholar]
- Quinlan, J.R. C4. 5: Programs for Machine Learning; Morgan Kaufmann Pub: Cambridge, MA, USA, 1993. [Google Scholar]
- Kass, G.V. An exploratory technique for investigating large quantities of categorical data. J. R. Stat. Soc. Ser. Appl. Stat. 1980, 29, 119–127. [Google Scholar] [CrossRef]
- Laber, E.; Murtinho, L.; Oliveira, F. Shallow decision trees for explainable k-means clustering. Pattern Recognit. 2023, 137, 109239. [Google Scholar] [CrossRef]
- Tavallali, P.; Tavallali, P.; Singhal, M. K-means tree: An optimal clustering tree for unsupervised learning. J. Supercomput. 2021, 77, 5239–5266. [Google Scholar] [CrossRef]
- Blockeel, H.; De Raedt, L.; Ramon, J. Top-down induction of clustering trees. arXiv 2000, arXiv:cs/0011032. [Google Scholar]
- Basak, J.; Krishnapuram, R. Interpretable hierarchical clustering by constructing an unsupervised decision tree. IEEE Trans. Knowl. Data Eng. 2005, 17, 121–132. [Google Scholar] [CrossRef]
- Fraiman, R.; Ghattas, B.; Svarc, M. Interpretable clustering using unsupervised binary trees. Adv. Data Anal. Classif. 2013, 7, 125–145. [Google Scholar] [CrossRef]
- Liu, B.; Xia, Y.; Yu, P.S. Clustering through decision tree construction. In Proceedings of the Ninth International Conference on Information and Knowledge Management, McLean, VA, USA, 6–11 November 2000; pp. 20–29. [Google Scholar]
- Gabidolla, M.; Carreira-Perpiñán, M.Á. Optimal interpretable clustering using oblique decision trees. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 400–410. [Google Scholar]
- Heath, D.; Kasif, S.; Salzberg, S. Induction of oblique decision trees. IJCAI 1993, 1993, 1002–1007. [Google Scholar]
- Bertsimas, D.; Orfanoudaki, A.; Wiberg, H. Interpretable clustering: An optimization approach. Mach. Learn. 2021, 110, 89–138. [Google Scholar] [CrossRef]
- Bertsimas, D.; Dunn, J. Optimal classification trees. Mach. Learn. 2017, 106, 1039–1082. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Dunn, J.C. Well-separated clusters and optimal fuzzy partitions. J. Cybern. 1974, 4, 95–104. [Google Scholar] [CrossRef]
- Adolfsson, A.; Ackerman, M.; Brownstein, N.C. To cluster, or not to cluster: An analysis of clusterability methods. Pattern Recognit. 2019, 88, 13–26. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Hartigan, P.M. The dip test of unimodality. Ann. Stat. 1985, 13, 70–84. [Google Scholar] [CrossRef]
- Chasani, P.; Likas, A. The UU-test for statistical modeling of unimodal data. Pattern Recognit. 2022, 122, 108272. [Google Scholar] [CrossRef]
- Kalogeratos, A.; Likas, A. Dip-means: An incremental clustering method for estimating the number of clusters. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 2393–2401. [Google Scholar]
- Maurus, S.; Plant, C. Skinny-dip: Clustering in a sea of noise. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1055–1064. [Google Scholar]
- Vardakas, G.; Kalogeratos, A.; Likas, A. UniForCE: The Unimodality Forest Method for Clustering and Estimation of the Number of Clusters. arXiv 2023, arXiv:2312.11323. [Google Scholar]
- Ultsch, A. Fundamental Clustering Problems Suite (Fcps); Technical Report; University of Marburg: Marburg, Germany, 2005. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2017. Available online: https://archive.ics.uci.edu (accessed on 20 May 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).