Identity-Based Online/Offline Encryption Scheme from LWE

Abstract

With quantum computers, the quantum resistance of cryptographic systems has gradually attracted attention. To overcome the shortcoming of existing identity-based encryption (IBE) schemes in resisting quantum attacks, we introduce an IBE scheme based on learning with errors (LWE). In addition, devices with limited computing power are becoming increasingly common in practice, making it increasingly important to improve the efficiency of online computation of encryption algorithms. The classic solution is to directly improve the efficiency of the Gaussian sampling algorithm, thereby increasing the overall efficiency of the scheme. However, our scheme combines the efficient Gaussian sampling algorithm, $\mathbf{G}$-trapdoor, with online/offline method to further improve the online encryption efficiency of the encryption algorithm. Our scheme completes partial computation before knowing the message and receiver’s identity, and once the message and receiver’s identity are obtained, the online part encryption can be efficiently completed. We construct an identity-based online/offline encryption (IBOOE) scheme from LWE with $\mathbf{G}$-trapdoor, improve the efficiency of online encryption while achieving quantum resistant security. We prove the scheme’s security under the standard model for chosen-plaintext attack (CPA). By comparing with relevant schemes in terms of experiments and analysis, our scheme has improved efficiency by 65% to 80% compared to the classical LWE IBE scheme (increasing with LWE security parameters), and by 60% to 70% compared to the recent IBE scheme from LWE. This greatly improves the efficiency of online computing for low-power encryption devices while ensuring security.

1. Introduction

In IBE schemes, user submits an arbitrary string corresponding to the identity to key generation center (KGC). This user’s private key which is authenticated is generated by the KGC and corresponds to the identity. Encrypting messages only requires knowing the identity of the recipient. This process does not require verifying the correctness of credentials in traditional public key architectures, especially for energy limited devices. With quantum computers’ computing technology, traditional encryption algorithms face the danger of being attacked by quantum computers. However, traditional IBE schemes do not have quantum resistant security.

Lattice-based cryptography system has the characteristics of simple structure and complex mathematics, and is the most prospective type of anti-quantum cryptography technology. The lattice-based IBE schemes deserve further research due to the excellent performance in practical application scenarios and scalability advantages. Gentry, Peikert, and Vaikuntanathan [1] designed an approach for lattice-based signature algorithms and proved the method’s security under the random oracle model; we abbreviate their scheme to GPV scheme. Cash et al. [2] proposed the LWE IBE scheme and proved this anti-quantum IBE scheme’s security under the standard model. Furthermore, Agrawal et al. [3] brought up an anti-quantum IBE scheme based on lattice under the standard model. In line with Agrawal et al.’s [3] work, their scheme has a simpler construct and shorter ciphertext compared to Cash et al.’s [2] scheme. Agrawal et al. treated identity as a chunk, and the lattice in their scheme consists of “left” and “right” lattices. The trapdoor for the left lattice is the true trapdoor for generating secrete keys, while the trapdoor for the right lattice is only used in security proof. Our scheme learns their idea of trapdoor generation and further improves based on it.

However, the current IBE algorithm based on lattice structure still has shortcomings in computational efficiency. The biggest reason is that lattice-based encryption schemes are closely related to Gaussian sampling, and thus, many efficiency improvement schemes focus on improving the efficiency of Gaussian sampling. Since the current implementations of Gaussian sampling are still achieved through extensive simulations to infinitely approximate Gaussian distributions, which still affects the overall computational efficiency. In an effort to carry the efficiency of existing lattice-based IBE schemes to a new and higher level, we apply online/offline method to delegate most of the Gaussian sampling and the parts that do not require identity and message knowledge to powerful devices for offline computation.

1.1. Our Motivation and Contributions

Although existing IBE schemes can protect the confidentiality of data without checking certificates, they cannot resist attacks from quantum computers. To address this issue, an anti-quantum IBE scheme can be achieved by constructing on LWE, the classic hard problem on lattice. However, the current LWE based IBE schemes are less efficient. Thus, we propose an IBOOE scheme based on LWE; the offline phase completes Gaussian sampling before obtaining the message to be encrypted and identity. In this way, our scheme ensures the efficiency of the scheme while achieving anti-quantum security. Our contributions are shown below.

(1)

We first investigate the coexistence of anti-quantum security and efficiency in the IBE system, and design an IBOOE scheme from the LWE problem.

(2)

We then construct our concrete IBOOE scheme from LWE and prove the CPA secure under the standard model.

(3)

Finally, we aim to test the feasibility and effectiveness of our scheme through the contrast of the original scheme [3], our scheme, and the recent anti-quantum IBE scheme [4].

1.2. Paper Organization

The rest of this article is organized as follows. We introduce the relevant work of our paper in Section 2. In Section 3, we introduce some concepts and related definitions, and describe the security model and system architecture. In Section 4, we propose the construction of our efficient IBOOE based on LWE and analyze its correctness and security. In Section 5, we compare our scheme with classical and recent LWE based IBE schemes. In Section 6, we conclude this article.

2. Related Work

The GPV scheme [1] provided the underlying scheme for the lattice-based IBE cryptographic algorithms. Regev [5] presented a typical lattice difficulty problem, the LWE problem. In the research of anti-quantum cryptography schemes, especially for IBE schemes, considering quantum circuits’ aspect, the proof of GPV scheme is conducted solely under the random oracle model, but without considering the security proof under the random oracle model from quantum technology. Zhandry [6] developed a new technology for random oracle model from the quantum technology, and then demonstrated that the GPV scheme is secure under the random oracle model from the quantum technology. Katsumata et al. [7] then provided more rigid proof for GPV scheme under the random oracle model from quantum technology. While Gao et al. [8] first constructed anti-quantum IBE scheme from LWE and a quantum circuit, they proved their quantum IBE scheme’s security under the random oracle model. Moreover, considering the enlargement of anti-quantum cryptography schemes in terms of functionality, Dutta et al. [9] first brought up the specific unidirectional construction of the proxy-re-encryption-based identity from LWE; they then proved under the standard model that the scheme is secure. In addition, for the sake of strengthening the security of proxy-re-encryption-based identity, on this basis, Wu et al. [10] added a function called re-encryption verifiability, which is a proxy re-encryption IBE scheme from basic lattice. Liu et al. [11] then extended the concept of server-aided revocable IBE to hierarchical IBE. In order to withstand side channel attack, Li et al. [12,13,14,15] presented some identity-based encryption schemes with leakage resilience. Furthermore, in terms of extending LWE itself, Abla et al. [16] brought up an IBE scheme based on ring LWE, with shorter main public key and stricter security analysis. Conversely, Fan et al. [17] brought up an adaptively secure scheme under the standard model, which is a fresh anti-quantum IBE scheme for middle product LWE. In addition, Lai et al. [18] promoted two-stage sampling approach of the GPV scheme, and proposed the new lattice two-stage sampling technology, which added noise not only to the ciphertext, but also to the key.

However, most of the current IBE schemes are inefficient, and they take up a lot of storage space. In terms of storage, the main issue is each user’s ID has a parameter matrix, which yields a sharp increase in the scale of the system’s public parameters. Zhang et al. [4] proposed a flexible trade-off mechanism using blocking technology to balance the scale of common parameters and the computational cost involved. They divide the identity into multiple parts and associate each part with a matrix, while slightly increasing the modulus of the lattice to maintain the same level of security. In the Gaussian sampling aspect, Weiden et al. [19] displayed that the running time consumed by Gaussian sampling accounts for half of the Lyubashevsky’s lattice signature scheme [20]. For the sake of improving the efficiency of Gaussian sampling, Micciancio and Peikert [21] brought up a new approach for generating a trapdoor in the lattice, which is more efficient with smaller hidden constants; this trapdoor is called $\mathbf{G}$-trapdoor. This method of generating trapdoors is more efficient because it does not involve any expensive Hermite normal form or matrix inversion computations. Next, Micciancio and Walter [22] developed a new Gaussian sampling algorithm and the algorithm is applicable to arbitrary and variable Gaussian distributions. By implementing more efficient Gaussian sampling, lattice-based cryptographic algorithms can be more widely applied. Furthermore, Sun et al. [23] also proposed a secure and efficient exponential Bernoulli sampling algorithm to achieve universal, efficient, and synchronized Gaussian sampling of integers.

Significantly, in the sake of improving the expense of Gaussian sampling in lattice encryption algorithms, the online/offline method is also an effective way. In 2008, Guo et al. [24] first brought up the IBOOE scheme. The principal idea is to complete computing that consume a lot of resources in the offline part through powerful devices. These calculations do not require knowledge of messages and identities. Under this mindset, we propose an online/offline IBE scheme from LWE with $\mathbf{G}$-trapdoor, complete Gaussian sampling during the offline phase. The offline part can be completed by powerful devices without the need to know identity and messages.

3. Preliminaries

We take values from the finite set $\mathsf{\Omega }$, and let $\mathit{A}$ and $\mathit{B}$ be random variables. Furthermore, the statistical distance between A and B, two ensembles of distributions indexed by s, is $△\left(\mathit{A};\mathit{B}\right)≔{\displaystyle \frac{1}{2}}{\sum }_{\mathit{s}\in \mathsf{\Omega }}\left|\mathit{A}\left(s\right)-\mathit{B}\left(s\right)\right|$. For an uniform and random variable ${\mathbf{U}}_{\mathsf{\Omega }}$ from $\mathsf{\Omega }$, if we have $△\left(\mathit{A};{\mathbf{U}}_{\mathsf{\Omega }}\right)\le \delta$, then we have the random variable $\mathit{A}$ is $\delta$-uniform over $\mathsf{\Omega }$. More specifically, we let $\mathit{A}\left(\kappa \right)$ and $\mathit{B}\left(\kappa \right)$ be the two sets of random variables. Furthermore, set $\mathit{d}\left(\kappa \right)≔△\left(\mathit{A}\left(\kappa \right);\mathit{B}\left(\kappa \right)\right)$, if $\mathit{d}\left(\kappa \right)$ is an ignorable function of $\kappa$, and in this way, we have that $\mathit{A}$ and $\mathit{B}$ are statistically approaching.

For vectors $S=\left\{s_1,\dots ,s_k\right\}\in {\mathbb{R}}^{n\times k}$. $L_2$ norm is the shortest distance to go from one point to another, which is the sum of squared differences between points. $∥S∥$ indicates the S’s longest vector’s $L_2$ length. $∥\tilde{S}∥≔\left\{{\tilde{s}}_1,\dots ,{\tilde{s}}_k\right\}$ indicates the Gram–Schmidt orthogonalization of the ordered vectors $s_1,\dots ,s_k$ as in above sequence.

We let $a_1,a_2,\dots ,a_n\in {\mathbb{R}}^{n\times n}$ be n linearly independent vectors and $\mathbf{Y}=\left(a_1,a_2,\dots ,a_n\right)$. Furthermore, the following additive discrete subgroup is called an n-dimensional lattice which is generated by $\mathbf{Y}$:

$$\Lambda =L\left(\mathbf{Y}\right)=\left\{\sum _{i=1}^n{x}_i{a}_i:x_i\in \mathbb{Z}\right\}$$

For the three positive integers $r,n$, and q, where q is a prime number, we define $\mathbf{X}\in {\mathbb{Z}}_{\mathit{q}}^{\mathit{r}\times \mathit{n}}$ and $\partial \in {\mathbb{Z}}_{\mathit{q}}^{\mathit{r}}$, and consider two kinds of n-dimensional lattices defined by $\mathbf{X}$. The transposed rows of $\mathbf{X}$ generates the first lattice and the first lattice is defined as:

$${\Lambda }_q\left(\mathbf{X}\right)≔\left\{\mu \in {\mathbb{Z}}^{\mathit{n}}:\exists s\in {\mathbb{Z}}_{\mathit{q}}^{\mathit{r}}where{\mathbf{X}}^{\top }s=\mu \mathsf{mod}q\right\}.$$

Those integer vectors are “orthogonal” under the modulus q to the rows of $\mathbf{X}$. Furthermore, they constitute the second lattice. The second lattice is defined as:

$${\Lambda }_q^{\perp }\left(\mathbf{X}\right)≔\left\{\mu \in {\mathbb{Z}}^{\mathit{n}}:\mathbf{X}\mu =0\mathsf{mod}q\right\}.$$

Moreover, we let ${\Lambda }_q^{\partial }=\left\{\mu \in {\mathbb{Z}}^n:\mathbf{X}\mu =\partial \mathsf{mod}q\right\}$ for the arbitrary $\partial \in {\mathbb{Z}}^r$ be the coset.

For $c\in {\mathbb{R}}^n$ and $s>0$, the Gaussian function is defined as ${\rho }_{s,c}\left(x\right)=exp\left(-\pi {∥\left(x-c\right)/s∥}^2\right)$. Then, we let ${\rho }_{s,c}\left(\Gamma \right)={\sum }_{x\in \Gamma }{\rho }_{s,c}\left(x\right)$ for any fixed countably subset $\Gamma \subseteq {\mathbb{R}}^n$. Next, the discrete Gaussian distribution for arbitrary $x\in \Gamma$ is defined as $D_{\Gamma ,s,c}\left(x\right)={\rho }_{s,c}\left(x\right)/{\rho }_{s,c}\left(\Gamma \right)$.

Definition 1.

Let ${\overline{\mathsf{\Psi }}}_{ϵ}$ over ${\mathbb{Z}}_q$ for an $ϵ\in \left(0,1\right)$ indicates the distribution of the random variable $⌊qA⌉modq$ and a prime number q, $⌊qA⌉$ means $⌊qA+1/2⌋$, where A is a normal random variable, the mean of A is zero, and the standard deviation of A is $ϵ/\sqrt{2\pi }$.

Definition 2.

For a prime number $\mathit{q}$, a positive integer $\mathit{r}$, and the distribution ${\overline{\mathsf{\Psi }}}_{ϵ}$ in ${\mathbb{Z}}_{\mathit{q}}$, the (${\mathbb{Z}}_{\mathit{q}},r,{\overline{\mathsf{\Psi }}}_{ϵ}$)-LWE problem is for the oracle access of samples, to differentiate between the distribution $\left({\partial }_i,v_i\right)=\left({\partial }_i,{\partial }_i^{\top }s+x_i\right)\in {\mathbb{Z}}_q^r\times {\mathbb{Z}}_q$ and the uniform distribution over ${\mathbb{Z}}_q^r\times {\mathbb{Z}}_q$, where $x_i\leftarrow {\overline{\mathsf{\Psi }}}_{ϵ}$, ${\partial }_i\leftarrow {\mathbb{Z}}_q^r$ and $s\leftarrow {\mathbb{Z}}_q^r$.

Theorem 1

([5]). There is an efficient algorithm for approaching the SIVP and the GapSVP problems in the worst case, to within $\tilde{O}\left(r/ϵ\right)$ factors in the $L_2$ norm, if for resolving the $\left({\mathbb{Z}}_q,r,{\overline{\mathsf{\Psi }}}_{ϵ}\right)$-LWE problem with $q>2\sqrt{r}/ϵ$ there exists an effective, probable quantum algorithm.

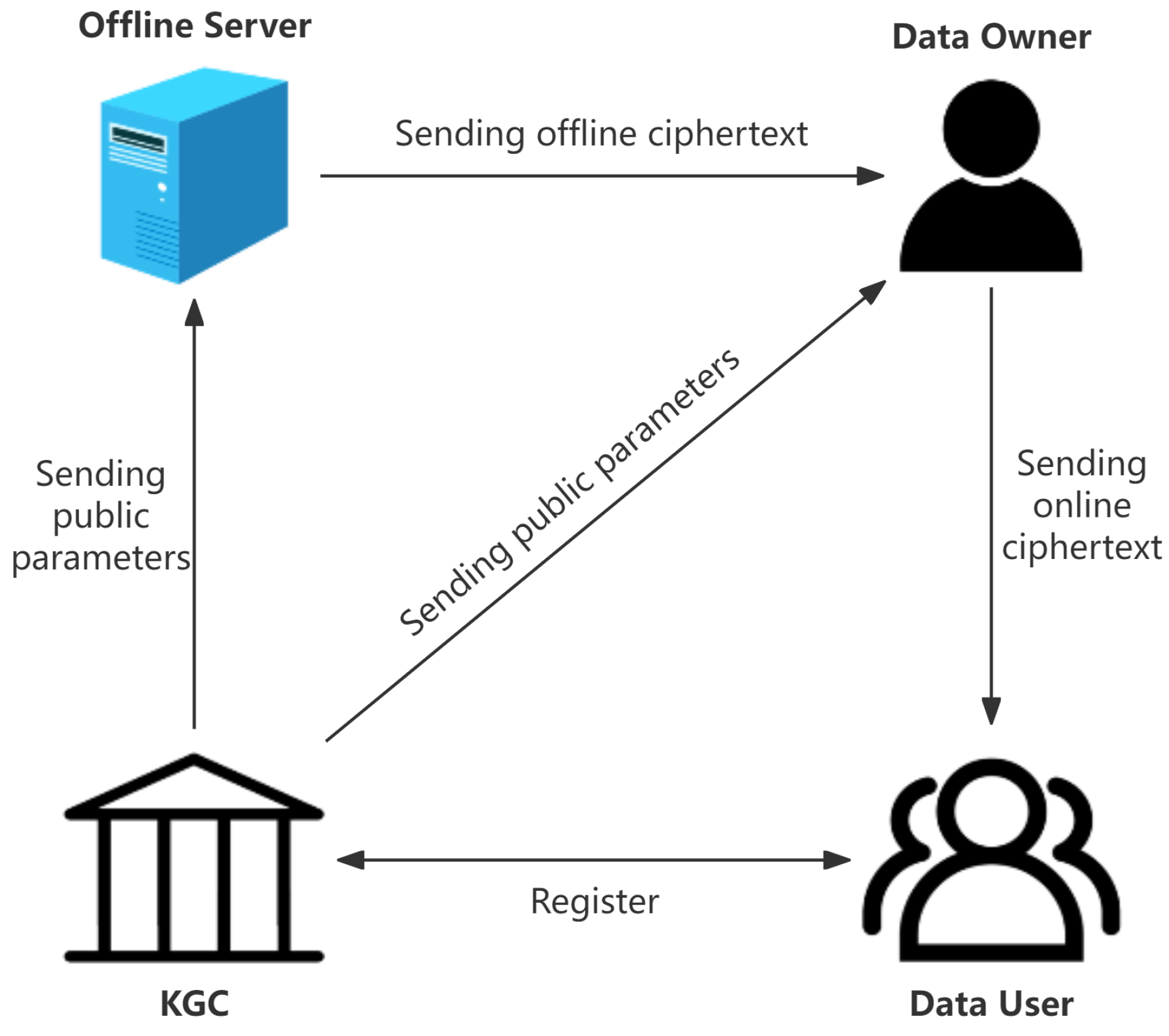
3.1. Framework and Security of IBOOE

Our IBOOE scheme is made up of the following five probabilistic polynomial-time (PPT) algorithms as below.

$\mathbf{Setup}$: In the setup phase, it takes security parameter $\lambda$ as the input, sets plaintext space and ciphertext space, then manufactures the global public parameters $\mathsf{PP}$ for following algorithms and the master secret key $\mathsf{MK}$ for the KGC.

$\mathbf{Extract}$: In the process of extracting secret key, it takes public parameters $\mathsf{PP}$, the master secret key $\mathsf{MK}$ and the $\mathsf{id}$ for generating the secret key ${\mathsf{SK}}_{\mathsf{id}}$, and ${\mathsf{SK}}_{\mathsf{id}}$ corresponds to the identity $\mathsf{id}$.

${\mathbf{Enc}}^{\mathbf{off}}$: During the offline encrypting phase, it takes public parameters $\mathsf{PP}$ as input for generating the offline ciphertext $\overline{\xi }$.

${\mathbf{Enc}}^{\mathbf{on}}$: During the online encrypting phase, it takes public parameters $\mathsf{PP}$, the message $mes$, the offline ciphertext $\overline{\xi }$, and the $\mathsf{id}$ as inputs for generating online ciphertext $\xi$.

$\mathbf{Dec}$: In the decrypting phase, it takes public parameters $\mathsf{PP}$, the ciphertext $\xi$ and the secret key ${\mathsf{SK}}_{\mathsf{id}}$ of the receiver, whose identity is $\mathsf{id}$ as inputs for decrypting the message $mes$.

For the security proof of our construction, we reduce our lattice based IBE scheme to a classical difficult problem on lattices, the LWE problem.

The (${\mathbb{Z}}_{\mathit{q}},r,{\overline{\mathsf{\Psi }}}_{ϵ}$)-LWE problem permits repetitive queries to the given challenge oracle $\mathcal{O}$. Furthermore, we say that if the following:

$$LWE-adv\left[\mathcal{A}\right]≔\left|Pr\left[{\mathcal{A}}^{{\mathcal{O}}_{\vartheta }}=1\right]-Pr\left[{\mathcal{A}}^{{\mathcal{O}}_{\mathsf{\$}}}=1\right]\right|$$

is non-ignorable for the random s from ${\mathbb{Z}}_{\mathit{q}}^{\mathit{r}}$, then the algorithm $\mathcal{A}$ resolves the (${\mathbb{Z}}_{\mathit{q}},r,{\overline{\mathsf{\Psi }}}_{ϵ}$)-LWE problem. ${\mathcal{O}}_{\vartheta }$ returns the real LWE sample and ${\mathcal{O}}_{\mathsf{\$}}$ is for the random case. The $Pr\left[{\mathcal{A}}^{{\mathcal{O}}_{\vartheta }}=1\right]$ means the probability of $\mathcal{A}$ guessing correctly when $\mathcal{A}$ accesses ${\mathcal{O}}_{\vartheta }$. The same applies to $Pr\left[{\mathcal{A}}^{{\mathcal{O}}_{\mathsf{\$}}}=1\right]$.

$\mathbf{Security}\mathbf{Game}.$ In order to ensure strong privacy in our IBOOE scheme, we describe a game that caches a character called “indistinguishable from random”. This implies that the challenge ciphertext from the ciphertext space appears to be a random element, making it difficult to decipher. For the security parameter $\lambda$, we define the scheme’s message space as ${\mathcal{M}}_{\lambda }$ and the scheme’s ciphertext space as ${\xi }_{\lambda }$. How the game works is described below.

$\mathbf{Init}$: In the initial phase, the adversary $\mathcal{A}$ first outputs its target identity ${\mathsf{id}}^{*}$.

$\mathbf{Setup}$: In the setup phase, the challenger then runs the algorithm $\mathbf{Setup}$ and gives the adversary $\mathcal{A}$ public parameters $\mathsf{PP}$. Furthermore, the challenger keeps the master key $\mathsf{MK}$ to itself.

$\mathbf{Phase}\mathbf{1}$: In the first phase, the adversary $\mathcal{A}$ sends private key queries $q_1,\dots ,q_n$ and the query $q_i$ is for ${\mathsf{id}}_i$. We request that ${\mathsf{id}}_i$ cannot equal to ${\mathsf{id}}^{*}$. For private key $d_i$ corresponds to the identity ${\mathsf{id}}_i$, and the challenger runs algorithm $\mathbf{Extract}$ to respond. Then, the challenger sends $d_i$ to $\mathcal{A}$. The above queries are all adaptive.

$\mathbf{Challenge}$: After adversary ${\mathcal{A}}^{\prime }s$ judgement of that the first phase is completed, a plaintext $M\in {\mathcal{M}}_{\lambda }$ will be output. Furthermore, this is the plaintext that $\mathcal{A}$ intends to be challenged. Then, for the following simulation, the challenger chooses the random bit $\mathit{a}\in \left\{0,1\right\}$ corresponding to different situation, and the challenger also chooses a random ciphertext $\xi \in {\xi }_{\lambda }$.

(1)

For $\mathit{a}=0$, challenger uses algorithm $\mathbf{Encrypt}$ for setting challenge ciphertext as ${\xi }^{*}$$≔\mathbf{Encrypt}$ $\left(\mathsf{PP},{\mathsf{id}}^{*},M\right)$.

(2)

For $\mathit{a}=1$, the challenger directly uses the challenge ciphertext chosen before and sets ${\xi }^{*}≔\xi .$

The challenger then sends ${\xi }^{*}$ as the ciphertext for challenge to adversary $\mathcal{A}$.

$\mathbf{Phase}\mathbf{2}$: Then, in the second phase, the adversary $\mathcal{A}$ adaptively sends the supplemental queries from $n+1$ to r, and the query $q_i$ corresponds to the ${\mathsf{id}}_i^{\prime }s$ private key extraction query, where ${\mathsf{id}}_i$ cannot be equivalent to ${\mathsf{id}}^{*}$. Just like in phase 1, the challenger sends $q_i$ to adversary $\mathcal{A}$.

$\mathbf{Guess}$: Lastly, adversary $\mathcal{A}$ sends the guess ${\mathit{a}}^{\prime }\in \left\{0,1\right\}$ as its output for result that the challenger chose before. $\mathcal{A}$ wins the game when $\mathit{a}={\mathit{a}}^{\prime }$. For the positive of adversary for attacking an IBE scheme, we define it as:

$$Ad{v}_{\mathcal{A}}\left(\lambda \right)=\left|Pr\left[\mathit{a}={\mathit{a}}^{\prime }\right]-1/2\right|.$$

The possibility of the adversary winning depends on the random bits which are used by the challenger and the adversary $\mathcal{A}$.

Definition 3.

If for every INDr-sID-CPA PPT adversary we have $Ad{v}_{\mathcal{A}}\left(\lambda \right)$, which is an ignorable function, then we are able to say that an IBE scheme is selective-identity, indistinguishable from random.

Lastly, we define the corresponding adaptive identity of our aforesaid concept, that is, in the attack game process, the init phase is removed so that the adversary can reveal the ${\mathsf{id}}^{*}$ that it wants to attack, namely its target identity, until the challenge phase. In the first phase, we permit the adversary to send random private key queries and then the adversary selects the random target identity ${\mathsf{id}}^{*}$. Furthermore, the only limitation is that in the phase 1, the adversary will not send the private key query for ${\mathsf{id}}^{*}$. Our security concept obtained in this way is defined in Definition 3, which is defined as INDr-ID-CPA.

3.2. Sampling Algorithms

For $r,q\in \mathbb{Z}$, q is an odd number, $k=⌈{log}_{2}q⌉$, namely the result of rounding up ${log}_{2}q$. We denote the $g^{\top }\in {\mathbb{Z}}_q^{1\times k}$ as $\left[\begin{array}{ccccc}1& 2& 4& \cdots & 2^{k-1}\end{array}\right]$. Let $\mathbf{G}={\mathbf{I}}_r\otimes g^{\top }\in {\mathbb{Z}}_q^{r\times rk}$ be a public matrix and ⊗ means tensor product. The $\mathbf{G}$-trapdoor for the lattice ${\Lambda }^{\perp }\left(\mathbf{X}\right)$ was proposed in the scheme [21].

Definition 4

([21]). Given a matrix $\mathbf{X}\in {\mathbb{Z}}_q^{r\times n},\mathbf{G}\in {\mathbb{Z}}_q^{r\times \omega }$ with $n\ge \omega \ge r$, q is an odd number. If there pertains some invertible matrix $\mathbf{S}\in {\mathbb{Z}}_q^{r\times r}$, and we have $\mathbf{X}\left[\begin{array}{c}{T}_{\mathbf{X}}\\ \mathbf{I}\end{array}\right]=\mathbf{SG}$, then $T_{\mathbf{X}}\in {\mathbb{Z}}_q^{\left(n-\omega \right)\times \omega }$ is named a $\mathbf{G}$-trapdoor for $\mathbf{X}$. We say that the greatest singular value of $T_{\mathbf{X}}$ is denoted as $s_1\left(T_{\mathbf{X}}\right)$, and the quality of this trapdoor $T_{\mathbf{X}}$ is judged by $s_1\left(T_{\mathbf{X}}\right).$

Theorem 2

([21]). Let $q\ge 2,r\ge 1$ and $\mathbf{S}\in {\mathbb{Z}}_q^{r\times r}$ is invertible matrix. For $k=⌈{log}_{2}q⌉$ and $n>rlogq$, there is a randomized algorithm $\mathbf{GenTrap}$$\left(1^r,1^n,q,\mathbf{S}\right)$, and the algorithm’s output is a parity-check matrix $\mathbf{X}\in {\mathbb{Z}}_q^{r\times n}$ with $\mathbf{G}$-trapdoor $T_{\mathbf{X}}$. The distribution of $\mathbf{X}$ approximately follows uniform distribution.

Moreover, for any $\partial \in {\mathbb{Z}}_q^r$ and sufficiently large $\varrho >\sqrt{rlogq}$, randomized algorithm $\mathbf{SampleD}$$\left(T_{\mathbf{X}},\mathbf{X},\mathbf{S},\partial ,\varrho \right)$, which outputs sampling results from distribution $D_{{\Lambda }_q^{\partial }\left(\mathbf{X}\right),\varrho }$ within $negl\left(r\right)$ statistical distance.

Lemma 1

([3]). Suppose that $n>\left(r+1\right)lo{g}_{2}q+\omega \left(logr\right)$, where $q>2$ and q is a prime number. Let $n\times k$ matrix $\mathbf{R}$ be an uniform matrix from ${\left\{1,-1\right\}}^{n\times k}$ mod q. Let $\mathbf{X}$ and $\mathbf{Y}$ be two uniform matrices from ${\mathbb{Z}}_q^{r\times n}$ and ${\mathbb{Z}}_q^{r\times k}$ separately. Then, for all of the vectors w from ${\mathbb{Z}}_q^n$, the distribution $\left(\mathbf{X},\mathbf{XR},{\mathbf{R}}^{\top }w\right)$ and the distribution $\left(\mathbf{X},\mathbf{Y},{\mathbf{R}}^{\top }w\right)$ is statistically approaching.

We look back at some sampling algorithms from [3,21]. Let $\mathbf{X},\mathbf{Y}$ be matrices in ${\mathbb{Z}}_q^{r\times n}$, the matrix ${\mathbf{M}}_1\in {\mathbb{Z}}_q^{r\times n_1}$, and $\mathbf{R}\in {\left\{-1,1\right\}}^{n\times n}$. Set $F_1≔\left(\mathbf{X}|{\mathbf{M}}_1\right)$, $F_2≔\left(\mathbf{X}|\mathbf{XR}+\mathbf{Y}\right)$.

–

$\mathbf{SampleL}$$\left(\mathbf{X},{\mathbf{M}}_1,T_{\mathbf{X}},\partial ,\varrho \right)\to \mu :$ For matrix $\mathbf{X}\in {\mathbb{Z}}_q^{r\times n}$ and its $\mathbf{G}$-trapdoor $T_{\mathbf{X}}$, matrix ${\mathbf{M}}_1\in {\mathbb{Z}}_q^{r\times n_1}$, vector $\partial \in {\mathbb{Z}}_q^r$ and parameter $\varrho \ge ∥\widetilde{T_{\mathbf{X}}}∥·\omega \left(\sqrt{log\left(n+n_1\right)}\right)$, the algorithm outputs a vector $\mu$ distributed statistically approaching to $D_{{\Lambda }_q^{\partial }\left({\mathbf{F}}_{\mathbf{1}}\right),\varrho }$.

–

$\mathbf{SampleR}$$\left(\mathbf{X},\mathbf{Y},\mathbf{R},T_{\mathbf{Y}},\partial ,\varrho \right)\to \mu :$ For matrix $\mathbf{Y}\in {\mathbb{Z}}_q^{r\times n}$ and its $\mathbf{G}$-trapdoor $T_{\mathbf{Y}}$, matrix $\mathbf{X}\in {\mathbb{Z}}_q^{r\times n}$, uniformly random matrix $\mathbf{R}$ from ${\left\{-1,1\right\}}^{n\times n}$, vector $\partial \in {\mathbb{Z}}_q^r$, and parameter $\varrho \ge ∥\widetilde{T_{\mathbf{Y}}}∥·\sqrt{n}·\omega \left(\sqrt{logn}\right)$, the algorithm outputs a vector $\mu$ distributed statistically close to $D_{{\Lambda }_q^{\partial }\left({\mathbf{F}}_{\mathbf{2}}\right),\varrho }$.

3.3. Encoding Identities as Matrices

The encoding function $\mathbf{N}$: ${\mathbb{Z}}_q^r\to {\mathbb{Z}}_q^{r\times r}$ is used to map identities in ${\mathbb{Z}}_q^r$ to matrices in ${\mathbb{Z}}_q^{r\times r}$. $\mathbf{N}$ is an explicit full-rank differences (FRD) construction, which means for all different $i{d}_1$ and $i{d}_2$ from ${\mathbb{Z}}_q^r$, the matrix $\left[\mathbf{N}\left(i{d}_1\right)-\mathbf{N}\left(i{d}_2\right)\right]\in {\mathbb{Z}}_q^{r\times r}$ is full-rank. Furthermore, the method is to build an additive subgroup $\mathbb{G}$ from ${\mathbb{Z}}_q^{r\times r}$ of size $q^r$. All of the non-zero matrices from $\mathbb{G}$ are full-rank. In this way, for all different $\mathbf{X},\mathbf{Y}\in \mathbb{G}$, the difference between them is also in $\mathbb{G}$, as a consequence, $\mathbf{X}-\mathbf{Y}$ is full-rank.

Although we are primarily interested in the finite field ${\mathbb{Z}}_q$, we represent the structure of a random field $\mathbb{P}$. In cases where polynomial $f\in \mathbb{P}\left[x\right]$ of degree less than r, we define the r-vector of coefficients of f as ces(f)$\in {\mathbb{P}}^r$ and express it as a row vector. However, in cases where f is of degree less than $r-1$, we add zeroes to the right of the coefficients vector, so it becomes r-vector. The case in point is, for r = 8 we have ces($x^5+7x^2+1$) = (1, 0, 7, 0, 0, 1, 0, 0) $\in {\mathbb{P}}^8$. We let p of degree r be some irreducible polynomial from $\mathbb{P}\left[x\right]$. Think back that the polynomial f from $\mathbb{P}\left[x\right]$ mod p has degree less than r, consequently, the ces(f mod p) is a vector from ${\mathbb{P}}^r$.

Yet, for an input $h=\left(h_0,\dots ,h_{r-1}\right)\in {\mathbb{P}}^r$, the polynomial $f_h\left(x\right)={\sum }_{i=0}^{r-1}{h}_i{x}^i\in \mathbb{P}\left[x\right]$. We define $\mathbf{N}\left(h\right)$ as:

$$\mathbf{N}\left(h\right)≔\left(\begin{array}{c}\mathsf{ces}\left(f_h\right)\\ \mathsf{ces}\left(x·f_h\mathsf{mod}p\right)\\ \mathsf{ces}\left(x^2·f_h\mathsf{mod}p\right)\\ ⋮\\ \mathsf{ces}\left(x^{r-1}·f_h\mathsf{mod}p\right)\end{array}\right)\in {\mathbb{P}}^{r\times r}.$$

Because for all of the prime numbers q and the integer $r>1$, there are irreducible polynomials of degree r from ${\mathbb{Z}}_q\left[x\right]$, and the structure can cater for any pair of q and r.

Theorem 3

([25]). Let $\mathbb{P}$ be a field and the p is a polynomial from $\mathbb{P}\left[x\right]$. The function $\mathbf{N}$ is an encoding with FRD, if the p is irreducible from $\mathbb{P}\left[x\right]$.

Let $r=4$, and $p\left(x\right)=x^4+x-1$. The function $\mathbf{N}\left(h\right)$, where $h=\left(h_0,h_1,h_2,h_3\right)$, works as below.

$$\mathbf{N}\left(h\right)=\mathbf{N}\left(h_0,h_1,h_2,h_3\right)≔$$

$$\left(\begin{array}{cccc}{h}_0& h_1& h_2& h_3\\ h_3& h_0-h_3& h_1& h_2\\ h_2& h_3-h_2& h_0-h_3& h_1\\ h_1& h_2-h_1& h_3-h_2& h_0-h_3\end{array}\right).$$

Theorem 3 proves that for all prime numbers q, the function $\mathbf{N}$ is FRD, where $x^4+x-1$ is irreducible from ${\mathbb{Z}}_q\left[x\right]$.

4. New Lattice-Identity-Based Online/Offline Encryption

The construction of our lattice based IBOOE scheme is on the basis of the following idea. In the offline phase, we generate offline ciphertext with high computational complexity and no need to know identity and messages. During the online phase, we generate online ciphertext by using identity, messages, and offline ciphertext.

4.1. Construction

As shown in Figure 1, in our IBOOE scheme, KGC generates public parameters and master secert key. With the master secret key, KGC generates the private key for the Data User. For performing the offline encryption operation, the Offline Server completes Gaussian sampling and sends offline ciphertext to the Data Owner. Using the offline ciphertext, the Data Owner completes online encryption with the Data User’s $\mathsf{id}$ and the message $mes$. The Data User decrypts ciphertext for the final message $mes$. The concrete algorithms are as below.

$\mathbf{Setup}$: KGC takes r to be the security parameter, sets $n=2r^{1+\delta },q=n^{2.5}·\omega \left(\sqrt{logr}\right)$, $\varrho =n·\omega \left(\sqrt{logr}\right),ϵ={\left[n^2·\omega \left(\sqrt{logr}\right)\right]}^{-1}$. Then, it rounds up n to next larger integer and rounds up q to next larger prime number. Among above formulas, $\delta$ is for $r^{\delta }=O\left(logr\right)$. By using algorithm $\mathbf{GenTrap}$, it selects a uniform and random $r\times n$-matrix ${\mathbf{X}}_0\in {\mathbb{Z}}_{\mathit{q}}^{\mathit{r}\times \mathit{n}}$ with the $\mathbf{G}$-trapdoor $T_{{\mathbf{X}}_0}$ as defined in Definition 4. It then selects two uniform and random $r\times n$ matrices ${\mathbf{X}}_1,\mathbf{Y}$ in ${\mathbb{Z}}_q^{\mathit{r}\times \mathit{n}}$. It selects a uniform and random r-vector ∂ in ${\mathbb{Z}}_{\mathit{q}}^{\mathit{r}}$. Lastly, KGC outputs public parameters $\mathsf{PP}$ and the master key $\mathsf{MK}$:

$$\mathsf{PP}=\left({\mathbf{X}}_0,{\mathbf{X}}_1,\mathbf{Y},\partial \right);\mathsf{MK}=T_{{\mathbf{X}}_0}.$$

$\mathbf{Extract}$: KGC takes public parameters $\mathsf{PP}$, the master key $\mathsf{MK}$, and an identity $\mathsf{id}\in {\mathbb{Z}}_{\mathit{q}}^{\mathit{r}}$ as inputs, then KGC samples $\mu \in {\mathbb{Z}}^{2\mathit{n}}$ as:

$$\mu \leftarrow \mathsf{SampleL}\left({\mathbf{X}}_0,{\mathbf{X}}_1+\mathbf{N}\left(\mathsf{id}\right)\mathbf{Y},T_{{\mathbf{X}}_0},\partial ,\varrho \right).$$

In the above formula, $\mathbf{N}$ is the FRD map as described in Section 3.3 and $\mu$ is distributed as $D_{{\Lambda }_q^{\partial }\left(F_{\mathsf{id}}\right),\varrho }$. Let $F_{\mathsf{id}}≔\left({\mathbf{X}}_0\right|{\mathbf{X}}_1+\mathbf{N}\left(\mathsf{id}\right)\mathbf{Y})$, which means $F_{\mathsf{id}}·\mu =\partial$. For the chosen $\mathsf{id}$, KGC outputs the following secret key:

$${\mathsf{SK}}_{\mathsf{id}}≔\mu .$$

${\mathbf{Enc}}^{\mathbf{off}}$: The Offline Server takes public parameters $\mathsf{PP}$ as input and completes Gaussian sampling, which does not need the identity and the message that needs to be encrypted in following online algorithm. It also chooses the uniform and random vector $s\stackrel{R}{\leftarrow }{\mathbb{Z}}_{\mathit{q}}^{\mathit{r}}$ and the uniform and random matrix $\mathbf{R}$ from ${\left\{-1,1\right\}}^{n\times n}$. It also chooses $x\stackrel{{\overline{\mathsf{\Psi }}}_{ϵ}}{\leftarrow }{\mathbb{Z}}_{\mathit{q}}$ and $y\stackrel{{\overline{\mathsf{\Psi }}}_{ϵ}^n}{\leftarrow }{\mathbb{Z}}_{\mathit{q}}^{\mathit{n}}$ for noise vectors, which both follow the distribution of Definition 1, and set $z\leftarrow {\mathbf{R}}^{T}y\in {\mathbb{Z}}_{\mathit{q}}^{\mathit{n}}$. Offline Server computes $\overline{{\xi }_0}={\partial }^{T}s+x\in {\mathbb{Z}}_{\mathit{q}}$ and $\overline{{\xi }_1}=\left[\begin{array}{c}y\\ z\end{array}\right]$ and stores the offline ciphertext for the online phase:

$$\overline{\xi }≔(\overline{{\xi }_0},\overline{{\xi }_1},s)$$

${\mathbf{Enc}}^{\mathbf{on}}$: The Data Owner takes $\mathsf{PP}$, identity $\mathsf{id}$, and a message $mes\in \left\{0,1\right\}$ as inputs. Then, it sets $F_{\mathsf{id}}$ as $\left({\mathbf{X}}_0|{\mathbf{X}}_1+\mathbf{N}\left(\mathsf{id}\right)\mathbf{Y}\right)$. It also sets ${\xi }_0=\overline{{\xi }_0}+mes⌊{\displaystyle \frac{q}{2}}⌋\in {\mathbb{Z}}_{\mathit{q}}$ and ${\xi }_1=F_{\mathsf{id}}^{\top }s+\left[\begin{array}{c}y\\ z\end{array}\right]\in {\mathbb{Z}}_{\mathit{q}}^{2\mathit{n}}$. The Data Owner outputs the online ciphertext:

$$\xi ≔({\xi }_0,{\xi }_1).$$

$\mathbf{Dec}$: The Data User takes public parameters $\mathsf{PP}$, the private key ${\mathsf{SK}}_{\mathsf{id}}$, and the online ciphertext $\xi$ as inputs, it then computes $\omega \leftarrow {\xi }_0-{\mathsf{SK}}_{\mathsf{id}}^{\top }{\xi }_1$ in ${\mathbb{Z}}_{\mathit{q}}$. It compares $\omega$ and $⌊{\displaystyle \frac{q}{2}}⌋$, the downward rounding of ${\displaystyle \frac{q}{2}}$, treat them as integers from $\mathbb{Z}$. If the two integers are approaching, namely, if $\left|\omega -⌊{\displaystyle \frac{q}{2}}⌋\right|<⌊{\displaystyle \frac{q}{4}}⌋$ from $\mathbb{Z}$, output 1, otherwise output 0.

In the above encryption, the matrix $\mathbf{R}$ has significant importance in security proof. The matrix is a tool for a specific distribution required by the simulation, which is used to sample noise vectors ($y,z$).

4.2. Parameters and Correctness

We define our scheme’s correctness below.

$\mathbf{Correctness}.$ If $\left(\mathsf{PP},\mathsf{MK}\right)\leftarrow \mathbf{Setup}\left(\lambda \right)$, the $\mathbf{Extract}$ algorithm runs as ${\mathsf{SK}}_{\mathsf{id}}\leftarrow \mathbf{Extract}$$\left(\mathsf{PP},\mathsf{MK},\mathsf{id}\right)$ and ciphertexts generated as $\overline{\xi }\leftarrow {\mathbf{Enc}}^{\mathbf{off}}\left(\mathsf{PP}\right)$, $\xi \leftarrow {\mathbf{Enc}}^{\mathbf{on}}\left(\mathsf{PP},\mathsf{id},mes,\overline{\xi }\right)$, then $\mathbf{Dec}\left(\mathsf{PP},{\mathsf{SK}}_{\mathsf{id}},\xi \right)$ outputs “$mes$” with an overwhelming probability.

Proof. 

When our scheme is operated as specified, during decryption, we have:

$$\omega ={\xi }_0-{\mathsf{SK}}_{\mathsf{id}}^{\top }{\xi }_1=mes⌊{\displaystyle \frac{q}{2}}⌋+x-{\mathsf{SK}}_{\mathsf{id}}^{\top }\left[\begin{array}{c}y\\ z\end{array}\right].$$

For recovering $mes$ correctly, we can compute the error term as $x-{\mathsf{SK}}_{\mathsf{id}}^{\top }\left[\begin{array}{c}y\\ z\end{array}\right]$, and it needs to be less than $q/5$. Since $x\in {\overline{\mathsf{\Psi }}}_{ϵ}$ and $y\in {\overline{\mathsf{\Psi }}}_{ϵ}^n$, we have $\left|x\right|<qϵ\omega \left(\sqrt{logn}\right)+1/2$ and $\left|y\right|<qϵ\omega \left(\sqrt{logn}\right)+\sqrt{n}/2$. For $∥{\mathsf{SK}}_{\mathsf{id}}∥$ is sampled by $\mathbf{SampleL}$, we have $∥{\mathsf{SK}}_{\mathsf{id}}∥\le \varrho \sqrt{2n}$. Let ${\mathsf{SK}}_{\mathsf{id}}=\left({\mu }_1,{\mu }_2\right)$, with the error term as follows:

$$x-{\mathsf{SK}}_{\mathsf{id}}^{\top }\left[\begin{array}{c}y\\ z\end{array}\right]=x-{\mu }_1^{\top }y-{\mu }_2^{\top }z=x-{\left({\mu }_1-\mathbf{R}{\mu }_2\right)}^{\top }y.$$

For a random matrix $\mathbf{R}$ chosen from ${\left\{-1,1\right\}}^{n\times n}$, we have $∥\mathbf{R}∥\le O\left(\sqrt{n}\right)$. Since $∥{\mu }_1-\mathbf{R}{\mu }_2∥\le ∥{\mu }_1∥+∥\mathbf{R}{\mu }_2∥\le O\left(\varrho n\right)$ ([3]), the error term $\left|x-{\mathsf{SK}}_{\mathsf{id}}^{\top }\left[\begin{array}{c}y\\ z\end{array}\right]\right|$ is then limited by:

$$\left|x\right|+\left|{\left({\mu }_1-\mathbf{R}{\mu }_2\right)}^{\top }y\right|\le qϵ\omega \left(\sqrt{logn}\right)+O\left(\varrho n^{3/2}\right).$$

In order for the system to function properly, we must make sure that the error term described as above in $\mathbf{Dec}$ is lower than $q/5$. $\mathbf{GenTrap}$ needs $n>rlogq$ and $\varrho >\sqrt{rlogq}$ to operate correctly. $\mathbf{SampleR}$ and $\mathbf{SampleL}$ need $\varrho$ to be large enough, $\varrho >n\omega \left(\sqrt{logn}\right)$. Furthermore, our security proof needs $q>2\sqrt{r}/ϵ$.

For the sake of meeting the requirements of accuracy and safety, we set the parameters as follows, using r as security parameter:

$$n=2r^{1+\delta },q=n^{2.5}·\omega \left(\sqrt{logr}\right)$$

$$\varrho =n·\omega \left(\sqrt{logr}\right),ϵ={\left[n^2·\omega \left(\sqrt{logr}\right)\right]}^{-1}$$

which round up n to the next greater integer, and round up q to the next greater prime number. Furthermore, $\delta$ is for $r^{\delta }>⌈logq⌉=O\left(logr\right)$. □

4.3. Security Proof

We demonstrate that our IBOOE scheme is indistinguishable from randomness under the selective identity attack in Definition 3. Being indistinguishable from randomness implies that, in the ciphertext space, the challenge ciphertext cannot be distinguished from randomly selected elements in the ciphertext space.

Theorem 4.

If the $\left({\mathbb{Z}}_{\mathit{q}},r,{\overline{\mathsf{\Psi }}}_{ϵ}\right)$-LWE assumption holds true, the IBOOE scheme is secure for INDr-sID-CPA.

Proof. 

Our security proof follows a series of games, where the first one of these games is identical as INDr-sID-CPA game, which is described in Definition 3. Furthermore, the adversary $\mathcal{A}$ has no positive in the final game. Because when the adversary gets the ciphertext in the last game, it is always a randomly selected element from ciphertext space. We demonstrate that the upside of the PPT adversary winning the rudimentary INDr-sID-CPA game is ignorable by demonstrating that the adversary cannot distinguish the series of games presented below. The proof of indistinguishability between the Game 2 and the Game 3 is reduced to the LWE difficulty problem. □

• $\mathbf{Game}\mathbf{0}$: The Game 0 is between the adversary $\mathcal{A}$ for our scheme and the INDr-sID-CPA challenger, it is just as described in Definition 3, namely the original game.

• $\mathbf{Game}\mathbf{1}$:

$\mathbf{Init}$: In the initial phase, the adversary $\mathcal{A}$ first outputs its target identity ${\mathsf{id}}^{*}$.

$\mathbf{Setup}$: In the setup phase, the challenger then runs algorithm $\mathbf{Setup}$ and chooses ${\mathbf{R}}^{*}$ to construct ${\mathbf{X}}_1$ as:

$$\begin{array}{c}{\mathbf{X}}_0{\mathbf{R}}^{*}-\mathbf{N}\left({\mathsf{id}}^{*}\right)\mathbf{Y}\end{array}$$

(1)

The challenger provides the system public parameters $\mathsf{PP}$ to the adversary $\mathcal{A}$ and keeps the master key $\mathsf{MK}$ secrete from $\mathcal{A}$.

$\mathbf{Phase}\mathbf{1}$: In the first phase, the adversary $\mathcal{A}$ sends the private key queries $q_1,\dots ,q_n$ to the challenger and the query $q_i$ is for ${\mathsf{id}}_i$. We request that ${\mathsf{id}}_i$ cannot equal to ${\mathsf{id}}^{*}$. For private key $d_i$ which corresponds to the identity ${\mathsf{id}}_i$, the challenger runs algorithm $\mathbf{Extract}$ to respond. The challenger sends $d_i$ to $\mathcal{A}$. The above queries are all adaptive.

$\mathbf{Challenge}$: After the adversary’s judgment of the first phase is completed, a plaintext $M\in {\mathcal{M}}_{\lambda }$ will be output. Furthermore, this is the plaintext that $\mathcal{A}$ intends to be challenged. Then, for the following simulation, the challenger selects a random bit $\mathit{a}\in \left\{0,1\right\}$ corresponding to a different situation, and it also picks a random ciphertext $\xi \in {\xi }_{\lambda }$.

(1)

For $\mathit{a}=0$, the challenger uses algorithm $\mathbf{Encrypt}$ for setting the challenge ciphertext as ${\xi }^{*}$$≔\mathbf{Encrypt}$($\mathsf{PP}$,${\mathsf{id}}^{*}$,M).

(2)

For $\mathit{a}=1$, the challenger directly uses the ciphertext chosen before and sets ${\xi }^{*}≔\xi .$

The challenger then sends ${\xi }^{*}$ as the ciphertext for challenge to adversary $\mathcal{A}$.

$\mathbf{Phase}\mathbf{2}$: Then, in the second phase, the adversary $\mathcal{A}$ adaptively sends supplemental queries from $n+1$ to r, and the query $q_i$ corresponds to the ${\mathsf{id}}_i^{\prime }s$ private key extraction query, where ${\mathsf{id}}_i$ cannot be equivalent to ${\mathsf{id}}^{*}$. Just like in phase 1, the challenger sends $q_i$ to adversary $\mathcal{A}$.

$\mathbf{Guess}$: Lastly, the adversary $\mathcal{A}$ sends the guess ${\mathit{a}}^{\prime }\in \left\{0,1\right\}$ as its output for result that the challenger chose before. $\mathcal{A}$ wins the game when $\mathit{a}={\mathit{a}}^{\prime }$. For the positive of adversary for attacking an IBE scheme, we define it as:

$$Ad{v}_{\mathcal{A}}\left(\lambda \right)=\left|Pr\left[\mathit{a}={\mathit{a}}^{\prime }\right]-1/2\right|.$$

• $\mathbf{Game}\mathbf{2}$:

$\mathbf{Init}$: In the initial phase, the adversary $\mathcal{A}$ first outputs its target identity ${\mathsf{id}}^{*}$.

$\mathbf{Setup}$: In the setup phase, the challenger then runs algorithm $\mathbf{Setup}$, generates ${\mathbf{X}}_0$ as a random matrix and generates $\mathbf{Y}$ using $\mathbf{GenTrap}$ with $\mathbf{G}$-trapdoor $T_{\mathbf{Y}}$, and constructs ${\mathbf{X}}_1\leftarrow {\mathbf{X}}_0{\mathbf{R}}^{*}-\mathbf{N}\left({\mathsf{id}}^{*}\right)\mathbf{Y}$. The challenger provides the system public parameters $\mathsf{PP}$ to the adversary $\mathcal{A}$ and keeps the master key $\mathsf{MK}$ secrete from $\mathcal{A}$.

$\mathbf{Phase}\mathbf{1}$: In the first phase, the adversary $\mathcal{A}$ sends the private key queries $q_1,\dots ,q_n$ to the challenger and the query $q_i$ is for ${\mathsf{id}}_i$. We request that ${\mathsf{id}}_i$ cannot equal to ${\mathsf{id}}^{*}$. For the private key $d_i$, which corresponds to the identity ${\mathsf{id}}_i$, the challenger runs $\mathbf{Extract}$ to respond. During $\mathbf{Extract}$, the challenger uses $\mathbf{SampleR}$$\left({\mathbf{X}}_0,\left(\mathbf{N}\left(\mathsf{id}\right)-\mathbf{N}\left({\mathsf{id}}^{*}\right)\right)\mathbf{Y},{\mathbf{R}}^{*},\partial ,\varrho \right)$ to get $\mu \in D_{{\Lambda }_q^{\partial }\left(F_{\mathsf{id}}\right),\varrho }$ where:

$$\begin{array}{c}{F}_{\mathsf{id}}≔\left({\mathbf{X}}_0\mid {\mathbf{X}}_0{\mathbf{R}}^{*}+\left(\mathbf{N}\left(\mathsf{id}\right)-\mathbf{N}\left({\mathsf{id}}^{*}\right)\right)\mathbf{Y}\right)\end{array}$$

(2)

The challenger then sends $d_i$ to $\mathcal{A}$. The above queries are all adaptive.

$\mathbf{Challenge}$: After the adversary’s judgement of the first phase is completed, a plaintext $M\in {\mathcal{M}}_{\lambda }$ will be output. Furthermore, this is the plaintext that $\mathcal{A}$ wants to be challenged. Then, for the following simulation, the challenger selects a random bit $\mathit{a}\in \left\{0,1\right\}$ corresponding to different situation, and it also picks a random ciphertext $\xi \in {\xi }_{\lambda }$.

(1)

For $\mathit{a}=0$, the challenger uses algorithm $\mathbf{Encrypt}$ for setting challenge ciphertext as ${\xi }^{*}$$≔\mathbf{Encrypt}$($\mathsf{PP}$,${\mathsf{id}}^{*}$,M).

(2)

For $\mathit{a}=1$, the challenger directly uses the ciphertext chosen before and sets ${\xi }^{*}≔\xi .$

The challenger then sends ${\xi }^{*}$ to adversary $\mathcal{A}$.

$\mathbf{Phase}\mathbf{2}$: Then, in the second phase, the adversary $\mathcal{A}$ adaptively sends the supplemental queries from $n+1$ to r, and the query $q_i$ corresponds to the ${\mathsf{id}}_i^{\prime }s$ private key extraction query, where ${\mathsf{id}}_i$ cannot be equivalent to ${\mathsf{id}}^{*}$. Just like in phase 1, challenger sends $q_i$ to adversary $\mathcal{A}$.

$\mathbf{Guess}$: Lastly, the adversary $\mathcal{A}$ sends the guess ${\mathit{a}}^{\prime }\in \left\{0,1\right\}$ as its output for result that the challenger chose before. $\mathcal{A}$ wins the game when $\mathit{a}={\mathit{a}}^{\prime }$. For the positive of adversary for attacking the IBE scheme, we define it as $Ad{v}_{\mathcal{A}}\left(\lambda \right)=\left|Pr\left[\mathit{a}={\mathit{a}}^{\prime }\right]-1/2\right|.$

• $\mathbf{Game}\mathbf{3}$:

$\mathbf{Init}$: In the initial phase, the adversary $\mathcal{A}$ first outputs its target identity ${\mathsf{id}}^{*}$.

$\mathbf{Setup}$: The challenger then runs algorithm $\mathbf{Setup}$, generates ${\mathbf{X}}_0$ as a random matrix and generates the matrix $\mathbf{Y}$ using $\mathbf{GenTrap}$ with $\mathbf{G}$-trapdoor $T_{\mathbf{Y}}$, and constructs ${\mathbf{X}}_1\leftarrow {\mathbf{X}}_0{\mathbf{R}}^{*}-\mathbf{N}\left({\mathsf{id}}^{*}\right)\mathbf{Y}$. The challenger provides the system public parameters $\mathsf{PP}$ to the adversary $\mathcal{A}$ and keeps the master key $\mathsf{MK}$ secrete from $\mathcal{A}$.

$\mathbf{Phase}\mathbf{1}$: In the first phase, the adversary $\mathcal{A}$ sends the private key queries $q_1,\dots ,q_n$ to the challenger and the query $q_i$ is for ${\mathsf{id}}_i$. We request that ${\mathsf{id}}_i$ cannot equal to ${\mathsf{id}}^{*}$. The private key $d_i$ corresponds to the identity ${\mathsf{id}}_i$, and the challenger runs $\mathbf{Extract}$ to respond. During $\mathbf{Extract}$, the challenger uses $\mathbf{SampleR}$ to get $\mu \in D_{{\Lambda }_q^{\partial }\left(F_{\mathsf{id}}\right),\varrho }$ where $F_{\mathsf{id}}$ is as in Formula (2). The challenger sends $d_i$ to $\mathcal{A}$. The above queries are all adaptive.

$\mathbf{Challenge}$: After the adversary’s judgement of the first phase is completed, a plaintext $M\in {\mathcal{M}}_{\lambda }$ will be output. Furthermore, this is the plaintext that $\mathcal{A}$ wants to be challenged. Then, for the following simulation, the challenger selects a random bit $\mathit{a}\in \left\{0,1\right\}$ corresponding to different situation, and it also picks a random ciphertext $\xi \in {\xi }_{\lambda }$, but always sets the challenge ciphertext as ${\xi }^{*}≔\xi$.

The challenger then sends ${\xi }^{*}$ to adversary $\mathcal{A}$.

$\mathbf{Phase}\mathbf{2}$: In the second phase, the adversary $\mathcal{A}$ adaptively sends the supplemental queries from $n+1$ to r, and the query $q_i$ corresponds to the ${\mathsf{id}}_i^{\prime }s$ private key extraction query, where ${\mathsf{id}}_i$ cannot be equivalent to ${\mathsf{id}}^{*}$. Just like in phase 1, the challenger responds $q_i$ to adversary $\mathcal{A}$.

$\mathbf{Guess}$: Lastly, the adversary $\mathcal{A}$ sends the guess ${\mathit{a}}^{\prime }\in \left\{0,1\right\}$ as its output for the result that challenger chose before. $\mathcal{A}$ wins the game when $\mathit{a}={\mathit{a}}^{\prime }$. For the positive of adversary for attacking an IBE scheme, we define it as $Ad{v}_{\mathcal{A}}\left(\lambda \right)=\left|Pr\left[\mathit{a}={\mathit{a}}^{\prime }\right]-1/2\right|.$

Theorem 5.

Game 0 and Game 1 are statistically indistinguishable.

Proof. 

The challenger uses random matrices ${\mathbf{X}}_0,{\mathbf{X}}_1,\mathbf{Y}$ to generate public parameters $\mathsf{PP}$ and the trapdoor $T_{{\mathbf{X}}_0}$ in Game 0. The challenger generates challenge ciphertext ${\xi }^{*}$ during the challenge phase. We use ${\mathbf{R}}^{*}$ from ${\left\{-1,1\right\}}^{n\times n}$ to represent a random matrix, which is used to generate ${\xi }^{*}$.

The challenger chooses ${\mathbf{R}}^{*}$ and constructs ${\mathbf{X}}_1$ as in Formula (1) in Game 1. Furthermore, identity ${\mathsf{id}}^{*}$ is the identity which will be attacked by $\mathcal{A}$. This means we change a little in how the challenger generates the matrix ${\mathbf{X}}_1$ in public parameters.

Lemma 1 shows that Game 0 is statistically indistinguishable from Game 1. We use martix ${\mathbf{R}}^{*}$ for constructing ${\mathbf{X}}_1$ and challenge ciphertext in Game 1. We are able to know that the distribution (${\mathbf{X}}_0,{\mathbf{X}}_0{\mathbf{R}}^{*},z$) is statistically approaching to (${\mathbf{X}}_0,{\mathbf{X}}_1^{\prime },z$) by Lemma 1. The ${\mathbf{X}}_1^{\prime }$ is a uniform matrix from ${\mathbb{Z}}_{\mathit{q}}^{\mathit{r}\times \mathit{n}}$. In this way, matrix ${\mathbf{X}}_0{\mathbf{R}}^{*}$ is statistically approaching to the uniform one in $\mathcal{A}$’s view. Therefore, the ${\mathbf{X}}_1$ as defined in Formula (1) is also approaching to the uniform one. As a result, ${\mathbf{X}}_1$ are indistinguishable in the Game 0 and the Game 1. □

Theorem 6.

Game 1 and Game 2 are statistically indistinguishable.

Proof. 

We construct matrix ${\mathbf{X}}_0$ as a random matrix in Game 2, and for $\mathbf{Y}$, we generate it by running algorithm $\mathsf{GenTrap}$ with $\mathbf{G}$-trapdoor $T_{\mathbf{Y}}$. Construct ${\mathbf{X}}_1$ as in Game 1. For private key queries, the challenger uses matrix $\mathbf{R}$ to respond. Furthermore, for $\mathsf{id}\ne {\mathsf{id}}^{*}$, for the sake of answering the private key queries, the challenger uses the short vector $\mu$ from ${\Lambda }_q^{\partial }\left(F_{\mathsf{id}}\right)$ and sets $F_{\mathsf{id}}$ as in Formula (2). According to the structure, the difference between $\mathbf{N}\left(\mathsf{id}\right)$ and $\mathbf{N}\left({\mathsf{id}}^{*}\right)$ is non-singular, namely $\left[\mathbf{N}\left(\mathsf{id}\right)-\mathbf{N}\left({\mathsf{id}}^{*}\right)\right]$. Now, for private key query, challenger runs algorithm $\mathbf{SampleR}$ to respond. As in Game 1, algorithm $\mathbf{SampleR}$ outputs the vector $\mu$ from ${\mathbb{Z}}^{2\mathit{n}}$, which is sampled from distribution statistically approaching to $D_{{\Lambda }_q^{\partial }\left(F_{\mathsf{id}}\right),\varrho }$.

In other aspects, Game 2 is as same as Game 1. Because the response to the private key queries is statistically very approaching to the response in the Game 1, $\mathcal{A}$’s positive over the Game 1 and Game 2 has an almost ignorable difference. □

Theorem 7.

Game 2 and Game 3 are statistically indistinguishable.

Proof. 

Game 3 is just like Game 2, although it differs in that the challenge ciphertext $\left({\xi }_0^{*},{\xi }_1^{*}\right)$ is always picked as an independent and random element from ${\mathbb{Z}}_{\mathit{q}}\times {\mathbb{Z}}_{\mathit{q}}^{2\mathit{n}}$. Since the challenge ciphertext in the ciphertext space is always a novel random element and adversary $\mathcal{A}$ has no positive in Game 3, then for a PPT adversary, the second and third games are computationally indistinguishable, and we do this by reducing it to the LWE problem.

Assuming $\mathcal{A}$ has significant superiority in differentiating between the Game 2 and the Game 3. Then, we apply the adversary $\mathcal{A}$ for an LWE algorithm $\mathcal{L}$.

As described in Definition 2, an LWE problem instance is to differentiate between truly random sample and noisy pseudo-random for some secret s in ${\mathbb{Z}}_{\mathit{q}}^{\mathit{r}}$. In our security game, we set ${\mathcal{O}}_{\mathsf{\$}}$ as the truly random sample and the ${\mathcal{O}}_{\vartheta }$ as the LWE sample. $\mathcal{L}$ makes a distinction between the two with the adversary $\mathcal{A}$, and operates as below:

$\mathbf{Instance}.$ Simulator $\mathcal{L}$ approaches from $\mathcal{O}$ and for each $i=0,\cdots ,n$, simulator $\mathcal{L}$ achieves a fresh pair $\left({\partial }_i,v_i\right)\in {\mathbb{Z}}_{\mathit{q}}^{\mathit{r}}\times {\mathbb{Z}}_{\mathit{q}}$.

$\mathbf{Targeting}.$ The adversary declares to $\mathcal{L}$ that the object it wants to attack is ${\mathsf{id}}^{*}$.

$\mathbf{Setup}.$ Simulator $\mathcal{L}$ generates the system’s public parameters $\mathsf{PP}$ as below:

(a)

From n of the given LWE samples, it makes the random matrix ${\mathbf{X}}_0\in {\mathbb{Z}}_{\mathit{q}}^{\mathit{r}\times \mathit{n}}$ and for all $i=1,\cdots ,n$ the i-th column of ${\mathbf{X}}_0$ is the r-vector ${\partial }_i$.

(b)

Specify the zeroth LWE sample as a publicly available random r-vector ${\partial }_0\in {\mathbb{Z}}_{\mathit{q}}^{\mathit{r}}$. The zeroth LWE sample has not been used yet.

(c)

Use ${\mathsf{id}}^{*}$ and ${\mathbf{R}}^{*}$ to create the remaining of public parameters as in Game 2.

(d)

Lastly, it sends public parameters $\mathsf{PP}=\left({\mathbf{X}}_0,{\mathbf{X}}_1,\mathbf{Y},{\partial }_0\right)$ to the adversary.

$\mathbf{Queries}.$ For each of the private key extraction query, simulator $\mathcal{L}$ answers just as in Game 2.

$\mathbf{Challenge}.$ With the target ${\mathsf{id}}^{*}$, when adversary prompts the message bit $me{s}^{*}\in \left\{0,1\right\}$ and the challenge ciphertext, $\mathcal{L}$ responds as below:

(a)

Set $v_0,\cdots ,v_n$ as the entries from the LWE instance and set $v^{*}=\left[\begin{array}{c}{v}_1\\ ⋮\\ v_n\end{array}\right]$ from ${\mathbb{Z}}_{\mathit{q}}^{\mathit{n}}$.

(b)

Letting ${\xi }_0^{*}=v_0+me{s}^{*}⌊{\displaystyle \frac{q}{2}}⌋\in {\mathbb{Z}}_{\mathit{q}}$ for masking message bit.

(c)

Set ${\xi }_1^{*}=\left[\begin{array}{c}{v}^{*}\\ \left({\mathbf{R}}^{*}\right)v^{*}\end{array}\right]\in {\mathbb{Z}}_{\mathit{q}}^{2\mathit{n}}$.

(d)

Send ${\xi }^{*}=\left({\xi }_0^{*},{\xi }_1^{*}\right)$ to the adversary.

If the LWE oracle is pseudo-random, namely $\mathcal{O}$ = ${\mathcal{O}}_{\vartheta }$, ${\xi }^{*}$ will be distributed as in Game 2. Firstly, inspect that the $F_{{\mathsf{id}}^{*}}=\left({\mathbf{X}}_0|{\mathbf{X}}_0{\mathbf{R}}^{*}\right)$. Secondly, by the definition of ${\mathcal{O}}_{\vartheta }$ we are able to know that for some random noise vector $y\in {\mathbb{Z}}_{\mathit{q}}^{\mathit{n}}$, which is distributed as ${\overline{\mathsf{\Psi }}}_{ϵ}^n$, $v^{*}={\mathbf{X}}_0^{\top }s+y$. Thus, ${\xi }_1^{*}$ defined as above in the step (c) satisfies:

$${\xi }_1^{*}=\left[\begin{array}{c}{\mathbf{X}}_0^{\top }s+y\\ {\left({\mathbf{R}}^{*}\right)}^{\top }{\mathbf{X}}_0^{\top }s+{\left({\mathbf{R}}^{*}\right)}^{\top }y\end{array}\right]={\left(F_{{\mathsf{id}}^{*}}\right)}^{\top }s+\left[\begin{array}{c}y\\ {\left({\mathbf{R}}^{*}\right)}^{\top }y\end{array}\right]$$

and the ${\xi }_1$ part in Game 2 is the quantity on the right, namely the efficacious challenge ciphertext. We also notice that $v_0={\partial }_0^{\top }s+x$, and the x’s distribution is as the ${\overline{\mathsf{\Psi }}}_{ϵ}$. In this way, ${\xi }_0^{*}$ in step (b) satisfies ${\xi }_0^{*}={\partial }_0^{\top }s+x+me{s}^{*}⌊{\displaystyle \frac{q}{2}}⌋$, just like the ${\xi }_0$ part of the challenge ciphertext described in the Game 2.

In the case that $\mathcal{O}$ = ${\mathcal{O}}_{\mathsf{\$}}$, we have $v_0$ is uniform from ${\mathbb{Z}}_{\mathit{q}}$ and $v^{*}$ is uniform from ${\mathbb{Z}}_{\mathit{q}}^{\mathit{n}}$. According to the standard left-over-hash-lemma, which describes the hash function defined by the matrix $\left({\mathbf{X}}_0^{\top }|v^{*}\right)$. It makes sure that the two quantities ${\mathbf{X}}_0{\mathbf{R}}^{*}$ and ${\left({\mathbf{R}}^{*}\right)}^{\top }{v}^{*}$ are uniformly independent. Thus, ${\xi }_1^{*}$, which is defined as in step (c) is uniformly independent in ${\mathbb{Z}}_{\mathit{q}}^{\mathit{2}\mathit{n}}$. As a result, the challenge ciphertext in ${\mathbb{Z}}_q\times {\mathbb{Z}}_q^{2n}$ is always uniform just as in Game 3. □

$\mathbf{Guess}.$ After allowing supplemental queries, $\mathcal{A}$ speculates that this is a challenger of Game 2 or Game 3. The simulator $\mathcal{L}$ finally outputs the guess of $\mathcal{A}$ as a solution to the LWE problem for which it is attempting to resolve.

We have mentioned before that in the case of $\mathcal{O}$ = ${\mathcal{O}}_{\vartheta }$, the adversary $\mathcal{A}$’s opinion is just like in the Game 2. Furthermore, in the case of $\mathcal{O}$ = ${\mathcal{O}}_{\mathsf{\$}}$, the adversary $\mathcal{A}$’s opinion is just like in the Game 3. Consequently, the positive of smulator $\mathcal{L}$ in resolving LWE is equal to the positive of $\mathcal{A}$ in differentiating between the Game 2 and the Game 3. At this point, we have fully introduce the algorithm $\mathcal{L}$ and provide corresponding proof.

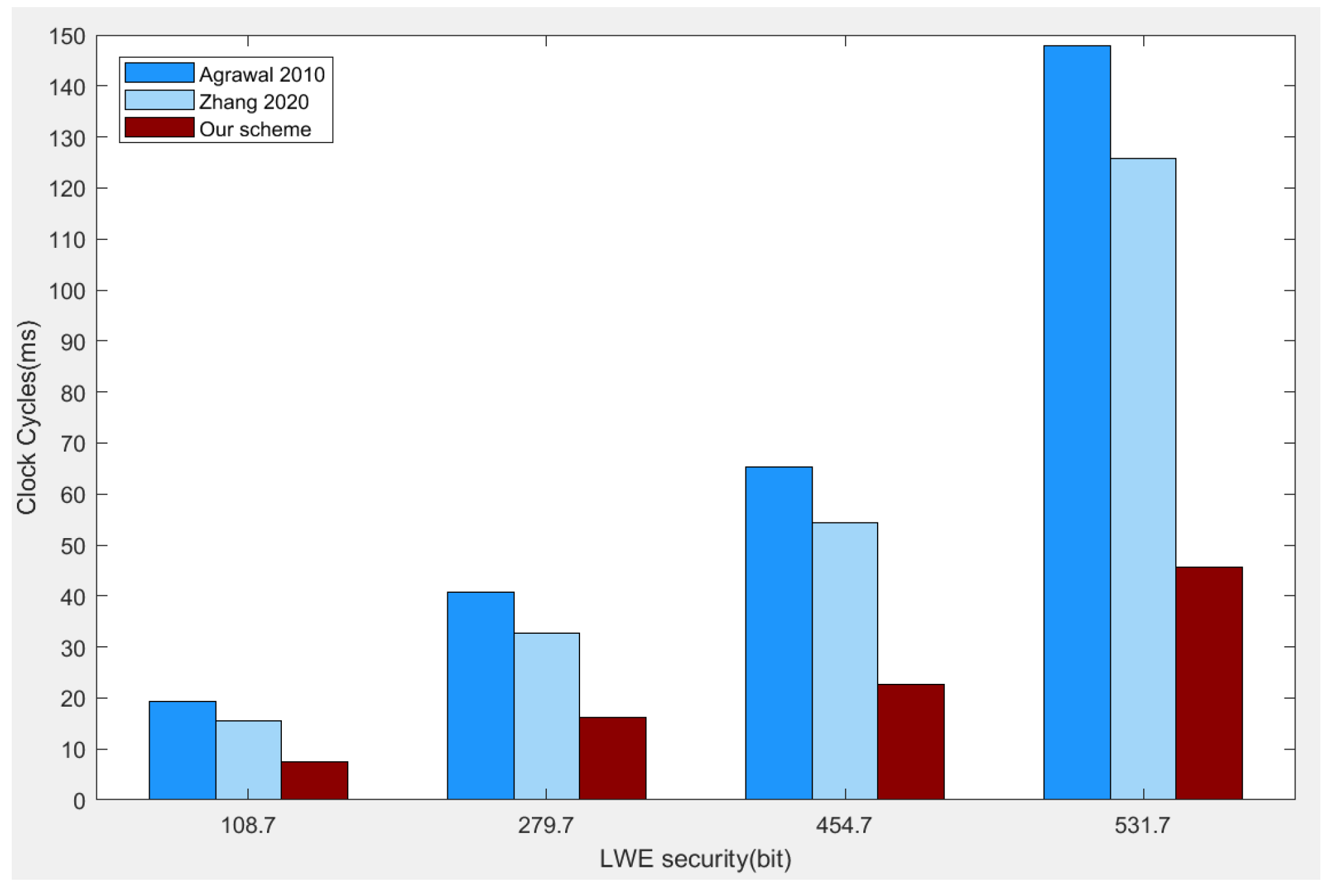
5. Comparison and Analysis

We compare our scheme with existing schemes [3,4] in terms of storage and computing. In

Table 1. Comparison of storage space.

	Scheme [3]	Scheme [4]	Our Scheme
PP Size	$2nrlogq$	$2nrlogq$	$2nrlogq$
SK Size	$2nlogq$	$2nrlogq$	$2nlogq$
Online Ciphertext Size	$\left(2n+1\right)logq$	$\left(2n+1\right)rlogq$	$\left(2n+1\right)logq$
Offline Ciphertext Size	-	-	$\left(2n+r+1\right)logq$
Security	CPA	CPA	CPA

, the performance of the schemes are analyzed from the aspects of $\mathsf{PP}$ size, $\mathsf{SK}$ size, online ciphertext size, offline ciphertext size, and security. We compare the computation efficiency of schemes in

Table 2. Comparison of computation efficiency.

	Online Computation	Offline Computation	Dimension
Scheme [3]	$r^2+4nr$	-	$6rlogq$
Scheme [4]	$r^2+3nr$	-	$2rlogq$
Our scheme	$2nr$	$r^2+2nr$	$2rlogq$

, from online computation, offline computation, and dimension. In addition, we also demonstrate through experimental simulations that our scheme is more efficient than existing schemes [3,4].

5.1. Theoretical Comparison

The schemes in Table 1 and Table 2 are secure against CPA under the standard model, where n is the dimension of the lattice, r is the security parameter, and q is the modulus. Furthermore, the limiting relationship between them is $n>rlogq$. Table 1 shows the storage cost and security among Agrawal et al.’s anti-quantum IBE scheme [3], our online/offline anti-quantum IBE scheme, and Zhang et al.’s anti-quantum IBE scheme [4]. Our scheme uses the more efficient trapdoor generation method $\mathbf{G}$-trapdoor to generate trapdoors in scheme. Moreover, the scheme [4] is a lattice based IBE scheme proposed by Zhang et al. in 2020, which is an efficient IBE scheme with short parameters over lattice. With the same security level, our scheme has a smaller $\mathsf{SK}$ size than scheme [4], and also has a smaller online ciphertext size. This is friendly to low-power encryption devices.

We also compare the efficiency of different schemes in Table 2 in terms of the computational cost of online ciphertext, the computational cost of offline ciphertext, and the dimension of lattice. It is easy to see through a comparison that our scheme has the highest efficiency in online ciphertext calculation compared to the scheme [3,4]. In addition, our scheme not only supports expansion into adaptive security scheme, but also into multi-bit encryption and HIBE, and has been proven to be secure in the standard model.

5.2. Experimental Simulation

Furthermore, we compare the clock cycles for implementing the online part of Agrawal et al.’s anti-quantum IBE scheme, Zhang et al.’s anti-quantum IBE scheme and our online/offline anti-quantum IBE scheme from LWE. In our scheme, the Gaussian sampling parts which do not request $\mathsf{id}$ and $mes$ are placed on the Offline Server for operation. Our implementation is carried out on an Intel i7-12700 2.7GHz CPU, which is manufactured by Intel, Shanghai, China, with double precision floating point numbers for non integers in C++. We use the “time.h” to measure clock cycles. The one-dimensional sampler [26] is a modified rejection sampler. We set q and r for different LWE security [27]. In our settings, $q=2^{12},r=2^9$ for 108.7-bit LWE security; $q=2^{24},r=2^{11}$ for 279.7-bit LWE security; $q=2^{34},r=2^{13}$ for 454.7-bit LWE security; and $q=2^{60},r=2^{14}$ for 531.7-bit LWE security.

The scheme in [3] is a classic IBE scheme based on LWE, while the scheme in [4] is a recently published efficient LWE IBE scheme. The scheme in [4] balances efficiency and public parameter size through clever ideas in identity processing, and our scheme focuses on improving the efficiency of online computing while ensuring security. As shown in Figure 2, for the efficiency of the online part, our online/offline scheme has improved by 65% to 80% compared to the initial anti-quantum IBE scheme [3] from LWE, and by 60% to 70% compared to the scheme [4]. The improvement in efficiency increases with the increase of LWE security parameters. Because our scheme not only uses the efficient trapdoor generation method of $\mathbf{G}$-trapdoor in generating trapdoors, but also performs offline calculation in advance to enable the online part to only complete necessary operations with lower cost. This is very practical in scenarios where encryption devices have low power consumption, because through online/offline technology, high calculation overhead can be completed in advance, and this part of the calculation does not require message and receiver’s identity. In this way, the efficiency of encryption devices can be maximized during the online phase.

6. Conclusions

With the rapid development of quantum computing technology, how to design efficient IBE schemes that resist quantum attacks is currently a hot research topic. In this paper, our innovative suggestion is to design an IBOOE scheme by utilizing the difficult problem of lattice-based cryptography, which can efficiently perform online encryption even if the device’s computing power is limited. Furthermore, the offline phase can be achieved without the need of the message to be encrypted and the recipient’s identity. In addition, we use $\mathbf{G}$-trapdoor for generating “strong trapdoors” in lattice. Compared to most existing schemes, our scheme is simpler and more efficient, greatly reducing online computing costs. We prove under the standard model that the scheme is CPA secure. Through the performance and security analysis, our scheme improve the performance of the classic LWE IBE scheme [3] by 65% to 80% (increased by LWE security parameters), and by 60% to 70% in comparison with the scheme [4]. This greatly increases the efficiency of online computing for low-power encryption devices while guaranteeing security.

Our online/offline scheme based on IBE from LWE materializes high performance while resisting quantum interference. Although our scheme can be easily expanded into an adaptive security scheme [3], and can also convert to the Hierarchical IBE scheme [2], it lacks practical features in daily life, such as flexible user changes. In the future, we will further design attribute-based encryption schemes [28,29,30,31] from LWE, which has fine-grained access control function.