FA-Seed: Flexible and Active Learning-Based Seed Selection
Abstract
1. Introduction
- Proposing an active seed selection strategy based on FMNN;
- Evaluating seed quality under limited label availability;
- Providing label suggestions to experts along with an optimized validation mechanism;
- Assessing performance on benchmark datasets.
2. Related Works
3. Proposed Method: FA-Seed
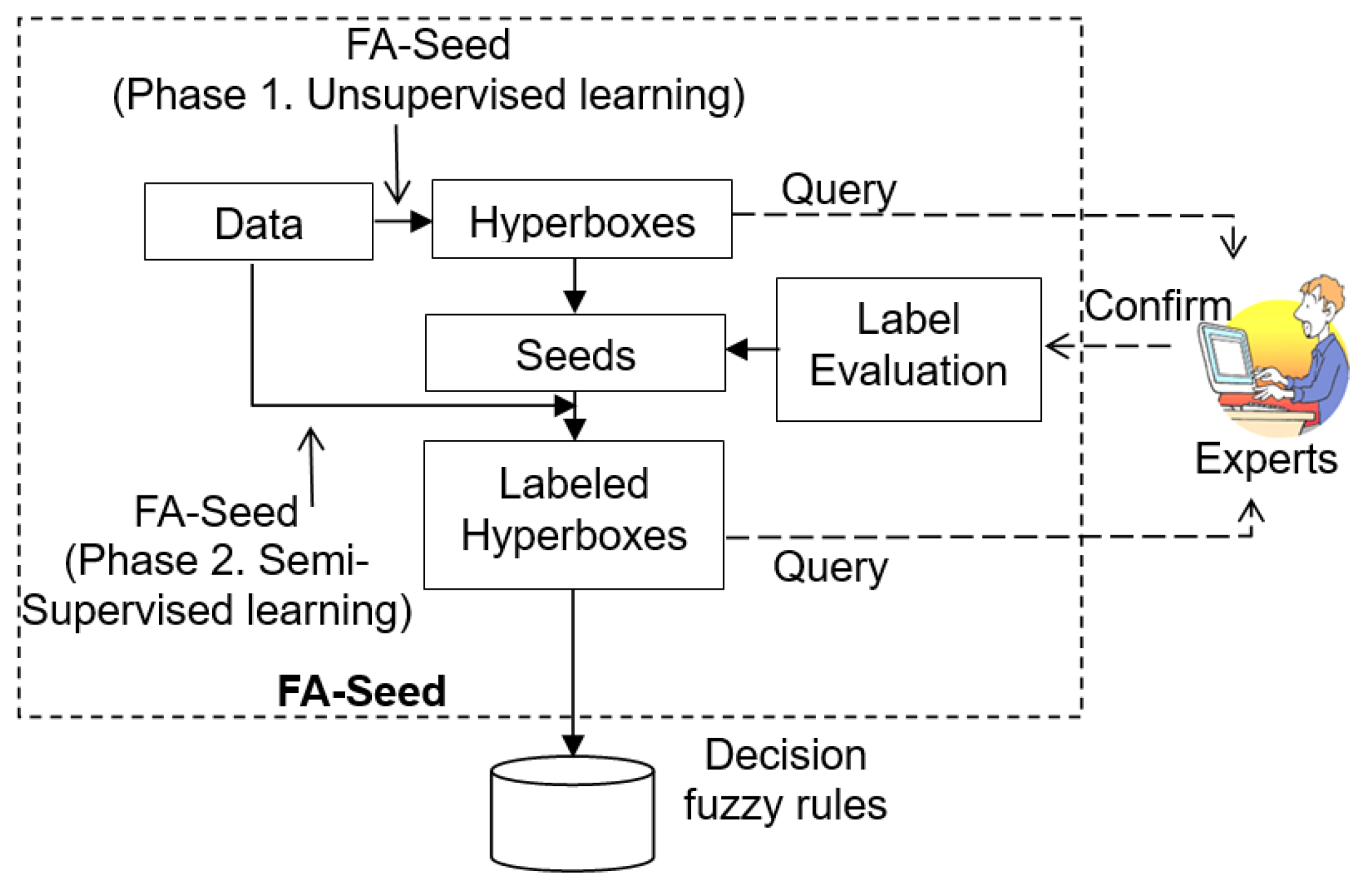
3.1. The Idea of Proposed Model
3.2. Setup and Definitions
3.2.1. Fuzzy Hyperbox and Membership
3.2.2. Seed Set Based on Centers and Purity
3.2.3. Adaptive Partition and Assignment with Fuzzy HXs
- Containment rule: if such that , assign x to that (uniqueness follows from ).
- Expansion: form the tentative expansion of , as defined in Equation (13). Accept it and set if all of the following hold:
- (1)
- Size constraint (as defined in Equation (14));
- (2)
- After any necessary contraction, the overlap constraint satisfies the constraint in Equation (16).
If accepted, assign x to the updated . - Create a new HX: if the expansion is not accepted, initialize a new HX around x, as in Equation (17).
3.2.4. Fuzzy HX-Level Labeling by Inheritance
3.2.5. Training Procedure
3.3. Model Architecture and Learning Process
3.3.1. Architecture of FA-Seed Model
- Seed scoring module: definition of seeds based on HX partitions, which evaluates candidate seeds using criteria such as data density, centroid deviation, and uncertainty, and assigns labels to reliable seeds within their respective HXs.
- Controlled label propagation and extended evaluation: This propagates labels from the verified seed set to the unlabeled data, ensuring consistency and accuracy across clusters. This component leverages the HX structure to minimize error propagation and actively queries uncertain samples that cannot be confidently assigned to a cluster.
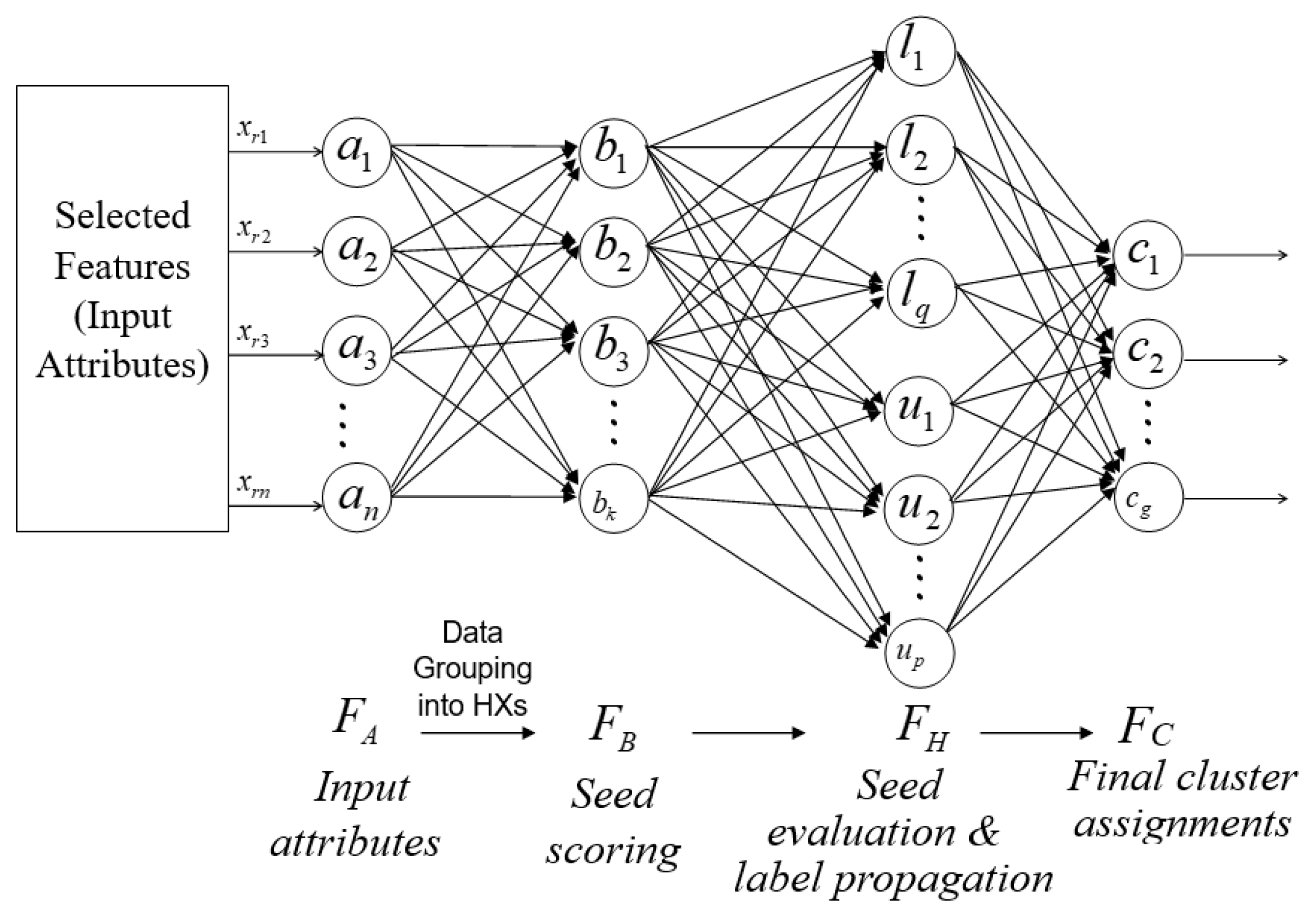
3.3.2. Neural Network Architecture of FA-Seed
- Input layer : This layer contains n nodes, each representing an input attribute. A sample is = and is mapped into HXs in using the min–max boundary vectors v and w.
- HX scoring layer : This layer includes K nodes (HXs) produced at Stage 1, each corresponding to an HX . These HXs are constructed incrementally and capture the local data structure in the input space. The activation is the membership
- Evaluation/propagation layer : HX nodes are partitioned into labeled and unlabeled sets: (size ) and (size ). This layer applies the gates and the inheritance rule to move HXs from to (at termination, so and typically ).
- Output layer : This layer contains G nodes, each representing one output cluster. The binary relationship between HX and class is represented by the matrix :The membership score of a sample to class is computed as:where is the activation of HX j. The set of HXs defining class g is given by:with G denoting the index set of HXs assigned to class g.
3.3.3. Learning Algorithm
| Algorithm 1: Seed Set Construction via Hyperbox Filtering. |
Input: Dataset X (); ; deviation threshold Output: Updated data set X, B
return B (the surviving HXs), (the reordered dataset) |
| Algorithm 2: Guided Hyperbox Expansion and Label Propagation. |
| Input: Reordered dataset X; S; ; ; . |
| Output: L. |
 |
4. Experiments
4.1. Experimental Objectives
4.2. Experimental Setup
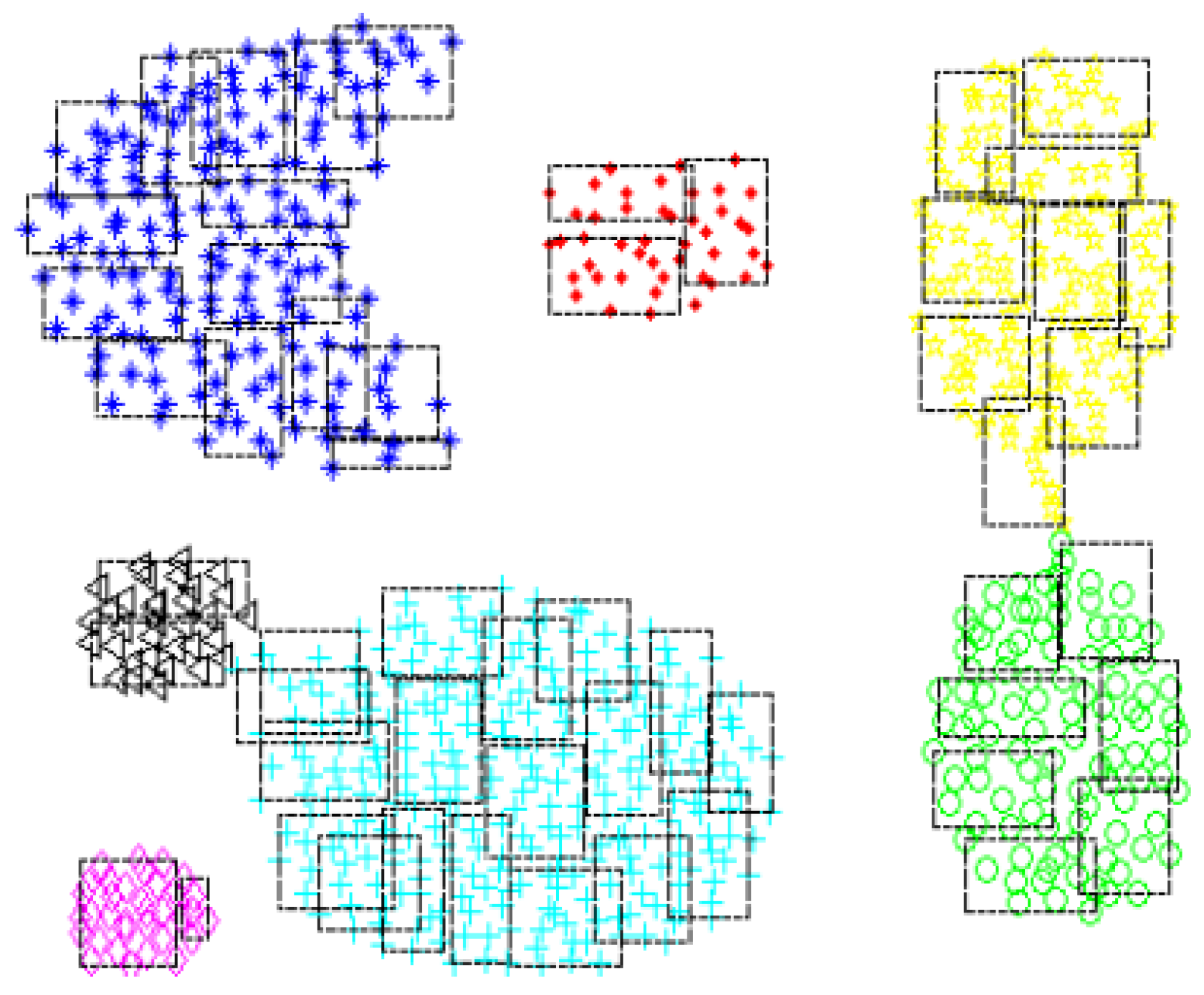
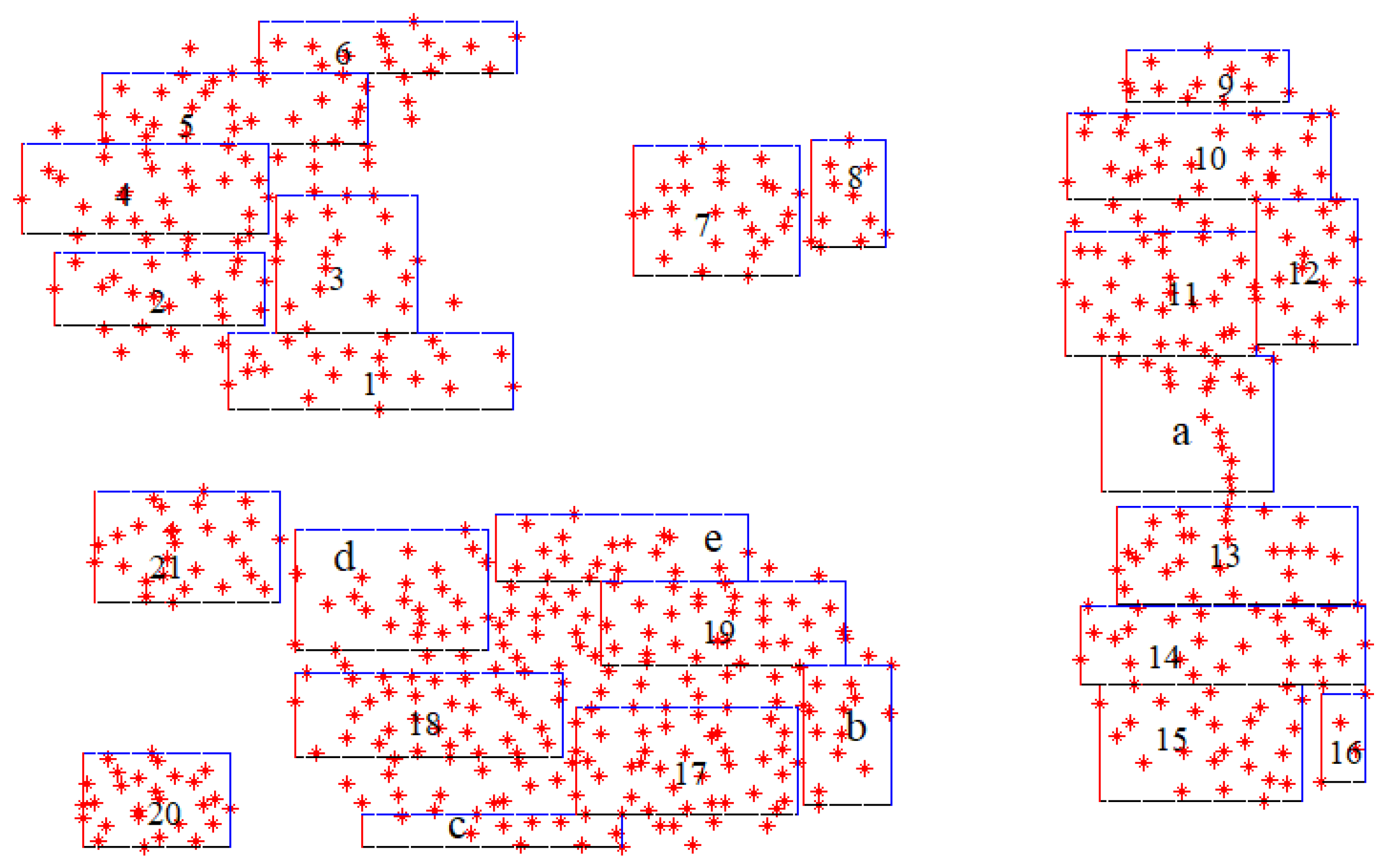
4.2.1. Datasets
4.2.2. Parameter Settings
4.2.3. Evaluation Metrics
- u is the number of correct decisions when in both clustering and ground truth.
- v is the number of correct decisions when in both clustering and ground truth.
- n is the total number of samples.
- if the prediction is correct; otherwise .
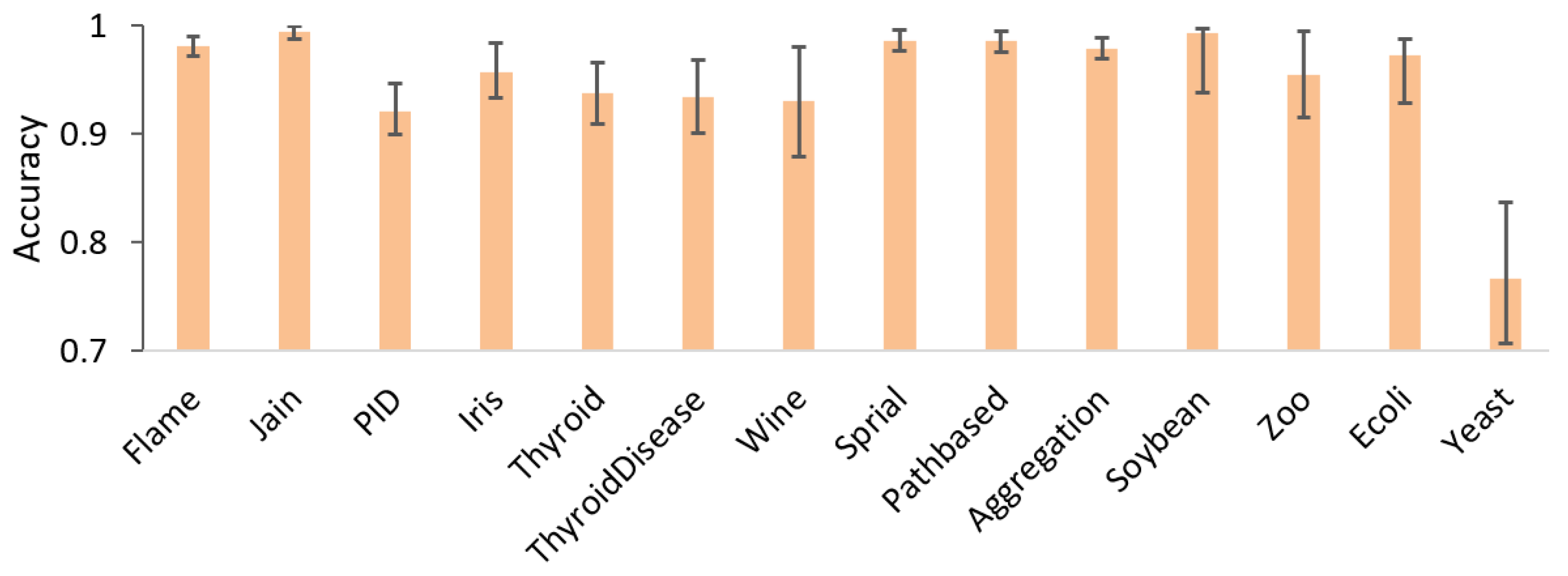
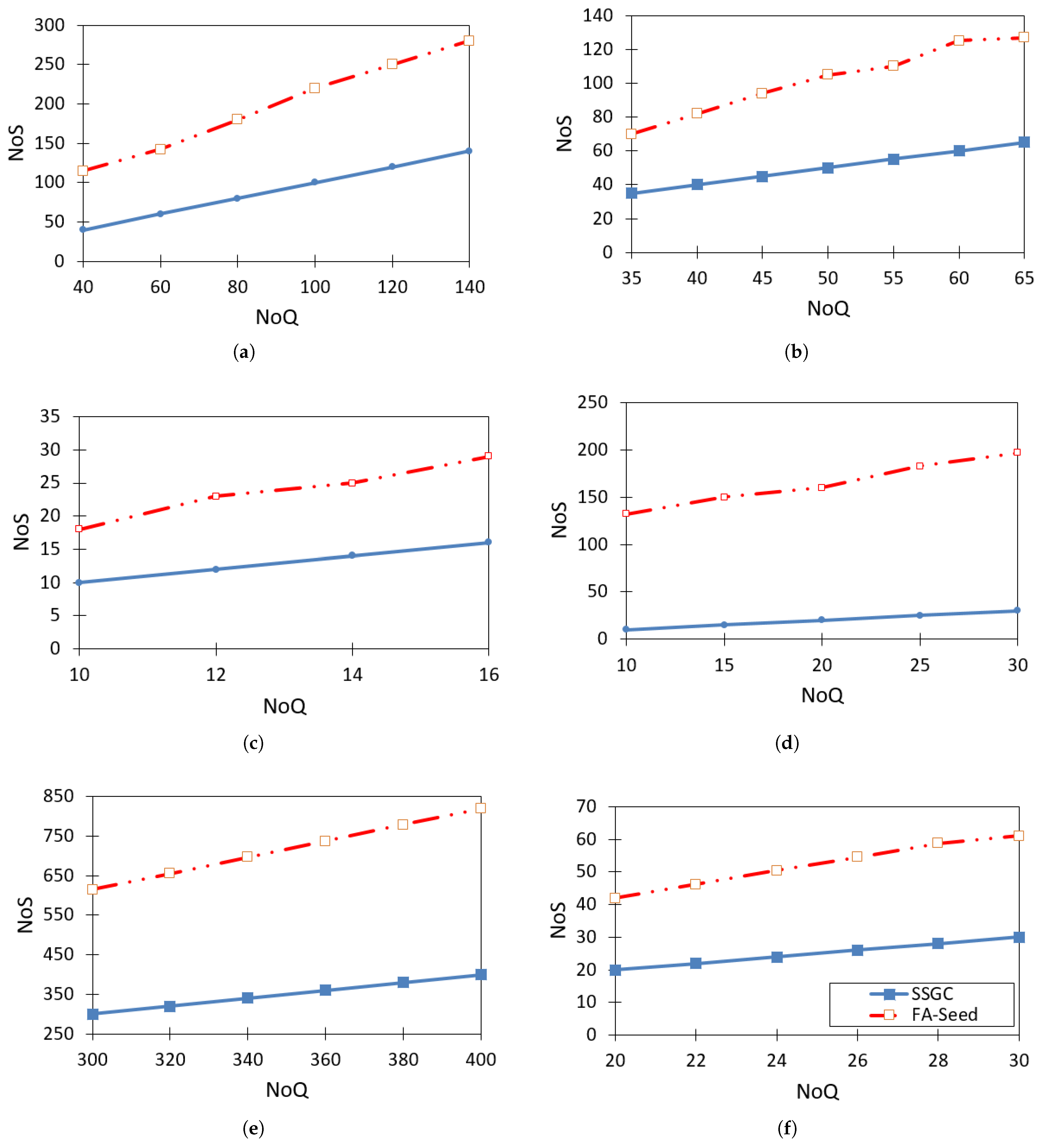
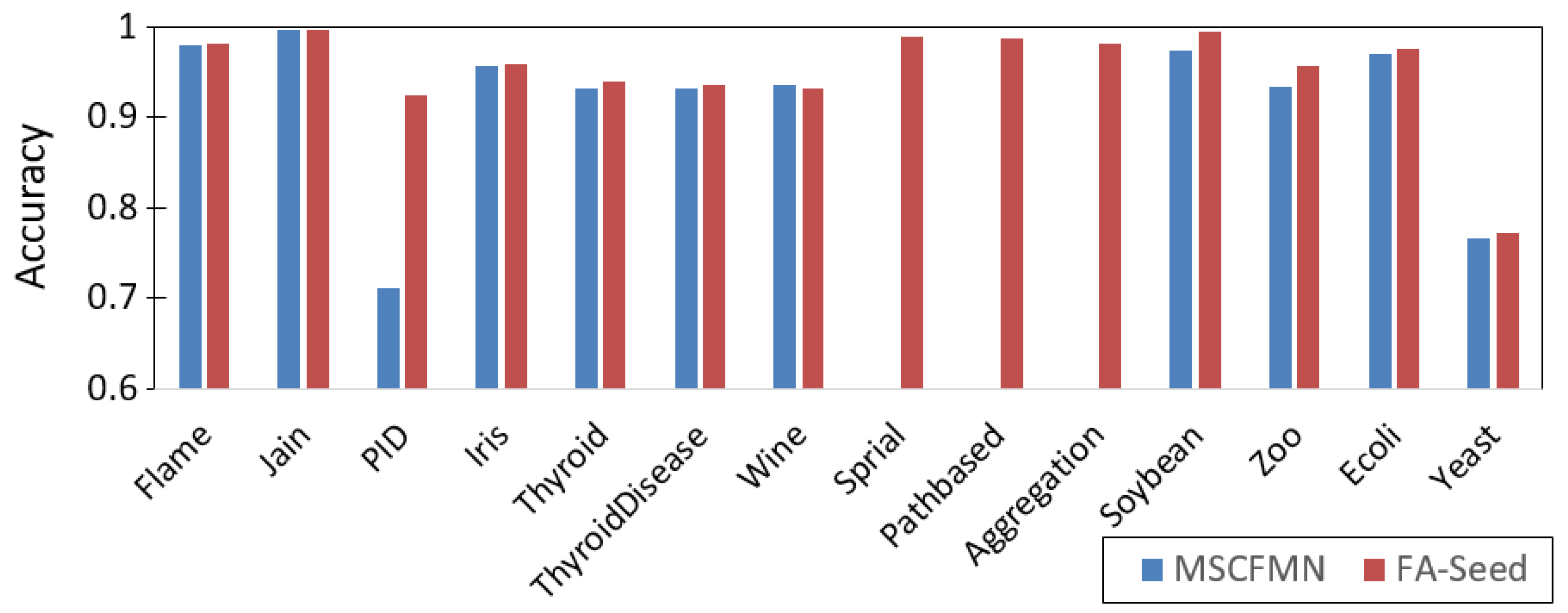
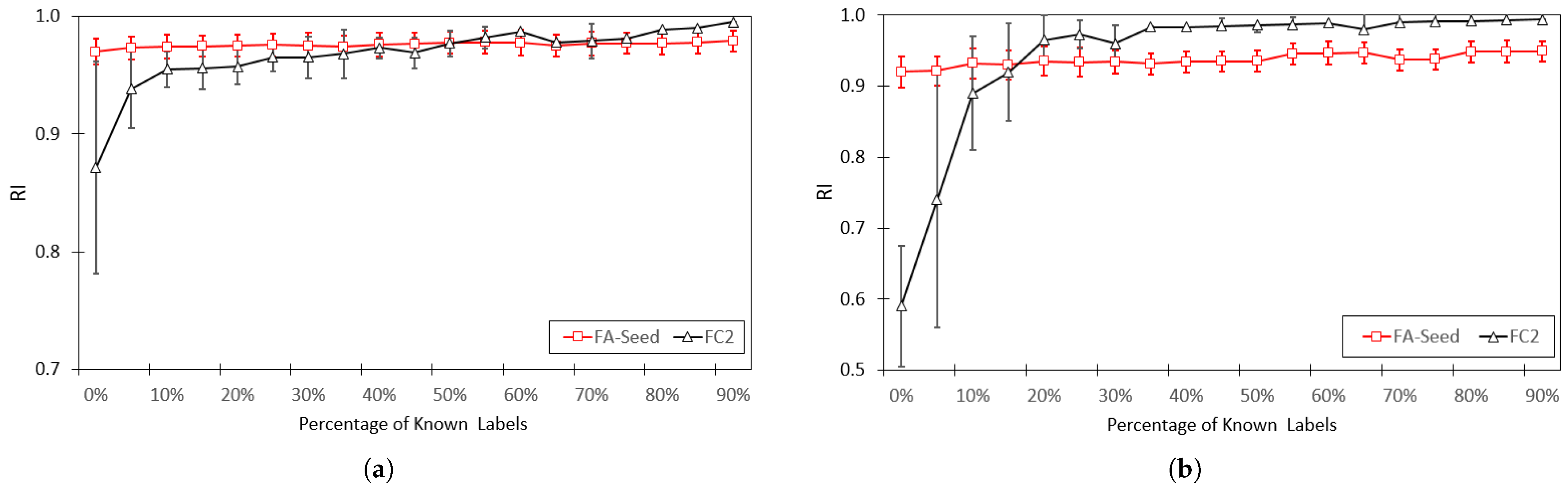
4.3. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CS-PDS | Constraints Self-learning from Partial Discriminant Spaces |
| DPP | Determinantal Point Processes |
| EM | Expectation Maximization |
| FC2 | Finding Clusters on Constraints |
| HX | Hyperbox |
| HXs | Hyperboxes |
| FMNN | Fuzzy Min–Max Neural Network |
| GFMNN | General FMNN |
| MSCFMN | Modified SCFMN |
| SCFMN | Semi-supervised Clustering in FMNN |
| SSGC | Semi-Supervised Graph-based Clustering |
| SSC | Semi-supervised Clustering |
| SSFC | Semi-supervised Fuzzy Clustering |
References
- Li, F.; Yue, P.; Su, L. Research on the convergence of fuzzy genetic algorithm based on rough classification. In Advances in Natural Computation, Proceedings of the Second International Conference, ICNC 2006, Xi’an, China, 24–28 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 792–795. [Google Scholar]
- Pedrycz, W.; Waletzky, J. Fuzzy clustering with partial supervision. IEEE Trans. Syst. Man Cybern. Part B 1997, 27, 787–795. [Google Scholar] [CrossRef] [PubMed]
- Gabrys, B.; Bargiela, A. General fuzzy min-max neural network for clustering and classification. IEEE Trans. Neural Netw. 2000, 11, 769–783. [Google Scholar] [CrossRef] [PubMed]
- Endo, Y.; Hamasuna, Y.; Yamashiro, M.; Miyamoto, S. On semi-supervised fuzzy c-means clustering. In Proceedings of the 2009 IEEE International Conference on Fuzzy Systems, Jeju, Republic of Korea, 20–24 August 2009; pp. 1119–1124. [Google Scholar]
- Minh, V.D.; Ngan, T.T.; Tuan, T.M.; Duong, V.T.; Cuong, N.T. An improvement in integrating clustering method and neural network to extract rules and application in diagnosis support. Iran. J. Fuzzy Syst. 2022, 19, 147–165. [Google Scholar]
- Vu, V.V. An efficient semi-supervised graph based clustering. Intell. Data Anal. 2018, 22, 297–307. [Google Scholar] [CrossRef]
- Almazroi, A.A.; Atwa, W. Semi-Supervised Clustering Algorithms Through Active Constraints. Int. J. Adv. Comput. Sci. Appl. 2024, 15, 7. [Google Scholar] [CrossRef]
- Shen, Z.; Lai, M.J.; Li, S. Graph-based semi-supervised local clustering with few labeled nodes. arXiv 2022, arXiv:2211.11114. [Google Scholar]
- Tran, T.N.; Vu, D.M.; Tran, M.T.; Le, B.D. The combination of fuzzy min–max neural network and semi-supervised learning in solving liver disease diagnosis support problem. Arab. J. Sci. Eng. 2019, 44, 2933–2944. [Google Scholar] [CrossRef]
- Bajpai, N.; Paik, J.H.; Sarkar, S. Balanced seed selection for K-means clustering with determinantal point process. Pattern Recognit. 2025, 164, 111548. [Google Scholar] [CrossRef]
- Sun, X. Semi-Supervised Clustering via Constraints Self-Learning. Mathematics 2025, 13, 1535. [Google Scholar] [CrossRef]
- Kämäräinen, J.K.; Kauppi, O.P.; Fränti, P. Clustering Datasets. Available online: https://cs.joensuu.fi/sipu/datasets/ (accessed on 2 August 2025).
- Khuat, T.T.; Gabrys, B. A comparative study of general fuzzy min-max neural networks for pattern classification problems. Neurocomputing 2020, 386, 110–125. [Google Scholar] [CrossRef]
- Simpson, P.K. Fuzzy min-max neural networks-part 2: Clustering. IEEE Trans. Fuzzy Syst. 2002, 1, 32. [Google Scholar] [CrossRef]
- Simpson, P.K. Fuzzy min-max neural networks. I. Classification. IEEE Trans. Neural Netw. 1992, 3, 776–786. [Google Scholar] [CrossRef]
- Aha, D. UC Irvine Machine Learning Repository. Available online: https://archive.ics.uci.edu/ (accessed on 2 August 2025).
- Batista, G.E.; Monard, M.C. An analysis of four missing data treatment methods for supervised learning. Appl. Artif. Intell. 2003, 17, 519–533. [Google Scholar] [CrossRef]



| Dataset | #Instances | #Features | #Clusters |
|---|---|---|---|
| Soybean | 47 | 35 | 4 |
| Zoo | 101 | 16 | 7 |
| Iris | 150 | 4 | 3 |
| Wine | 178 | 13 | 3 |
| Thyroid | 215 | 5 | 3 |
| Flame | 240 | 2 | 2 |
| Spiral | 312 | 2 | 3 |
| Pathbased | 317 | 2 | 3 |
| Ecoli | 336 | 8 | 8 |
| Jain | 373 | 2 | 2 |
| PID | 768 | 8 | 2 |
| Aggregation | 788 | 2 | 7 |
| Yeast | 1484 | 8 | 10 |
| ThyroidDisease | 7200 | 21 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, D.M.; Nguyen, T.S. FA-Seed: Flexible and Active Learning-Based Seed Selection. Information 2025, 16, 884. https://doi.org/10.3390/info16100884
Vu DM, Nguyen TS. FA-Seed: Flexible and Active Learning-Based Seed Selection. Information. 2025; 16(10):884. https://doi.org/10.3390/info16100884
Chicago/Turabian StyleVu, Dinh Minh, and Thanh Son Nguyen. 2025. "FA-Seed: Flexible and Active Learning-Based Seed Selection" Information 16, no. 10: 884. https://doi.org/10.3390/info16100884
APA StyleVu, D. M., & Nguyen, T. S. (2025). FA-Seed: Flexible and Active Learning-Based Seed Selection. Information, 16(10), 884. https://doi.org/10.3390/info16100884