Multi-Beam STAR MIMO Using Differential Arrays
Abstract
1. Introduction
2. Review of the Current MIMO Beamforming System
3. Twin-Array SIC Solution
3.1. Twin-Array Approaches
3.2. Past Work on Twin Arrays
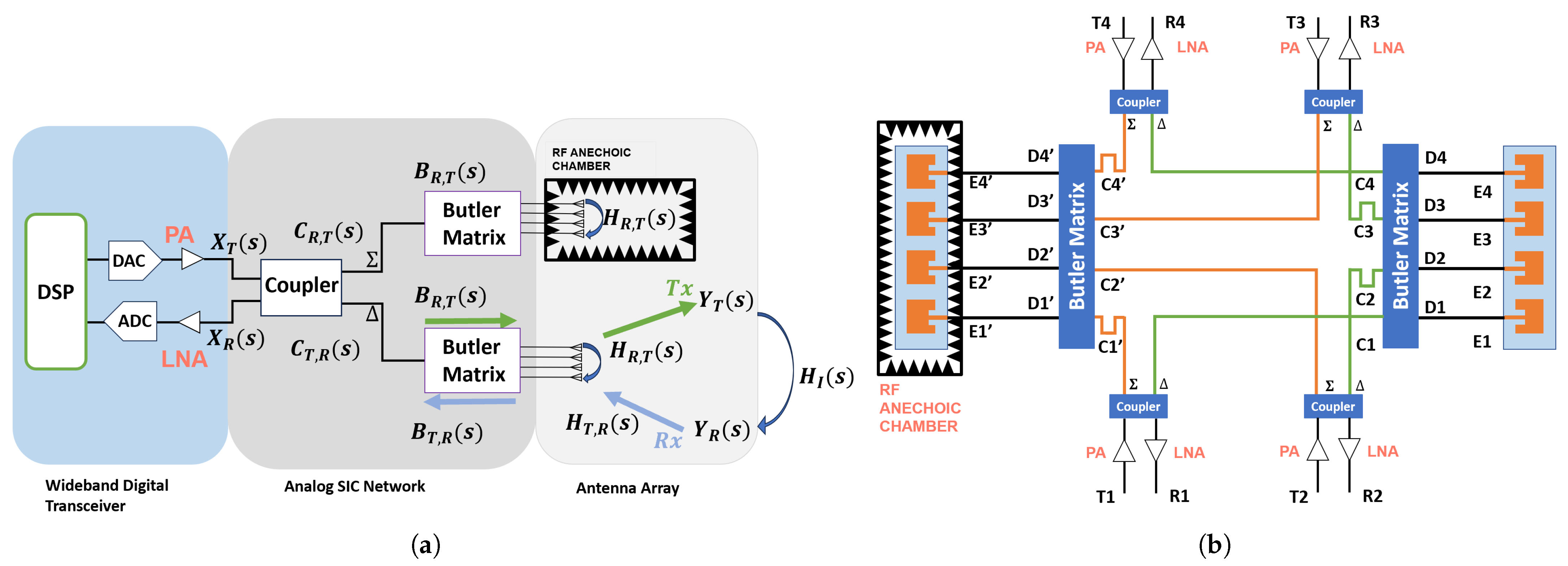
4. Proposed Twin Butler-Matrix Arrays
4.1. Twin-Array Analytical Model
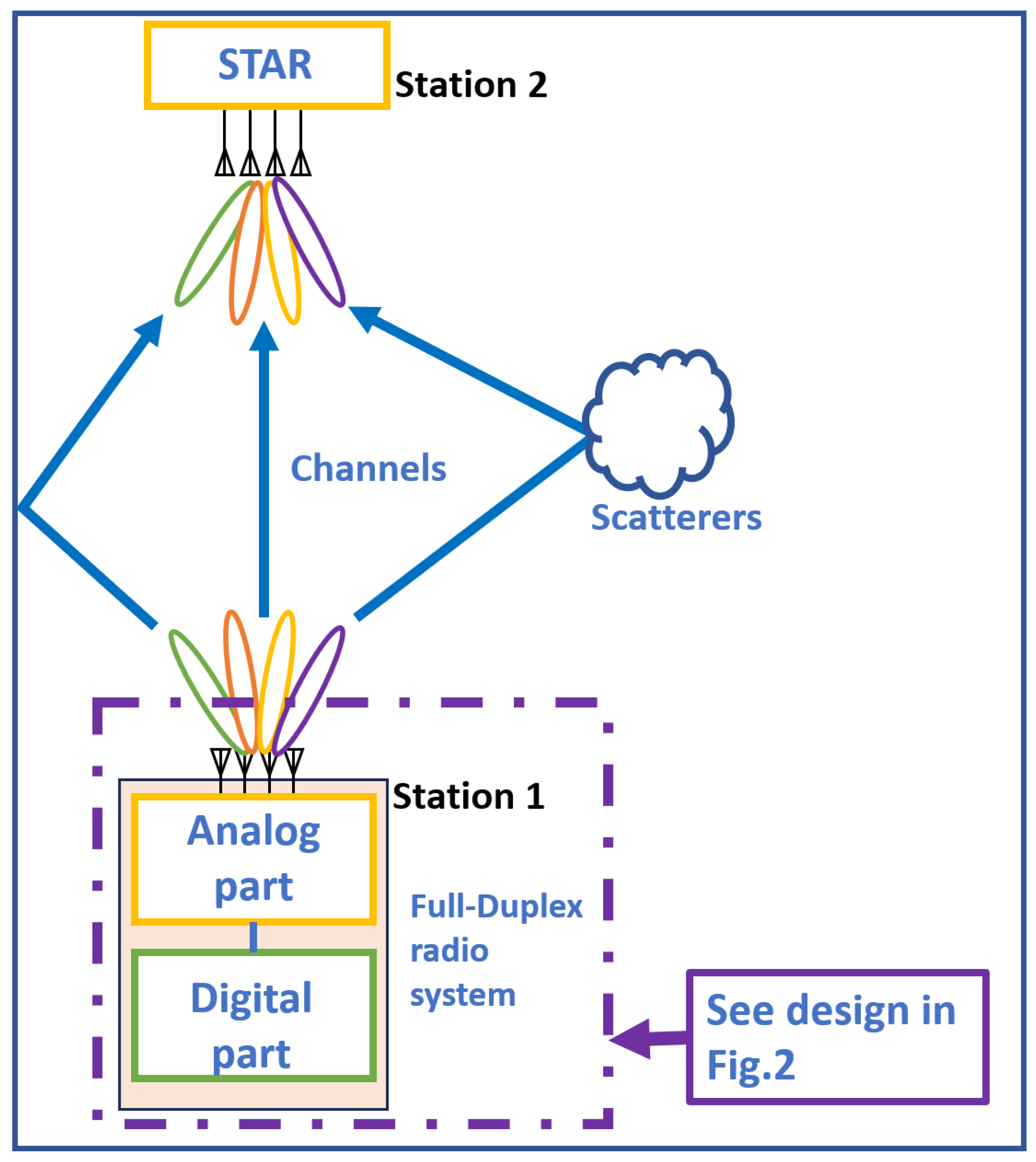
4.2. Radiowave Propagation
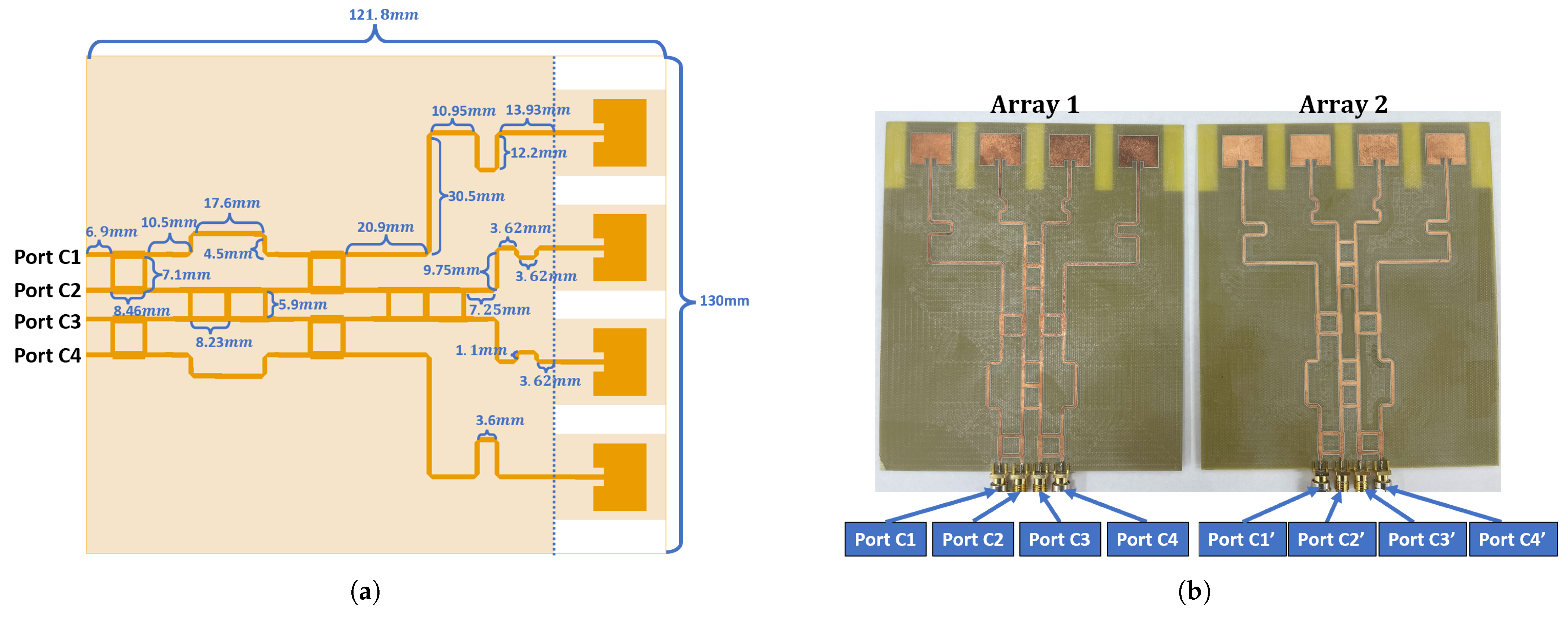
5. Antenna Array Aperture and Butler-Matrix Beams Design
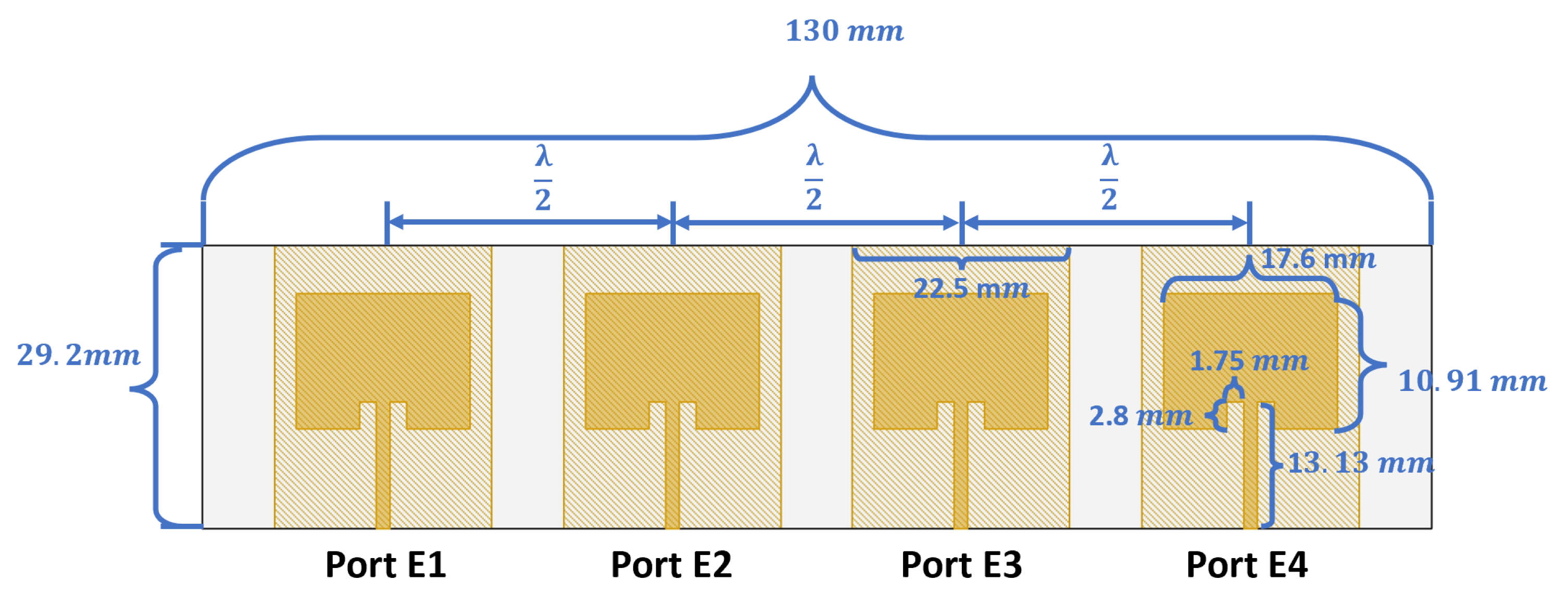
5.1. Design of a Single Patch Antenna Array
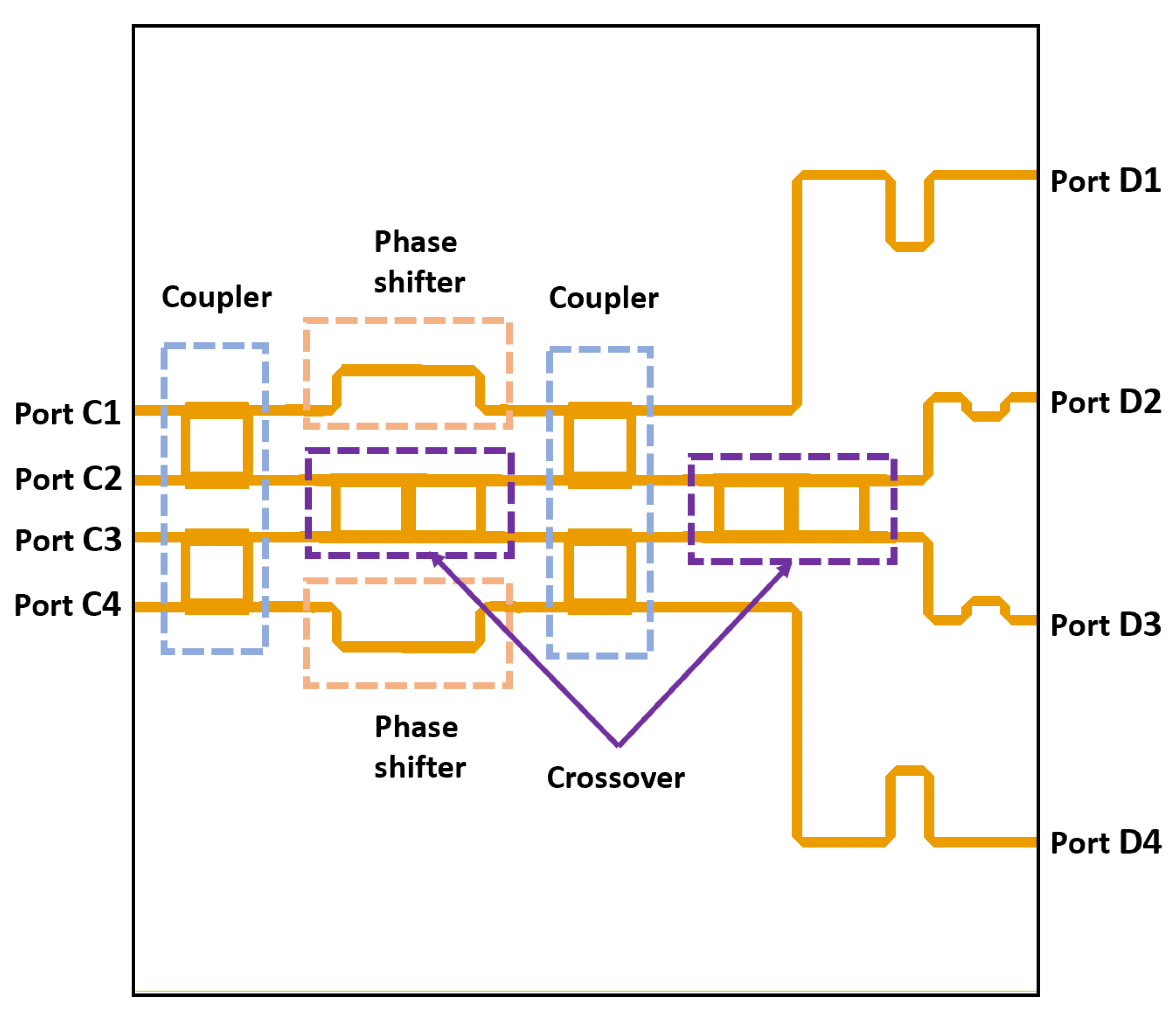
5.2. Design of Butler Matrix Network
5.3. Design of an Integrated Antenna Array with a Butler Matrix
6. MIMO STAR System
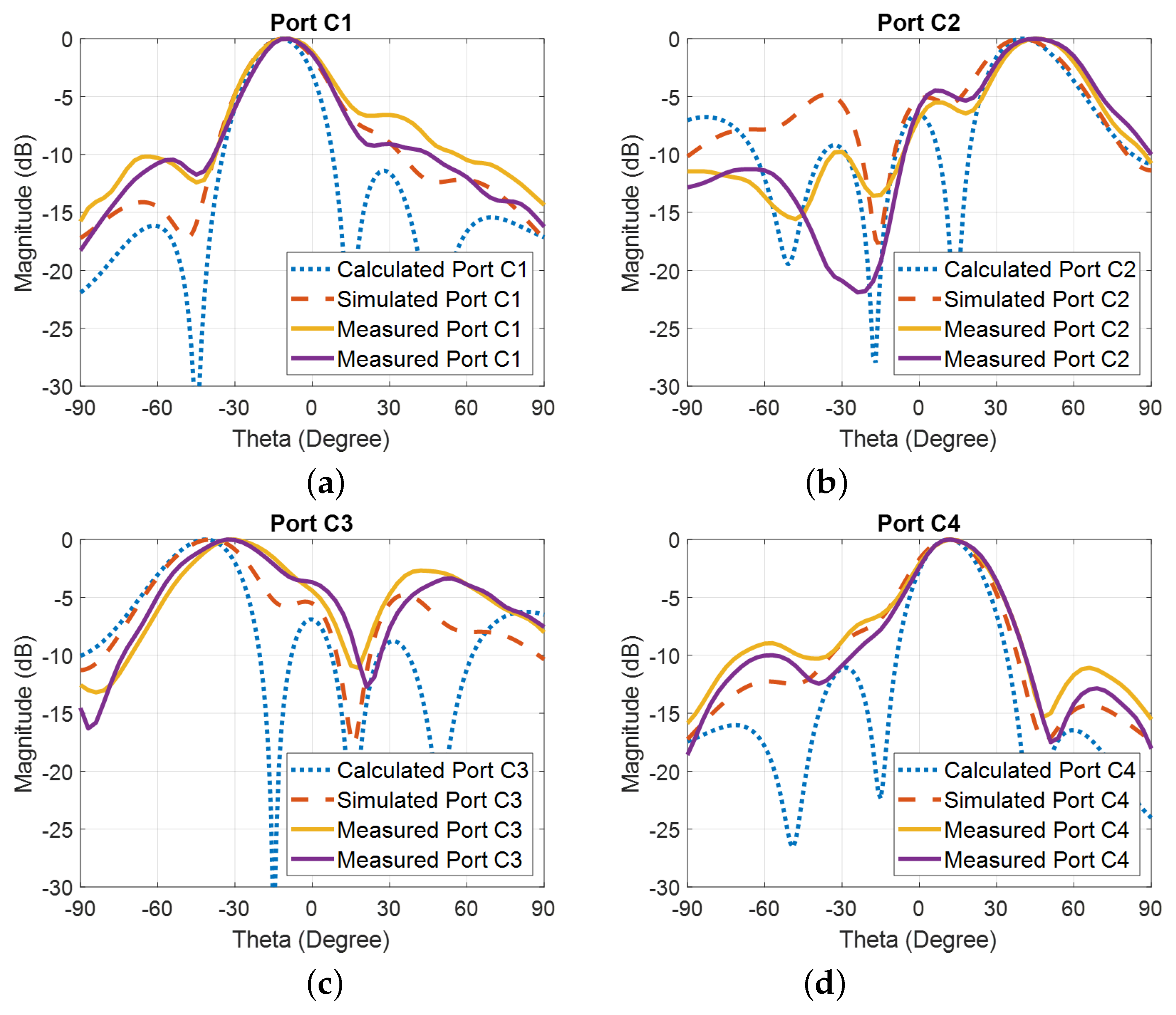
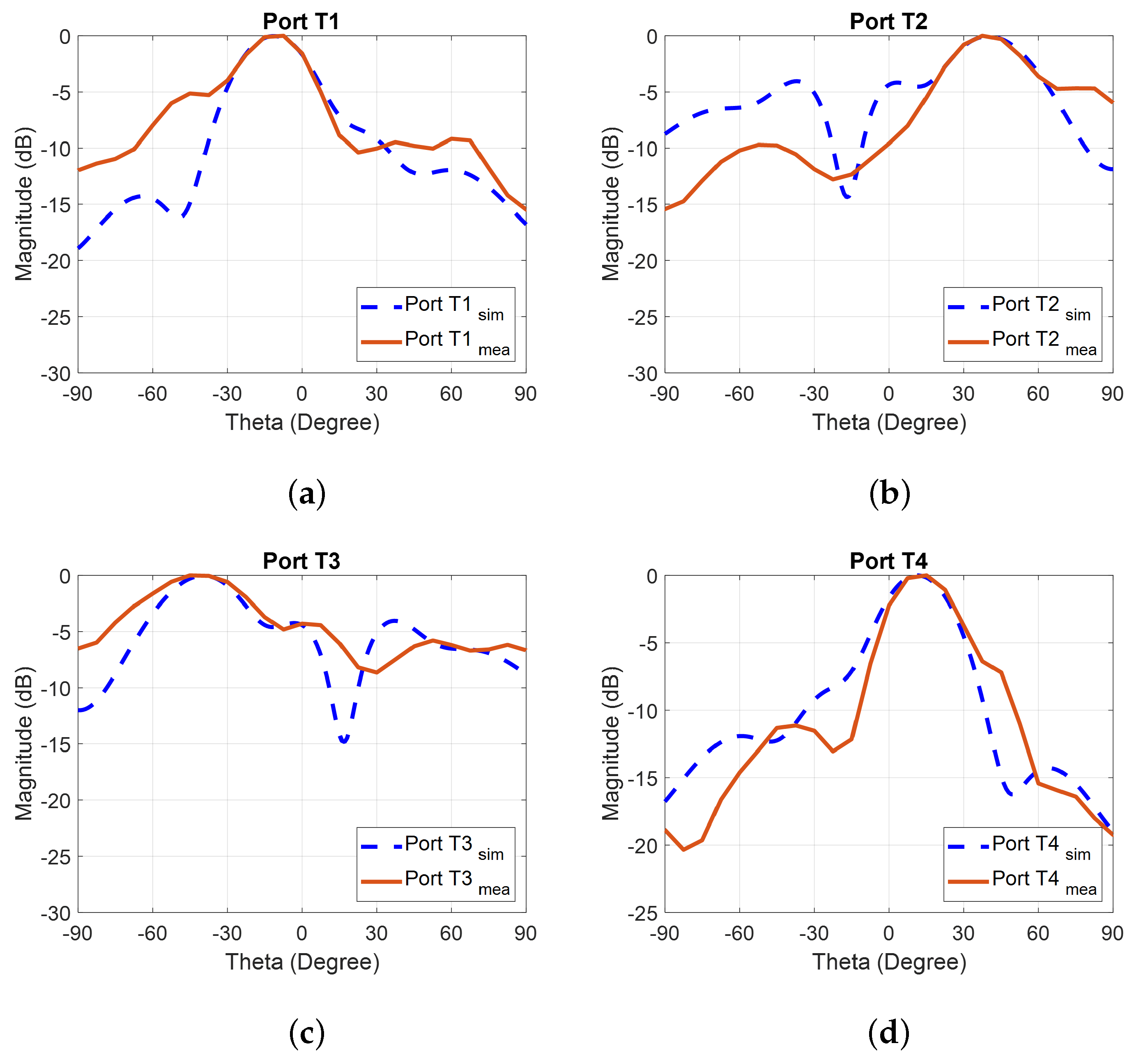
6.1. Radiated Beam-Measured Results
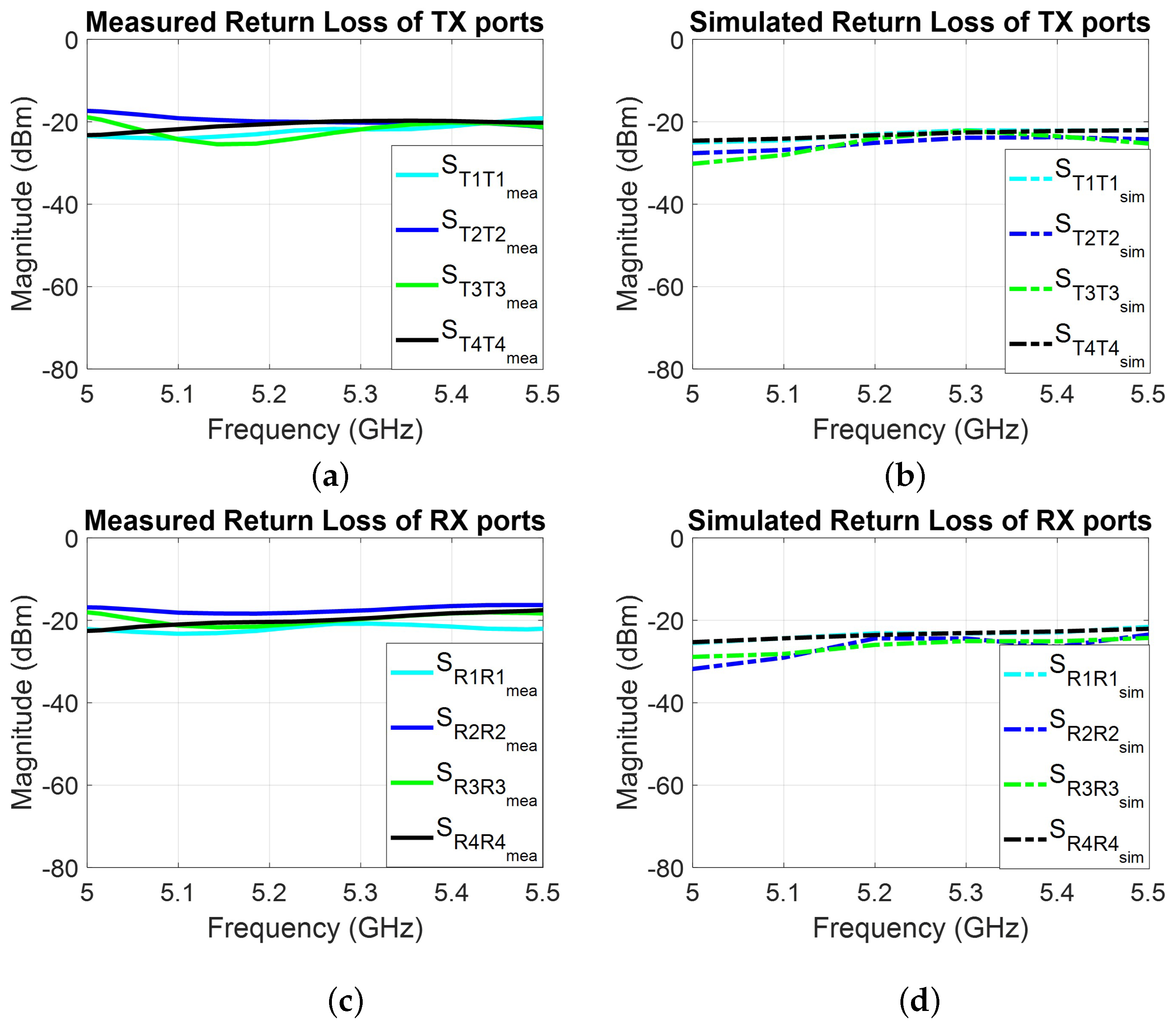
6.2. Measured System Return Loss
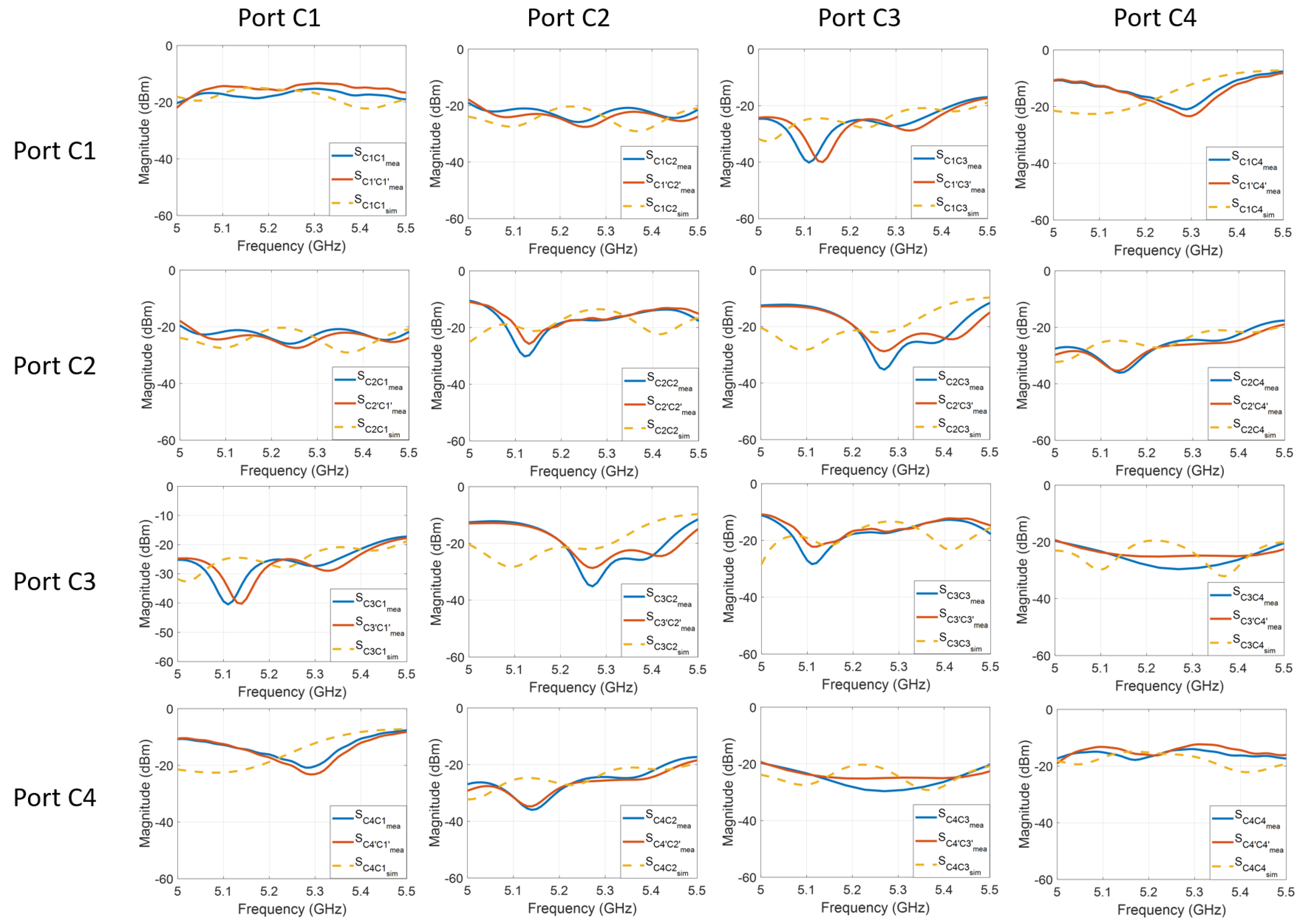
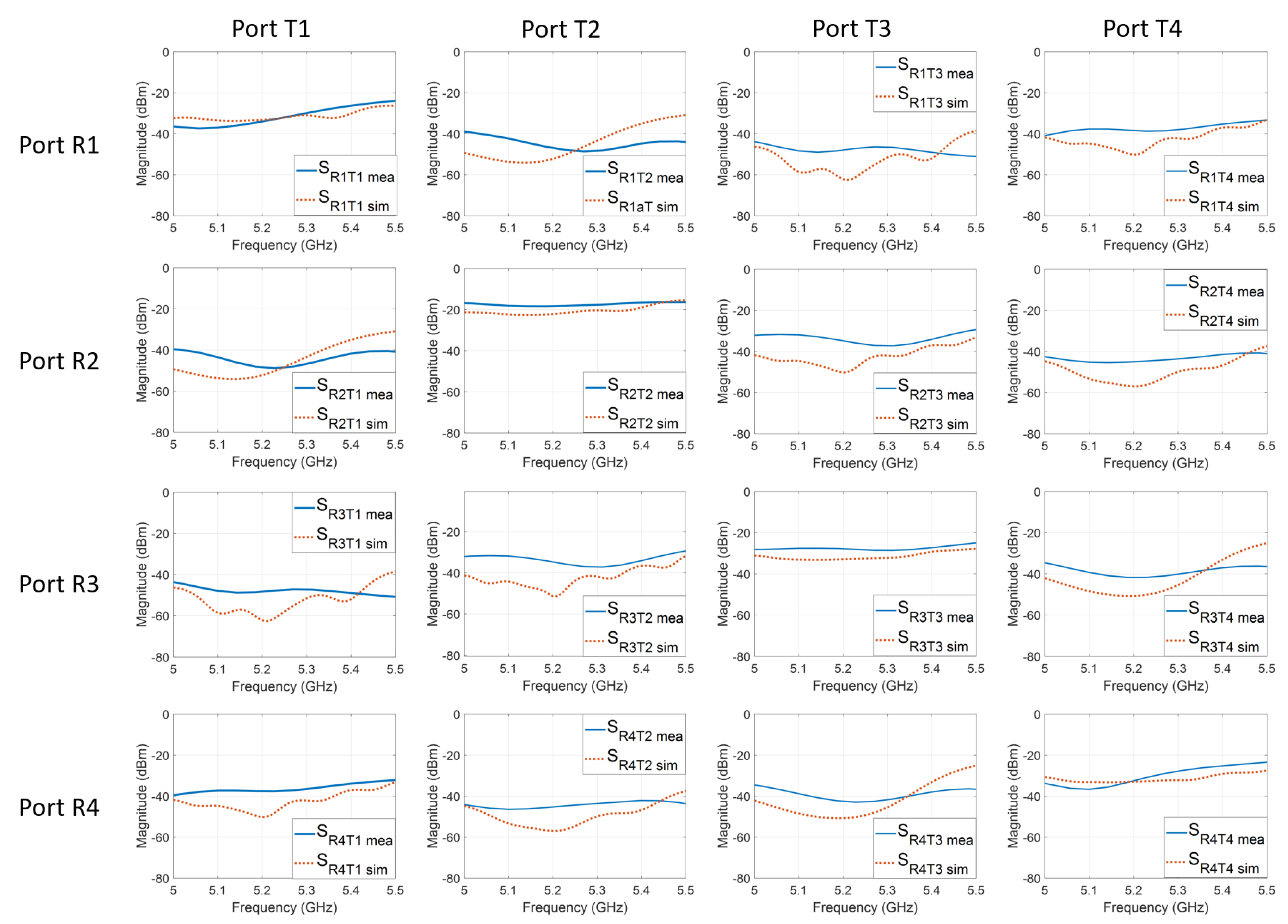
6.3. Designed Ports’ Isolation-Measured Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- John, D.M.; Vincent, S.; Pathan, S.; Kumar, P.; Ali, T. Flexible Antennas for a Sub-6 GHz 5G Band: A Comprehensive Review. Sensors 2022, 22, 7615. [Google Scholar] [CrossRef] [PubMed]
- Yao, G.; Hashemi, M.; Singh, R.; Shroff, N.B. Delay-Optimal Scheduling for Integrated mmWave – Sub-6 GHz Systems With Markovian Blockage Model. IEEE Trans. Mob. Comput. 2023, 22, 5124–5139. [Google Scholar] [CrossRef]
- Pirayesh, H.; Zeng, H. Jamming Attacks and Anti-Jamming Strategies in Wireless Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2022, 24, 767–809. [Google Scholar] [CrossRef]
- Smida, B.; Sabharwal, A.; Fodor, G.; Alexandropoulos, G.C.; Suraweera, H.A.; Chae, C.B. Full-Duplex Wireless for 6G: Progress Brings New Opportunities and Challenges. IEEE J. Sel. Areas Commun. 2023, 41, 2729–2750. [Google Scholar] [CrossRef]
- Skokowski, P.; Kelner, J.M.; Malon, K.; Maślanka, K.; Birutis, A.; Vazquez, M.A.; Saha, S.; Low, W.; Czapiewska, A.; Magiera, J.; et al. Jamming and Jamming Mitigation for Selected 5G Military Scenarios. Procedia Comput. Sci. 2022, 205, 258–267. [Google Scholar] [CrossRef]
- Zhao, H.; De Silva, U.; Pulipati, S.; Venkatakrishnan, S.B.; Bhardwaj, S.; Volakis, J.L.; Mandal, S.; Madanayake, A. A Broadband Multistage Self-Interference Canceller for Full-Duplex MIMO Radios. IEEE Trans. Microw. Theory Tech. 2021, 69, 2253–2266. [Google Scholar] [CrossRef]
- Dehghanzadeh, P.; Madanayake, A.; Zhao, H.; Venkatakrishnan, S.B.; Mandal, S. A Multiport Self-Interference Canceller for Wideband SIMO/MIMO-STAR Full-Duplex Arrays. IEEE Trans. Microw. Theory Tech. 2023, 72, 2640–2654. [Google Scholar] [CrossRef]
- Bojja Venkatakrishnan, S.; Papantonis, D.K.; Akhiyat, A.A.; Alwan, E.A.; Volakis, J.L. Experimental Validation of On-Site Coding Digital Beamformer With Ultra-Wideband Antenna Arrays. IEEE Trans. Microw. Theory Tech. 2017, 65, 4408–4417. [Google Scholar] [CrossRef]
- Venkatakrishnan, S.B.; Hovsepian, A.; Johnson, A.D.; Nakatani, T.; Alwan, E.A.; Volakis, J.L. Techniques for Achieving High Isolation in RF Domain for Simultaneous Transmit and Receive. IEEE Open J. Antennas Propag. 2020, 1, 358–367. [Google Scholar] [CrossRef]
- Bojja Venkatakrishnan, S.; Alwan, E.A.; Volakis, J.L. Wideband RF Self-Interference Cancellation Circuit for Phased Array Simultaneous Transmit and Receive Systems. IEEE Access 2018, 6, 3425–3432. [Google Scholar] [CrossRef]
- Foschini, G.; Golden, G.; Valenzuela, R.; Wolniansky, P. Simplified Processing for High Spectral Efficiency Wireless Communication Employing Multi-Element Arrays. IEEE J. Sel. Areas Commun. 1999, 17, 1841–1852. [Google Scholar] [CrossRef]
- Mohammadi, M.; Suraweera, H.A.; Krikidis, I.; Tellambura, C. Full-Duplex Radio for Uplink/Downlink Transmission with Spatial Randomness. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 1908–1913. [Google Scholar] [CrossRef]
- Yonis, A.; Abdullah, M.F.L.; Ghanim, M. LTE-FDD and LTE-TDD for cellular communications. In Proceedings of the Progress in Electromagnetics Research Symposium Proceedings, Kuala Lumpur, Malaysia, 27–30 March 2012. [Google Scholar]
- Kolodziej, K.E. In-Band Full-Duplex Wireless Systems Handbook; Artech House: Norwood, MA, USA, 2021. [Google Scholar]
- Rahman, M.A.; Rahman, M.M.; Alim, M.A. Design and Performance Analysis of an In-Band Full-Duplex MAC Protocol for Ad Hoc Networks. Telecom 2023, 4, 100–117. [Google Scholar] [CrossRef]
- Songzuo, L.; Iqbal, B.; Khan, I.U.; Ahmed, N.; Qiao, G.; Zhou, F. Full Duplex Physical and MAC layer-based Underwater Wireless Communication Systems and Protocols: Opportunities, challenges, and Future Directions. J. Mar. Sci. Eng. 2021, 9, 468. [Google Scholar] [CrossRef]
- Singh, K.; Wang, P.C.; Biswas, S.; Singh, S.K.; Mumtaz, S.; Li, C.P. Joint Active and Passive Beamforming Design for RIS-aided IBFD IoT communications: QoS and Power Efficiency Considerations. IEEE Trans. Consum. Electron. 2022, 69, 170–182. [Google Scholar] [CrossRef]
- Hassani, S.A.; Guevara, A.; Parashar, K.; Bourdoux, A.; van Liempd, B.; Pollin, S. An In-band Full-Duplex Transceiver for Simultaneous Communication and Environmental Sensing. In Proceedings of the 2018 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 1389–1394. [Google Scholar]
- Cox, C.H.; Ackerman, E.I. Photonics for Simultaneous Transmit and Receive. In Proceedings of the 2011 IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Raghavan, V.; Sayeed, A.M. Sublinear Capacity Scaling Laws for Sparse MIMO Channels. IEEE Trans. Inf. Theory 2010, 57, 345–364. [Google Scholar] [CrossRef]
- Sohrabi, F.; Yu, W. Hybrid Digital and Analog Beamforming Design for Large-Scale MIMO systems. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, Australia, 19–24 April 2015; pp. 2929–2933. [Google Scholar]
- Zhao, Y.; Venkatakrishnan, S.B.; Zekios, C.L.; Mandal, S.; Madanayake, A. Differential Arrays for Butler Multi-Beam STAR. In Proceedings of the 2024 International Applied Computational Electromagnetics Society Symposium (ACES), Orlando, FL, USA, 19–22 May 2024; pp. 1–2. [Google Scholar]
- Buinevich, M.; Vladyko, A. Forecasting Issues of Wireless Communication Networks’ cyber Resilience for an Intelligent Transportation System: An overview of cyber Attacks. Information 2019, 10, 27. [Google Scholar] [CrossRef]
- Bojja Venkatakrishnan, S. Simultaneous Transmit/Receive Multi-Functional Ultra-Wideband Transceiver with Reduced Hardware. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2017. [Google Scholar]
- Venkatakrishnan, S.B.; Hovsepian, A.; Volakis, J.L. Antenna Agnostic Feed Cancellation STAR System for Improved Cancellation. URSI Radio Sci. Bull. 2020, 2020, 46–53. [Google Scholar] [CrossRef]
- Bharadia, D.; Katti, S. Full Duplex MIMO Radios. In Proceedings of the 11th USENIX Symposium on Networked Systems Design and Implementation (NSDI 14), Seattle, WA, USA, 2–4 April 2014; pp. 359–372. [Google Scholar]
- Khaledian, S.; Farzami, F.; Smida, B.; Erricolo, D. Inherent Self-Interference Cancellation for In-Band Full-Duplex Single-Antenna Systems. IEEE Trans. Microw. Theory Tech. 2018, 66, 2842–2850. [Google Scholar] [CrossRef]
- Scherer, K.L.; Watt, S.J.; Alwan, E.A.; Akhiyat, A.A.; Dupaix, B.; Khalil, W.; Volakis, J.L. Simultaneous Transmit and Receive System Architecture with Four Stages of Cancellation. In Proceedings of the 2015 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 19–24 July 2015; pp. 520–521. [Google Scholar]
- Khojastepour, M.A.; Sundaresan, K.; Rangarajan, S.; Zhang, X.; Barghi, S. The Case for Antenna Cancellation for Scalable Full-Duplex Wireless Communications. In Proceedings of the 10th ACM Workshop on Hot Topics in Networks, Cambridge, MA, USA, 14–15 November 2011; pp. 1–6. [Google Scholar]
- Martin, K.; Psychogiou, D. Enhanced In-Band Self-Interference Suppression by Combining Bandpass Filter-Based RF Cancellers and Dual-Polarized Antennas. In Proceedings of the 2024 IEEE/MTT-S International Microwave Symposium—IMS 2024, Washington, DC, USA, 16–21 June 2024; pp. 741–744. [Google Scholar] [CrossRef]
- Elzayat, A.M.; Kouki, A.B. Tx/Rx Isolation Enhancement Based on a Novel Balanced Duplexer Architecture. In Proceedings of the 2011 IEEE MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Lin, J.Y.; Wong, S.W.; Yang, Y. Filtering In-Band Full-Duplex Slot Antenna Based on TM120 and TM210 Dual-Mode Resonators. In Proceedings of the 2021 IEEE MTT-S International Microwave Filter Workshop (IMFW), Perugia, Italy, 17–19 November 2021; pp. 249–251. [Google Scholar] [CrossRef]
- Schwartz, Y.; Cohen, E. An Ultra-Compact Wideband Tunable Autotransformer-Based Electrical-Balanced Duplexer Achieving 30 dB Isolation Across the 46–70 GHz Frequency Range. In Proceedings of the 2024 IEEE/MTT-S International Microwave Symposium—IMS 2024, Washington, DC, USA, 16–21 June 2024; pp. 446–449. [Google Scholar] [CrossRef]
- Cryan, M.; Hall, P.; Tsang, S.; Sha, J. Integrated Active Antenna with Full Duplex Operation. IEEE Trans. Microw. Theory Tech. 1997, 45, 1742–1748. [Google Scholar] [CrossRef]
- Dastjerdi, M.B.; Reiskarimian, N.; Chen, T.; Zussman, G.; Krishnaswamy, H. Full Duplex Circulator-Receiver Phased Array Employing Self-Interference Cancellation via Beamforming. In Proceedings of the 2018 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Philadelphia, PA, USA, 10–12 June 2018; pp. 108–111. [Google Scholar] [CrossRef]
- Shi, C.; Pan, W.; Shao, S. RF Wideband Self-Interference Cancellation for Full Duplex Phased Array Communication Systems. In Proceedings of the ICC 2022—IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 1094–1099. [Google Scholar] [CrossRef]
- Roberts, I.P.; Jain, H.B.; Vishwanath, S. Equipping Millimeter-Wave Full-Duplex with Analog Self-Interference Cancellation. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Masmoudi, A.; Le-Ngoc, T. Self-Interference Cancellation for Full-Duplex MIMO Transceivers. In Proceedings of the 2015 IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, LA, USA, 9–12 March 2015; pp. 141–146. [Google Scholar] [CrossRef]
- Dastjerdi, M.B.; Chen, T.; Reiskarimian, N.; Zussman, G.; Krishnaswamy, H. Self-Interference Cancellation via Beamforming in an Integrated Full Duplex Circulator-Receiver Phased Array. In Proceedings of the 2018 International Conference on Signal Processing and Communications (SPCOM), Bangalore, India, 16–19 July 2018; pp. 437–441. [Google Scholar] [CrossRef]
- Park, K.; Myeong, J.; Rebeiz, G.M.; Min, B.W. A 28-GHz Full-Duplex Phased Array Front-End Using Two Cross-Polarized Arrays and a Canceller. IEEE Trans. Microw. Theory Tech. 2021, 69, 1127–1135. [Google Scholar] [CrossRef]
- Wegener, A.T. Broadband Near-Field Filters for Simultaneous Transmit and Receive in a Small Two-Dimensional Array. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS2014), Tampa, FL, USA, 1–6 June 2014; pp. 1–3. [Google Scholar] [CrossRef]
- Lin, J.Y.; Yang, Y.; Wong, S.W.; Chen, R.S. In-Band Full-Duplex Filtering Antenna Arrays Using High-Order Mode Cavity Resonators. IEEE Trans. Microw. Theory Tech. 2023, 71, 1630–1639. [Google Scholar] [CrossRef]
- Le, A.T.; Huang, X.; Guo, Y.J. Analog Self-Interference Cancellation in Dual-Polarization Full-Duplex MIMO Systems. IEEE Commun. Lett. 2021, 25, 3075–3079. [Google Scholar] [CrossRef]
- Lee, C.; Khattak, M.K.; Kahng, S. Wideband 5G Beamforming Printed Array Clutched by LTE-A 4 × 4-multiple-input–multiple-output antennas with High Isolation. IET Microwaves Antennas Propag. 2018, 12, 1407–1413. [Google Scholar] [CrossRef]
- Kiani, S.H.; Savci, H.S.; Munir, M.E.; Sedik, A.; Mostafa, H. An Ultra-Wide Band MIMO Antenna System with Enhanced Isolation for Microwave Imaging Applications. Micromachines 2023, 14, 1732. [Google Scholar] [CrossRef] [PubMed]
- Roshna, T.K.; Deepak, U.; Sajitha, V.R.; Vasudevan, K.; Mohanan, P. A Compact UWB MIMO Antenna with Reflector to Enhance Isolation. IEEE Trans. Antennas Propag. 2015, 63, 1873–1877. [Google Scholar] [CrossRef]
- Tsakalaki, E.; Foroozanfard, E.; de Carvalho, E.; Pedersen, G.F. A 2-order MIMO full-duplex antenna system. In Proceedings of the The 8th European Conference on Antennas and Propagation (EuCAP 2014), The Hague, The Netherlands, 6–11 April 2014; pp. 2546–2550. [Google Scholar] [CrossRef]
- Li, M.; Jiang, L.; Yeung, K.L. A General and Systematic Method to Design Neutralization Lines for Isolation Enhancement in MIMO Antenna Arrays. IEEE Trans. Veh. Technol. 2020, 69, 6242–6253. [Google Scholar] [CrossRef]
- Zou, H.; Li, Y.; Xu, B.; Chen, Y.; Jin, H.; Yang, G.; Luo, Y. Dual-Functional MIMO Antenna Array With High Isolation for 5G/WLAN Applications in Smartphones. IEEE Access 2019, 7, 167470–167480. [Google Scholar] [CrossRef]
- Li, Y.; Sim, C.Y.D.; Luo, Y.; Yang, G. High-Isolation 3.5 GHz Eight-Antenna MIMO Array Using Balanced Open-Slot Antenna Element for 5G Smartphones. IEEE Trans. Antennas Propag. 2019, 67, 3820–3830. [Google Scholar] [CrossRef]
- Sokunbi, O.; Attia, H. Dual-layer Dual-patch EBG Structure for Isolation Enhancement and Correlation Reduction in MIMO Antenna Arrays. Prog. Electromagn. Res. C 2020, 100, 233–245. [Google Scholar] [CrossRef]
- Chen, Y.N.; Ding, C.; Liu, Y.; Guo, Y.J. A Four-Port Shared-Aperture In-Band Full-Duplex Antenna Array Based on Modes Combination Method. In Proceedings of the 2024 IEEE International Conference on Computational Electromagnetics (ICCEM), Nanjing, China, 15–17 April 2024; pp. 1–3. [Google Scholar] [CrossRef]
- Sepanek, R.; Hickle, M.; Stuenkel, M. In-Band Full-Duplex Self-Interference Canceller Augmented with Bandstop-Configured Resonators. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium (IMS), Los Angeles, CA, USA, 4–6 August 2020; pp. 1199–1202. [Google Scholar] [CrossRef]
- Nagulu, A.; Mekkawy, A.; Tymchenko, M.; Sounas, D.; Alù, A.; Krishnaswamy, H. Ultra-Wideband Switched-Capacitor Delays and circulators—Theory and Implementation. IEEE J.-Solid State Circuits 2021, 56, 1412–1424. [Google Scholar] [CrossRef]
- Malathi, A.C.J.; Thiripurasundari, D. Review on Isolation Techniques in MIMO Antenna systems. Indian J. Sci. Technol. 2016, 9, 1–10. [Google Scholar]
- Silva, U.D.; Pulipati, S.; Venkatakrishnan, S.B.; Bhardwaj, S.; Madanayake, A. A Passive STAR Microwave Circuit for 1-3 GHz Self-Interference Cancellation. In Proceedings of the 2020 IEEE 63rd International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, MA, USA, 9–12 August 2020; pp. 105–108. [Google Scholar] [CrossRef]
- Jonsson, J.C.; Smith, G.B.; Niklasson, G.A. Experimental and Monte Carlo analysis of isotropic multiple Mie scattering. Opt. Commun. 2004, 240, 9–17. [Google Scholar] [CrossRef]
- Zhensen, W.; Yi, Y.; Lihong, C. Monte Carlo simulation for millimeter wave propagation and scattering in rain medium. Int. J. Infrared Millim. Waves 1992, 13, 981–994. [Google Scholar] [CrossRef]
- Isabona, J.; Imoize, A.L.; Ojo, S.; Lee, C.C.; Li, C.T. Atmospheric Propagation Modelling for Terrestrial Radio Frequency Communication Links in a Tropical Wet and Dry Savanna Climate. Information 2022, 13, 141. [Google Scholar] [CrossRef]
- Kotake, H.; Abe, Y.; Kolev, D.R.; Saito, Y.; Takahashi, Y.; Fuse, T.; Satoh, Y.; Itahashi, T.; Yamakawa, S.; Tsuji, H.; et al. Experimental analysis of atmospheric channel model with misalignment fading for GEO satellite-to-ground optical link using “LUCAS” onboard optical data relay satellite. Opt. Express 2023, 31, 21351–21366. [Google Scholar] [CrossRef]
- Jiang, S.; Wang, W.; Miao, Y.; Fan, W.; Molisch, A.F. A Survey of Dense Multipath and Its Impact on Wireless Systems. IEEE Open J. Antennas Propag. 2022, 3, 435–460. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Balanis, C.; Ioannides, P. Introduction to smart antennas. Synth. Lect. Antennas 2007, 5, 1–179. [Google Scholar] [CrossRef]
- Vashist, S.; Soni, M.; Singhal, P. A review on the Development of Rotman Lens Antenna. Chin. J. Eng. 2014, 2014, 385385. [Google Scholar] [CrossRef]
- Mosca, S.; Bilotti, F.; Toscano, A.; Vegni, L. A Novel Design Method for Blass matrix Beam-Forming Networks. IEEE Trans. Antennas Propag. 2002, 50, 225–232. [Google Scholar] [CrossRef]
- Fonseca, N.J.G. Printed S-Band 4 × 4 Nolen Matrix for Multiple Beam Antenna Applications. IEEE Trans. Antennas Propag. 2009, 57, 1673–1678. [Google Scholar] [CrossRef]
- Comitangelo, R.; Minervini, D.; Piovano, B. Beam Forming Networks of Optimum Size and Compactness for Multibeam Antennas at 900 MHz. In Proceedings of the IEEE Antennas and Propagation Society International Symposium 1997. Digest, Montreal, QC, Canada, 13–18 July 1997; Volume 4, pp. 2127–2130. [Google Scholar] [CrossRef]

| Reference | Technology | Connection Type | Average Isolation (dB) | Center Frequency (GHz) | Bandwidth (GHz) | Metric |
|---|---|---|---|---|---|---|
| [47] | Microstrip | Discrete | 50 | 2.58 | 0.01 | 3.88 |
| [48] | Microstrip | Discrete | 25 | 2.4 | 0.2 | 0.26 |
| [43] | Microstrip | Integrated | 40 | 2.4 | 0.04 | 1.67 |
| [49] | Microstrip | Discrete | 34.6 | 3.5 | 0.2 | 1.65 |
| [50] | Microstrip | Discrete | 20 | 3.5 | 0.2 | 0.06 |
| [44] | Microstrip | Integrated | 38 | 2.5 | 0.3 | 7.57 |
| [45] | CPW-fed Microstrip | Integrated | 25 | 7 | 4 | 1.80 |
| [51] | EBG Microstrip | Integrated | 35 | 5.8 | 1.4 | 7.63 |
| [46] | CPS-fed Stripline | Integrated | 25 | 7 | 8 | 3.61 |
| [30] | Microstrip | Discrete | 50 | 2.4 | 0.02 | 8.33 |
| [33] | TSMC 65 nm CMOS | Integrated | 30 | 60 | 19 | 3.17 |
| [41] | Microstrip | Integrated | 30 | 3.45 | 0.1 | 0.3 |
| [27] | Microstrip | Integrated | 40 | 2.45 | 0.065 | 2.61 |
| [34] | Microstrip | Integrated | 45 | 4.04 | 0.02 | 1.57 |
| [40] | Microstrip | Discrete | 45 | 28 | 0.5 | 5.65 |
| [52] | Microstrip | Discrete | 38 | 3.5 | 0.5 | 9.01 |
| This work | Microstrip | Discrete | 40 | 5.2 | 0.5 | 9.62 |
| Port Name | Port C1 | Port C2 | Port C3 | Port C4 |
|---|---|---|---|---|
| Port D1 | 135° | 45° | 75° | 5° |
| Port D2 | 90° | 180° | −60° | 50° |
| Port D3 | 45° | −45° | 165° | 95° |
| Port D4 | 0° | 90° | 30° | 130° |
| Phase Difference | −45° | 135° | −135° | 45° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Venkatakrishnan, S.B.; Zekios, C.L.; Mandal, S.; Madanayake, A. Multi-Beam STAR MIMO Using Differential Arrays. Information 2025, 16, 321. https://doi.org/10.3390/info16040321
Zhao Y, Venkatakrishnan SB, Zekios CL, Mandal S, Madanayake A. Multi-Beam STAR MIMO Using Differential Arrays. Information. 2025; 16(4):321. https://doi.org/10.3390/info16040321
Chicago/Turabian StyleZhao, Yinyi, Satheesh Bojja Venkatakrishnan, Constantinos L. Zekios, Soumyajit Mandal, and Arjuna Madanayake. 2025. "Multi-Beam STAR MIMO Using Differential Arrays" Information 16, no. 4: 321. https://doi.org/10.3390/info16040321
APA StyleZhao, Y., Venkatakrishnan, S. B., Zekios, C. L., Mandal, S., & Madanayake, A. (2025). Multi-Beam STAR MIMO Using Differential Arrays. Information, 16(4), 321. https://doi.org/10.3390/info16040321










