A Lightweight Deep Learning Model for Profiled SCA Based on Random Convolution Kernels
Abstract
1. Introduction
- (1)
- Simplifying model architecture designA lightweight DL-based architecture for profiled SCA is proposed by using non-trained random convolution kernels [18], an attention mechanism, and a classifier (building upon the best CNNs introduced in [20]). Its random convolution layers are used as a non-trained transformer and then processed through a new attention layer in order to extract the mask information. Finally, this information is inputted into the (trained) classifier. Benefiting from this design, the model has fewer parameters and simpler structure. Compared with [15,16], the parameter number of this model is reduced by tens of thousands or even millions.
- (2)
- Processing diverse power traces (varying lengths and targets)We expand our model to support different input sizes and datasets of power traces, investigating the impact of the number of POIs (Point of Interest) selections. Furthermore, we also discuss the performance and complexity and evaluate the architecture in the identity (ID) leakage model. The notable superiority is that our architecture eliminates the dependents between the feature length of power consumption and the number of trainable parameters.
- (3)
- Lowering computational complexity of trainingWe evaluate and compare other relevant state-of-the-art works and demonstrate that our training efficiency is hundreds of times faster than other methods while at the same time requiring fewer power traces. Moreover, our architecture reduces the profiling traces and parameters by more than 70% and 94% compared to [15] and [16], respectively.
2. Profiled Side-Channel Analysis
2.1. The Profiling (Training) Phase
2.2. The Attack (Testing) Phase
3. Our Approach
3.1. Motivation
- (1)
- Avoid the use of heavy-weight and high-dimensional layers;
- (2)
- Minimize or avoid the stacking of traditional convolution layers, pooling layers, and activation layers;
- (3)
- Design a lightweight classifier with the ability to select and combine features from previous layers.
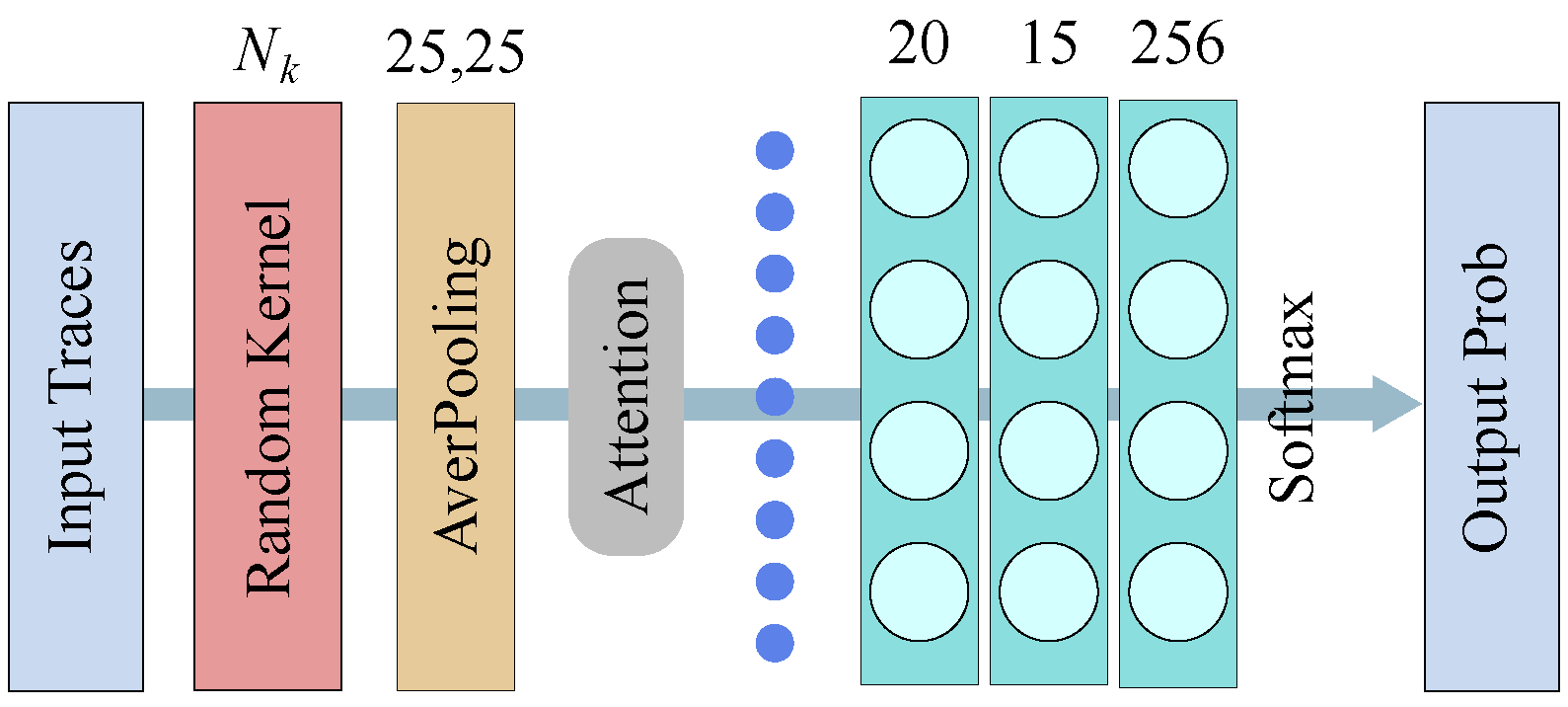
3.2. The Architecture
3.2.1. Kernel
3.2.2. The Attention Mechanism and Classifier
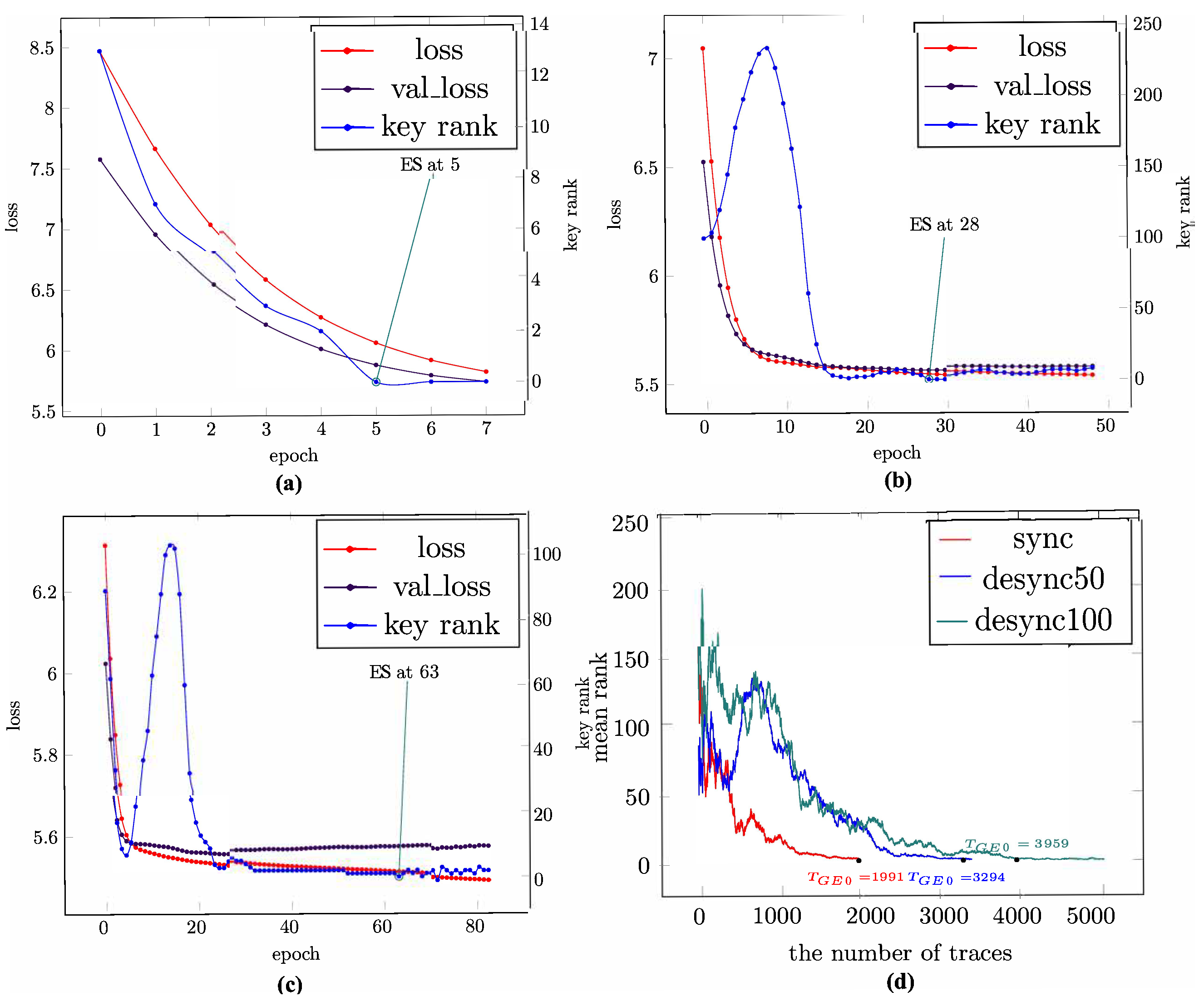
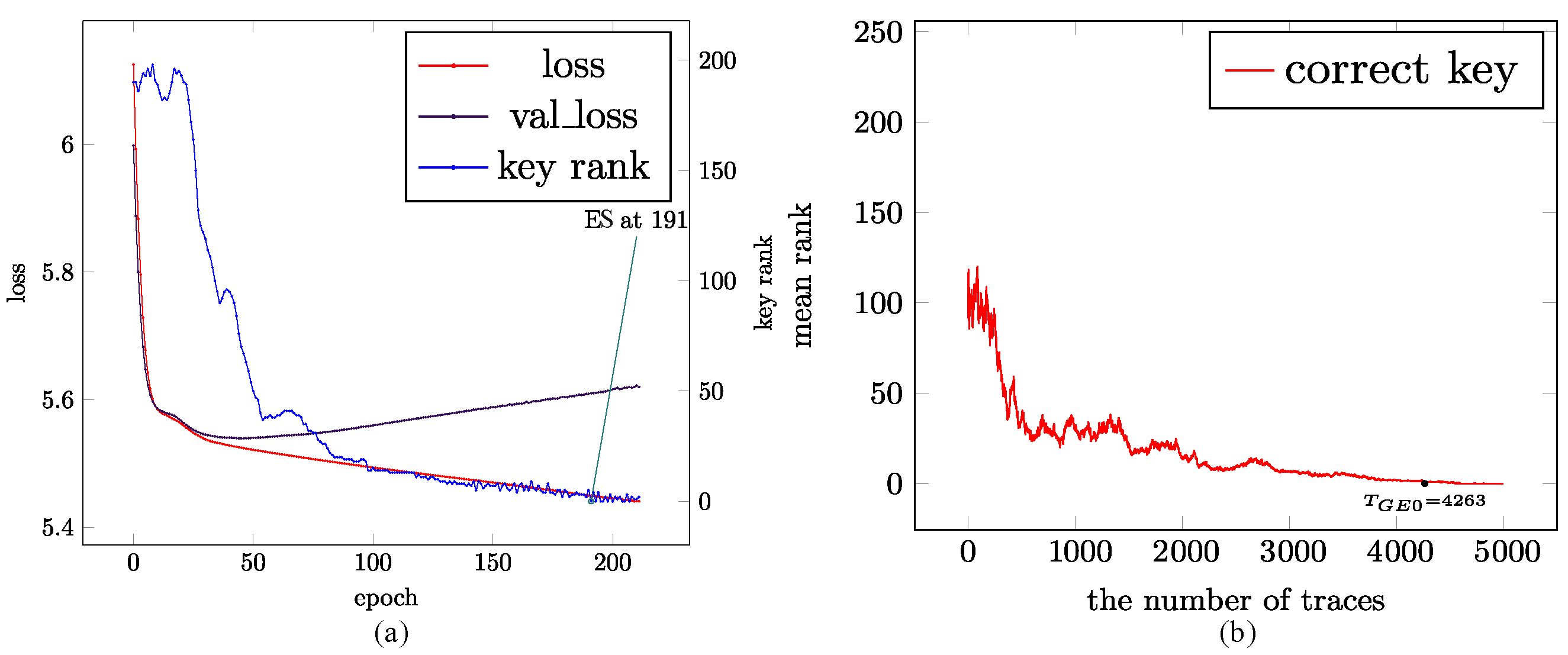
3.3. Training Procedure with Early Stopping
| Algorithm 1: The overall training procedure. |
 |
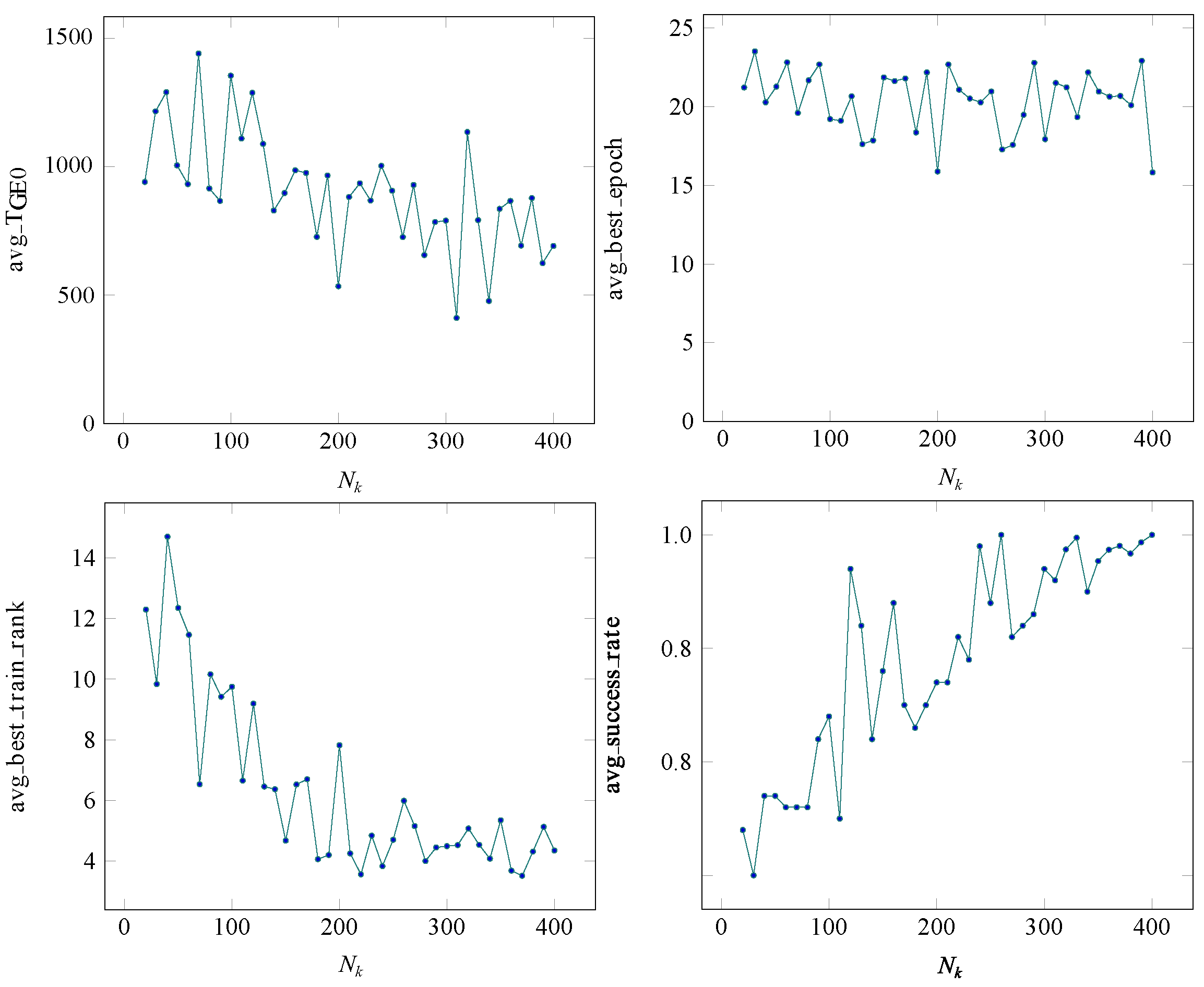
3.4. Performance Analysis of Random Kernels
3.5. Complexity Analysis
4. Experiments and Analysis
4.1. Datasets
4.2. Setups and Environments
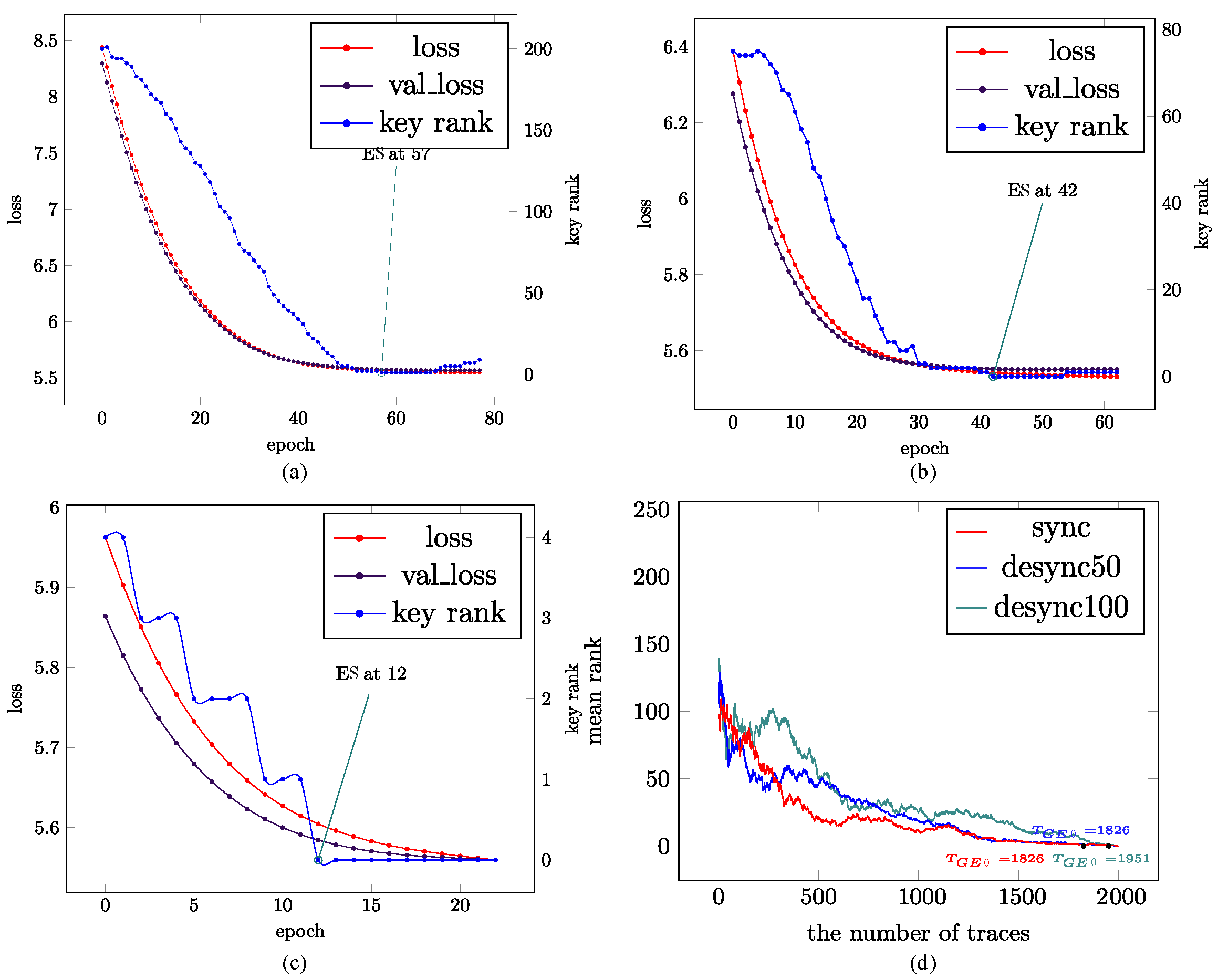
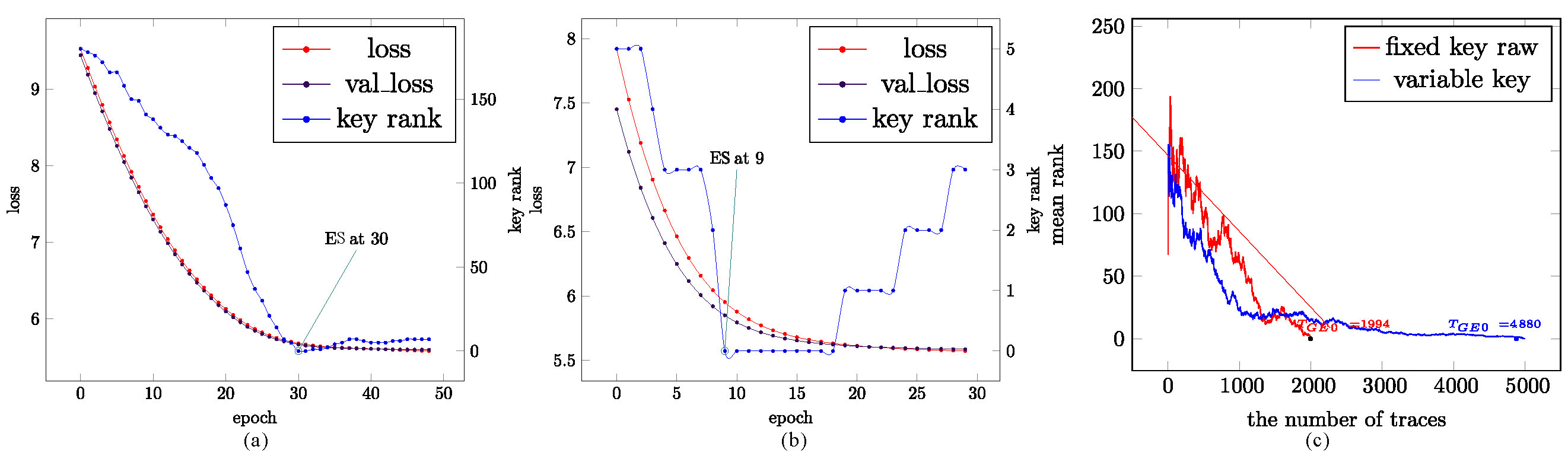
4.3. Experimental Results
4.4. Comparison and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kocher, P.C. Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems. In Proceedings of the Advances in Cryptology—CRYPTO’96, 16th Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 1996; Springer: Berlin/Heidelberg, Germany, 1996; pp. 104–113. [Google Scholar]
- Kocher, P.C.; Jaffe, J.; Jun, B. Differential power analysis. In Proceedings of the Advances in Cryptology—CRYPTO’99: 19th Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 1996; Springer: Berlin/Heidelberg, Germany, 1999; pp. 388–397. [Google Scholar]
- de la Fe, S.; Park, H.B.; Sim, B.Y.; Han, D.G.; Ferrer, C. Profiling Attack against RSA Key Generation Based on a Euclidean algorithm. Information 2021, 12, 462. [Google Scholar] [CrossRef]
- Maghrebi, H.; Portigliatti, T.; Prouff, E. Breaking Cryptographic Implementations Using Deep Learning Techniques. In Proceedings of the Security, Privacy, and Applied Cryptography Engineering: 6th International Conference, Hyderabad, India, 14–18 December 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 3–26. [Google Scholar]
- Kim, J.; Picek, S.; Heuser, A.; Bhasin, S.; Hanjalic, A. Make Some Noise. Unleashing the Power of Convolutional Neural Networks for Profiled Side-channel Analysis. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2019, 2019, 148–179. [Google Scholar] [CrossRef]
- Benadjila, R.; Prouff, E.; Strullu, R.; Cagli, E.; Dumas, C. Deep learning for side-channel analysis and introduction to ASCAD database. J. Cryptogr. Eng. 2020, 10, 163–188. [Google Scholar] [CrossRef]
- Picek, S.; Samiotis, I.P.; Kim, J.; Heuser, A.; Bhasin, S.; Legay, A. On the Performance of Convolutional Neural Networks for Side-Channel Analysis. In Proceedings of the Security, Privacy, and Applied Cryptography Engineering: 8th International Conference, Kanpur, India, 15–19 December 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 157–176. [Google Scholar]
- Li, L.; Ou, Y. A deep learning-based side channel attack model for different block ciphers. J. Comput. Sci. 2023, 72, 102078. [Google Scholar] [CrossRef]
- Wu, L.; Perin, G.; Picek, S. The Best of Two Worlds: Deep Learning-assisted Template Attack. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2021, 2022, 413–437. [Google Scholar] [CrossRef]
- Perin, G.; Wu, L.; Picek, S. Exploring Feature Selection Scenarios for Deep Learning-based Side-Channel Analysis. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2022, 2022, 828–861. [Google Scholar] [CrossRef]
- Acharya, R.Y.; Ganji, F.; Forte, D. Information Theory-based Evolution of Neural Networks for Side-channel Analysis. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2023, 2023, 401–437. [Google Scholar] [CrossRef]
- Hajra, S.; Chowdhury, S.; Mukhopadhyay, D. EstraNet: An Efficient Shift-Invariant Transformer Network for Side-Channel Analysis. Cryptology ePrint Archive, Paper 2023/1860. 2023. Available online: https://eprint.iacr.org/2023/1860 (accessed on 6 December 2023).
- Ahmed, A.A.; Salim, R.A.; Hasan, M.K. Deep Learning Method for Power Side-Channel Analysis on Chip Leakages. Elektron. Elektrotechnika 2023, 29, 50–57. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, A.A.; Fei, Y. A Guessing Entropy-Based Framework for Deep Learning-Assisted Side-Channel Analysis. IEEE Trans. Inf. Forensics Secur. 2023, 18, 3018–3030. [Google Scholar] [CrossRef]
- Liu, A.; Wang, A.; Sun, S.; Wei, C.; Ding, Y.; Wang, Y.; Zhu, L. CL-SCA: Leveraging Contrastive Learning for Profiled Side-Channel Analysis. Cryptology ePrint Archive, Paper 2024/049. 2024. Available online: https://eprint.iacr.org/2024/049 (accessed on 15 January 2024).
- Wu, L.; Weissbart, L.; Krček, M.; Li, H.; Perin, G.; Batina, L.; Picek, S. Label Correlation in Deep Learning-Based Side-Channel Analysis. IEEE Trans. Inf. Forensics Secur. 2023, 18, 3849–3861. [Google Scholar] [CrossRef]
- Ou, Y.; Li, L. Research on a high-order AES mask anti-power attack. IET Inf. Secur. 2020, 14, 580–586. [Google Scholar] [CrossRef]
- Dempster, A.; Petitjean, F.; Webb, G. ROCKET: Exceptionally fast and accurate time series classification using random convolutional kernels. Data Min. Knowl. Discov. 2020, 34, 1454–1495. [Google Scholar] [CrossRef]
- Salehinejad, H.; Wang, Y.; Yu, Y.; Jin, T.; Valaee, S. S-Rocket: Selective Random Convolution Kernels for Time Series Classification. arXiv 2022, arXiv:cs.LG/2203.03445. [Google Scholar]
- Rijsdijk, J.; Wu, L.; Perin, G.; Picek, S. Reinforcement learning for hyperparameter tuning in deep learning-based side-channel analysis. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2021, 2021, 677–707. [Google Scholar] [CrossRef]
- Zaid, G.; Bossuet, L.; Habrard, A.; Venelli, A. Methodology for efficient CNN architectures in profiling attacks. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 2020, 1–36. [Google Scholar] [CrossRef]
- Gupta, P.; Drees, J.P.; Hüllermeier, E. Automated Side-Channel Attacks using Black-Box Neural Architecture Search. Cryptology ePrint Archive, Paper 2023/093. 2023. Available online: https://eprint.iacr.org/2023/093 (accessed on 14 January 2024).
- Saxe, A.M.; Koh, P.W.; Chen, Z.; Bhand, M.; Suresh, B.; Ng, A.Y. On random weights and unsupervised feature learning. ICML 2011, 2, 6. [Google Scholar]
- Picek, S.; Heuser, A.; Jovic, A.; Bhasin, S.; Regazzoni, F. The Curse of Class Imbalance and Conflicting Metrics with Machine Learning for Side-channel Evaluations. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2019, 2019, 209–237. [Google Scholar] [CrossRef]
- Perin, G.; Wu, L.; Picek, S. AISY—Deep Learning-based Framework for Side-channel Analysis. Cryptology ePrint Archive, Paper 2021/357. 2021. Available online: https://eprint.iacr.org/2021/357 (accessed on 18 March 2021).
- Smith, L. A disciplined approach to neural network hyper-parameters: Part 1 – learning rate, batch size, momentum, and weight decay. arXiv 2018, arXiv:cs.LG/1803.09820. [Google Scholar]
- Smith, L.; Topin, N. Super-Convergence: Very Fast Training of Neural Networks Using Large Learning Rates. arXiv 2018, arXiv:cs.LG/1708.07120. [Google Scholar]
- Fisher, R.A. On the Mathematical Foundations of Theoretical Statistics. Philos. Trans. R. Soc. 1922, 222, 309–368. [Google Scholar]
- Saravanan, P.; Kalpana, P.; Preethisri, V.; Sneha, V. Power analysis attack using neural networks with wavelet transform as pre-processor. In Proceedings of the 18th International Symposium on VLSI Design and Test, Coimbatore, India, 16–18 July 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Ai, J.; Wang, Z.; Zhou, X.; Ou, C. Improved wavelet transform for noise reduction in power analysis attacks. In Proceedings of the 2016 IEEE International Conference on Signal and Image Processing (ICSIP), Beijing, China, 13–15 August 2016; pp. 602–606. [Google Scholar] [CrossRef]
- Bae, D.; Park, D.; Kim, G.; Choi, M.; Lee, N.; Kim, H.; Hong, S. Autoscaled-Wavelet Convolutional Layer for Deep Learning-Based Side-Channel Analysis. IEEE Access 2023, 11, 95381–95395. [Google Scholar] [CrossRef]
- Yang, G.; Li, H.; Ming, J.; Zhou, Y. Convolutional Neural Network Based Side-Channel Attacks in Time-Frequency Representations. In Smart Card Research and Advanced Applications; Bilgin, B., Fischer, J.B., Eds.; Springer: Cham, Switzerland, 2019; pp. 1–17. [Google Scholar]
- Garg, A.; Karimian, N. Leveraging Deep CNN and Transfer Learning for Side-Channel Attack. In Proceedings of the 2021 22nd International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 7–8 April 2021; pp. 91–96. [Google Scholar] [CrossRef]


| Hyperparameter Type | Hyperparameter Shape | Complexity * |
|---|---|---|
| Random kernel | time series length () | |
| number of kernels () | ||
| Attention | averagePooling1D () | 0 |
| dense (1) | 21 | |
| softmax (1) | 0 | |
| multiply (20) | 0 | |
| Classifier | dense (20) | 420 |
| dense (15) | 315 | |
| dense (c) | ||
| softmax (c) | 0 |
| Dataset | Trace Length | Profiling Traces | Attack Traces | Attack Byte |
|---|---|---|---|---|
| ASCAD_f | 700 | 15,000 | 5000 | 2 (224) |
| ASCAD_f_desync50 | 700 | 15,000 | 5000 | 2 (224) |
| ASCAD_f_desync100 | 700 | 15,000 | 5000 | 2 (224) |
| ASCAD_f_raw | 100,000 | 4500 | 5000 | 2 (224) |
| ASCAD_r | 1400 | 15,000 | 5000 | 2 (34) |
| AES_HD | 1250 | 15,000 | 5000 | 0 (0) |
| AES_HD_desync50 | 1250 | 15,000 | 5000 | 0 (0) |
| AES_HD_desync100 | 150 | 15,000 | 5000 | 0 (0) |
| AES_RD | 3500 | 15,000 | 5000 | 0 (43) |
| CHES CTF | 2200 | 15,000 | 5000 | 2 (94) |
| Pre-Processing Technique | Input (Trace) Length | Output (Feature) Length | Time Cost/s (1000 Traces) |
|---|---|---|---|
| Wavelet+PCA [29,30] | 700 | 520 | 6.84963298 |
| 1250 | 8.00765491 | ||
| 1400 | 8.87215233 | ||
| 2200 | 8.32040954 | ||
| 3500 | 9.62530255 | ||
| 100,000 | 41.92533708 | ||
| Time-Frequency image [32,33] * | 700 | / | 0.06076002/0.06228614 |
| 1250 | 0.24854016/0.30057955 | ||
| 1400 | 0.35778213/0.38010383 | ||
| 2200 | 1.24332047/1.30320311 | ||
| 3500 | 6.13667226/7.13198972 | ||
| 100,000 | -/- | ||
| Random Convolution Kernels | 700 | 520 | 0.41842961 |
| 1250 | 0.72135997 | ||
| 1400 | 0.77635646 | ||
| 2200 | 1.18555427 | ||
| 3500 | 1.77288055 | ||
| 100,000 | 46.68730211 |
| Model | Dataset Name | Num. Pro. Traces | Num. Param. | Time/(100 Batches) | |
|---|---|---|---|---|---|
| [6] | ASCAD_f | 50,000 | 66,652,544 | 244.6 s | 782 |
| ASCAD_f_desync100 | 8033 | ||||
| [15] | ASCAD_f | 10,000 | 47,778,176 | 167.7 s | 3860 |
| [16] | ASCAD_f | 50,000 | 79,695 | 2.10 s | 4050 |
| ASCAD_r | 151,375 | 3.92 s | 3684 | ||
| CHES CTF | 233,295 | 6.31 s | 1458 | ||
| [31] | ASCAD_f | 50,000 | 66,646,208 | 230.5 s | 133 |
| ASCAD_f_desync100 | 66,646,208 | 5512 | |||
| Ours | ASCAD_f | 15,000 | 4852 | 0.1173323 s | 1826 |
| ASCAD_f_raw | 0.0635662 s | 1948 | |||
| ASCAD_r | 0.3135437 s | 4880 | |||
| CHES CTF | 0.1166667 s | 1767 | |||
| AES_HD | 0.0676667 s | 1974 | |||
| AES_RD | 0.0681399 s | 1953 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, Y.; Wei, Y.; Rodríguez-Aldama, R.; Zhang, F. A Lightweight Deep Learning Model for Profiled SCA Based on Random Convolution Kernels. Information 2025, 16, 351. https://doi.org/10.3390/info16050351
Ou Y, Wei Y, Rodríguez-Aldama R, Zhang F. A Lightweight Deep Learning Model for Profiled SCA Based on Random Convolution Kernels. Information. 2025; 16(5):351. https://doi.org/10.3390/info16050351
Chicago/Turabian StyleOu, Yu, Yongzhuang Wei, René Rodríguez-Aldama, and Fengrong Zhang. 2025. "A Lightweight Deep Learning Model for Profiled SCA Based on Random Convolution Kernels" Information 16, no. 5: 351. https://doi.org/10.3390/info16050351
APA StyleOu, Y., Wei, Y., Rodríguez-Aldama, R., & Zhang, F. (2025). A Lightweight Deep Learning Model for Profiled SCA Based on Random Convolution Kernels. Information, 16(5), 351. https://doi.org/10.3390/info16050351







