Development of an ANFIS Model for the Optimization of a Queuing System in Warehouses
Abstract
1. Introduction
2. Literature Review
2.1. Models of Queuing System Theory in Traffic And Transportation
2.2. ANFIS Models in Traffic And Transportation
2.3. Methods of Multi-Criteria Decision-Making in Traffic And Transportation
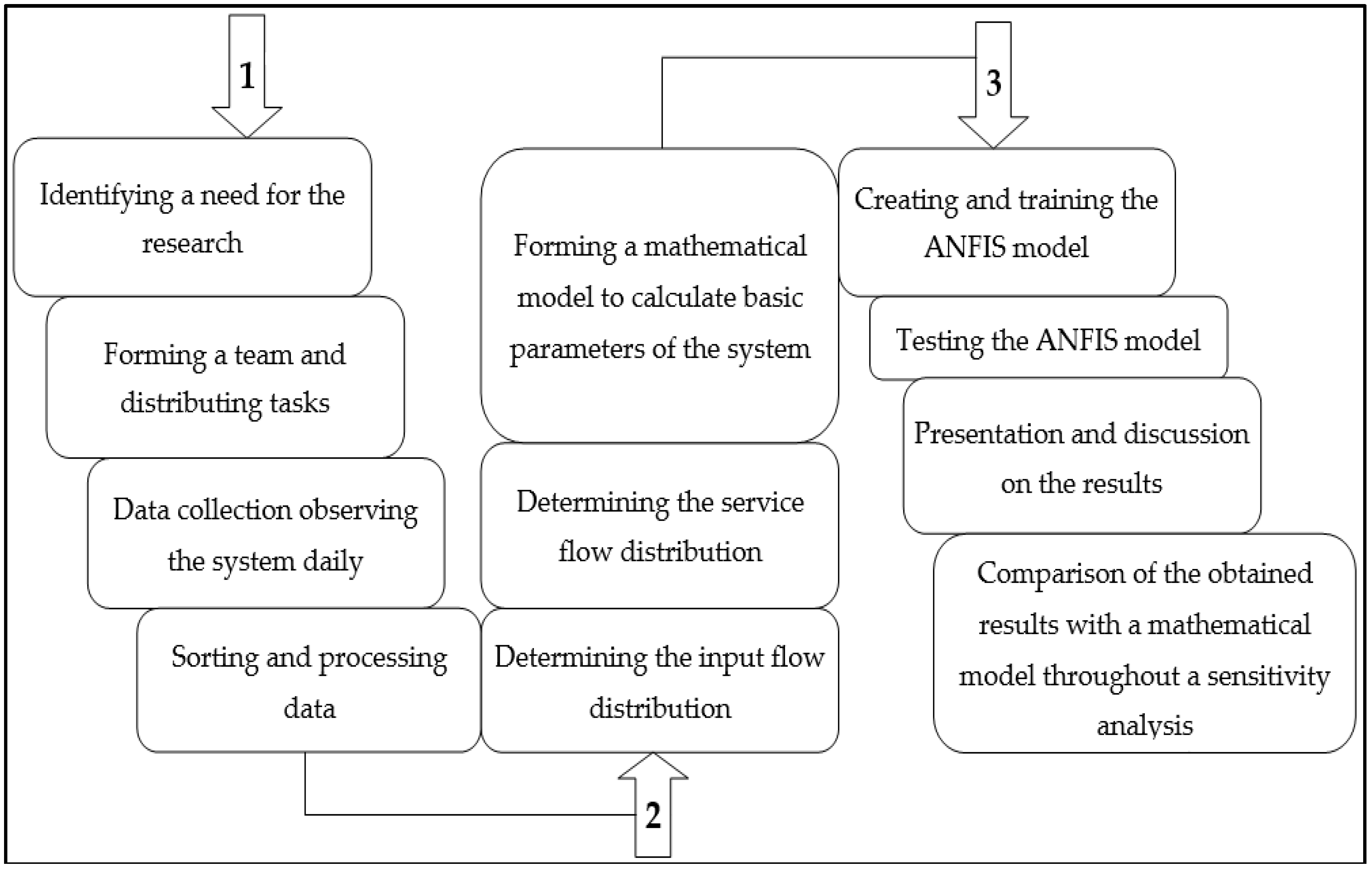
3. Methods
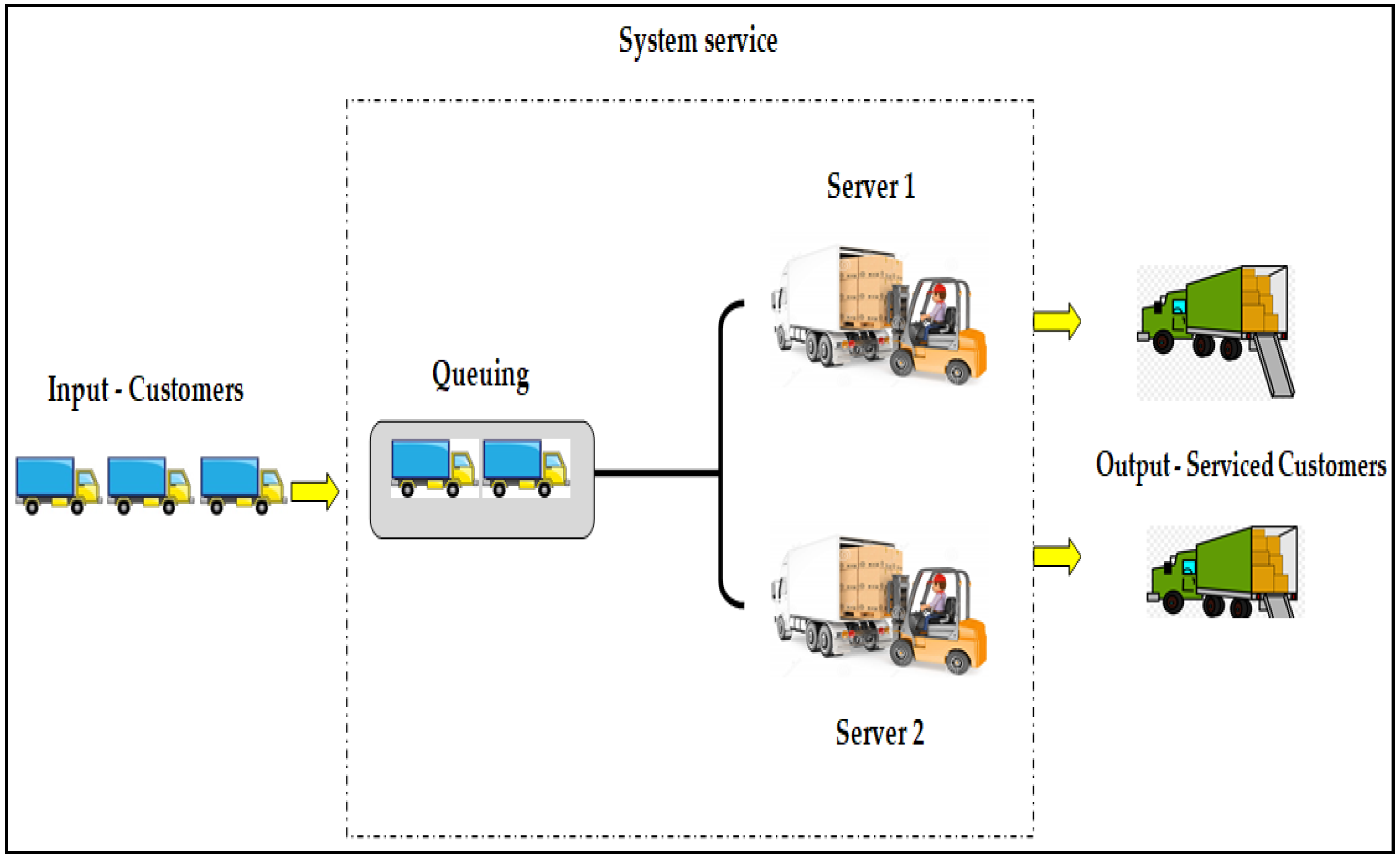
3.1. Basic Principles of Queuing Systems Theory
- The distribution of inter-arrival time; this most often corresponds to a Poisson, exponential or general distribution. Arrivals can be individual or in groups [40].
- The distribution of service time: exponential, hyper-exponential, hypo-exponential, constant, general.
- The number of servers can be one or more.
- The length of queue can be precisely defined or infinite. In case of arrival when the queue capacity is maximally filled, the costumer is denied, which is known as ‘balking’.
- System capacity implies the maximum number of customers in the system, being served or in the queue.
- FIFO (First in, First out)—in the order of arrival,
- LIFO (Last in, First out)—a customer that comes last will be served first,
- Random Service—customers are served in random order,
- Round Robin—a customer gets a time slot within which he/she will be served. If the service is not completed, the customer returns to the beginning of the queue,
- Priority Disciplines—the order of customer service is determined according to the priority that each one receives [37].
- A—the distribution of the inter-arrival time,
- B—the distribution of the service time. Positions A and B can be replaced by M (Markov processes, exponential distribution); D (deterministic distribution); E (Erlang distribution); H (hyper-exponential distribution); G (general distribution),
- m—the number of servers,
- K—system capacity,
- n—population size,
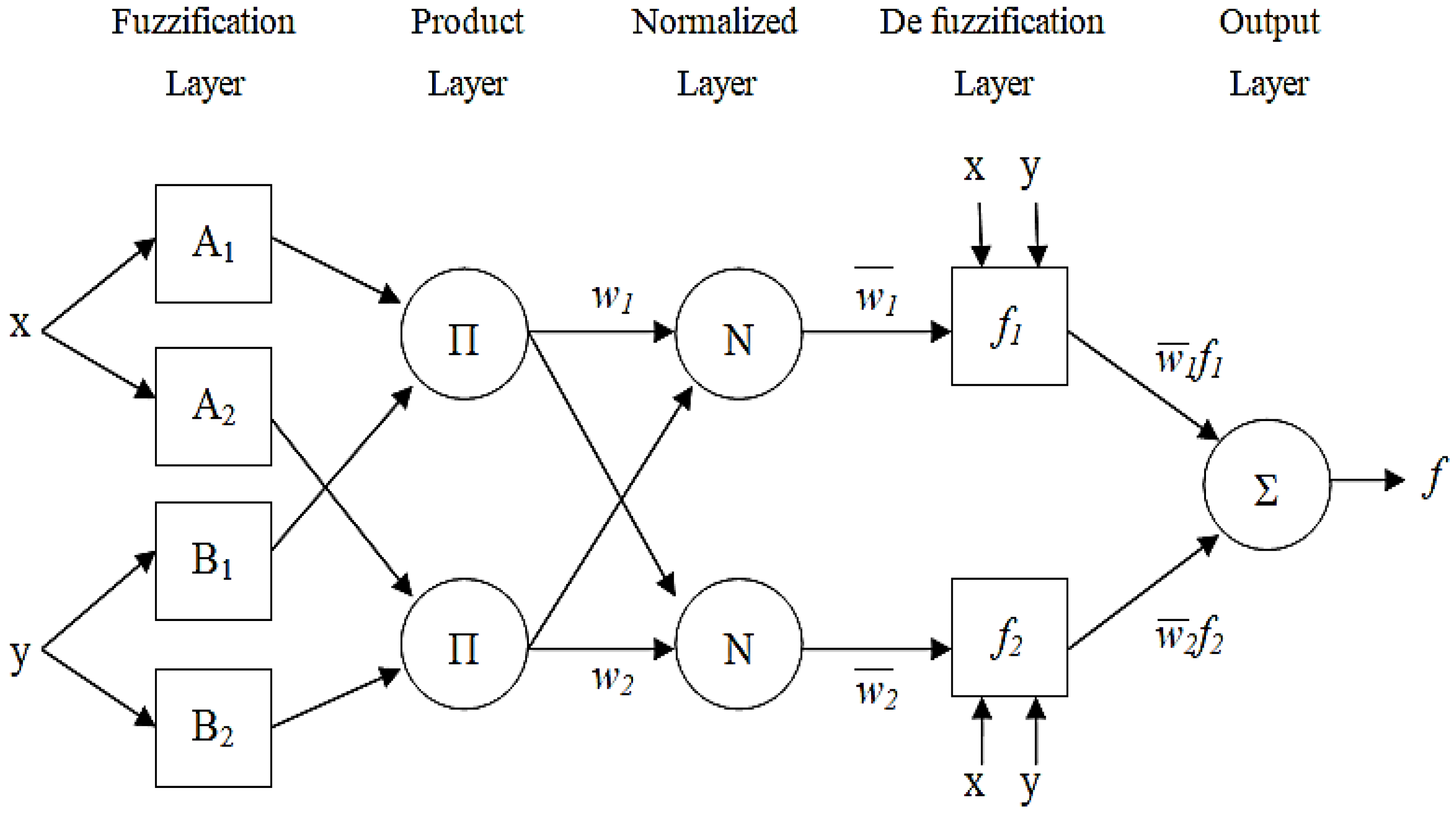
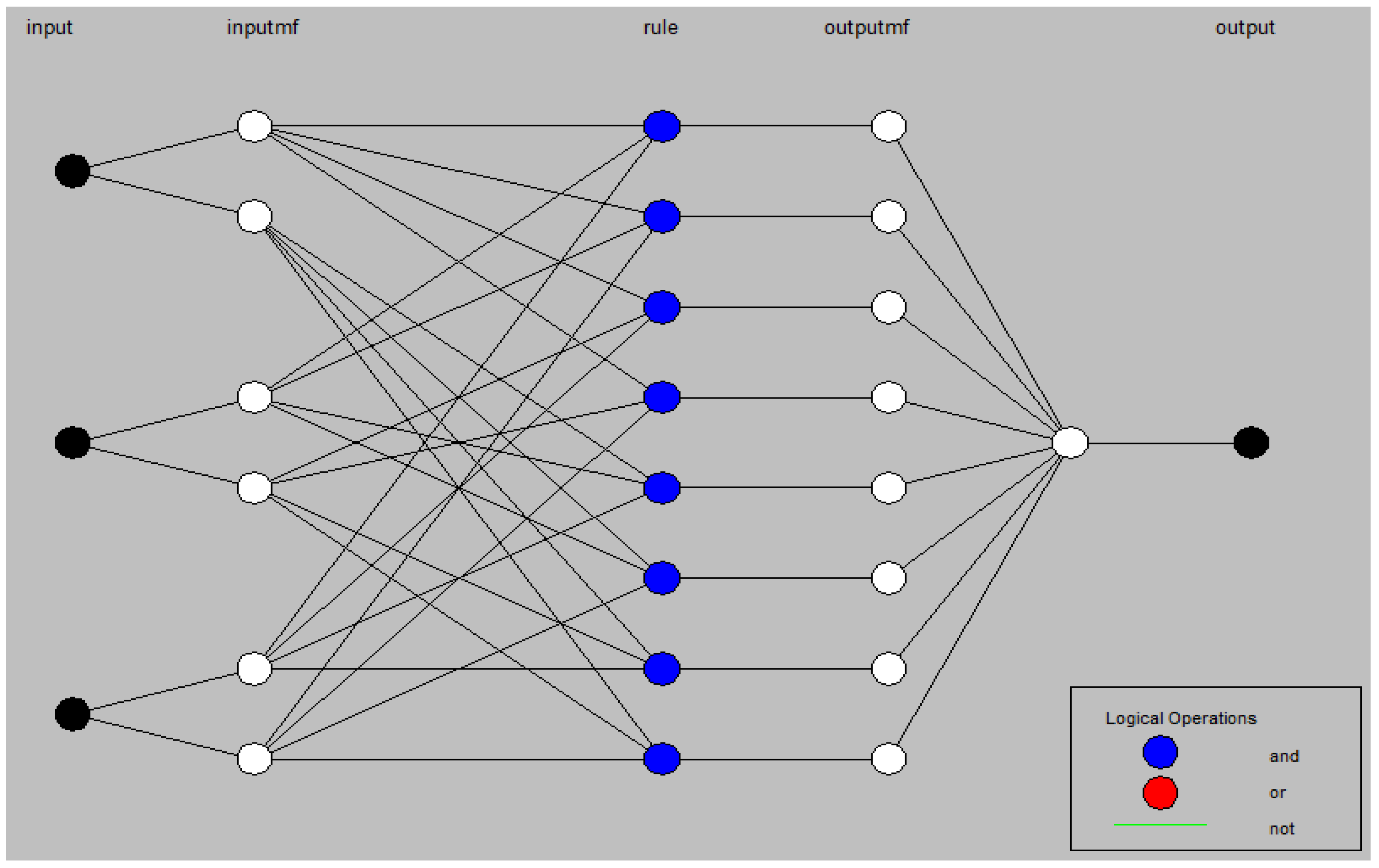
3.2. Adaptive Neuro-Fuzzy Inference Model
4. Case Study
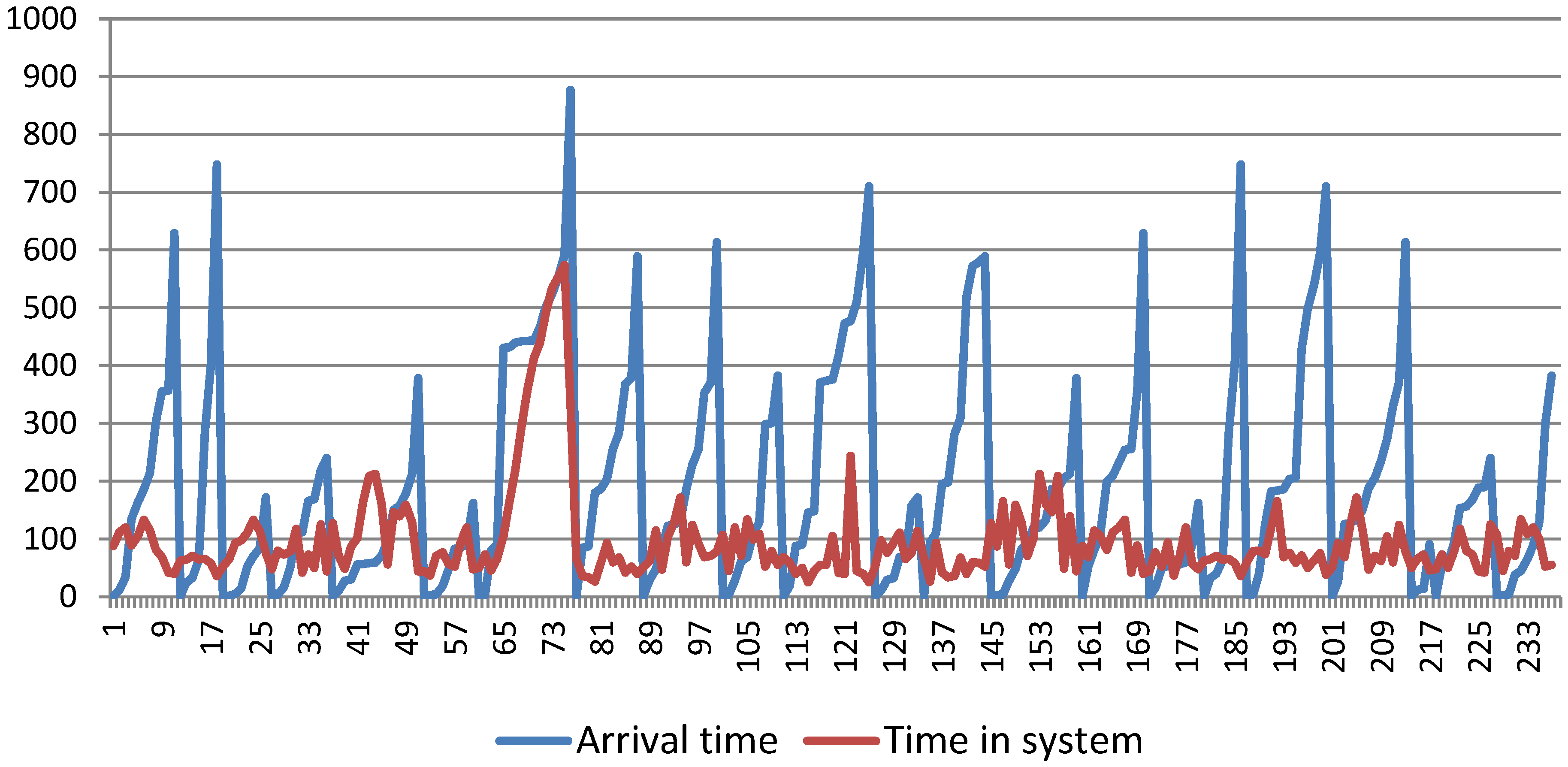
4.1. Data Collection
- the inter-arrival time of trucks,
- the cumulative arrival time since an initial time (for each day),
- the service time (transloading-manipulative operations) and
- the time in the system.
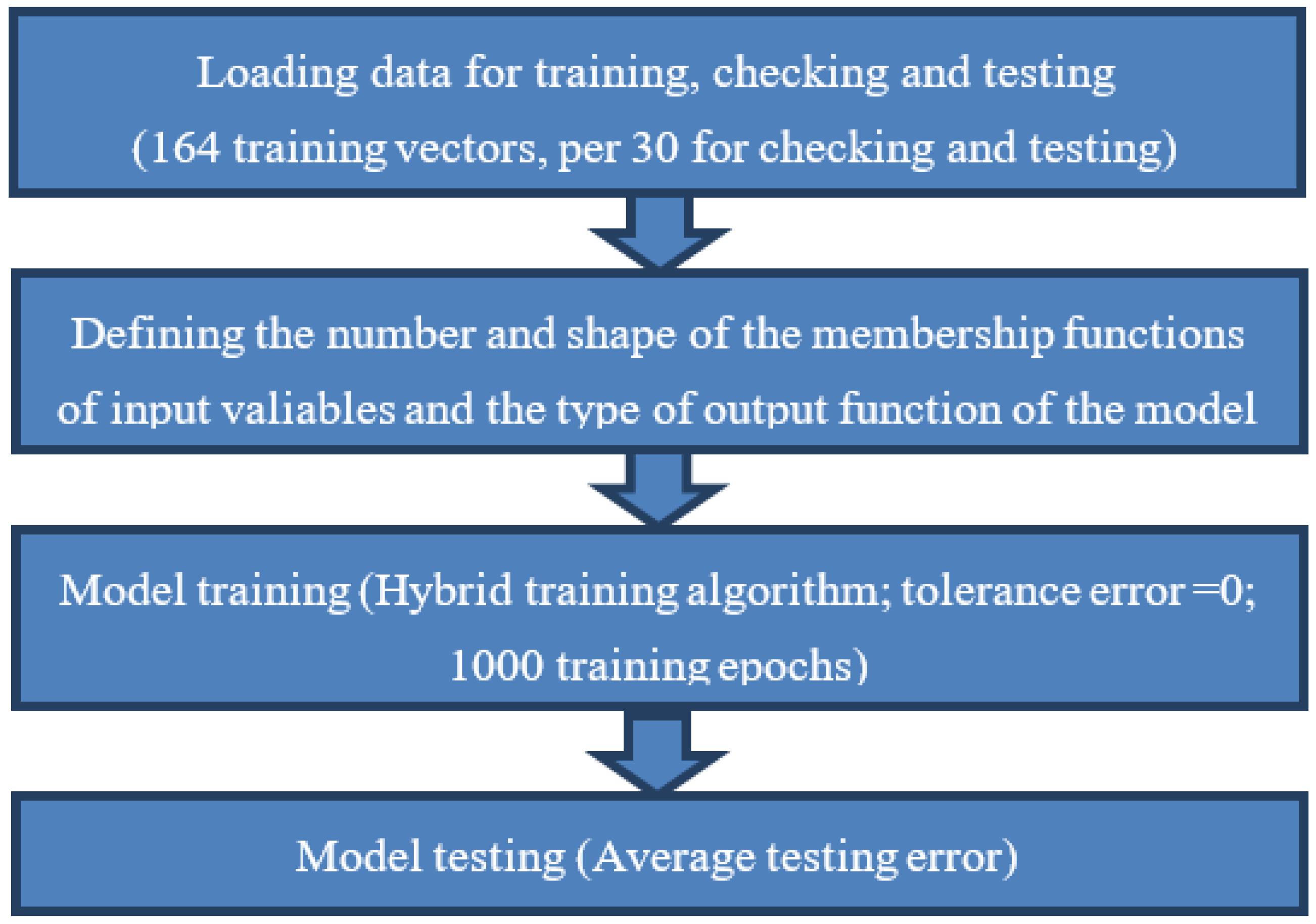
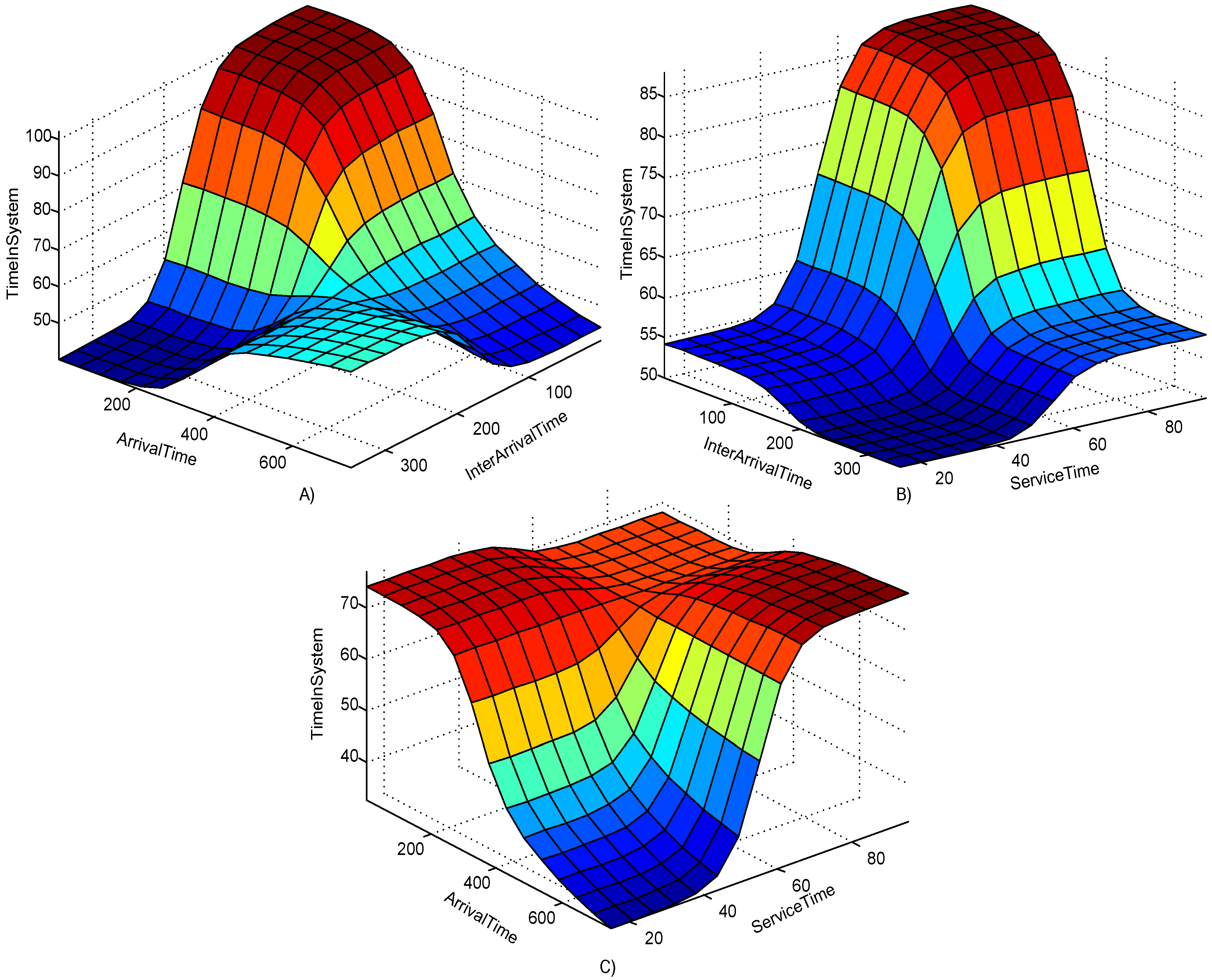
4.2. Creation and Training of the Model
- Training data, consisting of 73.21% or 164 input-output vectors, providing the so-called “Learning with a teacher”, where the outputs from the network are known in advance for appropriate inputs.
- Checking data, which is primarily aimed at preventing the occurrence of training data overfitting. The ANFIS model monitors the value of the checking error in each training epoch and retains learned parameters at its minimum value. Checking data consists of 13.39% or 30 input-output vectors.
- Testing data enables us to perform an evaluation of the abilities of the ANFIS model to perform a prediction of the time spent in the system as accurately as possible. The outputs of the ANFIS model are compared with known values, and the goal is to select a model that makes a minimum error. As well as checking data, testing data consists of 13.39% of the total set of data.
5. Results and discussion
6. Sensitivity Analysis
7. Conclusion
Author Contributions
Conflicts of Interest
References
- Stević, Ž.; Pamučar, D.; Kazimieras Zavadskas, E.; Ćirović, G.; Prentkovskis, O. The selection of wagons for the internal transport of a logistics company: A novel approach based on rough BWM and rough SAW methods. Symmetry 2017, 9, 264. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Vasiljević, M.; Stojić, G.; Korica, S. Novel Integrated multi-criteria model for supplier selection: Case study construction company. Symmetry 2017, 9, 279. [Google Scholar] [CrossRef]
- Stević, Ž.; Mulalić, E.; Božičković, Z.; Vesković, S.; Đalić, I. Economic analysis of the project of warehouse centralization in the paper production company. Serbian J. Manag. 2018, 13, 47–62. [Google Scholar] [CrossRef]
- Guerrouahane, N.; Aissani, D.; Bouallouche-Medjkoune, L.; Farhi, N. M/g/c/c state dependent queueing model for road traffic simulation. arXiv, 2016; arXiv:1612.09532. [Google Scholar]
- Raheja, T. Modelling traffic congestion using queuing networks. Sadhana 2010, 35, 427–431. [Google Scholar] [CrossRef]
- Van Woensel, T.; Vandaele, N. Queueing models for uninterrupted traffic flows. In Proceedings of the 13th Mini-EURO Conference Handling Uncertainty in the Analysis of Traffic and Transportation Systems, Bari, Italy, 2002; pp. 636–640. [Google Scholar]
- Vandaele, N.; Van Woensel, T.; Verbruggen, A. A queueing based traffic flow model. Transport. Res. D-Tr. E. 2000, 5, 121–135. [Google Scholar] [CrossRef]
- Osorio, C.; Bierlaire, M. Network performance optimization using a queueing network model. In Proceedings of the European Transport Conference, Langelaan, The Netherlands, 6–8 October 2008. [Google Scholar]
- Anokye, M.; Abdul-Aziz, A.R.; Annin, K.; Oduro, F.T. Application of queuing theory to vehicular traffic at signalized intersection in Kumasi-Ashanti region, Ghana. Am. Int. J. Cont. Res. 2013, 3, 23–29. [Google Scholar]
- Wang, F.; Ye, C.; Zhang, Y.; Li, Y. Simulation analysis and improvement of the vehicle queuing system on intersections based on MATLAB. Open Cybernet. Syst. J. 2014, 8, 217–223. [Google Scholar] [CrossRef]
- Chen, W.N. Application of queuing theory to dynamic vehicle routing problem. Glob. J. Bus. Res. 2009, 3, 85–91. [Google Scholar]
- Azizi, A.; Yarmohammadi, Y.; Yasini, A.; Sadeghifard, A. A queuing model to reduce energy consumption and pollutants production through transportation vehicles in green supply chain management. J. Sci. Res. Rep. 2015, 5, 571–581. [Google Scholar] [CrossRef]
- Aziziankohan, A.; Jolai, F.; Khalilzadeh, M.; Soltani, R.; Tavakkoli-Moghaddam, R. Green supply chain management using the queuing theory to handle congestion and reduce energy consumption and emissions from supply chain transportation fleet. J. Ind. Eng. Manag. 2017, 10, 213–236. [Google Scholar] [CrossRef]
- Gong, Y.; De Koster, R.B. A review on stochastic models and analysis of warehouse operations. Log. Res. 2011, 3, 191–205. [Google Scholar] [CrossRef]
- Masek, J.; Camaj, J.; Nedeliakova, E. Application the queuing theory in the warehouse optimization. Int. J. Soc. Behav. Educ. Econ. Bus. Ind. Eng. 2015, 9, 3744–3748. [Google Scholar]
- Cai, X.; Heragu, S.S.; Liu, Y. Modeling automated warehouses using semi-open queueing networks. In Handbook of Stochastic Models and Analysis of Manufacturing System Operations; Smith, J.M., Tan, B., Eds.; Springer-Verlag: New York, NY, USA, 2013; pp. 29–71. [Google Scholar]
- Bao-ping, C.; Zeng-Qiang, M. Short-term traffic flow prediction based on ANFIS. In Proceedings of the International Conference on Communication Software and Networks, Sichuan, China, 27–28 February 2009; pp. 791–793. [Google Scholar]
- Rahimi, A.M. Neuro-fuzzy system modelling for the effects of intelligent transportation on road accident fatalities. Tehnički Vjesn. 2017, 24, 1165–1171. [Google Scholar]
- Hosseinlou, M.H.; Sohrabi, M. Predicting and identifying traffic hot spots applying neuro-fuzzy systems in intercity roads. Int. J. Environ. Sci. Technol. 2009, 6, 309–314. [Google Scholar] [CrossRef]
- Suraj, S.; Jagrut, G. Smart traffic control using adaptive neuro-fuzzy Inference system (ANFIS). Int. J. Adv. Eng. Res. Dev. 2015, 2, 295–302. [Google Scholar]
- Araghi, S.; Khosravi, A.; Creighton, D. ANFIS traffic signal controller for an isolated intersection. In Proceedings of the International Conference on Fuzzy Computation Theory and Applications, Rome, Italy, 22–24 October 2014; pp. 175–180. [Google Scholar]
- Udofia, K.M.; Emagbetere, J.O.; Edeko, F.O. Dynamic traffic signal phase sequencing for an isolated intersection using ANFIS. Auto. Control Intell. Syst. 2014, 2, 21–26. [Google Scholar]
- Sharma, A.; Vijay, R.; Bodhe, G.L.; Malik, L.G. Adoptive neuro-fuzzy inference system for traffic noise prediction. Int. J. Comput. Appl. 2014, 98, 14–19. [Google Scholar] [CrossRef]
- Pamučar, D.; Ćirović, G. Vehicle route selection with an adaptive neuro fuzzy inference system in uncertainty conditions. Decis. Mak. Appl. Manag. Eng. 2018, 1, 13–37. [Google Scholar] [CrossRef]
- Andrade, K.; Uchida, K.; Kagaya, S. Development of transport mode choice model by using adaptive neuro-fuzzy inference system. Transport. Res. Rec.-J. Transport. Res. Board 2006, 1977, 8–16. [Google Scholar] [CrossRef]
- Mircetic, D.; Lalwani, C.; Lirn, T.; Maslaric, M.; Nikolicic, S. ANFIS expert system for cargo loading as part of decision support system in warehouse. In Proceedings of the 19th International Symposium on Logistics (ISL 2014), Ho Chi Minh City, Vietnam, 6–9 July 2014; pp. 10–20. [Google Scholar]
- Mirčetić, D.; Ralević, N.; Nikoličić, S.; Maslarić, M.; Stojanović, Đ. Expert system models for forecasting forklifts engagement in a warehouse loading operation: A case study. PROMET-Zagreb. 2016, 28, 393–401. [Google Scholar] [CrossRef]
- Marto, M.; Reynolds, K.; Borges, J.; Bushenkov, V.; Marques, S. Combining Decision Support Approaches for Optimizing the Selection of Bundles of Ecosystem Services. Forests 2018, 9, 438. [Google Scholar] [CrossRef]
- Al-Anbari, M.A.; Thameer, M.Y.; Al-Ansari, N. Landfill Site Selection by Weighted Overlay Technique: Case Study of Al-Kufa, Iraq. Sustainability 2018, 10, 999. [Google Scholar] [CrossRef]
- Sałabun, W.; Karczmarczyk, A. Using the COMET Method in the Sustainable City Transport Problem: An Empirical Study of the Electric Powered Cars. Procedia Comput. Sci. 2018, 126, 2248–2260. [Google Scholar] [CrossRef]
- Wątróbski, J.; Sałabun, W.; Karczmarczyk, A.; Wolski, W. Sustainable decision-making using the COMET method: An empirical study of the ammonium nitrate transport management. In Proceedings of the 2017 Federated Conference on Computer Science and Information Systems, Prague, Czech Republic, 3–6 September 2017; pp. 949–958. [Google Scholar]
- Wątróbski, J.; Sałabun, W.; Ladorucki, G. The temporal supplier evaluation model based on multicriteria decision analysis methods. In Proceedings of the Asian Conference on Intelligent Information and Database Systems, Kanazawa, Japan, 3–5 April 2017; pp. 432–442. [Google Scholar]
- Khalili-Damghani, K.; Dideh-Khani, H.; Sadi-Nezhad, S. A two-stage approach based on ANFIS and fuzzy goal programming for supplier selection. Int. J. Appl. Decis. Sci. 2013, 6, 1–14. [Google Scholar]
- Torkabadi, A.M.; Mayorga, R.V. Optimization of Supply Chain based on JIT Pull Control Policies: An Integrated Fuzzy AHP and ANFIS Approach. WSEAS Trans. Comput. 2017, 16, 366–377. [Google Scholar]
- Pirdavani, A.; Brijs, T.; Wets, G. A Multiple Criteria Decision-Making Approach for Prioritizing Accident Hotspots in the Absence of Crash Data. Transp. Rev. 2010, 30, 97–113. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Subotić, M.; Antuchevičiene, J.; Zavadskas, E. The Location Selection for Roundabout Construction Using Rough BWM-Rough WASPAS Approach Based on a New Rough Hamy Aggregator. Sustainability 2018, 10, 2817. [Google Scholar] [CrossRef]
- Stidham, S., Jr. Analysis, design, and control of queueing systems. Oper. Res. 2002, 50, 197–216. [Google Scholar] [CrossRef]
- Cooper, R.B. Introduction to queueing theory, 2nd ed.; Fineman, J., Schreiber, L.C., Eds.; North Holland: New York, NY, USA, 1981. [Google Scholar]
- Maragatha, S.; Srinivasan, S. Analysis of M/M/I queueing model for ATM facility. Glob. J. Theor.Appl. Mathematics Sci. 2012, 2, 41–46. [Google Scholar]
- Defraeye, M.; Van Nieuwenhuyse, I. Staffing and scheduling under nonstationary demand for service: A literature review. Omega 2016, 58, 4–25. [Google Scholar] [CrossRef]
- Stević, Ž. Calculation of the basic parameters of queuing systems using winqsb software. In Proceedings of the XI International May Conference on Strategic Management, Bor, Serbia, 29–31 May 2015; pp. 91–100. [Google Scholar]
- Sremac, S.; Tanackov, I.; Kopić, M.; Radović, D. ANFIS model for determining the economic order quantity. Decis. Mak. Appl. Manag. Eng. 2018, 1, 1–12. [Google Scholar] [CrossRef]
- Tiwari, S.; Babbar, R.; Kaur, G. Performance evaluation of two ANFIS models for predicting water quality Index of River Satluj (India). Adv. in Civ. Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Billah, M.; Waheed, S.; Ahmed, K.; Hanifa, A. Real time traffic sign detection and recognition using adaptive neuro fuzzy inference system. Commun. Appl. Electron. 2015, 3, 1–5. [Google Scholar] [CrossRef]
- Qasem, S.N.; Ebtehaj, I.; Riahi Madavar, H. Optimizing ANFIS for sediment transport in open channels using different evolutionary algorithms. J. Appl. Res. Water Wastewater 2017, 4, 290–298. [Google Scholar]
- Lukovac, V.; Pamučar, D.; Popović, M.; Đorović, B. Portfolio model for analyzing human resources: An approach based on neuro-fuzzy modeling and the simulated annealing algorithm. Expert Syst. Appl. 2017, 90, 318–331. [Google Scholar] [CrossRef]
- Pamučar, D.; Ljubojević, S.; Kostadinović, D.; Đorović, B. Cost and risk aggregation in multi-objective route planning for hazardous materials transportation—A neuro-fuzzy and artificial bee colony approach. Expert Syst. Appl. 2016, 65, 1–15. [Google Scholar] [CrossRef]
- Das, R.D.; Winter, S. Detecting urban transport modes using a hybrid knowledge driven framework from GPS trajectory. ISPRS Int. J. Geo-Inf. 2016, 5, 207. [Google Scholar] [CrossRef]
- Engmann, S.; Cousineau, D. Comparing distributions: The two-sample Anderson-Darling test as an alternative to the Kolmogorov-Smirnoff test. J. Appl. Quant. Methods 2011, 6, 1–17. [Google Scholar]
- Stephens, M.A. Tests based on EDF statistics. In Goodness of Fit. Techniques Chapter 4; D’Agostino, R.B., Stephens, M.A., Eds.; Routledge: New York, NY, USA, 1986. [Google Scholar]
- Barford, P.; Crovella, M. Generating representative web workloads for network and server performance evaluation. In ACM SIGMETRICS Performance Evaluation Review; ACM: New York, NY, USA, 1998; pp. 151–160. [Google Scholar]
- Jovanović, B.; Grbić, T.; Bojović, N.; Kujačić, M.; Šarac, D. Application of ANFIS for the Estimation of Queuing in a Postal Network Unit: A Case Study. Acta Polytech. Hung. 2015, 12, 25–40. [Google Scholar]
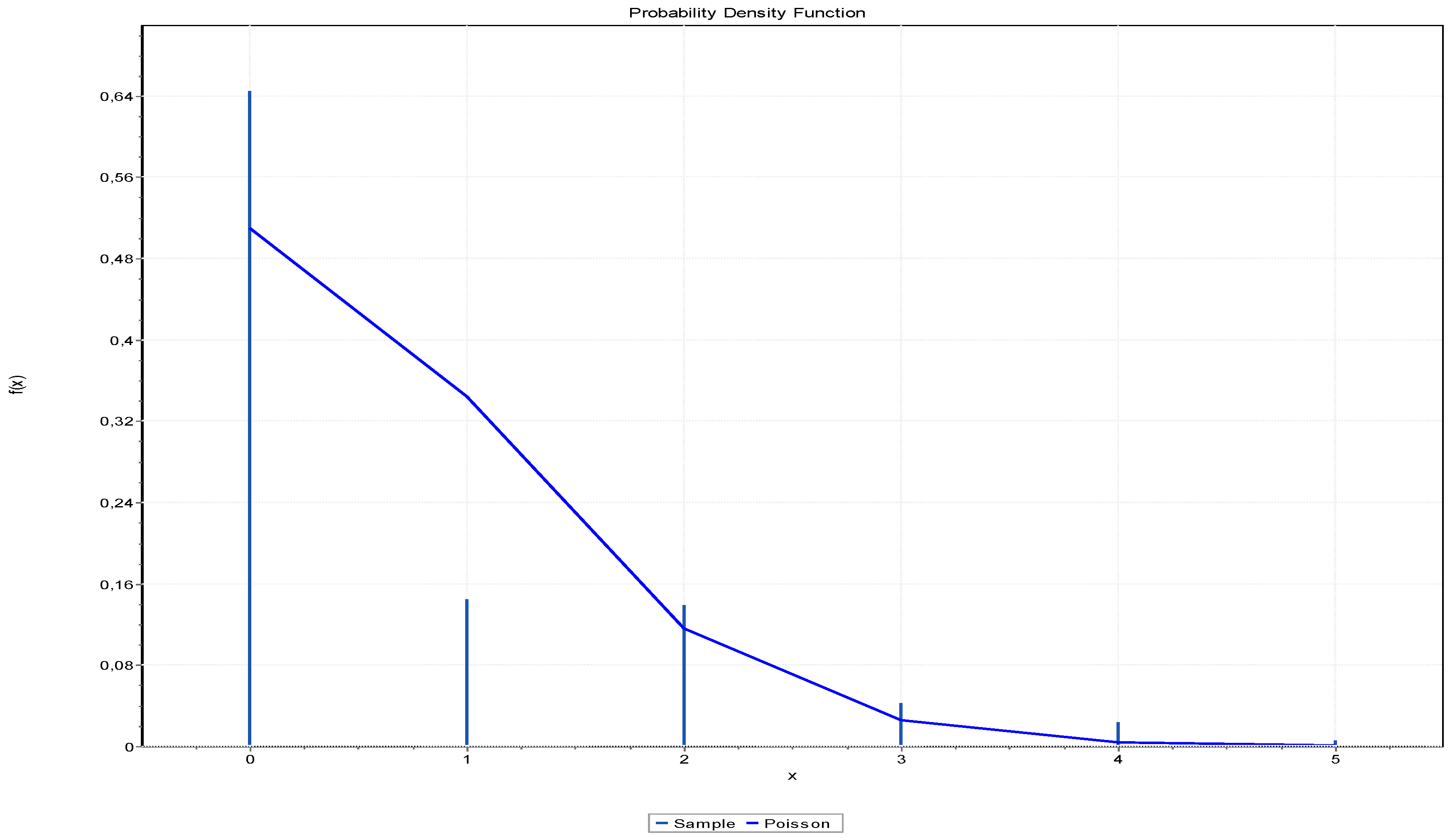
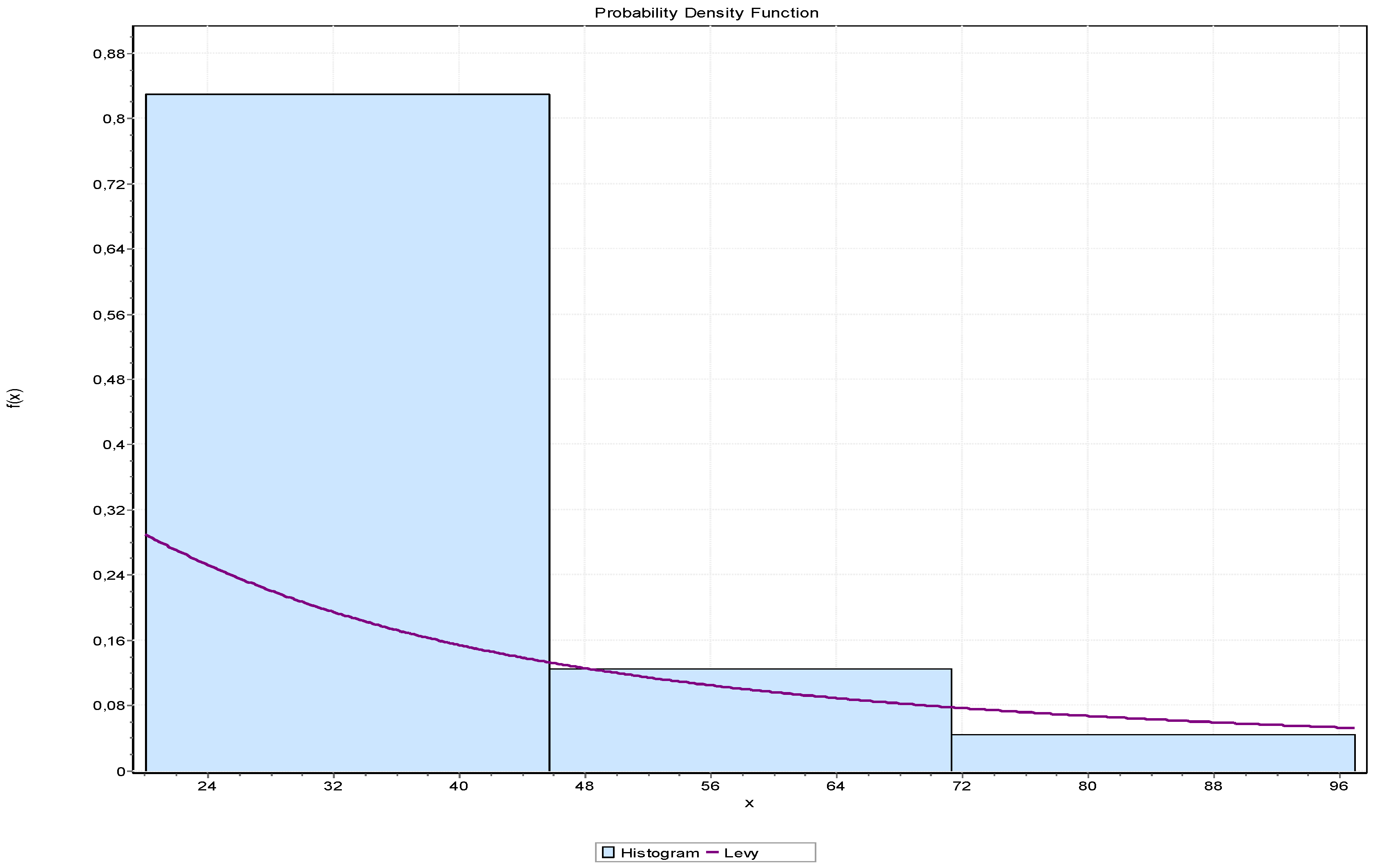
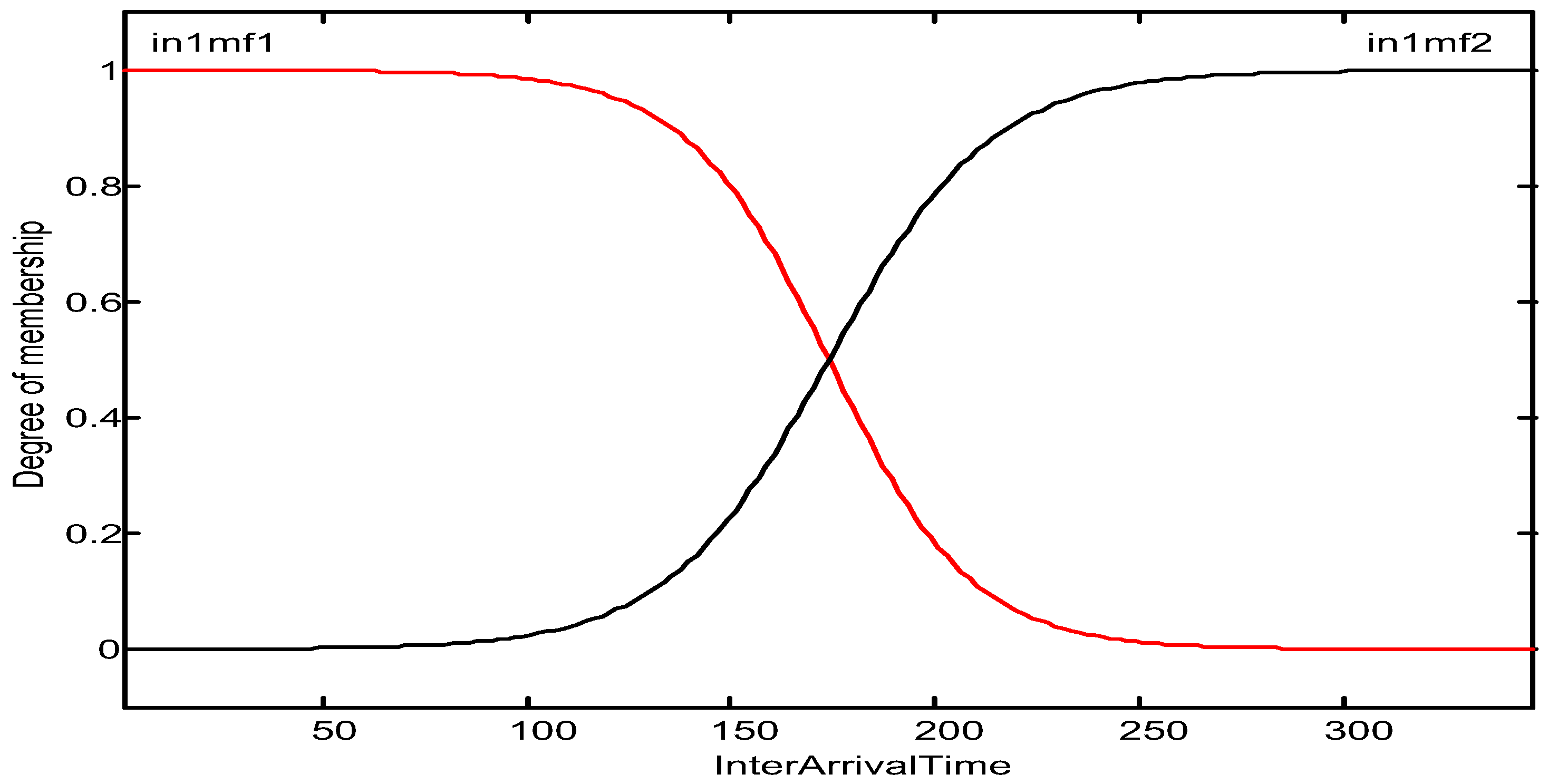

| Number of Trucks | Frequency |
|---|---|
| 0 | 214 |
| 1 | 48 |
| 2 | 46 |
| 3 | 14 |
| 4 | 8 |
| 5 | 2 |
| Distribution | Anderson Darling | |
|---|---|---|
| Statistic | Rank | |
| Poisson | 88.26 | 1 |
| Geometric | 112.79 | 2 |
| D. Uniform | 197.01 | 3 |
| Bernoulli | No fit (data max > 1) | |
| Binomial | No fit | |
| Hyper-geometric | No fit | |
| Logarithmic | No fit (data min < 1) | |
| Neg. Binomial | No fit | |
| Class Limits | Arithmetic Mean of Class-Interval | Frequency (Number of Trucks) |
|---|---|---|
| 15–25 | 20 | 46 |
| 26–36 | 31 | 72 |
| 37–47 | 42 | 68 |
| 48–58 | 53 | 22 |
| 59–69 | 64 | 6 |
| 70–80 | 75 | 0 |
| 81–91 | 83 | 6 |
| 92–102 | 97 | 4 |
| Distribution | Anderson Darling | |
|---|---|---|
| Statistic | Rank | |
| Levy | 1.5611 | 1 |
| Levy (2P) | 1.6041 | 2 |
| Pareto 2 | 2.3671 | 3 |
| Exponential | 2.9128 | 4 |
| Rayleigh | 3.6386 | 5 |
| Reciprocal | 3.8271 | 6 |
| Log-Logistic (3P) | 4.2251 | 7 |
| Fatigue Life (3P) | 4.4674 | 8 |
| Shape of Fuzzy Membership Functions | Number of Fuzzy Membership Functions for Each of Three Input Variables | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 2 2 | 3 3 3 | 2 2 3 | 2 3 2 | 2 3 3 | 3 3 2 | 3 2 3 | 3 2 2 | |
| Trimf | 18.66 | 64.64 | 21.53 | 22.94 | 30.46 | 66.73 | 23.30 | 20.72 |
| Trapmf | 14.23 | 27.72 | 16.16 | 14.33 | 16.64 | 16.46 | 20.55 | 18.11 |
| Gbellmf | 19.46 | 47.00 | 19.66 | 21.42 | 58.65 | 17.34 | 46.14 | 16.29 |
| Gaussmf | 16.91 | 307.84 | 20.26 | 17.81 | 26.91 | 31.49 | 22.64 | 17.79 |
| Gauss2mf | 14.30 | 20.50 | 63.56 | 15.70 | 22.40 | 26.89 | 19.16 | 17.83 |
| Pimf | 14.78 | 23.21 | 17.10 | 14.05 | 17.19 | 15.07 | 21.25 | 17.42 |
| Dsigmf | 13.67 | 64.43 | 24.38 | 17.09 | 60.50 | 28.00 | 19.29 | 17.46 |
| Psigmf | 13.67 | 64.43 | 24.38 | 17.09 | 60.50 | 28.00 | 19.29 | 17.46 |
| Shape of Fuzzy Membership Functions | Number of Fuzzy Membership Functions for Each of Three Input Variables | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 2 2 | 3 3 3 | 2 2 3 | 2 3 2 | 2 3 3 | 3 3 2 | 3 2 3 | 3 2 2 | |
| Trimf | 217.63 | 13557.47 | 577.56 | 836.02 | 1726.74 | 35925.48 | 19459.66 | 1219.73 |
| Trapmf | 116.57 | 318.80 | 219.14 | 38.82 | 25.42 | 60.76 | 294.55 | 44.87 |
| Gbellmf | 22.19 | 34006.56 | 187.06 | 5305.95 | 23183.85 | 14176.49 | 50418.31 | 6937.78 |
| Gaussmf | 33.02 | 24328.30 | 257.99 | 3293.97 | 11566.52 | 5466.29 | 51114.92 | 108.12 |
| Gauss2mf | 253.78 | 3727.55 | 319.52 | 9477.00 | 34019.82 | 3765.83 | 14012.94 | 2537.84 |
| Pimf | 841.49 | 597.19 | 2104.52 | 222.63 | 23.77 | 44.86 | 415.37 | 190.11 |
| Dsigmf | 588.50 | 4961.53 | 2289.36 | 774.68 | 65680.67 | 2563.84 | 19890.09 | 449.44 |
| Psigmf | 427.85 | 5027.61 | 1118.50 | 1120.38 | 62986.63 | 7788.29 | 15398.09 | 4170.70 |
| Ordinal Number | Checking Data | ANFIS Output | |||
|---|---|---|---|---|---|
| Inter-Arrival Interval | Arrival Time | Service Time | Time Spent in the System | ||
| 1st | 2 | 357 | 30 | 42 | 58.36 |
| 2nd | 272 | 629 | 25 | 40 | 37.84 |
| 3rd | 1 | 1 | 40 | 63 | 83.49 |
| 4th | 24 | 25 | 45 | 64 | 85.68 |
| 5th | 8 | 33 | 30 | 71 | 82.53 |
| 6th | 1 | 1 | 30 | 50 | 82.54 |
| 7th | 11 | 12 | 30 | 66 | 82.54 |
| 8th | 2 | 14 | 25 | 73 | 82.47 |
| 9th | 77 | 91 | 30 | 46 | 82.34 |
| 10th | 40 | 109 | 40 | 99 | 83.34 |
| 11th | 20 | 129 | 65 | 109 | 118.59 |
| 12th | 170 | 299 | 30 | 52 | 66.57 |
| 13th | 1 | 300 | 45 | 79 | 74.73 |
| 14th | 83 | 383 | 30 | 55 | 52.54 |
| 15th | 1 | 1 | 35 | 48 | 82.77 |
| 16th | 54 | 55 | 35 | 73 | 82.70 |
| 17th | 3 | 58 | 30 | 50 | 82.51 |
| 18th | 35 | 93 | 40 | 78 | 83.39 |
| 19th | 60 | 153 | 15 | 118 | 82.03 |
| 20th | 3 | 156 | 55 | 80 | 101.73 |
| 21st | 12 | 168 | 50 | 73 | 90.92 |
| 22nd | 21 | 189 | 15 | 44 | 81.54 |
| 23rd | 1 | 190 | 30 | 42 | 81.62 |
| 24th | 50 | 240 | 95 | 125 | 118.06 |
| 25th | 1 | 1 | 40 | 107 | 83.49 |
| 26th | 2 | 3 | 35 | 45 | 82.77 |
| 27th | 1 | 4 | 45 | 79 | 85.69 |
| 28th | 34 | 38 | 45 | 71 | 85.66 |
| 29th | 7 | 45 | 85 | 134 | 121.85 |
| 30th | 20 | 65 | 65 | 109 | 118.79 |
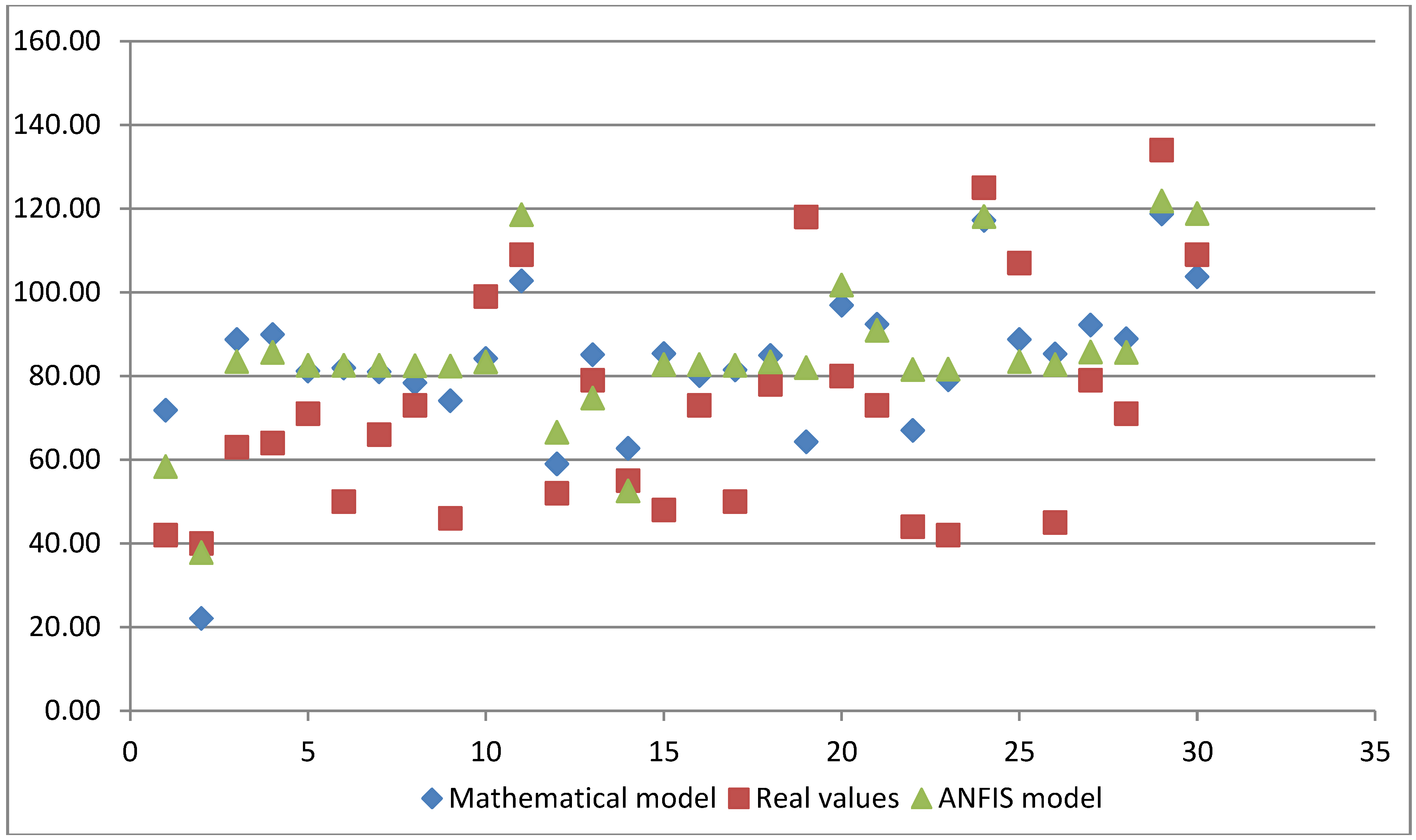
| Measured, Real Values | Mathematical Model | ANFIS Model |
|---|---|---|
| 42 | 71.84 | 58.36 |
| 40 | 22.03 | 37.84 |
| 63 | 88.75 | 83.49 |
| 64 | 89.95 | 85.68 |
| 71 | 81.17 | 82.53 |
| 50 | 81.92 | 82.54 |
| 66 | 80.96 | 82.54 |
| 73 | 78.39 | 82.47 |
| 46 | 74.12 | 82.34 |
| 99 | 84.15 | 83.34 |
| 109 | 102.73 | 118.59 |
| 52 | 59.03 | 66.57 |
| 79 | 85.11 | 74.73 |
| 55 | 62.72 | 52.54 |
| 48 | 85.33 | 82.77 |
| 73 | 80.11 | 82.70 |
| 50 | 81.46 | 82.51 |
| 78 | 84.87 | 83.39 |
| 118 | 64.29 | 82.03 |
| 80 | 96.90 | 101.73 |
| 73 | 92.33 | 90.92 |
| 44 | 66.99 | 81.54 |
| 42 | 79.09 | 81.62 |
| 125 | 117.19 | 118.06 |
| 107 | 88.75 | 83.49 |
| 45 | 85.24 | 82.77 |
| 79 | 92.16 | 85.69 |
| 71 | 88.95 | 85.66 |
| 134 | 118.76 | 121.85 |
| 109 | 103.70 | 118.79 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stojčić, M.; Pamučar, D.; Mahmutagić, E.; Stević, Ž. Development of an ANFIS Model for the Optimization of a Queuing System in Warehouses. Information 2018, 9, 240. https://doi.org/10.3390/info9100240
Stojčić M, Pamučar D, Mahmutagić E, Stević Ž. Development of an ANFIS Model for the Optimization of a Queuing System in Warehouses. Information. 2018; 9(10):240. https://doi.org/10.3390/info9100240
Chicago/Turabian StyleStojčić, Mirko, Dragan Pamučar, Eldina Mahmutagić, and Željko Stević. 2018. "Development of an ANFIS Model for the Optimization of a Queuing System in Warehouses" Information 9, no. 10: 240. https://doi.org/10.3390/info9100240
APA StyleStojčić, M., Pamučar, D., Mahmutagić, E., & Stević, Ž. (2018). Development of an ANFIS Model for the Optimization of a Queuing System in Warehouses. Information, 9(10), 240. https://doi.org/10.3390/info9100240







