Multiple Criteria Decision-Making in Heterogeneous Groups of Management Experts
Abstract
1. Introduction
- It is provided through a couple of algorithms and a nonlinear optimization approach concurrently applied.
- Through the Hadamard’s operator and some easy algebraic manipulations, objective functionals are synthesized (as it will be detailed further on), to be used in the optimization algorithm.
- When the I-MPRs improved by the methodology are reduced into an MPR (defined in the I-MPR), our approach can still give reliable results. For example, for this MPR, we can verify the results of IC or GC, with an alternative method.
- The IC or the GC accepted indices (threshold values) have been previously investigated and fixed. Nevertheless, the project designer could assign a different value depending on the project requirements.
- Obtained results are independent of the method of prioritization utilized in the consensus operation.
2. Preliminaries
Measuring the Dissimilarity between Matrices
3. Reliable Intervals for Individual Consistency and Group Consensus
3.1. Sequential Quadratic Programming Methodology
3.2. Matching the Problem with the SQP for Improving I-MPRs
3.2.1. Individual Consistency Objective Functional
3.2.2. Group Consensus Objective Functional
3.3. Improving the Individual Consistency of an I-MPR
| Algorithm 1: Algorithm IC-I-MPR |
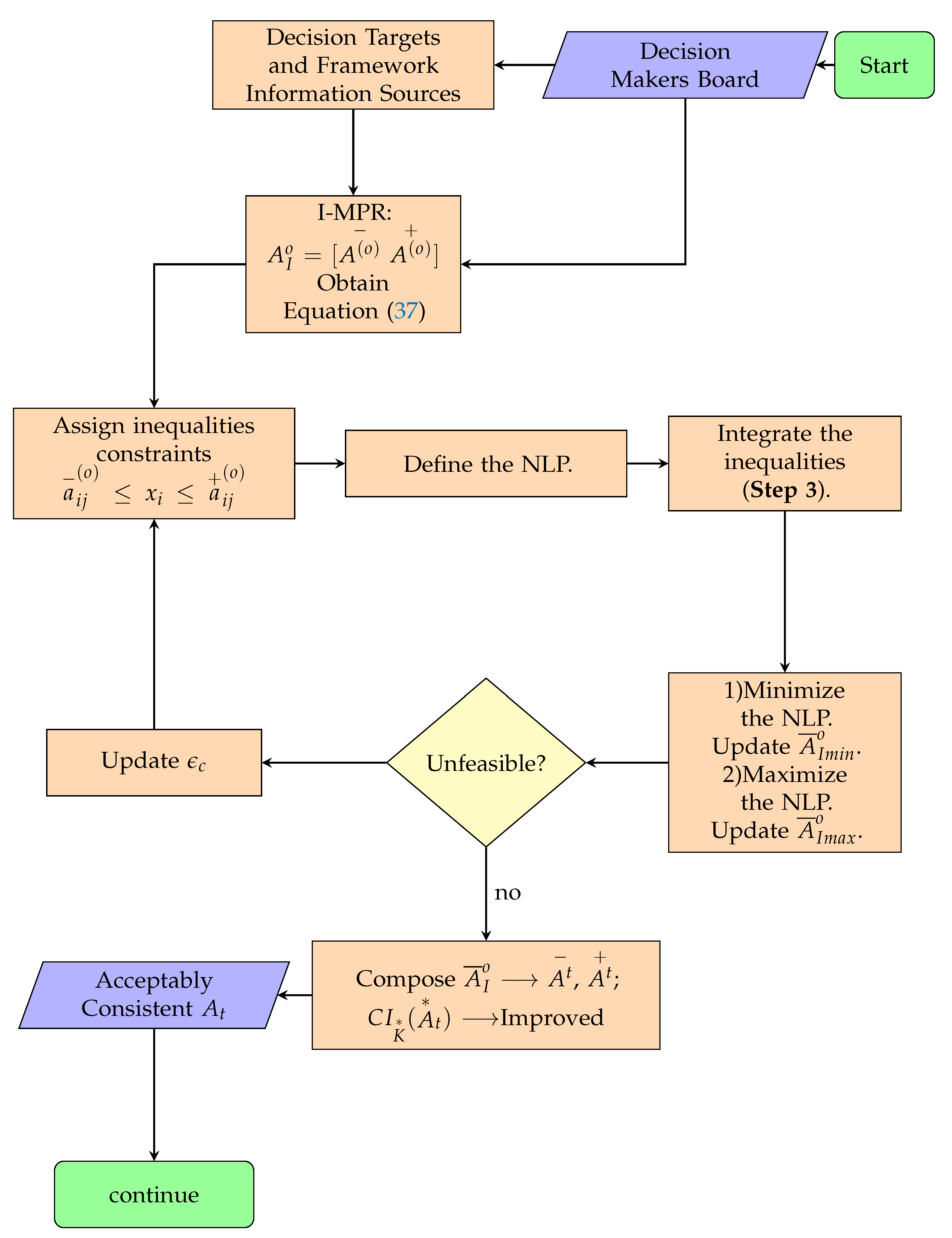
| Input: : the initial interval I-MPR; : the initialization value for the nonlinear optimization, which is to be defined within the corresponding interval or as the corresponding crisp value; the threshold value of for the Individual Consistency assessment; Design parameter value allowing the enlargement pace of the searching space of the algorithm. Output: : the consistency interval matrix computed and verifying interval conditions given by Equation (10). Step 1: Get the function for the assessment of Individual Consistency given by Equation (37). Step 2: Define for the nonlinear optimization algorithm, the allowed intervals: Step 4: Solve the former nonlinear optimization problem using the SQP algorithm to minimize it. Step 5: If an unfeasible solution is obtained, assign , where , increments at each iteration and return to Step 4. Otherwise, continue to the next step. Step 6: Obtain . Solve again the same nonlinear optimization problem but this time in order to maximize it. In order to do so, assign the objective functional as . Obtain . Step 7: Compose the Consistency Interval Matrix as follows: Step 8: end. |
3.4. Improving the Group Consensus of a Set of I-MPRs
| Algorithm 2: Algorithm GC-I-MPR |
| Input: : the initial interval I-MPRs; : the initialization value for the nonlinear optimization, which is to be defined within the corresponding interval or as the corresponding crisp value; for the Group consensus assessment; design parameter allowing the enlargement of the searching space of the algorithm. Output: : the I-MPRs computed and verifying interval conditions given by Equation (11). Step 1: Get the function for the assessment of Group Consensus given by Equation (39). Step 2: Define for the nonlinear optimization algorithm, the allowed intervals: Step 4: If , , then goto Step 9. Otherwise, continue with the next step. Step 5: Solve the former nonlinear optimization problem (NLP) using the SQP algorithm to minimize it. Step 6: If an unfeasible solution is obtained, assign , where , increments at each iteration and return to Step 4. Otherwise, continue to the next step. Step 7: Obtain the matrix . Solve again the same nonlinear optimization problem but this time in order to maximize it. Obtain . Step 8: Goto to Step 2. Step 9: Compose the Group Consensus Interval Matrix as follows: Step 10: end. |
- -
- In the case that an expert has provided a crisp value(s) in her/his judgement(s), this value(s) drives the process of nonlinear optimization since they will slightly change with the pace of . It is very useful since precisely in that value(s), the expert has shown her/his highest confidence level.
- -
- At the end of both algorithms, one gets reliable I-MPRs, i.e., where the consistency and consensus constraints are fulfilled.
4. Prioritization Method and Methodology Application
Interval Priority Vector Synthesis
5. Illustration of the Methodology through Numerical Examples
Case Study Discussions and Managerial Implications
6. Concluding Remarks and Future Work
- It is provided through a couple of algorithms and a nonlinear optimization approach (Sequential Quadratic Programming) concurrently applied.
- Through the Hadamard’s operator and some easy algebraic manipulations, objective functionals were synthesized to be used in the optimization algorithm.
- When the I-MPRs improved by the methodology are reduced into an MPR (defined in the I-MPR), our approach can still give reliable results. For example, for this MPR, we can verify the results of IC or GC with an alternative method.
- The IC or the GC accepted indices (threshold values) have been previously investigated and fixed. Nevertheless, the project designer could assign a different value depending on the project requirements.
- Obtained results are independent of the method of prioritization utilized in the consensus operation.
- The computational cost increases as the I-MPRs dimension and the number of DMs involved in the evaluation process are increased.
- For a real project where a high number of criteria and experts participate, it can be necessary to program this method through an exhaustive parallel computation system.
- For a real project where a high number of criteria and experts participate, the notation can be cumbersome.
- The application of our approach to various study cases where heterogenous groups of DMs with different weights participate in a collaborative manner.
- The integration of the complete methodology in a benchmark to compare the results of a diverse set of MCDM tools.
- The definition or employment of this methodology on different frameworks, v.gr. fuzzy or hesitant MCDM.
Funding
Acknowledgments
Conflicts of Interest
References
- Saaty, T. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Yntema, D.B.; Torgerson, W. Man-computer cooperation in decisions requiring common sense. IRE Trans. Hum. Factors Electron. 1961, 2, 20–26. [Google Scholar]
- Xia, W.; Wu, Z. Supplier selection with multiple criteria in volume discount environments. Omega 2007, 35, 494–504. [Google Scholar]
- Zadeh, L. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar]
- Seiford, M. A DEA Bibliography (1978 1992). In Data Envelopment Analysis: Theory, Methodology and Applications; Charnes, A., Cooper, W.W., Lewin, A.Y., Seiford, L.M., Eds.; Springer: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Aamodt, A.; Plaza, E. Case-based reasoning: Foundational issues. methodological variations and system approaches. Artif. Intell. Commun. 1994, 7, 39–59. [Google Scholar]
- Kusumadewi, S.; Hartati, S.; H, A.; Wardoyo, R. Fuzzy multi-attribute decision-making (FUZZY MADM); GrahaIlmu Publisher: Dresden, Germany, 2010. [Google Scholar]
- Benayoun, R.; Roy, B.; Sussman, B. ELECTRE: Une méthode pour guider le choix en présence de points de vue multiples. In SEMA; METRA International: Paris, France, 1996. [Google Scholar]
- Gwo-Hshiung, T.; Tzeng, G.; Huang, J.J. Multiple Attribute Decision Making: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Vincke, J.; Brans, P. A preference ranking organization method (the PROMETHEE method for MCDM). Manag. Sci. 1985, 31, 641–656. [Google Scholar]
- Wang, P.; Zhu, Z.; Wang, Y. A novel hybrid MCDM model combining the SAW, TOPSIS and GRA methods based on experimental design. Inf. Sci. 2016, 345, 27–45. [Google Scholar]
- Vicenc, T. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar]
- Liu, J.; Zhaoa, H.K.; Li, Z.B.; Liu, S.F. Decision process in MCDM with large number of criteria and heterogeneous risk preferences. Oper. Res. Perspect. 2017, 4, 106–112. [Google Scholar]
- Zhang, X.; Xu, Z. The Extended TOPSIS Method for Multi-criteria Decision Making Based on Hesitant Heterogeneous Information. In Proceedings of the 2nd International Conference on Software Engineering, Knowledge Engineering and Information Engineering (SEKEIE 2014), Singapore, 5–6 August 2014; pp. 81–86. [Google Scholar]
- Faizi, S.; Salabun, W.; Rashid, T.; Watróbski, J.; Zafar, S. Group Decision-Making for Hesitant Fuzzy Sets Based on Characteristic Objects Method. Symmetry 2017, 9, 136. [Google Scholar]
- Cheng, J.; Zhang, Y.; Feng, Y.; Liu, Z.; Tan, J. Structural Optimization of a High-Speed Press Considering Multi-Source Uncertainties Based on a New Heterogeneous TOPSIS. Appl. Sci. 2018, 8, 126. [Google Scholar]
- Faizi, S.; Rashid, T.; Salabun, W.; Zafar, S.; Watróbski, J. Decision Making with Uncertainty Using Hesitant Fuzzy Sets. Int. J. Fuzzy Syst. 2018, 20, 93–103. [Google Scholar]
- Watróbski, J.; Jankowski, J.; Ziemba, P.; Karczmarczyk, A.; Ziolo, M. Generalised framework for multi-criteria method selection. Omega 2018, in press. [Google Scholar]
- Linkov, I.; Bates, M.E.; Canis, L.J.; Seager, T.P.; Keisler, J.M. A decision-directed approach for prioritizing research into the impact of nanomaterials on the environment and human health. Nat. Nanotechnol. 2011, 6, 784–787. [Google Scholar]
- Karlson, M.; Karlsson, C.S.J.; Mortberg, U.; Olofsson, B.; Balfors, B. Design and evaluation of railway corridors based on spatial ecological and geological criteria. Transp. Res. Part D Transp. Environ. 2016, 46, 207–228. [Google Scholar]
- Liu, F.; Aiwu, G.; Lukovac, V.; Vukic, M. A multicriteria model for the selection of the transport service provider: A single valued neutrosophic DEMATEL multicriteria model. Decis. Mak. Appl. Manag. Eng. 2018, 1, 121–130. [Google Scholar]
- Veskovic, S.; Stevic, e.; Stojic, G.; Vasiljevic, M.; Milinkovic, S. Evaluation of the railway management model by using a new integrated model DELPHI-SWARA-MABAC. Decis. Mak. Appl. Manag. Eng. 2018, 1, 34–50. [Google Scholar]
- Petrovic, I.B.; Kankaraš, M. DEMATEL-AHP multi-criteria decision-making model for the determination and evaluation of criteria for selecting an air traffic protection aircraft. Decis. Mak. Appl. Manag. Eng. 2018, 1, 93–110. [Google Scholar]
- Pape, T. Prioritising data items for business analytics: Framework and application to human resources. Eur. J. Oper. Res. 2016, 252, 687–698. [Google Scholar]
- Cid-López, A.; Hornos, M.J.; Carrasco, R.A.; Herrera-Viedma, E. Applying a linguistic multi-criteria decision-making model to the analysis of ICT suppliers’ offers. Expert Syst. Appl. 2016, 57, 127–138. [Google Scholar]
- Shen, J.; Lu, H.; Zhang, Y.; Song, X.; He, L. Vulnerability assessment of urban ecosystems driven by water resources, human health and atmospheric environment. J. Hydrol. 2016, 536, 457–470. [Google Scholar]
- Mansour, F.; Al-Hindi, M.; Saad, W.; Salam, D. Environmental risk analysis and prioritization of pharmaceuticals in a developing world context. Sci. Total Environ. 2016, 557, 31–43. [Google Scholar]
- Azarnivand, A.; Malekian, A. Analysis of flood risk management strategies based on a group decision-making process via interval-valued intuitionistic fuzzy numbers. Water Resour. Manag. 2016, 30, 1903–1921. [Google Scholar]
- Ruiz-Padillo, A.; Torija, A.J.; Ramos-Ridao, A.; Ruiz, D.P. Application of the fuzzy analytic hierarchy process in multi-criteria decision in noise action plans: Prioritizing road stretches. Environ. Model. Softw. 2016, 81, 45–55. [Google Scholar]
- Maimoun, M.; Madani, K.; Reinhart, D. Multi-level multi-criteria analysis of alternative fuels for waste collection vehicles in the United States. Sci. Total Environ. 2016, 550, 349–361. [Google Scholar]
- Kim, Y.; Chung, E.S. Assessing climate change vulnerability with group multi-criteria decision-making approaches. Clim. Chang. 2013, 121, 301–315. [Google Scholar]
- Potić, I.; Golić, R.; Joksimović, T. Analysis of insolation potential of Knjazevac Municipality (Serbia) using multi-criteria approach. Renew. Sustain. Energy Rev. 2016, 56, 235–245. [Google Scholar]
- Franco, C.; Bojesen, M.; Hougaard, J.L.; Nielsen, K. A fuzzy approach to a multiple criteria and Geographical Information System for decision support on suitable locations for biogas plants. Appl. Energy 2015, 140, 304–315. [Google Scholar]
- Schmitz, S.; McCullagh, L.; Adams, R.; Barry, M.; Walsh, C. Identifying and revealing the importance of decision-making criteria for health technology assessment: A retrospective analysis of reimbursement recommendations in Ireland. PharmacoEconomics 2016, 34, 925–937. [Google Scholar]
- Linkov, I.; Trump, B.; Jin, D.; Mazurczak, M.; Schreurs, M. A decision-analytic approach to predict state regulation of hydraulic fracturing. Environ. Sci. Eur. 2014, 26, 20. [Google Scholar]
- Cabrerizo, F.J.; Herrera-Viedma, E.; Pedrycz, W. A method based on PSO and granular computing of linguistic information to solve group decision-making problems defined in heterogeneous contexts. Eur. J. Oper. Res. 2013, 230, 624–633. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Cabrerizo, F.J.; Kacprzyk, J.; Pedrycz, W. A review of soft consensus models in a fuzzy environment. Inf. Fusion 2014, 17, 4–13. [Google Scholar] [CrossRef]
- Sahin, R.; Yigider, M. A Multi-criteria neutrosophic group decision-making method based TOPSIS for supplier selection. arXiv, 2014; arXiv:1412.5077. [Google Scholar]
- Wu, Z.; Xu, J. A consistency and consensus based decision support model for group decision-making with multiplicative preference relations. Decis. Support Syst. 2012, 52, 757–767. [Google Scholar]
- Saaty, T.L.; Vargas, L.G. Uncertainty and rank order in the analytic hierarchy process. Eur. J. Oper. Res. 1987, 32, 107–117. [Google Scholar]
- Saaty, T. A ratio scale metric and the compatibility of ratio scales: The possibility of arrow’s impossibility theorem. Appl. Math. Lett. 1994, 7, 45–49. [Google Scholar]
- Wang, L. Compatibility and group decision-making. Syst. Eng. Theory Pract. 2002, 20, 92–96. [Google Scholar]
- López-Morales, V. A Reliable Method for Consistency Improving of Interval Multiplicative Preference Relations Expressed under Uncertainty. Int. J. Inf. Technol. Decis. Mak. 2018. [Google Scholar] [CrossRef]
- López-Morales, V. Reliable Group Decision-Making under Uncertain Judgments. Int. Tech. Rep. 2018, 1, 1–30. [Google Scholar]
- Beale, E.M.L. Numerical Methods in: Nonlinear Programming; Abadie, J., Ed.; North-Holland: Amsterdam, The Netherlands, 1967. [Google Scholar]
- Kou, G.; Lin, C. A cosine maximization method for the priority vector derivation in AHP. Eur. J. Oper. Res. 2014, 235, 225–232. [Google Scholar]
- Saaty, T. Decision-making with the AHP: Why is the principal eigenvector necessary? Eur. J. Oper. Res. 2003, 145, 85–91. [Google Scholar]
- Crawford, G.; Williams, C. A note on the analysis of subjective judgement matrices. J. Math. Psychol. 1985, 29, 387–405. [Google Scholar]
- Meng, F.; Zeng, X.; Li, Z. Research the priority methods of interval numbers complementary judgment matrix. In Proceedings of the 2007 IEEE International Conference on Grey Systems and Intelligent Services, Nanjing, China, 18–20 November 2007. [Google Scholar]
- Meng, F.; Chen, X.; Zhu, M.; Lin, J. Two new methods for deriving the priority vector from interval multiplicative preference relations. Inf. Fusion 2015, 26, 122–135. [Google Scholar]
- Ye, F. An extended TOPSIS method with interval-valued intuitionistic fuzzy numbers for virtual enterprise partner selection. Expert Syst. Appl. 2010, 37, 7050–7055. [Google Scholar]
- Liu, F.; Zhang, W.G.; Shang, Y.F. A group decision-making model with interval multiplicative reciprocal matrices based on the geometric consistency index. J. Comput. Ind. Eng. 2016, 101, 184–193. [Google Scholar]


© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Morales, V. Multiple Criteria Decision-Making in Heterogeneous Groups of Management Experts. Information 2018, 9, 300. https://doi.org/10.3390/info9120300
López-Morales V. Multiple Criteria Decision-Making in Heterogeneous Groups of Management Experts. Information. 2018; 9(12):300. https://doi.org/10.3390/info9120300
Chicago/Turabian StyleLópez-Morales, Virgilio. 2018. "Multiple Criteria Decision-Making in Heterogeneous Groups of Management Experts" Information 9, no. 12: 300. https://doi.org/10.3390/info9120300
APA StyleLópez-Morales, V. (2018). Multiple Criteria Decision-Making in Heterogeneous Groups of Management Experts. Information, 9(12), 300. https://doi.org/10.3390/info9120300



