Taylor Polynomials in a High Arithmetic Precision as Universal Approximators
Abstract
:1. Introduction
2. Description of the Method
3. Function Approximation in HAP
3.1. Basic Operations
3.2. Function Approximation
3.3. Extrapolation
3.4. Numerical Integration
3.5. Numerical Differentiation
3.6. Solution of Ordinary Differential Equations (ODEs)
3.7. System Identification
4. Functions in Multiple Dimensions
4.1. Multidimensional Interpolation
4.2. Solution of Partial Differential Equations
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| x | Variable x, corresponding to |
| Initial point in the approximation | |
| n | Number of terms in the Taylor series, also number of nodes |
| L | Length of the given domain |
| E | Modulus of elasticity |
| I | Inertia of the beam |
| Analytic function | |
| Vector of function values | |
| Vector of points | |
| r | Radius of convergence |
| Vandermonde matrix | |
| Vector of the derivatives of the function | |
| D | Flexural rigidity of plate |
| w | Deflection of the beam/plate |
| q | External load of beam/plate |
| Coefficient vector for Taylor polynomials | |
| v | Poisson constant |
| h | Slab’s thickness |
References
- Bakas, N.P. Numerical Solution for the Extrapolation Problem of Analytic Functions. Research 2019, 2019, 3903187. [Google Scholar] [CrossRef]
- Bailey, D.H.; Jeyabalan, K.; Li, X.S. A comparison of three high-precision quadrature schemes. Exp. Math. 2005, 14, 317–329. [Google Scholar] [CrossRef]
- Cheng, A.H. Multiquadric and its shape parameter—A numerical investigation of error estimate, condition number, and round-off error by arbitrary precision computation. Eng. Anal. Bound. Elem. 2012, 36, 220–239. [Google Scholar] [CrossRef]
- Huang, C.S.; Lee, C.F.; Cheng, A.H. Error estimate, optimal shape factor, and high precision computation of multiquadric collocation method. Eng. Anal. Bound. Elem. 2007, 31, 614–623. [Google Scholar] [CrossRef]
- Sharma, N.N.; Jain, R.; Pokkuluri, M.M.; Patkar, S.B.; Leupers, R.; Nikhil, R.S.; Merchant, F. CLARINET: A quire-enabled RISC-V-based framework for posit arithmetic empiricism. J. Syst. Archit. 2023, 135, 102801. [Google Scholar] [CrossRef]
- Lei, X.; Gu, T.; Xu, X. ddRingAllreduce: A high-precision RingAllreduce algorithm. CCF Trans. High Perform. Comput. 2023, 5, 245–257. [Google Scholar] [CrossRef]
- Wu, C.; Xia, Y.; Xu, Z.; Liu, L.; Tang, X.; Chen, Q.; Xu, F. Mathematical modelling for high precision ray tracing in optical design. Appl. Math. Model. 2024, 128, 103–122. [Google Scholar] [CrossRef]
- Friebel, K.F.A.; Bi, J.; Castrillon, J. Base2: An IR for Binary Numeral Types. In Proceedings of the 13th International Symposium on Highly Efficient Accelerators and Reconfigurable Technologies, Kusatsu, Japan, 14–16 June 2023; pp. 19–26. [Google Scholar] [CrossRef]
- Granlund, T. The GNU Multiple Precision Arithmetic Library. Free Softw. Found. Available online: https://gmplib.org/ (accessed on 13 January 2024).
- Amato, G.; Scozzari, F. JGMP: Java bindings and wrappers for the GMP library. SoftwareX 2023, 23, 101428. [Google Scholar] [CrossRef]
- Guessab, A.; Nouisser, O.; Schmeisser, G. Multivariate approximation by a combination of modified Taylor polynomials. J. Comput. Appl. Math. 2006, 196, 162–179. [Google Scholar] [CrossRef]
- Kalantari, B. Generalization of Taylor’s theorem and Newton’s method via a new family of determinantal interpolation formulas and its applications. J. Comput. Appl. Math. 2000, 126, 287–318. [Google Scholar] [CrossRef]
- Berz, M.; Makino, K. Verified Integration of ODEs and Flows Using Differential Algebraic Methods on High-Order Taylor Models. Reliab. Comput. 1998, 10, 361–369. [Google Scholar] [CrossRef]
- Yalçinbaş, S.; Sezer, M. The approximate solution of high-order linear Volterra-Fredholm integro-differential equations in terms of Taylor polynomials. Appl. Math. Comput. 2000, 112, 291–308. [Google Scholar] [CrossRef]
- Ranjan, R.; Prasad, H.S. A novel approach for the numerical approximation to the solution of singularly perturbed differential-difference equations with small shifts. J. Appl. Math. Comput. 2021, 65, 403–427. [Google Scholar] [CrossRef]
- Platte, R.B.; Trefethen, L.N.; Kuijlaars, A.B.J. Impossibility of Fast Stable Approximation of Analytic Functions from Equispaced Samples. SIAM Rev. 2011, 53, 308–318. [Google Scholar] [CrossRef]
- Boyd, J.P. Defeating the Runge phenomenon for equispaced polynomial interpolation via Tikhonov regularization. Appl. Math. Lett. 1992, 5, 57–59. [Google Scholar] [CrossRef]
- Zhang, S.Q.; Fu, C.H.; Zhao, X.D. Study of regional geomagnetic model of Fujian and adjacent areas based on 3D Taylor Polynomial model. Acta Geophys. Sin. 2016, 59, 1948–1956. [Google Scholar] [CrossRef]
- Boyd, J.P.; Xu, F. Divergence (Runge Phenomenon) for least-squares polynomial approximation on an equispaced grid and Mock-Chebyshev subset interpolation. Appl. Math. Comput. 2009, 210, 158–168. [Google Scholar] [CrossRef]
- Boyd, J.P.; Ong, J.R. Exponentially-convergent strategies for defeating the runge phenomenon for the approximation of non-periodic functions, part I: Single-interval schemes. Commun. Comput. Phys. 2009, 5, 484–497. [Google Scholar]
- Taylor, B. Principles of Linear Perspective; Knaplock, R., Ed.; British Library: London, UK, 1715. [Google Scholar]
- Babouskos, N.G.; Katsikadelis, J.T. Optimum design of thin plates via frequency optimization using BEM. Arch. Appl. Mech. 2015, 85, 1175–1190. [Google Scholar] [CrossRef]
- Yiotis, A.J.; Katsikadelis, J.T. Buckling of cylindrical shell panels: A MAEM solution. Arch. Appl. Mech. 2015, 85, 1545–1557. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Apostol, T.M. Calculus; John Wiley & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- Browder, A. Mathematical Analysis: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Katsoprinakis, E.S.; Nestoridis, V.N. Partial sums of Taylor series on a circle. Ann. L’Institut Fourier 2011, 39, 715–736. [Google Scholar] [CrossRef]
- Nestoridis, V. Universal Taylor series. Ann. de L’Institut Fourier 2011, 46, 1293–1306. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A. VWT, and FBP, Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Topics in Matrix Analysis; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Ycart, B. A case of mathematical eponymy: The Vandermonde determinant. arXiv 2012, arXiv:1204.4716. [Google Scholar] [CrossRef]
- Turner, L.R. Inverse of the Vandermonde Matrix with Applications; NASA–TN D-3547; NASA: Washington, DC, USA, 1966.
- Demanet, L.; Townsend, A. Stable extrapolation of analytic functions. Found. Comput. Math. 2019, 19, 297–331. [Google Scholar] [CrossRef]
- Boresi, A.P.; Sidebottom, O.M.; Saunders, H. Advanced Mechanics of Materials (4th Ed.). J. Vib. Acoust. Stress Reliab. Des. 1988, 110, 256–257. [Google Scholar] [CrossRef]
- Katsikadelis, J.T. System identification by the analog equation method. WIT Trans. Model. Simul. 1995, 10, 12. [Google Scholar]
- Katsikadelis, J.T. The Boundary Element Method for Plate Analysis; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Gregory, F.H. Arithmetic and Reality: A Development of Popper’s Ideas. Philos. Math. Educ. J. 2011, 26. [Google Scholar]
- Fousse, L.; Hanrot, G.; Lefèvre, V.; Pélissier, P.; Zimmermann, P. MPFR: A multiple-precision binary floating-point library with correct rounding. ACM Trans. Math. Softw. 2007, 33, 2. [Google Scholar] [CrossRef]


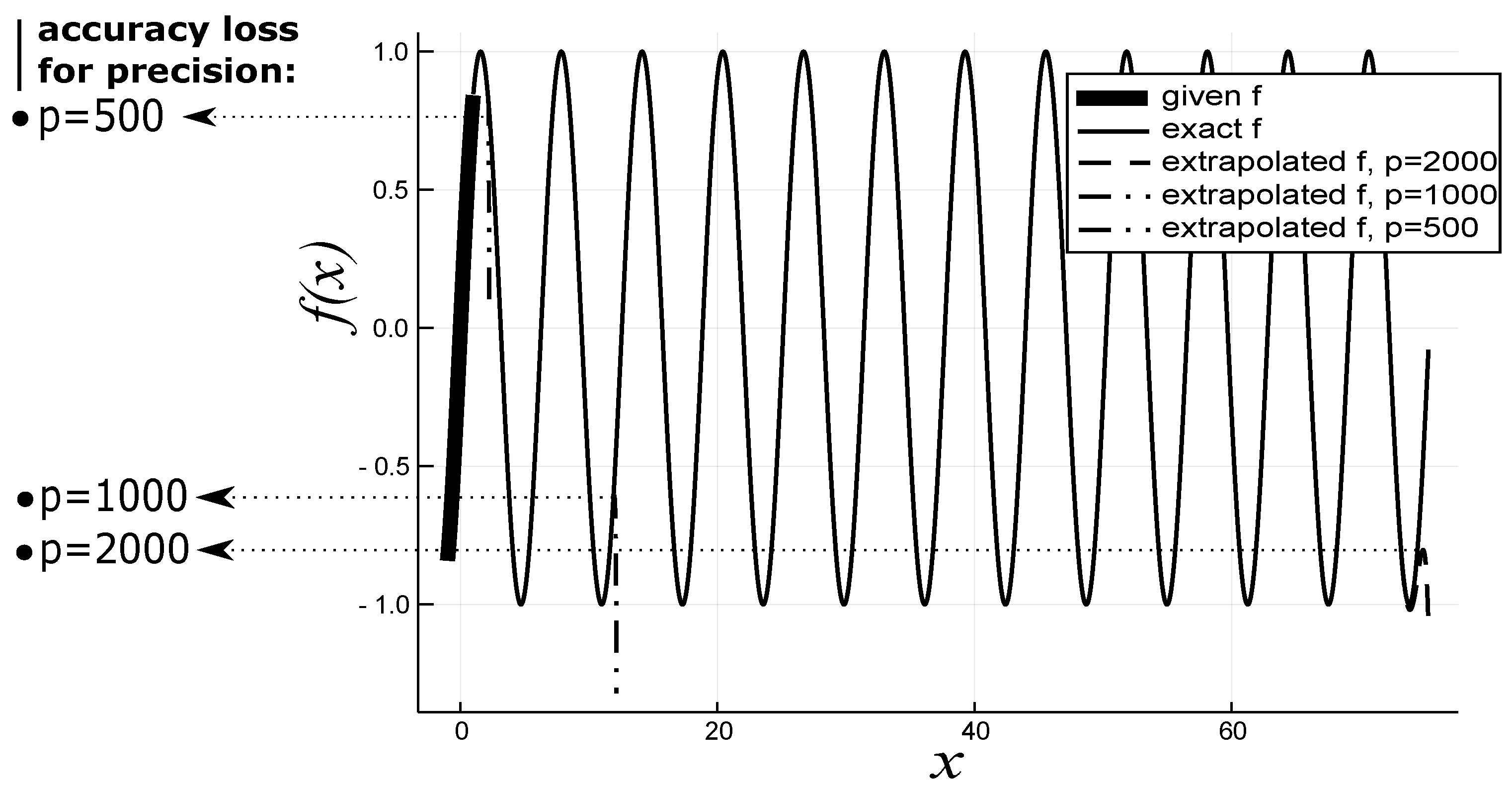
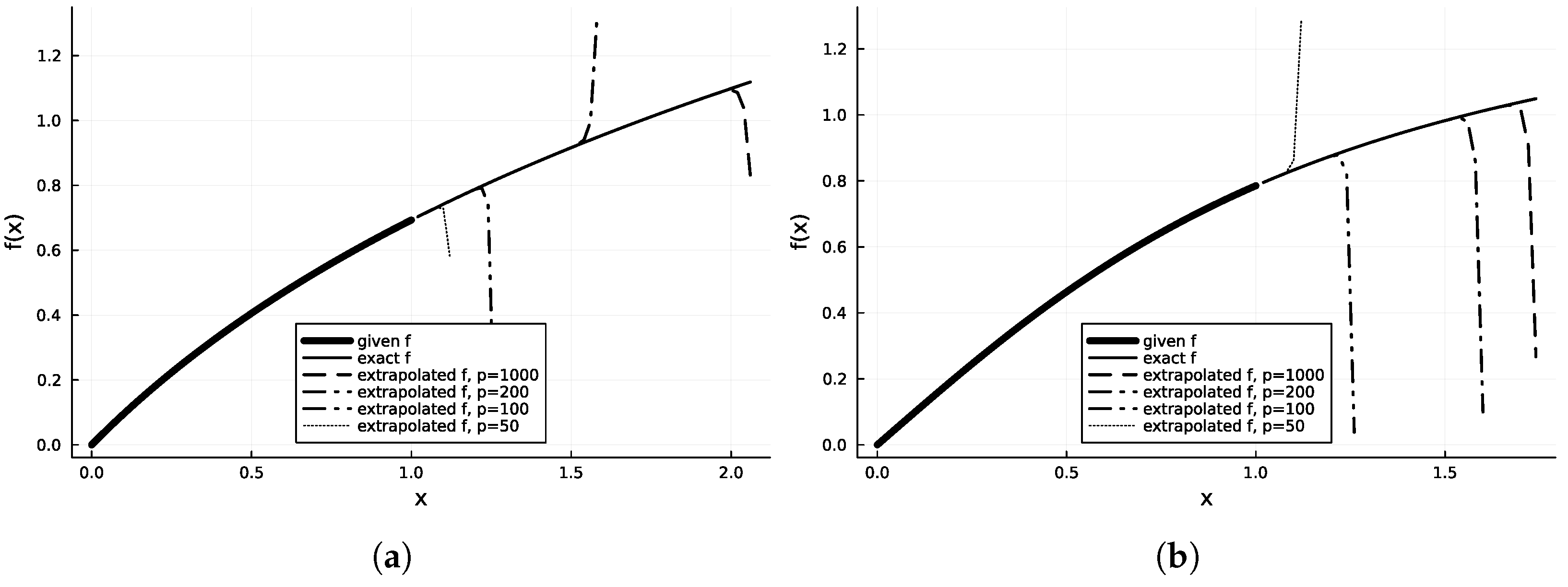


| Error vs. Precision (p) | |||||
|---|---|---|---|---|---|
| Error vs. Precision (p) | |||||
|---|---|---|---|---|---|
| Error vs. Precision (p) | |||||
|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakas, N. Taylor Polynomials in a High Arithmetic Precision as Universal Approximators. Computation 2024, 12, 53. https://doi.org/10.3390/computation12030053
Bakas N. Taylor Polynomials in a High Arithmetic Precision as Universal Approximators. Computation. 2024; 12(3):53. https://doi.org/10.3390/computation12030053
Chicago/Turabian StyleBakas, Nikolaos. 2024. "Taylor Polynomials in a High Arithmetic Precision as Universal Approximators" Computation 12, no. 3: 53. https://doi.org/10.3390/computation12030053
APA StyleBakas, N. (2024). Taylor Polynomials in a High Arithmetic Precision as Universal Approximators. Computation, 12(3), 53. https://doi.org/10.3390/computation12030053






