Development and Verification of Coupled Fluid–Structure Interaction Solver
Abstract
:1. Introduction
2. Numerical Methods
2.1. Fluid Solver
2.2. Structure Solver
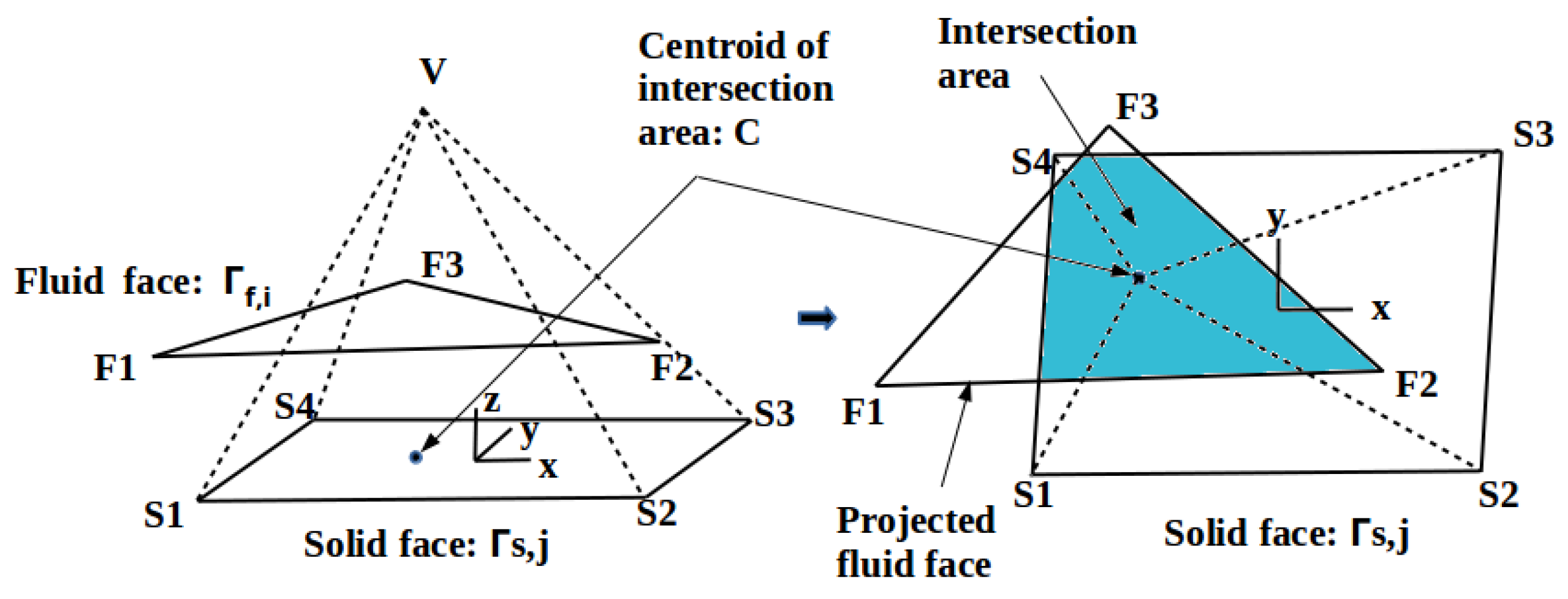
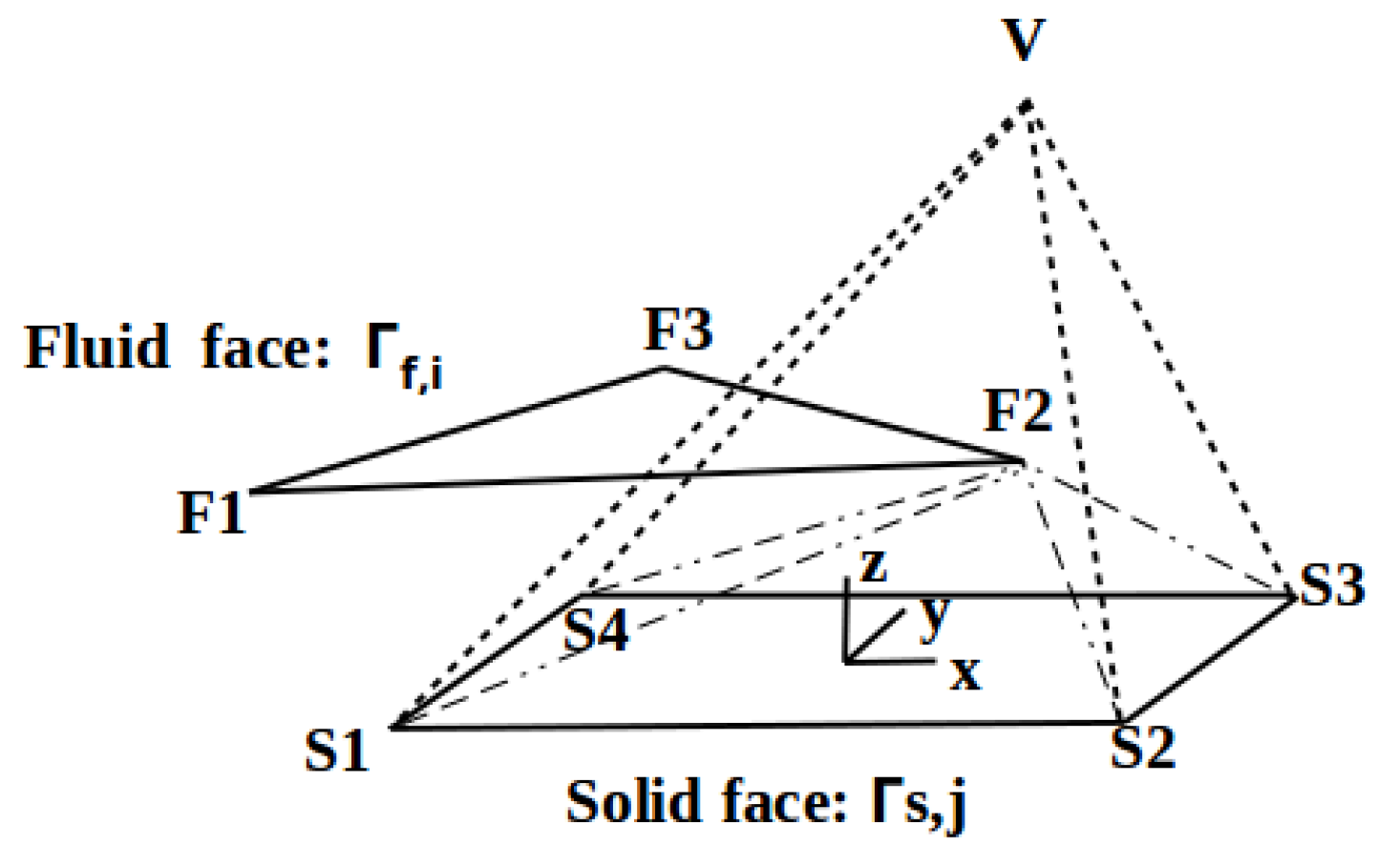
2.3. Coupling Algorithm
3. Computational Setup
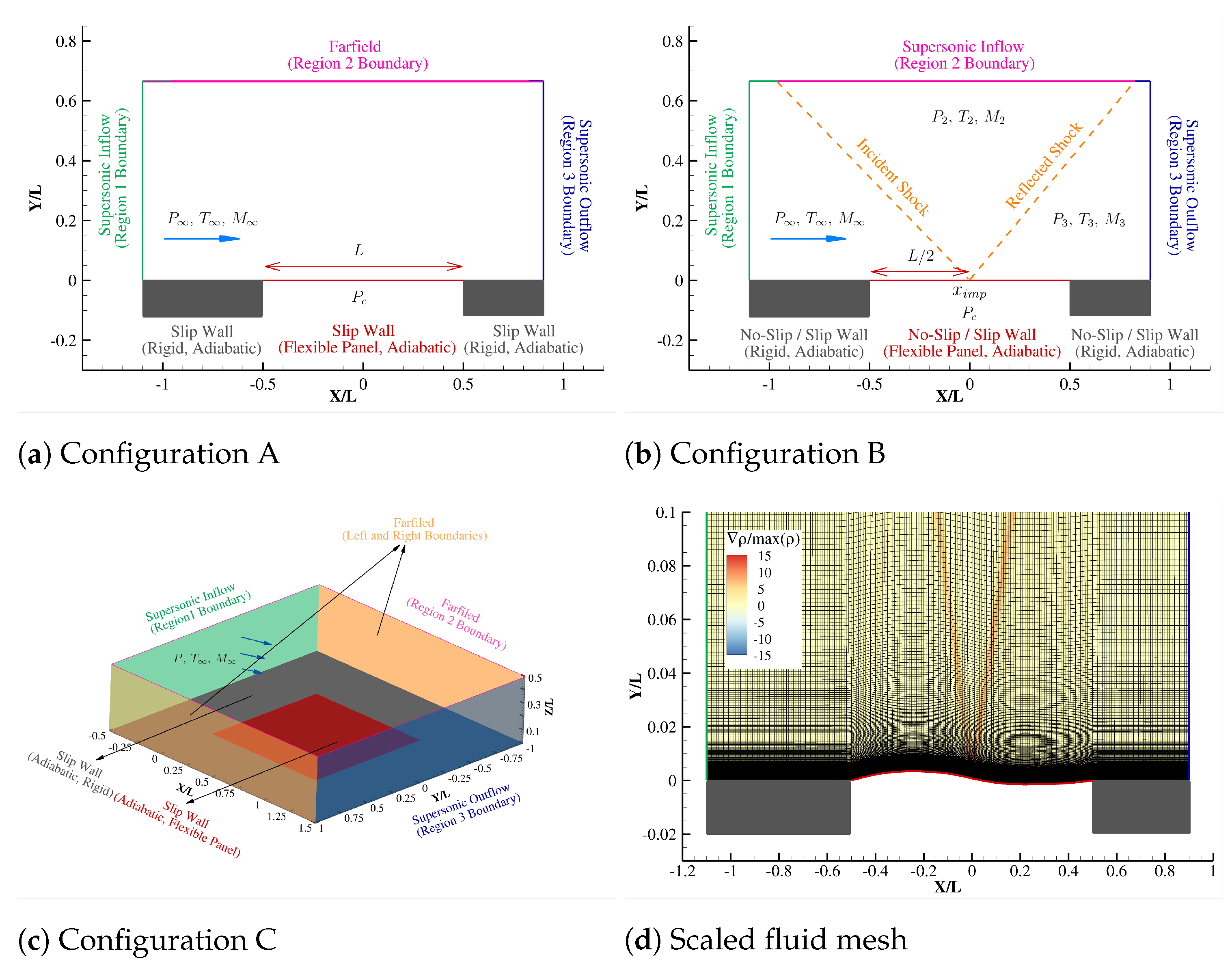
3.1. Problem Description
3.2. Domain and Grids
3.3. Simulation Conditions
3.4. Initial and Boundary Conditions
| Case | Flow Parameters | Structural Parameters | FSI Parameters | Grid Size | Time Step | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | [kg/m3] | [GPa], | Fluid | Structure | [s] | |||||||||||
| 1 | 2D Uniform Flow 1 | Inviscid | to | - | - | - | - | 0 | 2700 | 72, | 30 to 3000 | 35 K | 50 | 1 | ||
| to | 2 to 880 | |||||||||||||||
| 2 | 2D Oblique Shock 2 | Inviscid | - | - | , , , | - | 72, | 100 to 875 | 70 K | 50, 70, 100 | 1 | |||||
| 3 | Laminar 3 | , | 875 | 35 K | 50 | 4, 2, 1, , | ||||||||||
| 49 K | 70 | |||||||||||||||
| 70 K | 100 | |||||||||||||||
| 98 K | 140 | |||||||||||||||
| 140 K | 200 | |||||||||||||||
| 4 | 3D Uniform flow 4 | Inviscid | - | - | - | - | 1 | 500 to 3000 | 265 K | 1 | ||||||
4. Convergence Study
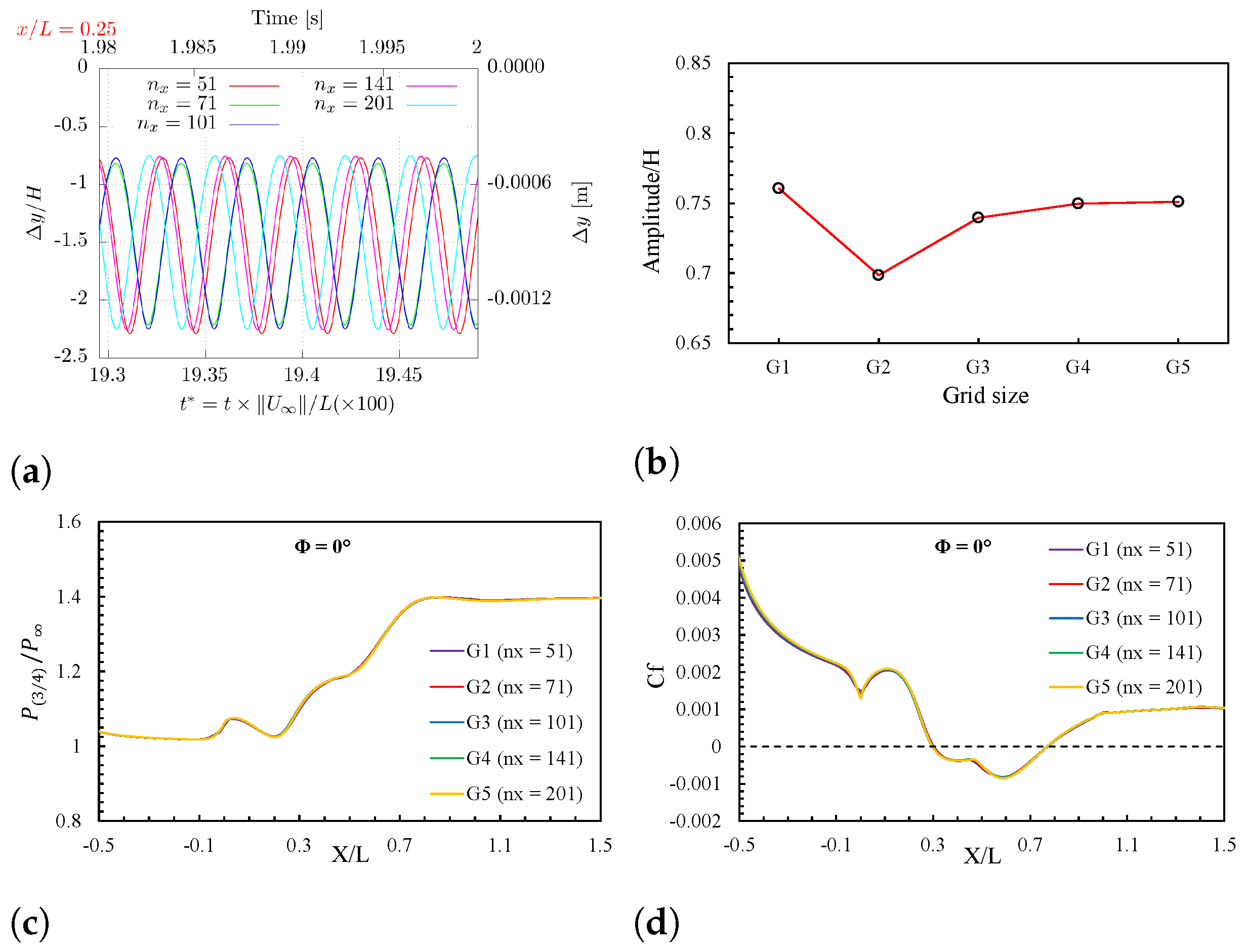
4.1. Grid Convergence Study
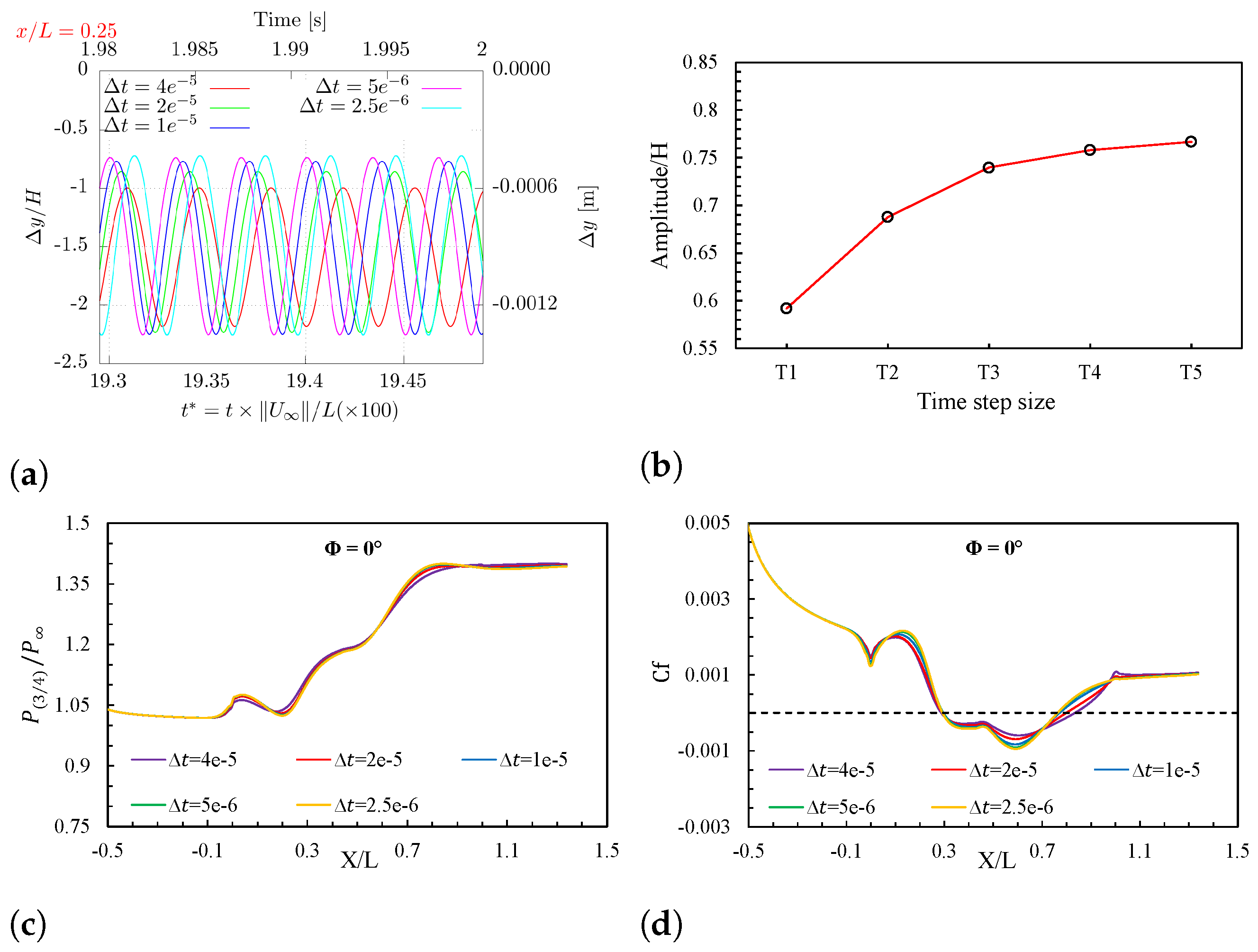
4.2. Time Independence Study
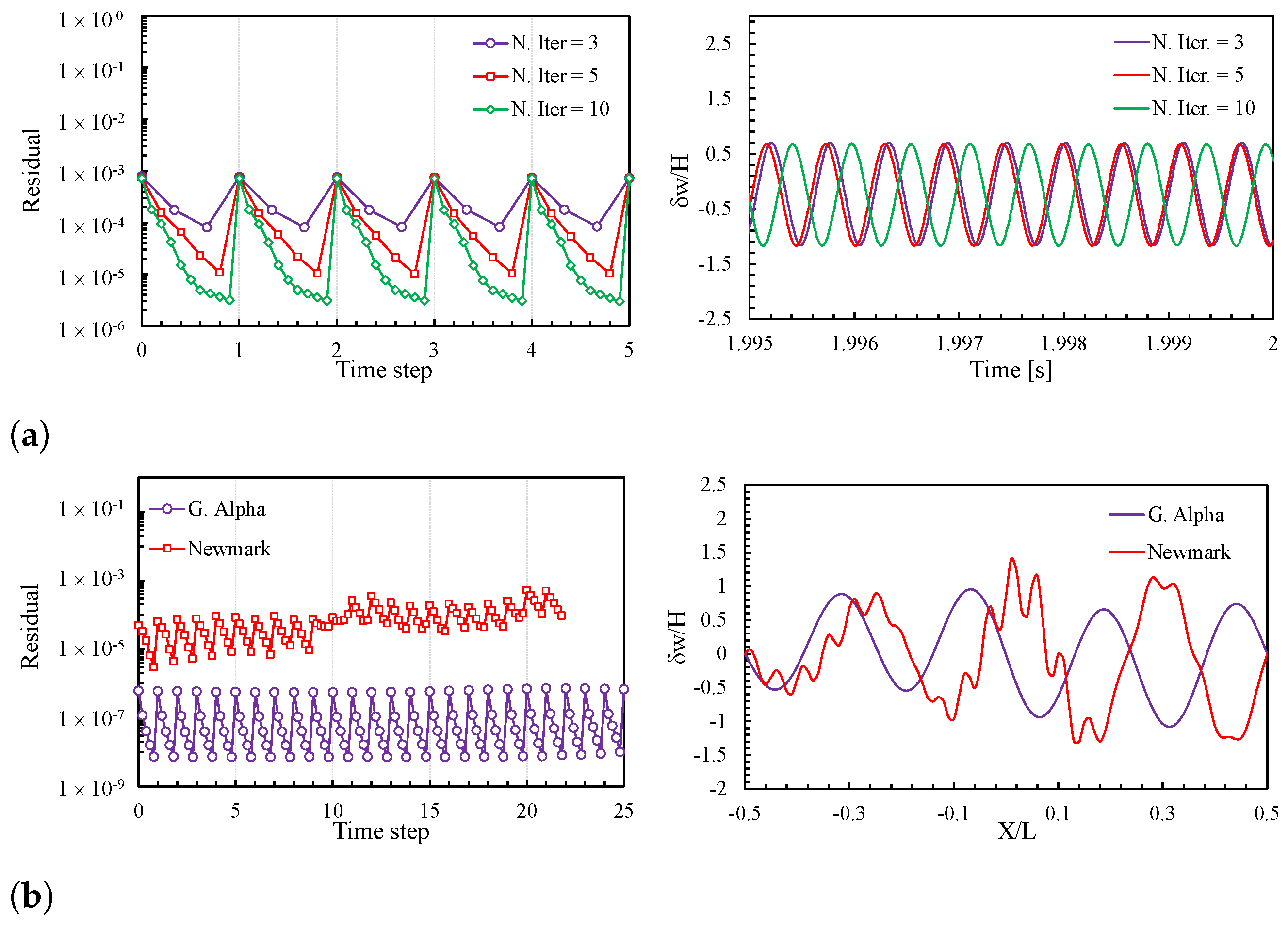
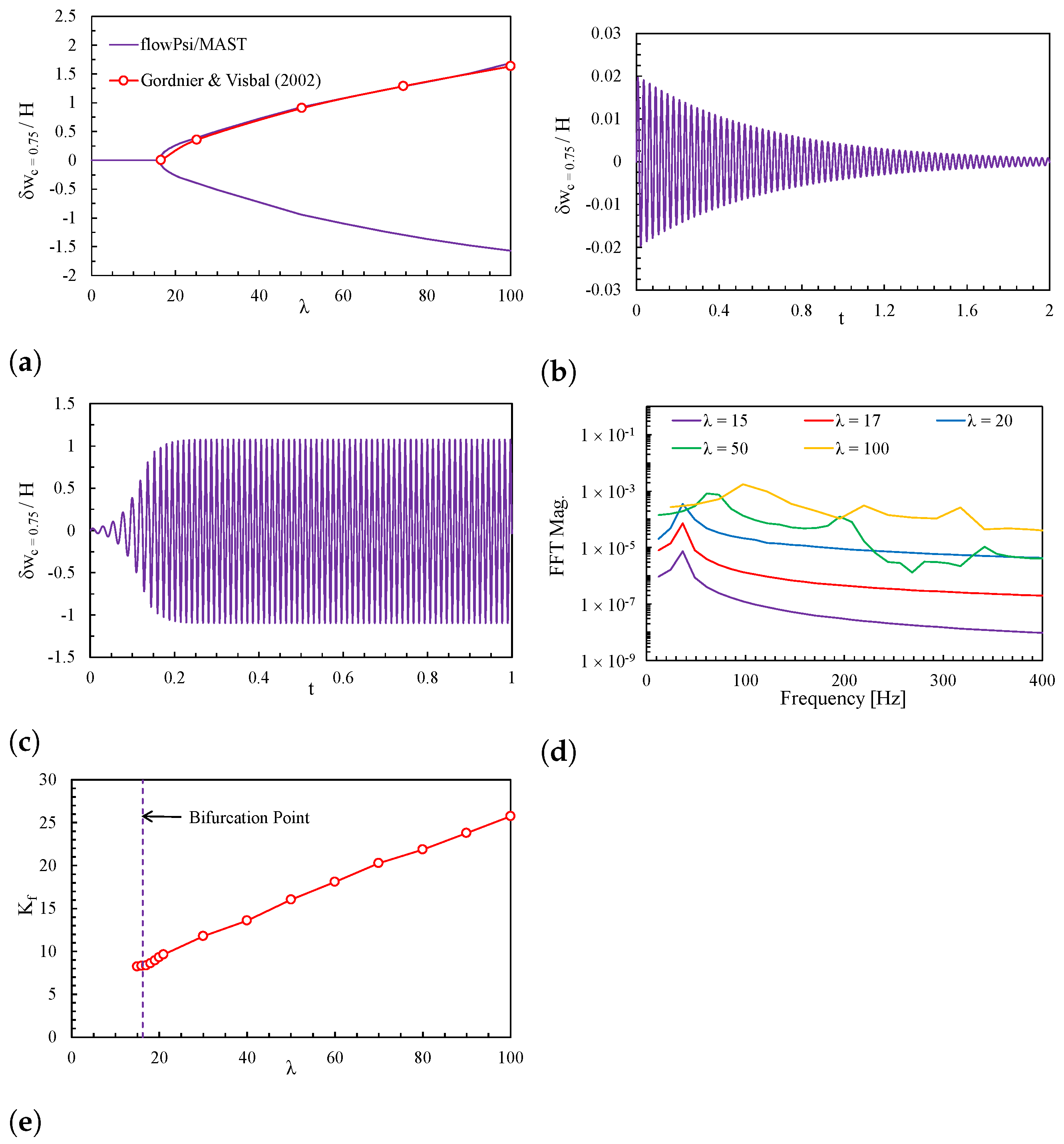
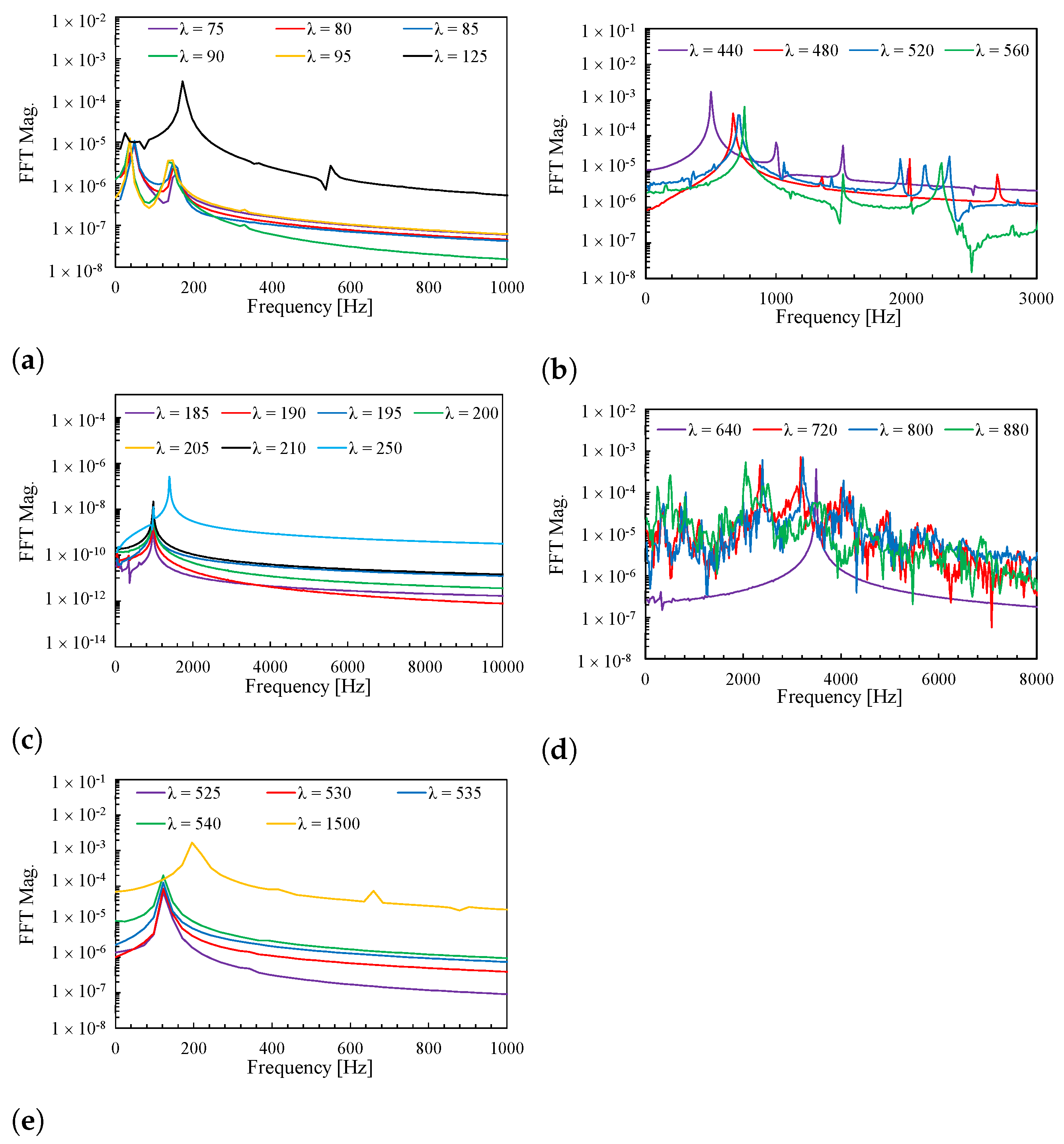
4.3. Stability of the FSI Solver
5. Results and Discussion
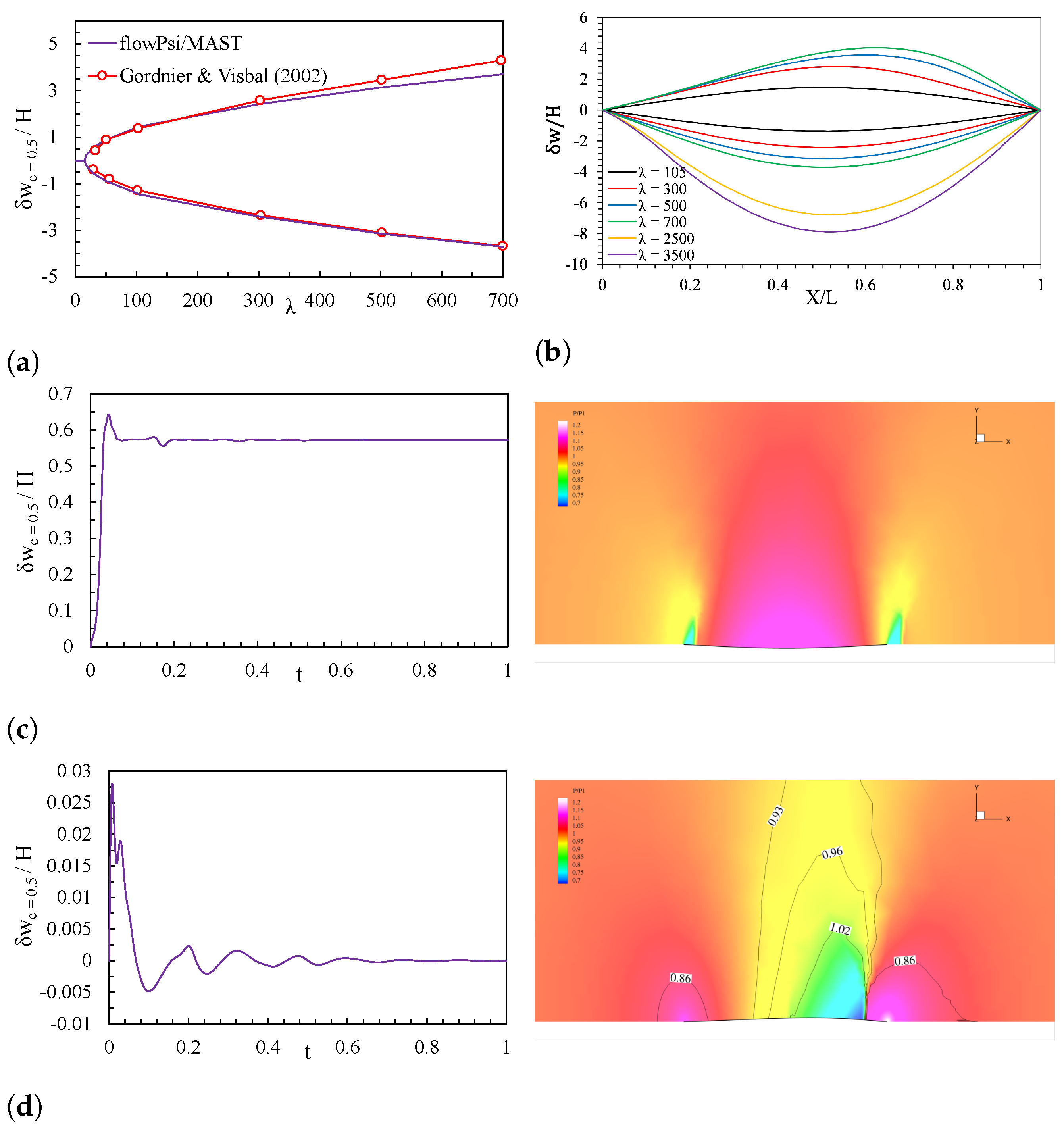
5.1. Configuration A: Uniform Flow (Set # 1)
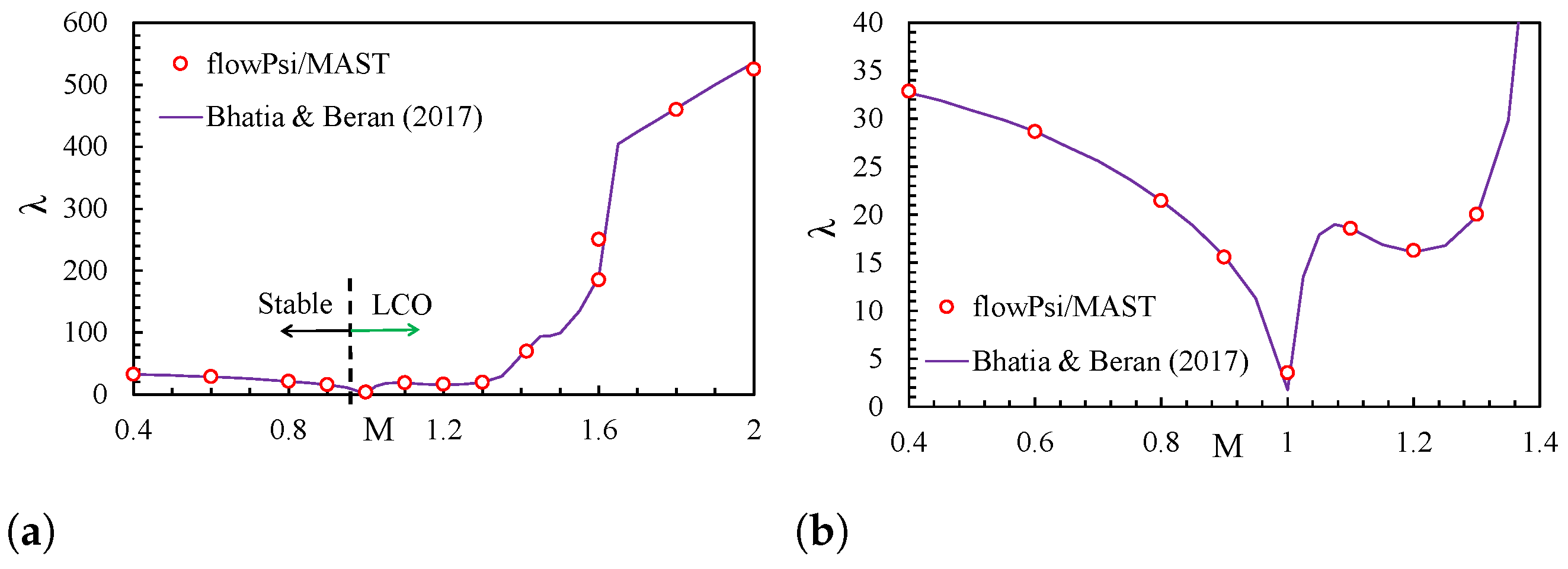
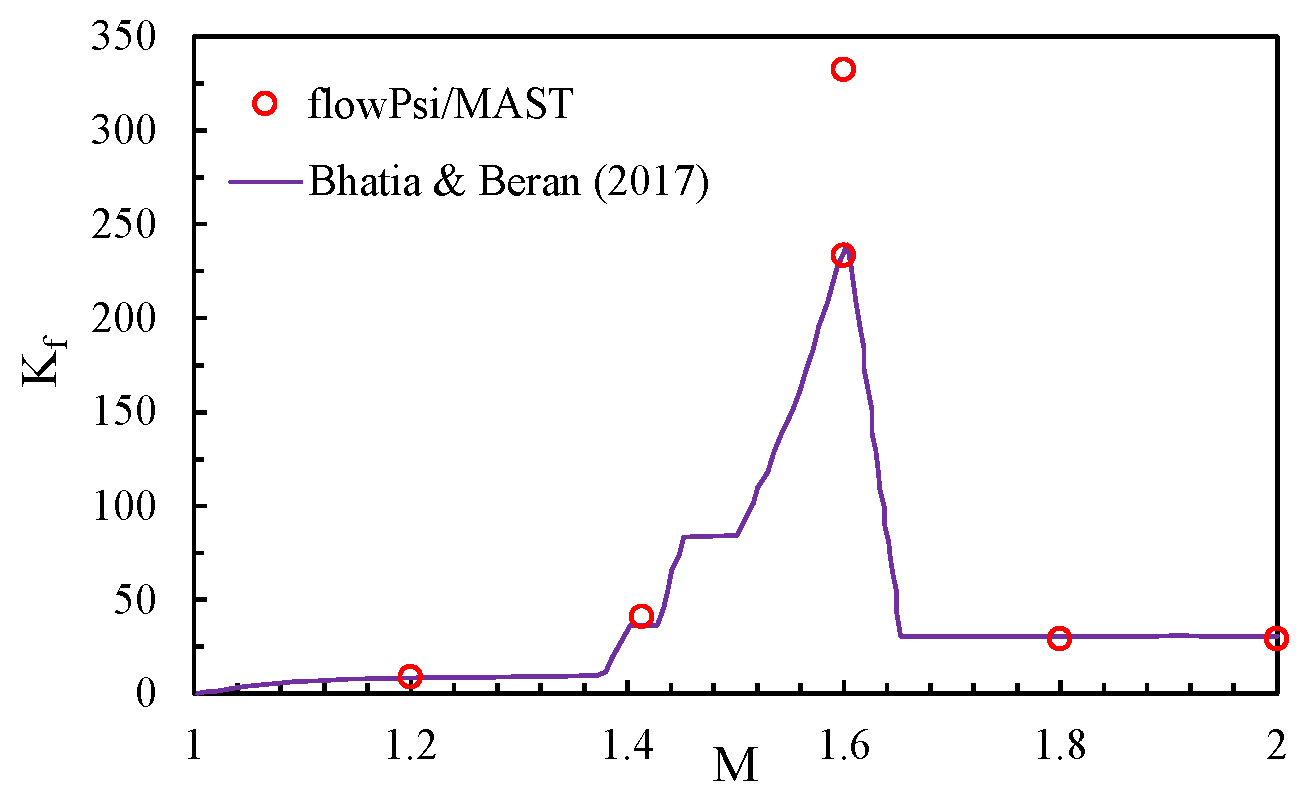
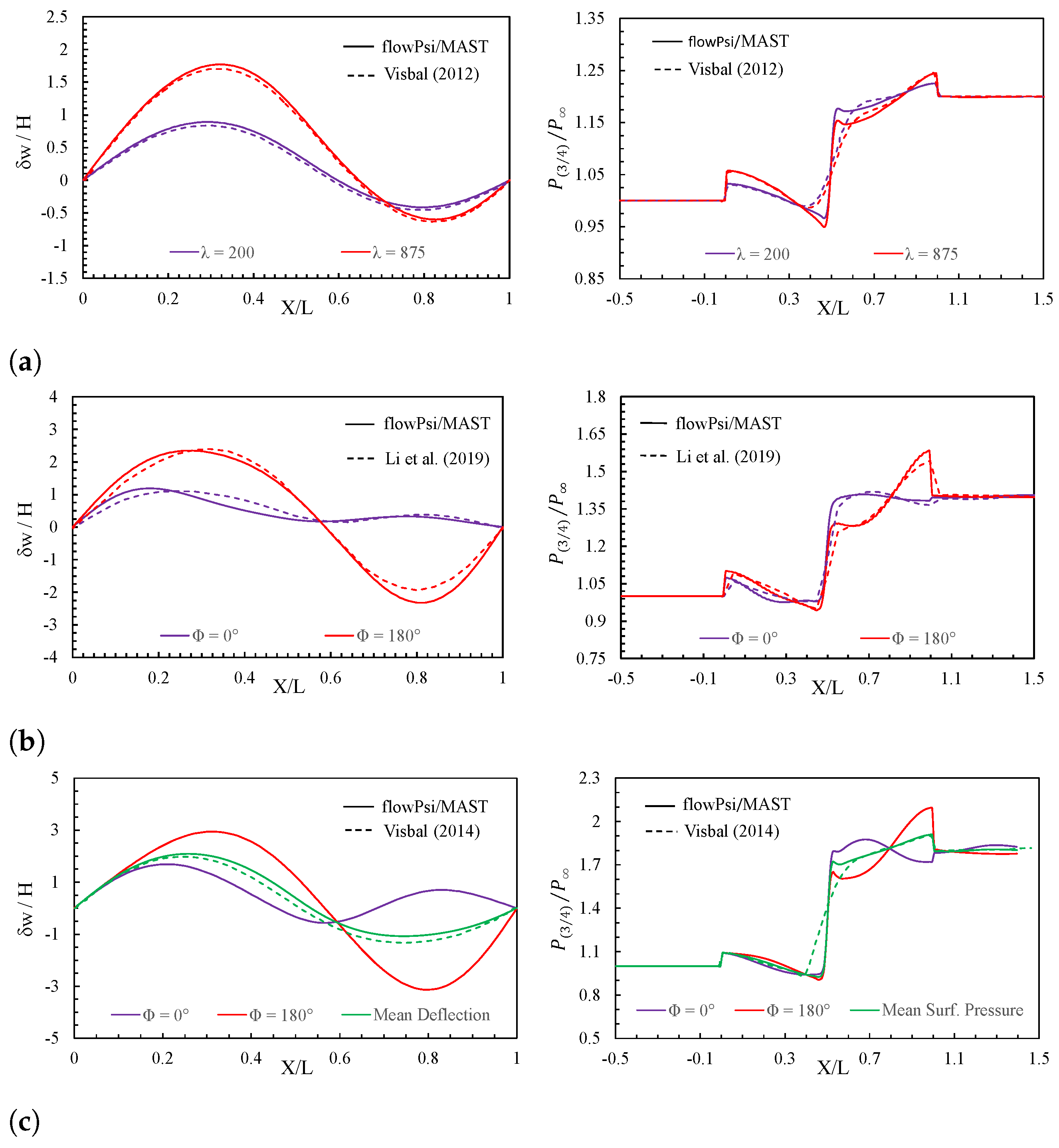
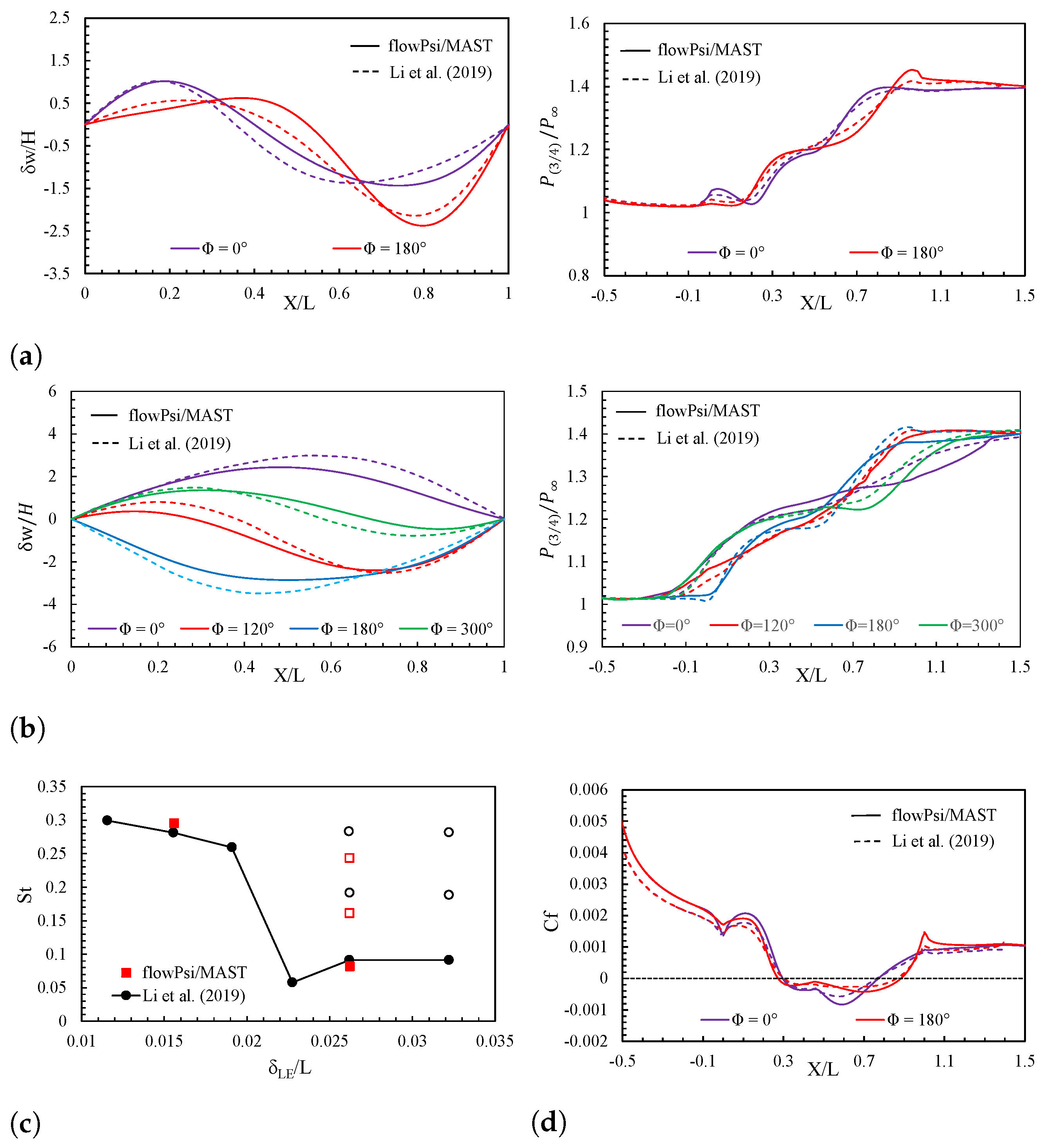
5.2. Configuration B: Supersonic Flow with Oblique Shock Wave
5.3. Configuration C: 3D Supersonic Uniform Flow (Set # 4)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| u | Fluid velocity [m/s] |
| T | Fluid temperature [K] |
| P | Fluid pressure [Pa] |
| Fluid density [kg/m3] | |
| Free stream fluid velocity [m/s] | |
| Free stream fluid temperature [K] | |
| Free stream fluid pressure [Pa] | |
| Free stream fluid density [kg/m3] | |
| Specific heat ratio | |
| R | Fluid specific gas constant [J/kg-K] |
| a | Speed of sound in the fluid [m/s] |
| Fluid specific heat at constant pressure [J/kg-K] | |
| Fluid dynamic viscosity [Pa-s] | |
| Fluid kinematic viscosity [m2/s] | |
| k | Fluid thermal conductivity [W/m-K] |
| M | Fluid Mach number |
| Prandtl number | |
| Reynold’s number , where is reference length | |
| Boundary layer thickness [m] | |
| Wall shear stress at a no-slip wall in the fluid domain | |
| Skin friction coefficient at no-slip walls in the fluid domain | |
| Solid temperature [K] | |
| Young’s modulus of the panel material [Pa] | |
| Poisson’s ratio of the panel material | |
| Structure thermal heat capacity [J/kg-K] | |
| Density of the panel material [kg/m3] | |
| H | Panel thickness [m] |
| L | Panel streamwise length [m] |
| D | Panel flexural rigidity [Pa-m3] |
| Panel deflection [m] | |
| f | Frequency [Hz] |
| Nondimensional frequency | |
| St | Strouhal number |
| Mass ratio | |
| Non-dimensional dynamic pressure | |
| Fluid freestream property | |
| Fluid stagnation property | |
| Fluid filtered quantity | |
| Fluid Favre averaged quantity [40] |
Appendix A. Fluid-Structure Coupling Algorithm

References
- Collar, A. The expanding domain of aeroelasticity. Aeronaut. J. 1946, 50, 613–636. [Google Scholar] [CrossRef]
- Costanzo, A. Experimental Investigation of Shock Wave-Boundary Layer Interaction on a Generic Oscillating Bump; KTH Industrial Engineering and Management: Stockholm, Sweden, 2014. [Google Scholar]
- Dowell, E.H. Panel flutter-A review of the aeroelastic stability of plates and shells. AIAA J. 1970, 8, 385–399. [Google Scholar] [CrossRef]
- Mei, C.; Abdel-Motagaly, K.; Chen, R. Review of nonlinear panel flutter at supersonic and hypersonic speeds. Appl. Mech. Rev. 1999, 52, 321–332. [Google Scholar] [CrossRef]
- Ganji, H.F.; Dowell, E.H. Panel flutter prediction in two dimensional flow with enhanced piston theory. J. Fluids Struct. 2016, 63, 97–102. [Google Scholar] [CrossRef]
- Brouwer, K.R.; McNamara, J.J. Enriched Piston Theory for Expedient Aeroelastic Loads Prediction in the Presence of Shock Impingements. AIAA J. 2019, 57, 1288–1302. [Google Scholar] [CrossRef]
- Chai, Y.; Gao, W.; Ankay, B.; Li, F.; Zhang, C. Aeroelastic analysis and flutter control of wings and panels: A review. Int. J. Mech. Syst. Dyn. 2021, 1, 5–34. [Google Scholar] [CrossRef]
- Panchal, J.; Benaroya, H. Review of control surface freeplay. Prog. Aerosp. Sci. 2021, 127, 100729. [Google Scholar] [CrossRef]
- Antimirova, E.; Jung, J.; Zhang, Z.; Machuca, A.; Gu, G.X. Overview of Computational Methods to Predict Flutter in Aircraft. J. Appl. Mech. 2024, 91, 050801. [Google Scholar] [CrossRef]
- Christian, M.; Steven J, H.; E, H.v.B.; Rene, d.B. A monolithic approach to fluid–structure interaction. Comput. Fluids 2004, 33, 839–848. [Google Scholar]
- Meduri, S.; Cremonesi, M.; Perego, U.; Bettinotti, O.; Kurkchubasche, A.; Oancea, V. A partitioned fully explicit Lagrangian finite element method for highly nonlinear fluid–structure interaction problems. Int. J. Numer. Methods Eng. 2018, 113, 43–64. [Google Scholar] [CrossRef]
- Davis, G.; Bendiksen, O. Transonic panel flutter. In Proceedings of the 34th Structures, Structural Dynamics and Materials Conference, La Jolla, CA, USA, 19–22 April 1993; p. 1476. [Google Scholar]
- Lee-Rausch, E.M.; Batina, J.T. Wing flutter boundary prediction using unsteady Euler aerodynamic method. J. Aircr. 1995, 32, 416–422. [Google Scholar] [CrossRef]
- Chen, X.; Zha, G.C.; Yang, M.T. Numerical simulation of 3-D wing flutter with fully coupled fluid-structural interaction. Comput. Fluids 2007, 36, 856–867. [Google Scholar] [CrossRef]
- Visbal, M. On the interaction of an oblique shock with a flexible panel. J. Fluids Struct. 2012, 30, 219–225. [Google Scholar] [CrossRef]
- Shishaeva, A.; Vedeneev, V.; Aksenov, A. Nonlinear single-mode and multi-mode panel flutter oscillations at low supersonic speeds. J. Fluids Struct. 2015, 56, 205–223. [Google Scholar] [CrossRef]
- Bhatia, M.; Beran, P. Transonic panel flutter predictions using a linearized stability formulation. AIAA J. 2017, 55, 3499–3516. [Google Scholar] [CrossRef]
- Boyer, N.R.; McNamara, J.; Gaitonde, D.; Barnes, C.J.; Visbal, M.R. Features of shock-induced panel flutter in three-dimensional inviscid flow. J. Fluids Struct. 2018, 83, 490–506. [Google Scholar] [CrossRef]
- Gordnier, R.E.; Visbal, M.R. Development of a three-dimensional viscous aeroelastic solver for nonlinear panel flutter. J. Fluids Struct. 2002, 16, 497–527. [Google Scholar] [CrossRef]
- Gordnier, R.E.; Visbal, M.R. Computation of three-dimensional nonlinear panel flutter. J. Aerosp. Eng. 2003, 16, 155–166. [Google Scholar] [CrossRef]
- Vedeneev, V. Interaction of panel flutter with inviscid boundary layer instability in supersonic flow. J. Fluid Mech. 2013, 736, 216–249. [Google Scholar] [CrossRef]
- Ostoich, C.M.; Bodony, D.J.; Geubelle, P.H. Interaction of a Mach 2.25 turbulent boundary layer with a fluttering panel using direct numerical simulation. Phys. Fluids 2013, 25, 110806. [Google Scholar] [CrossRef]
- Li, Y.; Luo, H.; Chen, X.; Xu, J. Laminar boundary layer separation over a fluttering panel induced by an oblique shock wave. J. Fluids Struct. 2019, 90, 90–109. [Google Scholar] [CrossRef]
- Boyer, N.R.; McNamara, J.; Gaitonde, D.; Barnes, C.J.; Visbal, M.R. Features of panel flutter response to shock boundary layer interactions. J. Fluids Struct. 2021, 101, 103207. [Google Scholar] [CrossRef]
- Shinde, V.; McNamara, J.J.; Gaitonde, D.V.; Barnes, C.J.; Visbal, M.R. Panel Flutter Induced by Transitional Shock Wave Boundary Layer Interaction. In Proceedings of the 2018 Fluid Dynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3548. [Google Scholar]
- Shinde, V.J.; McNamara, J.J.; Gaitonde, D.V. Shock wave turbulent boundary layer interaction over a flexible panel. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 and 19–21 January 2021; p. 0488. [Google Scholar]
- Cavagna, L.; Quaranta, G.; Mantegazza, P. Application of Navier–Stokes simulations for aeroelastic stability assessment in transonic regime. Comput. Struct. 2007, 85, 818–832. [Google Scholar] [CrossRef]
- Ozcatalbas, M.; Acar, B.; Uslu, S. Investigation of Aeroelastic Stability on AGARD 445.6 Wing at Transonic Regime. In Proceedings of the 2018 9th International Conference on Mechanical and Aerospace Engineering (ICMAE), Budapest, Hungary, 10–13 July 2018; pp. 565–569. [Google Scholar]
- Wang, J. Transonic static aeroelastic and longitudinal aerodynamic characteristics of a low-aspect-ratio swept wing. AIP Adv. 2019, 9, 045203. [Google Scholar] [CrossRef]
- Im, H.; Chen, X.; Zha, G. Prediction of a supersonic wing flutter boundary using a high fidelity detached eddy simulation. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; p. 39. [Google Scholar]
- Gan, J.; Zha, G. Delayed Detached Eddy Simulation of Supersonic Panel Aeroelasticity Using Fully Coupled Fluid Structure Interaction with High Order Schemes. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 4046. [Google Scholar]
- Luke, E.; Cinnella, P. Numerical simulations of mixtures of fluids using upwind algorithms. Comput. Fluids 2007, 36, 1547–1566. [Google Scholar] [CrossRef]
- Bhatia, M.; Beran, P.S. MAST: An Open-Source Computational Framework for Design of Multiphysics Systems. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018; p. 1650. [Google Scholar]
- Luke, E.; Collins, E.; Blades, E. A fast mesh deformation method using explicit interpolation. J. Comput. Phys. 2012, 231, 586–601. [Google Scholar] [CrossRef]
- Babinsky, H.; Harvey, J. (Eds.) Shock Wave-Boundary-Layer Interactions; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Gordnier, R.E.; Fithen, R. Coupling of a nonlinear finite element structural method with a Navier—Stokes solver. Comput. Struct. 2003, 81, 75–89. [Google Scholar] [CrossRef]
- Dowell, E.H. Nonlinear oscillations of a fluttering plate. II. AIAA J. 1967, 5, 1856–1862. [Google Scholar] [CrossRef]
- Chung, J.; Hulbert, G.M. A Time Integration Algorithm for Structural Dynamics with Improved Numerical Dissipation: The Generalized-α Method. J. Appl. Mech. 1993, 60, 371–375. [Google Scholar] [CrossRef]
- Visbal, M. Viscous and inviscid interactions of an oblique shock with a flexible panel. J. Fluids Struct. 2014, 48, 27–45. [Google Scholar] [CrossRef]
- Favre, A. Turbulence: Space-time statistical properties and behavior in supersonic flows. Phys. Fluids 1983, 26, 2851–2863. [Google Scholar] [CrossRef]
- Zope, A.D.; Schemmel, A.; Bhatia, M.; Bhushan, S.; Collins, E. Development and Validation of Fluid-Thermal Interaction Solver for High Fidelity Transient Simulations. In Proceedings of the AIAA Aviation 2020 Forum, Virtual Event, 15–19 June 2020; p. 3006. [Google Scholar]
- Sutherland, I.E.; Hodgman, G.W. Reentrant polygon clipping. Commun. ACM 1974, 17, 32–42. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schemmel, A.; Palakurthy, S.; Zope, A.; Collins, E.; Bhushan, S. Development and Verification of Coupled Fluid–Structure Interaction Solver. Computation 2024, 12, 129. https://doi.org/10.3390/computation12060129
Schemmel A, Palakurthy S, Zope A, Collins E, Bhushan S. Development and Verification of Coupled Fluid–Structure Interaction Solver. Computation. 2024; 12(6):129. https://doi.org/10.3390/computation12060129
Chicago/Turabian StyleSchemmel, Avery, Seshendra Palakurthy, Anup Zope, Eric Collins, and Shanti Bhushan. 2024. "Development and Verification of Coupled Fluid–Structure Interaction Solver" Computation 12, no. 6: 129. https://doi.org/10.3390/computation12060129
APA StyleSchemmel, A., Palakurthy, S., Zope, A., Collins, E., & Bhushan, S. (2024). Development and Verification of Coupled Fluid–Structure Interaction Solver. Computation, 12(6), 129. https://doi.org/10.3390/computation12060129








