Prediction of Bone Mineral Density (BMD) Adaptation in Pelvis–Femur Model with Hip Arthroplasties
Abstract
:1. Introduction
2. Materials and Methods
Bone Remodeling Mechanism
3. Results
3.1. Remodeling Behaviour in Pelvis–Femur Models
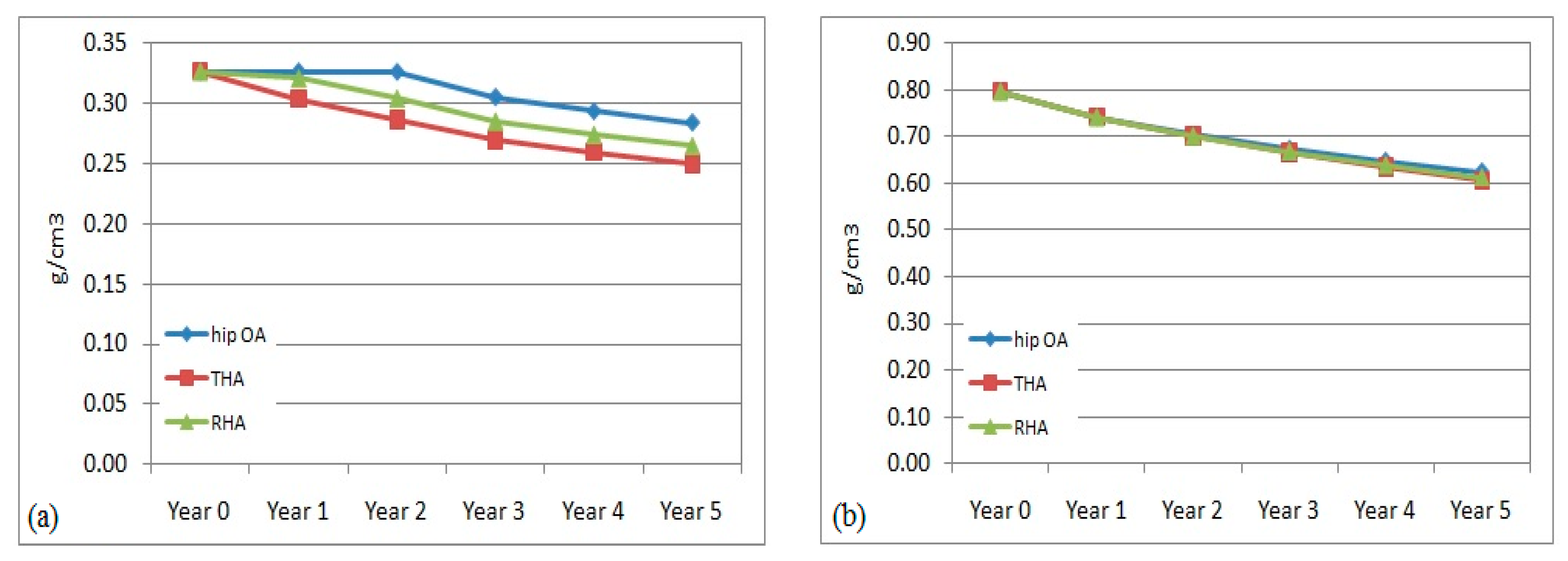
3.2. Bone Mineral Density (BMD) Adaptation in the Non-Operated Femur
3.3. Prediction of Bone Loss in Operated Femur
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sumitomo, N.; Koritake, K.; Hattori, T.; Morikawa, K.; Niwa, S.; Sato, K.; Niinomi, M. Experimental study on fracture fixation with low rigidity titanium alloy: Plate fixation of tibia fracture model in rabbit. J. Mat. Sci. 2008, 19, 1581–1586. [Google Scholar]
- Gong, H.; Kong, L.; Zhang, R.; Fang, J.; Zhao, M. A femur-implant model for the prediction of bone remodelling behaviour induced by cementless stem. J. Bionic Eng. 2013, 10, 350–358. [Google Scholar] [CrossRef]
- Van Rietbergen, B.; Huiskes, R.; Weinans, H.; Sumner, D.R.; Turner, T.M.; Galante, J.O. The Mechanism of Bone Remodeling and Resorption around Press-Fitted THA Stems. J. Biomech. 1993, 26, 369–382. [Google Scholar] [CrossRef]
- Weinans, H.; Huiskes, R.; Grootenboer, H.J. Effects of fit and bonding characteristics of femoral stems on adaptive bone remodelling. J. Biomech. Eng. Trans. ASME 1994, 116, 393–400. [Google Scholar] [CrossRef] [PubMed]
- Gong, H.; Wu, W.; Fang, J.; Dong, X.; Ahao, M.S.; Guo, T.T. Effects of materials of cementless femoral stem on the functional adaptation of bone. J. Bionic Eng. 2012, 9, 66–74. [Google Scholar] [CrossRef]
- Umeda, N.; Miki, H.; Nishii, T.; Yoshikawa, H.; Sugano, N. Progression off osteoarthritis of the knee after unilateral total hip arthroplasty: Minimum 10-year follow-up study. Arch. Orthop. Trauma Surg. 2009, 129, 149–154. [Google Scholar] [CrossRef] [PubMed]
- Nantel, J.; Termoz, N.; Vendittoli, P.A.; Lavigne, M.; Prince, F. Gait Patterns after Total Hip Arthroplasty and Surface Replacement Arthroplasty. Arch. Phys. Med. Rehabil. 2009, 90, 463–469. [Google Scholar] [CrossRef] [PubMed]
- Kiss, R.M. Effects of walking speed and severity of hip osteoarthritis on gait variability. J. Electromyogr. Kinesiol. 2010, 20, 1044–1051. [Google Scholar] [CrossRef]
- Dujardin, F.; Aucouturier, T.; Bocquet, G.; Dupare, F.; Weber, J.; Thormine, J.M. Kinematics of the healthy and arthritic hip joint during walking. A study of 136 subjects. Rev. Chir. Orthopédique Réparatrice L’Appareil 1998, 84, 689–699. [Google Scholar]
- Holnapy, G.; Iiiyes, A.; Kiss, R.M. Impact of the method of exposure in total hip arthroplasty on the variability of gait in the first 6 months of the postoperative period. J. Electromyogr. Kinesiol. 2013, 23, 966–976. [Google Scholar] [CrossRef]
- Bennet, D.; Ogonda, L.; Ellitt, D.; Humphreys, L.; Lawlor, M.; Beverland, D. Comparison of immediate postoperative walking ability in patients receiving minimally invasive and standard-incision hip arthroplasty. J. Arthop. 2007, 22, 490–495. [Google Scholar] [CrossRef] [PubMed]
- Keyak, J.H.; Rossi, S.A.; Jones, K.A.; Skinner, H.B. Prediction of femoral fracture load using automated finite element modelling. J. Biomech. 1998, 31, 125–133. [Google Scholar] [CrossRef]
- Keyak, J.H.; Skinner, H.B.; Fleming, J.A. Effect of force direction on femoral fracture load for two types of loading conditions. J. Orthop. Res. 2001, 19, 539–544. [Google Scholar] [CrossRef]
- Wang, Z.; Newell, K.M. Asymmetry of foot position and weight distribution channels the inter-leg coordination dynamics of standing. Exp. Brain Res. 2012, 222, 333–344. [Google Scholar] [CrossRef] [PubMed]
- Recnik, G.; Kralj-Iglic, V.; Iglic, A.; Antolic, V.; Kramberger, S.; Vengust, R. Higher peak contact hip stress predetermines the side of hip involved in idiopathic osteoarthritis. Clin. Biomech. 2007, 22, 1119–1124. [Google Scholar] [CrossRef]
- Gesso, H. Bone density equation in the femur. Jpn. J. Clin. Biomech. 1995, 16, 216. (In Japanese) [Google Scholar]
- Gesso, H. Simulation of adaptive bone remodelling after total hip replacement. Jpn. J. Clin. Biomech. 1997, 86, 33–38. (In Japanese) [Google Scholar]
- Herrera, A.; Rebollo, S.; Ibarz, E.; Mateo, J.; Gabarre, S.; Gracia, L. Mid-term study of bone remodelling after femoral cemented stem implantation: Comparison between DXA and finite element simulation. J. Arthop. 2014, 29, 90–100. [Google Scholar] [CrossRef]
- Hirata, Y.; Inaba, Y.; Kobayashi, N.; Ike, H.; Fujimaki, H.; Saito, T. Comparison of mechanical stress and change in bone mineral density between two types of femoral implant using finite element analysis. J. Arthop. 2013, 28, 1731–1735. [Google Scholar] [CrossRef]
- Huiskes, R.; Weinans, H.; van Rietbergen, B. The relationship between stress shielding and bone resorption around total hip stems and the effects of flexible materials. Clin. Orthop. Res. 1992, 274, 124–134. [Google Scholar] [CrossRef] [Green Version]
- Venesmaa, P.K.; Krojer, H.P.J.; Jurvelin, J.S.; Miettinen, H.J.A.; Suomalainen, O.T.; Alhava, E.M. Periprosthetic bone loss after cemented total hip arthroplasty: A prospective 5-year dual energy radiographic absorptiometry study of 15 patients. Acta Orthop. Scand. 2003, 74, 31–36. [Google Scholar] [CrossRef]
- Sychter, C.J.; Engh, C.A. The influence of clinical factor on periprosthetic bone remodeling. Clin. Orthop. Rel. Res. 1996, 322, 285–292. [Google Scholar] [CrossRef]
- Braun, A.; Papp, J.; Reiter, A. The periprosthetic bone remodeling process signs of vital bone reaction. Int. Orthop. 2003, 27 (Suppl. 1), 7–10. [Google Scholar]
- Nishii, T.; Sugano, N.; Masuhara, K.; Shibuya, T.; Ochi, T.; Tamura, S. Longitudinal evaluation of time-related bone remodeling after cementless total hip arthroplasty. Clin. Orthop. 1997, 339, 121–131. [Google Scholar] [CrossRef]
- Sabo, D.; Reiter, A.; Simank, H.G.; Thomsen, M.; Lukoschek, M.; Ewerbeck, V. Periprosthetic mineralisation around total hip endoprosthesis: Longitudinal study and cross-sectional study on titanium threaded acetabular cup and cementless Spotorno stem with DEXA. Calcif. Tissue Int. 1998, 62, 177–182. [Google Scholar] [CrossRef]
- Bobyn, J.D.; Mortimer, E.S.; Glassman, A.H.; Engh, C.A.; Miller, E.J.; Brooks, C.E. Producing and avoiding stress shielding: Laboratory and clinical observations of noncemented total hip arthroplasty. Clin. Orthop. 1992, 274, 79–96. [Google Scholar] [CrossRef]
- Kannus, P.; Jarvinen, M.; Sievanen, H.; Oja, P.; Vuori, I. Osteoporosis in men with a history of tibial fracture. J. Bone Miner. Res. 1994, 3, 423–429. [Google Scholar] [CrossRef]
- Hannan, M.T.; Felson, D.T.; Dawson-Hughes, B.; Tucker, K.L.; Cupples, L.A.; Wilson, P.W.F.; Kiel, D.P. Risks factors for longitudinal bone loss in elderly men and women: Framingham osteoporosis study. J. Bone Miner. Res. 2000, 4, 710–720. [Google Scholar] [CrossRef] [PubMed]
- Willis-Owen, C.A.; Atkinson, H.D.; Oakeshott, R.D. Bone mineral density in the femoral neck increases after hip resurfacing: A cohort with five-year follow-up. Int. Orthop. 2011, 35, 1303–1307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kishida, Y.; Sugano, N.; Nishii, T.; Miki, H.; Yamaguchi, K.; Yoshikawa, H. Prevention of the bone mineral density of the femur after surface replacement of the hip. J. Bone Jt. Surg. Br. Vol. 2004, 86, 185–189. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smolders, J.M.; Hol, A.; Rijnders, T.; van Susante, J.L. Changes in bone mineral density in the proximal femur after hip resurfacing and uncemented total hip replacement: A prospective randomised controlled study. J. Bone Jt. Surg. Br. Vol. 2010, 92, 1509–1514. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.; New, A.M.R.; Taylor, M. Bone remodelling inside a cemented resurfaced femoral head. Clin. Biomech. 2006, 21, 594–602. [Google Scholar] [CrossRef] [PubMed]
- Nunley, R.M.; Della Valle, C.J.; Barrack, R.L. Is Patient Selection Important for Hip Resurfacing? Clin. Orthop. Rel. Res. 2009, 467, 56–65. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dall’Ara, E.; Ohman, C.; Baleani, M.; Viceconti, M. Reduced tissue hardness of trabecular bone is associated with severe osteoarthritis. J. Biomech. 2011, 44, 1593–1598. [Google Scholar] [CrossRef] [PubMed]
- Findlay, D.M. Subchondral Bone in Osteoarthritis, Principles of Osteoarthritis-Its Definition, Character, Derivation and Modality-Related Recognition; In Tech.: Rijeka, Crotia, 2012. [Google Scholar]
- Li, G.; Yin, J.; Gao, J.; Cheng, T.S.; Pavlos, N.J.; Zhang, C.; Zheng, M.H. Subchondral bone in osteoarthritis: Insight into risk factors and microstructural changes. Arthritis Res. Ther. 2013, 15, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Häkkinen, A.; Borg, H.; Hakulinen, M.; Jurvelin, J.; Anttila, E.; Parviainen, T.; Kiviranta, I. Bone mineral density of the proximal femur after hip resurfacing arthroplasty: 1-year follow-up study. BMC Musculoskelet. Disord. 2011, 12, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdullah, A.H.; Todo, M. Effects of hip arthroplasties on bone adaptation in lower limbs: A computational study. J. Biosci. Med. 2015, 3, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Beaulieu, M.L.; Lamontagne, M.; Beaule, P.E. Lower limb biomechanics during gait do not return to normal following total hip arthroplasty. Gait Posture 2010, 32, 269–273. [Google Scholar] [CrossRef]
- Kobayashi, S.; Saito, N.; Horiuchi, H.; Iorio, R.; Takaoka, K. Poor bone quality or hip structure as risk factors affecting survival of total-hip arthroplasty. Lancet 2000, 355, 1499–1504. [Google Scholar] [CrossRef]
- Chung, C.Y.; Park, M.S.; Lee, K.M.; Lee, S.H.; Kim, T.K.; Kim, K.W.; Park, J.H.; Lee, J.J. Hip osteoarthritis and risk factors in elderly Korean population. Osteoarthr. Cartil. 2010, 18, 312–316. [Google Scholar] [CrossRef] [Green Version]
- Ringsberg, K.; Gerdhem, P.; Johansson, J.; Obrant, K.J. Is there a relationship between balance, gait performance and muscular strength in 75-year-old women? Age Ageing 1999, 28, 289–293. [Google Scholar] [CrossRef] [PubMed] [Green Version]







| Type | Model | Material | Elastic Modulus, E (GPa) | Poisson Ratio, v |
|---|---|---|---|---|
| THA | Acetabular cup | Ti-Alloy | 114 | 0.34 |
| Bearing liner | Alumina | 370 | 0.23 | |
| Femoral head | Alumina | 370 | 0.23 | |
| Prosthesis stem | Ti-Alloy | 114 | 0.34 | |
| RHA | Acetabular cup | Co-Chrome | 230 | 0.30 |
| Prosthesis pin | Co-Chrome | 230 | 0.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, A.H.; Todo, M. Prediction of Bone Mineral Density (BMD) Adaptation in Pelvis–Femur Model with Hip Arthroplasties. J. Funct. Biomater. 2021, 12, 49. https://doi.org/10.3390/jfb12030049
Abdullah AH, Todo M. Prediction of Bone Mineral Density (BMD) Adaptation in Pelvis–Femur Model with Hip Arthroplasties. Journal of Functional Biomaterials. 2021; 12(3):49. https://doi.org/10.3390/jfb12030049
Chicago/Turabian StyleAbdullah, Abdul Halim, and Mitsugu Todo. 2021. "Prediction of Bone Mineral Density (BMD) Adaptation in Pelvis–Femur Model with Hip Arthroplasties" Journal of Functional Biomaterials 12, no. 3: 49. https://doi.org/10.3390/jfb12030049
APA StyleAbdullah, A. H., & Todo, M. (2021). Prediction of Bone Mineral Density (BMD) Adaptation in Pelvis–Femur Model with Hip Arthroplasties. Journal of Functional Biomaterials, 12(3), 49. https://doi.org/10.3390/jfb12030049






