Lingering Dynamics of Type 2 Diabetes Mellitus Red Blood Cells in Retinal Arteriolar Bifurcations
Abstract
:1. Introduction
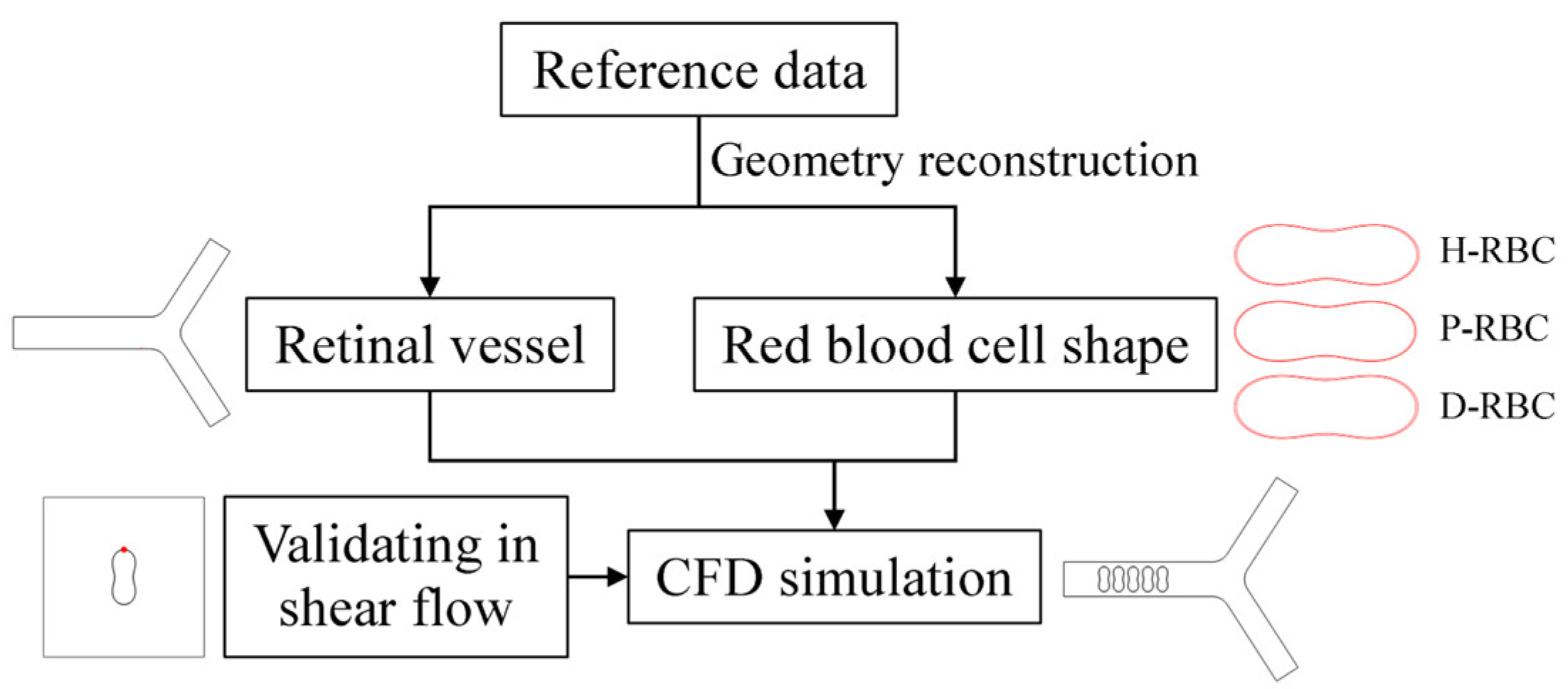
2. Materials and Methods
2.1. Retinal Vessel Model
2.2. RBC Model
2.3. Governing Equations
2.4. Boundary Conditions
3. Results
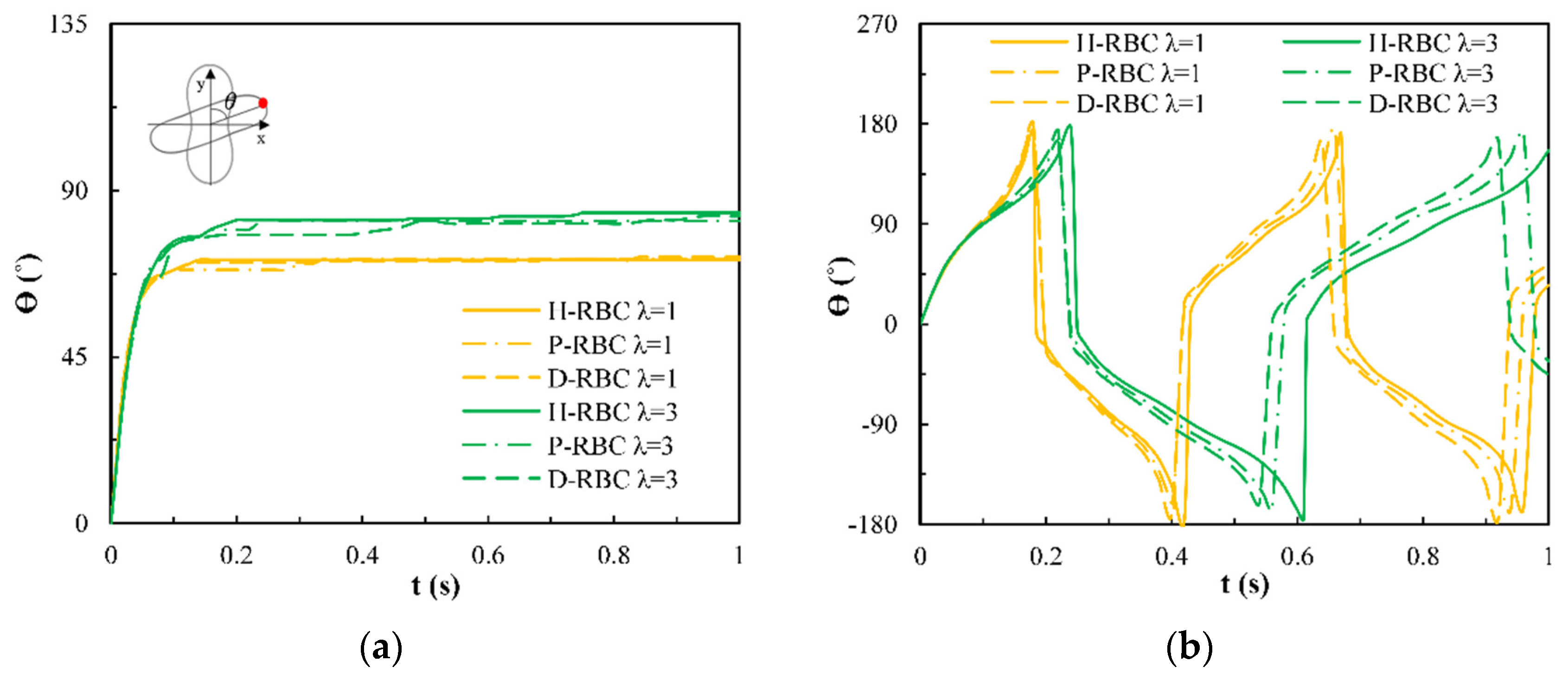
3.1. Dynamic Behavior of RBC in Shear Flow
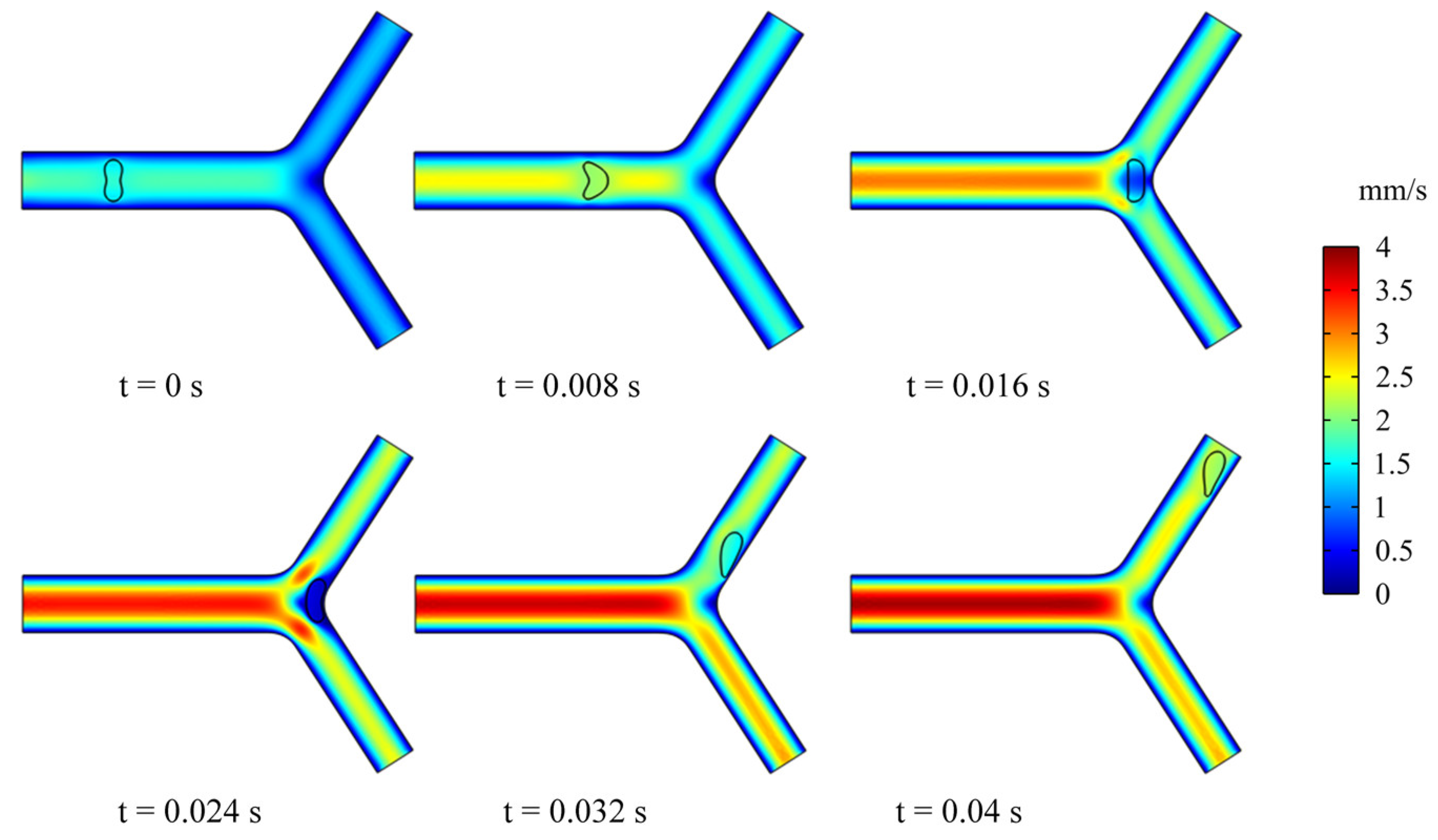
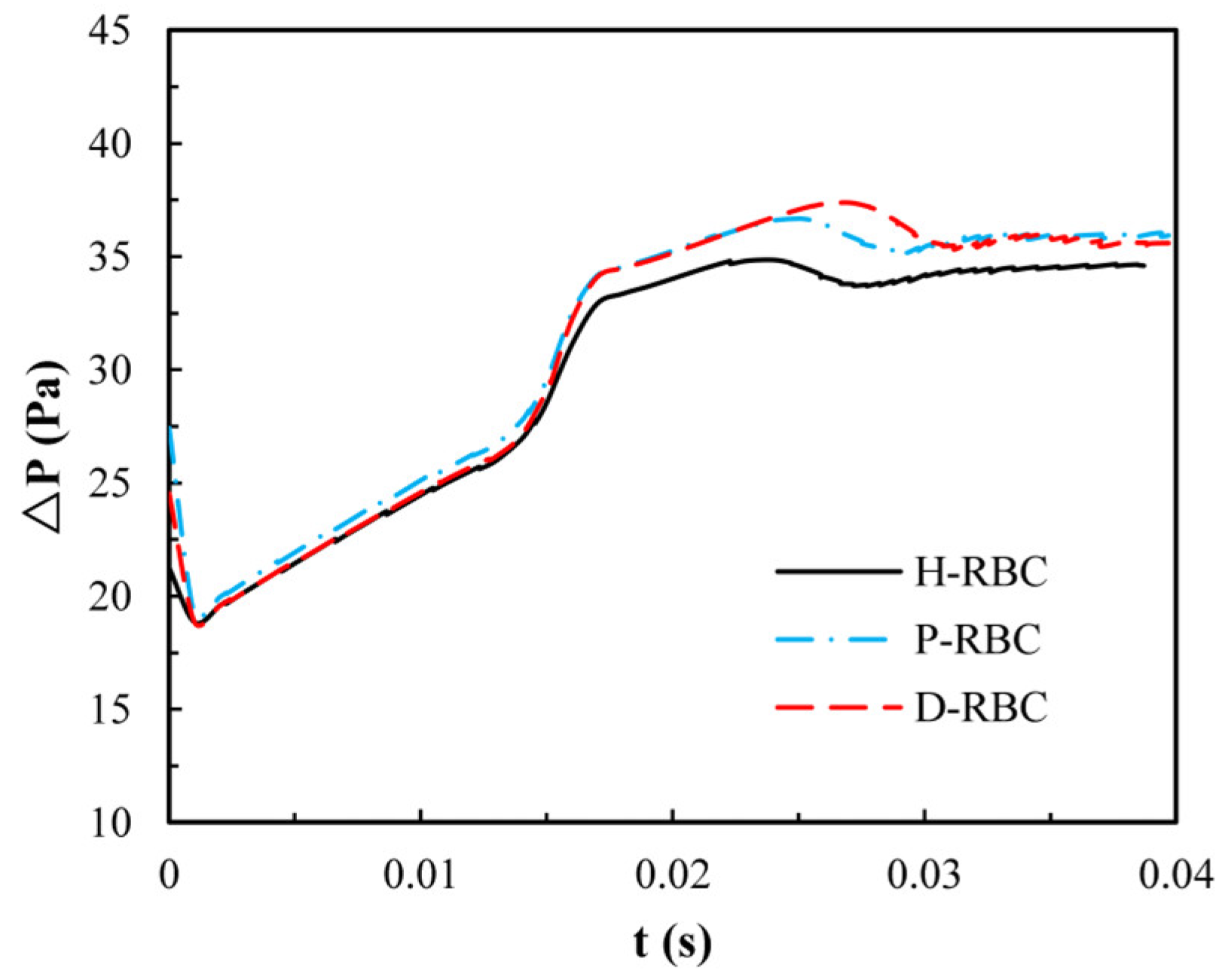
3.2. Dynamics of an RBC in Flowing through a Retinal Bifurcating Vessel
3.3. Dynamics of Multi-RBCs in Flowing through a Retinal Bifurcating Vessel
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ikram, M.K.; Cheung, C.Y.; Lorenzi, M.; Klein, R.; Jones, T.L.Z.; Wong, T.Y.; Retinal, N.J.W. Retinal Vascular Caliber as a Biomarker for Diabetes Microvascular Complications. Diabetes Care 2013, 36, 750–759. [Google Scholar] [CrossRef] [Green Version]
- Kavdia, M.; Popel, A.S. Venular endothelium-derived NO can affect paired arteriole: A computational model. Am. J. Physiol. Heart Circ. Physiol. 2006, 290, H716. [Google Scholar] [CrossRef] [Green Version]
- Peng, Z.; Li, X.; Pivkin, I.V.; Dao, M.; Suresh, S. Lipid bilayer and cytoskeletal interactions in a red blood cell. Proc. Natl. Acad. Sci. USA 2013, 110, 13356–13361. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diez-Silva, M.; Dao, M.; Han, J.Y.; Lim, C.T.; Suresh, S. Shape and Biomechanical Characteristics of Human Red Blood Cells in Health and Disease. MRS Bull. 2010, 35, 382–388. [Google Scholar] [CrossRef] [PubMed]
- Mohandas, N.; Evans, E. Mechanical Properties of the Red Cell Membrane in Relation to Molecular Structure and Genetic Defects. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 787–818. [Google Scholar] [CrossRef] [PubMed]
- Brown, C.D.; Ghali, H.S.; Zhao, Z.H.; Thomas, L.L.; Friedman, E.A. Association of reduced red blood cell deformability and diabetic nephropathy—Reply. Kidney Int. 2005, 67, 2066–2067. [Google Scholar] [CrossRef] [Green Version]
- Loyola-Leyva, A.; Loyola-Rodríguez, J.; Atzori, M.; Micron, F.G.J. Morphological changes in erythrocytes of people with type 2 diabetes mellitus evaluated with atomic force microscopy: A brief review. Micron 2017, 105, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Ciasca, G.; Papi, M.; Di Claudio, S.; Chiarpotto, M.; Palmieri, V.; Maulucci, G.; Nocca, G.; Rossi, C.; De Spirito, M. Mapping viscoelastic properties of healthy and pathological red blood cells at the nanoscale level. Nanoscale 2015, 7, 17030–17037. [Google Scholar] [CrossRef]
- Jin, H.; Xing, X.B.; Zhao, H.X.; Chen, Y.; Huang, X.; Ma, S.Y.; Ye, H.Y.; Cai, J.Y. Detection of erythrocytes influenced by aging and type 2 diabetes using atomic force microscope. Biochem. Biophys. Res. Commun. 2010, 391, 1698–1702. [Google Scholar] [CrossRef]
- AlSalhi, M.S.; Devanesan, S.; AlZahrani, K.E.; AlShebly, M.; Al-Qahtani, F.; Farhat, K.; Masilamani, V. Impact of Diabetes Mellitus on Human Erythrocytes: Atomic Force Microscopy and Spectral Investigations. Int. J. Environ. Res. Public Health 2018, 15, 2368. [Google Scholar] [CrossRef]
- Pozrikidis, C. Finite Deformation of Liquid Capsules Enclosed by Elastic Membranes in Simple Shear-Flow. J. Fluid Mech. 1995, 297, 123–152. [Google Scholar] [CrossRef]
- Wei, Y.; Mu, L.; Tang, Y.; Shen, Z.; He, Y. Computational analysis of nitric oxide biotransport in a microvessel influenced by red blood cells. Microvasc. Res. 2019, 125, 103878. [Google Scholar] [CrossRef] [PubMed]
- Balogh, P.; Bagchi, P. Direct Numerical Simulation of Cellular-Scale Blood Flow in 3D Microvascular Networks. Biophys. J. 2017, 113, 2815–2826. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takahashi, T. (Ed.) A Theoretical Model for the Microcirculatory Network. In Microcirculation in Fractal Branching Networks; Springer: Tokyo, Japan, 2014; pp. 25–45. [Google Scholar]
- Murray, C. The Physiological Principle of Minimum Work: I. The Vascular System and the Cost of Blood Volume. Proc. Natl. Acad. Sci. USA 1926, 12, 207–214. [Google Scholar] [CrossRef] [Green Version]
- Zamir, M. Nonsymmetrical bifurcations in arterial branching. J. Gen. Physiol. 1978, 72, 837. [Google Scholar] [CrossRef] [Green Version]
- Iberall, A.S. Anatomy and steady flow characteristics of the arterial system with an introduction to its pulsatile characteristics. Math. Biosci. 1967, 1, 375–395. [Google Scholar] [CrossRef]
- Zamir, M. On fractal properties of arterial trees. J. Theor. Biol. 1999, 197, 517–526. [Google Scholar] [CrossRef] [Green Version]
- Karch, R.; Neumann, F.; Neumann, M.; Schreiner, W. Staged growth of optimized arterial model trees. Ann. Biomed. Eng. 2000, 28, 495–511. [Google Scholar] [CrossRef]
- Luo, T.; Gast, T.J.; Vermeer, T.J.; Burns, S.A. Retinal Vascular Branching in Healthy and Diabetic Subjects. Investig. Ophth. Vis. Sci. 2017, 58, 2685–2694. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, T. Oxygen Consumption by Vascular Walls in the Retinal Vasculature. In Microcirculation in Fractal Branching Networks; Springer: Tokyo, Japan, 2014; pp. 47–69. [Google Scholar]
- Hochmuth, R.M.; Waugh, R.E. Erythrocyte-Membrane Elasticity and Viscosity. Annu. Rev. Physiol. 1987, 49, 209–219. [Google Scholar] [CrossRef]
- Vayo, H.W.; Shibata, M.K. Numerical Results on Red-Blood-Cell Geometry. Jpn. J. Physiol. 1982, 32, 891–894. [Google Scholar] [CrossRef] [PubMed]
- Nans, A.; Mohandas, N.; Stokes, D.L. Native Ultrastructure of the Red Cell Cytoskeleton by Cryo-Electron Tomography. Biophys. J. 2011, 101, 2341–2350. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heinrich, V.; Ritchie, K.; Mohandas, N.; Evans, E. Elastic thickness compressibilty of the red cell membrane. Biophys. J. 2001, 81, 1452–1463. [Google Scholar] [CrossRef] [Green Version]
- Loyola-Leyva, A.; Loyola-Rodriguez, J.P.; Teran-Figueroa, Y.; Camacho-Lopez, S.; Gonzalez, F.J.; Barquera, S. Application of atomic force microscopy to assess erythrocytes morphology in early stages of diabetes. A pilot study. Micron 2021, 141, 102982. [Google Scholar] [CrossRef]
- De Haan, M.; Zavodszky, G.; Azizi, V.; Hoekstra, A.G. Numerical Investigation of the Effects of Red Blood Cell Cytoplasmic Viscosity Contrasts on Single Cell and Bulk Transport Behaviour. Appl. Sci. 2018, 8, 1616. [Google Scholar] [CrossRef] [Green Version]
- Bagchi, P.; Johnson, P.C.; Popel, A.S. Computational fluid dynamic simulation of aggregation of deformable cells in a shear flow. J. Biomech. Eng. 2005, 127, 1070–1080. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Johnson, P.C.; Popel, A.S. Effects of erythrocyte deformability and aggregation on the cell free layer and apparent viscosity of microscopic blood flows. Microvasc. Res. 2009, 77, 265–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohandas, N.; Groner, W. Cell-Membrane and Volume Changes during Red-Cell Development and Aging. Ann. N. Y. Acad. Sci. 1989, 554, 217–224. [Google Scholar] [CrossRef]
- Tsukada, K.; Sekizuka, E.; Oshio, C.; Minamitani, H. Direct measurement of erythrocyte deformability in diabetes mellitus with a transparent microchannel capillary model and high-speed video camera system. Microvasc. Res. 2001, 61, 231–239. [Google Scholar] [CrossRef] [Green Version]
- Biro, K.; Feher, G.; Vekasi, J.; Kenyeres, P.; Toth, K.; Koltai, K. Hemorheological Parameters in Diabetic Patients: Role of Glucose Lowering Therapies. Metabolites 2021, 11, 806. [Google Scholar] [CrossRef]
- Baskurt, O.K.; Meiselman, H.J. Determination of red blood cell shape recovery time constant in a Couette system by the analysis of light reflectance and ektacytometry. Biorheology 1996, 33, 489–503. [Google Scholar] [CrossRef] [PubMed]
- Hochmuth, R.M.; Worthy, P.R.; Evans, E.A. Red-Cell Extensional Recovery and the Determination of Membrane Viscosity. Biophys. J. 1979, 26, 101–114. [Google Scholar] [CrossRef] [Green Version]
- Chang, H.Y.; Li, X.J.; Karniadakis, G.E. Modeling of Biomechanics and Biorheology of Red Blood Cells in Type 2 Diabetes Mellitus. Biophys. J. 2017, 113, 481–490. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fischer, T.M. Tank-tread frequency of the red cell membrane: Dependence on the viscosity of the suspending medium. Biophys. J. 2007, 93, 2553–2561. [Google Scholar] [CrossRef] [Green Version]
- Shen, Z.Y.; Farutin, A.; Thiebaud, M.; Misbah, C. Interaction and rheology of vesicle suspensions in confined shear flow. Phys. Rev. Fluids 2017, 2, 103101. [Google Scholar] [CrossRef]
- Fischer, T.; Schmidschonbein, H. Tank Tread Motion of Red-Cell Membranes in Viscometric Flow—Behavior of Intracellular and Extracellular Markers (with Film). Blood Cells 1977, 3, 351–365. [Google Scholar]
- Fischer, T.M.; Korzeniewski, R. Angle of Inclination of Tank-Treading Red Cells: Dependence on Shear Rate and Suspending Medium. Biophys. J. 2015, 108, 1352–1360. [Google Scholar] [CrossRef] [Green Version]
- Noguchi, H. Swinging and synchronized rotations of red blood cells in simple shear flow. Phys. Rev. E 2009, 80, 021902. [Google Scholar] [CrossRef] [Green Version]
- Sugihara, M. Motion and deformation of a red blood cell in a shear flow: A two-dimensional simulation of the wall effect. Biorheology 1985, 22, 1–19. [Google Scholar] [CrossRef]
- Kihm, A.; Quint, S.; Laschke, M.W.; Menger, M.D.; John, T.; Kaestner, L.; Wagner, C. Lingering Dynamics in Microvascular Blood Flow. Biophys. J. 2021, 120, 432–439. [Google Scholar] [CrossRef]
- Mazzanti, L.; Faloia, E.; Rabini, R.A.; Staffolani, R.; Kantar, A.; Fiorini, R.; Swoboda, B.; Depirro, R.; Bertoli, E. Diabetes-Mellitus Induces Red-Blood-Cell Plasma-Membrane Alterations Possibly Affecting the Aging Process. Clin. Biochem. 1992, 25, 41–46. [Google Scholar] [CrossRef]
- Dodson, W.R.; Dimitrakopoulos, P. Tank-treading of swollen erythrocytes in shear flows. Phys. Rev. E 2012, 85, 021922. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sui, Y.; Chew, Y.T.; Roy, P.; Cheng, Y.P.; Low, H.T. Dynamic motion of red blood cells in simple shear flow. Phys. Fluids 2008, 20, 112106. [Google Scholar] [CrossRef]
- Chien, S.; Usami, S.; Dellenback, R.J.; Gregersen, M.I. Shear-Dependent Deformation of Erythrocytes in Rheology of Human Blood. Am. J. Physiol. 1970, 219, 136–142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forsyth, A.M.; Wan, J.D.; Ristenpart, W.D.; Stone, H.A. The dynamic behavior of chemically “stiffened” red blood cells in microchannel flows. Microvasc. Res. 2010, 80, 37–43. [Google Scholar] [CrossRef] [PubMed]
- Peduzzi, M.; Melli, M.; Fonda, S.; Codeluppi, L.; Guerrieri, F. Comparative-Evaluation of Blood-Viscosity in Diabetic-Retinopathy. Int. Ophthalmol. 1984, 7, 15–19. [Google Scholar] [CrossRef] [PubMed]
- Grindle, C.F.; Buskard, N.A.; Newman, D.L. Hyperviscosity retinopathy. A scientific approach to therapy. Trans. Ophthalmol. Soc. U K (1962) 1976, 96, 216–219. [Google Scholar]
- Fornal, M.; Lekka, M.; Pyka-Fosciak, G.; Lebed, K.; Grodzicki, T.; Wizner, B.; Styczen, J. Erythrocyte stiffness in diabetes mellitus studied with atomic force microscope. Clin. Hemorheol. Microcirc. 2006, 35, 273–276. [Google Scholar]
- Tamariz, L.J.; Young, J.H.; Pankow, J.S.; Yeh, H.C.; Schmidt, M.I.; Astor, B.; Brancati, F.L. Blood viscosity and hematocrit as risk factors for type 2 diabetes mellitus: The atherosclerosis risk in communities (ARIC) study. Am. J. Epidemiol. 2008, 168, 1153. [Google Scholar] [CrossRef] [Green Version]
- Lowe, G.D.O.; Lee, A.J.; Rumley, A.; Price, J.F.; Fowkes, F.G.R. Blood viscosity and risk of cardiovascular events: The Edinburgh Artery Study. Brit. J. Haematol. 1997, 96, 168–173. [Google Scholar] [CrossRef]
- Babu, N.; Singh, M. Influence of hyperglycemia on aggregation, deformability and shape parameters of erythrocytes. Clin. Hemorheol. Microcirc. 2004, 31, 273–280. [Google Scholar] [PubMed]
- Pelikanova, T.; Kohout, M.; Valek, J.; Base, J.; Stefka, Z. Fatty acid composition of serum lipids and erythrocyte membranes in type 2 (non-insulin-dependent) diabetic men. Metabolism 1991, 40, 175–180. [Google Scholar] [CrossRef]
- Kiani, M.F.; Cokelet, G.R. Additional Pressure-Drop at a Bifurcation Due To the Passage of Flexible Disks in a Large-Scale Model. J. Biomech. Eng. 1994, 116, 497–501. [Google Scholar] [CrossRef]
- Fiorentino, T.V.; Prioletta, A.; Zuo, P.; Folli, F. Hyperglycemia-induced Oxidative Stress and its Role in Diabetes Mellitus Related Cardiovascular Diseases. Curr. Pharm. Des. 2013, 19, 5695–5703. [Google Scholar] [CrossRef] [PubMed]
- Amiya, E. Interaction of hyperlipidemia and reactive oxygen species: Insights from the lipid-raft platform. World J. Cardiol. 2016, 8, 689–694. [Google Scholar] [CrossRef] [PubMed]
- Vekasi, J.; Marton, Z.; Kesmarky, G.; Cser, A.; Russai, R.; Horvath, B. Hemorheological alterations in patients with diabetic retinopathy. Clin. Hemorheol. Microcirc. 2001, 24, 59–64. [Google Scholar] [PubMed]
- Wautier, J.L. Blood cell—Vessel wall interactions. Clin. Hemorheol. Microcirc. 1992, 12, 55–58. [Google Scholar] [CrossRef]
- Cho, Y.I.; Mooney, M.P.; Cho, D.J. Hemorheological Disorders in Diabetes Mellitus. J. Diabetes Sci. Technol. 2008, 2, 1130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moon, J.S.; Kim, J.H.; Kim, J.H.; Park, I.R.; Lee, J.H.; Kim, H.J.; Lee, J.; Kim, Y.K.; Yoon, J.S.; Won, K.C.; et al. Impaired RBC deformability is associated with diabetic retinopathy in patients with type 2 diabetes. Diabetes Metab. 2016, 42, 448–452. [Google Scholar] [CrossRef]








| Symbol | Value, Units | Description |
|---|---|---|
| 9.5 μm | parent vessel diameter | |
| 2.36 | vessel index | |
| 1 | asymmetry index | |
| 1060 kg/m3 | plasma density and cytoplasmic density | |
| 1090 kg/m3 | RBC membrane density | |
| 5 | physiological viscosity ratio | |
| 1, 3, 5, 7, 9 | viscosity ratio | |
| 50, 100, 150 1/s | shear flow rate |
| Parameters | H-RBC | P-RBC | D-RBC |
|---|---|---|---|
| Diameter (μm) | 6.91 [26] | 6.82 [26] | 6.89 [26] |
| Thickness (μm) | 2.36 [26] | 2.4 [26] | 2.68 [26] |
| Concave depth (μm) | 0.43 [26] | 0.37 [26] | 0.143 [26] |
| (Pa·s) | 0.00128 [32] | 0.00131 | 0.00133 [32] |
| (kPa) | 1820 [8] | 2020 | 2520 [8] |
| (s) | 0.1 [33,34] | 0.08 [35] | 0.07 [35] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, L.; Chen, H.; He, Y.; Mu, L.; Luan, Y. Lingering Dynamics of Type 2 Diabetes Mellitus Red Blood Cells in Retinal Arteriolar Bifurcations. J. Funct. Biomater. 2022, 13, 205. https://doi.org/10.3390/jfb13040205
Long L, Chen H, He Y, Mu L, Luan Y. Lingering Dynamics of Type 2 Diabetes Mellitus Red Blood Cells in Retinal Arteriolar Bifurcations. Journal of Functional Biomaterials. 2022; 13(4):205. https://doi.org/10.3390/jfb13040205
Chicago/Turabian StyleLong, Lili, Huimin Chen, Ying He, Lizhong Mu, and Yong Luan. 2022. "Lingering Dynamics of Type 2 Diabetes Mellitus Red Blood Cells in Retinal Arteriolar Bifurcations" Journal of Functional Biomaterials 13, no. 4: 205. https://doi.org/10.3390/jfb13040205
APA StyleLong, L., Chen, H., He, Y., Mu, L., & Luan, Y. (2022). Lingering Dynamics of Type 2 Diabetes Mellitus Red Blood Cells in Retinal Arteriolar Bifurcations. Journal of Functional Biomaterials, 13(4), 205. https://doi.org/10.3390/jfb13040205






