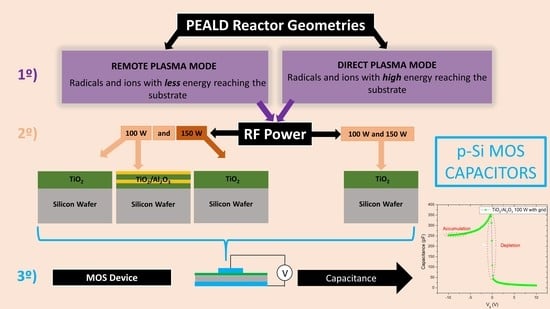
MOS Capacitance Measurements for PEALD TiO2 Dielectric Films Grown under Different Conditions and the Impact of Al2O3 Partial-Monolayer Insertion
Abstract
:1. Introduction
2. Materials and Methods
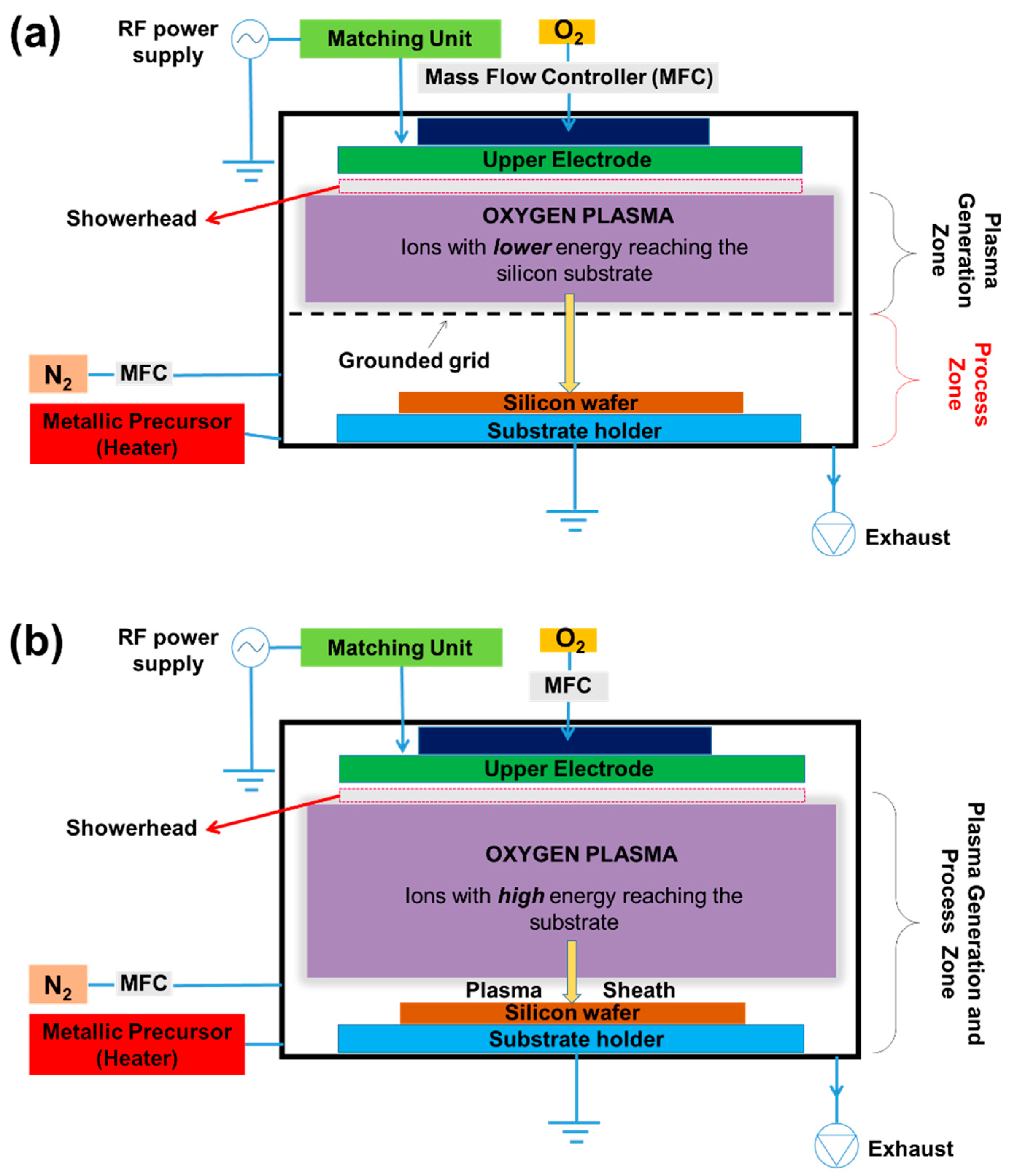
2.1. Film Preparation
2.2. Nanolaminate Preparation
2.3. Thin-Film Characterization
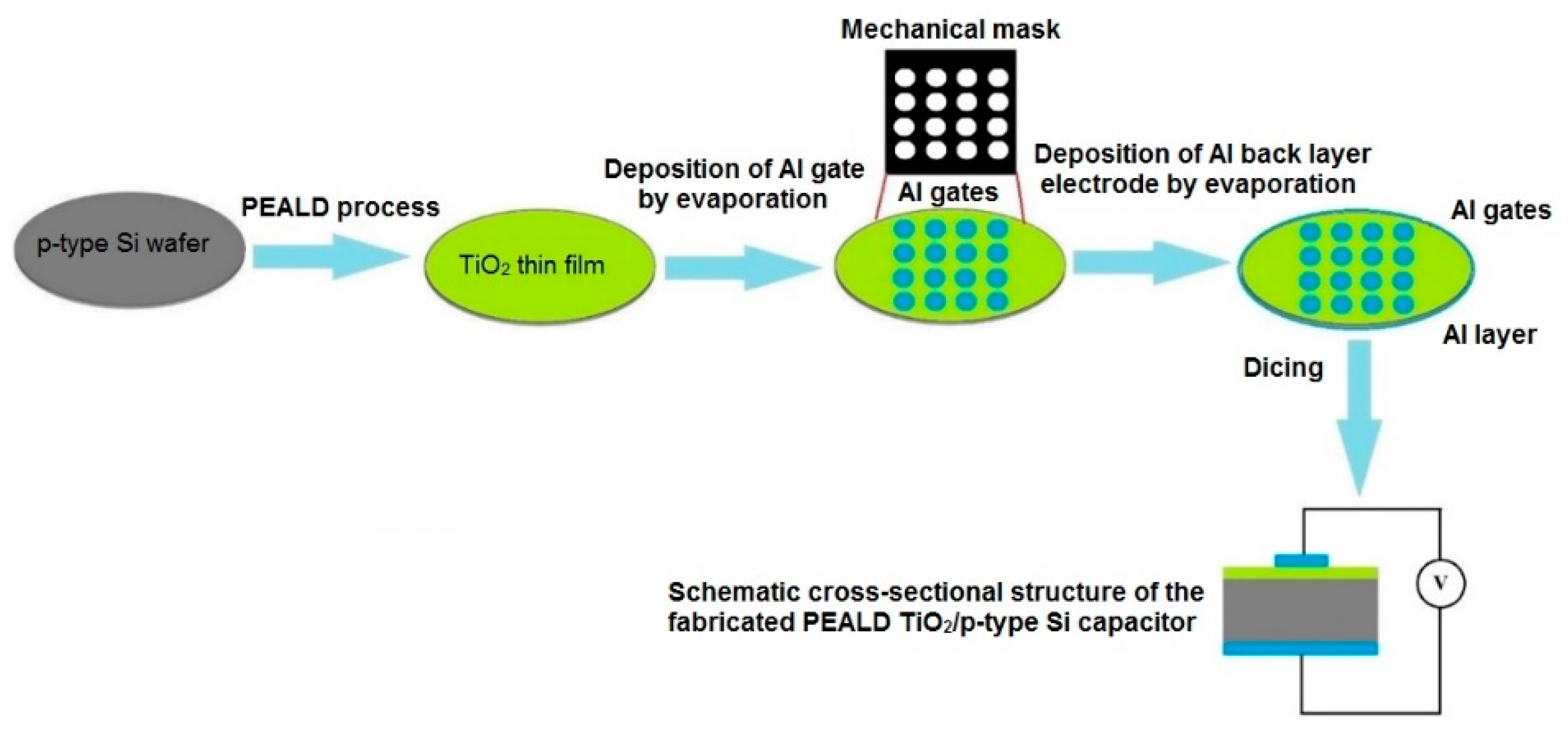
2.4. Fabrication and Characterization of the MOS Structures
3. Results and Discussion
3.1. Film Characterization
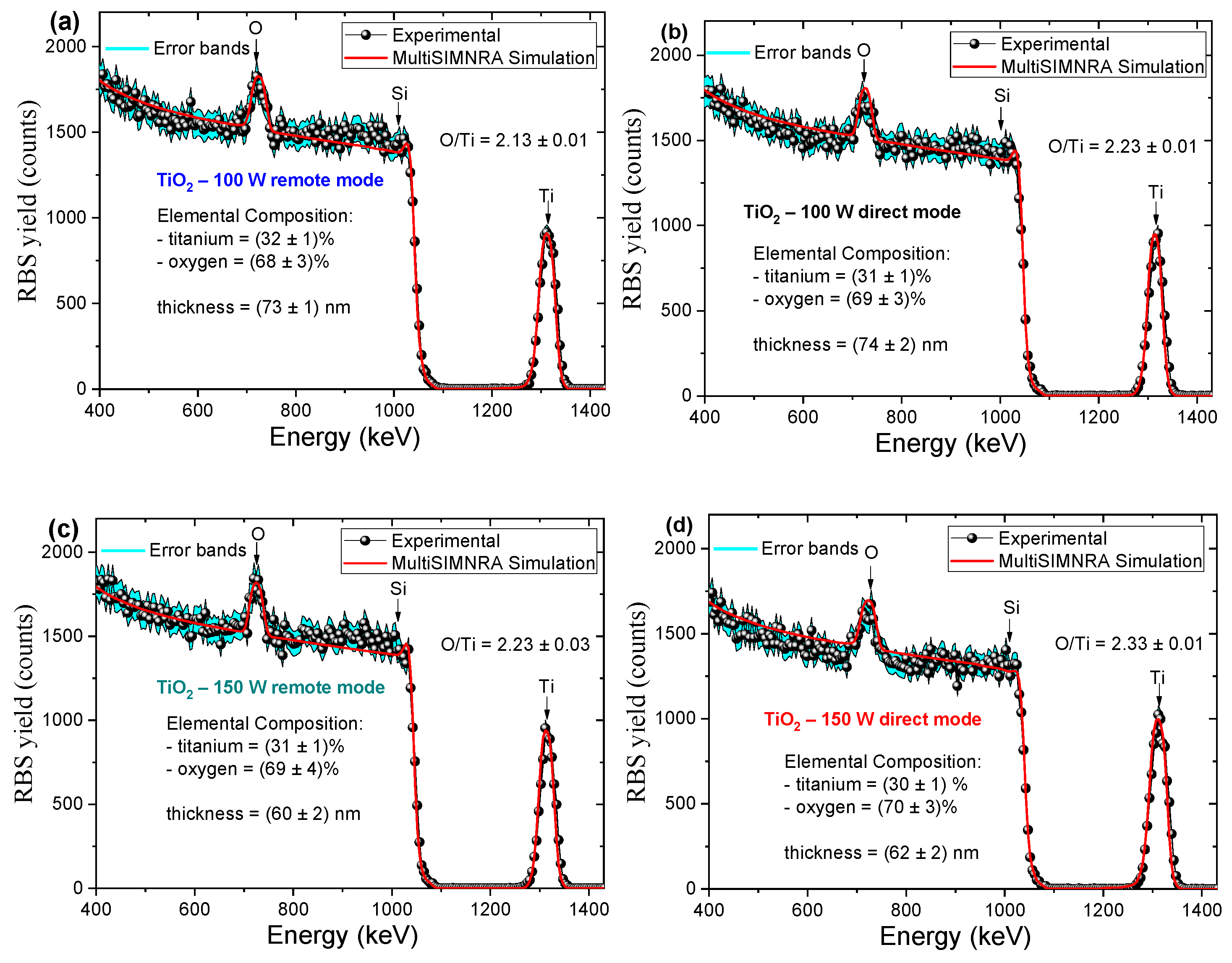
3.1.1. Chemical Composition
3.1.2. Structure and Morphology
3.2. Electrical Characterization of TiO2/p-Si MOS Capacitors
3.2.1. Current Density-Voltage Measurements
3.2.2. Capacitance-Voltage and Conductance-Voltage Measurements
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baek, Y.; Lim, S.; Kim, L.H.; Park, S.; Lee, S.W.; Oh, T.H.; Kim, S.H.; Park, C.E. Al2O3/TiO2 nanolaminate gate dielectric films with enhanced electrical performances for organic field-effect transistors. Org. Electron. 2016, 28, 139–146. [Google Scholar] [CrossRef]
- Wei, D.; Edgar, J.H.; Briggs, D.P.; Retterer, S.T.; Srijanto, B.; Hensley, D.K.; Meyer, H.M., III. Atomic layer deposition TiO2-Al2O3 stack: An improved gate dielectric on Ga-polar GaN metal oxide semiconductor capacitors. J. Vac. Sci. Technol. B 2014, 32, 060602. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Kim, Y.I.; Lee, J.Y.; Choi, S.-Y. A low-temperature-grown TiO2-based device for the flexible stacked RRAM application. Nanotechnology 2010, 21, 115203. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Kong, J.-Z.; Cao, Z.-Y.; Li, A.-D.; Wang, L.-G.; Zhu, L.; Li, X.; Cao, Y.-Q.; Wu, D. Bipolar resistive switching characteristics of HfO2/TiO2/HfO2 trilayer-structure RRAM devices on Pt and TiN-coated substrates fabricated by atomic layer deposition. Nanoscale Res. Lett. 2017, 12, 393. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.; Hossain, T.; Garces, N.Y.; Nepal, N.; Meyer, H.M., III; Kirkham, M.J.; Eddy, C.R., Jr.; Edgar, J.H. Influence of atomic layer deposition temperatures on TiO2/n-Si MOS capacitor. ECS J. Solid State Sci. Technol. 2013, 2, N110–N114. [Google Scholar] [CrossRef] [Green Version]
- Maeng, W.J.; Kim, W.-H.; Lim, S.J.; Lee, C.-S.; Lee, T.; Kim, H. Flatband voltage control in p-metal gate metal-oxide-semiconductor field effect transistor by insertion of TiO2 layer. Appl. Phys. Lett. 2010, 96, 082905. [Google Scholar] [CrossRef] [Green Version]
- Zardetto, V.; Williams, B.L.; Perrota, A.; Di Giacomo, F.; Verheijen, M.A.; Andriessen, R.; Kessels, W.M.M.; Creatore, M. Atomic layer deposition for perovskite solar cells: Research status, opportunities, and challenges. Sustain. Energy Fuels 2017, 1, 30–55. [Google Scholar] [CrossRef]
- Wang, W.-C.; Tsai, M.-C.; Yang, J.; Hsu, C.; Chen, M.-J. Efficiency enhancement of nanotextured black silicon solar cells using Al2O3/TiO2 dual-layer passivation stack prepared by atomic layer deposition. ACS Appl. Mater. Interfaces 2015, 7, 10228–10237. [Google Scholar] [CrossRef]
- Pessoa, R.S.; Fraga, M.A.; Santos, L.V.; Massi, M.; Maciel, H.S. Nanostructured thin films based on TiO2 and/or SiC for use in photoelectrochemical cells: A review of the material characteristics, synthesis and recent applications. Mater. Sci. Semicond. Process. 2015, 29, 56–68. [Google Scholar] [CrossRef]
- Nakata, K.; Fujishima, A. TiO2 photocatalysis: Desing and applications. J. Photochem. Photobiol. C 2012, 13, 169–189. [Google Scholar] [CrossRef]
- Daghrir, R.; Drogui, P.; Robert, D. Modified TiO2 for environmental photocatalytic applications: A review. Ind. Eng. Chem. Res. 2013, 52, 3581–3599. [Google Scholar] [CrossRef]
- Pessoa, R.S.; Fraga, M.A.; Chiappim, W.; Maciel, H.S. Exploring the Properties and Fuel Cell Applications of Ultrathin Atomic Layer Deposited Metal Oxide Films. In Emerging Materials for Energy Conversion and Storage, 1st ed.; Cheong, K.Y., Impellizzeri, G., Fraga, M.A., Eds.; Elsevier: Cambridge, MA, USA, 2018; pp. 83–114. [Google Scholar]
- Sharma, R.K.; Bhatnagar, M.C.; Sharma, G.L. Influence of doping on sensitivity and response time of TiO2 oxygen gas sensor. Rev. Sci. Instrum. 1999, 71, 1500–1509. [Google Scholar] [CrossRef]
- Bao, S.-J.; Li, C.M.; Zang, J.-F.; Cui, X.-Q.; Qiao, Y.; Guo, J. New nanostructured TiO2 for Direct electrochemistry and glucose sensor applications. Adv. Funct. Mater. 2008, 18, 591–599. [Google Scholar] [CrossRef]
- Fraga, M.A.; Furlan, H.; Pessoa, R.S.; Rasia, L.A.; Mateus, C.F.R. Studies on SiC, DLC and TiO2 thin films as piezoresistive sensor materials for high-temperature applications. Microsyst. Technol. 2012, 8, 1027–1033. [Google Scholar] [CrossRef]
- Rathee, D.; Kumar, M.; Arya, S.K. CMOS development and optimization, scaling issue and replacement with high-k material for future microelectronics. Int. J. Comput. Appl. 2010, 8, 10–17. [Google Scholar] [CrossRef]
- Pfeiffer, K.; Schulz, U.; Tünnermann, A.; Szeghalmi, A. Antireflection coating for strongly curved glass lenses by atomic layer deposition. Coatings 2017, 7, 118. [Google Scholar] [CrossRef] [Green Version]
- Pessoa, R.S.; Fraga, M.A. Biomedical applications of ultrathin atomic layer deposited metal oxide films on polymeric materials. In Frontiers of Nanoscience, 1st ed.; Benelmekki, M., Erbe, A., Eds.; Elsevier: Cambridge, MA, USA, 2019; Volume 14, pp. 291–307. [Google Scholar]
- Pessoa, R.S.; dos Santos, V.P.; Cardoso, S.B.; Doria, A.C.O.C.; Figueira, F.R.; Rodrigues, B.V.M.; Testoni, G.E.; Fraga, M.A.; Marciano, F.R.; Lobo, A.O.; et al. TiO2 coatings via atomic layer deposition on polyurethane and polydimethylsiloxane substrate: Properties and effects on C. Albicans growth and inactivation process. Appl. Surf. Sci. 2017, 422, 73–84. [Google Scholar] [CrossRef]
- Dias, V.; Maciel, H.S.; Fraga, M.A.; Lobo, A.O.; Pessoa, R.S.; Marciano, F.R. Atomic layer deposited TiO2 and Al2O3 thin films as a coating for Aluminum food packing application. Materials 2019, 12, 682. [Google Scholar] [CrossRef] [Green Version]
- Uchiyama, H.; Bando, T.; Kozuka, H. Effect of the amount of H2O and HNO3 in Ti(OC3H7i)4 solutions on the crystallization of sol-gel-derived TiO2 films. Thin Solid Film. 2019, 669, 157–161. [Google Scholar] [CrossRef]
- Abbas, F.; Bensaha, R.; Taroré, H. The influence of Zn+2 doping and annealing temperature on grown-up of nanostructures TiO2 thin films prepared by the sol-gel dip-coating method and their photocatalytic application. Optik 2019, 180, 361–369. [Google Scholar] [CrossRef]
- Toku, H.; Pessoa, R.S.; Maciel, H.S.; Massi, M.; Mengui, U.A. The effect of oxygen concentration on the low temperature deposition of TiO2 thin films. Surf. Coat. Technol. 2008, 202, 2126–2131. [Google Scholar] [CrossRef]
- Toku, H.; Pessoa, R.S.; Maciel, H.S.; Massi, M.; Mengui, U.A. Influence of process parameters on the growth of pure-phase anatase and rutile TiO2 thin films deposited by low temperature reactive magnetron sputtering. Braz. J. Phys. 2010, 40, 340–343. [Google Scholar] [CrossRef] [Green Version]
- Astinchap, B.; Laelabadi, K.G. Effects of substrate temperature and precursor amount on optical properties and microstructure of CVD deposited amorphous TiO2 thin films. J. Phys. Chem. Solids 2019, 129, 217–226. [Google Scholar] [CrossRef]
- Manova, D.; Arias, L.F.; Holefe, A.; Alani, I.; Kleiman, A.; Asenova, I.; Decker, U.; Marquez, A.; Mändl, S. Nitrogen incorporation during PVD deposition of TiO2: N thin films. Surf. Coat. Technol. 2017, 312, 61–65. [Google Scholar] [CrossRef]
- Pessoa, R.S.; Pereira, F.P.; Testoni, G.E.; Chiappim, W.; Maciel, H.S.; Santos, L.V. Effect of substrate type on the structure of TiO2 thin films deposited by atomic layer deposition technique. JICS 2015, 1, 38–42. [Google Scholar]
- Chiappim, W.; Testoni, G.E.; Moraes, R.S.; Sagás, J.C.; Origo, F.D.; Vieira, L.; Maciel, H.S. Structural, morphological, and optical properties of TiO2 thin films grown by atomic layer deposition on fluorine-doped tin oxide conductive glass. Vacuum 2016, 123, 91–102. [Google Scholar] [CrossRef]
- Lim, J.W.; Yuu, S.J.; Lee, J.H. Characteristics of TiO2 films prepared by ALD with and without plasma. Electrochem. Solid State Lett. 2004, 11, F73–F76. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.J.; Han, W.B.; Jeon, H.; Park, J.; Jang, W.; Yoon, C.S.; Jeon, H. Deposition temperature dependence of titanium oxide thin films grown by remote-plasma atomic layer deposition. Phys. Status Solidi A 2013, 210, 276–284. [Google Scholar] [CrossRef]
- Kilpi, L.; Ylivaara, O.M.E.; Vaajoki, A.; Liu, X.; Rontu, V. Tribological properties of thin films made by atomic layer deposition sliding against silicone. J. Vac. Sci. Technol. A 2018, 36, 01A122. [Google Scholar] [CrossRef] [Green Version]
- Faraz, T.; Knoops, H.C.M.; Verheijen, M.A.; van Helvoirt, C.A.A.; Karwal, S.; Sharma, A.; Beladiya, V.; Szeghalmi, A.; Hausmann, D.M.; Henri, J.; et al. Tuning material properties of oxides and nitrides by substrates biasing during plasma-enhanced atomic layer deposition on planar and 3D substrate topographies. ACS Appl. Mater. Interfaces 2018, 10, 13158–13180. [Google Scholar] [CrossRef] [Green Version]
- Chaker, A.; Szkutnik, P.D.; Pointet, J.; Gonon, P.; Vallée, C.; Bsiesy, A. Understanding the mechanisms of interfacial reaction during TiO2 layer growth on RuO2 by atomic layer deposition with O2 plasma or H2O as oxygen source. J. Appl. Phys. 2016, 120, 085315. [Google Scholar] [CrossRef]
- Choi, W.-S. X-ray photoelectron spectroscopy analyses of atomic layer deposition-prepared titanium-dioxide thin films with oxygen sources and their annealing effect. Sci. Adv. Mater. 2016, 8, 336–341. [Google Scholar] [CrossRef]
- Ratzsch, S.; Kley, E.-B.; Tünnermann, A.; Szeghalmi, A. Influence of the oxygen plasma parameters on the atomic layer deposition of titanium dioxide. Nanotechnology 2015, 26, 024003. [Google Scholar] [CrossRef] [PubMed]
- Schindler, P.; Logar, M.; Provine, J.; Prinz, F.B. Enhanced step coverage of TiO2 deposited on high aspect ratio surfaces by plasma-enhanced atomic layer deposition. Langmuir 2015, 31, 5057–5062. [Google Scholar] [CrossRef]
- Puurunen, R.L. Surface chemistry of atomic layer deposition: A case study for the trimethylaluminum/water process. J. Appl. Phys. 2005, 97, 121301. [Google Scholar] [CrossRef]
- Profijt, H.B.; Potts, S.E.; van de Sanden, M.C.M.; Kessels, W.M.M. Plasma-assisted atomic layer deposition: Basics, opportunities, and challenges. J. Vac. Sci. Technol. A 2011, 29, 050801. [Google Scholar] [CrossRef] [Green Version]
- Potts, S.E.; Kessels, W.M.M. Energy-enhanced atomic layer deposition for more process and precursor versatility. Coord. Chem. Rev. 2013, 257, 3254–3270. [Google Scholar] [CrossRef]
- Liu, G.X.; Shan, F.K.; Park, J.J.; Lee, W.J.; Lee, G.H.; Kim, I.S.; Shin, B.C.; Yoon, S.G. Electrical properties of Ga2O3-based dielectric thin films prepared by plasma enhanced atomic layer deposition (PEALD). J. Electroceram. 2006, 17, 145–149. [Google Scholar] [CrossRef]
- Hudec, B.; Huseková, K.; Aarik, J.; Tarre, A.; Kasikov, A.; Frölich, K. RuO2/TiO2 based MIM capacitors for DRAM applications. In Proceedings of the 8th International Conference on Advanced Semiconductor Devices and Microsystems, Smolenice Castle, Slovakia, 25–27 October 2010; pp. 341–344. [Google Scholar]
- Cunha, J.M.V.; Fernandes, P.A.; Hultqvist, A.; Teixeira, J.P.; Bose, S.; Vermang, B.; Garud, S.; Buldu, S.; Gaspar, J.; Edoff, Leitão, J.P.; et al. Insulator Materials for Interface Passivation of Cu(In, Ga)Se2 thin films. IEEE J. Photovolt. 2018, 8, 1313–1319. [Google Scholar] [CrossRef]
- Kim, H.; Oh, I.-K. Review of plasma-enhanced atomic layer deposition: Technical enabler of nanoscale device fabrication. Jpn. J. Appl. Phys. 2014, 53, 03DA01. [Google Scholar] [CrossRef]
- Choi, G.-J.; Kim, S.K.; Won, S.-J.; Kim, H.J.; Hwang, C.S. Plasma-enhanced atomic layer deposition of TiO2 and Al-doped TiO2 films using N2O and O2 reactants. J. Electrochem. Soc. 2009, 156, G138–G143. [Google Scholar] [CrossRef]
- Chiappim, W.; Testoni, G.E.; Doria, A.C.O.C.; Pessoa, R.S.; Fraga, M.A.; Galvão, N.K.A.M.; Grigorov, K.G.; Vieira, L.; Maciel, H.S. Relationships among growth mechanism, structure and morphology of PEALD TiO2 films: The influence of O2 plasma power, precursors chemistry and plasma exposure mode. Nanotechnology 2016, 27, 305701. [Google Scholar] [CrossRef] [PubMed]
- Kääriäinen, T.O.; Cameron, D.C. Plasma-enhanced atomic layer deposition of Al2O3 at room temperature. Plasma Process. Polym. 2009, 6, S237–S241. [Google Scholar] [CrossRef]
- Nogueira, W.A.; dos Santos Filho, S.G. Influência das limpezas químicas úmidas H2O/H2O2/NH4OH e H2O/HF/HNO3 na micro-rugosidade de lâminas de silício. Revista Brasileira de Aplicações de Vácuo 2001, 20, 46–51. [Google Scholar]
- Faraz, T.; Arts, K.; Karwal, S.; Knoops, H.C.M.; Kessels, W.M.M. Energetic ions during plasma-enhenced atomic layer deposition and their role in tailoring materials properties. Plasma Sources Sci. Technol. 2019, 28, 024002. [Google Scholar] [CrossRef]
- Testoni, G.E.; Chiappim, W.; Pessoa, R.S.; Fraga, M.A.; Miyakawa, W.; Sakane, K.K.; Galvão, N.K.A.M.; Vieira, L.; Maciel, H.S. Influence of the Al2O3 partial-monolayer number on the crystallization mechanism of TiO2 in ALD TiO2/Al2O3 nanolaminates and its impact on the material properties. J. Phys. D Appl. Phys. 2016, 49, 375301. [Google Scholar] [CrossRef]
- LAMFI. Available online: http://deuterio.if.usp.br/multisimnra/ (accessed on 3 December 2019).
- MPCDF. Available online: https://home.mpcdf.mpg.de/~mam/Mayer-AIP-Conference-Proceedings-475- (accessed on 20 December 2019).
- Chiappim, W.; Testoni, G.E.; de Lima, J.S.B.; Medeiros, H.S.; Pessoa, R.S.; Grigorov, K.G.; Vieira, L.; Maciel, H.S. Effect of process temperature and reaction cycle number on atomic layer deposition of TiO2 thin films using TiCl4 and H2O precursors: Correlation between material properties and process environment. Braz. J. Phys. 2016, 46, 56–69. [Google Scholar] [CrossRef]
- Bousoulas, P.; Michelakaki, I.; Tsoukalas, D. Influence of oxygen content of room temperature TiO2−x deposited films for enhanced resistive switching memory performance. J. Appl. Phys. 2014, 115, 034516. [Google Scholar] [CrossRef]
- Ohsaka, T.; Izumi, F.; Fujiki, Y. Raman spectrum of anatase, TiO2. J. Raman Spectrosc. 1978, 7, 321–324. [Google Scholar] [CrossRef]
- Parker, J.C.; Siegel, R.W. Calibration of the Raman spectrum to the oxygen stoichiometry of nanophase TiO2. Appl. Phys. Lett. 1990, 57, 943. [Google Scholar] [CrossRef]
- Bassi, A.L.; Cattaneo, D.; Russo, V.; Bottani, C.E.; Barborini, E.; Mazza, T.; Piseri, P.; Miliani, P.; Ernst, F.O.; Wegner, K.; et al. Raman spectroscopy characterization of titania nanoparticles produced by flame pyrolysis: The influence of size and stoichiometry. J. Appl. Phys. 2005, 98, 074305. [Google Scholar] [CrossRef]
- Gates-Rector, S.; Blanton, T. The powder diffraction file: A quality materials characterization database. Powder Diffr. 2019, 34, 352–360. [Google Scholar] [CrossRef] [Green Version]
- Avila, J.R.; Qadri, S.B.; Freitas, J.A., Jr.; Nepal, N.; Boris, D.R.; Walton, S.G.; Eddy, C.R., Jr.; Wheeler, V.D. Impact of growth conditions on the phase selectivity and epitaxial quality of TiO2 films grown by plasma-assisted atomic layer deposition. Chem. Mater. 2019, 31, 3900–3908. [Google Scholar] [CrossRef]
- Patterson, A.L. The Scherrer formula for X-ray particle size determination. Phys. Rev. 1939, 56, 978. [Google Scholar] [CrossRef]
- Ortiz-Conde, A.; Sánchez, F.J.G.; Muci, J. New method to extract the model parameters of solar cells from the explicit analytic solutions of their illuminated I–V characteristics. Sol. Energy Mater. Sol. Cells 2006, 90, 352–361. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W Function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Shockley, W. The theory of p-n junctions in semiconductors and p-n junction transistors. Bell Syst. Tech. J. 1949, 28, 435–489. [Google Scholar] [CrossRef]
- Sah, C.; Noyce, R.N.; Shockley, W. Carrier generation and recombination in p-n junctions and p-n junction characteristics. Proc. IRE 1957, 45, 1228–1243. [Google Scholar] [CrossRef]
- Faulkner, E.A.; Buckingham, M.J. Modified theory of the current/voltage relation in silicon p-n junctions. Electron. Lett. 1968, 4, 359–360. [Google Scholar] [CrossRef]
- Nussbaum, A. Generation-recombination characteristic behavior of silicon diodes. Phys. Status Solidi A 1973, 19, 441–450. [Google Scholar] [CrossRef]
- Jain, A.; Kapoor, A. A new method to determine the diode ideality factor of real solar cell using Lambert W-function. Sol. Energy Mater. Sol. Cells 2005, 85, 391–396. [Google Scholar] [CrossRef]
- Rajab, S.M.; Oliveira, I.C.; Massi, M.; Maciel, H.S.; dos Santos Filho, S.G.; Mansano, R.D. Effect of the thermal annealing on the electrical and physical properties of SiC thin films produced by RF magnetron sputtering. Thin Solid Film. 2006, 512, 170–175. [Google Scholar] [CrossRef]
- Oliveira, I.C.; Massi, M.; Santos, S.G.; Otani, C.; Maciel, H.S.; Mansano, R.D. Dieletric characteristics of AlN films grown by d.c.-magnetron sputtering discharge. Diam. Relat. Mater. 2001, 10, 1317–1321. [Google Scholar] [CrossRef]
- Schroder, D.K. Semiconductor Material and Device Characterization, 3rd ed.; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Dingemans, G.; Terlinden, N.M.; Verheijen, M.A.; van de Sanden, M.C.M.; Kessels, W.M.M. Controlling the fixed charge and passivation of Si (100)/Al2O3 interfaces using ultrathin SiO2 interlayers synthesized by atomic layer deposition. J. Appl. Phys. 2011, 110, 093715. [Google Scholar] [CrossRef]
- Tang, X.; Francis, L.A.; Simonis, P.; Haslinger, M.; Delamare, R.; Deschaume, O.; Flandre, D.; Defrance, P.; Jonas, A.M.; Vigneron, J.P.; et al. Room temperature atomic layer deposition of Al2O3 and replication of butterfly wings for photovoltaic application. J. Vac. Sci. Technol. A 2011, 30, 01A146. [Google Scholar] [CrossRef]
- Kotipali, R.; Delemare, R.; Poncelet, O.; Tang, X.; Francis, L.A.; Flandre, D. Passivation effects of atomic-layer-deposited aluminum oxide. EPJ Photovolt. 2013, 4, 1–8. [Google Scholar] [CrossRef]
- Liao, B.; Hoex, B.; Arbele, A.G.; Chi, D.; Bhatia, C.S. Excellent c-Si surface passivation by low-temperature atomic layer deposited titanium oxide. Appl. Phys. Lett. 2014, 104, 253903. [Google Scholar] [CrossRef]
- Hill, W.A.; Coleman, C.C. A single-frequency approximation for interface-state density determination. Solid State Electron. 1979, 23, 987–993. [Google Scholar] [CrossRef]
- Nicollian, E.H.; Brews, J.R. MOS (metal oxide semiconductor) physics and technology. J. Vac. Sci. Technol. 1982, 21, 1048. [Google Scholar]
- Yoshitsugu, K.; Horita, M.; Ishikawa, Y.; Uraoka, Y. Leakage current reduction in ALD-Al2O3 dieletric deposited on Si by pressure deuterium oxide annealing. ECS Trans. 2015, 67, 205–210. [Google Scholar] [CrossRef]
- Zougar, L.; Sali, S.; Kermadi, S.; Boucheham, A.; Boumaour, M.; Kechouane, M. Annealling impact on interface properties of sprayed Al2O3-based MIS structure for silicon surface passivation. J. Electron. Mater. 2019, 48, 916–924. [Google Scholar] [CrossRef]
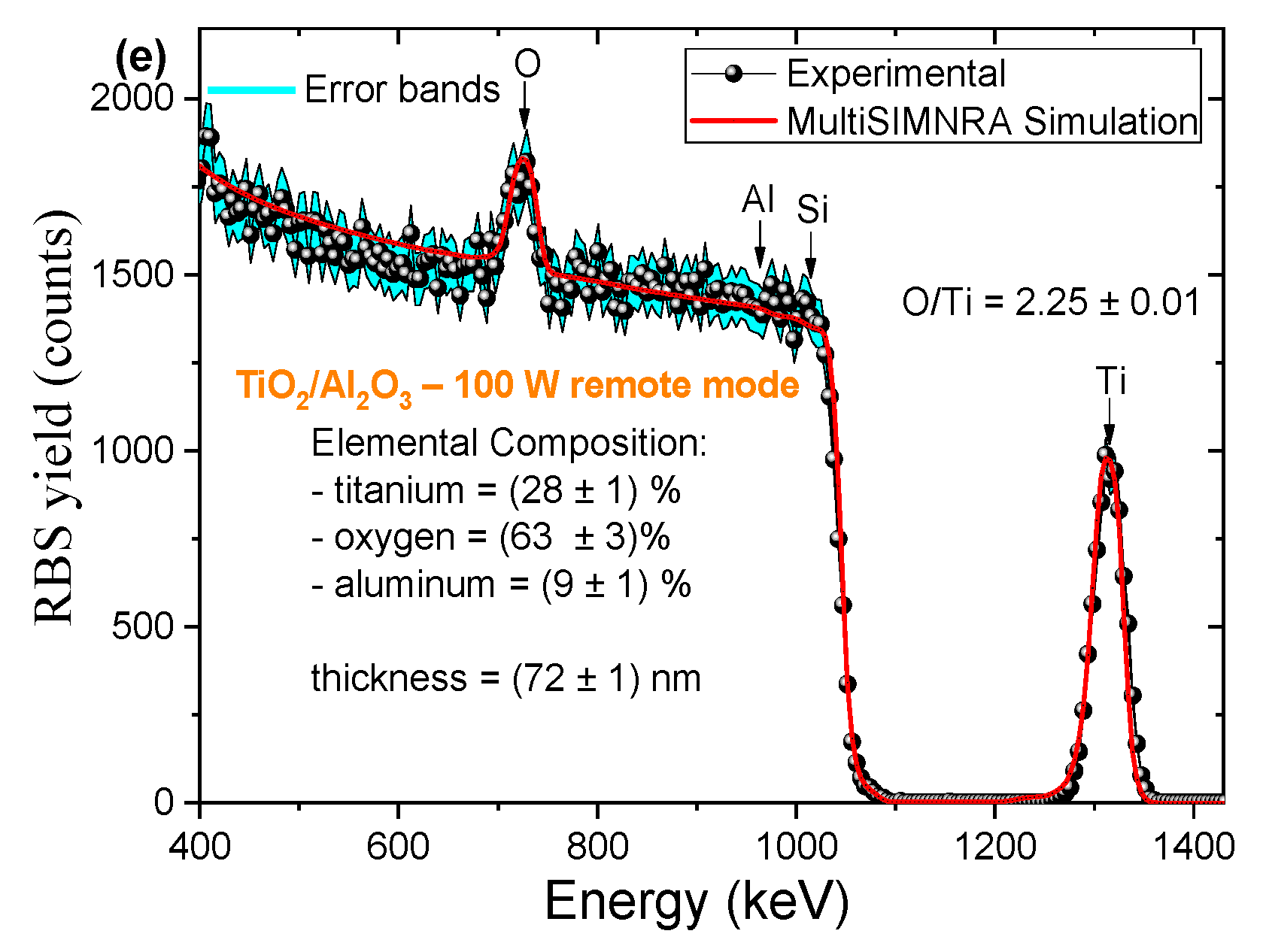
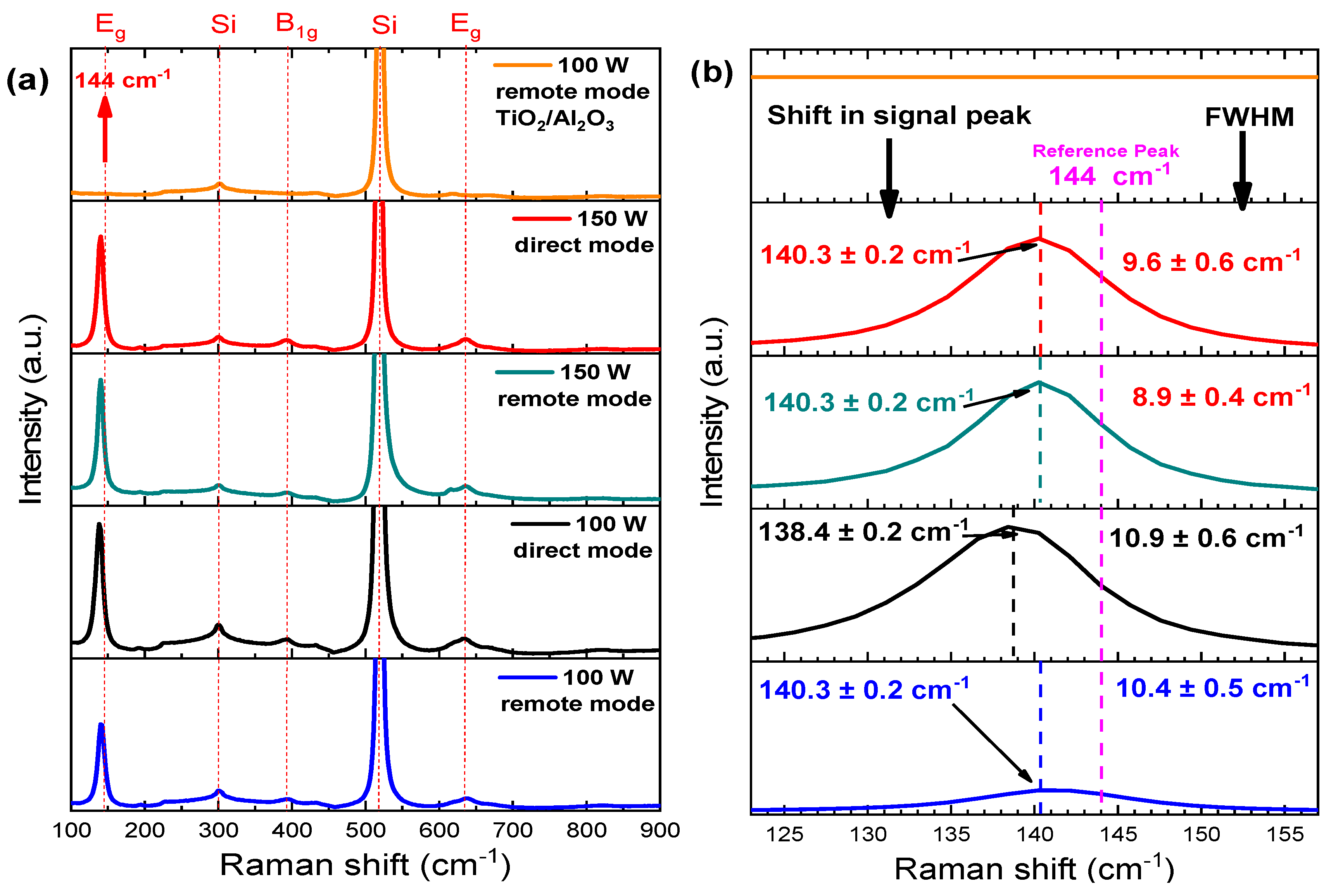



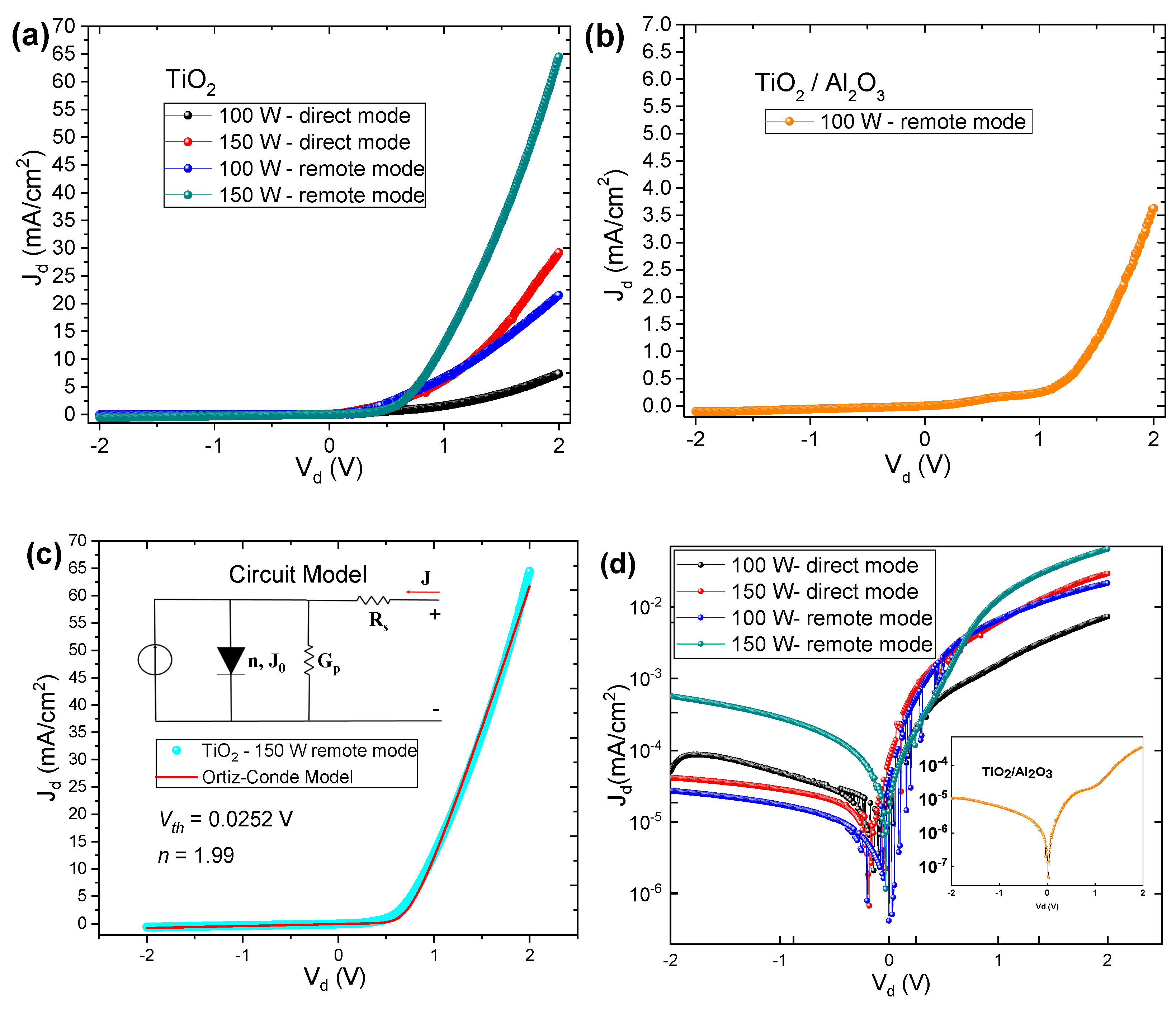
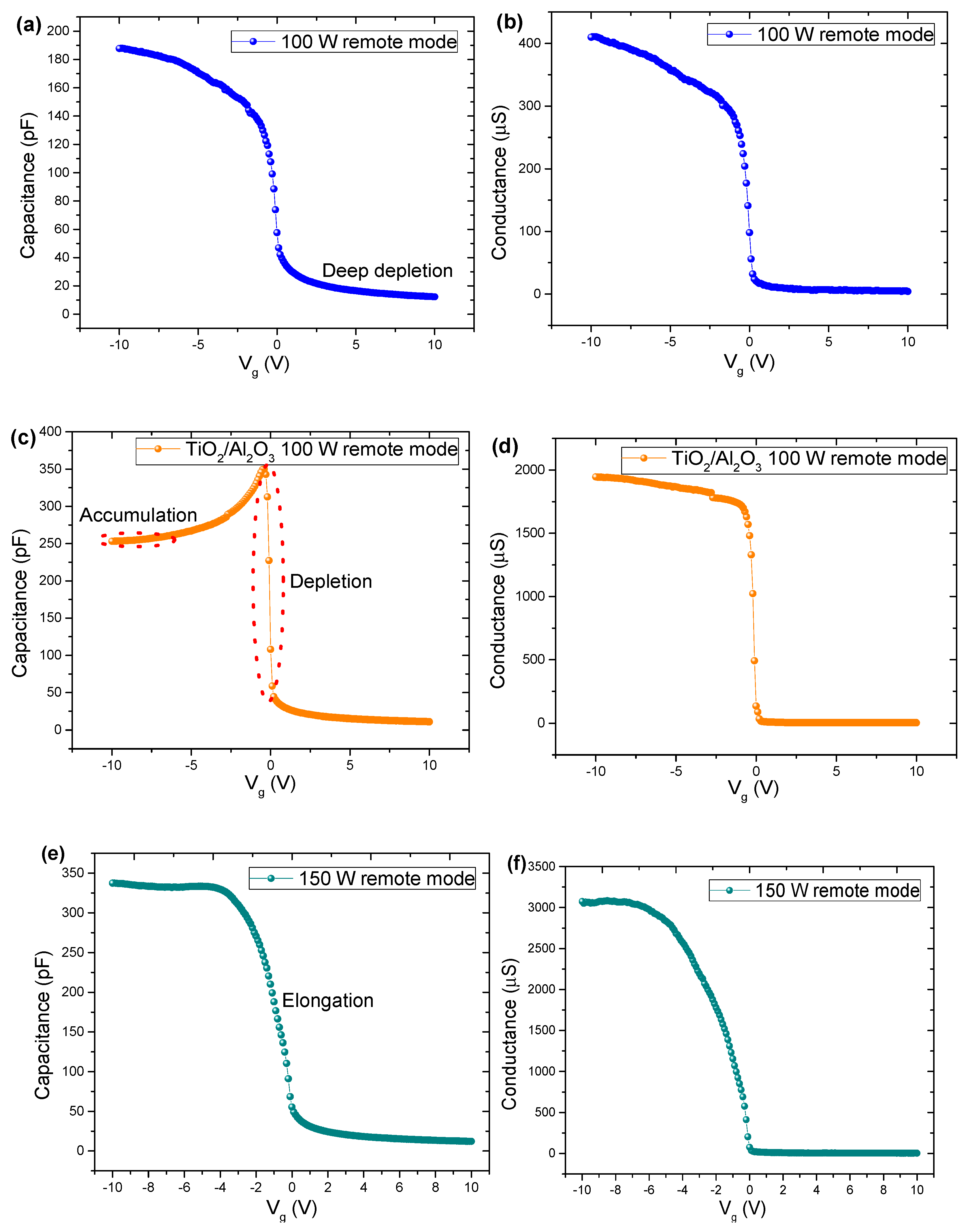
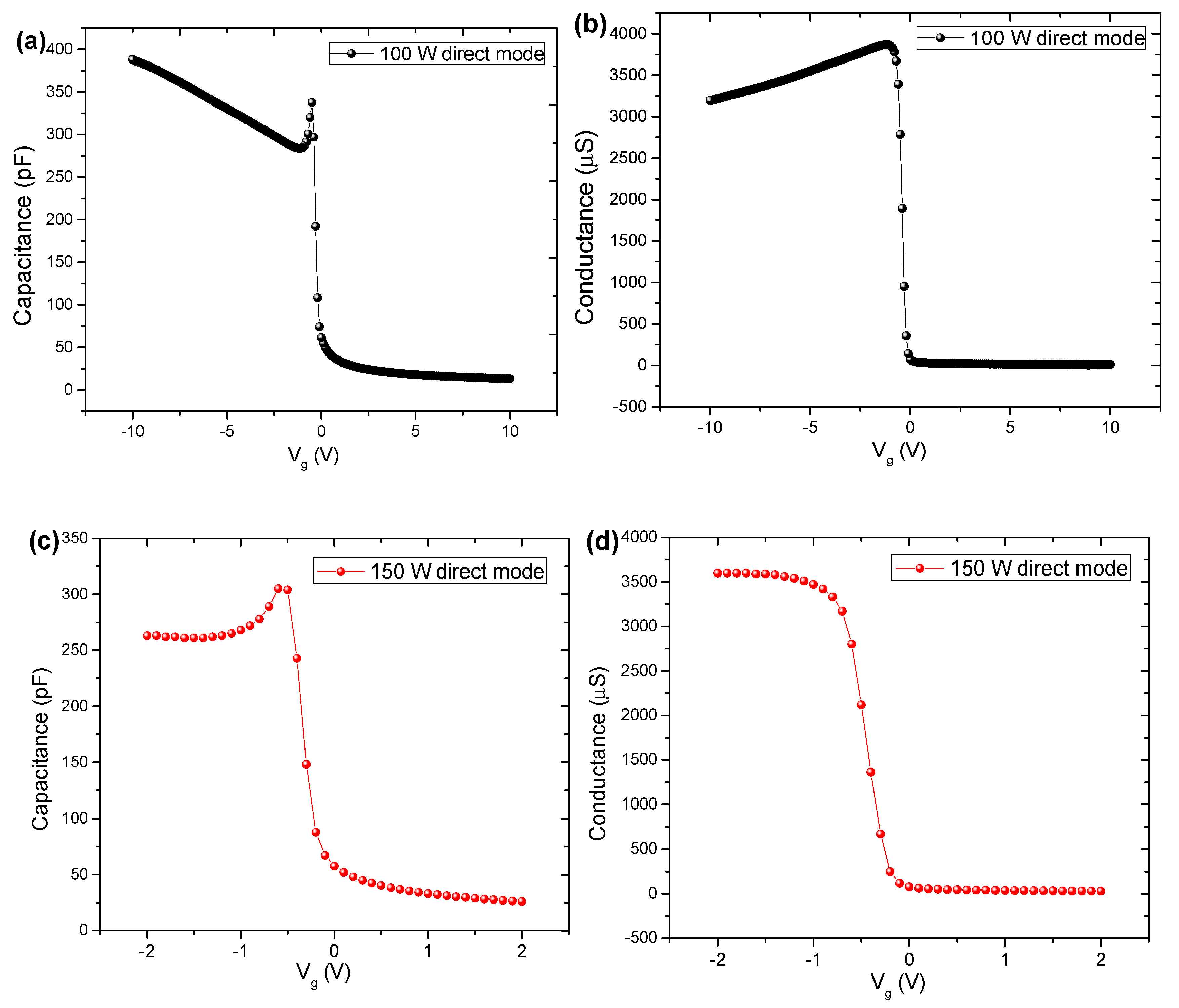
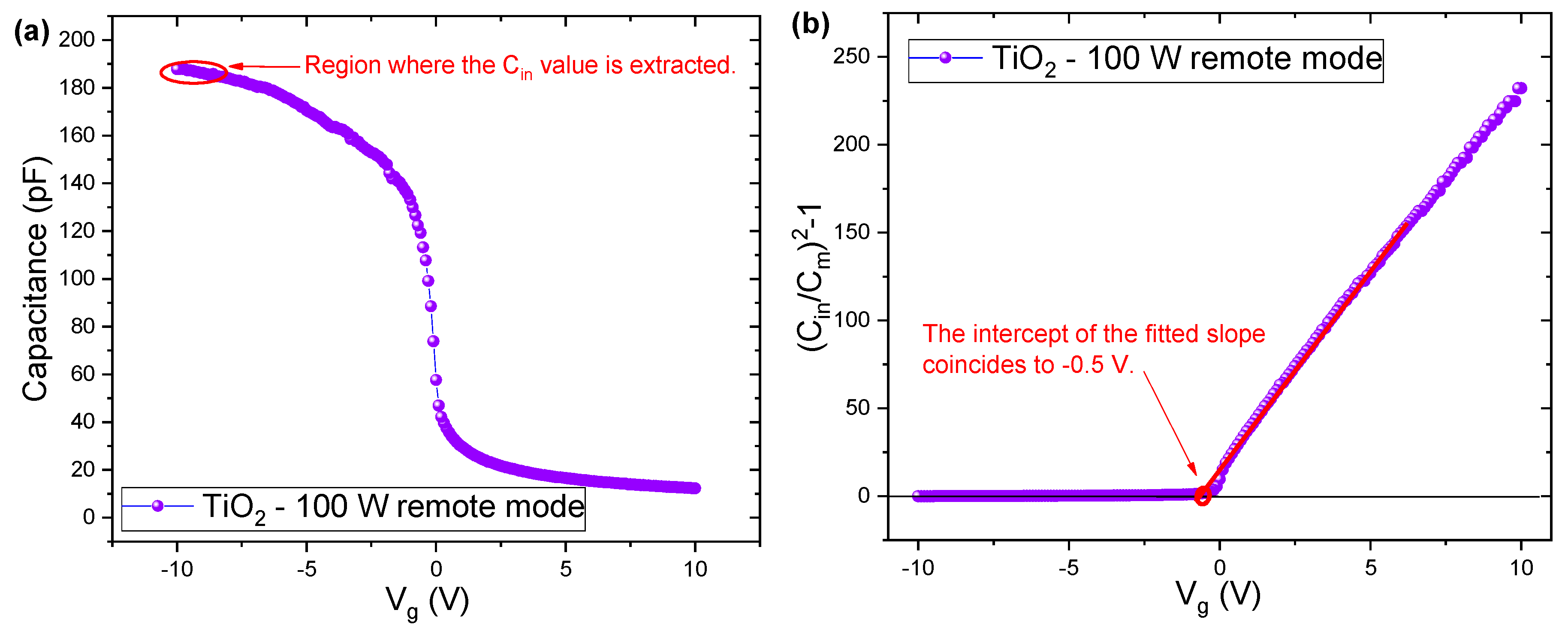
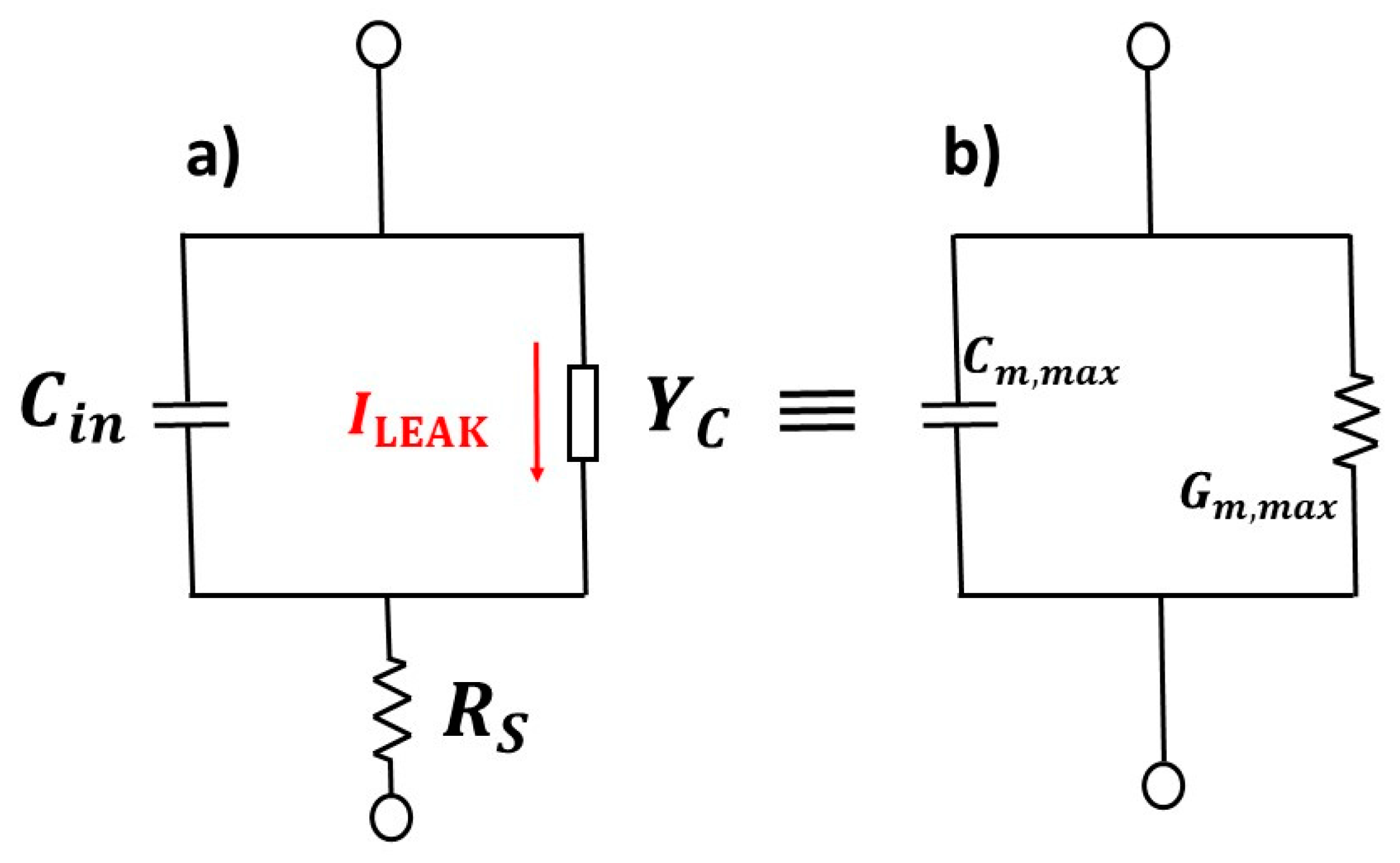
| Sample | Rs (Ω) | Gp (µS) | n (Ideality Factor) |
|---|---|---|---|
| TiO2-100 W remote mode | 70 | 36 | 1.79 |
| TiO2/Al2O3-100 W remote mode | 1110 | 6.8 | 1.59 |
| TiO2-100 W direct mode | 180 | 256 | 1.93 |
| TiO2-150 W direct mode | 47 | 89 | 1.99 |
| TiO2-150 W remote mode | 50 | 84 | 1.99 |
| Sample | Vfb (V) | Qf (cm−2) |
|---|---|---|
| TiO2-100 W remote mode | −0.5 | −3.54 × 1011 |
| TiO2/Al2O3-100 W remote mode | −0.4 | −8.41 × 1011 |
| TiO2-100 W direct mode | −0.2 | −2.41 × 1012 |
| TiO2-150 W direct mode | −0.4 | −2.10 × 1012 |
| TiO2-150 W remote mode | −0.3 | −8.80 × 1011 |
| Sample | Dit (eV−1.cm−2) |
|---|---|
| TiO2/Al2O3-100 W remote mode | 5.52 × 1011 |
| TiO2-100 W direct mode | 7.08 × 1011 |
| TiO2-100 W remote mode | 2.44 × 1011 |
| TiO2-150 W direct mode | 3.48 × 1011 |
| TiO2-150 W remote mode | 6.74 × 1011 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiappim, W.; Watanabe, M.; Dias, V.; Testoni, G.; Rangel, R.; Fraga, M.; Maciel, H.; dos Santos Filho, S.; Pessoa, R. MOS Capacitance Measurements for PEALD TiO2 Dielectric Films Grown under Different Conditions and the Impact of Al2O3 Partial-Monolayer Insertion. Nanomaterials 2020, 10, 338. https://doi.org/10.3390/nano10020338
Chiappim W, Watanabe M, Dias V, Testoni G, Rangel R, Fraga M, Maciel H, dos Santos Filho S, Pessoa R. MOS Capacitance Measurements for PEALD TiO2 Dielectric Films Grown under Different Conditions and the Impact of Al2O3 Partial-Monolayer Insertion. Nanomaterials. 2020; 10(2):338. https://doi.org/10.3390/nano10020338
Chicago/Turabian StyleChiappim, William, Marcos Watanabe, Vanessa Dias, Giorgio Testoni, Ricardo Rangel, Mariana Fraga, Homero Maciel, Sebastião dos Santos Filho, and Rodrigo Pessoa. 2020. "MOS Capacitance Measurements for PEALD TiO2 Dielectric Films Grown under Different Conditions and the Impact of Al2O3 Partial-Monolayer Insertion" Nanomaterials 10, no. 2: 338. https://doi.org/10.3390/nano10020338
APA StyleChiappim, W., Watanabe, M., Dias, V., Testoni, G., Rangel, R., Fraga, M., Maciel, H., dos Santos Filho, S., & Pessoa, R. (2020). MOS Capacitance Measurements for PEALD TiO2 Dielectric Films Grown under Different Conditions and the Impact of Al2O3 Partial-Monolayer Insertion. Nanomaterials, 10(2), 338. https://doi.org/10.3390/nano10020338