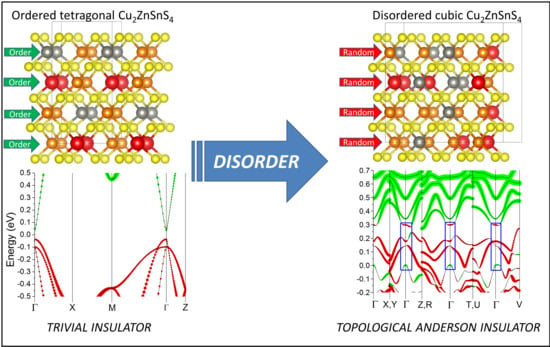
Topological Anderson Insulator in Cation-Disordered Cu2ZnSnS4
Abstract
:1. Introduction
2. Computational Methodology
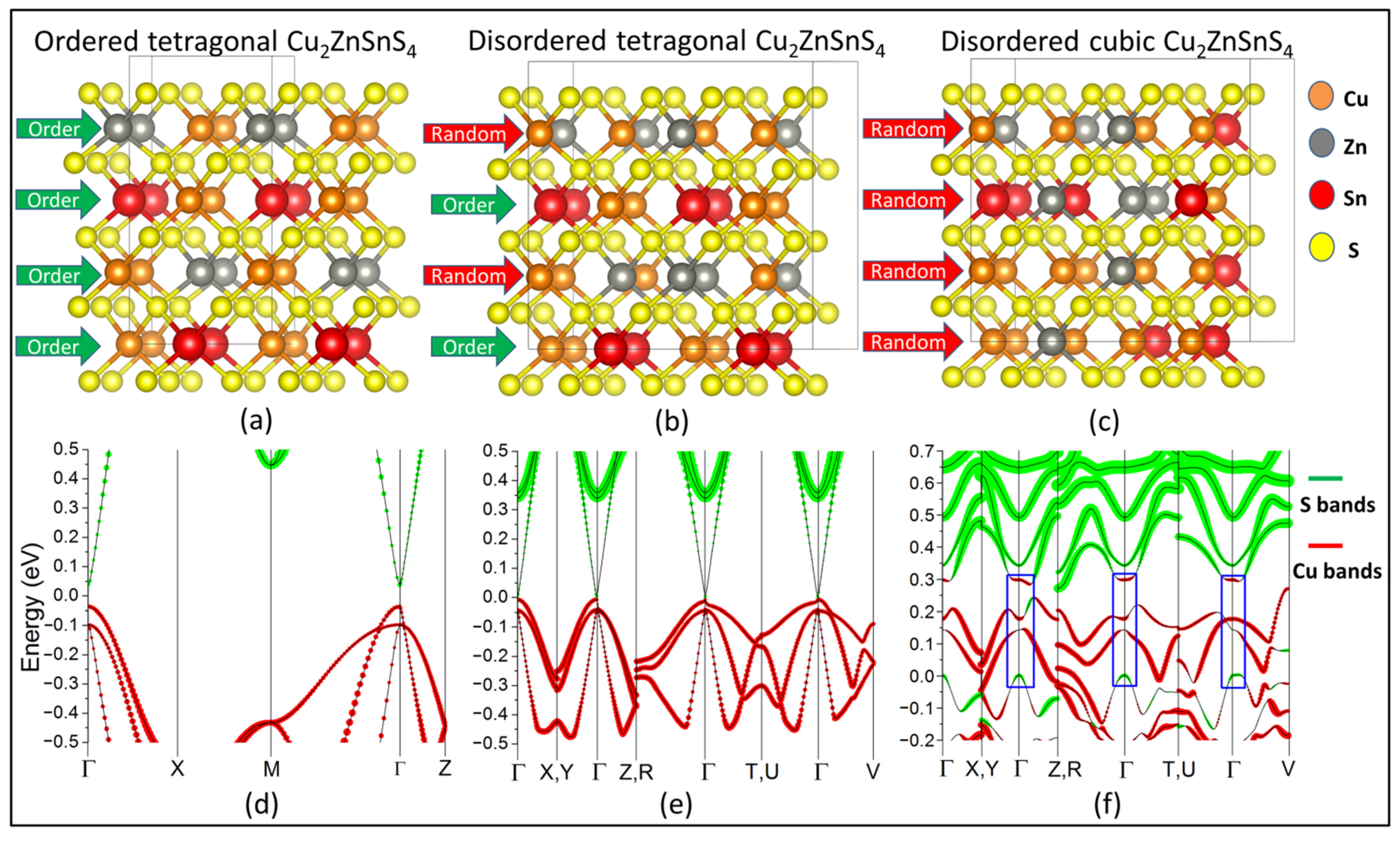
3. Results and Discussion
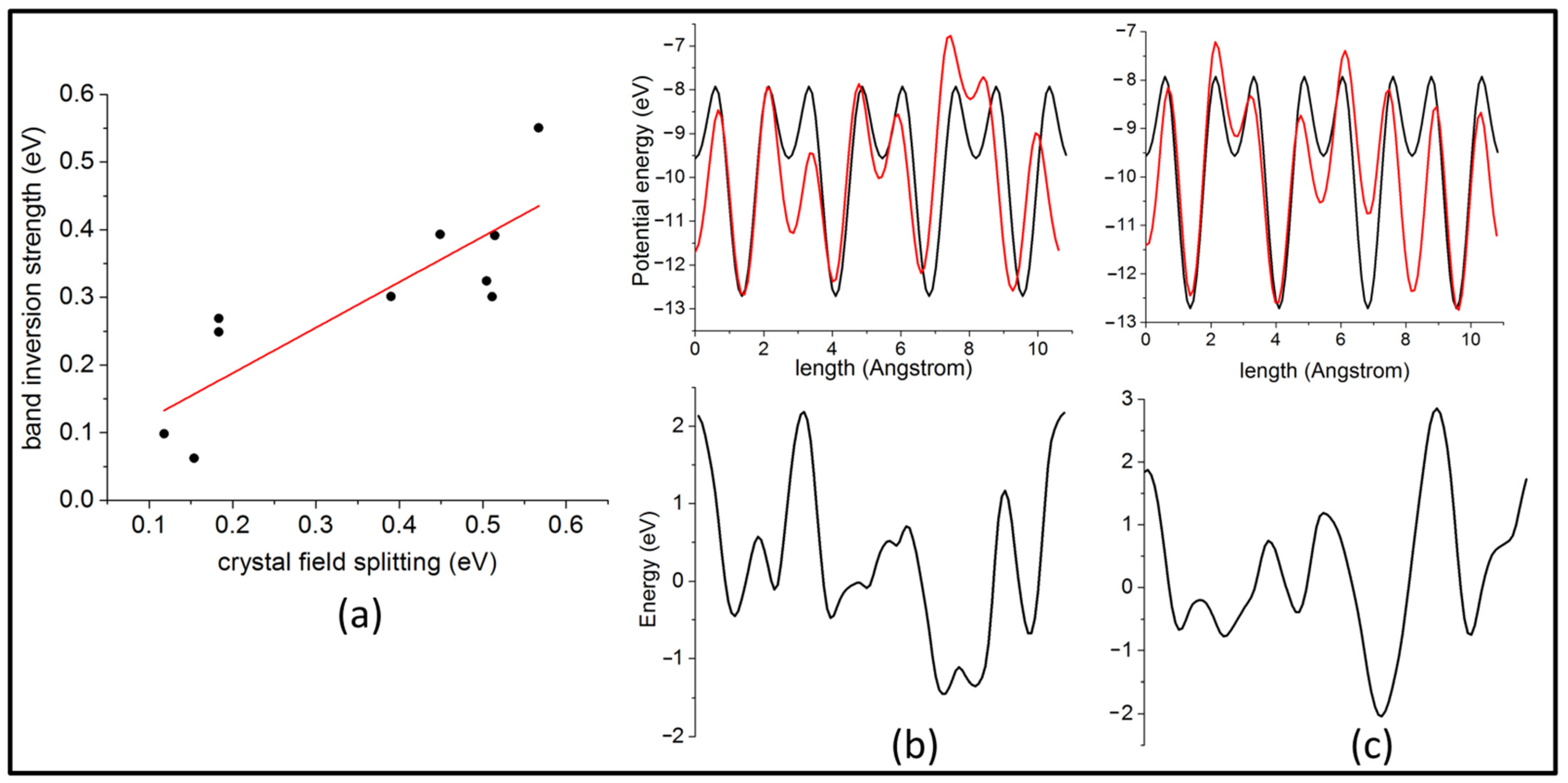
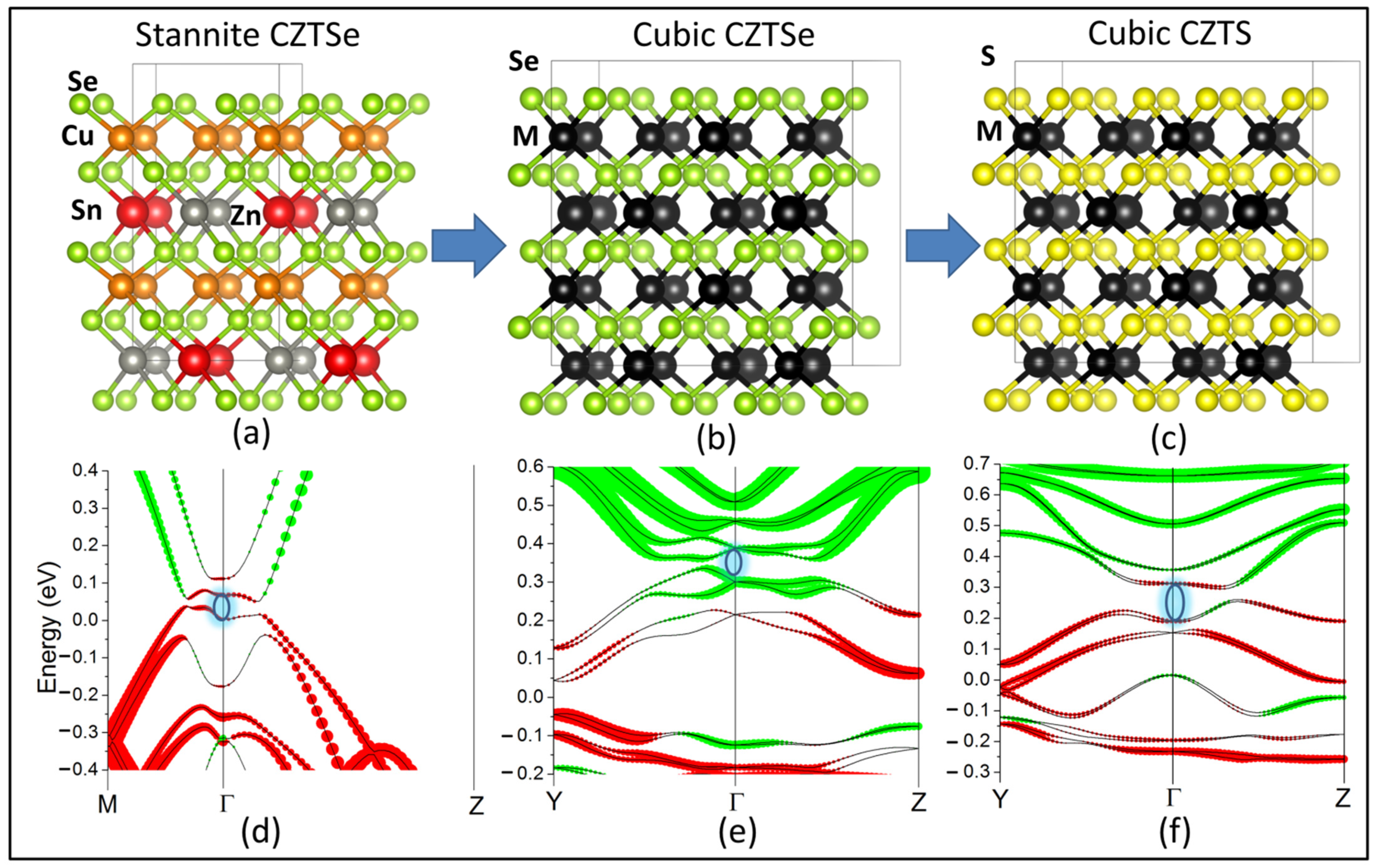
3.1. Band Inversion in the Bulk
3.2. Adiabatic Continuity
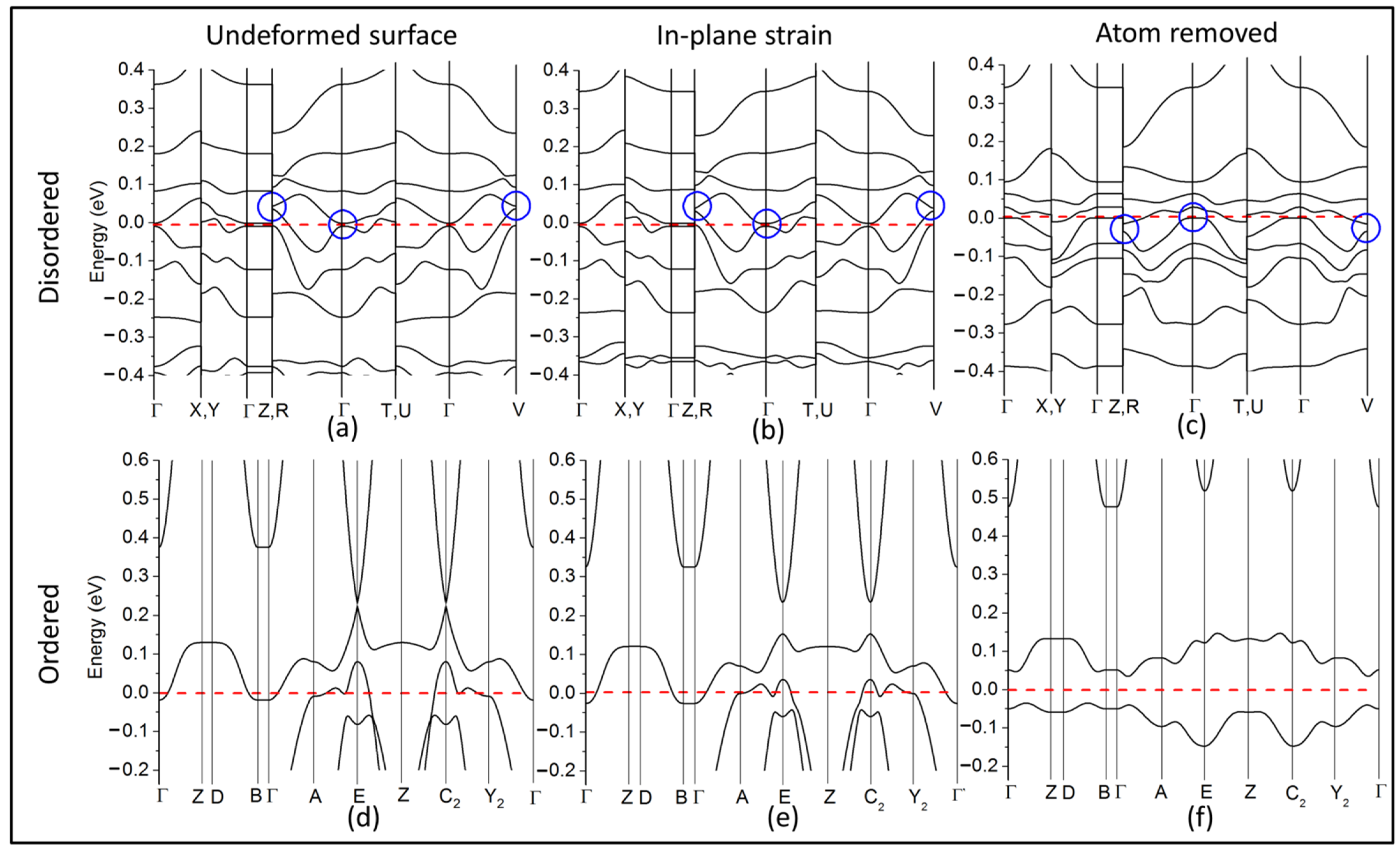
3.3. Topological Surface States
3.4. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef] [Green Version]
- Xu, N.; Xu, Y.; Zhu, J. Topological insulators for thermoelectrics. NPJ Quantum Mater. 2017, 2, 51. [Google Scholar] [CrossRef]
- Pal, K.; Anand, S.; Waghmare, U.V. Thermoelectric properties of materials with nontrivial electronic topology. J. Mater. Chem. C 2015, 3, 12130–12139. [Google Scholar] [CrossRef]
- Müchler, L.; Casper, F.; Yan, B.; Chadov, S.; Felser, C. Topological insulators and thermoelectric materials. Phys. Status Solidi-Rapid Res. Lett. 2013, 7, 91–100. [Google Scholar] [CrossRef] [Green Version]
- Moore, J.E. The birth of topological insulators. Nature 2010, 464, 194–198. [Google Scholar] [CrossRef]
- He, M.; Sun, H.; He, Q.L. Topological insulator: Spintronics and quantum computations. Front. Phys. 2019, 14, 43401. [Google Scholar] [CrossRef]
- Pesin, D.; MacDonald, A.H. Spintronics and pseudospintronics in graphene and topological insulators. Nat. Mater. 2012, 11, 409–416. [Google Scholar] [CrossRef]
- Paudel, H.P.; Leuenberger, M.N. Three-dimensional topological insulator quantum dot for optically controlled quantum memory and quantum computing. Phys. Rev. B-Condens. Matter Mater. Phys. 2013, 88, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Klitzing, K.V.; Dorda, G.; Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance. Phys. Rev. Lett. 1980, 45, 494–497. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Kane, C.L.; Mele, E.J. Topological insulators in three dimensions. Phys. Rev. Lett. 2007, 98, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. A topological Dirac insulator in a quantum spin Hall phase. Nature 2008, 452, 970–974. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Liu, C.X.; Qi, X.L.; Dai, X.; Fang, Z.; Zhang, S.C. Topological insulators in Bi 2 Se 3, Bi 2 Te 3 and Sb 2 Te 3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438–442. [Google Scholar] [CrossRef]
- Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.S.; Cava, R.J.; et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 398–402. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.L.; Analytis, J.G.; Chu, J.; Liu, Z.K.; Mo, S.; Qi, X.L.; Zhang, H.J.; Lu, D.H.; Dai, X.; Fang, Z.; et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3. Science 2009, 325, 178–181. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Wang, Y.; Chen, M.; Li, Z.; Song, C.; He, K.; Wang, L.; Chen, X.; Ma, X.; Xue, Q.K. Landau quantization and the thickness limit of topological insulator thin films of Sb 2Te 3. Phys. Rev. Lett. 2012, 108, 2–6. [Google Scholar] [CrossRef] [Green Version]
- Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 2011, 106, 106802. [Google Scholar] [CrossRef] [Green Version]
- Alexandradinata, A.; Fang, C.; Gilbert, M.J.; Bernevig, B.A. Spin-Orbit-free topological insulators without time-reversal symmetry. Phys. Rev. Lett. 2014, 113, 245202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, S.; Gong, X.G.; Duan, C.G.; Zhu, Z.Q.; Chu, J.H.; Walsh, A.; Yao, Y.G.; Ma, J.; Wei, S.H. Band structure engineering of multinary chalcogenide topological insulators. Phys. Rev. B-Condens. Matter Mater. Phys. 2011, 83, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.J.; Lin, H.; Das, T.; Hasan, M.Z.; Bansil, A. Topological insulators in the quaternary chalcogenide compounds and ternary famatinite compounds. New J. Phys. 2010, 13, 085017. [Google Scholar] [CrossRef]
- Huang, H.; Liu, F. Quantum Spin Hall Effect and Spin Bott Index in a Quasicrystal Lattice. Phys. Rev. Lett. 2018, 121, 126401. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Liu, F. A Unified View of Topological Phase Transition in Band Theory. Research 2020, 2020, 1–7. [Google Scholar] [CrossRef]
- Ni, X.; Huang, H.; Liu, F. Robustness of topological insulating phase against vacancy, vacancy cluster, and grain boundary bulk defects. Phys. Rev. B 2020, 101, 125114. [Google Scholar] [CrossRef]
- Li, J.; Chu, R.L.; Jain, J.K.; Shen, S.Q. Topological anderson insulator. Phys. Rev. Lett. 2009, 102, 136806. [Google Scholar] [CrossRef] [PubMed]
- Groth, C.W.; Wimmer, M.; Akhmerov, A.R.; Tworzydło, J.; Beenakker, C.W.J. Theory of the Topological Anderson Insulator. Phys. Rev. Lett. 2009, 103, 196805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, H.M.; Rosenberg, G.; Refael, G.; Franz, M. Topological Anderson insulator in three dimensions. Phys. Rev. Lett. 2010, 105, 2–5. [Google Scholar] [CrossRef] [Green Version]
- Meier, E.J.; An, F.A.; Dauphin, A.; Maffei, M.; Massignan, P.; Hughes, T.L.; Gadway, B. Observation of the topological Anderson insulator in disordered atomic wires. Science 2018, 933, 929–933. [Google Scholar] [CrossRef] [Green Version]
- Nakajima, S.; Takei, N.; Sakuma, K.; Kuno, Y.; Marra, P.; Takahashi, Y. Competition and interplay between topology and quasi-periodic disorder in Thouless pumping of ultracold atoms. Nat. Phys. 2021, 17, 844–849. [Google Scholar] [CrossRef]
- Isotta, E.; Mukherjee, B.; Fanciulli, C.; Ataollahi, N.; Sergueev, I.; Stankov, S.; Edla, R.; Pugno, N.M.; Scardi, P. Origin of a Simultaneous Suppression of Thermal Conductivity and Increase of Electrical Conductivity and Seebeck Coefficient in Disordered Cubic Cu2ZnSnS4. Phys. Rev. Appl. 2020, 14, 064073. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 169–186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Lim, D.H.; Wilcox, J. DFT-based study on oxygen adsorption on defective graphene-supported Pt nanoparticles. J. Phys. Chem. C 2011, 115, 22742–22747. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef] [Green Version]
- Paier, J.; Asahi, R.; Nagoya, A.; Kresse, G. Cu2 ZnSnS4 as a potential photovoltaic material: A hybrid Hartree-Fock density functional theory study. Phys. Rev. B-Condens. Matter Mater. Phys. 2009, 79, 115126. [Google Scholar] [CrossRef]
- Hinuma, Y.; Pizzi, G.; Kumagai, Y.; Oba, F.; Tanaka, I. Band structure diagram paths based on crystallography. Comput. Mater. Sci. 2017, 128, 140–184. [Google Scholar] [CrossRef] [Green Version]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Zhou, H.; Hsu, W.C.; Duan, H.S.; Bob, B.; Yang, W.; Song, T.B.; Hsu, C.J.; Yang, Y. CZTS nanocrystals: A promising approach for next generation thin film photovoltaics. Energy Environ. Sci. 2013, 6, 2822–2838. [Google Scholar] [CrossRef]
- Ravindiran, M.; Praveenkumar, C. Status review and the future prospects of CZTS based solar cell–A novel approach on the device structure and material modeling for CZTS based photovoltaic device. Renew. Sustain. Energy Rev. 2018, 94, 317–329. [Google Scholar] [CrossRef]
- Ataollahi, N.; Bazerla, F.; Malerba, C.; Chiappini, A.; Ferrari, M.; Maggio, R.D.; Scardi, P. Synthesis and Post-Annealing of Cu 2 ZnSnS 4 Absorber Layers Based on Oleylamine/1-dodecanethiol. Materials 2019, 12, 3320. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Syafiq, U.; Ataollahi, N.; Di Maggio, R.; Scardi, P. Solution-based synthesis and characterization ofcu2znsns4 (czts) thin films. Molecules 2019, 24, 3454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ataollahi, N.; Malerba, C.; Cappelletto, E.; Ciancio, R.; Edla, R.; Di Maggio, R.; Scardi, P. Control of composition and grain growth in Cu 2 ZnSnS 4 thin films from nanoparticle inks. Thin Solid Films 2019, 674, 12–21. [Google Scholar] [CrossRef]
- Syafiq, U.; Ataollahi, N.; Scardi, P. Progress in CZTS as hole transport layer in perovskite solar cell. Sol. Energy 2020, 196, 399–408. [Google Scholar] [CrossRef]
- Ali, A.; Jacob, J.; Arshad, M.I.; Ajaz un Nabi, M.; Ashfaq, A.; Mahmood, K.; Amin, N.; Ikram, S.; Rehman, U.; Hussain, S.; et al. Enhancement of thermoelectric properties of sulphurized CZTS nano-crystals by the engineering of secondary phases. Solid State Sci. 2020, 103, 106198. [Google Scholar] [CrossRef]
- Ashfaq, A.; Jacob, J.; Bano, N.; Ali, A.; Ahmad, W.; Mahmood, K.; Arshad, M.I.; Ikram, S.; Rehman, U.; Hussain, S. Tailoring the thermoelectric properties of sol-gel grown CZTS/ITO thin films by controlling the secondary phases. Phys. B Condens. Matter 2019, 558, 86–90. [Google Scholar] [CrossRef]
- Ashfaq, A.; Jacon, J.; Ali, A.; Mehboob, K.; Mahmood, K.; Rehman, U.; Ahmad, W.; Ikram, S.; Amin, N.; Tahir, S.; et al. Designing of Seebeck coefficient and electrical conductivity in CZTS thin films for giant power factor. Ceram. Int. 2020, 46, 9646–9655. [Google Scholar] [CrossRef]
- Isotta, E.; Pugno, N.M.; Scardi, P. Nanostructured kesterite (Cu2ZnSnS4) for applications in thermoelectric devices. Powder Diffr. 2019, 32, 42–47. [Google Scholar] [CrossRef] [Green Version]
- Isotta, E.; Fanciulli, C.; Pugno, N.M.; Scardi, P. Effect of the Order-Disorder Transition on the Seebeck Coefficient of Nanostructured Thermoelectric. Nanomaterials 2019, 9, 762. [Google Scholar] [CrossRef] [Green Version]
- Isotta, E.; Mukherjee, B.; Fanciulli, C.; Pugno, N.M.; Scardi, P. Order-Disorder Transition in Kesterite Cu2ZnSnS4: Thermopower Enhancement via Electronic Band Structure Modification. J. Phys. Chem. C 2020, 124, 7091–7096. [Google Scholar] [CrossRef]
- Scragg, J.J.S.; Choubrac, L.; Lafond, A.; Ericson, T.; Platzer-Björkman, C. A low-temperature order-disorder transition in Cu2ZnSnS4 thin films. Appl. Phys. Lett. 2014, 104, 2–6. [Google Scholar] [CrossRef] [Green Version]
- Persson, C. Electronic and optical properties of Cu2ZnSnS4 and Cu2ZnSnSe4. J. Appl. Phys. 2010, 107, 053710. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 34, 1757–1762. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Liu, H.; Jiang, H.; Sun, Q.F.; Xie, X.C. Dependence of topological Anderson insulator on the type of disorder. Phys. Rev. B-Condens. Matter Mater. Phys. 2012, 85, 195125. [Google Scholar] [CrossRef] [Green Version]
- Girschik, A.; Libisch, F.; Rotter, S. Topological insulator in the presence of spatially correlated disorder. Phys. Rev. B-Condens. Matter Mater. Phys. 2013, 88, 014201. [Google Scholar] [CrossRef] [Green Version]
- Bansil, A.; Lin, H.; Das, T. Colloquium: Topological band theory. Rev. Mod. Phys. 2016, 88, 021004. [Google Scholar] [CrossRef] [Green Version]
- Al-Sawai, W.; Lin, H.; Markiewicz, R.S.; Wray, L.A.; Xia, Y.; Xu, S.Y.; Hasan, M.Z.; Bansil, A. Topological electronic structure in half-Heusler topological insulators. Phys. Rev. B-Condens. Matter Mater. Phys. 2010, 82, 125208. [Google Scholar] [CrossRef] [Green Version]
- Chadov, S.; Kiss, J.; Kübler, J.; Felser, C. Topological phase transition in bulk materials described by the coherent potential approximation technique. Phys. Status Solidi-Rapid Res. Lett. 2013, 7, 82–89. [Google Scholar] [CrossRef] [Green Version]
- Lin, H.; Wray, L.A.; Xia, Y.; Xu, S.; Jia, S.; Cava, R.J.; Bansil, A.; Hasan, M.Z. Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nat. Mater. 2010, 9, 546–549. [Google Scholar] [CrossRef] [Green Version]
- Lin, H.; Das, T.; Wang, Y.J.; Wray, L.A.; Xu, S.Y.; Hasan, M.Z.; Bansil, A. Adiabatic transformation as a search tool for new topological insulators: Distorted ternary Li2AgSb-class semiconductors and related compounds. Phys. Rev. B-Condens. Matter Mater. Phys. 2013, 87, 121202. [Google Scholar] [CrossRef] [Green Version]
- Feng, W.; Xiao, D.; Ding, J.; Yao, Y. Three-dimensional topological insulators in I-III-VI2 and II-IV-V2 chalcopyrite semiconductors. Phys. Rev. Lett. 2011, 106, 016402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, S.M.; Xuc, S.Y.; Belopolski, I.; Lee, C.C.; Chang, G.; Chang, T.R.; Wang, B.K.; Alidoust, N.; Bian, G.; Neupane, M.; et al. New type of Weyl semimetal with quadratic double Weyl fermions. Proc. Natl. Acad. Sci. USA 2016, 113, 1180–1185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meng, L.; Zhang, Y.; Ni, S.; Li, B.; Wu, W. Unique Schrödinger semimetal state in ternary Be2P3N honeycomb lattice. J. Mater. Chem. C 2019, 7, 4118–4123. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukherjee, B.; Isotta, E.; Fanciulli, C.; Ataollahi, N.; Scardi, P. Topological Anderson Insulator in Cation-Disordered Cu2ZnSnS4. Nanomaterials 2021, 11, 2595. https://doi.org/10.3390/nano11102595
Mukherjee B, Isotta E, Fanciulli C, Ataollahi N, Scardi P. Topological Anderson Insulator in Cation-Disordered Cu2ZnSnS4. Nanomaterials. 2021; 11(10):2595. https://doi.org/10.3390/nano11102595
Chicago/Turabian StyleMukherjee, Binayak, Eleonora Isotta, Carlo Fanciulli, Narges Ataollahi, and Paolo Scardi. 2021. "Topological Anderson Insulator in Cation-Disordered Cu2ZnSnS4" Nanomaterials 11, no. 10: 2595. https://doi.org/10.3390/nano11102595
APA StyleMukherjee, B., Isotta, E., Fanciulli, C., Ataollahi, N., & Scardi, P. (2021). Topological Anderson Insulator in Cation-Disordered Cu2ZnSnS4. Nanomaterials, 11(10), 2595. https://doi.org/10.3390/nano11102595