Combined Structural and Voltage Control of Giant Nonlinearities in Semiconductor Superlattices
Abstract
1. Introduction
2. Materials and Methods
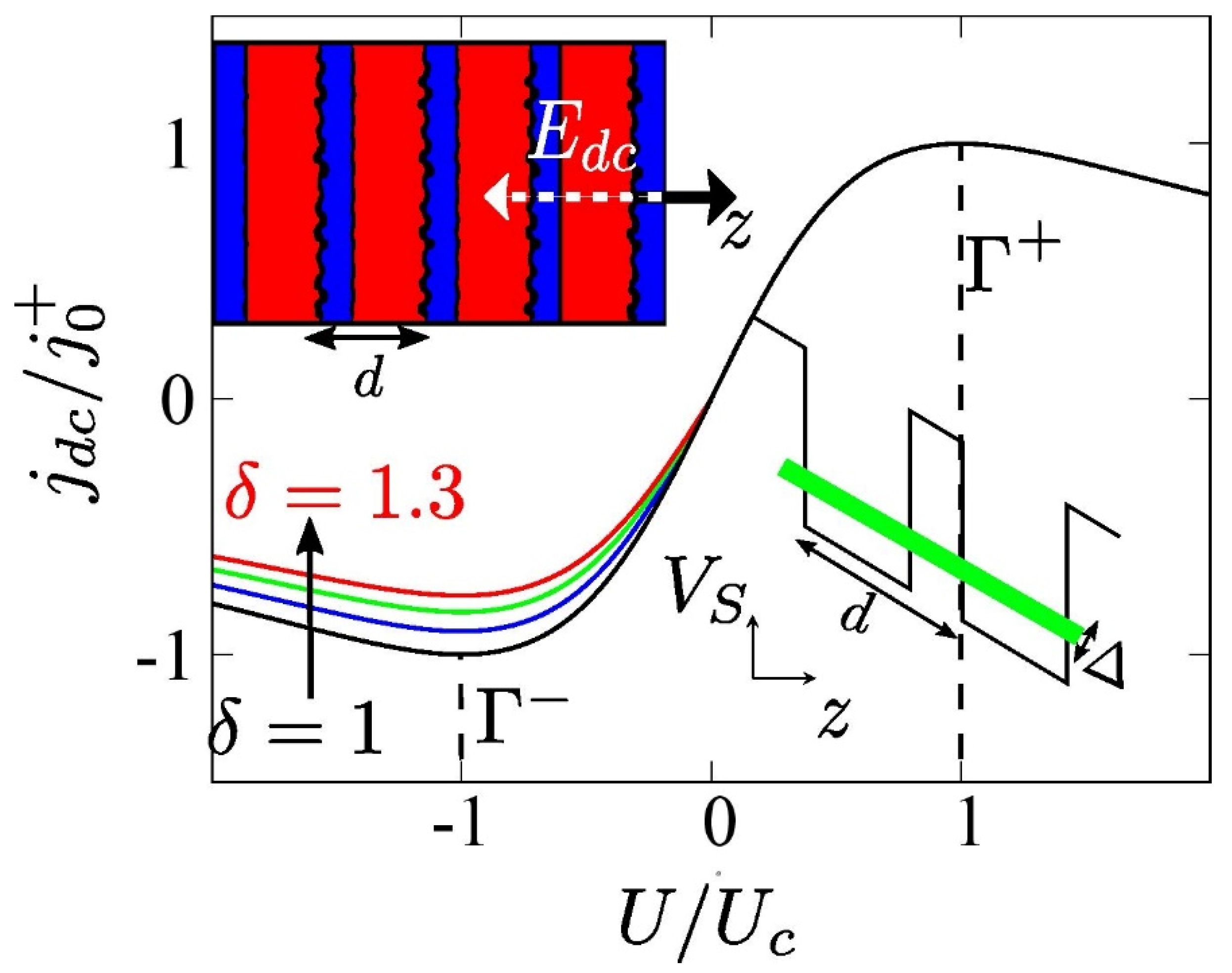
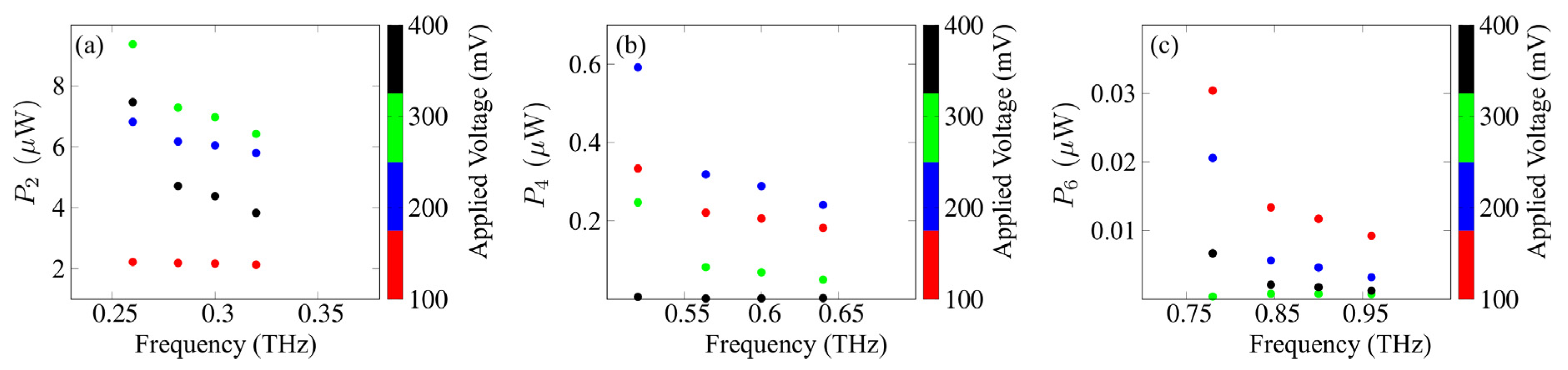
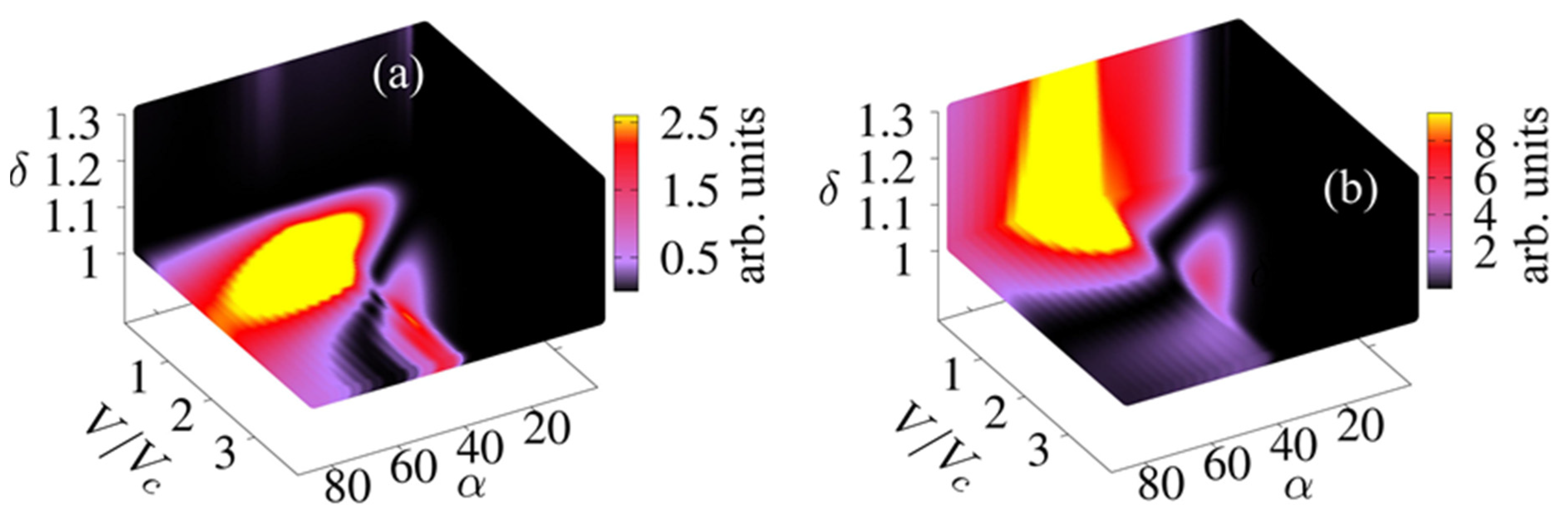
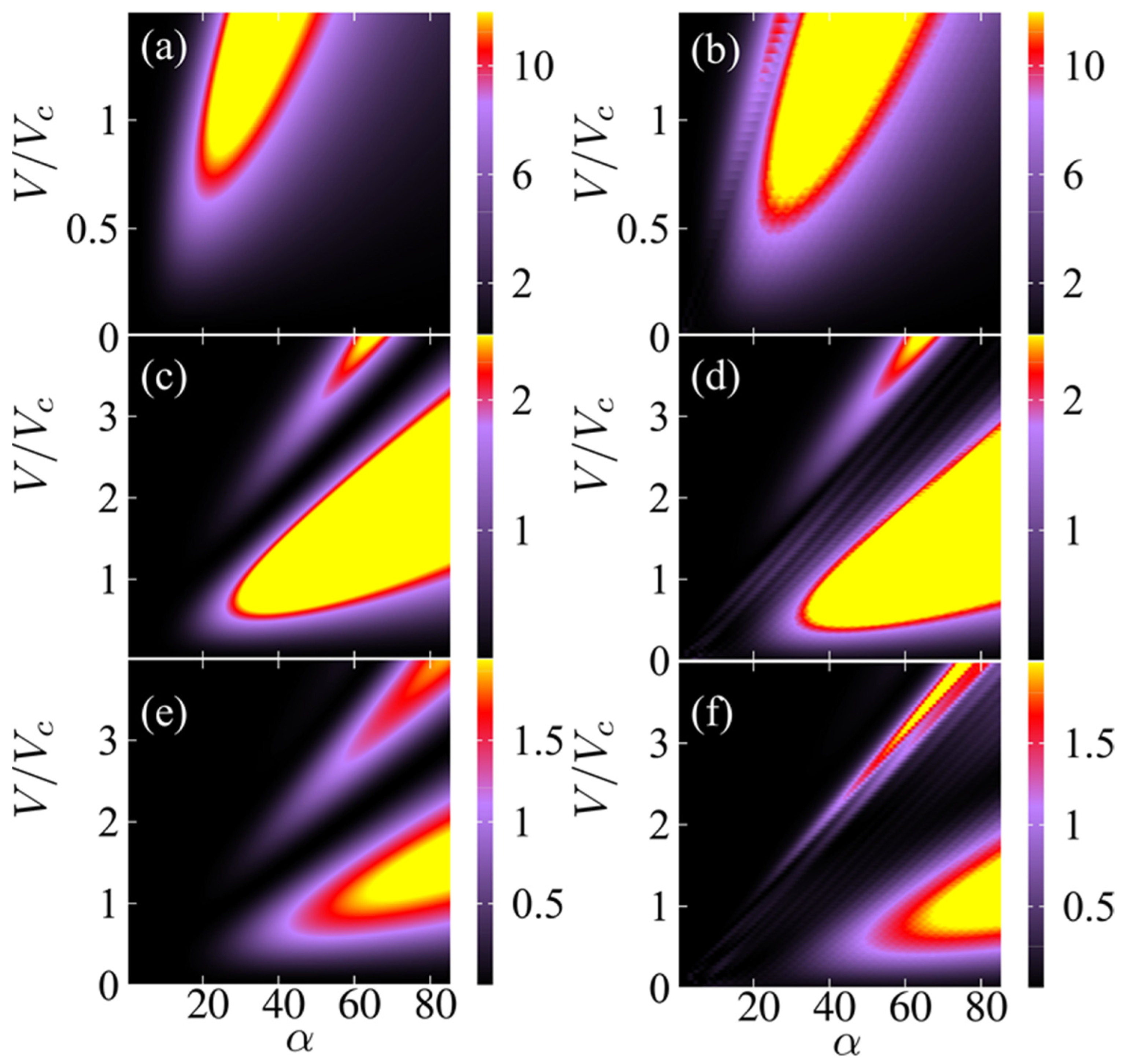
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wacker, A. Semiconductor superlattices: A model system for nonlinear transport. Phys. Rep. 2002, 357, 1–111. [Google Scholar] [CrossRef]
- Alfadhli, S.A.; Savel’ev, S.E.; Kusmartsev, F.V. Dirac-Weyl points’ manipulation using linear polarized laser field in Floquet crystals for various Graphene superlattices. J. Phys. Conf. Ser. 2018, 961, 012012. [Google Scholar] [CrossRef]
- Pereira, M. Analytical Expressions for Numerical Characterization of Semiconductors per Comparison with Luminescence. Materials 2018, 11, 2. [Google Scholar] [CrossRef]
- Waschke, C.; Roskos, H.G.; Schwedler, R.; Leo, K.; Kurz, H.; Köhler, K. Coherent Submillimeter-Wave Emission from Bloch Oscillations in a Semiconductor Superlattice. Phys. Rev. Lett. 1993, 70, 3319–3322. [Google Scholar] [CrossRef] [PubMed]
- Vaks, V. High-Precise Spectrometry of the Terahertz Frequency Range: The Methods, Approaches and Applications. J. Infrared Milli. Terahz. Waves 2012, 33, 43–53. [Google Scholar] [CrossRef]
- Pavelyev, D.G.; Skryl, A.S.; Bakunov, M.I. High-resolution broadband terahertz spectroscopy via electronic heterodyne detection of photonically generated terahertz frequency comb. Opt. Lett. 2014, 39, 5669–5672. [Google Scholar] [CrossRef] [PubMed]
- Eisele, H.; Li, L.; Linfield, E.H. High-performance GaAs/AlAs superlattice electronic devices in oscillators at frequencies 100–320 GHz. Appl. Phys. Lett. 2018, 112, 172103. [Google Scholar] [CrossRef]
- Gaifullin, M.B.; Alexeeva, N.V.; Hramov, A.E.; Makarov, V.V.; Maksimenko, V.A.; Koronovskii, A.A.; Greenaway, M.T.; Fromhold, T.M.; Patané, A.; Mellor, C.J.; et al. Balanov, Microwave Generation in Synchronized Semiconductor Superlattices. Phys. Rev. Appl. 2017, 7, 044024. [Google Scholar] [CrossRef]
- Dhillon, S.S.; Vitiello, M.S.; Linfield, E.H.; Davies, A.G.; Hoffmann, M.C.; Booske, J.; Paoloni, C.; Gensch, M.; Weightman, P.; Williams, G.P.; et al. The 2017 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2017, 50, 043001. [Google Scholar] [CrossRef]
- Mittelstädt, A.; Greif, L.A.T.; Jagsch, S.T.; Schliwa, A. Terahertz lasing at room temperature: A numerical study of a vertical-emitting quantum cascade laser based on a quantum dot superlattice. Phys. Rev. B 2021, 103, 115301. [Google Scholar] [CrossRef]
- Ferrari, A.C. Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems. Nanoscale 2015, 7, 4598–4810. [Google Scholar] [CrossRef]
- Pereira, M.F.; Shulika, O. Terahertz and Mid Infrared Radiation: Detection of Explosives and CBRN (Using Terahertz). In NATO Science for Peace and Security Series B: Physics and Biophysics; Springer: Dordrecht, The Netherlands, 2014; ISBN 978-94-017-8571-6. [Google Scholar]
- Pereira, M.F.; Shulika, O. Terahertz and Mid Infrared Radiation: Generation, Detection and Applications. In NATO Science for Peace and Security Series B: Physics and Biophysics; Springer Science & Business Media B.V.: Berlin, Germany, 2011; ISBN 978-94-007-0768-9. [Google Scholar]
- Faist, J.; Capasso, F.; Sivco, D.L.; Sirtori, C.; Hutchinson, A.L.; Cho, A.Y. Quantum Cascade Laser. Science 1994, 264, 553–556. [Google Scholar] [CrossRef]
- Köhler, R.; Tredicucci, A.; Beltram, F.; Beere, H.E.; Linfield, E.H.; Davies, A.G.; Ritchie, D.A.; Iotti, R.C.; Rossi, F. Terahertz semiconductor-heterostructure laser. Nature 2002, 417, 156–159. [Google Scholar] [CrossRef]
- Razeghi, M.; Lu, Q.Y.; Bandyopadhyay, N.; Zhou, W.; Heydari, D.; Bai, Y.; Slivken, S. Quantum cascade lasers: From tool to product. Opt. Express 2015, 23, 8462–8475. [Google Scholar] [CrossRef]
- Schmielau, T.; Pereira, M.F. Nonequilibrium many body theory for quantum transport in terahertz quantum cascade lasers. Appl. Phys. Lett. 2009, 95, 231111. [Google Scholar] [CrossRef]
- Pereira, M.F.; Lee, S.-C.; Wacker, A. Controlling many-body effects in the midinfrared gain and terahertz absorption of quantum cascade laser structures. Phys. Rev. B 2004, 69, 205310. [Google Scholar] [CrossRef]
- Pereira, M.F.; Wenzel, H. Interplay of Coulomb and nonparabolicity effects in the intersubband absorption of electrons and holes in quantum wells. Phys. Rev. B 2004, 70, 205331. [Google Scholar] [CrossRef]
- Pereira, M.F. Intervalence transverse-electric mode terahertz lasing without population inversion. Phys. Rev. B 2008, 78, 245305. [Google Scholar] [CrossRef]
- Pereira, M.F.; Tomić, S. Intersubband gain without global inversion through dilute nitride band engineering. Appl. Phys. Lett. 2011, 98, 061101. [Google Scholar] [CrossRef]
- Pereira, M.F. The Linewidth Enhancement Factor of Intersubband Lasers: From a Two-Level Limit to Gain without Inversion Conditions. Appl. Phys. Lett. 2016, 109, 222102. [Google Scholar] [CrossRef]
- Winge, D.O.; Franckie, M.; Verdozzi, C.; Wacker, A.; Pereira, M.F. Simple electron-electron scattering in non-equilibrium Green’s function simulations. J. Phys. Conf. Ser. 2016, 696, 012013. [Google Scholar] [CrossRef]
- Wacker, A.; Lindskog, M.; Winge, D.O. Nonequilibrium Green’s Function Model for Simulation of Quantum Cascade Laser Devices Under Operating Conditions. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1200611. [Google Scholar] [CrossRef]
- Franckié, M.; Faist, J. Bayesian optimization of terahertz quantum cascade lasers. Phys. Rev. Appl. 2020, 13, 034025. [Google Scholar] [CrossRef]
- Gajić, A.; Radovanović, J.; Vuković, N.; Milanović, V.; Boiko, D.L. Theoretical approach to quantum cascade micro-laser broadband multimode emission in strong magnetic fields. Phys. Lett. A 2021, 387, 127007. [Google Scholar] [CrossRef]
- Vukovic, N.; Radovanovic, J.; Milanovic, V.; Boiko, D.L. Numerical study of Risken–Nummedal–Graham–Haken instability in mid-infrared Fabry–Pérot quantum cascade lasers. Opt. Quantum Electron. 2020, 52, 91. [Google Scholar] [CrossRef]
- Pereira, M.F.; Winge, D.; Wacker, A.; Zubelli, J.P.; Rodrigues, A.S.; Anfertev, V.; Vaks, V. Theory and Measurements of Harmonic Generation in Semiconductor Superlattices with Applications in the 100 GHz to 1 THz Range. Phys. Rev. B 2017, 96, 045306. [Google Scholar] [CrossRef]
- Winnerl, S.; Schomburg, E.; Brandl, S.; Kus, O.; Renk, K.F.; Wanke, M.C.; Allen, S.J.; Ignatov, A.A.; Ustinov, V.; Zhukov, A.; et al. Frequency doubling and tripling of terahertz radiation in a GaAs/AlAs superlattice due to frequency modulation of bloch oscillations. Appl. Phys. Lett. 2000, 77, 1259. [Google Scholar] [CrossRef]
- Schomburg, E.; Grenzer, J.; Hofbeck, K.; Dummer, C.; Winnerl, S.; Ignatov, A.; Renk, K.; Pavel’Ev, D.; Koschurinov, J.; Melzer, B.; et al. Superlattice frequency multiplier for generation of submillimeter waves. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 724. [Google Scholar] [CrossRef]
- Ignatov, A.A.; Schomburg, E.; Grenzer, J.; Renk, K.F.; Dodin, E.P. THz-field induced nonlinear transport and dc voltage generation in a semiconductor superlattice due to bloch oscillations. Z. Phys. 1995, 98, 187–195. [Google Scholar] [CrossRef]
- Romanov, Y.A.; Romanova, Y.Y. Bloch oscillations in superlattices: The problem of a terahertz oscillator. Semiconductors 2005, 39, 147. [Google Scholar] [CrossRef]
- Le Person, H.; Minot, C.; Boni, L.; Palmier, J.F.; Mollot, F. Gunn oscillations up to 20 GHz optically induced in GaAs/AlAs superlattice. Appl. Phys. Lett. 1992, 60, 2397. [Google Scholar] [CrossRef]
- Schomburg, E. Current oscillation in superlattices with different miniband widths. Phys. Rev. B 1998, 58, 4035. [Google Scholar] [CrossRef]
- Meier, T.; Von Plessen, G.; Thomas, P.; Koch, S.W. Coherent electric-field effects in semiconductors. Phys. Rev. Lett. 1994, 73, 902. [Google Scholar] [CrossRef]
- Dignam, M. Excitonic bloch oscillations in a terahertz field. Phys. Rev. B 1999, 59, 5770. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, A.; Yang, L.; Dignam, M.M. Tunable terahertz amplification in optically excited biased semiconductor superlattices: Influence of excited excitonic states. Phys. Rev. B 2008, 77, 115307. [Google Scholar] [CrossRef]
- Pereira, M.F.; Anfertev, V.; Zubelli, J.P.; Vaks, V. THz Generation by GHz Multiplication in Superlattices. J. Nanophotonics 2017, 11, 046022. [Google Scholar] [CrossRef]
- Apostolakis, A.; Pereira, M.F. Controlling the harmonic conversion efficiency in semiconductor superlattices by interface roughness design. AIP Adv. 2019, 9, 015022. [Google Scholar] [CrossRef]
- Apostolakis, A.; Pereira, M.F. Potential and limits of superlattice multipliers coupled to different input power sources. J. Nanophotonics 2019, 13, 036017. [Google Scholar] [CrossRef]
- Apostolakis, A.; Pereira, M.F. Superlattice nonlinearities for Gigahertz-Terahertz generation in harmonic multipliers. Nanophotonics 2020, 9, 3941–3952. [Google Scholar] [CrossRef]
- Pereira, M.F.; Anfertev, V.; Shevchenko, Y.; Vaks, V. Giant controllable gigahertz to terahertz nonlinearities in superlattices. Sci. Rep. 2020, 10, 15950. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, M.F.; Apostolakis, A. Combined Structural and Voltage Control of Giant Nonlinearities in Semiconductor Superlattices. Nanomaterials 2021, 11, 1287. https://doi.org/10.3390/nano11051287
Pereira MF, Apostolakis A. Combined Structural and Voltage Control of Giant Nonlinearities in Semiconductor Superlattices. Nanomaterials. 2021; 11(5):1287. https://doi.org/10.3390/nano11051287
Chicago/Turabian StylePereira, Mauro Fernandes, and Apostolos Apostolakis. 2021. "Combined Structural and Voltage Control of Giant Nonlinearities in Semiconductor Superlattices" Nanomaterials 11, no. 5: 1287. https://doi.org/10.3390/nano11051287
APA StylePereira, M. F., & Apostolakis, A. (2021). Combined Structural and Voltage Control of Giant Nonlinearities in Semiconductor Superlattices. Nanomaterials, 11(5), 1287. https://doi.org/10.3390/nano11051287






