Funneling Spontaneous Emission into Waveguides via Epsilon-Near-Zero Metamaterials
Abstract
1. Introduction
2. Materials and Methods
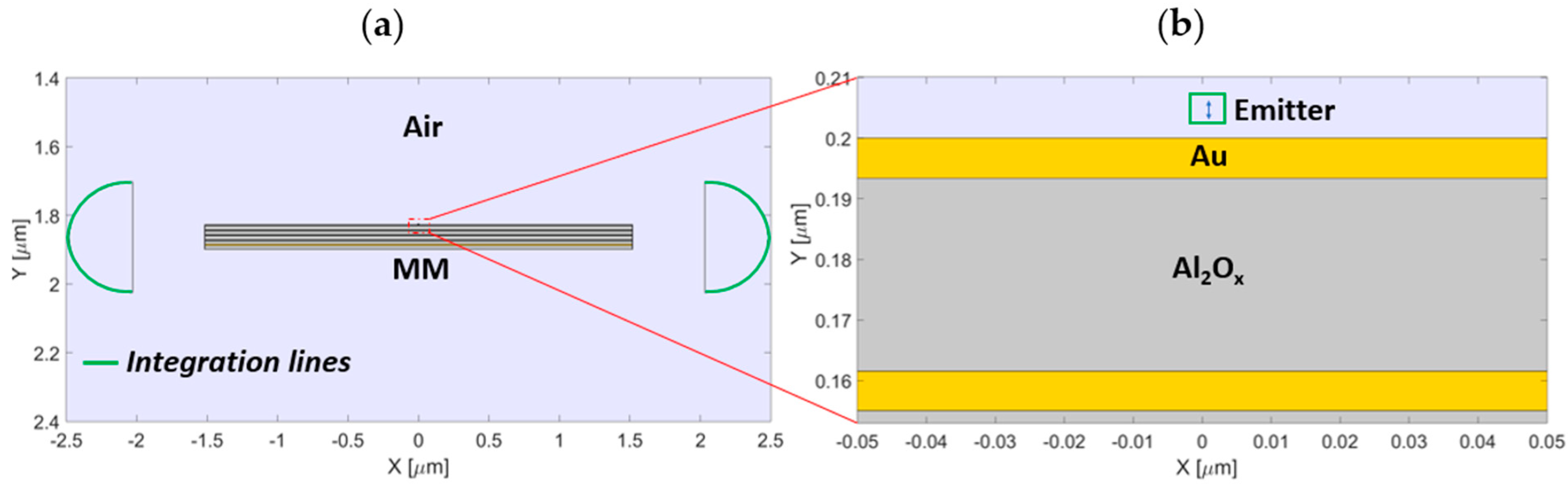
2.1. Methodology for Preliminary Results
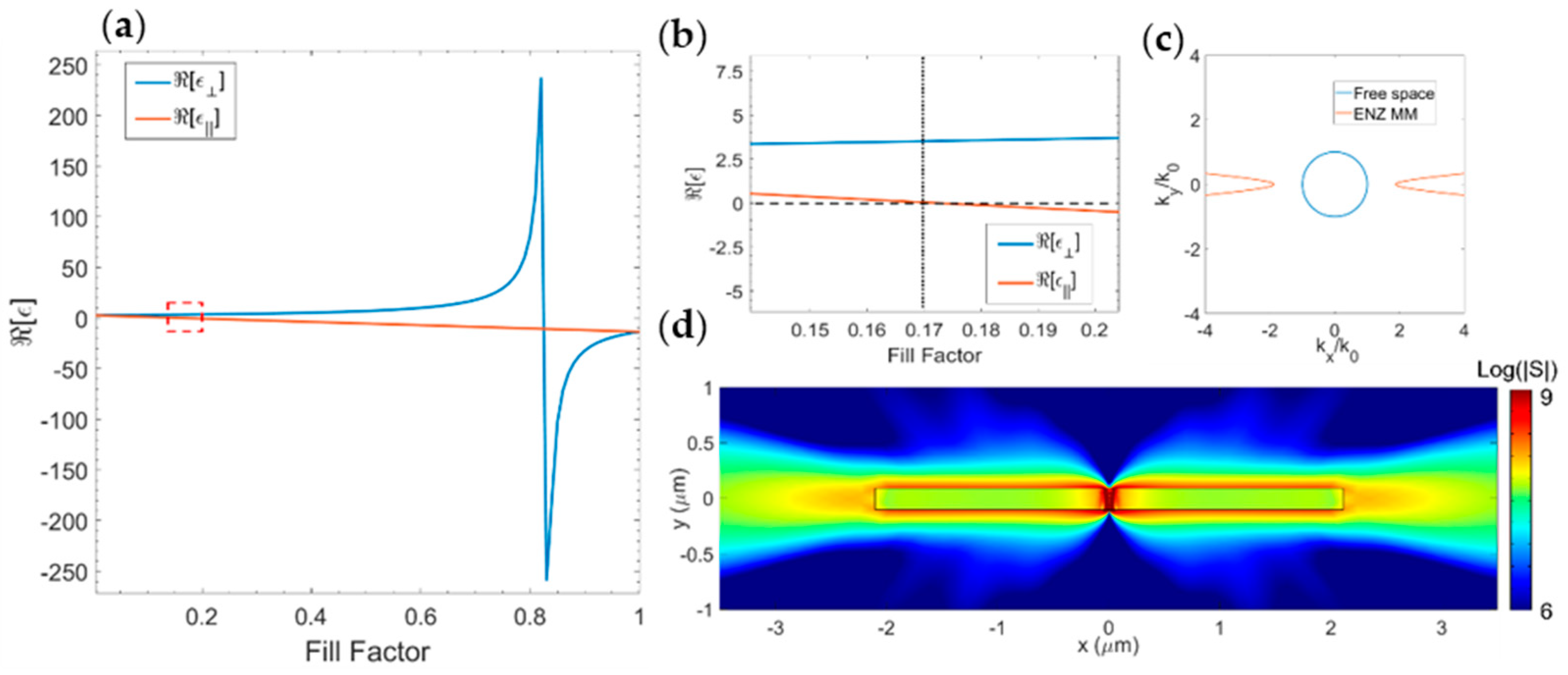
2.2. Methodology for Modal Analysis
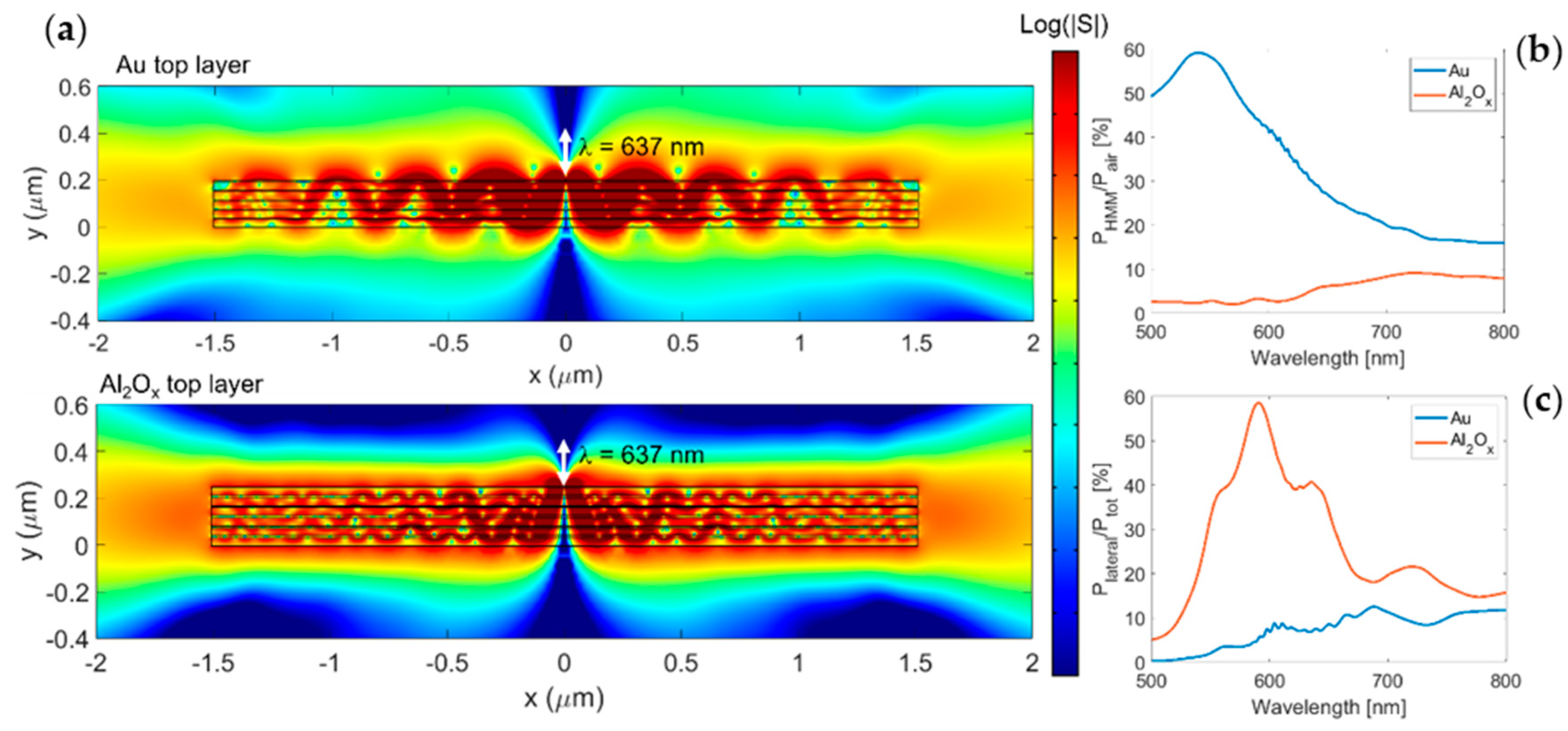
2.3. Methodology for Performance Analysis
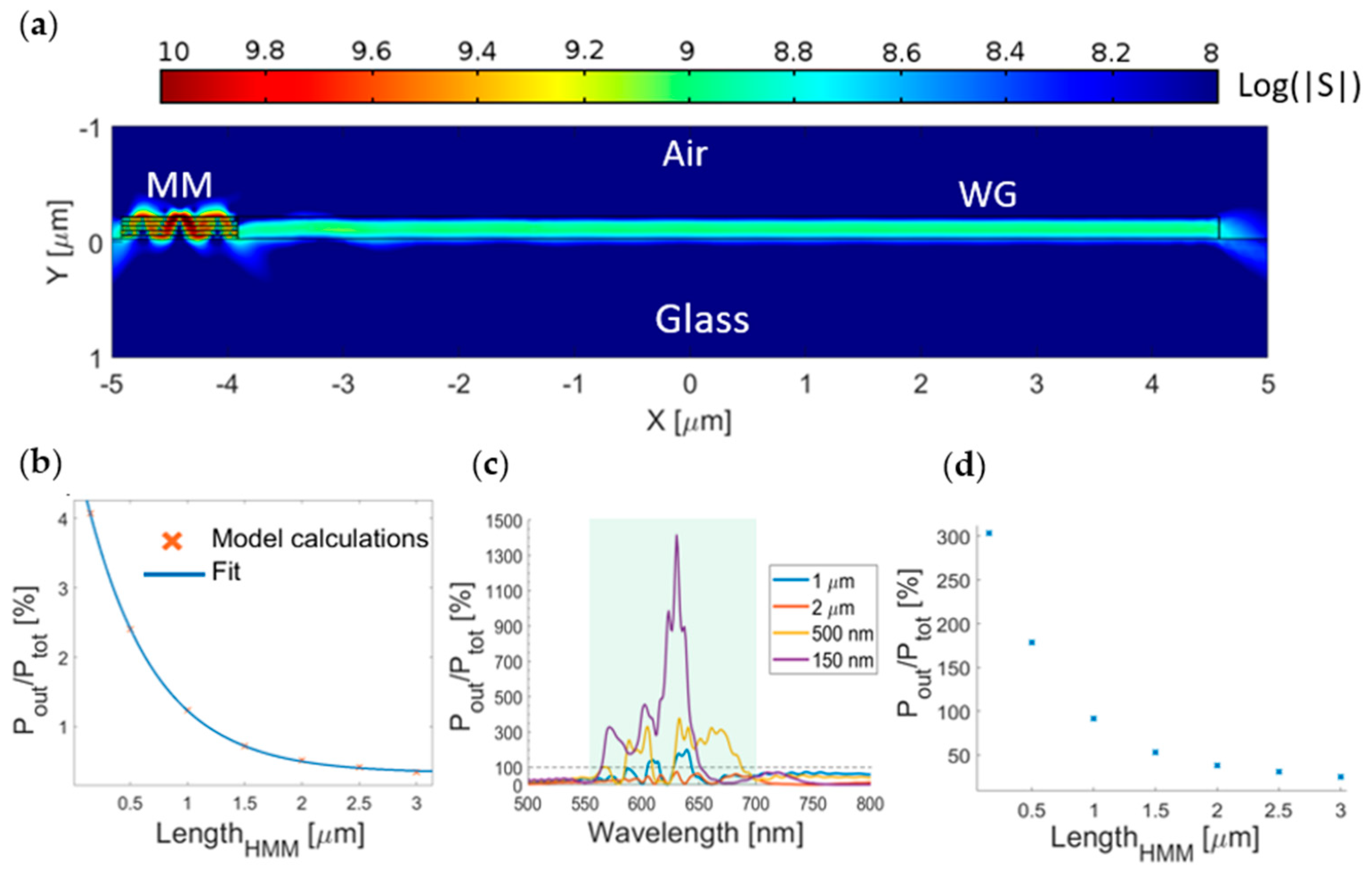
2.4. Methodology for Waveguide Coupling Analysis
3. Results
3.1. Preliminary Results
3.2. Modal Analysis
3.3. Performance Analysis
3.4. Waveguide Coupling Analysis
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Sciarrino, F.; Laing, A.; Thompson, M.G. Integrated photonic quantum technologies. Nat. Photonics 2020, 14, 273–284. [Google Scholar] [CrossRef]
- Damulira, E.; Yusoff, M.N.S.; Omar, A.F.; Taib, N.H.M. A Review: Photonic Devices Used for Dosimetry in Medical Radiation. Sensors 2019, 19, 2226. [Google Scholar] [CrossRef] [PubMed]
- Shekhar, P.; Atkinson, J.; Jacob, Z. Hyperbolic metamaterials: Fundamentals and applications. Nano Converg. 2014, 1, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
- Newman, W.D.; Cortes, C.L.; Jacob, Z. Enhanced and directional single-photon emission in hyperbolic metamaterials. J. Opt. Soc. Am. B 2013, 30, 766–775. [Google Scholar] [CrossRef]
- Ferrari, L.; Smalley, J.S.T.; Fainman, Y.; Liu, Z. Hyperbolic metamaterials for dispersion-assisted directional light emission. Nanoscale 2017, 9, 9034–9048. [Google Scholar] [CrossRef] [PubMed]
- Dickson, W.; Liebscher, L. Amplified spontaneous emission of surface plasmon polaritons and limitations on the increase of their propagation length. Opt. Lett. 2010, 35, 1197–1199. [Google Scholar]
- Bozhevolnyi, S.I.; Jacob, B.K. Fundamental limitations in spontaneous emission rate of single-photon sources. Optica 2016, 3, 1418–1421. [Google Scholar] [CrossRef]
- Lu, D.; Kan, J.J.; Fullerton, E.E.; Liu, Z. Enhancing spontaneous emission rates of molecules using nanopatterned multilayer hyperbolic metamaterials. Nat. Nanotechnol. 2014, 9, 48–53. [Google Scholar] [CrossRef] [PubMed]
- Laucht, A.; Pütz, S.; Günthner, T.; Hauke, N.; Saive, R.; Frederick, S.; Bichler, M.; Amann, M.-C.; Holleitner, A.W.; Kaniber, M.; et al. A Waveguide-Coupled On-Chip Single-Photon Source. Phys. Rev. X 2012, 2, 011014. [Google Scholar] [CrossRef]
- Kidwai, O.; Zhukovsky, S.V.; Sipe, J.E. Dipole radiation near hyperbolic metamaterials: Applicability of effective-medium approximation. Opt. Lett. 2011, 36, 2530–2532. [Google Scholar] [CrossRef] [PubMed]
- Aharonovich, I.; Englund, D.; Toth, I.A.M. Solid-state single-photon emitters. Nat. Photonics 2016, 10, 631–641. [Google Scholar] [CrossRef]
- Schirhagl, R.; Chang, K.; Loretz, M.; Degen, C.L. Nitrogen-Vacancy Centers in Diamond: Nanoscale Sensors for Physics and Biology. Annu. Rev. Phys. Chem. 2014, 65, 83–105. [Google Scholar] [CrossRef] [PubMed]
- Fabbri, N.; Hernández-Gómez, S. Quantum control for nanoscale spectroscopy with diamond NV centers: A short review. Front. Phys. 2020, 8, 652. [Google Scholar]
- Ginzburg, P.; Roth, D.J.; E Nasir, M.; Segovia, P.; Krasavin, A.V.; Levitt, J.; Hirvonen, L.M.; Wells, B.; Suhling, K.; Richards, D.; et al. Spontaneous emission in non-local materials. Light. Sci. Appl. 2017, 6, e16273. [Google Scholar] [CrossRef] [PubMed]
- Törmä, P.; William, L.B. Strong coupling between surface plasmon polaritons and emitters: A review. Rep. Prog. Phys. 2014, 78, 013901. [Google Scholar] [CrossRef] [PubMed]
- Ding, P.; Liang, E.; Cai, G.; Hu, W.; Fan, C.; Xue, Q. Dual-band perfect absorption and field enhancement by interaction between localized and propagating surface plasmons in optical metamaterials. J. Opt. 2011, 13, 075005. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Tavassoli, S.H.; Lavrinenko, A. Mode-resolved directional enhancement of spontaneous emission inside/outside finite multilayer hyperbolic metamaterials. Mater. Today Commun. 2020, 23, 100859. [Google Scholar] [CrossRef]
- Jiang, P.; Ma, N.; Liu, P.; Wu, W.; Zhang, K. An Easy-Implemented On-Chip Waveguide Coupled Single Photon Source Based on Self-Assembled Quantum Dots Membrane. Appl. Sci. 2021, 11, 695. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Channab, M.; Pirri, C.F.; Angelini, A. Funneling Spontaneous Emission into Waveguides via Epsilon-Near-Zero Metamaterials. Nanomaterials 2021, 11, 1410. https://doi.org/10.3390/nano11061410
Channab M, Pirri CF, Angelini A. Funneling Spontaneous Emission into Waveguides via Epsilon-Near-Zero Metamaterials. Nanomaterials. 2021; 11(6):1410. https://doi.org/10.3390/nano11061410
Chicago/Turabian StyleChannab, M., C. F. Pirri, and A. Angelini. 2021. "Funneling Spontaneous Emission into Waveguides via Epsilon-Near-Zero Metamaterials" Nanomaterials 11, no. 6: 1410. https://doi.org/10.3390/nano11061410
APA StyleChannab, M., Pirri, C. F., & Angelini, A. (2021). Funneling Spontaneous Emission into Waveguides via Epsilon-Near-Zero Metamaterials. Nanomaterials, 11(6), 1410. https://doi.org/10.3390/nano11061410






